Robust information routing by dorsal subiculum neurons

The dorsal subiculum robustly routes multiple types of navigation-associated information to downstream areas.

Abstract

The dorsal hippocampus conveys various information associated with spatial navigation; however, how the information is distributed to multiple downstream areas remains unknown. We investigated this by identifying axonal projections using optogenetics during large-scale recordings from the rat subiculum, the major hippocampal output structure. Subicular neurons demonstrated a noise-resistant representation of place, speed, and trajectory, which was as accurate as or even more accurate than that of hippocampal CA1 neurons. Speed- and trajectory-dependent firings were most prominent in neurons projecting to the retrosplenial cortex and nucleus accumbens, respectively. Place-related firing was uniformly observed in neurons targeting the retrosplenial cortex, nucleus accumbens, anteroventral thalamus, and medial mammillary body. Theta oscillations and sharp-wave/ripples tightly controlled the firing of projection neurons in a target region–specific manner. In conclusion, the dorsal subiculum robustly routes diverse navigation-associated information to downstream areas.

INTRODUCTION

The hippocampus is crucially involved in spatial navigation and memory. Through interactions with intra- and extrahippocampal areas (1–7), hippocampal neurons diversely represent a variety of spatial navigation parameters, such as place (8), speed (9), trajectory (10–12), head direction (9, 13), and time (14–16). The spike timing of these neurons is secured by multiple hippocampal neural oscillations, including theta oscillations, gamma oscillations, and sharp-wave/ripples (SPW-Rs) (17–19), thus facilitating temporally precise information transmission within and between brain regions. To support navigational behavior output, hippocampal information is likely distributed to extrahippocampal areas. However, little is known about how diverse hippocampal information is distributed to downstream areas.

The subiculum (SUB) is the major hippocampal output structure, receiving hippocampal CA1 and entorhinal cortical output and projecting to various cortical/subcortical areas, including the nucleus accumbens (NAC), anteroventral thalamic nucleus (AV), interanteromedial thalamic nucleus (ITN), retrosplenial cortex (RSC), and medial mammillary body (MMB) (20). The CA1-SUB projection is topographically organized so that proximal and distal CA1 areas project to the distal (far from CA1) and proximal (close to CA1) SUB, respectively (20). The CA1 area shows graded spatial tuning along its proximodistal axis (21). In addition, SUB neurons located at proximal and distal areas innervate different target areas (22), suggesting that these projections potentially convey distinct information. Consistent with this idea, suppression of the proximal or distal SUB has a distinct impact on memory acquisition (23). Analogous to CA1 neurons, SUB neurons represent multiple variables associated with spatial navigation, such as place (24–26), axis (27), boundary (28), reward (29), and memory (30). Such anatomical and physiological evidence imply a pivotal role for the SUB in the distribution of multimodal information; however, little is known about the nature of information distribution from this structure. An enigmatic point of subicular representation is that the overall subicular spatial firing is apparently dispersed (24, 25). Thus, it remains elusive whether the SUB fails to inherit the information content from the CA1 area or whether it inherits the information but converts it into a distinct form of representation suitable for interregional distribution to downstream areas. Moreover, it is unknown whether the SUB routes multiple types of information uniformly to all target areas or selectively routes distinct information to different targets. We anticipated that the SUB processes navigational information received from the CA1 area and routes the information to downstream targets in a projection-specific manner.

We investigated the above hypothesis by identifying axonal projections using optogenetics (31) while performing large-scale extracellular recordings (32, 33) of the rat dorsal SUB and CA1 area during multiple spatial tasks and sleep. We found that the SUB has a noise-resistant, accurate representation of multiple types of navigation-associated information and routes this information uniformly or selectively to target areas depending on the type of information.

RESULTS

The SUB comprises projection neurons targeting distinct downstream areas

Anterograde tracing revealed that the major projection targets of the rat dorsal SUB include the NAC, AV, anterodorsal thalamic nucleus, ITN, nucleus reuniens, RSC, and MMB (Fig. 1, A to E). A moderate projection was also observed in the dorsal tenia tecta and dorsal peduncular cortex (Fig. 1B). These projections were consistent with those reported by a previous study (22). Next, we determined the somata locations of SUB projection neurons by injecting the retrograde tracer cholera toxin B subunit conjugated with Alexa Fluor 488 (CTB488) into one of the above target areas. In addition to the well-characterized differences between the proximal and distal SUB areas (22), we observed robust differences between the superficial and deep locations of SUB projection neurons (Fig. 1F and fig. S1) (34). Deeply located SUB neurons have been recently reported to have different gene expression patterns from other SUB neurons (23, 35). Projection-specific visualization of neuronal morphology (Fig. 1, G to L) revealed that dendritic spine density was lower in AV-projecting (AV-p) and ITN-projecting (ITN-p) neurons than in NAC-projecting (NAC-p) and RSC-projecting (RSC-p) neurons (Fig. 1M). These results, together with accumulating previous evidence (22, 23, 36), indicate that SUB projection neurons comprise at least partly separated groups of neurons that target distinct downstream areas.

Fig. 1. The subiculum comprises projection neurons targeting distinct downstream areas.

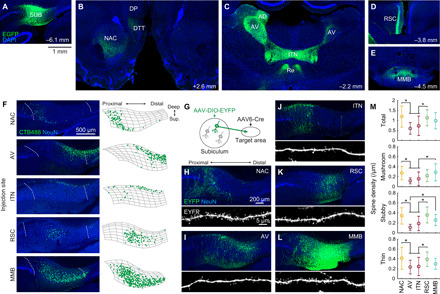
(A to E) After the injection of AAV1/2-EF1α-EGFP into the left dorsal SUB (A), EGFP-labeled axons were observed in the ipsilateral NAC, ipsilateral dorsal tenia tecta (DTT), ipsilateral dorsal peduncular cortex (DP) (B), bilateral AV, anterodorsal thalamic nucleus (AD), ITN, nucleus reuniens (Re) (C), the superficial layer of the ipsilateral granular RSC (D), and MMB (E). All images show coronal sections. Numbers, approximate distances of the sections from the bregma. (F) SUB coronal sections containing cholera toxin B subunit conjugated with Alexa Fluor 488 (CTB488)–labeled projection neurons (left) and the corresponding cell counting (right). Left: Dotted curves, borders of the SUB cell layer. Right: Segmented SUB cell layer (mesh) and detected CTB488-positive neurons (dots). (G to M) Dendritic morphology of SUB projection neurons. (G) Schematic of visualization of projection-specific neuronal morphology. (H to L) SUB coronal sections containing EYFP-labeled projection neurons (top) and apical dendrites (bottom). The AAV6-pgk-Cre was injected in one of the following areas: NAC (H), AV (I), ITN (J), RSC (K), and MMB (L). (M) Dendritic spine density per unit length of the apical dendrite. n = 17, 17, 25, 21, and 20 cells for NAC-p, AV-p, ITN-p, RSC-p, and MMB-p SUB neurons, respectively. *P < 0.05, Tukey test. Means ± SD.

Optogenetic identification of projection targets

The anatomical observations led us to hypothesize that SUB projection neurons convey distinct information depending on the projection targets. To investigate this, we combined large-scale extracellular recordings (32, 33) from the SUB and CA1 area of freely behaving rats with optogenetic identification of the projection targets (31) of the recorded SUB neurons (Fig. 2A). We stereotaxically introduced adeno-associated virus (AAV) expressing channelrhodopsin-2 under the control of synapsin promoter, AAV1-hSyn-hChR2(H134R)-enhanced yellow fluorescent protein (EYFP), into the dorsal SUB, inserted a 256-channel silicon probe into the dorsal SUB and CA1 area, and implanted up to four optical fibers to each projection target (NAC, AV, RSC, and MMB) in each rat (Fig. 2, B to F, and fig. S2). We selected these four target areas because they were strongly innervated by the SUB (Fig. 1) while being anatomically distant from each other, which would maximize the anatomical specificity of optical simulation. Rats performed multiple spatial tasks, including an open-field, a linear-track, and an alternating T-maze task, and rested/slept in a small enclosure before and after the tasks. We monitored and analyzed a total of 315 and 319 putative principal cells in the CA1 and SUB, respectively, from 22 recording sessions in 11 rats (fig. S3, A to C, and table S1).

Fig. 2. Optogenetic identification of SUB projection neurons.

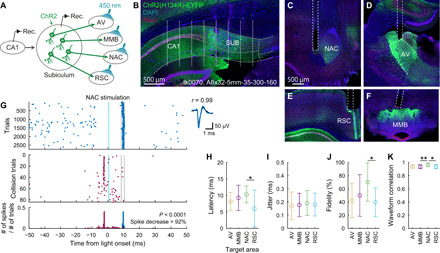
(A) Schematic of optogenetic identification. (B) Coronal section indicating ChR2 expression (green) and the estimated recording sites (white dots). Gray curves, borders of the CA1, SUB, and their cell layers. Text, animal ID and silicon probe name. (C to F) NAC (C), AV (D), RSC (E), and MMB (F) coronal sections containing ChR2-expressing SUB axons (green) and the reconstructed optical fiber locations (dotted lines). (G) Left: Spike responses of a SUB neuron upon light irradiation to the NAC. Evoked spikes (top) decreased when spontaneous spikes occurred shortly before the expected latency of evoked spikes (middle and bottom). Shaded blue areas, light stimulation periods. Gray lines, bin ranges of evoked spikes. Right: Mean waveforms of spontaneous (black) and evoked (blue) spikes. (H to J) Latency (H), jitter (I), and fidelity (J) of evoked spikes. (K) Waveform correlation between the evoked and spontaneous spikes. (H to K) Means ± SD. *P < 0.05 and **P < 0.01, Tukey test.

To identify the projection targets of activity-monitored neurons with antidromic spikes (31), we irradiated blue light pulses sequentially to each target area during the rest sessions. In response to the light pulses, a proportion of SUB neurons generated short-latency (<25 ms; 8.7 ± 4.0 ms, means ± SD), low-jitter (<0.5 ms, 0.18 ± 0.09 ms) spikes with high fidelity (>20%, 51.8 ± 30.2%), and these neurons were identified as projection neurons innervating the irradiated area (Fig. 2, G to K, and fig. S3D). The locations of the identified projection neurons in the SUB cell layer were consistent with the distribution of retrogradely labeled CTB488-positive neurons (fig. S3E). RSC-p neurons had a shorter latency than NAC-p neurons (Fig. 2H), presumably reflecting differences in the anatomical distance between the SUB and these target areas. Among SUB principal cells, we identified 11 AV-p (3.4% of SUB principal cells), 28 MMB-p (8.8%), 18 NAC-p (5.6%), and 16 RSC-p (5.0%) SUB neurons (table S1). Previous anatomical studies demonstrated that moderate proportions of SUB neurons have collateral projections to more than one area with several combinations of target areas (22, 23, 36, 37). Consistently, several SUB neurons were identified as projecting to more than one area (fig. S3E).

The SUB represents place information as accurately as the CA1, and subicular projection neurons uniformly carry this information

The hippocampal CA1 area and the SUB contain spatially tuned cells that fire whenever animals move through particular places in an environment (8, 24–26). We compared place representation in CA1 and SUB neurons while rats were running on a linear track. While many CA1 neurons fired at specific places along the track, SUB neurons fired at broader locations (Fig. 3A). Rate maps of eastbound and westbound trials were uncorrelated both in the CA1 and SUB (CA1: r = −0.03 ± 0.46, SUB: r = −0.07 ± 0.44; t₄₁₄ = 0.96, P = 0.34, CA1 versus SUB). This is consistent with the known directionality of place representation on a linear environment (9, 26). Per-spike spatial information, expressed by the I_spike value, a measure of the spatial specificity of individual cells (38), was lower in SUB than in CA1 neurons (means ± SD: CA1, 0.94 ± 0.77 bits/spike; SUB, 0.34 ± 0.46 bits/spike; Z = 9.73, P < 0.0001, Wilcoxon rank sum test; Fig. 3B and fig. S4A). In contrast, SUB neurons had higher mean firing rates (during trials in the preferred direction; CA1, 3.7 ± 5.4 Hz; SUB, 9.8 ± 12.9 Hz; Z = 7.78, P < 0.0001; Fig. 3C and fig. S4A) and peak firing rates (in the preferred direction; CA1, 9.3 ± 9.0 Hz; SUB, 17.1 ± 17.0 Hz; Z = 5.83, P < 0.0001; Fig. 3D) than CA1 neurons. Because of this high firing rate, per-second spatial information, I_sec (38), which is equal to I_spike multiplied by the mean firing rate, was comparable between CA1 and SUB neurons (CA1, 1.43 ± 1.69 bits/s; SUB, 1.39 ± 1.87 bits/s; Z = 0.98, P = 0.33; Fig. 3E and fig. S4A). Moreover, SUB and CA1 neurons showed similar mutual information (39) of firing rates and places (CA1, 0.26 ± 0.17 bits; SUB, 0.29 ± 0.23 bits; Z = 0.51, P = 0.61; Fig. 3F). The mutual information correlated with I_sec (CA1: r = 0.87, P < 0.0001; SUB: r = 0.84, P < 0.0001) but not with I_spike (CA1: r = 0.004, P = 0.96; SUB: r = 0.11, P = 0.08). These results suggest that, despite the apparent decrease in spatial specificity shown by the lower I_spike value, SUB neurons convey a comparable amount of spatial information per unit time with that conveyed by CA1 neurons owing to the subicular high firing rate. The idea that SUB neurons robustly represent place information is further supported by the observation that their firing was anchored more to place than to the elapsed time from the start of trials (fig. S5, A to D) and by the fact that SUB rate maps were more temporally stable than the CA1 rate maps (fig. S5E).

Fig. 3. Place representation on a linear track.

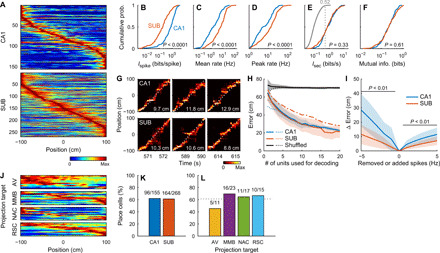
(A) Peak-normalized rate maps of CA1 (top) and SUB (bottom) neurons sorted by peak positions. (B to F) Cumulative distribution of I_spike (B), mean firing rate (C), peak firing rate (D), I_sec (E) (gray curve, the distribution of shuffled data; number and dotted line, its 99th percentile), and mutual information (F) of CA1 and SUB neurons. P values: Wilcoxon rank sum test. (G) Example position decoding from simultaneously recorded CA1 (top) or SUB (bottom) neurons in three consecutive trials. Color maps, probabilities of estimated animal positions. Dotted curves, observed animal positions. Numbers, decoding errors of the trials. (H) Error of position decoding averaged across all animals. Decoding errors were calculated either from all time bins irrespective of the number of spikes in the bins (solid lines and shaded areas, means ± SDs) or from time bins containing one or more spikes (dotted lines, mean). Dashed-dotted line, SUB decoding error calculated after randomly removing spikes from SUB neurons to match the CA1 mean firing rate (mean). Black line, decoding error obtained from the shuffling procedure. (I) Difference in decoding errors after randomly removing (negative x values) or adding (positive x values) spikes to each neuron. Group data were averaged across all animals. P < 0.01, Bonferroni test after two-way repeated-measures ANOVA. Means (solid lines) ± SD (shaded areas). (J) Peak-normalized rate maps of SUB projection neurons sorted by peak positions. (K and L) Percentage of place cells in the CA1 and SUB (K) and SUB projection neurons (L). Numbers, number of place cells to the total number of neurons. Dotted line, percentage of place cells in SUB neurons.

Next, we investigated whether the SUB also represents place information as accurately as the CA1 at a cell population level using Bayesian decoding of animal position (Fig. 3, G and H) (40). The decoding errors obtained from CA1 and SUB neuronal populations were both smaller than those obtained using shuffled data, even when single neurons were used for decoding (P < 0.001, Tukey test), and became even smaller by increasing the number of neurons used [F_{19, 700} = 90.87, P < 0.001, two-way analysis of variance (ANOVA); Fig. 3H, solid lines]. The decoding errors were comparable between the CA1 and SUB, irrespective of the number of neurons used (P > 0.2, Bonferroni test after two-way ANOVA; Fig. 3H, solid lines), suggesting that CA1 and SUB neuronal populations of the same size convey a comparable amount of decodable spatial information. Randomly removing spikes from SUB neurons to match the mean firing rate of SUB neurons to that of CA1 neurons increased the decoding errors (F_{1, 917} = 220.10, P < 0.001; Fig. 3H, dashed-dotted line), suggesting that the SUB high firing rate supports its accurate spatial representation.

To clarify how the spatial firing of single neurons relates to population coding, we estimated the contribution of single neurons to the decoding performance. The decoding improvement obtained by adding single units (see Materials and Methods) correlated with I_sec (CA1: r = 0.76, P < 0.0001; SUB: r = 0.69, P < 0.0001) and mutual information (CA1, r = 0.78, P < 0.0001; SUB, r = 0.73, P < 0.0001) but not with I_spike (CA1, r = 0.06, P = 0.46; SUB, r = 0.04, P = 0.40) in both the CA1 and SUB, highlighting the tight association between I_sec and population coding.

We hypothesized that the subicular representation gains robustness against noise owing to its high firing rate. We tested this idea by adding noise to the original spike trains before proceeding with the decoding analysis. In response to simple additive noise (41), we found a smaller increase in the decoding error in the SUB than in the CA1 (Fig. 3I), suggesting that population spatial coding in the SUB is more resistant to additive noise than that in the CA1.

Next, we asked how spatial information is conveyed by SUB projection neuron groups targeting distinct downstream areas (Fig. 3J). The proportions of place cells (defined by I_sec) were similar in the CA1 and SUB (χ² = 0.02, P = 0.88, χ² test; Fig. 3K and fig. S4A), as well as among the groups of SUB projection neurons targeting the AV, MMB, NAC, or RSC (χ² = 1.99, P = 0.57; Fig. 3L). Neither peak nor centroid positions of rate maps were significantly different among the four SUB projection neuron groups (P > 0.1, Steel-Dwass test; Fig. 3J). These results suggest that the SUB projection neurons targeting these four downstream areas uniformly display place-related firing. The results for the spatial representation were consistent, irrespective of the sizes of a position bin and a time window, and were consistent across animals (fig. S6, A to K). We observed a similar spatial representation in a two-dimensional (2D) open field (figs. S4B and S7).

The SUB represents speed information more accurately than the CA1, and this information is most prominently conveyed by RSC-p neurons

The hippocampus contains neurons that respond to the running speed of animals (9). We thus investigated speed representation in CA1 and SUB neurons while rats foraged in an open field. Both the CA1 and SUB contained neurons with instantaneous firing rates that correlated with the rat’s instantaneous running speed (Fig. 4A). To estimate the amount of speed information, as in the case of spatial information, we calculated per-spike speed information I_spike and per-second speed information I_sec (42). The I_spike value was lower in SUB than in CA1 neurons (CA1, 0.054 ± 0.057 bits/spike; SUB, 0.028 ± 0.059 bits/spike; Z = 9.12, P < 0.0001, Wilcoxon rank sum test), while the mean firing rate of SUB neurons was higher than that of CA1 neurons (CA1, 1.5 ± 1.9 Hz; SUB, 5.6 ± 5.2 Hz; Z = 11.48, P < 0.0001) (Fig. 4, B and C, fig. S4C). Consequently, the I_sec value was similar between all CA1 and SUB neurons (CA1, 0.046 ± 0.052 bits/s; SUB, 0.077 ± 0.114 bits/s; Z = 1.12, P = 0.26; Fig. 4D and fig. S4C). However, when comparing only neurons with an I_sec value exceeding the 99th percentile of the shuffled data, the I_sec value was higher for SUB than for CA1 neurons (CA1, 0.118 ± 0.060 bits/s; SUB, 0.205 ± 0.137 bits/s; Z = 5.19, P < 0.0001; Fig. 4D). To distinguish positively and negatively modulated speed cells, we calculated the speed score (43). The absolute speed score was tightly correlated with I_sec (CA1, r = 0.75, P < 0.0001; SUB, r = 0.80, P < 0.0001) but was only modestly correlated with I_spike (CA1, r = 0.32, P < 0.0001; SUB, r = 0.32, P < 0.0001). The speed score was higher for SUB than for CA1 neurons (CA1, 0.141 ± 0.043; SUB, 0.201 ± 0.087; Z = 5.74, P < 0.0001, Wilcoxon rank sum test) when comparing neurons with a speed score exceeding the 99th percentile of the shuffled data distribution (Fig. 4E). Conversely, the speed score was smaller for SUB than for CA1 neurons (CA1, −0.100 ± 0.006; SUB, −0.142 ± 0.041; Z = 2.34, P = 0.019) when comparing neurons with a speed score smaller than the first percentile of the shuffled data distribution (Fig. 4E). The speed scores obtained from the first and second halves of the sessions were positively correlated both for the CA1 and the SUB (CA1, r = 0.51, P < 0.0001; SUB, r = 0.79, P < 0.0001). These results suggest that, despite the broader speed tuning, as shown by the lower I_spike values, SUB neurons convey a larger amount of speed information per unit time than that conveyed by CA1 neurons.

Fig. 4. Speed representation in an open field.

(A) Rate maps (left), z-scored running speed (gray) and firing rate (color) (middle), and mean firing rate as a function of running speed (right). Each row shows the firing patterns of a single neuron. Numbers, peak firing rates in the figure (left and middle) and speed scores (right). (B to E) Cumulative distribution of I_spike (B), mean firing rates (C), I_sec (D), and speed scores (E). P values: Wilcoxon rank sum test. (D and E) Gray curves, numbers, and dotted lines, the distribution of shuffled data and its 1st (E) and 99th (D and E) percentiles. *P = 0.019 and ****P < 0.0001, CA1 versus SUB neurons exceeding either the 1st or 99th percentile threshold, Wilcoxon rank sum test. (F) Example decoding of speed from simultaneously recorded CA1 (top) and SUB (bottom) neuron activity. Gray, observed speed. Color, decoded speed. Numbers, decoding accuracy. (G) Decoding accuracy averaged across all animals. Dashed-dotted line, SUB decoding accuracy calculated after randomly removing spikes from SUB neurons to match the CA1 mean firing rate (mean). Black line, decoding error obtained from a shuffling procedure. (G and H) Means (solid lines) ± SD (shaded areas). (H) Normalized decoding accuracy after randomly removing (negative x values) or adding (positive x values) spikes to each neuron. Group data were averaged across all animals. P < 0.05, Bonferroni test after two-way repeated-measures ANOVA. (I and J) Percentage of n-speed (left) and p-speed (right) cells in the CA1 and SUB (I) and among SUB projection neurons (J). Numbers, number of speed cells to the total number of neurons. (I) ***P = 0.0002, χ² test. (J) Dotted lines, percentage of n-speed (left) and p-speed (right) cells in SUB neurons. *P < 0.05, bootstrap analysis.

We asked whether the stronger speed representation in individual SUB neurons is reflected by the speed representation at the population level. To this end, we constructed a linear decoder of speed (Fig. 4, F and G) (43). The decoding accuracy was higher in the SUB than in the CA1 irrespective of the number of neurons used (P < 0.05, Bonferroni test after two-way ANOVA; Fig. 4G and fig. S6L). The SUB decoding accuracy decreased when spikes were randomly removed from SUB neurons to match the CA1 mean firing rate (P < 0.001, Bonferroni test after two-way ANOVA; Fig. 4G, dashed-dotted line); however, it was still higher than the CA1 decoding accuracy (P < 0.001). The single-unit decoding accuracy better correlated with the I_sec (CA1: r = 0.68, P < 0.0001; SUB: r = 0.75, P < 0.0001) than with the I_spike (CA1: r = 0.27, P < 0.0001; SUB: r = 0.28, P < 0.0001) value both in the CA1 and SUB (CA1: Z = 5.85, P < 0.0001; SUB: Z = 8.03, P < 0.0001; test of the difference between two correlation coefficients). Speed decoding by the SUB was more resistant to additive noises than that by the CA1 (Fig. 4H and fig. S6L).

We then investigated the proportion of positively (p-speed cells) and negatively (n-speed cells) modulated speed cells (see Materials and Methods). While the proportion of p-speed cells was similar between the SUB and CA1 (χ² = 1.12, P = 0.29; Fig. 4I), that of n-speed cells was higher in the SUB than in the CA1 (χ² = 13.71, P = 0.0002; Fig. 4I and fig. S4C). The I_sec value was higher in the p-speed SUB cells than in the n-speed SUB cells and p-speed CA1 cells (n-speed cells, CA1, 0.062 ± 0.037 bits/s, SUB, 0.096 ± 0.099 bits/s; p-speed cells, CA1, 0.086 ± 0.066 bits/s, SUB, 0.153 ± 0.143 bits/s; P < 0.05, Steel-Dwass test). The proportion of p-speed cells among RSC-p neurons was larger than that among the entire SUB cell population (P < 0.05, bootstrap analysis; Fig. 4J), indicating that speed-dependent firing is most prominent in RSC-p neurons.

The SUB represents trajectory information as accurately as the CA1, and this information is most prominently conveyed by NAC-p neurons

Next, we investigated trajectory-dependent firing at the start point of an alternating T-maze task (Fig. 5A) (12). A fraction of CA1 and SUB neurons showed different firing rates in the start box according to the next choice of arm (Fig. 5B). To measure the information encoded regarding the next choice (left or right), as signaled by the firing rate in the start box, we defined the trajectory I_spike and I_sec. Compared with CA1 neurons, SUB neurons showed lower I_spike values (Z = 5.73, P < 0.0001, Wilcoxon rank sum test; Fig. 5C and fig. S4D) and a lower rate change ratio (see Materials and Methods, Z = 5.72, P < 0.0001; Fig. 5D). However, SUB neurons had a higher mean firing rate in the start box (Z = 10.16, P < 0.0001; Fig. 5E and fig. S4D) and consequently had comparable I_sec values to those of CA1 neurons (Z = 0.02, P = 0.99; Fig. 5F and fig. S4D). In addition, the area under the receiver operating characteristic (auROC), indicating the goodness of fit of the binary classifier, was similar between CA1 and SUB neurons (Z = 0.92, P = 0.36; Fig. 5G). We performed trajectory decoding from the firing rates in the start box, as described previously (5). SUB neurons showed moderately higher decoding accuracy than did CA1 neurons (F_{1, 432} = 17.02, P < 0.001; Fig. 5H and fig. S6M) and were more resistant to additive noise (Fig. 5I and fig. S6M). Random spike removal from SUB neurons to match the CA1 firing rate decreased the decoding accuracy (F_{1, 495} = 46.36, P < 0.001; Fig. 5H, dashed-dotted line).

Fig. 5. Trajectory-dependent firing during an alternating T-maze task.

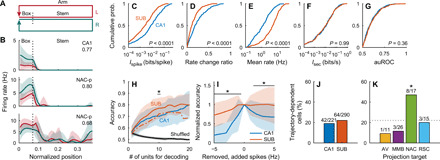
(A) Schematic of the behavioral task. (B) Rate maps of a CA1 and two NAC-p SUB neurons while rats were in the start box (normalized position, 0.02 to 0.07) and stem (normalized position, 0.07 to 0.38) of the T-maze. Numbers, auROC of the neuron. Red, left-arm trials. Green, right-arm trials. Means (solid lines) ± SD (shaded areas). (C to G) Cumulative distribution of I_spike (CA1, 0.034 ± 0.064 bits/spike; SUB, 0.011 ± 0.023 bits/spike) (C), rate change ratio (CA1, 0.24 ± 0.19; SUB, 0.15 ± 0.13) (D), mean firing rate (CA1, 2.3 ± 3.2 Hz; SUB, 6.8 ± 6.8 Hz) (E), I_sec (CA1, 0.034 ± 0.063 bits/s; SUB, 0.040 ± 0.089 bits/s) (F), and auROC (CA1, 0.601 ± 0.084; SUB, 0.609 ± 0.091) (G) in the start box. P values: Wilcoxon rank sum test. (H) Accuracy of trajectory decoding averaged across all animals. Dashed-dotted line, SUB decoding accuracy calculated after randomly removing spikes from SUB neurons to match the CA1 mean firing rate (mean). Black line, chance level of decoding error estimated by a shuffling procedure. *P < 0.05, CA1 versus SUB solid lines, Bonferroni test after two-way ANOVA. (H and I) Means (solid lines) ± SD (shaded areas). (I) Normalized decoding accuracy after randomly removing (negative x values) or adding (positive x values) spikes to each neuron. Group data were averaged across all animals. *P < 0.05, Bonferroni test after two-way repeated-measures ANOVA. (J and K) Percentage of trajectory-dependent cells in the CA1 and SUB (J) and SUB projection neurons (K). Numbers, number of trajectory-dependent cells to the total number of neurons. Dotted line, percentage of trajectory-dependent cells in SUB neurons. *P < 0.05, bootstrap analysis.

Both the CA1 and SUB contained ~20% of trajectory-dependent cells (χ² = 0.72, P = 0.40; Fig. 5J and fig. S4D). Among the groups of SUB projection neurons, NAC-p neurons contained a higher proportion of trajectory-dependent cells than the other groups of projection neurons (χ² = 9.06, P = 0.03) and the entire population of SUB neurons (P < 0.05, bootstrap analysis; Fig. 5K).

In the stem, only small proportions of cells showed trajectory-dependent firing (CA1, 9.6%; SUB, 7.7%; χ² = 0.53, P = 0.47). This is consistent with a previous study demonstrating that CA1 neurons exhibit trajectory-dependent firing in the start box but not in the stem when a delay is introduced between trials (12).

Weak head-direction tuning in subicular projection neurons

Although neuronal firing associated with head direction emerges in the CA1 and SUB in cue-rich (13) and multipath environments (27), respectively, head-direction tuning is generally weak in both regions in non–cue-rich open fields (25, 27, 44). Consistently, CA1 and SUB neurons displayed weak head-direction tuning in an open field (Fig. 6A). While per-spike directional information, I_spike (CA1, 0.120 ± 0.122 bits/spike; SUB, 0.047 ± 0.089 bits/spike; Z = 11.55, P < 0.0001, Wilcoxon rank sum test; Fig. 6B and fig. S4E) and mean vector length (CA1, 0.134 ± 0.095; SUB, 0.078 ± 0.076; Z = 8.47, P < 0.0001; Fig. 6C) were higher in CA1 neurons than in SUB neurons, per-second directional information, I_sec, was comparable between them (CA1, 0.081 ± 0.058 bits/s; SUB, 0.099 ± 0.110 bits/s; Z = 0.28, P = 0.78; Fig. 6D and fig. S4E). Bayesian decoding of head direction (45) revealed statistically significant (P < 0.001, CA1 versus shuffled, SUB versus shuffled, Bonferroni test after two-way ANOVA) but marginal decoding performance for both CA1 and SUB neurons (Fig. 6, E and F). While the proportion of head-direction cells was higher in the SUB than in the CA1 (χ² = 10.88, P = 0.001; Fig. 6G and fig. S4E), all four groups of SUB projection neurons contained only small proportions of head-direction cells (Fig. 6H).

Fig. 6. Head-direction representation in an open field.

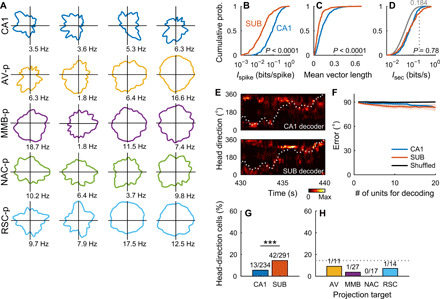
(A) Directional rate maps of CA1 and SUB projection neurons. Each map shows the firing patterns of a single neuron. Numbers, peak firing rates in the figure. (B to D) Cumulative distribution of I_spike (B), mean vector length (C), and I_sec (D). P values: Wilcoxon rank sum test. (E) Example head-direction decoding from simultaneously recorded CA1 (top) or SUB (bottom) neurons. Color maps, probabilities of estimated head directions. Dotted curves, observed head directions. (F) Angular error of head-direction decoding averaged across all animals. Solid lines and shaded areas, means ± SDs. (G and H) Percentage of head-direction cells in the CA1 and SUB (G) and SUB projection neurons (H). Numbers, number of head-direction cells to the total number of neurons. Dotted line, percentage of head-direction cells in SUB neurons. ***P = 0.001, χ² test.

Projection-specific phase locking to theta oscillations

Next, we asked whether the CA1, SUB, and SUB projection neurons have specific temporal firing patterns during theta oscillations. During running, we observed robust theta oscillations both in the CA1 and SUB (Fig. 7, A to C). Using theta oscillations at the center of the SUB cell layer as a reference (recording site location, 47 ± 13% and 51 ± 15% along proximal [0%]–distal [100%] and superficial [0%]–deep [100%] axes of the SUB cell layer, respectively), we examined theta phase locking of neuronal firing during RUN periods. Virtually, all CA1 and SUB neurons were significantly phase-locked (P < 0.05, Rayleigh test) to subicular theta oscillations (CA1, 100%; SUB, 99.0%; Fig. 7D). The preferred theta phases of SUB neurons were at earlier phases of theta cycles than those of CA1 neurons (CA1, 46.1 ± 45.4°; SUB, 332.6 ± 54.7°; circular mean ± angular deviation; U² = 4.30, P < 0.001, Watson U² test; Fig. 7, D and E, and fig. S4F). We measured the strength of phase locking using pairwise phase consistency (PPC) (46). While CA1 neurons locked to the ascending phase of theta oscillations showed higher PPC than those locked to the descending phase (F_9,267 = 4.80, P < 0.0001, one-way ANOVA), SUB neurons locked to the peaks of theta oscillations showed higher PPC than those locked to troughs (F_{9, 290} = 2.69, P = 0.005) (Fig. 7D). For the entire population, PPC was modestly smaller in the SUB than in the CA1 (CA1, 0.060 ± 0.058; SUB, 0.052 ± 0.065; Z = 2.94; P = 0.003, Wilcoxon rank sum test).

Fig. 7. Projection-specific theta phase locking during RUN periods.

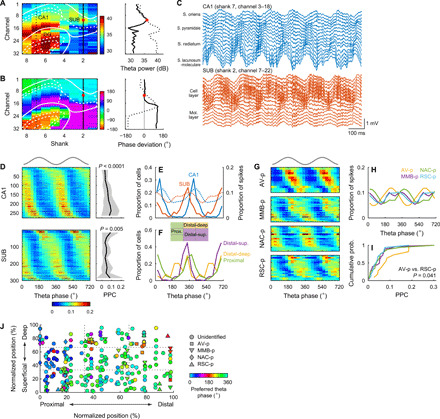
(A and B) Distribution of theta power (A) and theta phase deviations (B) in an open field (left). White lines, borders of the CA1, SUB, and dentate gyrus (DG). Values along the CA1 (black dotted lines) and SUB (solid black lines) are plotted in the right. Red dots, the reference recording site with the maximal theta power in the SUB cell layer. (C) Wide-band local field potentials (LFPs) simultaneously recorded from the CA1 (top) and SUB (bottom). (D) Spike phase distribution along the reference SUB theta oscillations (left) and corresponding PPC (right) in the CA1 (top) and SUB (bottom). P values, one-way ANOVA. Means (solid lines) ± SD (shaded areas). (D and G) Top gray traces, idealized reference theta cycles. (E) Distribution of the preferred theta phases (left y axis, solid lines) and spike theta phases (right y axis, dotted lines). (F) Distribution of preferred theta phases for neurons located at proximal (green), distal-deep (yellow), and distal-superficial (purple) part of the SUB cell layer. (G) Spike phase distribution along the reference SUB theta oscillations in SUB projection neurons. (H and I) Distribution of the spike theta phases (H) and PPC (I) of SUB projection neurons. (J) Preferred theta phase plotted against cell location and projection target. Normalized positions indicate the anatomical cell location within the SUB cell layer.

SUB neurons had distinct preferred theta phases depending on the location of their somata. SUB neurons located at the distal-deep part (distal two-thirds and deep one-third of the cell layer) of the SUB cell layer fired at the earliest phases of theta cycles (285.4 ± 63.2°), followed by neurons at the distal-superficial part (distal two-thirds and superficial two-thirds of the cell layer, 321.2 ± 39.6°), and lastly neurons at the proximal part (proximal one-third of the cell layer, 9.6 ± 54.8°; Fig. 7F and fig. S4F). These three distributions of preferred theta phases were different from each other (P < 0.01, Watson U² test with Bonferroni correction). In agreement with this location-dependent sequential firing, SUB projection neurons showed differences in theta phase locking (Fig. 7, G and H). The earliest preferred theta phases were observed in AV-p neurons (250.8 ± 50.0°), followed by RSC-p neurons (292.1 ± 53.6°), MMB-p neurons (297.8 ± 57.0°), and lastly NAC-p neurons (29.3 ± 48.6°). The preferred phases of NAC-p neurons were different from those of MMB-p, RSC-p, and AV-p neurons (P < 0.02, Watson U² test with Bonferroni correction). AV-p neurons were more strongly phase-locked to theta oscillations than RSC-p neurons (t = 2.64, P = 0.041, Steel-Dwass test; Fig. 7I). To assess which of the cell location and projection target better explain the preferred theta phases, we performed multiple regression analysis of preferred phases using the following six parameters as predictor variables: proximal-distal cell location, superficial-deep cell location, AV-p or not, MMB-p or not, NAC-p or not, and RSC-p or not (Fig. 7J). Among them, only the following four variables significantly predicted the preferred theta phase: proximal-distal location (standardized coefficient β: −0.30, P < 0.001), AV-p or not (β: −0.20, P < 0.001), MMB-p or not (β: −0.23, P < 0.001), and NAC-p or not (β: 0.20, P = 0.001), suggesting that preferred theta phase is conjunctively determined by these factors. These results demonstrate that theta oscillations robustly control the spike timing of SUB neurons in a target-specific manner. We observed similar patterns of theta phase locking during rapid eye movement (REM) sleep in both the CA1 and SUB (figs. S8 and S4F).

Projection-specific firing modulation by SPW-Rs

Next, we investigated the temporal firing patterns along SPW-Rs during slow-wave sleep (SWS). We observed synchronous SPW-Rs in the CA1 and SUB areas (Fig. 8, A and B). Using the ripple events detected at the center of the SUB cell layer as a reference, we examined the peri-ripple event firing rates of individual neurons. While most CA1 (92.7%) and SUB (73.7%) neurons showed significantly higher firing rates during ripple events than during baseline periods (P < 0.01, t test), a small fraction of SUB neurons, but not of CA1 neurons, were significantly (P < 0.01, t test) suppressed during ripples (CA1, 0%; SUB, 4.4%; χ² = 14.11, P = 0.0002; Fig. 8, C and D) (47). These suppressed neurons were mostly localized in the distal-deep part of the SUB cell layer (proximal: 2.3%, distal-superficial: 1.5%, and distal-deep: 16.7%; P < 0.001 by χ² test; Fig. 8E and fig. S4G). Consistent with this location-dependent firing modulation, 73% of AV-p neurons were significantly suppressed during ripples, while only 18% of them were activated (Fig. 8F). In contrast, nearly all MMB-p (93%) and NAC-p (100%) neurons were activated during ripples (Fig. 8F). RSC-p neurons comprised a mixture of activated (63%) and suppressed (31%) neurons (Fig. 8F). Consequently, AV-p neurons showed the lowest normalized peak height among all projection neuron groups, while RSC-p neurons showed a lower normalized peak height than did MMB-p neurons (Fig. 8G). The ripple-triggered activation/suppression was maintained regardless of the variations in ripple power (P < 0.01 by Bonferroni test after two-way repeated-measures ANOVA, AV-p versus all other projection neuron groups, MMB-p versus RSC-p; P = 0.017, NAC-p versus RSC-p; Fig. 8H), duration (P < 0.01, AV-p versus all other projection neuron groups, MMB-p versus RSC-p; P = 0.024, NAC-p versus RSC-p; Fig. 8I), or frequency (P < 0.01, AV-p versus all other projection neuron groups, MMB-p versus RSC-p; Fig. 8J). Essentially the same pattern of firing modulation was observed in SPW-Rs during the awake rest periods (figs. S4G and S9).

Fig. 8. Projection-specific firing modulation by SPW-Rs during SWS.

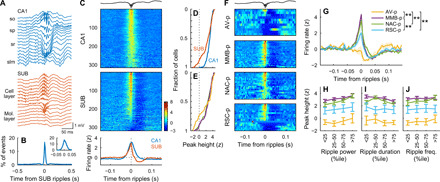
(A) Wide-band LFPs simultaneously recorded in the CA1 (top) and SUB (bottom) showing SPW-Rs. so, stratum oriens; sp, stratum pyramidale; sr, stratum radiatum; slm, stratum lacunosum-moleculare. (B) Cross-correlogram (CCG) of ripple events detected in the CA1 and SUB cell layers. Inset: The same CCG at a finer temporal scale. Means (solid line) ± SD (shaded area). (C) Ripple-triggered average of firing rates (z-scored) of CA1 (top) and SUB (middle) neurons and the firing rates averaged over CA1 or SUB neurons (bottom). Ripple events detected in single recording sites at the center of the SUB cell layer were used as the reference in (C) to (J). (C and F) Topmost trace, example SUB LFP showing SPW-Rs. (D and E) Mean z-scored firing rate averaged around the negative ripple peaks (−10 to 10 ms) for CA1 and SUB neurons (D) and for SUB neurons located at the proximal (green), distal-superficial (purple), and distal-deep (yellow) part of the SUB cell layer (E). (F) Ripple-triggered average of z-scored firing rates of individual SUB projection neurons. (G) Ripple-triggered average of z-scored firing rates of SUB projection neurons. **P < 0.01, Tukey test for peak height. Means (solid lines) ± SEM (shaded areas). (H to J) Mean z-scored firing rate averaged around negative ripple peaks (−10 to 10 ms) as a function of ripple power (H), ripple duration (I), and ripple frequency (J). The plot colors are the same as in (G). Means ± SEM.

DISCUSSION

To the best of our knowledge, this is the first report demonstrating the pathway-specific information routing from the SUB. Three main findings were noted. First, SUB neurons robustly represented multiple types of navigation-associated information as accurately as or even more accurately than CA1 neurons. Second, depending on the type, the information was carried either uniformly or selectively by SUB projection neurons targeting distinct areas. Third, the firing of SUB projection neurons was distinctly controlled by theta oscillations and SPW-Rs in a target region–specific manner. These three findings address “how,” “which,” and “when” information is emitted from the SUB to downstream targets, respectively, providing a comprehensive view of information routing from the dorsal hippocampal formation.

A key feature of the subicular representations was that SUB neurons conveyed comparable (i.e., place and trajectory) or even greater (i.e., speed) information per unit time than that conveyed by CA1 neurons, despite their broader tuning. A previous study using a U-shaped track task suggested that SUB neurons carry more positional information per unit time than do CA1 neurons (26). They used model neurons derived from experimental data to estimate information content, partly because they could simultaneously record only a few SUB neurons. A limitation of their study is that it modeled neither bursting and history dependence in the spike trains (48, 49) nor transient synchrony between neurons (50), which is a hallmark of “cell assembly” (51). Such spike timing correlations both in single neurons and among multiple neurons are known to affect the amount of information encoded (52). In contrast, we measured spatial information directly from the experimental data by simultaneously monitoring a larger number of SUB neurons using 256-channel silicon probes. Further, by using multiple behavioral tasks, we found that SUB neurons have accurate representations for speed and trajectory, which expands the concept of SUB place representation (26) to that of multiple navigation-associated variables.

Our results suggest that the sharply tuned, low–firing rate representation in the CA1 area is converted into a broadly tuned, high–firing rate representation in the SUB without losing the information content. This change in representation may be caused by the converging inputs onto single SUB neurons from multiple CA1 neurons, as proposed by previous studies (24, 25). In addition, the richer speed information in the SUB might be due to further convergence of entorhinal speed signals (42, 43). The high firing rate in the SUB is crucially important for supporting per-second information rate in single neurons, decoding performance as a population, and the noise-resistant robust coding, which may be suitable for long-range projections suffering from substantial noise (41). These coding strategies were common across place, speed, and trajectory information. Thus, we propose that a key role of the SUB is to generate noise-resistant, accurate representations for multiple types of navigation-associated information. The coding strategy of constructing such a high–firing rate, noise-resistant representation may apply not only for the SUB but also for the entire hippocampal circuit. The mean firing rates of principal cells progressively increase as they pass through the feed-forward network of the hippocampal formation (i.e., dentate gyrus ➔ CA3 ➔ CA1 ➔ SUB) (24, 53–55). Thus, one of the roles of the hippocampal circuit might be to convert the sparse firing in the dentate gyrus (55–58) to progressively denser and more robust representations.

We found that groups of SUB projection neurons uniformly (i.e., place) or selectively (i.e., speed and trajectory) carry information. Place information may be used in all target areas; in particular, the AV, MMB, and RSC are all implicated in spatial learning (59). As SUB neurons showed comparable spatial coding with CA1 neurons both at single-cell and population levels, we predict that SUB neurons projecting to regions other than the four that we identified also show strong place coding. Speed information prominently routed to the RSC may interact with visual-locomotion integration in this area (60, 61). Trajectory information routed to the NAC may help goal-directed action to obtain a reward, which is thought to be the major function of the NAC (62). Head-direction tuning was weak in all four groups of SUB projection neurons, suggesting that head-direction information in the AV (63) and RSC (64) is derived not from the SUB but from other regions innervating these areas. Considering that the ventral CA1 routes information related to anxiety, goal approach, and task engagement to distinct target areas, including the prefrontal cortex, amygdala, and NAC (31), the entire dorsoventral axis of the hippocampal formation might route distinct, relevant information to different target areas. Note that such discussion of functional allocations to different projections is based on the assumption that projection neurons sampled by optogenetics represent the neuronal population in the target pathways (31, 65). In addition, the information routed to downstream areas is not necessarily passed on to the neurons in the target areas. To precisely link the information routing to its network and behavioral functions, deliberate future studies would be necessary. For instance, whether the NAC-routed trajectory information is required for spatial working memory remains unknown. In line with our result, the disconnection of the SUB-NAC pathway has been shown to impair spatial working memory in a radial arm maze task but only when no delay was inserted between the training and test phases (66). In contrast, inactivation of the distal SUB, but not the proximal SUB containing NAC-p neurons, has been shown to impair spatial working memory in a Morris water maze task (23). In addition, Nelson et al. (67) found that the reciprocal connection between the SUB and anterior thalamic nuclei, including the AV, is required for a modified T-maze task, in which animals could not use intramaze cues. Collectively, while multiple SUB projections are recruited in spatial working memory tasks, their necessity appears to depend on various factors, including the type of behavioral task, task difficulty, delay length, and richness of available cues.

SUB projection neurons showed different preferred spike timing during theta oscillations, suggesting that distinct information is sent out sequentially to different target areas in each theta cycle. A potential determinant of the preferred spike timing is the topographically graded input from the entorhinal cortex. The medial and lateral entorhinal cortex (MEC and LEC, respectively) preferentially innervate the distal and proximal SUB, respectively (68). MEC layer 3 neurons, which project to the SUB (69), fire maximally around the peaks of theta oscillations measured in the CA1 pyramidal cell layer (70, 71), which matches the observed phase preference of distal SUB neurons. Therefore, the spike timing of distal SUB neurons during theta oscillations may be under strong control of MEC layer 3 inputs. By contrast, the LEC displays weaker theta oscillations/modulation (72). Thus, the theta phase preference of proximal SUB neurons may be mainly determined by CA1 inputs, which show a theta phase preference similar to that of proximal SUB neurons. All four downstream areas examined in this study exhibit theta-modulated activity, which is often coherent with hippocampal theta oscillations (59, 63, 73, 74). Thus, the SUB potentially coordinates theta-paced activity in multiple downstream areas with fine temporal precision. SUB projection neurons were also distinctly activated or suppressed during ripples. Because of the widespread projections of the SUB, precisely timed activity broadcasted from the SUB might organize the brain-wide activity (75) through the modulation of downstream areas (47, 74, 76, 77). Exactly how the routed information from the SUB is used in the target areas remains to be elucidated. Further studies are warranted to investigate the impact of SUB activity on information processing in downstream areas.

MATERIALS AND METHODS

All procedures of animal care and use were approved by the Institutional Animal Care and Use Committee of Osaka City University and were performed in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals.

Anatomical tracing

AAVs for anatomical tracing were produced by cotransfecting plasmids into 293T cells (RCB2202, Riken BRC), purified with heparin columns (HiTrap, GE Healthcare), and titered via quantitative polymerase chain reaction, as described previously (6). Plasmids used for AAV production were as follows: pAAV-EF1α-EGFP (6), pAAV-EF1α-DIO-EYFP (no. 20296, Addgene), pAAV-pgk-Cre (no. 24593, Addgene), pXR1 (National Gene Vector Biorepository), pAAV2/6 (PL-T-PV0004, Penn Vector Core), pAAV-RC (AAV Helper-Free System, Stratagene), and pHelper (AAV Helper-Free System).

Stereotaxic injections were performed on male Long-Evans rats (n = 2, 13, and 12 rats for anterograde tracing, retrograde tracing, and projection-specific labeling, respectively; 262 to 382 g; 7.9 to 10 weeks old on the day of surgery; SLC, Japan) under ~2% isoflurane anesthesia. For anterograde tracing, 400 nl of AAV1/2-EF1α-EGFP [2.9 × 10¹³ genome copies (GC)/ml] was injected into the left dorsal SUB [anterior-posterior from bregma (AP): −6.1 mm, mediolateral from the midline (ML): 3.0 mm, dorsoventral from the cortical surface (DV): 2.8 mm]. For retrograde tracing, either 400 or 1200 nl per site of 0.5% (w/v) CTB488 (C34775, Thermo Fisher Scientific) was injected into one of the following brain areas: bilateral NAC (n = 4 rats; AP: +2.4 mm, ML: ±1.8 mm, DV: 6.4 mm), bilateral AV (n = 2 rats; AP: −2.0 or −1.7 mm, ML: ±1.6 mm, and DV: 5.2 mm), ITN (n = 2 rats; AP: −2.0 mm, ML: 1.0 mm, DV: 6.6 mm, inserted from the right hemisphere at an angle of 10° in the coronal plane with the tip pointing toward the medial direction), bilateral RSC (n = 2 rats; AP: −3.8 mm, ML: ±0.4 mm, DV: 1.6 mm), and MMB (n = 3 rats; AP: −4.7, −4.2, or −3.2 mm; ML: 1.5 mm; DV: 8.9, 9.1, or 9.3 mm, at a 10° angle as described above). For projection-specific labeling, 1000 nl per site of AAV1/2-EF1α-DIO-EYFP (9.2 × 10¹¹ GC/ml) was injected into the bilateral dorsal SUB (AP: −6.1 mm, ML: ±3.0 mm, DV: 2.8 mm), and 400 nl per site of AAV6-pgk-Cre (2.4 × 10¹² GC/ml) was injected into one of the following brain areas: bilateral NAC (n = 3 rats; AP: +2.4 mm, ML: ±1.8 mm, DV: 6.4 mm), bilateral AV (n = 2 rats; AP: −2.0 mm, ML: ±1.6 mm, DV: 5.2 mm), ITN (n = 2 rats; AP: −2.0 mm, ML: 1.0 mm, DV: 6.4 mm, at a 10° angle as described above), bilateral RSC (n = 3 rats; AP: −3.8 mm, ML: ±0.4 mm, DV: 2.0 mm), and MMB (n = 2 rats; AP: −4.7 mm, ML: 1.5 mm, DV: 8.9 mm, at a 10° angle as described above).

Immunohistochemistry was performed as described in the “Histology” section. Cells positive for CTB488, NOS, or PCP4 were counted manually using Fiji software at four or five AP levels of the SUB (350 to 2150 μm posterior to the posterior commissure). In individual images, 10 × 2 and 10 × 5 grids were placed on the deep cell layer, rich in PCP4-positive cells (35), and the superficial cell layer, scarce in PCP4-positive cells, of the SUB, respectively. The density of CTB488-positive cells in each grid was obtained as the number of CTB488-positive cells in the grid divided by the grid area. Dendritic spines of EYFP-labeled dendrites were semiautomatically detected and measured from confocal image stacks (voxel size, 0.1 μm × 0.1 μm × 0.5 μm) using the NeuronStudio software, as described previously (78). Spines were classified into three groups according to their shape: mushroom, thin, and stubby. Spine density was calculated as the number of spines divided by the dendrite length.

Materials for extracellular recordings

We used three types of 256-channel silicon probes (NeuroNexus). All types had eight shanks, with each shank containing linearly aligned 32 recording sites (160 to 177 μm² per site, 0.61 ± 0.23 megohm at 1 kHz) but differing in their horizontal shank separation and vertical site spacing. Buzsaki256 probes had 300-μm shank separation and 50-μm vertical site spacing. A8x32-5mm-35-300-160 probes had 300-μm shank separation and 35-μm site spacing. A8x32-Edge-5mm-25-200-177 probes had 200-μm shank separation and 25-μm site spacing. The silicon probes were mounted on a 3D-printed microdrive with a movable screw (R0090B500, J.I. Morris), with which the silicon probe was gradually lowered to the SUB/CA1 area after implantation. For 8 of the 11 implantations, all recording sites were coated with poly(3,4-ethylenedioxythiophene) conducting polymer (79) with a 1-μA direct current for 3 s (nanoZ, White Matter) to lower the impedance (0.44 ± 0.20 megohm at 1 kHz after coating).

Laser diodes (450-nm light; PL450B, Osram) were coupled with a short optic fiber of 105-μm (FG105LCA, Thorlabs) or 200-μm (FP200URT, Thorlabs) core diameter (3.0 to 22.0 mm length depending on the target brain area). Light emission was controlled by a laser diode driver (LD202C, Thorlabs) and was measured before surgery from the tip of the optic fibers to reach 24 to 31 mW (with FG105LCA) and 42 to 88 mW (with FP200URT) with 100% laser output power.

Surgery for recordings

Eleven male Long-Evans rats (293 to 490 g; 8.9 to 15.3 weeks old on the day of surgery; SLC) were used. Under 1.6 to 2.0% isoflurane anesthesia, eight rats were stereotaxically implanted with four laser diode–coupled optic fibers targeting the left NAC (AP: +2.4 mm, ML: 1.8 mm, DV: 6.3 mm), left AV (AP: −2.0 mm, ML: 1.6 mm, DV: 4.6 to 4.8 mm), left RSC (AP: −3.8 mm, ML: 0.4 mm, DV: 1.5 mm), and MMB (AP: −4.7 mm, ML: 1.5 mm, DV: 8.7 mm, inserted from the right hemisphere at an angle of 10 degrees in the coronal plane with the tip pointing toward the medial direction) and were then injected with 800 nl per site of AAV1-hSyn-hChR2(H134R)-EYFP (2.3 × 10¹³ GC/ml; Penn Vector Core; diluted 1:1 to 1:5 before injection) using a pulled glass pipet (G-1, Narishige) into two sites in the left dorsal SUB (AP: −5.7 mm, ML: 2.2 to 2.5 mm, DV: 2.9 to 3.0 mm and AP: −6.1 mm, ML: 3.2 to 3.5 mm, DV: 2.9 to 3.0 mm). Rats were lastly implanted with a silicon probe targeting above the left dorsal SUB and distal CA1 area (center of the eight shanks at AP: −5.9 to −6.1 mm, ML: 2.7 to 3.3 mm, DV: 2.4 mm, with shanks parallel to the coronal plane). Two stainless steel screws (B000FN0J58, Antrin Miniature Specialties) inserted above the cerebellum served as indifferent and ground electrodes. A faraday cage connected to the ground electrode was placed around the implants. One rat was subjected to the same surgery, but the optic fiber implantation to the MMB was omitted for a technical reason. Two rats were implanted only with a silicon probe above the dorsal SUB and distal CA1 area (center of shanks at AP: −5.9 mm, ML: 2.8 to 3.3 mm, DV: 2.4 mm). All rats were housed individually after surgery.

Data collection

Electrophysiological data from behaving rats were acquired using a 256-channel, multiplexed recording system (KJE-1001, Amplipex) during behavioral tasks and sleep. Neurophysiological signals were amplified on a pre-amplifier module (HS-10, Amplipex) and acquired continuously at 20 kHz with 16-bit resolution. The silicon probe was lowered daily toward the SUB/CA1 area until large-amplitude units appeared approximately at the center of vertically aligned recording sites at a depth of 2.7 to 3.8 mm from the cortical surface. Characteristic features (power, phase, and polarity) of theta oscillations and SPW-Rs were used as additional guides to determine the approximate locations of the recording sites relative to the SUB/CA1 cell layer (17, 19). The animal’s position and head direction were tracked by monitoring two small light-emitting diodes (LEDs; green and red, 5-cm separation) mounted above the head-stage using an overhead camera (c930e, Logicool) at ~30-Hz sampling rate. Single camera pixels corresponded to 0.41 cm for linear track and 0.52 cm for open-field, T-maze, zigzag maze, and rest sessions. LED positions were extracted and resampled to 39.0625 Hz for further analysis.

After the recording, to identify the location of recording sites, small electric lesions were made by passing anodal DC current (3 μA for 10 s; A365, World Precision Instruments) through the most dorsal and ventral recording sites of each shank under anesthesia. Immunohistochemistry was performed as described in the “Histology” section. The tracks of silicon probe shanks and optic fibers were reconstructed from the images of serial sections.

The acquired local field potential (LFP) signals were downsampled to 1250 Hz for further analysis. Positive polarity is plotted upward throughout the study. Spike sorting was first performed automatically using the Kilosort software (https://github.com/cortex-lab/KiloSort and https://github.com/MouseLand/Kilosort2), and then, clusters were adjusted manually using the phy gui (https://github.com/cortex-lab/phy), according to the developers’ instructions. We measured cluster quality via the isolation distance and interspike interval (ISI) index, defined as the number of ISIs less than 2 ms divided by the number of ISIs between 2 and 10 ms multiplied by 4 (6, 32). Units satisfying all the following criteria were included for further analysis: isolation distance > 20, ISI index < 0.2, trough-to-peak amplitude > 50 μV, and overall mean firing rate > 0.1 Hz. Although we set these stringent criteria for unit quality, we cannot exclude that some units recorded in different sessions could have been identical, since spikes from sessions recorded on different days were clustered separately (table S1). We confirmed that even when single sessions per animal were used for analysis to remove this potential double counting, the statistical significance of pathway-specific information routing (Figs. 4J and 5K) was maintained.

Behavioral procedures

Rats were trained to perform four types of water-rewarded spatial tasks—namely, open-field, linear track, alternating T-maze, and zigzag maze tasks—daily for 7 to 9 days before and 4 to 8 days after surgery. During training, the experimenter gave water drops randomly in the arena (for the open-field task) or at the reward ports (for the other tasks, see below) to motivate animal movement. In the alternating T-maze task, only correct trials were rewarded. Then, 13 to 22 days after surgery (6 to 13 days for two rats not injected with AAV), the recording sessions were carried out for two to three consecutive days, with the four behavioral tasks performed each day for 20 min each, and intertask rest sessions performed for 40 to 80 min each. Rest sessions were also carried out before the first behavioral task and after the final task. On the recording days, optical stimulation sessions to identify axonal projections were performed once (after all recording sessions of the day; one of the nine rats) or thrice (before, in the middle of, and after the recording sessions of the day; eight of the nine rats) while rats were resting in a small enclosure. During the periods of the behavioral experiments, rats were water-deprived in a way to maintain ~90% of their free-feeding body weight. All behavioral experiments were performed during the light period of the 12-hour light/dark cycle.

The open-field task was performed using a square black arena (118 cm by 118 cm, 40 cm deep, with an A4-sized white cue card on one of the walls), in which rats freely foraged for randomly dispersed drops of water. The linear track task was performed on an elevated black linear track (234-cm long, 6.5-cm wide, 54-cm high) on which rats were required to run back and forth to receive a 30-μl water drop supplied alternately at the edges of the track.

The alternating T-maze task was performed in a square black arena (118 cm by 118 cm, 40-cm deep) consisting of a start box (30 cm by 10 cm), central runway (stem, 98-cm long, 10-cm wide), and left/right arms (10-cm wide). Rats were enclosed by doors in the start box for ~8 s before allowed to run through the stem and arm. Rats were subjected to trials continuously and had to choose the other arm from that chosen in the previous trial to be rewarded with a 30-μl water drop at the end of the arm.

The zigzag maze task was performed in a square black arena (118 cm by 118 cm, 40-cm deep), in which seven additional partitions (101-cm long, 30-cm high) were placed to form eight runways (118-cm long, 14-cm wide) connected with hairpin curves. Rats were rewarded with an 80-μl water drop alternately placed at the edges of the entire runway. During rest sessions, rats were placed in a small black enclosure (18 cm by 18 cm, 40-cm deep) not containing a water reward; optical stimulation to identify axonal projections was also performed in this enclosure.

Optogenetic identification of projection targets

To identify the projection targets of recorded cells with antidromic spikes (31), we sequentially irradiated blue light pulses to the projection targets of the SUB while recording from the SUB and CA1. A single stimulation train consisted of 200 light pulses (10 pulses at 5 Hz repeated for 20 times with ~1-s intervals) and was repeated for combinations of 1- or 5-ms pulse durations with 12.5, 25, 50, 75, or 100% laser output power. Following these stimulation trains, closed-loop stimulation was performed to efficiently detect spike collisions. For this, spikes were detected online by high-pass filtering the extracellular signals at 300 Hz and by thresholding at 3 × root mean square, using a multi I/O processor (RX8, Tucker-Davis Technologies). Triggered by the detected spikes, a single light pulse (1-ms duration, 100% laser output power) was delivered to the target region with 1.8-ms delay. To avoid burst stimulation, the minimum interstimulation interval was set to 200 ms.

We identified projection neurons offline as follows. The peri-stimulus time histogram (0.5-ms bins) of individual cells was constructed for each stimulation train. Spikes in the first peak bin after stimulation onset (≥10 spikes and >mean + 3 SD of the prestimulus baseline period) and in its contiguous bins (>mean + 1 SD of the baseline period) were regarded as optically evoked spikes. Stimulation trains that gave low waveform correlation between the evoked and spontaneous spikes (r < 0.9) were excluded from further analysis. Fidelity for each stimulation train was calculated as the number of evoked spikes divided by that of stimulation trials (i.e., 200). Jitter was defined as the SD of time from stimulation onset to the evoked spikes. Latency was defined as the mean time from stimulation onset to the evoked spikes. In the stimulation train with the highest fidelity, the units satisfying all following criteria were defined as the neurons projecting to the stimulated area: fidelity > 20%, jitter < 0.5 ms, and latency < 25 ms. These criteria were determined on the basis of the units that passed the spike collision test (see below).

Spike collision test was performed as follows. For a given evoked spike latency t ms, optical stimulation trials were divided into two types: collision trials that had one or more spontaneous spikes between −t + 1 ms and t − 1 ms (i.e., shortly before the expected evoked spike latency t) and the rest of the trials (noncollision trials). If the fidelity of optical spike generation in the collision trials was significantly less than that in noncollision trials (P < 0.05, χ² test), the unit was regarded to pass the collision test. We used units that passed the spike collision test to define the criteria to identify projection target areas, so that 80% of the test-passed units were included in the criteria described above (fidelity > 20%, jitter < 0.5 ms, latency < 25 ms) (fig. S3).

Histology

At specific days after the surgery for anatomical tracing (anterograde tracing: 15 days, retrograde tracing: 7 days, projection-specific labeling: 20 to 21 days) or soon after the electric lesions for localizing silicon probes, rats were transcardially perfused with 0.9% saline, followed by 4% paraformaldehyde in 0.1 M phosphate buffer. The implanted silicon probe was pulled out before the brain was removed from the skull. Brains were stored in the same fixative overnight at 4°C and then sectioned using a vibratome (VT1200S, Leica) at a 50-μm thickness parallel to the coronal plane. Sections were incubated sequentially with 5% bovine serum albumin (BSA)/0.3% Triton X-100 in phosphate-buffered saline (PBS) for 30 min at room temperature, primary antibodies in 5% BSA/PBS overnight at 4°C, and the corresponding secondary antibodies conjugated with Alexa Fluor dyes in 5% BSA/PBS for either 2 hours at room temperature or overnight at 4°C. Some sections were counterstained with DAPI (4′,6-diamidino-2-phenylindole; 0.5 μg/ml; D1306, Thermo Fisher Scientific) and/or NeuroTrace Red fluorescent Nissl (1:200; N21482, Thermo Fisher Scientific). Between the incubation procedures, sections were washed with PBS. The primary antibodies used were as follows: chicken anti-GFP (green fluorescent protein) (1:2000; ab13970, Abcam), mouse anti-Cre recombinase (1:2000; MAB3120, Millipore), mouse anti-NeuN (1:2000; MAB377, Millipore), rabbit anti-PCP4 (1:200; HPA005792, Sigma-Aldrich), and sheep anti-NOS (1:10,000; gift from T. Fukuda, originally from P. C. Emson) (35). The following secondary antibodies were used at 1:800 dilution: goat anti-chicken immunoglobulin Y (IgY) conjugated with Alexa Fluor 488 (A-11039, Thermo Fisher Scientific), goat anti-mouse IgG with Alexa Fluor 594 (A-11032, Thermo Fisher Scientific), donkey anti-mouse IgG with Alexa Fluor 405 (ab175659, Abcam), donkey anti-rabbit IgG with Alexa Fluor 594 (A-21207, Thermo Fisher Scientific), and donkey anti-sheep IgG with Alexa Fluor 647 (A-21448, Invitrogen). Stained sections were mounted on coverslips with antifade mountant (P36961, Thermo Fisher Scientific). Tiled fluorescent images were taken using a confocal microscope (LSM700, Zeiss) equipped with 10× [numerical aperture (NA) = 0.45, for anterograde tracing and for localizing silicon probe and optic fibers], 20× (NA = 0.8, for retrograde tracing), and 63× (NA = 1.2, for dendritic spines) objectives.

Cell classification

We recorded a total of 791 well-isolated, large-amplitude units. Of these, 353 and 339 units were histologically identified to be localized in the CA1 area and SUB, respectively. Putative CA1 principal cells were defined as units that had >0.4-ms trough-to-peak spike width and <10-Hz overall mean firing rate. Putative SUB principal cells were defined as units that had >0.4-ms trough-to-peak spike width. The threshold of the mean firing rate was omitted when classifying SUB principal cells because a proportion of these cells shows high firing rates (fig. S3) (25). Accordingly, 315 and 319 units were identified as CA1 principal cells and SUB principal cells, respectively.

We verified the criteria of principal cell classification of CA1 and SUB neurons by detecting putative monosynaptic interactions (80). Cross-correlograms (CCGs) of spike timing were constructed for all pairs of simultaneously recorded cells (0.1-ms bins, Gaussian smoothing with 0.5-ms σ). For each pair, 199 surrogate CCGs were also constructed from data with random jittering of spike timing by −5 to 5 ms in one of the paired cells. The 99% global band significance level was calculated as described previously (80). CCGs with a peak or trough crossing the 99% significance level between 0 and 5 ms were taken as the candidate pairs of monosynaptic excitation or inhibition, respectively. Of these, dull peaks and troughs unlikely to be due to monosynaptic spike transmission and suppression were excluded by visual inspection. Nearly all CCG-based putative excitatory cells (CA1: 44 of 45 neurons, SUB: 40 of 40 neurons) were confirmed to meet the criteria of principal cells described above, and all CCG-based putative inhibitory cells (CA1: 6 of 6 neurons, SUB: 5 of 5 neurons) had <0.4-ms spike width (fig. S3, A to C). Hereafter, we analyzed only the CA1 and SUB principal cells.

Place representation on a linear track

We examined the spatial firing patterns on a linear track by constructing 1D rate maps for individual cells. A rate map consisted of firing rates at position bins (2-cm long, excluding the edges of the track), calculated by dividing the number of spikes in each position bin by the duration spent in that bin, after having individually smoothed both the numerator and denominator with a Gaussian filter (σ = 2 cm). For each cell, rate maps were constructed separately for eastbound and westbound trials, and the rate map with the higher peak firing rate (i.e., the rate map of the cell’s preferred direction) was used for further analysis. Cells with peak firing rates less than 1 Hz in the preferred direction were excluded from the analysis. The mean rate was defined as the mean firing rate during trials in the preferred direction. Spatial information per spike (I_spike, bits/spike) and spatial information per second (I_sec, bits/s) were calculated by

$$I_{\text{spike}}={\displaystyle \sum _i}{p}_i\frac{{\mathrm{\lambda }}_i}{\mathrm{\lambda }}{\text{log}}_2\left(\frac{{\mathrm{\lambda }}_i}{\mathrm{\lambda }}\right)$$ (1)

$$I_{\text{spike}}={\displaystyle \sum _i}{p}_i{\mathrm{\lambda }}_i{\text{log}}_2\left(\frac{{\mathrm{\lambda }}_i}{\mathrm{\lambda }}\right)$$ (2)

where p_i is the proportion of time spent in the ith position bin, λ_i is the firing rate in the ith position bin, and λ is the mean firing rate during trials (38).

The chance level of I_sec was obtained by a trial-wise shuffling procedure, by which the rate map of every trial was circularly shifted relative to the track position by a random interval, with the end of the trial wrapped to the beginning before obtaining the rate map averaged over trials. The shuffling was repeated 1000 times for each cell. A cell was defined as a place cell if its I_sec value exceeded the 99th percentile of the I_sec value from the shuffled data obtained from all CA1 and SUB cells.

Mutual information (bits) of firing rates and places was estimated according to a previous study (39) by

$$\text{Mutual information}={\displaystyle \sum _i}{\displaystyle \sum _j}{p}_{i\mathit{j}}{\text{log}}_2\left(\frac{p_{\mathit{ij}}}{p_i{p}_j}\right)$$

where p_i is the probability that the animal is in the ith position bin (bin size, 2 cm), p_j is the probability that the instantaneous firing rate of a cell is in the jth firing rate bin (four bins, see below), and p_ij is the joint probability between the ith position bin and jth firing rate bin. The instantaneous firing rate of a cell was obtained by sorting the cell’s spike timing into 25.6-ms bins, followed by Gaussian smoothing (σ = 128 ms) of the binned firing rate. The instantaneous firing rates were sorted into four firing rate bins with threshold values at 25, 50, and 75 percentiles of the nonzero instantaneous firing rate values.

Place decoding on a linear track

We performed memoryless Bayesian decoding of the rat’s position to estimate the positional information conveyed by CA1 and SUB cell populations (40). The probability of the rat’s position (pos) across M total position bins in time window τ (250 ms) containing neural spikes (spikes) was

$$\text{Pr}(\text{pos}\mid \text{spikes})=U/{\displaystyle \sum _{i=1}^M}U$$

where

$$U=({\displaystyle \prod _{j=1}^N}{f}_j{(\text{pos})}^{n_j}) \mathit{\text{exp}}(-\mathrm{\tau }{\displaystyle \sum _{j=1}^N}{f}_j(\text{pos}))$$

The f_j(pos) is the rate map of the jth unit, n_j is the number of spikes of the jth unit in the time window, and N is the number of units used for decoding. Decoding performance was estimated using leave-one-out cross-validation as follows. From a given set of trials in the recording session, a trial was chosen as test data, and the rest of the trials were used as training data. The decoding result, Pr(pos | spikes), was obtained using rate maps f_j(pos) constructed from the training data and spike train n_j in the test data. The position with the highest Pr(pos|spikes) across the position bins was defined as the decoded position of the given time window. The decoding error of the test data was calculated as the mean Euclidean distance between the decoded and the observed positions. The decoding error was calculated either from all time bins, irrespective of the number of spikes in the bins, or from time bins containing one or more spikes, both of which gave essentially the same results (Fig. 3H). This procedure was repeated to assign every trial as test data, and the decoding errors from all test data were averaged to obtain the decoding error of the session. The chance-level distribution of the decoding error was estimated by a shuffling procedure repeated 100 times: The decoded positions were randomly permuted along time windows, and the decoding error was calculated.

Dependency of the decoding performance on the number of used cells was measured by random cell subsampling. Of the total simultaneously recorded CA1 or SUB cells (N_total), decoding was performed using a certain number of random cell subsets, and the decoding error was calculated. This procedure was repeated 100 times (or for all possible combinations of the cell group if the number of combinations was less than 100), and the obtained decoding errors were averaged over the repetition. By changing the number of units supplied for the decoding from 1 to N_total, we obtained the decoding error for each number of units.

To control the decoding performance for SUB high firing rate, the mean firing rate of SUB neurons was matched to that of CA1 neurons by randomly removing (1 − λ_CA1/λ_SUB) × 100% of spikes out of all spikes generated by SUB neurons, where λ_CA1 and λ_SUB were the mean firing rates averaged across CA1 and SUB neurons, respectively. We then performed the decoding analysis as described above using these subsampled SUB spikes.

To estimate the contribution of single units to the decoding performance, we performed a Jackknife procedure after random subsampling of the units. Of the total simultaneously recorded CA1 or SUB units, one unit was chosen as a test unit, and nine were randomly chosen from the remaining units. Recording sessions with less than 10 simultaneously recorded CA1 or SUB units were excluded from this analysis. Decoding was performed using the nine units with or without the test unit, and the decoding improvement of the test unit was calculated as the difference in the decoding error between the two decoding error values. The random choice of nine units was repeated 100 times from all possible combinations of nine units without replacement (or for all possible combinations of choices if the number of combinations was less than 100), and the decoding improvement of the test unit was averaged over the repetition. This procedure was further repeated to assign every recorded unit as a test unit once.

The robustness of the decoding performance against noise was estimated by randomly removing (up to 99% of the number of spikes of each unit) or adding spikes to every unit at a fixed frequency over the entire recording session before performing the decoding procedure with all simultaneously recorded CA1 or SUB cells. The removal/addition procedure was repeated 100 times to obtain the decoding error, averaged over the repetition. Recording sessions with less than five simultaneously recorded units were excluded from this analysis. The entire decoding procedure was performed separately for eastbound and westbound runs, which were pooled later.

Place representation in an open field

We analyzed the spatial firing patterns in the open field similarly to those on the linear track. A rate map was constructed by 2 × 2 cm position bins using a 2D Gaussian filter (σ = 4 cm) for smoothing. Units with a mean firing rate less than 0.1 Hz in the open field were excluded from the analysis. Spatial information per spike (I_spike, bits/spike) and that per second (I_sec, bits/s) was calculated exactly as those on the linear track. A session-wise shuffling procedure was performed, by which the spike train of the whole open-field session was circularly time-shifted relative to the rat’s position by a random interval between 30 s and the length of the session minus 30 s, with the end of the trial wrapped to the beginning.

We performed memoryless Bayesian decoding (τ = 1 s) as in the case of the linear track. Decoding performance was estimated using fivefold cross-validation as follows. The four-fifth periods of the recording session (e.g., 0 to 960 s of the 1200-s session) were chosen as the training data, and the remaining periods (e.g., 960 to 1200 s) were assigned as the test data. The probability of the rat’s position across position bins, Pr(pos|spikes), was calculated from rate maps f_j(pos) constructed from the training data and spike train n_j in the test data, as described above. This procedure was repeated five times to decode from all periods of the recording session, and the decoding errors from the five periods were averaged to obtain the decoding error of the session. The chance-level distribution of the decoding error was estimated by a shuffling procedure (100 repetitions), by which the decoded positions were randomly permuted along time bins, and the decoding error was calculated from the shuffled decoded positions and the observed positions. To control the decoding performance for SUB high firing rate, spikes were randomly removed from SUB neurons as described above, before performing the decoding analysis. Dependency of the decoding performance on the number of used cells and the robustness of the decoding performance against noise were also estimated as described for the linear track.

Speed representation in an open field

Speed representation in the open field was analyzed as described previously (42, 43). Neuronal spikes were sorted into 25.6-ms time bins. The instantaneous firing rate was obtained by dividing the numbers of spikes for each cell by the bin size and smoothed with a Gaussian filter (σ = 256 ms). Units with mean firing rate less than 0.1 Hz in the open field were excluded from the analysis. Each rat’s positions were smoothed with a Gaussian filter (σ = 256 ms). Instantaneous running speed was calculated by dividing the distance of the smoothed position between adjacent bins by the bin size (25.6 ms). Changing the SD of Gaussian filters to 128 or 512 ms for both firing rate and position gave similar results. Periods slower than 2 cm/s and faster than 50 cm/s were removed from the analysis. Speed scores were defined for each cell as the Pearson product-moment correlation coefficients between the cell’s instantaneous firing rate and the rat’s instantaneous running speed. We calculated speed information as follows (42). First, for each cell, the speed tuning curve of the firing rate against speed was constructed using bins of 4 cm/s, from 2 to 50 cm/s. Then, speed information per spike (I_spike, bits/spike) and speed information per second (I_sec, bits/s) were obtained by Eqs. 1 and 2, respectively, where p_i is the proportion of time spent in the ith speed bin, λ_i is the firing rate in the ith speed bin, and λ is the mean firing rate in the open field.

Chance-level statistics were calculated by a shuffling procedure (100 repetition), by which the spike train was circularly time-shifted relative to the rat’s position by a random interval between 30 s and the length of the session minus 30 s, with the end of the trial wrapped to the beginning. A cell was defined as a positive speed (p-speed) cell or negative speed (n-speed) cell if its speed score exceeded the 99th percentile or was lower than the 1st percentile, respectively, of the distribution of speed scores from the shuffled data from all CA1 and SUB principal cells. We used bootstrap analysis to determine whether a SUB projection neuron group contained a significantly higher proportion of p-speed cells (31).

Decoding of running speed

Decoding of running speed was performed using fivefold cross-validation similar to a previous study (43). Of the 1200-s recording session in the open field, one-fifth of the period (e.g., 0 to 240 s) was assigned as test data, and the remaining four-fifths (e.g., 240 to 1200 s) were used as training data. A linear relationship between the firing rate and running speed averaged over 1-s bins was expressed as

$$S_{\text{tr}}=R_{\text{tr}}f$$

where S_tr is a column vector with the speed bins of the training data, R_tr is a matrix containing the corresponding firing rate bins for each neuron as columns and an additional column of 1s to account for y intercepts, and f is a linear filter used as a column vector with a length equal to the number of cells plus 1. The linear filter f was obtained by

$$f={R_{\text{tr}}}^{+}{S}_{\text{tr}}$$

where R_tr⁺ is the Moore-Penrose pseudoinverse of R_tr. Once f was obtained, the decoded speed S_dec was calculated by

$$S_{\text{dec}}=R_{\text{test}}f$$

where R_test is the firing rate matrix of the test data. Decoding accuracy was defined as the Pearson correlation coefficient between S_dec and the observed speed S_test. The chance level of the decoding accuracy was estimated by a shuffling procedure repeated 100 times, by which S_dec was time-shifted by a random interval between 30 and 210 s relative to S_test. The decoding procedure was repeated five times to decode all periods of the recording session, and the obtained decoding accuracy was averaged over the five periods. Dependency of the decoding performance on the number of used cells was measured by random subsampling of the cells, as described above. The single-unit decoding accuracy refers to the accuracy obtained from the decoding using single units. To control the decoding performance for SUB high firing rate, spikes were randomly removed from SUB neurons as described above, before performing the decoding analysis.

Robustness of the decoding performance against noise was estimated by randomly removing (up to 99% of the number of spikes of the unit) or adding spikes to every unit at a fixed frequency over the entire recording session before performing the decoding procedure with all the simultaneously recorded CA1 or SUB units. The removal/addition procedure was repeated 100 times to obtain the decoding accuracy, averaged over the repetition. The normalized accuracy was obtained as the decoding accuracy values divided by the corresponding decoding accuracy without the spike removal/addition. Recording sessions containing less than five units were excluded from this analysis.

Trajectory-dependent firing in an alternating T-maze

Trajectory-dependent firing in the start box of the T-maze was analyzed. A trial comprised a wait period of ~8 s in the start box, running through the stem and left or right arm, reward acquisition at the end of the arm, and return to the start box. To estimate the strength of trajectory-dependent firing in the start box, we obtained the following parameters for each neuron using firing rates in the start box: trajectory information per spike (I_spike, bits/spike) and trajectory information per second (I_sec, bits/s), calculated by Eqs. 1 and 2, respectively, where i is the identifier of left or right choices, p_i is the proportion of choice i, λ_i is the mean firing rate in the start box for the subsequent choice i, and λ is the mean firing rate in the start box. Units with λ_i < 0.1 Hz for both left and right choices were excluded from the analysis. The rate change ratio was defined as |λ_L − λ_R| / max(λ_L, λ_R), where λ_L and λ_R are the firing rates in the start box averaged over left- and right-arm trials, respectively. The auROC (ranging from 0 to 1) was calculated to estimate the goodness of fit of the binary classifier (i.e., left- or right-arm trials) from the mean firing rates in the start box using the “perfcurve” function in MATLAB. For auROC values less than 0.5, 1 − auROC was assigned as the new auROC value, as the experimenter had no prior knowledge on the type of trials (left or right) that neurons showed a higher firing rate. We defined trajectory-dependent cells as neurons whose firing rates in the start box were significantly different between left- and right-arm trials (P < 0.05, Wilcoxon rank sum test). We used bootstrap analysis to determine whether a SUB projection neuron group contained a significantly higher proportion of trajectory-dependent cells (31).

Decoding of trajectory

Trajectory decoding was performed using a support vector machine algorithm and leave-one-out cross-validation, according to a previous study (5). From a given set of trials in the recording session, one trial was assigned as test data, and the remaining trials were used as the training dataset. A binary classifier was constructed to predict the next trajectory (left or right) from the firing rates in the start box, using the “fitcsvm” function in MATLAB, in which the input arguments were matrix F consisting of the firing rates of individual neurons (columns) in the training trials (rows) and vector y consisting of the trajectory label (−1, 1) of the training trials. Using the firing rates in the test trial as an input to the constructed classifier, the trajectory in the test trial was predicted. This decoding procedure was repeated to assign every trial as test data once, and the decoding accuracy was defined as the proportion of correctly predicted trials. Dependency of the decoding performance on the number of used cells was measured by random subsampling of the cells, as described above. The chance level of the decoding accuracy was estimated by a shuffling procedure repeated 100 times, by which trajectory labels were randomly shuffled before constructing the classifier. To control the decoding performance for SUB high firing rate, spikes were randomly removed from SUB neurons as described above, before performing the decoding analysis.

The robustness of the decoding performance against noise was estimated by randomly removing (up to 99% of the number of spikes of the unit) or adding spikes to every unit at a fixed frequency over the entire recording session before performing the decoding procedure with all the simultaneously recorded CA1 or SUB units. The removal/addition procedure was repeated 100 times to obtain the decoding accuracy averaged over the repetition. The normalized accuracy was obtained as follows: (decoding accuracy − 0.5)/(corresponding decoding accuracy without the spike removal/addition − 0.5). Recording sessions containing less than five units were excluded from this analysis.

Head-direction representation in an open field

We analyzed the head-direction tuning in the open field by constructing directional rate maps for individual cells. A directional rate map consisted of firing rates at 1° directional bins smoothed by Gaussian filter (σ = 5°). Units with a mean firing rate less than 0.1 Hz in the open field were excluded from the analyses. Directional information per spike (I_spike, bits/spike) and that per second (I_sec, bits/s) were calculated by Eqs. 1 and 2, respectively, where p_i is the proportion of time spent in the ith directional bin, λ_i is the firing rate in the ith directional bin, and λ is the mean firing rate in the open field. The chance level of I_sec was obtained by a session-wise shuffling procedure of spike timing against the rat’s position. A cell was defined as a head-direction cell if its I_sec value exceeded the 99th percentile of the I_sec value from the shuffled data obtained from all CA1 and SUB cells. Strength of directional tuning was measured with the mean vector length of head directions when spikes occurred. We performed memoryless Bayesian decoding of head direction (τ = 250 ms, 1° directional bins) similarly with place decoding in an open field. Decoding performance was estimated using fivefold cross-validation. The decoding error was obtained as the mean of the absolute angular differences between the decoded and observed head direction.

Behavioral states

Throughout the recording sessions, each second of behavior was classified into four states: RUN, REST, REM sleep, or SWS. This classification was carried out by visual inspection of the power spectra of SUB LFPs, SUB raw LFP traces, and electromyogram (EMG)–related signals extracted as correlations of LFPs in distant channels after filtering at 300 to 600 Hz (81). RUN states were defined as the periods during behavioral tasks with prominent theta oscillations and EMG-related signals. REST was defined as the awake, resting state detected during rest sessions without theta oscillations but with EMG-related signals. REM sleep was detected by the presence of robust theta oscillations and the absence of EMG-related signals during rest sessions. SWS was detected by the absence of both theta oscillations and EMG-related signals during rest sessions.

Theta oscillations

The power spectra density of LFP during RUN and REM periods was obtained using the Welch periodogram method (50% overlapping Hamming windows with a length of 2 s). Theta power was obtained as the mean power spectra density (in decibels) between 5 and 10 Hz. A recording site with maximal theta power approximately at the center of the SUB cell layer was used as the reference site to determine phase deviation and phase locking. Instantaneous theta phase was derived from the Hilbert transform of the bandpass-filtered (5- to 10-Hz) LFP trace (troughs = 0° and 360° and peaks = 180° throughout this study). Theta phase deviation was calculated as the mean circular distance of instantaneous theta phases between the reference recording site and the recording site of interest. Spike theta phase, i.e., the theta phase at which the spike occurred, was obtained for every spike. The preferred theta phase of each neuron was defined as the circular mean of the spike theta phases. PPC, a firing rate–insensitive measure of phase-locking strength, was calculated by

$$\text{PPC}=\frac{2}{N(N-1)}{\displaystyle \sum _{i=1}^{N-1}}{\displaystyle \sum _{j=i+1}^N}\{\text{cos} ({\mathrm{\theta }}_i) \text{cos} ({\mathrm{\theta }}_j)+\text{sin} ({\mathrm{\theta }}_i) \text{sin} ({\mathrm{\theta }}_j)\}$$

where N is the total spike number, and θ_i is the spike theta phase of the ith spike (46).

SPW-R–associated firing

Spike timing along SPW-Rs was examined during SWS and REST periods. The ripple-band LFP signal was obtained as the bandpass-filtered LFP signal (140 to 230 Hz) at the center of the SUB cell layer. Normalized ripple power was calculated as the z-scored moving average (window size, 11 samples) of squared ripple-band LFP signals. Periods with a normalized ripple power exceeding three were collected as candidate ripple events. Temporally close candidate events (<30-ms interevent intervals) were merged into single events. The candidate events with low peak normalized ripple power (<7), too short duration (<15 ms), or too long duration (>300 ms) were discarded, and the remaining events were defined as ripple events. Ripple timing was determined as the timing of the negative peak of the bandpass-filtered LFP signal (140 to 230 Hz) in each event. Ripple power was defined as the peak value of the normalized ripple power in each ripple event. Ripple duration was defined as the duration of the normalized ripple power exceeding three. Ripple frequency was defined as the frequency with maximal wavelet power between 140 and 230 Hz at the ripple timing. A peri-event time histogram (5-ms bins) was constructed for each ripple event for each cell, averaged across all events, and z-scored. The peak height for each neuron was defined as the mean z-scored peri-event time histogram between −10 and +10 ms. All data analyses were performed by custom-written MATLAB codes.

Statistical analysis

Statistical analysis was performed using MATLAB (MathWorks) and SPSS Statistics (IBM). All statistical tests were two-sided. Error bars indicate means ± SD unless otherwise noted.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/11/eabf1913/DC1

View/request a protocol for this paper from Bio-protocol.