Right Ventricular Myocardial Mechanics: Multi-Modal Deformation, Microstructure, Modeling, and Comparison to the Left Ventricle

Abstract

The right ventricular myocardium, much like the rest of the right side of the heart, has been consistently understudied. Presently, little is known about its mechanics, its microstructure, and its constitutive behavior. In this work, we set out to provide the first data on the mechanics of the mature right ventricular myocardium in both simple shear and uniaxial loading and to compare these data to the mechanics of the left ventricular myocardium. To this end, we tested ovine tissue samples of the right and left ventricle under a comprehensive mechanical testing protocol that consisted of six simple shear modes and three tension/compression modes. After mechanical testing, we conducted a histology-based microstructural analysis on each right ventricular sample that yielded high resolution fiber distribution maps across the entire samples. Equipped with this detailed mechanical and histological data, we employed an inverse finite element framework to determine the optimal form and parameters for microstructure-based constitutive models. The results of our study show that right ventricular myocardium is less stiff then the left ventricular myocardium in the fiber direction, but similarly exhibits non-linear, anisotropic, and tension/compression asymmetric behavior with direction-dependent Poynting effect. In addition, we found that right ventricular myocardial fibers change angles transmurally and are dispersed within the sheet plane and normal to it. Through our inverse finite element analysis, we found that the Holzapfel model successfully fits these data, even when selectively informed by rudimentary microstructural information. And, we found that the inclusion of higher-fidelity microstructural data improved the Holzapfel model’s predictive ability. Looking forward, this investigation is a critical step towards understanding the fundamental mechanical behavior of right ventricular myocardium and lays the groundwork for future whole-organ mechanical simulations.

Graphical abstract

1. Introduction

The right side of the heart has historically received little attention from the medical and scientific communities. This includes not only the famously dubbed “forgotten valve [1]– the tricuspid valve –, but also the “forgotten [2], “neglected [3], “unnecessary” [4], or “dispensable chamber [5]– the right ventricle. This unbalanced effort toward understanding right ventricular function and disease has in part been due to early reports that proposed that substantial damage to the right ventricle did not significantly affect global hemodynamics [6, 7, 8]. Its anatomic location below the sternum and away from the esophagus, smaller wall thickness, and complex, crescent-shaped geometry have further inhibited its study by complicating imaging [9, 10]. Of course, we now appreciate that a healthy right ventricle is essential to a healthy cardiovascular system as exemplified in patients with pulmonary hypertension [11], myocardial infarction [12], and left ventricular dysfunction [13]. Furthermore, during the present COVID-19 pandemic, we are reminded of the right ventricle’s vital importance because the right ventricle appears to be disproportionately negatively affected in COVID-19 patients [14]. However, due to the historic neglect and the challenges associated with imaging, relatively little is known about the right ventricle.

Gaps in our knowledge about right ventricular micro- and macro-structure, kinematics, and kinetics cannot be filled by extrapolating from what is known about the left ventricle. This is because the two ventricles, albeit connected, are distinct anatomic entities. Aside from differences in location, thickness, and shape, the right ventricular myocardium has a different microstructural organization [15]. Specifically, myocardial fibers have been reported to run primarily in the circumferential direction [16]. Additionally, right ventricular cardiomyocytes may be of a different phenotype than their left-sided equivalents [17]. A sensible starting point for understanding the right ventricle and its function is to study its passive constitutive behavior; that is, to study the tissues mechanical response to deformation. Examples of noteworthy exceptions to the general neglect of right ventricular myocardial mechanics are the studies on right ventricular free wall mechanics in large animals under planar conditions [18] and under diverse loading modes but in immature animals [19] as well as the recent studies in a murine model by Sacks’ group [20, 21, 22].

Despite the differences between the left and right ventricle, we can learn from left ventricle research as we fill the gaps in right ventricle research. For example, studies on left ventricular constitutive behavior have created a comprehensive framework for myocardial tissue characterization that we will draw from in our current work. This previous work on left ventricular myocardial constitutive behavior differs in four essential aspects: i) the mechanical testing modes, ii) the form of the constitutive law, iii) the fitting procedures, and finally, iv) the inclusion of microstructural information. As to the deformation mode, while myocardium has previously been tested under planar conditions [23], those tests do not fully capture the natural deformation modes of the tissue that are dominated by shear. Thus, Dokos et al. in their seminal work performed the first simple shear experiments of left ventricular myocardium [24]. Recognizing the orthotropic nature of the material, they performed a total of six shear experiments on porcine tissue. Shear experiments have since become standard and have been repeated by Sommer et al. on human tissue [25]. With the exception of the work by Sacks et al., who have developed a complex shear device to perform experiments with non-traction-free boundary conditions, this class of experiments have implemented simple shear [26]. Shear data from Dokos et al. [24], Sommer et al.[25], and Avazmohammadi et al.[26] were subsequently fit with multiple different constitutive models. Among those models, the Holzapfel model has emerged as the de facto standard [27, 28, 29, 30], with the Guccione model as a popular alternative [31, 32, 33]. In order to identify the material parameters of these constitutive models, most previous studies employed gradient-based methods to minimize objective functions via homogeneous, analytical solutions to the simple shear problem. However, simple shear is not so simple, and thus inverse finite element methods are required to accurately capture the heterogeneous solution to a simple shear problem with traction free inclined edges [34]. Accordingly, Schmid et al. and Avazmohammadi et al. performed inverse finite element analyses to determine the parameters for their constitutive models of interest [35, 26]. Finally, myocardium is a highly heterogeneous tissue. Inclusion of material heterogeneity in previous work has ranged from ignoring it all together to detailed inclusion based on sample-specific characterization of tissue microstructure via 2-Photon imaging [25] or diffusion-tensor imaging [36].

Inspired by these previous works on the right and left ventricles, the objective of our current work is to further study the passive mechanics of right ventricular myocardium. Specifically, our work will add to these previous studies by reporting detailed, spatially-resolved mechanical and histological data, and by combining these data to test and inform different constitutive assumptions and models for right ventricular myocardium.

2. Methods

2.1. Animal model procedures

We performed all animal-related procedures according to the Principles of Laboratory Animal Care by the National Society for Medical Research and followed the Guide for Care and Use of Laboratory Animals by the National Academy of Science and published by the National Institutes of Health. Furthermore, this protocol was approved by our local Institutional Animal Care and Use Committee (IACUC #: 17–05).

We included right and left ventricular myocardial tissue samples from twelve healthy, male, Dorsett sheep in our study. At the time of sacrifice the animals were approximately six months old and weighed 61 ± 3 kgs (mean ± SD). We sacrificed the animals via injection of sodium pentothal (100 mg/kg IV) and a potassium chloride bolus (80 mEq IV) before placing the whole hearts in physiological solution supplemented with a myosin inhibitor (2,3 Butanedione monoxime) to minimize the risk of rigor mortis. Immediately after excising the hearts, we shipped the tissue from our procurement site overnight to our testing facility on ice. Upon receipt, we placed the hearts in 4° chilled Fomblin and performed a 60 minute-long whole-heart MRI protocol (data not included here). Then, we prepared the test samples by identifying areas of the right and left ventricular free wall that were at least 8mm thick and equally far from the base, the apex, and the interventricular septum. Using a surgical blade, we removed an approximately cube-shaped sample whose principal axes aligned with the transmural (N), the fiber (F), and longitudinal (S) directions, see Figure 1A. Once the excision was completed, we measured the sample dimensions using a digital caliper. Note, we used differently colored sutures on two of the sample edges to uniquely identify the samples’ orientation throughout our experimental protocol. Next, we glued the cubes in their first orientation to sample holders and mounted the sample complex (sample plus holders) to our custom mechanical testing machine.

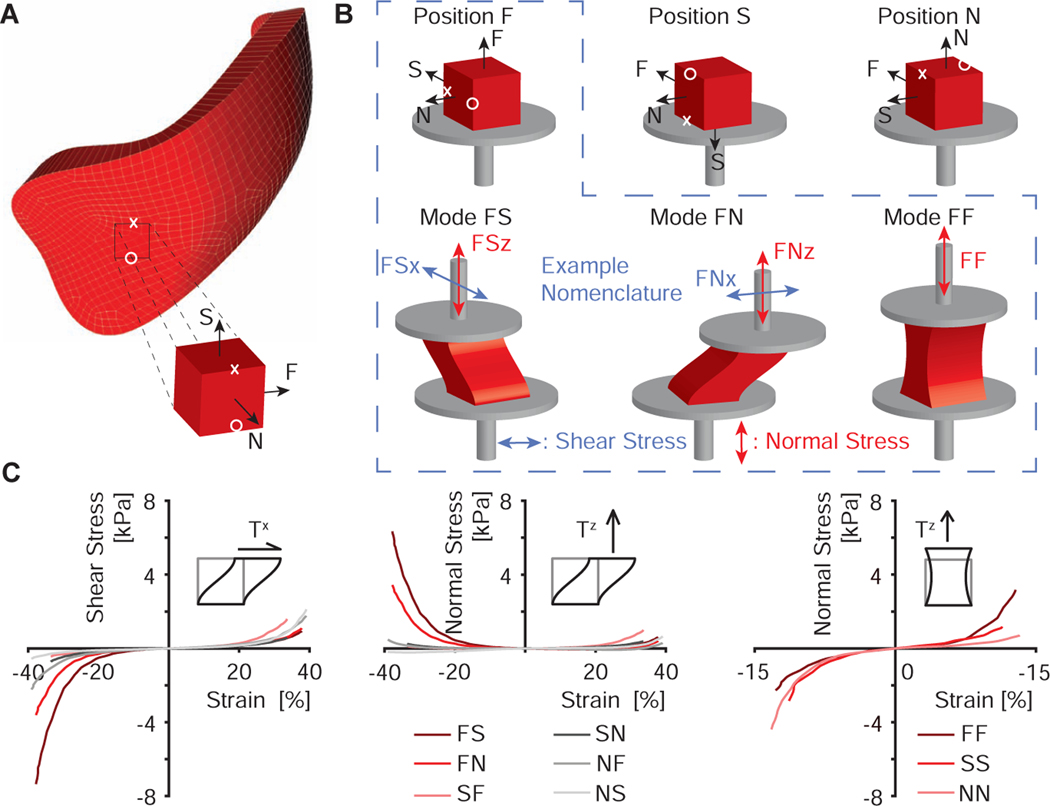
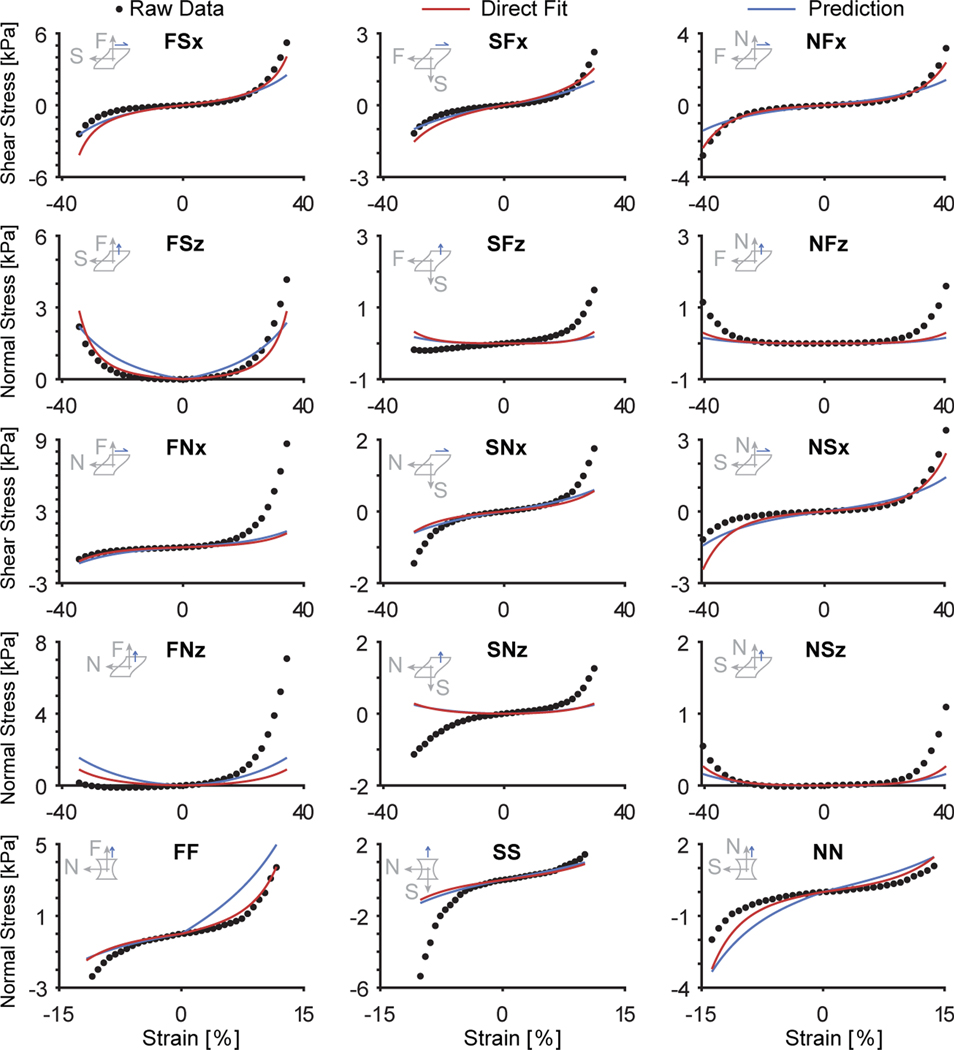
Figure 1:

Triaxial shear experiments of right ventricular myocardium. (A) Approximate anatomic location from which the samples were excised, where Fiber-Sheet-Normal (FSN) reference frame describes the anatomic directions of each sample. (B) Nomenclature for sample orientation and measurement directions. During simple shear experiments, we simultaneously measured forces, i.e., stress, in shear direction (x) and normal direction (z). Under uniaxial tension and compression, we only report stress in normal direction. In total, we conducted nine unique tests for each sample via three tests modes in three different orientations. (C) Examples for stress-strain curves for one selected sample

2.2. Simple shear and tensile/compression testing

During testing, we performed simple shear experiments in both in-plane directions as well as uniaxial tensile/compression tests, all at rates of 1mm/s. The strain magnitude varied between samples as a function of the original sample size between 28 and 57% shear strain, and from 9 to 27% normal strain for uniaxial tensile/compression tests of the right ventricular samples. The corresponding magnitudes for the left ventricular samples ranged between 10 and 51% shear strain, while the normal strain varied from 5 to 21%. All test conditions are also illustrated in Figure 1B. After one testing round was completed, we removed the sample complex, carefully dissected the tissue from the holders, and re-glued the same sample in a different orientation. Upon re-orientation of the sample, we repeated the same testing protocol. Finally, we removed the sample again, and re-orientated and re-glued the sample to perform the final testing cycle. Note, before every test, we preconditioned the samples to at least 5 cycles, see Figure 1C for a representative data set. Also note, that we permuted the order of the orientations in which we tested the samples to avoid a time/direction-dependent bias. Throughout testing, samples remained submerged at 37°C in the physiological shipping solution with myosin inhibitor. The total protocol took less than 90 minutes per sample.

2.3. Histology and microstructural organization

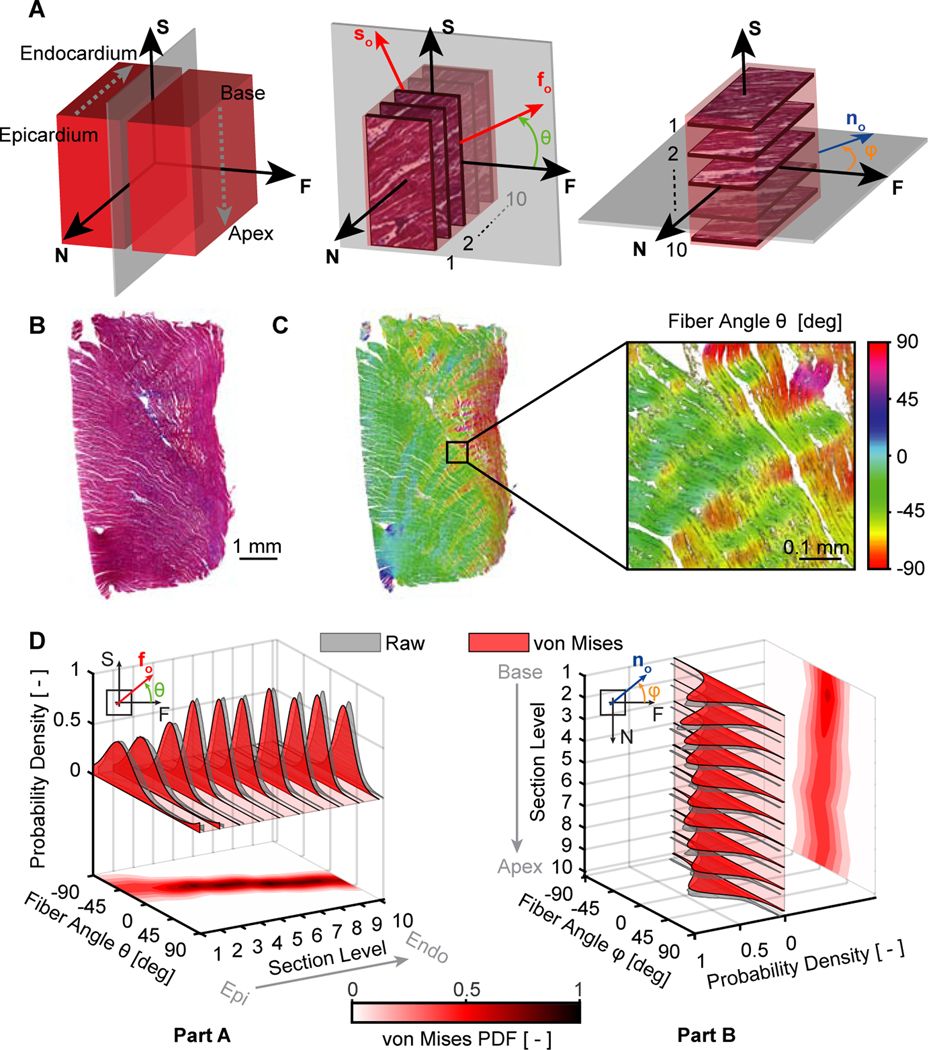
After concluding all mechanical tests, we removed the tissue from the holders, carefully inspected the samples, and removed all remaining glue residue. For histological preparations of right ventricular samples, we fix the tissue in formalin, and subsequently shipped all samples in 70% alcohol to a commercial histology service (Histoserv Inc., MD, USA) that divided the samples into two equal parts via separation along the plane normal to the fiber direction. For both tissue parts, they prepared Massons trichrome stains in ten sections. For the first part, they sectioned the samples from the epicardial side to the endocardial side, i.e., transmurally. For the second part, they sectioned the samples from the basal side to the apical side, i.e., longitudinally, see Figure 2A. Please note that one histological data set was not usable. Therefore, histological data and histology-based models are available only for n = 11 samples.

Figure 2:

Histology-based microstructural analysis of right ventricular myocardium. (A) We divided each sample into two parts along a plane normal to the fiber direction. We sectioned the first part in ten 1mm-steps in the transmural direction, and we sectioned the second part in ten 1mm-steps along the basal-apical direction, i.e, longitudinally. (B) Representative example of a histological section stained with Masson’s trichrome. (C) Identification of fiber orientation distributions via ImageJ’s OrientationJ plugin, where the color scale represents the in-plane fiber angle with respect to the horizontal axis. (D) We also fit π-periodic von Mises probability density functions (PDF) to the OrientationJ-derived normalized pixel occurrence per fiber angle for each section in both sample parts

Next, we acquired high resolution images of each stain and quantified the fiber orientation distribution for all sections via ImageJ’s OrientationJ plugin [37], see Figure 2B–C. In order to approximate the fiber distribution as a probability density function, we used non-linear least squares regression to fit the π-periodic, 2D orthotropic von Mises distribution [38],

$$R(\theta \text{ or }\varphi )=\frac{\exp (b\cos (2[\theta \text{ or }\phi -\mu ]))}{2\pi I_o(b)},$$ (1)

where θ is the fiber angle in the sheet-plane (FS-plane) and ϕ is the fiber angle normal to the sheet-plane (NF-plane), I_o the modified Bessel function, and μ and b are the von Mises location and concentration parameters, respectively. We repeated this process for each transmural and longitudinal section and subsequently interpolated the distribution functions throughout each samples’ thickness and height, see Figure 2D for this process on a representative sample.

2.4. Constitutive modeling

We modeled the right ventricle tissue as a nearly incompressible hyperelastic material according to Holzapfel et al. [27]. This strain energy function is based on the microstructural characteristics of myocardial tissue with strain energy terms accounting for the fibrous constituent of the myocardium (ostensibly muscle and/or collagen fibers), the contribution of the amorphous matrix, and their coupling interactions. Based on goodness of fit studies with an eight parameter version and a twelve parameter version of the Holzapfel model, we chose the eight parameter model because the twelve parameter model rendered only marginal improvements, see Supplementary document. Finally, as we describe in Section 2.4.2, we extended this model by including muscle fiber dispersion in the sheet-plane to take advantage of our microstructural data.

In each case below, we decompose the deformation gradient F into a volumetric, J^1/3I, and isochoric part, $\overline{F}=J^{-1/3}F$. The corresponding deviatoric right Cauchy-Green deformation tensor thus reads $\overline{C}={\overline{F}}^T\overline{F}$. The total strain energy function W constitutes the isochoric, W_iso, and the volumetric part, U [39], i.e.,

$$W(\text{C})=W_{\text{iso}}+U(J),$$ (2)

where U(J) = K [ln(J)]² /2 with K being the bulk modulus and J = det(F) [40].

We will test two general classes of material models. The first class, Class 1, represents the tissue microstructure via mean fiber direction vectors only. The second class, Class 2, accounts for dispersion of fibers around the mean fiber direction.

2.4.1. Model Class 1: Holzapfel model without fiber dispersion

Based on the (undeformed) mean fiber direction of the tissue, we defined the orthonormal material axes (f_o,s_o,n_o) where f_o is the in-plane fiber vector, s_o is the sheet-plane vector and n_o is the normal vector to the f_o − s_o plane, see Figure 2A. We assumed the normal vector to be aligned with the transmural direction and, thus, normal to the epicardial surface. Considering the uncoupled formulation of the strain energy, we can write the following isochoric invariants as [27, 36]

$${\overline{I}}_1=\overline{\mathbf{C}}:\mathbf{I};{\overline{I}}_{4f}={\mathbf{\text{f}}}_o\cdot {\overline{\mathbf{\text{C}}}\mathbf{\text{f}}}_o;{\overline{I}}_{4s}={\mathbf{\text{s}}}_o\cdot {\overline{\mathbf{\text{C}}}\mathbf{\text{s}}}_o;{\overline{I}}_{8fs}={\mathbf{\text{f}}}_{\mathbf{\text{o}}}\cdot \overline{\mathbf{\text{C}}}{\mathbf{s}}_o,$$ (3)

while the isochoric part of the strain energy is

$$W_{i\text{SO}}=W_g+W_f+W_s+W_{fs},$$ (4)

with the following individual terms

$$\begin{array}{l}{W}_g=\frac{a}{2b}\left[\exp \left(b\left[{\overline{I}}_1-3\right]\right)-1\right]\\ W_f=\frac{a_f}{2b_f}\left[\exp \left(b_f{\left[{\overline{I}}_{4f}-1\right]}^2\right)-1\right]\\ W_s=\frac{a_s}{2b_s}\left[\exp \left(b_s{\left[{\overline{I}}_{4s}-1\right]}^2\right)-1\right]\\ W_{fs}=\frac{a_{fs}}{2b_{fs}}\left[\exp \left(b_{fs}{\overline{I}}_{8fs}^2\right)-1\right].\end{array}$$ (5)

Of the total eight material parameters, the a’s are expressed in units of stress and the b’s are dimensionless. Fibers (W_f and W_s terms) contribute to the strain energy function only under tension or equivalently when Ī_4f > 1 or Ī_4s > 1. Note, the W_fs term effectively couples the material behavior in fiber and sheet direction as discussed in [41]. We implemented this form of the Holzapfel model in FEBio by utilizing the FEBio plugin development framework (FEBio, Version 2.9.1) [42].

2.4.2. Model Class 2: Holzapfel model with fiber dispersion

To expand the assumption of a single fiber vector capturing the microstructural organization of the tissue, we modified the initial constitutive models (Model Class 1) to also include fiber dispersion about the mean fiber direction. Thus, we include fiber dispersion via continuous fiber distributions (CFD). Note, the parameters of these functions were directly informed by fits to our histological data, see Section 2.3. To this end, the updated form of the strain energy function reads

$$W_{\text{iso }}=W_g+W_f^{CFD}+W_s+W_{fs},$$ (6)

where every term remains as stated in Section 2.4.1, except for the new term, $W_f^{CFD}$ which reads [43, 44]

$$W_f^{CFD}=\underset{S}{{\displaystyle \int }}H\left({\overline{I}}_{4f}-1\right)W_f^{\ast }R(n)\text{d}A,$$ (7)

With

$$W_f^{\ast }=\frac{a_f}{2b_f}\left[\exp \left(b_f{\left[{\overline{I}}_{4f}-1\right]}^2\right)-1\right].$$ (8)

In Equation (7), H is the Heaviside step function that enforces fibers contributing to the stored energy only if Ī_4f > 1. In addition, R(n) captures the fiber dispersion according to a 2D von Mises distribution within the sheet-plane only). The function R(n) is normalized so that ∫_SR(n)dA = 1. To integrate Equation (7), we used a common trapezoidal integration scheme with n_θ = 31 integration points over the unit circle.

2.5. Microstructure-inclusion strategies

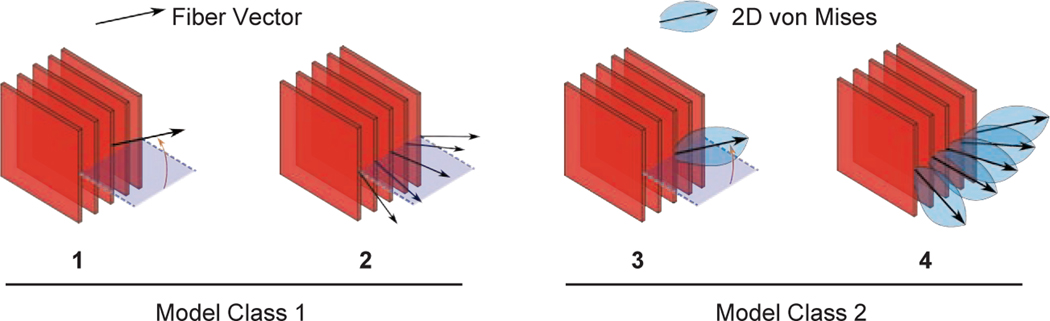
In addition to our investigation of the two model cases, we considered multiple different strategies for including microstructural information. In total we considered four different constitutive approaches which differed in their inclusion of transmural heterogeneity and assumptions about fiber distribution parameters, see Figure 3. A summary of the different cases is as follows:

Figure 3:

Microstructure-inclusion strategies. In Strategies 1–2 we used the model version without fiber dispersion (Model Class 1). In Strategies 3–4 we account for the fiber dispersion that we informed with histological data (Model Class 2)

Cases without fiber dispersion (Model Class 1):

• Strategy 1: Identical fiber angle throughout the thickness based on the histology-derived average data across all sections

• Strategy 2: One fiber angle per section based on the histology-derived average data for each section individually

Cases with fiber dispersion (Model Class 2):

• Strategy 3: Identical fiber angle and 2D distribution throughout the thickness based on the histology-derived data across all sections

• Strategy 4: One fiber angle and 2D distribution per section based on the histology-derived average data for each section individually

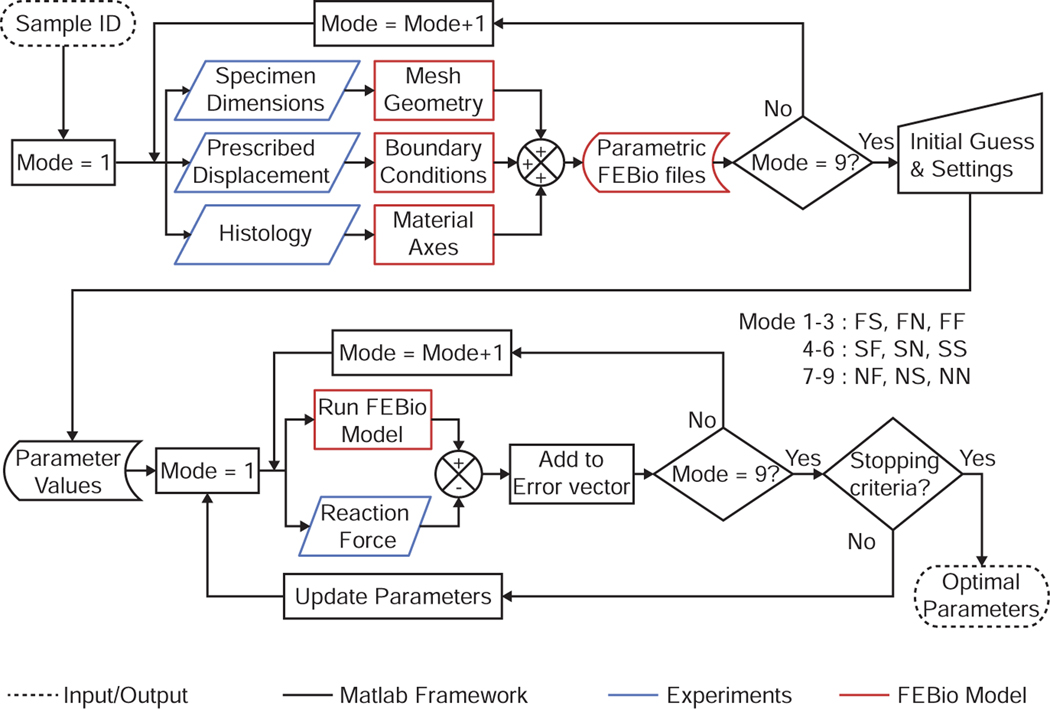
2.6. Inverse analysis

To identify the material parameters for each sample, we developed a custom inverse analysis pipeline using MATLAB (Mathworks, Version 2019) and FEBio [40], see Figure 4. Specifically, we performed a non-linear regression analysis via a trust region reflective algorithm (lsqnonlin function in MATLAB [45, 46]) to minimize following objective function:

$$\min Z(c)={\displaystyle \sum }_i^{mode}{\displaystyle \sum }_j^{\text{force}}{\displaystyle \sum }_k^n{\left|f_{\text{fem}}\left(s_k,c\right)-f_{\exp }\left(s_k\right)\right|}_{i,j}^2$$ (9)

$$\begin{array}{l}mode=\{\begin{array}{ll}1-3:& \text{FS},\text{FN},\text{FF}\\ 4-6:& \text{SF},\text{SN},\text{SS}\\ 7-9:& \text{NF},\text{NS},\text{NN}\end{array},\\ force=\{\begin{array}{ll}x,z:& \text{Simple shear modes}\\ z:& \text{Uniaxial tension/compression modes}\end{array},\end{array}$$

where c represents the material parameter set, i refers to the loading mode index, j to the force, and s_k to the displacement points (n = 100). The gradient of the objective function was evaluated numerically using forward finite differences, where each function evaluation corresponds to a finite element forward simulation of the test problem in FEBio. We evaluated the quality of our constitutive fit by computing the normalized mean square error written as:

$$e{\left(c^{\ast }\right)}_{\text{NMSE}}=1-\frac{Z\left(c^{\ast }\right)}{{{\displaystyle \sum }}_i^{mode}{{\displaystyle \sum }}_j^{\text{force}}{{\displaystyle \sum }}_k^n{\left|f_{\exp }\left(s_k\right)-{\overline{f}}_{\exp }\right|}_{i,j}^2},$$ (10)

where c* is the optimal set of material parameters and ${\overline{f}}_{\exp }$ is the mean force over all modes and data points. According to the definition in Equation 10, e = 1 represents a perfect fit, with the poorest fit quality being e →−∞.

Figure 4:

Inverse finite element analysis pipeline

For each forward simulation, we built a finite element model for each test mode, test position, and sample. The sample geometry was approximated as a rectangular prism with dimensions corresponding to the experimental measurements described in Section 2.1. Next, we discretized the geometry isotropically via mixed linear hexahedral (Q1P0) elements. We aligned the material axes of each element with our histologically-derived, or estimated (depending on the model assumptions), fiber direction vectors. For the boundary conditions, we fixed the displacements of the bottom surface and attached the top surface to a rigid body, representing the moving parts of the testing device. Additionally, we prescribed the motion of the rigid body (actuator) as a shear- or uniaxial translation and constrained the remaining five degrees of freedom. Following a mesh refinement study based on the peak values of the rigid body reaction force and strain energy density for every loading mode, we discretized our do main with 10³ elements and enforced incompressibility via the penalty method. See Figure 5 for representative finite element model simulation results. Additional studies of framework sensitivity to initial parameter guess, mesh density, bulk modulus, element type, and incompressibility enforcement strategy are included in the Supplementary document. Note, recent work has indicated that the use of the deviatoric split when modeling incompressible materials may lead to non-physical volume growth [47, 48, 49]. We specifically investigated this phenomenon in our framework and found no evidence thereof, see also the Supplementary document for additional detail.

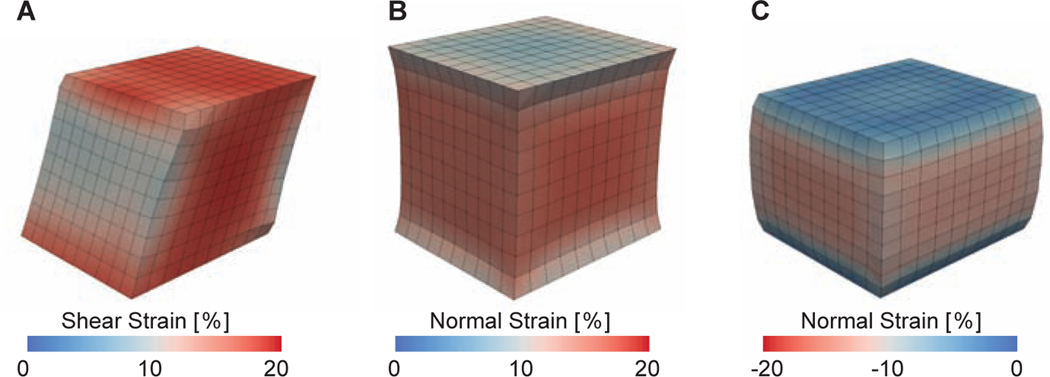
Figure 5:

Representative finite element simulation outcomes for (A) a simple shear mode, (B) a tensile mode, and (C) a compressive mode. Color corresponds to Green-Lagrange strains

2.7. Statistics

All data are reported as means ± standard error. Where we statistically compared multiple groups, we employed a linear mixed model as implemented through the afex package in R and declared tests with p-values smaller than 0.05 as statistically significant [50]. In the linear mixed model, we accounted for fixed main effects and interactions as well as random effects due to subject. If we found a statistical difference among groups, we performed multi-comparison via Tukey post-hoc analyses, also in R. The only exception to our use of linear mixed models was when we identified whether normal stress under simple shear were larger or smaller than zero to determine whether positive or negative Poynting effects were present. To this end, we used a simple Student’s t-test as implemented in Excel (Microsoft, Version 2016).

3. Results

Note, all mechanical raw data and histological imaging data are available through the Texas Data Repository as per Section 6.

3.1. Right ventricular myocardium shows strain-stiffening, anisotropy, Poynting effect, and tension-compression non-linearity

In Figure 6, we present the mean stresses among our n=12 right ventricular myocardium samples (red) with their respective standard errors. We found that the tissue response was highly non-linear and anisotropic.

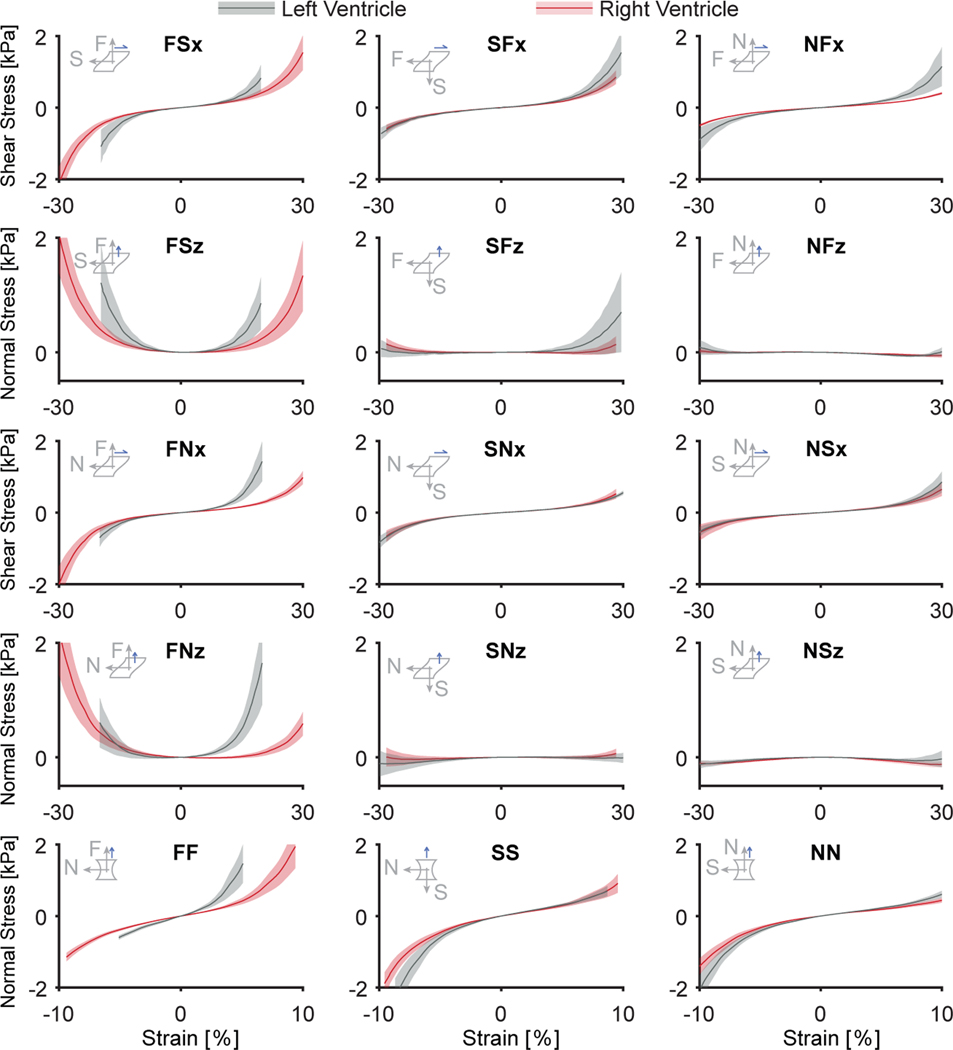
Figure 6:

Right ventricular myocardium demonstrates non-linear, strain-stiffening, and anisotropic behavior and is less stiff than left ventricular myocardium. Average stress-strain data for n = 12 right ventricular myocardium samples are shown in red, while average stress-strain data for n = 11 left ventricular myocardium samples are shown in grey for all test modes. Shaded areas represent the standard error among samples

Specifically, we found that the material was anisotropic (p < 0.0001), by determining that the shear stress in the FS mode, FSx, was higher than the shear stress in the NF, NS, SF, and SN modes, i.e., NFx, NSx, SFx, and SNx (all p < 0.01), and that the shear stress in the FN mode, FNx, was higher than in the NF, NS, SF, and SN modes, i.e., NFx, NSx, SFx, and SNx (all p < 0.05), see also Figure 7A. The normal stress in response to simple shear also indicated an anisotropic material response (p < 0.0001). Specifically, we observed the highest normal stresses for the F modes, FSz and FNz, and both were different from the other normal stresses under all other modes (p < 0.005 for all), see Figure 7B. Note, for these comparisons we evaluated stress for all modes at ±28.2% strain in shear. Further note that in our numeric results, a positive normal stress implies that the shear sample was trying to pull the sheared surfaces together rather than spread them apart. When sheared in the fiber modes FS and FN, the normal stresses, FSz and FNz, were statistically significantly larger than zero (p < 0.05). Thus, right ventricular myocardium exhibited a negative Poynting effect when the fibers were activated under shear [51]. On the other hand, when sheared under the other modes that do not correspond to the dominant fiber direction, normal stresses where either not different from zero (SFz, SNz, NFz, p > 0.05 for all), or smaller than zero (NSz, p < 0.05), i.e. the material exhibited positive Poynting effect.

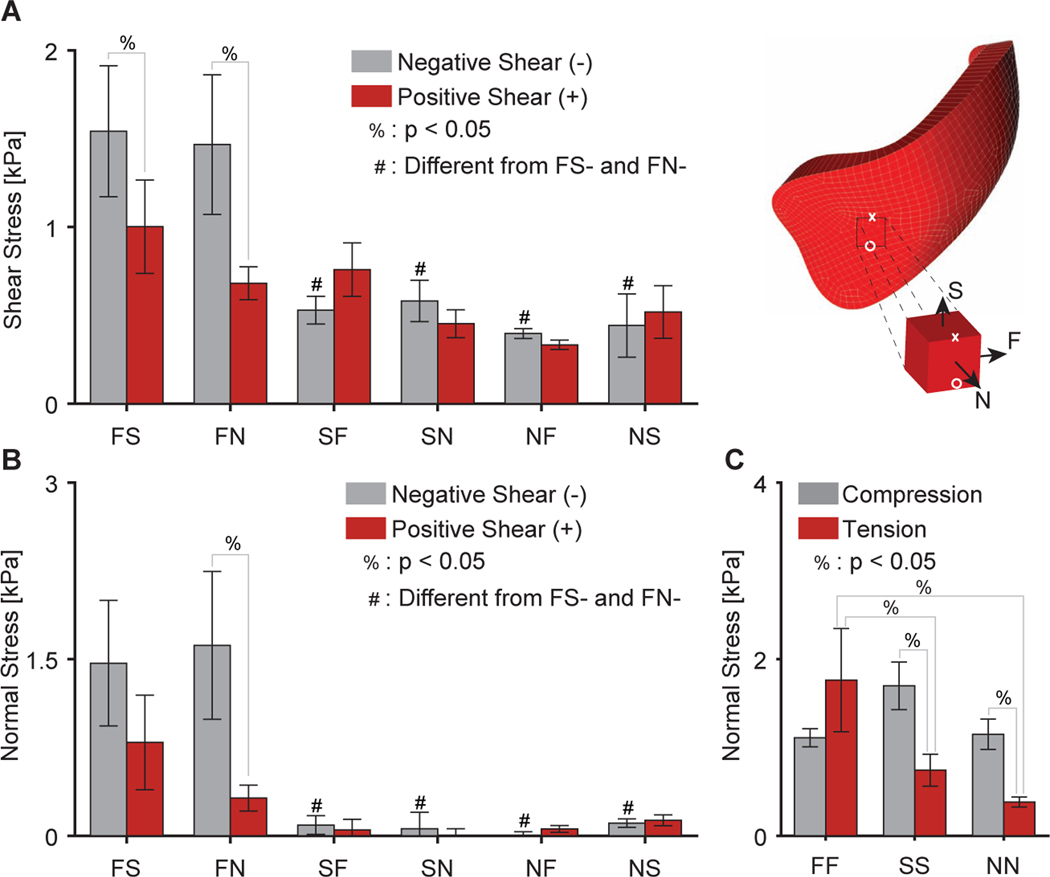
Figure 7:

Summary of differences in (A) shear stress and (B) normal stress of right ventricular myocardium under simple shear and (C) normal stress under uniaxial tension/compression. Note, stresses were evaluated for n = 12 samples at ±28.2% in shear and ±9.4% in tension/compression. Further note, that stresses are shown by their magnitude

When comparing between the tensile modes at 9.4% strain we, again, found that the material was anisotropic (p=0.023). The right ventricular myocardium demonstrated larger stresses in the FF mode than in the SS and NN modes (p = 0.011 and p = 0.001, respectively), see Figure 7C. On the other hand, comparing the compressive modes at −9.4% strain did not reveal any statistically significant anisotropy. While, we did not observe a statistically significant difference in direction-dependence as a main effect, i.e., tension-compression non-linearity (p = 0.076), we found a significant interaction between anisotropy and load-direction (p = 0.002). And, once corrected for material anisotropy, the material exhibited tension-compression non-linearity. Specifically, the material demonstrated higher stresses under compression than under tension in the SS and NN modes (p = 0.007 and p = 0.028). In the FF mode, the material showed higher stresses in tension than in compression. However, these differences did not reach statistical significance (p = 0.061).

3.2. Right ventricular myocardium is less stiff than left ventricular myocardium in the fiber direction

In Figure 6, we also present the mean stresses comparing n=12 right ventricular myocardium samples (red) with n=11 left ventricular myocardium samples (grey). Qualitatively, the right and left ventricular myocardium mechanical response was similar. However, there were marked quantitative differences between the two. First, our statistical analysis revealed a strong difference in shear stress between samples from the right and left ventricles (p < 0.001). Differences were drive primarily by lower stresses in the right ventricular myocardium than in the left ventricular myocardium when sheared in the FS mode, i.e., FSx, and FN mode, i.e., FNx (p = 0.045 and p < 0.0001, respectively). Similarly, normal stresses under simple shear also differed significantly between the right and left ventricular myocardium (p < 0.01). Specifically, these differences were due to the right ventricular myocardium producing lower normal stresses in the FN mode, i.e., FNz (p < 0.0001), and the FS mode, i.e., FSz (p < 0.05). The myocardium from both ventricles also differed in the uniaxial direction (p = 0.003), where differences were driven by a lower stresses of the right ventricular myocardium in the FF mode (p < 0.0001) but not the other modes. Note, stresses between right ventricular and left ventricular myocardium where compared at 19.7% shear strain and ±5% tensile/compressive strain.

3.3. Right ventricular myocardium fibers are dispersed in the sheet-plane and in the plane perpendicular to the sheet-plane

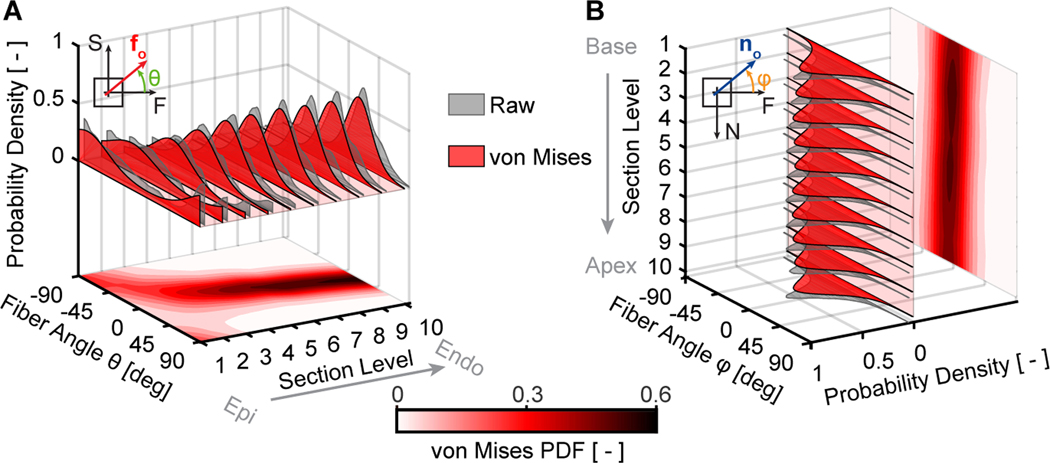
Figure 8 illustrates the results of our microstructural analysis averaged among n=11 right ventricular myocardial samples. Figure 8A illustrates the fiber dispersion transmurally. We found that fibers were dispersed according to a single-mode probability function (grey) that was well represented by a von Mises distribution (red). The mean fiber direction shifted from approximately −76.4° degrees at the epicardial side, to +22.9° degrees at the endocardial side. In other words, fibers were oriented approximately longitudinally at the epicardial surface and approximately circumferentially at the endocardial surface. In addition, the dispersion spread was the largest at the epicardial side (von Mises concentration parameter b = 0.8) and decreased toward the endocardial side (b = 2.5).

Figure 8:

Right ventricular myocardium has a spatially heterogeneous microstructure with dispersed organization within the sheet-plane and the plane perpendicular to the sheet-plane. (A) Average within sheet-plane fiber angle distributions among n=11 right ventricular myocardium samples based on Masson’s trichrome staining throughout the samples’ thickness, i.e., transmurally. (B) Average perpendicular-to-the-sheet-plane fiber angle distribution among the same samples throughout the basal-apical sample direction, i.e., longitudinally

Figure 8B illustrates the fiber dispersion in the plane perpendicular to the sheet plane. Interestingly, we found that similar to the sheet-plane, fibers were not perfectly aligned. Specifically, fibers were dispersed and could be well-represented by a von Misses distribution. However, in contrast to the fiber dispersion within the sheet-plane, the dispersion in the plane perpendicular to the sheet-plane did not shift between sections and was consistently centered around 0°. The von Mises concentration parameter, a measure of the fiber dispersion spread, was comparable to the concentration parameters of the within sheet-plane dispersion (on average b = 1.9).

3.4. Right ventricular myocardial mechanics are well represented by the Holzapfel constitutive model

In Table 1, we present the goodness of fit for all samples and all microstructure-inclusion strategies. All four microstructure-inclusion strategies yielded satisfying fits, see Figure 9 for an example. For the readers convenience, we scaled the NMSE from the value of 1 for the worst fit (minimum NMSE) to the value of 10 for the best fit (maximum NMSE). We achieved the best average scaled score with microstructure-inclusion Strategy 2 that is the model that represents the samples’ spatially heterogeneous microstructure with transmurally-varying fiber direction vectors, but without fiber dispersion. On the other hand, we observed the lowest average score for Strategy 1, which models the samples’ microstructure via only one mean fiber direction without dispersion. However, these findings should be treated with caution as the differences between the best and worst fits were marginal as indicted by the similarity between the minimum and maximum NMSE as listed in the last two columns of Table 1.

Table 1:

Quality of constitutive parameter fits for all samples and microstructure-inclusion strategies (see Figure 3). We scaled the goodness of fit from 1.0 (worst fit among the strategies) to 10.0 (best fit among the strategies). The last two columns display the best and worst Normalized Mean Square Error (NMSE) among the strategies. A higher NMSE value implies a better fit with an upper limit of NMSE=1

		Strategy			NMSE
Sample	1	2	3	4	min	max
1	1.0	3.2	10.0	9.3	0.913	0.932
2	1.0	10.0	8.4	5.8	0.852	0.901
3	6.1	4.6	10.0	1.0	0.858	0.868
4	10.0	9.9	1.0	3.0	0.636	0.734
5	10.0	9.6	9.1	1.0	0.713	0.761
6	1.0	1.2	10.0	1.3	0.750	0.765
7	1.0	9.3	4.9	10.0	0.692	0.781
8	7.1	10.0	1.0	4.7	0.642	0.683
9	1.0	4.1	3.5	10.0	0.569	0.582
10	1.0	6.0	8.7	10.0	0.799	0.893
11	10.0	9.8	1.5	1.0	0.813	0.835
Mean	4.5	7.1	6.2	5.2
SE	1.3	1.0	1.2	1.2

Figure 9:

Mechanics of right ventricular myocardium can be accurately predicted based on microstructural data. Shown are raw data for a selected sample, which also serves as the “test data” (black circles). The red line shows a direct, or optimal, constitutive fit via Strategy 4, that is using the Holzapfel model that accounts for spatial variation in histology-informed fiber dispersion through the sample’s thickness. Note, this fit quality is typical in that it falls between the best and worst fits. We also show a prediction based on constitutive parameters that were informed via training on the other ten samples and the microstructural data from the sample itself

3.5. Right ventricular myocardial microstructure cannot be easily predicted from mechanical response alone

It would be convenient to estimate microstructural information from mechanical tests alone. For example, it would be convenient to estimate microstructural data in-vivo via inverse methods. To evaluate our ability to accomplish this, we used our comprehensive set of mechanical data and our inverse pipeline. Specifically, in microstructure-inclusion Strategy 3, we assumed the microstructural parameters were unknown. Thus, in addition to fitting the eight parameters of the constitutive law, we also fit the the 2D von Mises distribution parameters mu and b. Table 2 summarizes our findings. In short, there are significant discrepancies between microstructural parameters derived from histology (ground truth) and those estimated through our inverse approach.

Table 2:

Estimation of microstructural information from mechanical data alone (Est.) and comparison to histology-based measurements (Exp.). Using microstructure-inclusion Strategy 3, we inversely identified not only the eight parameters of the material model, but also the mean fiber direction (μ) and concentration parameter b of the π-periodic 2D von Mises distribution

	μ (°)		b		NMSE
Sample	Exp.	Est.	Exp.	Est.	Exp.	Est.
1	55.7	−35.5	0.86	7.17	0.932	0.942
2	−5.9	−12.3	1.22	2.03	0.892	0.912
3	41.7	−32.8	1.24	0.04	0.868	0.896
4	6.4	6.2	1.07	26.65	0.636	0.736
5	−15.5	−9.4	2.30	5.20	0.756	0.775
6	−5.0	13.7	2.50	4.06	0.765	0.856
7	1.7	24.0	4.56	4.99	0.730	0.884
8	−15.6	2.3	0.90	2.96	0.642	0.675
9	−1.3	39.2	2.18	99.90	0.572	0.674
10	3.7	11.5	2.01	3.39	0.879	0.919
11	18.2	14.8	8.18	99.26	0.814	0.838

3.6. Right ventricular myocardial mechanics can be reliably predicted from microstructural data

After finding that all microstructure-inclusion strategies provided satisfying fits to the experimental data, we set out to identify the inclusion strategy with the best predictive ability [52, 53]. To this end, we modified our pipeline to simultaneously estimate the material parameters for ten randomly chosen samples (the “training set”). We repeated these fits for all microstructure-inclusion strategies. Subsequently, we compared their ability to predict the constitutive behavior of the eleventh, unseen sample (the “test set”).

We found that training based on ten samples led to excellent fits on the unseen data, see Table 3. We achieved fits with NMSE ranging from 0.500 to 0.515. These values correspond to 84.8% and 88.5% of the NMSE from the best individual or direct fit for this sample, see Figure 9 as an example. Compellingly, a clear pattern emerged: the more sample-specific microstructural data that we included, the better our predictions were. Strategy 1, which represented the entire microstructure via only one fiber direction vector without dispersion performed the worst. Adding spatial heterogeneity by representing the microstructure with ten fiber direction vectors throughout the thickness in Strategy 2 improved upon the prediction of Strategy 1. Further, adding dispersion to a single fiber in Strategy 3 improved upon both Strategy 1 and 2. Finally, including both spatial heterogeneity and dispersion in Strategy 4 yielded the best predictions.

Table 3:

Material parameters identified by fitting the Holzapfel model simultaneously to ten “training data sets,” for each microstructure-inclusion strategy separately. With these data, we predicted the behavior of the “test data set,” a held-out sample, based only on its microstructural data (Prediction) and compared it to a direct fit to the data (Direct Fit)

			Strategy
		1	2	3	4
a	(Pa)	2088.75	2163.74	2176.85	2113.71
b	(—)	4.427	4.239	4.200	4.319
af	(Pa)	4254.81	3847.00	5402.66	6595.44
bf	(—)	5.027	10.794	7.174	4.340
as	(Pa)	966.50	634.37	78.53	0.82
bs	(—)	0.0	0.002	0.110	0.004
afs	(Pa)	1152.72	1119.13	0.0	393.86
bfs	(—)	9.149	1.263	0.0	1.154
Direct Fit	NMSE	0.569	0.573	0.572	0.582
Prediction	NMSE	0.500	0.510	0.512	0.515

4. Discussion

Much about the right ventricle remains to be studied and understood to make up for decades of neglect. In our current work, we report on the constitutive behavior and microstructure of ovine right ventricular myocardium. Through detailed mechanical and histological characterization we also critically evaluated the performance of the most promising constitutive framework for right ventricular myocardium introduced, modified, and popularized by Holzapfel et al., Li et al., Guan et al. and others [27, 36, 54, 55].

We chose simple shear tests for our current study as we believe they best represent the natural deformation mode of myocardium. Additionally, we included tension and compression tests as these modes enforce larger volumetric changes and may thus activate deformation modes that were not activated under simple shear. During triaxial simple shear testing, the right ventricular myocardium exhibited mechanical behavior consistent with its complex laminar and fibrous structure [24, 25]. We found that its mechanical response is non-linear, strain-stiffening, and anisotropic. Consistent with our understanding of myocardium, we found that right ventricular myocardium is stiffest in the directions that align with the myocardial fiber directions. We also found that right ventricular myocardium exhibits Poynting effect. That is, under simple shear, it produces a normal force. Interestingly, it did so in a directionally-dependent manner. Specifically, it expressed significant normal tensile stresses when sheared againstthe fiber direction (negative Poynting) while normal stresses were either insignificant or compressive when sheared in the other directions (positive Poynting). This discrepancy may indicate that the negative Poynting effect stems from the mechanical response of the muscle fibers or their collagen support. Additionally, we found that right ventricular myocardium exhibits tension-compression non-linearity under uniaxial loading. In other words, tissue stiffness was different under tensile and compressive loading. Again, this effect depended on the orientation in which the tissue was loaded with respect to the tissue microstructure. When loaded in the fiber direction, the material acted stiffer under tension than under compression. When loaded in the other two directions, the material was stiffer in compression than in tension. Consistent with this mechanism, in the absence of fiber activation, increasing stiffness under compression likely stems from the material’s incompressible behavior.

Finally, we also compared the mechanics of the right ventricular myocardium to that of the left ventricular myocardium. Our data on left ventricular myocardium reflects the findings of many before us in that the muscle of the left ventricle showed non-linear, strain-stiffening, and anisotropic behavior also [24, 25, 30, 23]. Critically, we found that the right ventricular myocardium was less stiff than the left ventricular myocardium, but only in the directions in which muscle fibers were activated. This finding is consistent with our expectation that the left ventricular myocardium, which has to resist and produce larger forces in-vivo, is stiffer in the force-producing direction. Finding that the materials don’t significantly differ in the direction in which fibers are not activated points to a preservation of the amorphous tissue structure and properties between the two sides of the heart.

Our qualitative observations on the mechanics of right ventricular myocardium are well-aligned with those of others [19, 18, 22, 20, 21], who also found that right ventricular myocardium is a non-linear, strain-stiffening, and anisotropic material. The closest comparison to our data are those by Ahmad et al. who used uniaxial, biaxial, and simple shear testing to compare the right ventricular and left ventricular myocardium in piglets [19]. Interestingly, they found, in contrast to us, and against their expectations, that the right ventricular myocardium was stiffer than the left ventricular myocardium. They argued their counter-intuitive result likely stemmed from the immaturity of the tissue in which collagen cross-linking had not yet been concluded. It is noteworthy that Sacks et al., who compared left and right ventricular myocardium using planar biaxial testing only, also found that right ventricular myocardium was stiffer in the fiber direction than left ventricular myocardium [18]. Difference in our findings are difficult to resolve as experiments were done using different test modalities, species, and age of subjects. Future studies will have to resolve this 450 apparent paradox.

In our work, we found that the fiber directions varied significantly in the transmural direction, but were highly consistent between samples. Specifically, we found that the fiber directions varied across our samples by approximately 100°. This number is well-aligned with findings by Avazmohammadi et al. [29] and Sharifi Kia et al. [56] on murine right ventricles. They found that fiber directions varied by 100° and 60° across the entire wall, respectively. Importantly, on the left ventricle it has previously been reported that rodent and large animal models show significantly different transmural fiber directions [57]. In contrast, our data indicates that microstructural data for the right ventricle appears to be well-aligned between large and small animals. In addition to mean fiber direction, we also explored fiber dispersion as a measure of fiber organization. In agreement with reports by Avazmohammadi et al. and Ahmad et al. [58], we found that fibers were dispersed within the sheet-plane. Moreover, fibers appeared to be most dispersed at the epicardial surface and least dispersed toward the endocardial surface. To date, the teleological reasons of this heterogeneous fiber dispersion are unknown but are likely driven by functional needs and natural demand for cardiac efficiency. Importantly, and surprisingly to us, fibers were also dispersed in the plane perpendicular to the sheet-plane. Interestingly, few or no current models of myocardium (either for the left or right ventricle) support asymmetric three dimensional fiber dispersion and the functional importance of such distributions have not been explored. Future studies will hopefully fill these gaps.

To obtain these detailed microstructural data, we acquired ten histological sections across our samples. This process is not only destructive and expensive, but also time-consuming. Thus, one of the questions we tried to answer in our current work was: How much microstructural data is necessary to accurately reproduce the constitutive behavior of right ventricular myocardium? Additionally, we explored the question: Can we use the inverse fits to our mechanical data to correctly identify fiber direction and dispersion? Finally, we set out to answer: How much microstructural data is necessary to predict the behavior of an unseen tissue sample?

To answer these questions, we developed an inverse analysis pipeline with microstructurally-informed finite element models. We implemented four different microstructure-inclusion strategies with increasing levels of complexity. To answer our first question, we fit our model for eleven samples individually. We found that our fits reached similar levels of goodness between the varying strategies. In short, it appears that even drastically simplifying assumptions about the tissue microstructure can yield satisfying fits. The answer to our second question is closely related to our answer to the first question. If models with vastly simplified microstructure satisfyingly fit our mechanical data, it is unlikely that an inverse approach will be able to uniquely identify the microstructure based on only the mechanical data acquired. Indeed, we found that predicted microstructural parameters compared poorly to actual measurements. This finding highlights the danger of interpreting constitutive laws as having microstructural meaning without supporting microstructural characterization. Finally, to answer our third question, we identified a set of parameters that fit ten of our data sets best. Again, we repeated this identification for each microstructure-inclusion strategy. Subsequently, we tested the predictive ability against a randomly selected eleventh, held-out data set. Here we found that increasing the information about microstructural data improves our predictions. Thus, perhaps not surprisingly, we find that the more microstructural data about a sample is known, the more confident the modeler can be in parameter predictions that are based on historic data. In more detail, we found that including fiber dispersion had a stronger, positive effect on predictive power than including spatial heterogeneity. From an entirely pragmatic perspective, this is useful for researchers whose own labs are capable of collecting histological data but may lack the equipment and computational resources to perform triaxial mechanical testing and the corresponding finite element simulations.

Of course, some limitations arise from the methodology that we followed in this study. Mechanical testing was conducted more than 12 hours after sacrificing these animals. Although, we kept tissues in solution with myosin inhibitor to avoid rigor mortis, we cannot ensure that tissue properties did not decay during transport and storage. Concerns could also arise as to the effect of Fomblin on the mechanics of our tissue samples. To address this concern, we note that Fomblin is a hydrophobic reagent. Penetration of highly hydrated soft tissues is therefore unlikely. Additionally, we did not observe any remarkable tissue characteristics during histological studies. In a similar vein, our samples were glued to the test apparatus. To ensure that gluing samples did not significantly affect our tissue properties, we checked for glue penetration in all of our histological preparations. We did not see any glue penetration under Picrosirius Red or Massons Trichrome staining, or on unstained slides. Concerns may also be raised about the boundary effects stemming from gluing the sample to our sample holders. While we cannot rule out that the stress-field of our sample may be effected, we also highlight that alternative fixation methods, such as sutures, rakes, or clamps, likely have the same or larger effects. Finally, for our histological studies, staining and sectioning the embedded tissue may have also resulted in fiber re-orientation from their fresh, untreated state. However, we expect this effect to be minimal.

5. Conclusion

Based on our comprehensive mechanical testing protocol of six simple shear modes and three tension/compression modes, we found that right ventricular myocardium exhibits non-linear, strain-stiffening, and anisotropic behavior with Poynting effect. The mechanics of right ventricular myocardium were qualitatively and quantitatively very comparable to the mechanics of the left ventricular myocardium. The exception being the sample stiffness in the fiber direction, in which the right ventricular myocardium was less stiff. When interpreting and using our mechanical data on right and left ventricular myocardium, we remind the reader of the limitations above. Additionally, we conducted detailed microstructural analyses via serial histological sections that revealed that muscle fibers in the right ventricular myocardial were dispersed in the sheet-plane and in the plane perpendicular to the sheet-plane. While fiber distributions varied in the transmural direction, they were consistent in the longitudinal direction. Additionally, we investigated fundamental questions about constitutive modeling of right ventricular myocardium and found that the Holzapfel model provides an excellent fit to our data even when limited microstructural data is provided. We also demonstrated that including more microstructural data improves the ability of this model to predict mechanical behavior. Finally, we demonstrated that inversely identifying microstructural data may provide erroneous results and should thus be done with care. In conclusion, we provide previously unreported mechanical, microstructural, and modeling data that continues to fill gaps in our knowledge of the right ventricle.