Abstract
The Drosophila montium species group is a clade of 94 named species closely related to the model species D. melanogaster. The montium species group is distributed over a broad geographic range throughout Asia, Africa, and Australasia. Species of this group possess a wide range of morphologies, mating behaviors, and endosymbiont associations, making this clade useful for comparative analyses. We use genomic data from 42 available species to estimate the phylogeny and relative divergence times within the montium species group, and its relative divergence time from D. melanogaster. To assess the robustness of our phylogenetic inferences, we use 3 non-overlapping sets of 20 single-copy coding sequences and analyze all 60 genes with both Bayesian and maximum likelihood methods. Our analyses support monophyly of the group. Apart from the uncertain placement of a single species, D. baimaii, our analyses also support the monophyly of all seven subgroups proposed within the montium group. Our phylograms and relative chronograms provide a highly resolved species tree, with discordance restricted to estimates of relatively short branches deep in the tree. In contrast, age estimates for the montium crown group, relative to its divergence from D. melanogaster, depend critically on prior assumptions concerning variation in rates of molecular evolution across branches, and hence have not been reliably determined. We discuss methodological issues that limit phylogenetic resolution – even when complete genome sequences are available – as well as the utility of the current phylogeny for understanding the evolutionary and biogeographic history of this clade.
Keywords: Bayesian inference, maximum likelihood inference, biogeography, chronograms, Drosophila phylogeny, phylogenetic discordance
1. Introduction
Reference genomes from species at increasing phylogenetic distances provide insights into the evolution of genomes, phenotypes, and host-symbiont interactions. For instance, the genome sequences of extinct Homo species and multiple non-human primates have elucidated which genomic features – such as gene family expansions/contractions, de novo gene origin, and structural rearrangements – are human-specific, and which are more deeply conserved (Burbano et al., 2012; Green et al., 2010; Reich et al., 2010). Similarly, as evidenced by their numerous citations, reference genomes from Mus and Drosophila congeners greatly advanced our understanding of these model systems (e.g., Clark et al., 2007; Thybert et al., 2018). The success of these comparative genomic studies has spawned more extensive projects; – for example, the recent sequencing of the genomes of every butterfly species in North America (Zhang et al., 2019), 5000 arthropod genomes (https://i5k.github.io/), the genomes of all living bat species (https://bat1k.ucd.ie/), and at least one genome for every vertebrate genus (https://genome10k.soe.ucsc.edu/). As whole-genome sequencing becomes increasingly commonplace, dense sampling of genomes from entire clades (“model clade genomics”; Rogers, 2018) will greatly advance comparative genomics and genome-enabled studies of phenotypic evolution. For instance, convergent genomic features have been used to explore the genetic basis of marine and subterranean lifestyles in distantly related mammals (Chikina et al., 2016; Partha et al., 2017). As the number of densely sequenced clades grows, increasingly fine-grained analyses of divergent and convergent genomic features within and among clades may yield novel insights into the molecular underpinnings of phenotypic and ecological diversity, as well as patterns of association of hosts with their microbiomes (e.g., Nishida and Ochman, 2019) and endosymbionts (e.g., Turelli et al., 2018).
The Drosophila montium species group was originally established as a subgroup within the larger melanogaster species group (Hsu 1949). At that time, the melanogaster group consisted of only 13 described species, including five in the montium subgroup (two of which were subsequently reassigned to other clades). Following decades of research, the melanogaster species group has grown to almost 200 species, including 94 described species in the montium subgroup alone (Bock and Wheeler, 1972; Bock, 1980; Toda, 1991; Bächli 2020 database; Toda 2020 database). The monophyly of the montium clade has remained undisputed (Da Lage et al. 2007; Yang et al. 2012; Russo et al. 2013), while new evidence refutes the monophyly of the wider melanogaster group as originally described (Pelandakis and Solignac 1993; Prigent et al. 2017; Kopp et al. 2019). For these and other reasons, some authors have proposed upgrading the montium subgroup to species group status (Da Lage et al. 2007; Yassin 2013, 2018), with Yassin (2018) formally subdividing the new montium species group into seven subgroups. This classification has been adopted by Drosophila taxonomic databases (Bächli 2020; Toda 2020) and several recent comparative analyses (e.g., Chen et al. 2019; Yassin et al. 2019; Bronski et al. 2020), and we follow it here.
The montium species group is estimated to have diverged from D. melanogaster 28 to 41 million years (MY) ago in Asia (Russo et al., 2013; Tamura et al., 2004), subsequently spreading to Africa and Oceania (Yassin, 2018). This species-rich lineage harbors diverse behavioral, morphological, and physiological traits, making it well-suited for model clade genomics. Genomic comparisons of distantly related Drosophila species have yielded important insights into evolutionary mechanisms —for example, revealing the functional conservation of cis-regulatory elements despite extensive sequence divergence and reorganization of transcription factor binding sites (Ludwig & Kreitman, 1995; Ludwig et al., 1998; Ludwig et al., 2000; Hare et al., 2008; Kim et al., 2009; Swanson et al., 2011). However, these approaches pose significant challenges. Distantly related species have often accumulated so many sequence differences that it can be difficult to identify functionally important changes or to determine the order of key evolutionary events. Furthermore, highly diverged sequences from multiple species are sensitive to alignment error, especially for small features such as binding sites (Stark et al., 2007; Kim et al., 2009). These problems are ameliorated by starting with many closely related species and studying enhancer evolution at the earliest stages of divergence. Such comparisons are more likely to reveal when important changes occur (e.g., the order of binding site gains and losses), and to identify compensatory changes before they are obscured by additional sequence evolution.
Genome assemblies and a robust phylogeny for the montium species group will also facilitate evolutionary analyses of divergent and convergent phenotypes and their genetic bases. For example, several species in the montium group have evolved an unusual mating behavior, where males emit courtship songs after mounting the female (Chen et al., 2019, 2013). This behavior is accompanied by frequent evolutionary losses of pre-copulatory mating song, as well as by many transitions between different song types (pulse, sine, and high pulse repetition, Chen et al., 2019). Morphological traits, such as sex-specific pigmentation, also change rapidly in the montium clade; in particular, a female-limited color polymorphism appears to have evolved convergently in several species (Kopp et al., 2000; Yassin et al., 2016). Species of this clade have also repeatedly evolved physiological adaptations that correlate with environmental variables, such as desiccation and temperature tolerance (Goto et al., 2000; Kellermann et al., 2009). Despite the intriguing gains and losses of phenotypes across the clade, genome-based analyses of these traits have lagged because only a few genomes are available (Allen et al., 2017; Chen et al., 2014) and the phylogeny of the clade remains uncertain.
Initial montium group phylogenies, estimated from allozymes or mitochondrial loci, involved a handful of species and were unable to provide a comprehensive overview (Ohnishi, 1983; Kim et al., 1989; Nikolaidis and Scouras, 1996). Subsequent studies included nearly half of all described species but used only partly overlapping taxon samples and relied on only one to four loci, chosen largely for historical reasons (Chen et al., 2013; Goto et al., 2000; Yassin et al., 2016; Zhang et al., 2003). The most recent phylogeny of Yassin et al. (2016) is based on four loci, the largest data set available at the time. This phylogeny, which differs from previous phylogenies, subdivided the montium species group into seven subgroups: kikkawai, montium, orosa, parvula, punjabiensis, serrata, and seguyi, with further subdivision of some of these subgroups into species complexes (Yassin, 2018; Yassin et al., 2019).
To better resolve the montium group phylogeny and provide genomic resources for comparative analyses, we have sequenced the genomes of 42 montium-clade species (including those already published by Bronski et al., 2020). We find that the subgroups proposed by Yassin (2018) are almost completely supported by our analyses, the primary exception being the placement of a single species, D. baimaii. In contrast, our estimated relationships among these subgroups differ substantially from those of Yassin et al. (2016). This type of discordance is common among Drosophila studies in which the phylogeny of a clade has been estimated using different datasets [e.g., compare the analyses of the D. melanogaster species group (sensu Hsu 1949) by Schawaroch, 2002; Kopp and True, 2002; Da Lage et al., 2007; Barmina and Kopp, 2007]. Repeatedly, increasingly refined analyses suggest that most nodes are often resolved with relatively little data, but a subset of deep nodes remain ambiguous even with essentially unlimited data. As genome-scale data become increasingly prevalent in phylogenetic studies, defining major clades is likely to prove much easier than eliminating lingering uncertainties within and among clades. We discuss the implications of our revised phylogeny for the biogeographic history, phenotypic evolution and molecular evolution of the montium species group and for understanding host-symbiont coevolution.
2. Material and Methods
2.1. Fly stocks
We acquired stocks from the U.S. National Drosophila Species Stock Center, the Ehime Drosophila Species Stock Center in Japan, colleagues, and our own collecting. The strains and species used are reported in Supplemental Table 1, which also indicates the sources of the genome assemblies. Our study includes every montium group species for which we could obtain a living strain (42 species, representing 45% of the 94 described species in the species group). We include seven species not in the phylogeny of Yassin et al. (2016): D. greeni, anomelani, ohnishii, ogumai, orosa, fengkainensis, and trapezifrons. The Yassin et al. (2016) phylogeny includes eight montium species that we could not obtain as live strains: D. biauraria, subauraria, khaoyana, cauverii, neoasahinai, nagarholensis, dossoui, and davidi. Finally, three species in our data set were used in Yassin et al. (2016) but have been subsequently renamed: D. bicornuta has been provisionally renamed aff. bicornuta because the available strain was found to belong to a new species closely related to D. bicornuta (T. K. Katoh and M. Watada, unpubl.), chauvacae has been renamed cf. chauvacae (Prigent et al., 2020), and curta has been renamed aff. tsacasi (Yassin et al., 2019).
2.2. Sequencing
Sequencing was divided between two labs. The Eisen lab sequenced and assembled genomes for 23 montium species: D. asahinai, auraria, cf. bakoue, birchii, bocki, bunnanda, burlai, jambulina, kanapiae, lacteicornis, leontia, mayri, nikananu, pectinifera, punjabiensis, rufa, seguyi, serrata, tani, triauraria, truncata, vulcana, and watanabei (NCBI: PRJNA554346; methods reported in Bronski et al., 2020). Briefly, DNA was extracted from three flies per strain and sheared to a mean fragment size of 350 bp with a Covaris E220 sonicator. Libraries were constructed with an Illumina TruSeq DNA PCR-free kit (Illumina 20015962) and 100-bp paired-end reads were sequenced on an Illumina HiSeq 2000 or HiSeq 2500 instrument.
The Cooper lab sequenced 31 additional lines from 22 montium species (only auraria, bocki and triauraria overlap with the species sequenced by the Eisen lab): D. anomelani, auraria (×4), baimaii, barbarae, aff. bicornuta, bocki, cf. bocqueti, burlai, cf. chauvacae, diplacantha, fengkainensis, greeni, lini, malagassya, ogumai, ohnishii, orosa, parvula, trapezifrons, triauraria (×6), tsacasi, and aff. tsacasi (×2). As in Meany et al. (2019), DNA was extracted from a pool of 10 male and 10 female flies per strain and sheared to an average size of 400 bp with a Covaris E220 sonicator. Libraries were prepared with a NEBNext® Ultra™ II DNA Library Prep Kit (NEB E7645). Between 20–24 libraries were pooled per lane and 150-bp paired-end reads were sequenced on the HiSeq4000 at Novogene. Short-read data generated for this paper are archived on NCBI, and assemblies and phylogenetic analysis scripts on DRYAD (NCBI: PRJNA680378; DRYAD: doi:10.25338/B8P614).
2.3. Assemblies
We used 59 genome assemblies, including the 5 publicly available assemblies from the ananassae and melanogaster groups that we used as outgroups: D. ananassae (NCBI: GCA_000005115.1), D. biarmipes (NCBI: GCA_000233415.2), D. elegans (NCBI: GCA_000224195.2), D. melanogaster (NCBI: GCF_000001215.4), and D. simulans (NCBI: GCF_000754195.2). This set includes genome assemblies from 22 of the 23 montium species (omitting D. burlai) assembled by the Eisen lab (DRYAD doi: https://doi.org/10.6078/D1CH5R; Bronski et al. 2020) and D. kikkawai (NCBI: GCA_000224215.2). In addition, we generated new assemblies for another 22 montium species (31 strains).
To generate the new genome assemblies, we trimmed the reads with Sickle v. 1.33 (Joshi and Fass, 2011) and assembled them with ABySS v. 2.0.2 (Jackman et al., 2017). Kmer values of 51, 61…91 were tested and the assembly with the highest N50 was kept. Assembly statistics for each species are reported in Supplementary Table 2. Total scaffold lengths ranged from 100 Mb to 204 Mb, and the mean and median contig N50 across the assemblies were 41,478 bp and 17,233 bp, respectively. Assemblies have been archived on DRYAD (doi:10.25338/B8P614).
2.4. Gene extraction for phylogenetic analyses
We used three sets of 20 distinct loci, each set analyzed independently, to determine the robustness of our estimated phylogenies (Table 1). We selected loci whose coding regions were roughly comparable in length, 500–2000 bp, single copy, with unique homologs across all of the species analyzed. We obtained coding sequences for each gene in D. melanogaster, D. simulans, D. biarmipes, D. elegans and D. ananassae from FlyBase as query sequences and used tBLASTn to identify orthologous sequences from the genome assemblies of each montium species. All sequences were aligned with MAFFT v. 7 with default parameters (Katoh and Standley, 2013) and trimmed (i.e., introns extracted) using the D. melanogaster sequences as a guide. For each locus, we used data corresponding to the full length of the coding sequence in D. melanogaster (see Table 1).
Table 1.
Three sets of 20 loci used in phylogenetic analyses
| Gene set 1 (36,753 bp)1 | location in D. melanogaster (chromosome arm-centimorgans) | Length of coding region (bp) in D. melanogaster2 |
|---|---|---|
| mAcon1 (FBgn0010100) | 2L-54 | 2364 |
| Ald1 (FBgn0000064) | 3R-90 | 1092 |
| bcd (FBgn0000166) | 3R-48 | 1242 |
| e (FBgn0000527) | 3R-71 | 2640 |
| enolase (FBgn0000579) | 2L-3 | 1503 |
| esc (FBgn0000588) | 2L-45 | 1278 |
| Zw (FBgn0004057) | X-63 | 1509 |
| GlyP (FBgn0004507) | 2L-4 | 2535 |
| GlyS (FBgn0266064) | 3R-56 | 2070 |
| ninaE (FBgn0002940) | 3R-67 | 1122 |
| Pepck (FBgn0034356) | 2R-86 | 1917 |
| Pgi (FBgn0003074) | 2R-59 | 1677 |
| Pgm1 (FBgn0003076) | 3L-44 | 1683 |
| pic (FBgn0260962) | 3R-53 | 3423 |
| ptc (FBgn0003892) | 2R-59 | 3861 |
| Tpi (FBgn0086355) | 3R-100 | 744 |
| Taldo (FBgn0023477) | 2R-105 | 996 |
| w (FBgn0003996) | X-1.5 | 2064 |
| wg (FBgn0284084) | 2L-25 | 1407 |
| y (FBgn0004034) | X-0 | 1626 |
| Gene set 2 (23,127 bp) | ||
| Gαi (FBgn0001104) | 3L-18 | 1068 |
| Hex-A (FBgn0001186) | X-28 | 1626 |
| me31B (FBgn0004419) | 2L-40 | 1287 |
| nuf (FBgn0013718) | 3L-42 | 957 |
| MAPk-Ak2 (FBgn0013987) | X-13 | 1080 |
| Rab14 (FBgn0015791) | 2L-50 | 720 |
| TfIIEβ (FBgn0015829) | 3L-10 | 750 |
| crq (FBgn0015924) | 2L-0.7 | 1476 |
| colt (FBgn0019830) | 2L-7 | 921 |
| hfp (FBgn0028577) | 3L-0.5 | 1638 |
| Ldsdh1 (FBgn0029994) | X-22 | 963 |
| CG1434 (FBgn0030554) | X-48 | 1422 |
| CG17760 (FBgn0033756) | 2R-67 | 1062 |
| Trh (FBgn0035187) | 3L-0 | 1668 |
| CG12766 (FBgn0035476) | 3L-10 | 963 |
| FRG1 (FBgn0036964) | 3L-47 | 789 |
| PH4αEFB (FBgn0039776) | 3R-100 | 1653 |
| Lst8 (FBgn0264691) | X-29 | 942 |
| CG55245 (FBgn0265180) | 2R-94 | 1323 |
| vib (FBgn0267975) | 3R-66 | 819 |
| Gene set 3 (24,315 bp) | ||
| Hsp27 (FBgn0001226) | 3L-29 | 642 |
| Obp84a (FBgn0011282) | 3R-48 | 666 |
| Aldh (FBgn0012036) | 2L-35 | 1563 |
| Rlip (FBgn0026056) | 3R-70 | 1878 |
| l(1)G0193 (FBgn0027280) | X-21 | 1941 |
| CCT6 (FBgn0027329) | X-51 | 1602 |
| Aladin (FBgn0030122) | X-27 | 1401 |
| Brms1 (FBgn0030434) | X-41 | 780 |
| CG8952 (FBgn0030688) | X-51 | 831 |
| CG11601 (FBgn0031244) | 2L-0.5 | 828 |
| Tpr2 (FBgn0032586) | 2L-52 | 1527 |
| CG8728 (FBgn0033235) | 2R-57 | 1671 |
| CG5757 (FBgn0034299) | 2R-84 | 636 |
| Osi2 (FBgn0037410) | 3R-47.5 | 1173 |
| CG4338 (FBgn0038313) | 3R-56 | 825 |
| Trax (FBgn0038327) | 3R-57 | 897 |
| comm2 (FBgn0041160) | 3L-43 | 1032 |
| CG41520 (FBgn0087011) | 2R-55 | 1545 |
| 26–29-p (FBgn0250848) | 3L-41 | 1650 |
| mRpL37 (FBgn0261380) | 3R-50 | 1227 |
Loci used in Turelli et al. (2018).
We used coding sequences of this length from each genome.
Before combining the loci into sets, phylogenies were estimated from each locus. We initially examined 61 loci, but discarded one (FBgn0250874, D. melanogaster map position, X-1.5 with length 1287) because it produced a phylogram in which a single branch had length exceeding 75% of the total tree length. We conjecture that this artifact was produced by mis-identified homology (e.g., either we used an unexpected paralog or the coding region of the locus was changed by indels in one or more of the species). For our 60 loci, the alignments have been archived on DRYAD (doi:10.25338/B8P614).
2.5. Phylogenetic analyses
We initially performed Bayesian analyses using the GTR + Γ(discrete) model for sequence evolution, but then repeated our Bayesian phylogram estimates using GTR + Γ(discrete) + I (invariant sites); we also estimated phylograms using maximum likelihood (ML) under both models for sequence evolution [i.e., GTR + Γ(discrete), with and without I]. We initially avoided the invariant sites parameter, I, because of uncertainty about the reliability of estimates (reviewed in Nguyen et al., 2018) and because posterior-predictive simulations (Bollback 2002) in our recent phylogenetic analysis of nine Drosophila species, spanning the clade that includes D. melanogaster and D. ananassae (and, hence, including all montium group species), indicated that the GTR + Γ(discrete) model, with four rate categories, adequately described our sequence data (Turelli et al. 2018). The nine-species analysis of Turelli et al. (2018) used only the first set of 20 loci in Table 1. Our Bayesian analyses were performed with RevBayes v. 1.0.9 (Höhna et al., 2016), largely following the procedures used in Turelli et al. (2018); but our more extensive data precluded some of their model testing and validation procedures. With only 9 species and 20 loci, Turelli et al. (2018) were able to perform posterior-predictive simulations (Bollback, 2002) to assess the adequacy of their model of molecular evolution and stepping-stone simulations (Xie et al., 2011) to calculate marginal likelihoods for comparing the fit of models imposing different constraints on relative rates of evolution across data partitions. Comparable simulation analyses were not feasible with our computing resources for the larger number of species and loci in this study. Hence, our model choices rely on prior experience and the simulation studies cited below.
Our analyses used alignments of either 20 or 60 concatenated genes. For each gene set, we partitioned the coding sequences by gene and by codon position to accommodate potential variation in the substitution process among genes and codon positions. Guided by our previous analyses, including tests of model adequacy, and published simulation studies suggesting little loss of accuracy associated with using overparameterized models, either in terms of the number of partitions (e.g., Kainer and Lanfear, 2015; but see Wang et al., 2019) or the parameters describing sequence evolution (Huelsenbeck and Rannala, 2004; Abadi et al., 2019), we did not explore alternative partitioning schemes or models of sequence evolution simpler than GTR + Γ(discrete). We accommodated variation in the overall substitution rates among data partitions by assigning a rate multiplier, σ, to each data partition.
Our Bayesian analyses used flat, symmetrical (α = 1) Dirichlet priors both on the stationary base frequencies, π, and on the relative-rate parameters, η, of the GTR model [i.e., Dirichlet(1,1,1…)]. As in Turelli et al. (2018), we used a Γ(2,1) hyperprior on the shape parameter, α, of the discrete-Γ model (adopting the conventional assumption that the rate parameter of this Γ distribution, β, is equal to α, so that the mean rate is 1; Yang 1994). (The gamma distribution, Γ(α,β), is parameterized so that the mean and variance are α/β and α/β2, respectively.) The Γ(α,α) model for rate variation assigns significant probability near zero when α < 1 (accommodating invariant sites). The Γ(2,1) hyperprior on α assigns 95% probability to the interval (0.36, 4.74), allowing for both small and large values of α. As expected, the mean of the posterior distribution for Γ rate variation is smaller when the substitution model explicitly includes I. The prior we used for the substitution-rate multiplier for the ith data partition, σi, differs between our phylogram and chronogram analyses; we describe these priors below.
For the RevBayes analyses, four independent runs were performed for each gene set; in all cases, the runs produced concordant topologies. We diagnosed MCMC performance using Tracer 1.7 (Rambaut et al. 2018). Nodes with posterior probabilities below 0.95 were collapsed into polytomies. (Apart from our analyses of multiple strains of D. auraria and D. triauraria, only two polytomies appear in our Bayesian results, both in one 20-gene phylogram [Fig. 1B], as discussed below. All other nodes have posterior support > 0.99 using either GTR + Γ or GTR + Γ + I.)
Fig. 1.
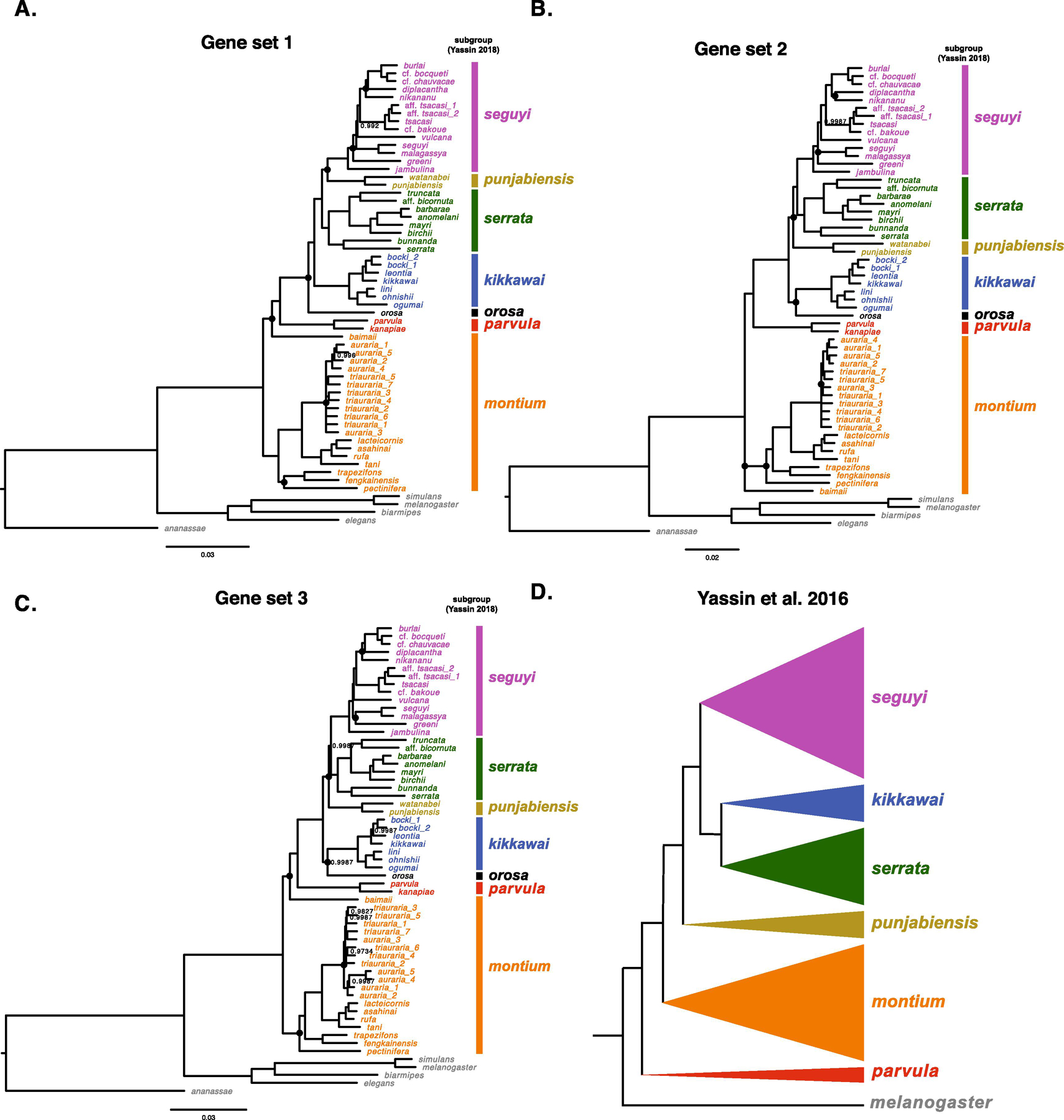
Alternative estimates of the D. montium species group phylogeny. Panels A, B and C show the results from three independent Bayesian analyses, each based on concatenated complete coding sequences of 20 nuclear loci, with no overlap among gene sets (Table 1). Panel D shows the relationships of the subgroups within the montium species group proposed by Yassin (2018). In A–C, we label the groups using the same colors as in D. Nodes with posterior probabilities < 0.999 are indicated, and nodes with posterior probabilities below 0.95 are presented as polytomies. Nodes that vary among the three phylogenies in A–C are marked with a black dot. The scale bars show the average number of estimated substitutions per site over the specified branch length.
2.5.1. Phylograms
The data include 42 montium species, with D. melanogaster, D. simulans, D. biarmipes, D. elegans and D. ananassae as outgroups. We used RevBayes to estimate phylograms from three sets of 20 concatenated genes, extracted from all the genome assemblies in Supplemental Table 1 (including multiple representatives from individual species). For each 20-gene set, we used the GTR + Γ and GTR + Γ + I models with four rate categories, partitioning by gene and codon position, for a total of 60 partitions. In the phylograms, branch lengths are scaled to the expected number of substitutions per site, averaged over the 60 partitions (which were analyzed separately for each gene set). To test the robustness of our results to the discretization of Γ-distributed rate variation, we ran the first and second gene sets with six rate categories as well as four with GTR + Γ. Each partition had an independent rate multiplier with prior Γ(1,1) [i.e., Exp(1)]. Our analyses assumed a uniform prior over all possible topologies. Branch lengths were drawn from a flat, symmetrical Dirichlet distribution and thus summed to 1. Because the expected number of substitutions along a branch equals the branch length times the rate multiplier, the expected number of substitutions across the entire tree for a partition is equal to the rate multiplier for the partition. We also performed a Bayesian analysis using all 60 genes (with 180 partitions).
We reanalyzed our data using ML analyses with RAxML v.8 (Stamatakis, 2014) and the default settings, with 1000 bootstraps to assess robustness of the point estimates. We used the GTR + Γ + I model with four rate categories (omitting I changed bootstrap support values only slightly).
2.5.2. Chronograms
Using RevBayes we estimated relative chronograms, whose branch lengths are proportional to time, to determine the relative ages of splits separating the seven subgroups of the montium species group designated in Yassin (2018). Based on the invariance of our phylogram inferences to the inclusion of I in the model of sequence evolution (see below), chronograms were estimated using only the GTR + Γ model. Times are scaled relative to the divergence time of the montium species group from D. melanogaster because of deep uncertainties concerning absolute divergence times of drosophilids (Obbard et al., 2012; Russo et al., 2013; Izumitani et al., 2016). Following Turelli et al. (2018), our analyses assumed a birth-death prior on the tree topology. Our chronogram analyses were restricted to 17 species for computational reasons. We set ρ, the sampling parameter of the birth-death process, to 0.1, corresponding to the approximate fraction of the 190 species of the melanogaster species group (sensu Hsu 1949) considered.
Following Yassin et al. (2016), we first used a strict-clock model assuming constant (but partition-specific) rates of molecular evolution across each branch. We also estimated relaxed-clock relative chronograms using different prior assumptions concerning rate variation across branches. We used two different Γ branch-rate priors (modeling variation in rates of molecular evolution across branches, assuming that the relative rates across all partitions remain constant): Γ(2,2), which allows for fairly extreme variation, and the more constrained Γ(7,7). (The strict-clock chronogram corresponds to the limiting case of a Γ(n,n) prior with n →∞.). For each assumption concerning variation across branches, we fixed the root age at 1. As with our phylograms, we partitioned the data by gene and codon position, but used all 60 genes. For each model of rate variation across branches, we used the GTR + Γ model for rate variation across sites within a partition, with four Γ rate categories. For tree shape, we used the same birth-death prior on the tree topology and node ages as Turelli et al. (2018) (see Yang and Rannala, 1997); in this prior model, τi is the length of branch i in units of (relative or absolute) time. As in our phylogram analyses, we assigned a rate multiplier, σi, to each data partition; but we assigned a diffuse Γ(0.001, 0.001) prior on the data-partition-specific substitution-rate multipliers, σ. This diffuse prior is known to behave well over a wide range of datasets (Andrew Rambaut, pers. comm.).
To reduce chronogram run times, we used only 17 montium species, but they spanned all seven subgroups proposed by Yassin (2018): the seguyi subgroup (D. burlai, D. tsacasi, D. bakoue, D. jambulina), punjabiensis subgroup (D. watanabei), serrata subgroup (D. truncata, D. serrata), kikkawai subgroup (D. kikkawai, D. leontia), parvula subgroup (D. kanapiae), orosa subgroup (D. orosa), and montium subgroup (D. baimaii, D. auraria, D. triauraria, D. lacteicornis, D. rufa, D. pectinifera). We also included D. melanogaster as an outgroup. When using the Γ(2,2) prior, we constrained the analysis to ensure that D. melanogaster was the outgroup (discussed below). Even for this restricted data set, the run times for our individual chronograms were nearly a month. Hence, we were not able to use “best practice” Bayesian model selection (Bollback, 2002) to determine which relaxed-clock model best approximates our data, because that would increase the calculation times by more than an order of magnitude.
3. Results
3.1. Phylograms
3.1.1. Bayesian analyses
For each set of 20 genes and each model of molecular evolution, all four replicate runs produce the same estimated topology. For gene sets 1 and 2, we obtain the same topology using the GTR + Γ model whether we discretize the Γ into four or six partitions (gene set 3 and the entire set of 60 loci were analyzed only with four partitions). For each of the four data sets (three sets of 20 genes, one using all 60), we obtained identical topologies in our Bayesian analyses whether we used GTR + Γ or GTR + Γ + I to model sequence evolution. Fig. 1 presents the results for our GTR + Γ analyses. Small differences in a few posterior support values using GTR + Γ + I are discussed below. Our description follows the taxonomy of Yassin (2018) and refers to the major subdivisions within the 94-species montium species group as subgroups.
We sought to determine the relationships among the subgroups proposed by Yassin (2018), to determine whether these subgroups are clades, and to understand species relationships within each subgroup. Thus, our phylograms (Fig. 1A, 1B, 1C) are shaded and labeled corresponding to the Yassin (2018) subgroups (Fig. 1D). Our three 20-gene sets produced largely concordant results, but there are notable exceptions concerning the placement of the small punjabiensis and orosa subgroups and the placement of D. baimaii, D. greeni, D. nikananu and D. pectinifera. The discrepancies among the three 20-gene phylograms mostly involve resolving relatively short branches relatively deep in the tree. The ambiguities involving D. greeni, D. nikananu and D. pectinifera concern only their placements within their respective subgroups. The placement of D. baimaii is more problematic. Gene sets 1 and 3 both produce fully resolved phylogenies with posterior probabilities > 0.99 for each node; but they do not fully agree on subgroup relationships. Gene set 2 produces two unresolved trichotomies, concerning the placements of D. baimaii and D. greeni, as discussed below. We first compare the relationships among the clades in our phylogenies to the subgroup relationships in Yassin (2018) (Fig. 1D), which are based on a strict-clock chronogram from Yassin et al. (2016).
The topologies produced by gene sets 1 and 3 indicate that the montium subgroup is sister to the remaining montium species, i.e., the montium subgroup arose from the deepest divergence in the montium group. For gene set 2, the deepest node for all montium species is associated with an unresolved trichotomy resulting from the uncertain placement of D. baimaii, consistent with the montium subgroup diverging first. In contrast, Yassin et al. (2016) suggested that the parvula subgroup diverged first, i.e., is sister to a clade containing all other subgroups. This hypothesis is rejected by all of our phylograms. As indicated below, we expect this parvula subgroup placement in Yassin et al. (2016) was an artifact of their strict-clock assumption and the limited sequence data then available. All three of our phylograms place the parvula subgroup sister to a clade that includes the seguyi, punjabiensis, serrata, kikkawai and orosa subgroups, making it younger than the montium subgroup, a conclusion consistent with our relaxed-clock chronograms estimated from all 60 genes, discussed below. Yassin et al. (2016) and Yassin (2018) placed D. baimaii within the montium subgroup. None of our analyses support this. Gene sets 1 and 2 (Fig. 1A and 1C) and our 60-gene analyses (Fig. 2) place D. baimaii outside of the montium subgroup and as sister to the remaining montium group species (i.e., the large clade that includes the distantly related parvula and seguyi subgroups). Gene set 2 (Fig. 1B) provides weak support for the hypothesis that D. baimaii is sister to all other montium group species, but the posterior support is only 0.65 using GTR + Γ and 0.74 using GTR + Γ + I. Clearly, the lineage leading to D. baimaii arose very early in the radiation of the 94 extant montium species, but its placement remains uncertain. With this single exception involving D. baimaii, our analyses suggest that all of the subgroups proposed by Yassin (2018) are clades.
Fig. 2.
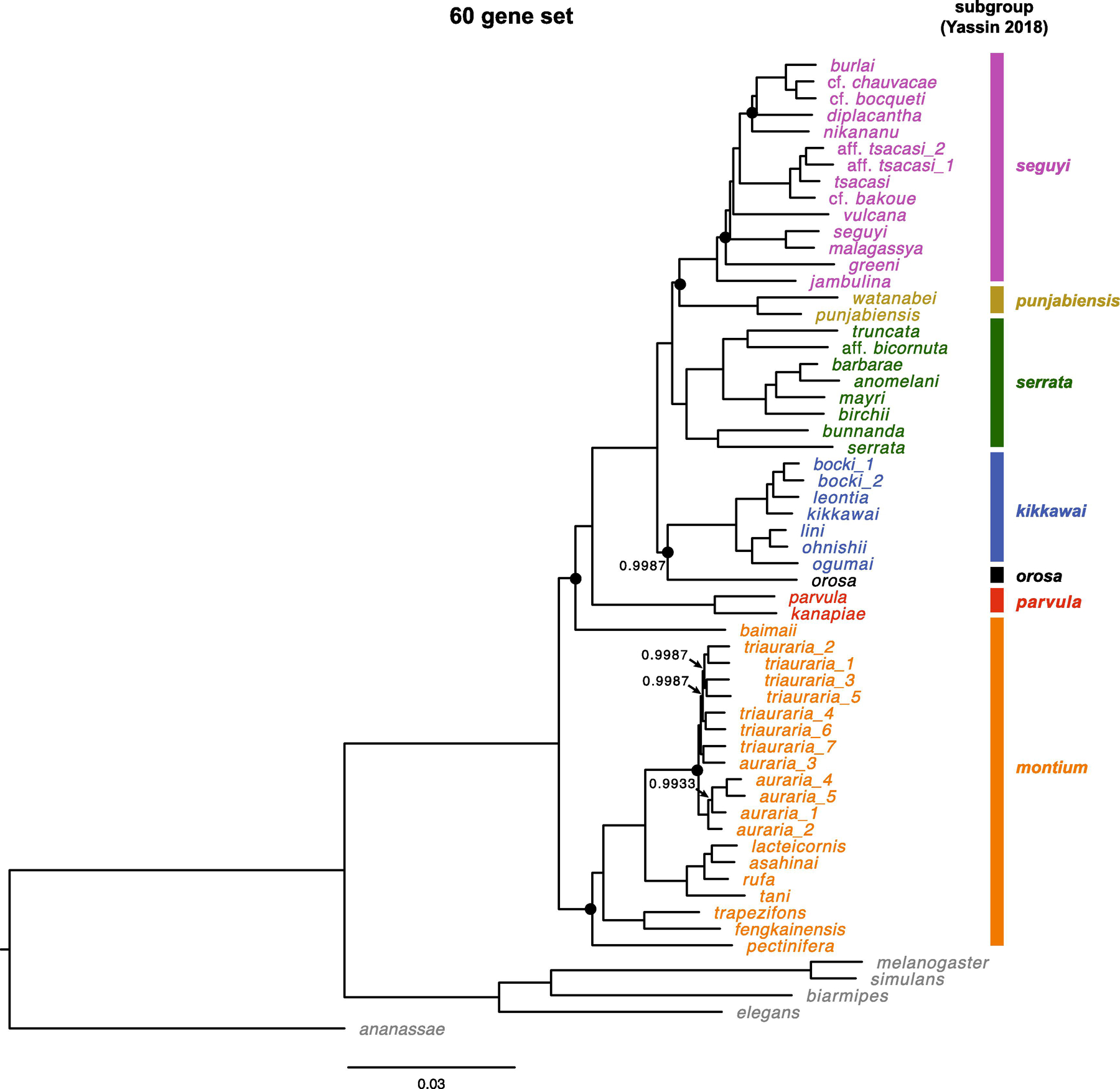
Estimate of the D. montium species group phylogeny based on all 60 loci (Table 1). We present posterior probabilities only for nodes with support < 0.999. Nodes that vary among the three phylogenies in Fig. 1 are marked with a black dot. The scale bars show the average number of estimated substitutions per site over the specified branch length.
Consistent with Yassin et al. (2016), which did not include D. orosa, our analyses all agree that the combined species of the seguyi, serrata, punjabiensis and kikkawai subgroups form a clade, which also includes the orosa subgroup. In this clade, our analyses all place the parvula subgroup sister to the rest. In agreement with Yassin et al. (2016), the seguyi-subgroup species form a clade, with D. jambulina diverging earliest. (Note that D. jambulina is Asian, whereas the remaining seguyi subgroup species are African.) The placement of the orosa subgroup is uncertain: in gene sets 2 and 3, it forms a sister lineage to the kikkawai subgroup (Fig. 1B and 1C), whereas gene set 1 places it sister to a larger clade composed of the seguyi, punjabiensis, serrata, and kikkawai subgroups (Fig. 1A). The phylograms also differ in the placement of the punjabiensis subgroup. Gene set 1 (Fig. 1A) places it sister to the seguyi subgroup, whereas gene sets 2 and 3 (Fig. 1B, 1C) place the punjabiensis subgroup sister to a clade that consists of the seguyi and serrata subgroups. The differences in the positions of both the orosa and the punjabiensis subgroups involve short branches at the base of the radiation that leads to the seguyi, serrata, punjabiensis, kikkawai, and orosa subgroups.
In addition to uncertainty in the placement of D. baimaii and D. orosa, our phylograms differ slightly in the placement of three other species within their subgroups: D. nikananu and D. greeni in the seguyi subgroup, and D. pectinifera in the montium subgroup. Using gene set 2, D. nikananu is sister to D. diplacantha (Fig. 1B), but it branches prior to D. diplacantha when using gene sets 1 and 3 (Fig. 1A and 1C). Gene set 1 (Fig. 1A) places the lineage leading to D. greeni diverging just after D. jambulina at the base of the seguyi clade radiation, gene set 3 (Fig. 1C) places D. greeni as sister to (D. seguyi, D. malagassya), and gene set 2 (Fig. 1B) does not confidently resolve the placement of D. greeni. Finally, gene sets 2 and 3 place D. pectinifera as diverging earliest from the remainder of the montium subgroup (ignoring D. baimaii), whereas gene set 1 places it sister to (D. fengkainensis, D. trapezifrons). Again, these discrepancies arise from estimating short branches near the base of a radiation.
In the auraria species complex, we have included multiple strains for D. triauraria (n = 8) and D. auraria (n = 5). Only gene set 1 (Fig. 1A) supports the monophyly of each species. This is expected, given the close relationship of these species (Gan et al., 2017; Kim et al., 1989; Miyake and Watada, 2007; Watada et al., 2011).
When we use all 60 genes in a single analysis (Fig. 2), we again produce a fully resolved phylogeny with posterior probabilities > 0.995 for every node. Our 20-gene estimates produce only six ambiguous nodes in the phylogeny of the 42 montium species. For five of those six nodes, two 20-gene analyses support one topology while the third supports an alternative (all three analyses differ concerning D. greeni). In four of those five cases (involving the placement of D. nikananu, D. orosa, D. baimaii and D. pectinifera), the 60-gene analysis agrees with the resolution inferred from two of the three 20-gene analyses. In contrast, the placement of punjabiensis subgroup in the 60-gene tree contradicts the resolution inferred from both gene sets 2 and 3, but agrees with that from gene set 1. As discussed below, we believe these ambiguities reflect limitations of current phylogenetic methods rather than a lack of data.
For all four data sets, the interspecific topologies obtained using GTR + Γ + I are identical to those presented in Fig. 1 and 2. The results differ only trivially in support values. For instance, in the 60-gene analysis, the support for the node denoting the most recent common ancestor (MRCA) of D. vulcana and D. burlai decreases from > 0.999 (GTR + Γ) to 0.997 (GTR + Γ + I), whereas the support for the MRCA of D. orosa and the kikkawai subgroup increases from 0.9987 to > 0.999. Notably, for gene set 2, the trichotomies involving placements of D. baimaii and D. greeni remain unresolved under both models. Using GTR + Γ + I instead of GTR + Γ, the support for D. baimaii being sister to all other montium group species increases from 0.65 to 0.74, while the support for D. greeni being sister to (D. malagassya, D. seguyi) decreases from 0.90 to 0.65.
3.1.1. Maximum likelihood analyses
We obtained an alternative estimate of the phylogram using ML. Fig. 3 shows the result obtained using RAxML v.8 (Stamatakis, 2014) with GTR + Γ + I on the 60-gene data set with 1000 bootstrap replicates. There are three central results: (1) the most likely phylogeny is generally concordant with our Bayesian estimate (Fig. 2); (2) bootstrap support values indicate significantly lower confidence in the estimated topology than suggested by the Bayesian posterior probabilities; and (3) with one exception, the only interspecific nodes with less than 99% bootstrap support are those showing discordance among our three 20-gene Bayesian estimates. The one exception occurs in the seguyi subgroup. The ML analysis provides only 67% bootstrap support for D. vulcana being sister to the clade that spans D. burlai to sp. cf. bakoue. This relationship has posterior support > 0.995 in all four of our Bayesian analyses, but has support < 0.999 for our Bayesian analyses of gene sets 1 and 2. The largest discrepancy between the ML topology in Fig. 3 and the 60-gene Bayesian result in Fig. 2 concerns the relationships of the three subgroups: punjabiensis, seguyi and serrata. The ML tree gives 82% bootstrap support to (punjabiensis, (seguyi, serrata)), whereas the Bayesian tree gives posterior probability > 0.999 to (serrata, (punjabiensis, seguyi)). Notably the ML topology, (punjabiensis, (seguyi, serrata)), is supported by two of the three 20-gene Bayesian analyses (gene sets 2 and 3, see Fig. 1).
Fig. 3.
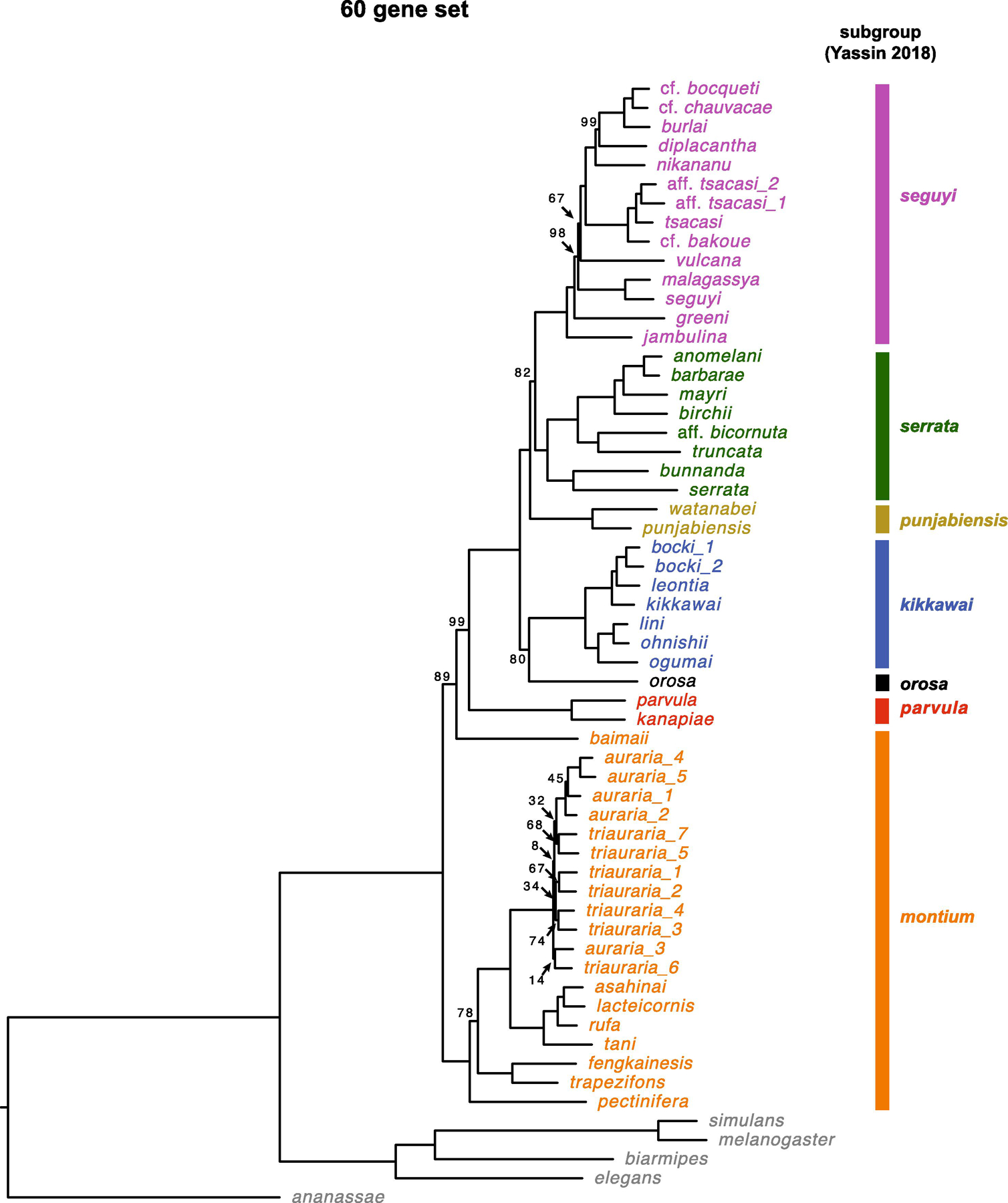
Estimate of the D. montium species group phylogeny based on all 60 loci (Table 1) using RAxML. We present bootstrap support values based on 1000 bootstrap replicates. The scale bars show the average number of estimated substitutions per site over the specified branch length.
Finding lower bootstrap support values than Bayesian posterior probabilities is common, as is the observation that Bayesian posterior values can strongly support incorrect topologies due to model misspecification (Douady et al., 2003; Erixon et al., 2003; Yang and Zhu, 2018). Overall, the ML results in Fig. 3 reinforce both the principal topological inferences from our Bayesian analyses and the uncertainties revealed by our three independent 20-gene analyses (Fig. 1 and 2). Moreover, the 60-gene ML analysis supports our Bayesian conclusions that disagree with the topology of Yassin et al. (2016) (Fig. 1D, e.g., the kikkawai subgroup is sister to a clade formed by the three subgroups punjabiensis, seguyi and serrata, and the montium subgroup splits first from the remaining subgroups in the montium group).
3.2. Chronograms
Using all 60 loci, we estimated three chronograms with RevBayes using priors that allowed for different levels of variation in rates of molecular evolution across branches: Γ(2,2), Γ(7,7) and strict-clock (corresponding Γ(n,n) as n →∞). These models, like those used to estimate our phylograms, all assume that the ratios of rates of evolution for each partition remain constant across the tree (an assumption refuted by some of the earliest analyses of molecular evolution, e.g., Langley and Fitch, 1974). However, chronogram estimates also impose an additional constraint: constant multipliers must be found for each partition to achieve a constant length from each tip to the root (phylograms allow these distances to vary among tips). This additional constraint increases the degree of model misspecification and hence increases the chance that Bayesian analyses might strongly support to an incorrect topology (Yang and Zhu, 2018).
In Fig. 4, we use the same colors as in the phylograms to indicate the subgroups designated by Yassin (2018). The strict-clock (Fig. 4A) and the Γ(7,7) chronogram (Fig. 4B) correctly place D. melanogaster as the outgroup. For those analyses, we provide 95% posterior confidence intervals. Using the more variable Γ(2,2) branch-rate prior, we found it necessary to impose the constraint that D. melanogaster is the outgroup. With that constraint, the Γ(2,2) and Γ(7,7) chronograms produce identical topologies that agree with our 60-gene phylograms (Fig. 2 and 3). The strict-clock chronogram differs from the relaxed-clock chronograms (and all of our phylograms) in the placement of D. baimaii and D. kanapiae. Consistent with our phylograms (Fig. 1–3), the Γ(7,7) and Γ(2,2) chronograms place the parvula subgroup species D. kanapiae as sister to the clade composed of the seguyi, serrata, punjabiensis, kikkawai and orosa subgroups. In contrast, the topology inferred under the strict-clock assumption contradicts all five phylograms (Bayesian and ML), placing (D. kanapiae, D. baimaii) as sister to the montium subgroup. None of our chronograms place D. baimaii within the montium subgroup. (Consistent with this conclusion, Yassin (2018) noted that the morphology of the inner paraphyses in D. baimaii males was atypical for the montium subgroup.)
Fig. 4.
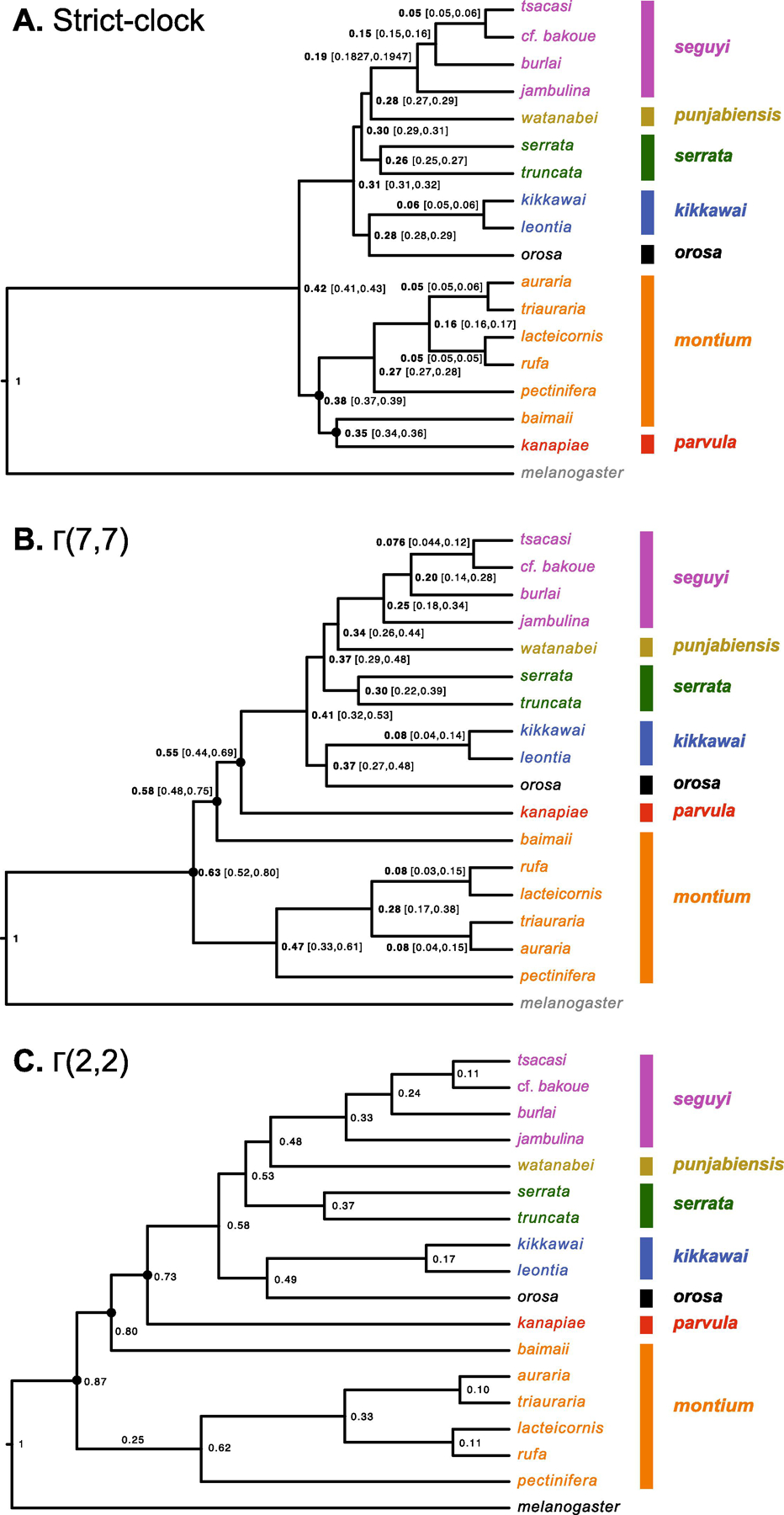
Alternative relative chronograms for the D. montium species group. Numbers at the nodes are times scaled relative to the divergence time between the D. melanogaster and the montium species group. The three analyses differ only in the priors assumed for relative rates of molecular evolution across branches: A) assumes a strict molecular clock, as in Yassin et al. (2016) (corresponding to a Γ(n,n) branch-rate prior with n →∞), B) assumes a relaxed clock with rates of evolution across branches following a Γ(7,7) distribution, and C) assumes a more relaxed clock with Γ(2,2) prior. Each analysis uses all 60 loci from Table 1. Nodes that vary among the three chronograms are marked with a black dot. To reduce computation times, we used only a subset of the genomes analyzed in Fig. 1 and 2. Strains triauraria_7 and auraria_1 were used.
Overall, allowing for non-clock-like patterns of substitutions leads to inferring an older age for the divergence of the montium species relative to their divergence from D. melanogaster. Under the strict clock, this relative divergence time is 0.42, but it increases to 0.63 under Γ(7,7) and to 0.87 under Γ(2,2). Given that we have not independently calibrated the age of the 190-member melanogaster group (sensu Hsu 1949), we cannot assess whether the alternative variable branch-length models produce different absolute ages for the montium crown group.
4. Discussion
Our results generally support the taxonomic revision and proposed phylogeny of the montium clade from Yassin (2018). However, our much more extensive sequence data and alternative methods for inferring phylogenies and estimating chronograms produce greater phylogenetic resolution while also highlighting difficult-to-resolve relationships and uncertain divergence times. The unresolved phylogenetic questions involve a small number of nodes subtended by short branches relatively deep in the tree. As discussed below, genomic data do not provide a magic bullet for resolving these phylogenetic ambiguities. Our chronograms based on alternative priors also illustrate some of the difficulties associated with estimating clade ages. Nevertheless, we suspect that more refined resolutions of these estimation problems are unlikely to affect the utility of the montium species group for comparative evolutionary studies. Below, we first discuss methodological issues concerning phylogenetic inference, focusing on: alternative biological causes for conflicting topologies estimated from different loci, the difficulty of accurately modeling molecular evolution and speciation, and the limitations imposed on the complexity of models of cladogenesis and molecular anagenesis by computing resources and available software. We then consider the biological implications of our results and prospects for future analyses.
4.1. Why use only 60 loci when full draft genomes are available?
Whole-genome methods for phylogenetic inference are proliferating. However, to estimate phylogenies using data from thousands of loci, compromises must be made in determining orthology and in choosing a model of molecular evolution, a model of cladogenesis, and statistical methodology (reviewed in Rannala and Yang, 2008; Degnan and Rosenberg, 2009; Lemmon and Lemmon, 2013; Flouri et al,. 2018; Lees et al., 2018). Rather than trying to align our draft genomes, we have chosen instead to focus on a relatively small number of carefully curated, single-copy loci for which we are highly confident of orthology. By focusing on only 60 genes, we could perform full Bayesian analyses for relatively complex substitution models using modest computational resources.
Why not use more data? Since the advent of likelihood-based molecular phylogenetics in the 1980s (Felsenstein, 1981, 1988), studies have generally sought to use ever more sequence data to fully and confidently resolve phylogenies (e.g., Prum et al., 2015 for birds; Edelman et al., 2019 for Heliconius butterflies). The general goal is to produce a fully resolved topology, with strong statistical support for each node, as indicated by high posterior probabilities and/or high bootstrap support values. Our three separate Bayesian estimates based on DNA coding sequences for sets of 20 orthologous proteins (Fig. 1A–C) show that data from a moderate number of loci generally suffice to produce fully resolved trees for the montium clade, with Bayesian posterior values > 0.999 for almost every node. Hence, our limited data do not lack statistical resolving power. Nevertheless, our alternative data sets imply essentially complete confidence in topologies that are inconsistent with each other at a small subset of nodes. The inconsistencies are almost surely due to model misspecification (Yang and Zhu 2018). Using even more data, as when we combined all 60 loci (Fig. 2), will produce yet another fully resolved, highly supported tree. What remains uncertain is whether any of the estimated phylogenies correctly reconstruct species relationships.
Measures of statistical confidence are reliable only if the stochastic model for sequence change is accurate (Huelsenbeck and Rannala, 2004; Brown and Thomson, 2018), the aligned sequences reliably reflect lineage divergence (i.e., orthologs are accurately distinguished from paralogs, Fitch, 1970), and lineage divergence is accurately modeled, typically under the assumption of a strictly bifurcating tree (cf. Schumer et al., 2018; Edelman et al., 2019). Different loci can lead to different estimated topologies for at least five reasons: 1) incomplete lineage sorting (ILS), associated with alternative coalescent patterns produced by polymorphisms in ancestral lineages (Gillespie and Langley, 1979; Maddison, 1997; Edwards, 2009); 2) misidentification of paralogous loci as orthologous (Fitch, 1970); 3) introgression (Edelman et al., 2019); 4) inaccurate models of lineage divergence, for instance assuming purely allopatric speciation versus speciation with gene flow or, more extreme, monoploid hybrid speciation (e.g., Rieseberg et al., 2003; Schumer et al., 2018); or 5) inaccurate models of molecular evolution (Brown and Thomson, 2018). No currently available software attempts to control for all of these sources of ambiguity. Compromises are necessary, suggesting that consistency across methods and data sets may be a plausible ad hoc guide to accuracy, with the caveat that counterexamples are known (e.g., Degnan and Rosenberg (2006) show that with ILS, the majority of single-gene estimates may favor an incorrect topology).
ILS is the source of gene-tree conflicts most often considered, because of its connection to well-developed neutral coalescent theory from population genetics. It is widely appreciated that split times associated with individual gene trees generally do not accurately reflect species divergence times (Gillespie and Langley, 1979), and that molecular polymorphisms can generate gene-tree, species-tree conflicts (Maddison, 1997; Hudson and Coyne, 2002). ILS is surely common, but standard ILS models implicitly assume purely allopatric speciation without gene flow and attempt to account for between-locus inconsistencies solely in terms of ancestral polymorphisms. By not concatenating data across loci, multispecies coalescent analyses can correct for statistical inconsistencies caused by ILS (Degnan and Rosenberg, 2006; Flouri et al., 2018). However, currently implemented programs make severe constraints on the models of molecular evolution or use questionable priors or ad hoc statistical methods. Moreover, introgression is probably as pervasive as ILS, at least for Drosophila. Although the geography of speciation is unknowable for nodes deep in the species tree, the evidence for reinforcement presented by Coyne and Orr (1989, 1997) suggests that roughly half of Drosophila speciation events involve hybridization of diverging lineages (Turelli et al., 2014). The importance of introgression in Heliconius speciation is illustrated by Edelman et al. (2019). No software is widely available to deal with both ILS and introgression – and even when such software appears, the models of molecular evolution are likely to impose severe (and unrealistic) restrictions to make the calculations manageable.
In one of the earliest empirical studies of protein evolution across multiple species, Langley and Fitch (1974) demonstrated that different genes show different relative rates of substitution along different parts of the tree. None of the programs we used account for this heterogeneity. Its effect on phylogenetic inferences may be negligible or may artificially inflate statistical confidence in biased estimates (Duchene et al., 2020). These issues certainly merit further investigation. None of the widely available species-tree estimation programs account for relative-rate differences across loci that vary across branches of the tree. For simplicity, we have limited our inferences to Bayesian and maximum likelihood analyses using concatenated data, ignoring ILS, relative rate variation across the tree, and introgression. We encourage others to revisit our genomic data and analyses using alternative methods or alternative data types (e.g., insertion elements, Springer et al., 2020). The contrast and similarities between the conflicting conclusions of highly resolved Bayesian inferences (Fig. 1 and 2) and the uncertainties indicated by ML bootstrap support (Fig. 3) make clear the value of comparing alternative phylogeny estimates in assessing robustness.
4.2. Phylograms versus relative chronograms
By contrasting a strict-clock chronogram (Fig. 4A) with two relaxed-clock chronograms, assuming different branch-rate priors (Fig. 4B,C), we see that the strict-clock assumption leads to an inferred topology that differs from all of our phylograms in its placement of the parvula-subgroup species D. kanapiae. Assuming a molecular clock can produce artifactual topologies in the face of pervasive evidence for time-varying rates (e.g., Kolaczkowski and Thornton 2008). Hence, some of the discrepancies between our results and those of Yassin et al. (2016) are likely to arise from their assumption of a molecular clock. Because branch lengths confound time and substitution rates, it is well known that branch-rate priors can significantly affect estimates of relative divergence times (cf. dos Reis et al., 2018). This effect is clearly illustrated in Fig. 4.
4.3. Implications for the history of the montium species group
Due to the paucity of suitable amber fossils (Grimaldi, 1987), the absolute timescale of Drosophila evolution is uncertain. The available calibration approaches are based either on sequence comparisons between Drosophila species endemic to Hawaiian islands of different age (Tamura et al., 2004; Obbard et al., 2012; Gao et al., 2011; Izumitani et al. 2011; Russo et al., 2013) or on mutation rates measured in laboratory strains of D. melanogaster (Cutter 2008; Obbard et al., 2012). The resulting estimates vary widely depending on the calibration method, the sequence data, and the model used (Obbard et al., 2012). Yassin (2018), following Russo et al. (2013), assumed the split between D. melanogaster and the montium species group to have occurred ~28 MY ago, and estimated the montium crown group to be ~19.3 MY old. Our results suggest that this analysis may have underestimated the age of the montium group due to the use of a strict-clock model; relaxed clock analyses (Fig. 4) suggest that the montium crown group is closer in age to the melanogaster-montium split.
Our results largely confirm that the subgroups within the montium species group proposed by Yassin (2018) are monophyletic. However, the assignment of D. baimaii to the montium subgroup seems doubtful; and we obviously cannot assess the monophyly of the orosa subgroup, for which we have data from only one species. On the other hand, the relationships we infer among subgroups differ substantially from Yassin (2018). The new phylogeny indicates that the montium subgroup branched first (in particular, earlier than the parvula subgroup), while the punjabiensis subgroup is closer to the seguyi subgroup than suggested by Yassin (2018).
Our data support the overall conclusion of Yassin (2018) that the montium species group originated in Southeast Asia and spread gradually westward and northward, but the details of this spread may differ slightly from his proposal. For instance, D. jambulina, the most basal species in the seguyi subgroup, is the only South Asian member of that otherwise African clade, and the seguyi subgroup as a whole forms a clade with the South Asian punjabiensis subgroup. This suggests that the last common ancestor of the punjabiensis and seguyi subgroups occurred in South Asia (following, presumably, dispersal from Southeast Asia), and that South Asia served as a stepping stone for a single invasion of Africa. The Southeast Asian parvula subgroup, which occupied the most basal position in the phylogeny of Yassin (2018), seems actually to be more recently derived than the mainly Northeast Asian montium subgroup. In the latter clade, the most basal branch is D. pectinifera, endemic to the Ogasawara Islands in the southeast of Japan; this is followed by the split between the D. trapezifrons + D. fengkainensis species pair (which is distributed across Southern China, Taiwan, and South Asia) and a large clade composed of the auraria and rufa species complexes (sensu Yassin, 2018), which have a predominantly Northeast Asian distribution. These observations highlight an interesting pattern: although most subgroups in the montium species group (including the kikkawai, serrata, and parvula subgroups) have occupied Southeast Asia since their origin, only the montium subgroup experienced northward expansion.
4.4. Persistent ambiguities: Do they matter for comparative studies?
Not surprisingly, the species-rich montium species group encompasses significant phenotypic diversity. It has been used as a model to study the evolution of sex-specific pigmentation (Yassin et al., 2016), the structure of male external genitalia (Yassin, 2018, 2019), and male courtship behavior (Chen et al., 2019). These studies were based on a phylogenetic hypothesis that differs from ours at both among-subgroup and within-subgroup levels. Despite using much more data, several ambiguities persist between our replicate phylogenetic analyses. These changes and ambiguities may revise estimates of the order and direction of change for some characters. However, central features of phenotypic evolution in the montium species group appear to be robust to these uncertainties. For instance, abdominal pigmentation is highly variable in both males and females across the clade (Yassin et al., 2016). Although our revised phylogeny implies a different scenario of trait evolution, it does not change the key conclusions – namely, that pigmentation evolves at a higher rate in females than in males, that female-limited color polymorphism has evolved multiple times, and that dark male pigmentation is the most likely ancestral state for the montium species group (Yassin et al., 2016). Similarly, our updated phylogeny that places the montium subgroup more basally than the parvula subgroup does not affect the inference that post-mounting male courtship song evolved at the base of the entire montium species group (Chen et al., 2019). Since most losses of pre-mounting song, and most transitions between different song types, are observed within individual subgroups, our revision of phylogenetic relationships among subgroups is consistent with the general conclusion that pre-mounting song has been lost multiple times, and that the diversity of song types in the montium species group reflects many independent transitions (Chen et al., 2019).
4.5. Wolbachia-host dynamics and coevolution
A central question for Wolbachia-host interactions is the tempo and mode of Wolbachia acquisition, which can elucidate patterns of coevolution. Currently about half of all insect species, including Drosophila species, are known to harbor Wolbachia infections (Weinert et al., 2015). Phylogenetically informed comparative genomic analyses, involving host nuclear and mitochondrial genomes and Wolbachia genomes, are needed to untangle how Wolbachia are acquired. Such analyses indicate that many Wolbachia infections, at least among Drosophila, have been relatively recently obtained, within 103–105 years, by a combination of introgression between close relatives and non-sexual horizontal transmission (Conner et al., 2017; Turelli et al. 2018, Cooper et al., 2019). The time-scales of Wolbachia and host divergence can be understood only by cross-calibrations, which quantify the relative rates of divergence for host nuclear and mitochondrial genomes – and for Wolbachia genomes in cases of cladogenic transmission from common ancestors. To date, the only calibrations based on co-speciation of Wolbachia and its hosts come from Nasonia wasps (Raychoudhury et al., 2009) and Nomada bees (Gerth and Bleidorn, 2016). Our ongoing genomic analyses of these montium species seem to provide the first example of cladogenic Wolbachia transmission between Drosophila species, with close relatives retaining Wolbachia from a common ancestor (Cooper, Hoffmann and Turelli, unpubl.). Such discoveries are facilitated by species-level phylogenies and relatively complete taxon sampling. They depend primarily on the confident identification of sister species and other close relatives and are relatively robust to uncertainties deeper in the species tree.
4.6. Conclusion
Overall, we hope our comprehensive phylogenetic analysis of species relationships within the montium species group will enable genomic analyses that clarify evolutionary inferences across this diverse clade.
Supplementary Material
Highlights.
We estimate phylogenies and chronograms for 42 of 94 species of the montium group
20 nuclear loci suffice to produce well-resolved Bayesian phylogenetic estimates
3 non-overlapping sets of 20 loci produce slightly discordant Bayesian phylogenies
Maximum likelihood and bootstrap analyses of 60 loci reinforce these uncertainties
Divergence time estimates depend critically on difficult-to-test prior assumptions
Acknowledgements
We thank our following funding sources: NIH NRSA 1 F32 GM120893–01A1 & UC Chancellor’s Fellowship (EKD), NIH MIRAs R35GM124701 (BSC) and R35GM122592 (AK), NIH R01-GM-104325 (MT & AAH), and the Howard Hughes Medical Institute (MBE). We also thank Amir Yassin, Mike May, Matt Hahn and an anonymous reviewer for comments and suggestions that significantly improved our analyses and presentation.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declarations of interest: none.
References
- Abadi S, Azouri D, Pupko T, Mayrose T, 2019. Model selection may not be a mandatory step for phylogeny reconstruction. Nature Comm 10, 934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen SL, Delaney EK, Kopp A, Chenoweth SF, 2017. Single-molecule sequencing of the Drosophila serrata genome. G3 Genes, Genomes, Genet 7, 781–788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barmina O, Kopp A 2007. Sex-specific expression of a HOX gene associated with rapid morphological evolution. Developmental Biol 311, 277–286. [DOI] [PubMed] [Google Scholar]
- Bächli G 2020. The database on Taxonomy of Drosophilidae http://www.taxodros.uzh.ch/, accessed September 2020.
- Bock IR, 1980. Current status of the Drosophila melanogaster species-group. (Diptera). Syst. Ent 5, 341–356. [Google Scholar]
- Bock IR, Wheeler MR, 1972. The Drosophila melanogaster species group. Univ. Texas Publ VII, 1–102. [Google Scholar]
- Bollback JP, 2002. Bayesian model adequacy and choice in phylogenetics. Mol. Biol. Evol 19, 1171–1180. [DOI] [PubMed] [Google Scholar]
- Bronski MJ, Martinez CC, Weld HA, Eisen MB, 2020. Whole genome sequences of 23 species from the Drosophila montium species group (Diptera : Drosophilidae): a resource for testing evolutionary hypotheses. G3 Genes, Genomes, Genet 10, 1443–1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown JM, Thomson RC, 2018. Evaluating model performance in evolutionary biology. Ann. Rev. Ecol. Evol. Syst 49, 95–114. [Google Scholar]
- Burbano HA, Green RE, Maricic T, Lalueza-Fox C, de la Rasilla M, Rosas A, Kelso J, Pollard KS, Lachmann M, Pääbo S, 2012. Analysis of human accelerated DNA regions using archaic hominin genomes. PLoS One 7, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen A, Chen C-C, Katoh T, Katoh TK, Watada M, Toda MJ, Ritchie MG, Wen S-Y, 2019. Evolution and diversity of the courtship repertoire in the Drosophila montium species group (Diptera: Drosophilidae). J. Evol. Biol 32, 1124–1140. [DOI] [PubMed] [Google Scholar]
- Chen C-C, Watada M, Miyake H, Katoh TK, Sun Z, Li Y-F, Ritchie MG, Wen S-Y, 2013. Courtship patterns in the Drosophila montium species subgroup: repeated loss of precopulatory courtship? Zoolog. Sci 30, 1056–1062. [DOI] [PubMed] [Google Scholar]
- Chen Z-X, Sturgill D, Qu J, Jiang H, Park S, Boley N, Suzuki AM, Fletcher AR, Plachetzki DC, FitzGerald PC, et al. , 2014. Comparative validation of the D. melanogaster modENCODE transcriptome annotation. Genome Res 24, 1209–1223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chikina M, Robinson JD, Clark NL, 2016. Hundreds of genes experienced convergent shifts in selective pressure in marine mammals. Mol. Biol. Evol 33, 2182–2192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark AG, Eisen MB, Smith DR, Bergman CM, Oliver B, Markow TA, Kaufman TC, Kellis M, Gelbart W, Iyer VN, et al. , 2007. Evolution of genes and genomes on the Drosophila phylogeny. Nature 450, 203–218. [DOI] [PubMed] [Google Scholar]
- Conner WR, Blaxter ML, Anfora G, Ometto L, Rota-Stabelli O, Turelli M, 2017. Genome comparisons indicate recent transfer of wRi-like Wolbachia between sister species Drosophila suzukii and D. subpulchrella. Ecology and Evolution 7, 9391–9404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper BS, Vanderpool D, Conner WR, Matute DR, Turelli M, 2019. Wolbachia acquisition by Drosophila yakuba-clade hosts and transfer of incompatibility loci between distantly related Wolbachia. Genetics 212, 1399–1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coyne JA, Orr HA, 1989. Patterns of speciation in Drosophila. Evolution 43, 362–381. [DOI] [PubMed] [Google Scholar]
- Coyne JA, Orr HA, 1997. “Patterns of speciation in Drosophila” revisited. Evolution 51, 295–303. [DOI] [PubMed] [Google Scholar]
- Cutter AD, 2008. Divergence times in Caenorhabditis and Drosophila inferred from direct estimates of the neutral mutation rate. Mol. Biol. Evol 25, 778–786. [DOI] [PubMed] [Google Scholar]
- Da Lage JL, Kergoat GJ, Maczkowiak F, Silvain JF, Cariou ML, Lachaise D, 2007. A phylogeny of Drosophilidae using the Amyrel gene: Questioning the Drosophila melanogaster species group boundaries. J. Zool. Syst. Evol. Res 45, 47–63. [Google Scholar]
- Degnan JH, Rosenberg NA, 2006. Discordance of species trees with their most likely gene trees. PLoS Genet 2, e68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Degnan JH, Rosenberg NA, 2009. Gene tree discordance, phylogenetic inference and the multispecies coalescent. Trends Ecol. Evol 24, 332–340. [DOI] [PubMed] [Google Scholar]
- dos Reis M, Gunnell GF, Barba-Montoya J, Wilkins A, Yang Z, Yoder AD, 2018. Using phylogenomic data to explore the effects of relaxed clocks and calibration strategies on divergence time estimation: primates as a test case. Syst. Biol 67, 594–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douady CJ, Delusc F, Boucher Y, Doolittle WF, Douzery EJP 2003. Comparison of Bayesian and maximum likelihood bootstrap measures of phylogenetic reliability. Mol. Biol. Evol 20, 248–254. [DOI] [PubMed] [Google Scholar]
- Duchene DA, Tong KJ, Foster CSP, Duchene S, Lanfear R, Ho SYW, 2020. Linking branch lengths across sets of loci provides the highest statistical support for phylogenetic inference. Mol. Biol. Evol 37, 1202–1210. [DOI] [PubMed] [Google Scholar]
- Edelman NB, Frandsen PB, Miyagi M, Clavigo B, Davey J, Dikow RB, Garcia-Accinelli G, Van Belleghem SM, Patterson N, Neafsey DE, et al. , 2019. Genetic architecture and introgression shape a butterfly radiation. Science 366, 594–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards SV, 2009. Is a new and general theory of molecular systematics emerging? Evolution 63, 1–19. [DOI] [PubMed] [Google Scholar]
- Erixon P, Svennblad B, Britton T, Oxelman B 2003. Reliability of Bayesian posterior probabilities and bootstrap frequencies in phylogenetics. Syst. Biol 52, 665–673. [DOI] [PubMed] [Google Scholar]
- Felsenstein J, 1981. Evolutionary trees from DNA sequences: a maximum likelihood approach. J. Mol. Evol 17, 368–376. [DOI] [PubMed] [Google Scholar]
- Felsenstein J, 1988. Phylogenies from molecular sequences: inference and reliability. Ann. Rev. Genet 22, 521–565. [DOI] [PubMed] [Google Scholar]
- Fitch WM, 1970. Distinguishing homologous from analogous proteins. Syst. Zool 19, 99–113. [PubMed] [Google Scholar]
- Flouri T, Jiao X, Rannala B, Yang Z, 2018. Species tree inference with BPP using genome sequences and the multispecies coalescent. Mol. Biol. Evol 35, 2585–2593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gan L, Li G, Li W, Zeng Q, Yang Y, 2017. Increase data characters to construct the molecular phylogeny of the Drosophila auraria species complex. Open J. Genet 7, 40–49. [Google Scholar]
- Gao J. j., Hu Y. g., Toda MJ, Katoh T, Tamura K, 2011. Phylogenetic relationships between Sophophora and Lordiphosa, with proposition of a hypothesis on the vicariant divergences of tropical lineages between the Old and New Worlds in the family Drosophilidae. Mol. Phylogenet. Evol 60, 98–107. [DOI] [PubMed] [Google Scholar]
- Gerth M, Bleidorn C, 2016. Comparative genomics provides a timeframe for Wolbachia evolution and exposes a recent biotin synthesis operon transfer. Nature Microbiology 2, 16241. [DOI] [PubMed] [Google Scholar]
- Gillespie JH, Langley CH, 1979. Are evolutionary rates really variable? J. Mol. Evol 13, 27–34. [DOI] [PubMed] [Google Scholar]
- Goto SG, Kitamura HW, Kimura MT, 2000. Phylogenetic relationships and climatic adaptations in the Drosophila takahashii and montium species subgroups. Mol. Phylogenet. Evol 15, 147–156. [DOI] [PubMed] [Google Scholar]
- Green RE, Krause J, Briggs AW, Maricic T, Stenzel U, Kircher M, Patterson N, Li H, Zhai W, Fritz MHY, Hansen NF, et al. , 2010. A draft sequence of the Neandertal genome. Science 328, 710–722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grimaldi DA, 1987. Amber fossil Drosophilidae (Diptera), with particular reference to the Hispaniolan taxa. American Museum Novitates 2888, 1–23. [Google Scholar]
- Hare EE, Peterson BK, Iyer VN, Meier R, Eisen MB, 2008. Sepsid even-skipped enhancers are functionally conserved in Drosophila despite lack of sequence conservation. PLoS Genet 4, e1000106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hohna S, Landis MJ, Heath TA, Boussau B, Lartillot N, Moore BR, Huelsenbeck JP, Ronquist F, 2016. RevBayes: Bayesian phylogenetic inference using graphical models and an interactive model-specification language. Syst. Biol 65, 726–736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson RR, Coyne JA, 2002. Mathematical consequences of the genealogical species concept. Evolution 56, 1557–1565. [DOI] [PubMed] [Google Scholar]
- Hsu TC, 1949. The external genital apparatus of male Drosophilidae in relation to systematics. Univ. Texas Publ 4920, 80–142. [Google Scholar]
- Huelsenbeck JP, Rannala B, 2004. Frequentist properties of Bayesian posterior probabilities of phylogenetic trees under simple and complex substitution models. Syst. Biol 53, 904–913. [DOI] [PubMed] [Google Scholar]
- Izumitani HF, Kusaka Y, Koshikawa S, Toda MJ, Katoh T, 2016. Phylogeography of the subgenus Drosophila (Diptera: Drosophilidae): evolutionary history of faunal divergence between the old and new worlds. PLoS ONE 11, e0160051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackman SD, Vandervalk BP, Mohamadi H, Chu J, Yeo S, Hammond SA, Jahesh G, Khan H, Coombe L, Warren RL, Birol I, 2017. ABySS 2.0: resource-efficient assembly of large genomes using a Bloom filter. Genome Res 27, 768–777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi NA, Fass JN, 2011. Sickle: A sliding-window, adaptive, quality-based trimming tool for FastQ files. (Version 1.33) [Software] Available at https://github.com/najoshi/sickle.
- Kainer D, Lanfear R, 2015. The effects of partitioning on phylogenetic inference. Mol. Biol. Evol 32, 1611–1627. [DOI] [PubMed] [Google Scholar]
- Katoh K, Standley DM, 2013. MAFFT Multiple sequence alignment software version 7: improvements in performance and usability. Mol. Biol. Evol 30, 772–780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kellermann V, van Heerwaarden B, Sgro CM, Hoffmann AA, 2009. Fundamental evolutionary limits in ecological traits drive Drosophila species distributions. Science 325, 1244–1246. [DOI] [PubMed] [Google Scholar]
- Kim BK, Kitagawa O, Watanabe TK, 1989. Evolutionary genetics of the Drosophila montium subgroup. I. Reproductive isolations and the phylogeny. Japanese J. Genet 64, 177–190. [DOI] [PubMed] [Google Scholar]
- Kim J, He X, Sinha S, 2009. Evolution of regulatory sequences in 12 Drosophila species. PLoS Genet 5, e1000330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolaczkowski B, Thornton JW, 2008. A mixed branch length model of heterotachy improves phylogenetic accuracy. Mol. Biol. Evol 25, 1054–1066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopp A, True JR, 2002. Phylogeny of the Oriental Drosophila melanogaster species group: a multilocus reconstruction. Syst. Biol. 51, 786–805. [DOI] [PubMed] [Google Scholar]
- Kopp A, Barmina O, Prigent SR, 2019. Phylogenetic position of the Drosophila fima and dentissima lineages, and the status of the D. melanogaster species group. Mol. Phylogenet. Evol 139, 106543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopp A, Duncan I, Carroll SB, 2000. Genetic control and evolution of sexually dimorphic characters in Drosophila. Nature 408, 553–559. [DOI] [PubMed] [Google Scholar]
- Langley CH, Fitch WM, 1974. An examination of the constancy of the rate of molecular evolution. J. Mol. Evol 3, 161–177. [DOI] [PubMed] [Google Scholar]
- Lees JA, Kendall M, Parkhill J, Colijn C, Bentley SD, Harris SR, 2018. Evaluation of phylogenetic reconstruction methods using bacterial whole genomes: a simulation based study. Wellcome Open Research 3, 33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemmon EM, Lemmon AR, 2013. High-throughput genomic data in systematics and phylogenetics. Ann. Rev. Ecol. Evol. Syst 44, 99–121. [Google Scholar]
- Lemeunier F, David JR, Tsacas L, Ashburner M, 1986. The melanogaster species group. In: Ashburner M, Carson HL, Thompson JN (Eds.), The Genetics and Biology of Drosophila. Academic Press, New York, NY, pp. 147–256. [Google Scholar]
- Ludwig MZ, Kreitman M 1995. Evolutionary dynamics of the enhancer region of even-skipped in Drosophila. Mol. Biol. Evol 12, 1002–1111. [DOI] [PubMed] [Google Scholar]
- Ludwig MZ, Patel NH, Kreitman M, 1998. Functional analysis of eve stripe 2 enhancer evolution in Drosophila: rules governing conservation and change. Development 125, 949–958.9449677 [Google Scholar]
- Ludwig MZ, Bergman C, Patel NH, Kreitman M, 2000. Evidence for stabilizing selection in a eukaryotic enhancer element. Nature 403, 564–567. [DOI] [PubMed] [Google Scholar]
- Maddison WP, 1997. Gene trees in species trees. Syst. Biol 46, 523–536. [Google Scholar]
- Meany MK, Conner WR, Richter SV, Bailey JA, Turelli M, Cooper BS, 2019. Loss of cytoplasmic incompatibility and minimal fecundity effects explain relatively low Wolbachia frequencies in Drosophila mauritiana. Evolution 73, 1278–1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyake H, Watada M, 2007. Molecular phylogeny of the Drosophila auraria species complex and allied species of Japan based on nuclear and mitochondrial DNA sequences. Genes Genet. Syst 82, 77–88. [DOI] [PubMed] [Google Scholar]
- Nikolaidis N, Scouras ZG, 1996. The Drosophila montium subgroup species. Phylogenetic relationships based on mitochondrial DNA analysis. Genome 39, 874–883. [DOI] [PubMed] [Google Scholar]
- Nishida AH, Ochman H, 2019. A great-ape view of the gut microbiome. Nature Reviews Genetics 20, 195–206. [DOI] [PubMed] [Google Scholar]
- Nguyen L-T, von Haeseler A, Minh BQ 2018. Complex models of sequence evolution require accurate estimators as exemplified by the invariable site plus gamma model. Syst. Biol 67, 552–558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Obbard DJ, Maclennan J, Kim K-W, Rambaut A, O’Grady PM, Jiggins FM, 2012. Estimating divergence dates and substitution rates in the Drosophila phylogeny, Mol. Biol. Evol 29:3459–3473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohnishi S, Kim K, Watanabe TK, 1983. Biochemical phylogeny of the Drosophila montium species subgroup. Japanese J. Genet 58, 141–151. [Google Scholar]
- O’Grady PM, DeSalle R, 2018. Phylogeny of the genus Drosophila. Genetics 209, 1–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Partha R, Chauhan BK, Ferreira Z, Robinson JD, Lathrop K, Nischal KK, Chikina M, Clark NL, 2017. Subterranean mammals show convergent regression in ocular genes and enhancers, along with adaptation to tunneling. Elife 6, 1–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson JT, Stone WS, 1952. Evolution in the genus Drosophila. Macmillan, New York. [Google Scholar]
- Prigent SR, Lang M, Nagy O, Acurio A, Matamoro-Vidal A, David JR, 2020. Field collections reveal that São Tomé is the Afrotropical island with the highest diversity of drosophilid flies (Diptera: Drosophilidae). Ann. la Soc. Entomol. Fr 56, 1–14. [Google Scholar]
- Prum RO, Berv JS, Dornburg A, Field DJ, Townsend JP, Lemmon EM, Lemmon AR, 2015. A comprehensive phylogeny of birds (Aves) using targeted next-generation DNA sequencing. Nature 526, 656–660. [DOI] [PubMed] [Google Scholar]
- Rambaut A, Drummond AJ, Dong X, Baele G, Suchard MA 2018. Posterior summarization in Bayesian phylogenetics under Tracer 1.7. Syst. Biol 67, 901–904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rannala B, Yang Z, 2008. Phylogenetic inference using whole genomes. Ann. Rev. Genomics Hum. Genet 9, 217–231. [DOI] [PubMed] [Google Scholar]
- Raychoudhury R, Baldo L, Oliveira DCSG, Werren JH, 2009. Modes of acquisition of Wolbachia: horizontal transfer, hybrid introgression, and codivergence in the Nasonia species complex. Evolution 63, 165–183. [DOI] [PubMed] [Google Scholar]
- Reich D, Green RE, Kircher M, Krause J, Patterson N, Durand EY, Viola B, Briggs AW, Stenzel U, Johnson PLF, et al. 2010. Genetic history of an archaic hominin group from Denisova cave in Siberia. Nature 468, 1053–1060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rieseberg LH, Raymond O, Rosenthal DM, Lai Z, Livingstone K, Nakazato T, Durphy JL, Schwarzbach AE, Donovan LA, Lexer C, 2003. Major ecological transitions in wild sunflowers facilitated by hybridization. Science 301, 1211–1216. [DOI] [PubMed] [Google Scholar]
- Rogers J, 2018. Adding resolution and dimensionality to comparative genomics: Moving from reference genomes to clade genomics. Genome Biol 19, 18–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russo C. a. M., Mello B, Frazão A, Voloch CM, 2013. Phylogenetic analysis and a time tree for a large drosophilid data set (Diptera: Drosophilidae). Zool. J. Linn. Soc 169, 765–775. [Google Scholar]
- Schawaroch V, 2002. Phylogeny of a paradigm lineage: the Drosophila melanogaster species group (Diptera: Drosophilidae). Biol. J. Linn. Soc 76, 21–37. [Google Scholar]
- Schumer M, Xu C, Powell DL, Durvasula A, Skov L, Holland C, Blazier JC, Sankararaman S, Andolfatto P, Rosenthal GG, Przeworski M, 2018. Natural selection interacts with recombination to shape the evolution of hybrid genomes. Science 360, 656–660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Springer S, Molloy EK, Sloan DB, Simmons MP, Gatesy J, 2020. ILS-aware analysis of low-homoplasy retroelement insertions: inference of species trees and introgression usingg quartets. J. Heredity 111, 147–168. [DOI] [PubMed] [Google Scholar]
- Stamatakis A, 2014. RAxML version 8: a tool for phylogenetic analysis and post-analysis for large phylogenies. Bioinformatics 30, 1312–1313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stark A, Lin MF, Kheradpour P, Pedersen JS, Parts L, Carlson JW, Crosby MA, Rasmussen MD, Roy S, Deoras AN, et al. , 2007. Discovery of functional elements in 12 Drosophila genomes using evolutionary signatures. Nature 450, 219–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swanson CI, Schwimmer DB, Barolo S, 2011. Rapid evolutionary rewiring of a structurally constrained eye enhancer. Curr. Biol 21, 1186–1196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamura K, Subramanian S, Kumar S, 2004. Temporal patterns of fruit fly (Drosophila) evolution revealed by mutation clocks. Mol. Biol. Evol 21, 36–44. [DOI] [PubMed] [Google Scholar]
- Thybert D, Roller M, Navarro FCP, Fiddes I, Streeter I, Feig C, Martin-Galvez D, Kolmogorov M, Janoušek V, Akanni W, et al. , 2018. Repeat associated mechanisms of genome evolution and function revealed by the Mus caroli and Mus pahari genomes. Genome Res 28, 448–459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toda MJ, 1991. Drosophilidae (Diptera) in Myanmar (Burma) VII. The Drosophila melanogaster species-group, excepting the D. montium subgroup. Oriental Insects 25, 69–94. [Google Scholar]
- Toda MJ 2020. DrosWLD-Species database https://bioinfo.museum.hokudai.ac.jp/db/index.php, accessed September 2020.
- Turelli M, Lipkowitz JR, Brandvain Y, 2014. On the Coyne and Orr-igin of species: effects of intrinsic postzygotic isolation, ecological differentiation, X-chromosome size, and sympatry on Drosophila speciation. Evolution 68, 1176–1187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turelli M, Cooper BS, Richardson KM, Ginsberg PS, Peckenpaugh B, Antelope CX, Kim KJ, May MR, Abrieux A, Wilson DA, et al. , 2018. Rapid global spread of wRi-like Wolbachia across multiple Drosophila. Curr. Biol 28, 963–971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H-C, Susko E, Roger AJ, 2019. The relative importance of modeling site pattern heterogeneity versus partition-wise heterotachy in phylogenetic inference. Syst. Biol 68, 1003–1019. [DOI] [PubMed] [Google Scholar]
- Watada M, Matsumoto M, Kondo M, Kimura MT, 2011. Taxonomic study of the Drosophila auraria species complex (Diptera: Drosophilidae) with description of a new species. Entomol. Sci 14, 392–398. [Google Scholar]
- Weinert LA, Araujo-Jnr EV, Ahmed MZ, Welch JJ, 2015. The incidence of bacterial endosymbionts in terrestrial arthropods. Proc. Roy. Soc. Lond. B 282, 20150249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie W, Lewis PO, Fan Y, Kuo L, Chen M-H, 2011. Improving marginal likelihood estimation for Bayesian phylogenetic model selection. Syst. Biol 60, 150–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z, 1994. Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J. Mol. Evol 39, 306–314. [DOI] [PubMed] [Google Scholar]
- Yang Z, Rannala B, 1997. Bayesian phylogenetic inference using DNA sequences: a Markov Chain Monte Carlo method. Mol. Biol. Evol 14, 717–724. [DOI] [PubMed] [Google Scholar]
- Yang Z, Zhu T, 2018. Bayesian selection of misspecified models is overconfident and may cause spurious posterior probabilities for phylogenetic trees. Proc. Natl. Acad. Sci. USA 115, 1854–1859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yassin A, 2018. Phylogenetic biogeography and classification of the Drosophila montium species group (Diptera: Drosophilidae). Ann. la Soc. Entomol. Fr 54, 167–175. [Google Scholar]
- Yassin A, Suwalski A, Raveloson Ravaomanarivo LH, 2019. Resolving the synonymy and polyphyly of the ‘Drosophila bakoue species complex’ (Diptera: Drosophilidae: ‘D. montium species group’) with descriptions of two new species from Madagascar. European J. Taxonomy 532, 1–26. [Google Scholar]
- Yassin A, Delaney EK, Reddiex AJ, Seher TD, Bastide H, Appleton NC, Lack JB, David JR, Chenoweth SF, Pool JE, et al. , 2016. The pdm3 locus is a hotspot for recurrent evolution of female-limited color dimorphism in Drosophila. Curr. Biol 26, 2412–2422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Cong Q, Shen J, Opler PA, Grishin NV, 2019. Genomics of a complete butterfly continent. bioRxiv 829887. 10.1101/829887 [DOI]
- Zhang Z, Inomata N, Cariou ML, Da Lage JL, Yamazaki T, 2003. Phylogeny and the evolution of the Amylase multigenes in the Drosophila montium species subgroup. J. Mol. Evol 56, 121–130. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


