Improved Sampling Strategies for Protein Model Refinement based on Molecular Dynamics Simulation

Abstract

Protein structures provide valuable information for understanding biological processes. Protein structures can be determined by experimental methods such as X-ray crystallography, nuclear magnetic resonance (NMR) spectroscopy, or cryogenic electron microscopy. As an alternative, in silico methods can be used to predict protein structures. Those methods utilize protein structure databases for structure prediction via template-based modeling or for training machine-learning models to generate predictions. Structure prediction for proteins distant from proteins with known structures often results in lower accuracy with respect to the true physiological structures. Physics-based protein model refinement methods can be applied to improve model accuracy in the predicted models. Refinement methods rely on conformational sampling around the predicted structures, and if structures closer to the native states are sampled, improvements in the model quality become possible. Molecular dynamics simulations have been especially successful for improving model qualities but although consistent refinement can be achieved, the improvements in model qualities are still moderate. To extend the refinement performance of a simulation-based protocol, we explored new schemes that focus on an optimized use of biasing functions and the application of increased simulation temperatures. In addition, we tested the use of alternative initial models so that the simulations can explore conformational space more broadly. Based on the insight of this analysis we are proposing a new refinement protocol that significantly outperformed previous state-of-the-art molecular dynamics simulation-based protocols in the benchmark tests described here.

Graphical Abstract

INTRODUCTION

The computational modeling of protein structures has become an essential approach for studying biological systems in atomistic detail as an alternative to experimental structure determination methods.^1–2 As the number of experimentally determined protein structures keeps growing, protein structure prediction based on homologous structures has become more widely applicable and reliable.^3–4 At the same time, the growth in structures as well as the rapid growth in sequence databases has enabled accurate predictions based on predicted inter-residue distances. Such distance information can be inferred from co-evolutionary couplings⁵, especially via deep neural network models that take advantage of recent progress with machine-learning techniques.^{3–4, 6–7} This approach has been groundbreaking, especially for protein sequences for which close homolog structures have not yet been determined. Using either approach, it is now possible to predict protein structures from their primary sequence with reasonable accuracy in most cases. However, predicted structures still need to be optimized further to reach experimental accuracy as minor structural differences resulting from variations in the primary sequences are most difficult to capture with knowledge-driven techniques.⁸ Models generated by template-based modeling by construction resemble the structures of the templates. These models are expected to be similar to the structure for a homologous target sequence when the degree of sequence identity is high, but such template-based models cannot usually capture how sequence variations may modulate the structure in detail. Because of differences in sidechains, homology models may have poor structure packing. Also, models can be incorrectly predicted in some regions if the sequences are very distant from the sequence of the modeling templates and/or when sequence alignments do not optimally reflect structural equivalency of residues in homologous structures. On the other hand, models based on machine-learning methods may also deviate from their native structures, since current machine learning-based methods rely on co-evolutionary analysis of many close sequence homologs.^9–10 Thus, the predicted contacts essentially focus on the average structure of an ensemble of a homologous set of sequences, rather than individual structural deviations of a given target sequence.

Protein model refinement addresses these defects. Refinement aims at improving initial model qualities towards the accuracy of experimental structures in terms of global structure arrangement, local structure packing, and stereochemical correctness.^11–17 Several methods have been proposed that address these tasks. Earlier methods primarily focused on the refinement of local structures by improving sidechain packing or hydrogen bond networks, whereas the global structure could only be refined slightly along with the local structure improvements.^18–22 More recently, molecular dynamics (MD) simulations have been applied to improve global structure more substantially.^{8, 15, 23–26} MD simulations allow extensive sampling and refinement becomes possible when the force field is good enough to guide sampling to the native state at the lowest free energy. Moreover, ensemble-averaging has been found to be key to the success of MD-based structure refinement as the resulting models better resemble how experimental structures are obtained. At the same time, ensemble-averaging also reduces the sensitivity to inaccuracies in the force field or scoring functions.²⁵ MD-based refinement via ensemble-averaging has been one of the most successful strategies for consistently refining both global and local structure features. With state-of-the-art MD-based refinement protocols, it has become possible to consistently bring initial models significantly closer to their experimental structures for most protein structures.^{24, 27} There are examples, where refined models reached root-mean-square-deviations of Cα atoms (Cα-RMSD) of around 1 Å from the native structures as demonstrated during CASP13. In the past, refinement has been mostly applied to models built based on homology modeling because only those had sufficiently high initial model qualities. With the advances in structure prediction based on machine-learning methods, the resulting models are also good starting points for refinement. Recently, it was shown that refinement is also able to improve these models.²⁸ MD-based refinement was in particular able to improve the structure packing between sidechains as well as loop structures.

Most protein model refinement protocols are based on a combination of conformational sampling from an initial model for refinement with a scheme for deriving an improved structure from the sampled conformations.⁸ Therefore, effective conformational sampling is one of the key parts for successful refinement. Some previously proposed protocols have used Monte Carlo minimization with structure perturbation operations and followed relaxation using MD simulations.²² Global optimization methods, such as genetic algorithm and conformational space annealing, have also been adopted in a few protocols.^29–31 Most recently, MD simulations have become a popular choice for conformational sampling during refinement. MD simulations have had success by reaching the native state of smaller proteins via in silico protein folding simulations that started from extended states.³² Therefore, using such simulations to reach the native state from an initial model that is already close to the native state has been an obvious choice. However, the initial model for refinement usually lies off the protein folding pathway and direct transition to the native state is hindered by significant kinetic barriers, e.g. due to mispacked side chains. In essence, refinement often requires that structures are partially unfolded and refolded. These transitions demand a long time due to kinetic barriers. From a systematic analysis of energy landscapes between initial homology models and the native states it was found that effective time scales for crossing the kinetic barriers during refinement may be on the order of a few microseconds to sub-milliseconds for small proteins and probably even longer for larger systems. Very extensive MD simulations³³ and/or the application of enhanced sampling methods such as replica exchange MD simulation^34–36 have been proposed to overcome the sampling challenge. However, such protocols can be technically challenging and may require significant computational resources that limit their practical use in routine applications of refinement methods. Therefore, standard MD simulations have remained the most effective sampling approach for exploring diverse conformational states with limited computational expense and complexity.

Conformational sampling is restrained in most successful refinement methods in order to prevent large-scale unfolding and focus sampling on reaching the native state. Unrestrained MD simulations from protein models usually result in a significant deterioration of model qualities, at least over the time scales that can be reached via simulations today.³³ The force field used in the simulations may have deficits that drive the simulated models towards the unfolded state, or, more likely, there are simply unfavorable contacts in the initial models that lead to rapid unfolding in order to reach a conformation with more favorable interactions. Once unfolded, there is not enough time to refold to the native state. Under the assumption that the native state is indeed the most favorable state based on free energies, restraints are applied to prevent unfolding so that sampling can find the native state more quickly. However, there is a compromise between the application of restraints and the need for conformational transitions since some degree of unfolding may be crucial for the refinement of structural defects in the initial model^{24, 33, 37}. Other reasons for applying restraints to an initial conformation is that simulations of a monomeric apo structure may neglect important stabilizing interactions due to oligomerization, ligand binding, or other biomolecular interactions in the physiological environment. During structure prediction, such factors could be transferred implicitly from known structures via restraints.

Here, we focus on several aspects for improving structure sampling via MD simulations during protein model refinement. First, we systematically benchmarked different restraining protocols. In particular, we focused on analyzing the application of restraints with flat-bottom harmonic function that was introduced by us earlier.²⁷ Because of its functional form, flat-bottom restraints do not limit sampling within some range, while at same time still preventing large deviations from the initial model such as significant unfolding. Second, we explored the application of higher temperatures during the MD simulations. Elevated temperatures are expected to accelerate sampling such as in temperature replica exchange simulations^34–36, but increased temperatures can also cause thermal denaturation or alter the free energy landscape compared to physiological conditions in other ways. We tested here to what extent increased temperatures can be beneficial during structure refinement, especially when combined with restraints. Third, we tested an idea of enhancing sampling by initiating simulations from an augmented set of similar initial models. We hypothesized that refinement may be easier from some models than others and therefore refinement may be overall more successful than if only a single model is used, even if it is the best initial model in terms of distance from the true native structures. More specifically, we built alternative models starting from the initial model using additional template-based information for targets where this is possible. Simply combining simulations from multiple initial models also allowed a broader exploration of different parts of conformational space that may otherwise be separated by high kinetic barriers. Based on the insights from the detailed analysis of different aspects of our MD-based refinement method, we are presenting a new refinement protocol that leads to improved prediction accuracies based on our benchmark tests.

METHODS

Overview of refinement protocol

We tested different sampling strategies for protein model refinement within a previously established framework (see Figure 1)²⁷ to investigate how they affect refinement performance and to improve it. Starting from an initial model, a common pre-sampling stage consists of the application of locPREFMD³⁸ to resolve stereochemical errors such as severe atomic clashes, cis-peptide bonds, and poor rotamer states that may cause problems during simulations. The initial model after locPREFMD was then solvated in an explicit water box, and equilibrated by heating up to a chosen simulation temperature. The subsequent sampling stage involved MD simulations according to different strategies as described below with the goal of generating an ensemble of structures. During the post-sampling stage, again common to all protocols, a set of structures was selected among the sampled structures to be ensemble averaged. We used two ensemble selection schemes: (1) the 25% lowest-scoring conformations according to RWplus³⁹ were selected; (2) a combined score based on RWplus and the deviation from the initial structure was applied to select the sub-ensemble.²⁵ The selected structures were then averaged based on Cartesian coordinates. Stereochemical problems due to averaging were removed via local relaxation using short MD simulation, followed by SCWRL4⁴⁰ to rebuild side chains, and again the application of locPREFMD to polish the quality of the final models.

Figure 1.

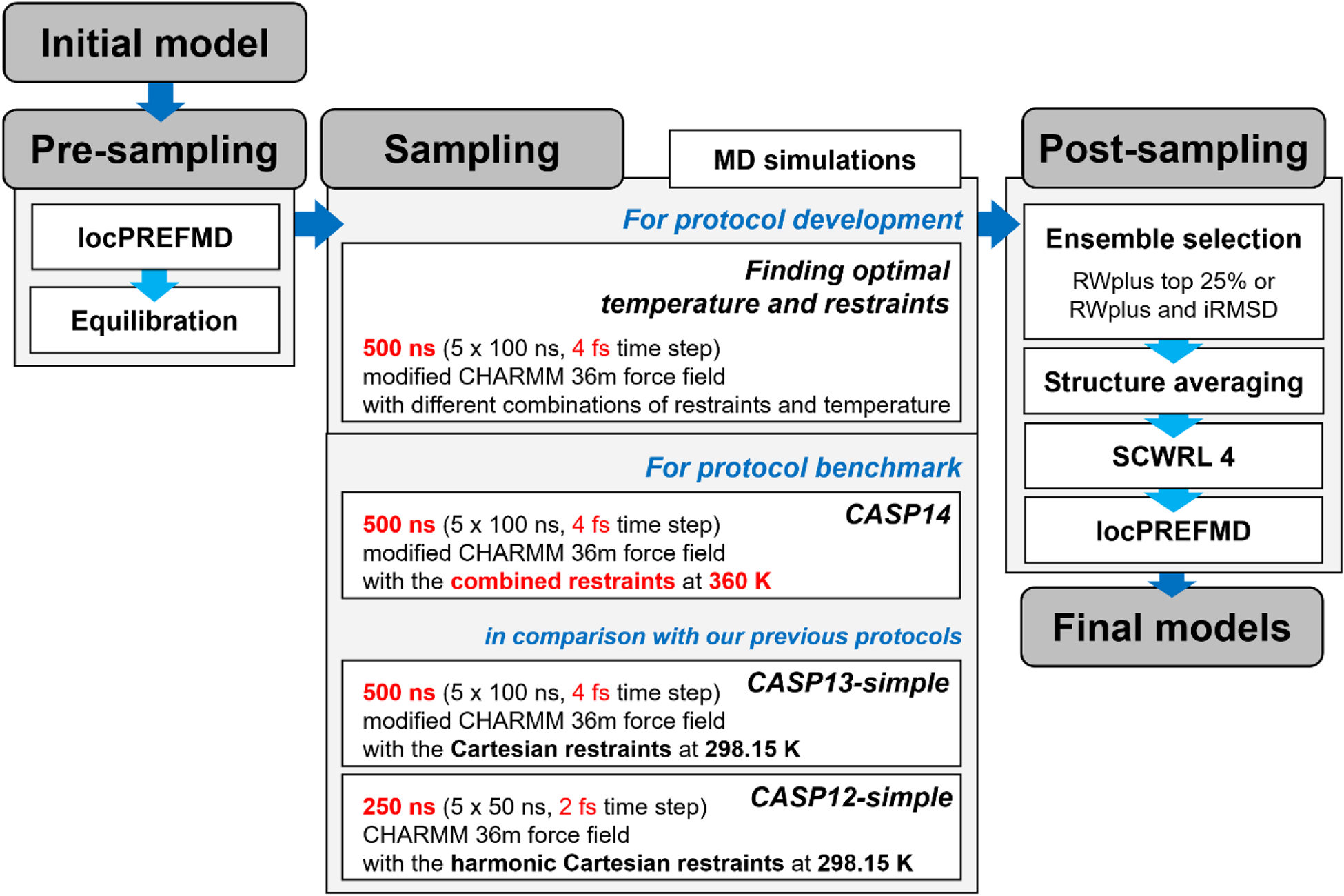
Overview of the refinement protocol benchmark framework

In all protocols, MD simulations were carried out with the CHARMM 36m force field⁴¹ or a modified version²⁷ in combination with explicit water molecules described by the CHARMM version of the TIP3P water model.⁴² For locPREFMD and during the local relaxation of the averaged structure, the original version of the CHARMM 36m force field was used. For the simulations during the main sampling stage and its preceding equilibration step, a modified version of CHARMM 36m force field was applied except when running our previous CASP12 procedure for benchmark purposes. In the modified force field version, lower energy barriers for backbone dihedral angles terms between major secondary structure regions were implemented via alternative CMAP terms. This modification was meant to accelerate transitions between backbone dihedral angles but without significantly affecting protein stability since relative free energies of the conformational minima were retained. For nonbonded interactions, we used a switching function between 8 and 10 Å. Particle-mesh Ewald summation was applied to evaluate full electrostatic energy in a periodic system.⁴³ Bonds involving hydrogens were kept rigid with the SHAKE algorithm.⁴⁴ Hydrogen mass repartitioning⁴⁵ was applied, where heavier hydrogen masses (3 a.m.u.) allowed simulations to be run with a 4-fs integration time step in combination with the SHAKE algorithm. This allowed us to sample twice as much at the same computational cost.

The initial equilibration of each simulated system involved the following steps: A given initial protein model was rotated to align its principal component axes to X, Y, and Z-axes and centered at a periodic rectangular simulation box with a marginal distance from the protein to the box edges of 9 Å. This protocol minimized overall system sizes to reduce computational costs. Explicit waters filled up the rest of the simulation box. Some of the water molecules were replaced randomly with either sodium or chloride ions as needed to neutralize the total charge of each system. Solvated systems were then locally minimized by the l-BFGS-b algorithm for up to 500 steps. Initial Langevin dynamics simulations were started from the minimized system for 1 ns in total with a 2-fs time step and a 0.01/ps friction coefficient. During these equilibration simulations, the temperature was first gradually heated up to the temperature used in the production simulations using the NVT ensemble. Then, equilibration was continued in the NpT ensemble at 1 bar with a Monte Carlo barostat to allow the box sizes to adjust. Throughout the equilibration, harmonic restraints were applied to Cα atoms with respect to their initial positions with a force constant of 0.5 kcal/mol/Ų. From the equilibrated structures, production simulations were carried out by using Langevin dynamics simulations with a 0.01/ps friction coefficient in the NVT ensemble. We used either a 4-fs time step with hydrogen mass repartitioning or a 2-fs time step with standard atomic masses (to reproduce our earlier CASP12 protocol).

Refinement with various restraint biases

Various types of restraints were tested to bias sampling. The use of restraints with respect to the initial model is a common approach for consistent refinement.^{8, 15, 22, 26–27, 30} Restraints keep structures close to their initial models, so that structure sampling can focus on finding the correct structure in the vicinity of the initial model. However, at the same time, restraints may hinder transitions between conformational states by raising the energy barriers for such transitions. As a result, structure sampling and refinement can become more difficult, especially when initial models deviate significantly from the native state. Previously, we introduced flat-bottom harmonic restraints applied to Cartesian coordinates of Cα atoms (Eq. 1).²⁷

$$E_{\text{Catesian }}\left({\mathbf{r}}_i;{\mathbf{r}}_i^o\right)=k_0\text{max}{\left(0,\left|{\mathbf{r}}_i-{\mathbf{r}}_i^o\right|-b_{\text{flat}}\right)}^2$$ (1)

where r_i and r_i^o are Cartesian coordinates of Cα atoms of the i-th residue for a conformation and the reference model, respectively. k₀ is the force constant and b_flat is the flat-bottom width of the flat-bottom harmonic restraint. We used here k₀ = 0.025 kcal/mol/Ų and b_flat = 4 Å. Such potentials were successful in allowing some structure transitions within “restraint-free” regions; and this allowed remarkable structural improvements in some cases.²⁷

Here we tested additional variants of restraints. First, we tested flat-bottom harmonic restraints applied to distances between Cα atoms (Eq. 2)

$$E_{\text{Distance }}\left(d_{ij};d_{ij}^o\right)=k_0\text{max}{\left(0,\left|d_{ij}-d_{ij}^o\right|-b_{\mathit{\text{flat}}}\right)}^2$$ (2)

where d_ij and d_ij^o are distances between Cα atoms of the i-th and j-th residues for an instantaneous conformation and the initial model, respectively. This restraint was applied to residue pairs with distances below 10 Å in the initial model and separated by more than three residues. For the distance-based flat-bottom harmonic restraint potential, we used k₀ = 0.05 kcal/mol/Ų and b_flat = 2 Å. This choice of values gave a comparable biasing strength compared to the Cartesian restraints. Second, we tested a combined restraint between Cartesian and distance restraints (Eq. 3).

$$E_{\text{Combined }}\left(\lambda \right)=\lambda \sum _i{E}_{\text{Cartesian }}\left({\mathbf{r}}_i;{\mathbf{r}}_i^o\right)+(1-\lambda )\sum _{j-i>3}{E}_{\text{Distance }}\left(d_{ij};d_{ij}^o\right)$$ (3)

where λ is a switching parameter between the types of restraints. As each type of restraints limits conformational sampling differently, we tried to maximize the benefit from both types of restraints by gradually switching from the Cartesian restraints (λ=1) to the distance restraints (λ=0) throughout the simulations.

To compare the performance, refinement runs were carried out with each type of restraints. In addition to the refinement with restraints, simulations without restraints were conducted to revisit and reaffirm the benefit of using restraints with current simulation protocols. Sampling in each refinement run involved five trajectories of MD simulations, each performed for 100 ns. Sampled protein conformations were recorded for every 50 ps. Consequently, 10,000 structures were generated during each refinement run.

Refinement at higher temperatures

While previous refinement protocols simply assumed room temperature (i.e. 298K), we tested here elevated temperatures during the MD simulations. Temperature is one of the key parameters for conformational sampling since transitions between conformational states can be accelerated at high temperatures. Considering that protein models need to be partially unfolded and refolded to be refined, MD simulations at elevated temperatures may boost this process. This benefit is counteracted by a loss of stability and increased tendency towards thermal denaturation. However, since restraints were applied with respect to the initial model, protein unfolding may be prevented. Thus, improved sampling may be possible with moderately increased temperatures together with restraints. We explored here whether there is an optimal temperature for refinement simulations in the presence of restraints where improved sampling can be achieved without a loss of protein stability. To address this question, refinement runs were tested at different temperatures: 298.15, 320, 340, 360, and 380 K. In these simulations, we used the combined restraint according to Eq. 3.

Refinement with multiple alternative initial models

We examined whether refinement is more effective when alternative models for a given target are used as initial models. We hypothesized that an initial model that is closest to the native structure from a set of similar models does not necessarily guarantee a better model after refinement because refinement success is more dependent on what kinetic barriers exist between the initial model and the native state than the distance according to a given metric such as GDT-HA or RMSD. Alternative models could potentially result in better refined models if they are less trapped kinetically even as they are initially deviating more from the native state than the best initial model. Therefore, we examined an expanded protocol where a given initial model was augmented with alternative initial models.

Alternative initial models were generated from the initial model with additional template information via template-based modeling. A sequence profile was generated by searching sequences against the UniClust30 database⁴⁶ by using HHblits.⁴⁷ Structure homologs were identified via the generated sequence profile from HHsearch^48–49 with the Viterbi algorithm using the local alignment mode. The top 100 searched structures were compared with the initial model by using TM-align⁵⁰, and structures that had a similar fold to the initial model (TM-score > 0.6) were selected for further model building. For each selected structure, the sequence alignment between the target sequence and the template structure was generated by using HHalign^48–49 with the MAC algorithm and using the global alignment mode. We allowed up to three alternative sequence alignments that had comparable alignment scores. Twelve models were generated for each sequence alignment by using MODELLER⁵¹, and the best-scored model was selected as a final model for sequence alignment. Among the generated models, up to ten models were selected for further optimization based on a structure similarity cutoff, i.e. a TM-score of 0.6 or the best TM-score-0.2, whichever was greater. If less than two models were selected, we did not test the idea of alternative models for the target. Also, if there were any chain breaks, we did not try to build alternative models. During the benchmark, we identified experimental structures that were released after the first day of CASP of each target and removed them from the template list in order to generate refined models that can be compared to the performance of other groups during the respective rounds of CASP.

To further explore the idea of using multiple templates, the selected models and the initial model were hybridized. We used the scripts for the Rosetta “Iterative hybridize” protocol using the “simple” option that prevents “mutation” operations³⁰. We repurposed the scripts to generate diverse structures, but requiring that structures did not deviate much from the initial model by applying different types of restraints. The restraints were based on the restraint generation scheme of the original Rosetta method, which uses “bounded” restraints (Eq. 4) with σ = 1 Å, s = 0.5. Parameters of residue type-dependent contact distance upper bound, $d_{ij}^{ub}$, are taken from the original work. For structurally conserved regions, we used flat-bottom harmonic restraints (Eq. 2) instead of the “bounded” restraints. Conserved regions were defined as those where the root-mean-square difference of Cα-Cα distances between the selected models and the initial model was less than 2 Å. The flat-bottom harmonic restraints were used with k₀ = 0.25 kcal/mol/Ų and b_flat = 1 Å. Extensive optimization was not needed for our purposes. Therefore, we hybridized structures with only ten populations over ten iterations rather than 50 populations over 50 iterations as in the original method. The starting populations at each iteration consisted of the initial model and selected models from the previous iteration. If there were insufficient models, they were replicated to fill up the starting population. Four out of ten hybridized models obtained at the end of the iterations were selected for the further refinement as alternative initial models.

$$E_{\mathit{\text{bounded}}}\left(d_{ij};d_{ij}^{ub}\right)=\{\begin{array}{ll}0\hfill & ,d_{ij}\le d_{ij}^{ub}\hfill \\ {\left(\frac{d_{ij}-d_{ij}^{ub}}{\sigma }\right)}^2\hfill & ,d_{ij}^{ub}<d_{ij}\le d_{ij}^{ub}+s\sigma \hfill \\ \frac{1}{\sigma }\left(d_{ij}-\left(d_{ij}^{ub}+s\sigma \right)\right)+s^2\hfill & ,d_{ij}>d_{ij}^{ub}+s\sigma \hfill \end{array}$$ (4)

Refinement via MD simulations was carried out with the original initial model and the alternative models generated via hybridization. For each initial model, five trajectories of MD simulations were performed for 100 ns with restraints with respect to each initial model, and a refined model was generated via post-sampling processes. In addition to the refined models for each initial model, another refined model was obtained by aggregating all the sampled conformation from the original initial model and the alternative initial models.

Refinement protocols

The refinement performance with the new sampling protocol with the original initial model and additional alternative models were benchmarked and compared with our previous refinement protocols. For comparison, a protocol, named CASP12-simple, which is similar to the protocol during CASP12³⁷ or the conservative protocol used during CASP13²⁷, was used as a reference for MD simulations with harmonic restraints on Cα coordinates and at a temperature of 298.15 K. Another protocol, named CASP13-simple, was also used as a reference protocol for using MD simulations with flat-bottom harmonic restraints on Cα coordinates and again at a temperature of 298.15 K. The CASP13-simple protocol is a simplified protocol of the iterative protocol used during CASP13.²⁷ The key differences were that the iterative sampling part was omitted and RWplus³⁹ scoring was used for the ensemble selection step. A new sampling protocol, named CASP14, adopted the combined restraints and performed MD simulations at 360 K. For the new sampling protocol, we tested a single initial model-based protocol, which uses the original initial model, as well as a multiple initial model-based protocol, which uses the original initial model and additional alternative initial models.

For each simulation protocol, refinement was performed three times independently for every target. Statistical analyses of the refinement results are reported based on the average values of the independent runs.

Benchmark sets

Two benchmark sets were used. The first set consisted of 28 CASP10 refinement targets.¹³ The second set consisted of 103 CASP11–13 refinement targets.^{14, 16–17} We note that five CASP12 targets were excluded because of a lack of experimental structures. The first set was used to examine the effect of parameters for MD simulation procedures such as simulation temperature and the type of bias restraints. The second set was utilized as a test set to compare the performances between refinement protocols.

Analysis of residue-wise improvements and their dependence on initial quality

We hypothesized that residue-wise improvement depends on its initial quality. To validate the hypothesis, we evaluated the residue-wise S-score⁹ (Eq. 5) and the lDDT score.⁵² The residue-wise S-score was calculated based on residue-wise Cα deviations, d, from the structure alignment by using LGA⁵³ in sequence-dependent mode and a 4 Å distance cutoff.

$$\mathrm{S}-\text{score}=\frac{1}{\left(1+{\left(d/d_0\right)}^2\right)}$$ (5)

where d₀ was set to 5 Å, and the minimum S-score was set to 0.1. To consider neighboring residues together, the residue-wise scores were averaged according to Eq. 6 and 7.

$$X_{\text{neighbor }}\left(r\right)=\frac{\sum _{s}w\left(s\right)X\left(r+s\right)}{\sum _{s}w\left(s\right)}$$ (6)

$$w\left(s\right)=e^{-{\left(s/s_0\right)}^2/2}$$ (7)

where X is either the residue-wise S-score or lDDT, s is the sequence separation to a neighboring residue, and s₀ was set to 1. We did statistical analysis of residue-wise improvements dependence on its initial quality with consideration of neighboring residues.

Analysis of refinement of biologically important regions

To validate the utility of physics-based refinement for biologically important regions of a protein, we focused on model quality improvements at ligand binding sites and structurally variable regions, where homolog structures have diverse conformations. These regions can be important for protein functions, so it would be beneficial if model quality at these regions can be improved via physics-based refinement. For ligand binding sites, we analyzed biologically relevant ligands only, and molecules or ions used only for crystallization such as polyethylene glycol (PEG) were excluded. Ligand binding sites were defined as residues where any heavy atom distance from a binding ligand is closer than 5 Å. The performance of physics-based refinement was assessed based on backbone atom RMSD of residues in the ligand binding site. For structurally variable regions, we defined variable local regions (VLRs), which are analogous to unreliable local regions (ULRs).⁹ A VLR is comprised of more than three consecutive residues where the RMSF for a residue between single template-based homology models and the initial model is greater than 3.8 Å. In contrast, an ULR is defined by deviations from the experimental structure. For the homology models for this analysis, we only included models with a TM-score > 0.75 relative to the initial model.

Software

The manipulation of PDB files, preparation for the MD simulations and locPREFMD was done by the MMTSB Tool Set⁵⁴ with CHARMM⁵⁵ and the MDTraj Python library.⁵⁶ MD simulations were carried out by using the OpenMM Python library.⁵⁷

The refinement scripts used for this work are available at https://github.com/feiglab/prefmd2. The refinement protocol with single initial model is available at PREFMD web server (http://feiglab.org/prefmd).

RESULTS

Refinement with different forms of restraints

Refinement with the combined restraints was overall the best choice among the tested types of restraints (Figure 2A). Refinement with different types of restraints was tested at two simulation temperatures, 298.15 K and 360 K. Regardless of the simulation temperature, the combined restraints generally worked well for improving both global and local structure features. Comparing performances between the Cartesian restraints and the distance restraints, the Cartesian restraints showed better performance in terms of improving global structure similarity (based on RMSD and GDT-HA scores⁵³), whereas the distance restraints did as good or slightly better for local structure refinement (based on lDDT⁵² and SphereGrinder⁵⁸ scores) (Figure 2A and Figure S1).

Figure 2. Refinement performance dependence on the MD simulation protocols.

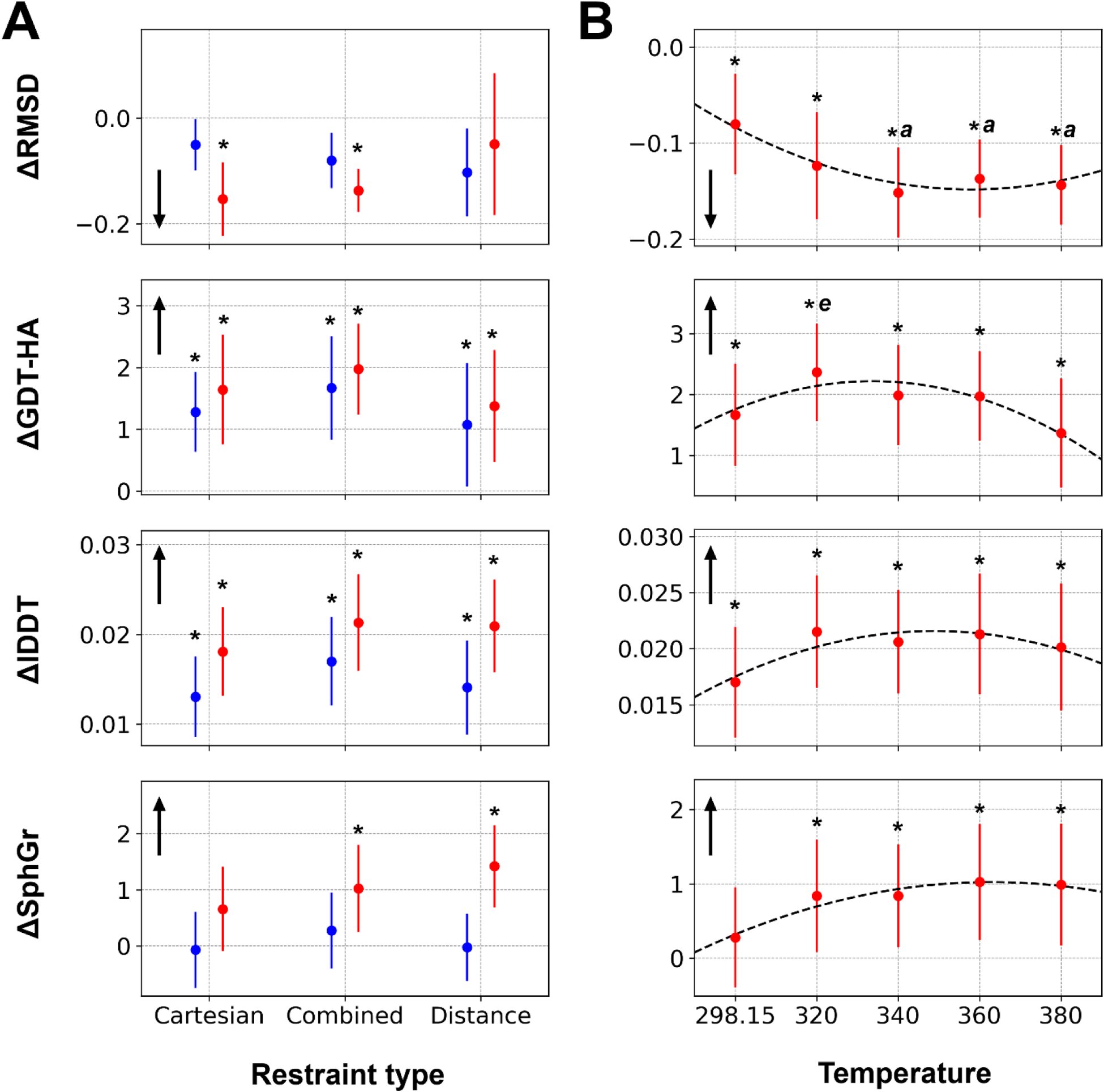
Model quality changes with different restraint types at 298.15 K and 360 K are presented in blue and red, respectively (A). The average values and the target-averaged values of standard deviations from three independent runs are shown as circles and error bars. Refinement results at different MD simulation temperature with the combined restraints are presented in the same way (B). Cubic spline with consideration of the standard deviations are overlaid as dashed lines. Parameters that were statistically significantly improved (p-value < 0.05 from ANOVA test and followed Tukey HSD test) over the initial models are marked with asterisks. Similarly, if a parameter is significantly better than another parameter, it is marked with a letter representing the parameter for which results are compared: r for Cartesian restraints (A); a and e for 298.15 K and 380 K, respectively (B). The direction of improvement for each measure is indicated with a black arrow.

By applying restraints, structure sampling is limited to in the vicinity of the initial model. Otherwise, structure sampling randomly explores conformational space. The use of restraints is effective because the initial model usually has correct structural features and restraints are meant to preserve them. We analyzed in more detail how different types of restraints maintain different structural features of the initial model (Figure S2). Sampling with the Cartesian restraints showed less deviation of global similarities, especially in terms of RMSD, since the Cartesian restraints focus on maintaining the overall structure. On the other hand, sampling with the distance restraints showed less deviation of local similarities based on lDDT and SphereGrinder. This is expected as distance restraints focus more on local interactions instead of the overall global conformation. The combined restraints, however, seemed to able to combine both effects of maintaining and improving both global and local structural features relative to the initial model.

Some examples of refinement with different restraints are illustrated in Figure S3. Refinement of TR663 (PDB ID: 4EXR) was successful regardless of the restraint type, but it was most successful with the distance restraints (Figure S3A). With the distance restraints, collective motions of larger structure elements such as secondary structure elements became possible as they are linked by restraints. As a result, orientation error of a helix and β-sheet curvature were improved, while keeping their local structures. These improvements led to significant improvements in both global and local structure qualities. With Cartesian restraints, it was also possible to improve these regions, but the refinement was not as extensive as with the distance restraints because the sampling necessary to achieve the improvements required too much deviation from the initial model in terms of RMSD. Therefore, the Cartesian restraints limited the ability to reach the lower energy states closer to the native (Figure 3A).

Figure 3. Comparisons of conformational sampling with different types of restraints.

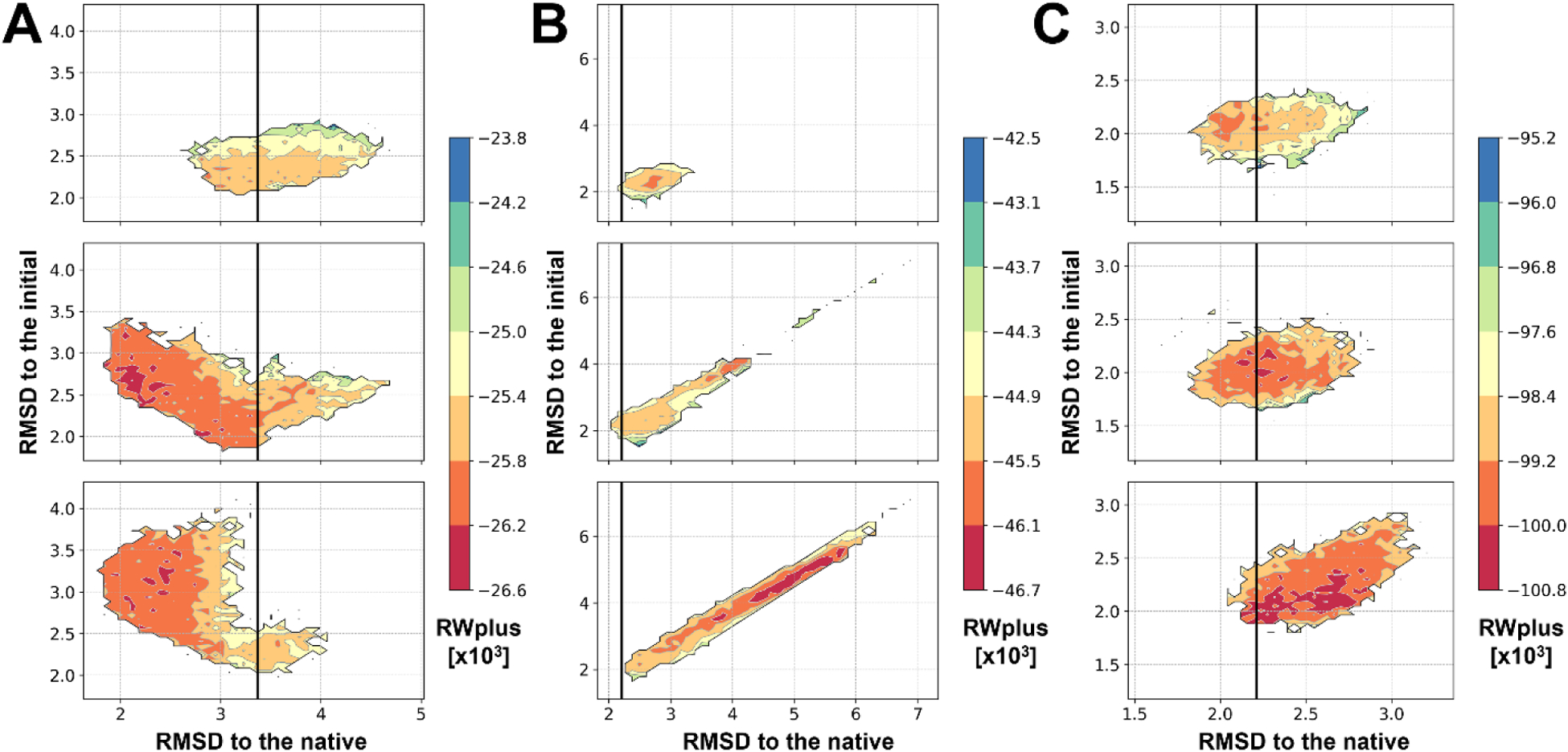
Cα-RMSDs with respect to the native and the initial structures are shown as contour maps with the corresponding RWplus scores for the sampled conformations of TR663 (A), TR699 (B), and TR699 as dimer (C) with the Cartesian restraints (top), the combined restraints (middle), and the distance restraints (bottom). The initial model qualities are marked with black vertical lines.

Unfortunately, refinement with the distance restraints is more susceptible to global effects on protein structure such as oligomerization, ligand binding, and protein-protein interactions. As an example, refinement of TR699 (PDB ID: 4KT7) was unsuccessful with the distance restraints (Figure S3B). A β-turn was misplaced after the refinement as it was not stable by itself (Figure 3B). It turned out that the structure forms a dimer, and the β-turn is at the binding interface with significant interactions. The structure changed significantly because there was no restraint or significant energy barrier for preventing it. On the other hand, in this case, refinement with the Cartesian restraints were the better choice as they largely preserved the initial model as the global restraints prevented the β-turn from moving freely. We note that when we refined the model as dimer, the model could be refined using any types of restraints without losing the β-turn conformation (Figure S3C). However, in practical applications, reliable inference of the oligomerization state, ligand binding, or protein-protein interactions is often not possible.

Refinement with the combined restraints appears to be an optimal choice of restraints. By beginning sampling with the Cartesian restraints before gradually switching to distance restraints, it allows sampling to benefit from both types of restraints. Sampled structures with the combined restraints cover the conformational space for both types of sampling (Figure 3). The scoring function, RWplus, could then select better conformations among the sampled structures. As a result, it could achieve refinement comparable to or even better than the best results with either Cartesian or distance restraints (Figure 2 and Figure S3).

Refinement without restraints generally led to significant deterioration of model qualities. The model quality changes without restraints in terms of Cα-RMSD, GDT-HA, lDDT, and SphereGrinder were −0.08 Å, −1.03, 0.0029, −1.12 at 298.15 K and 0.26 Å, −4.65, −0.0175, −3.53 at 360 K, respectively. These results confirm previous studies that found that restraints are necessary for successful refinement³³ with the exception of a few successful cases involving very small protein models.²⁴

Refinement at higher temperatures

Refinement via MD simulations was more successful at higher temperatures (Figure 2B). The refinement performance improved as MD simulation temperature increased up until 360 K before decreasing at higher temperatures, especially for GDT-HA scores. Refinement at higher temperatures is expected to be effective for overcoming energy barriers, so that conformational transitions would be more likely to occur and a wider range of conformations can be sampled. This is indeed what we find (see example in Figure 4). At moderately increased temperatures (i.e. 360 K), the additional sampling includes more native-like structures (Figure 4) but when the temperature is too high (i.e. 380 K) sampling shifts to non-native states. Moreover, while sampling based on simulations at 298.15 K resulted in sampled conformations that were well packed with low RWplus scores, the conformations shifted to less-well packed structures at 380K with higher RWplus scores even although secondary structure arrangements were overall improved (Figure 4A). At 360 K, structures were overall improved and retained favorable RWplus scores indicative of good packing resulting in the best refinement predictions after application of the post-sampling stage.

Figure 4.

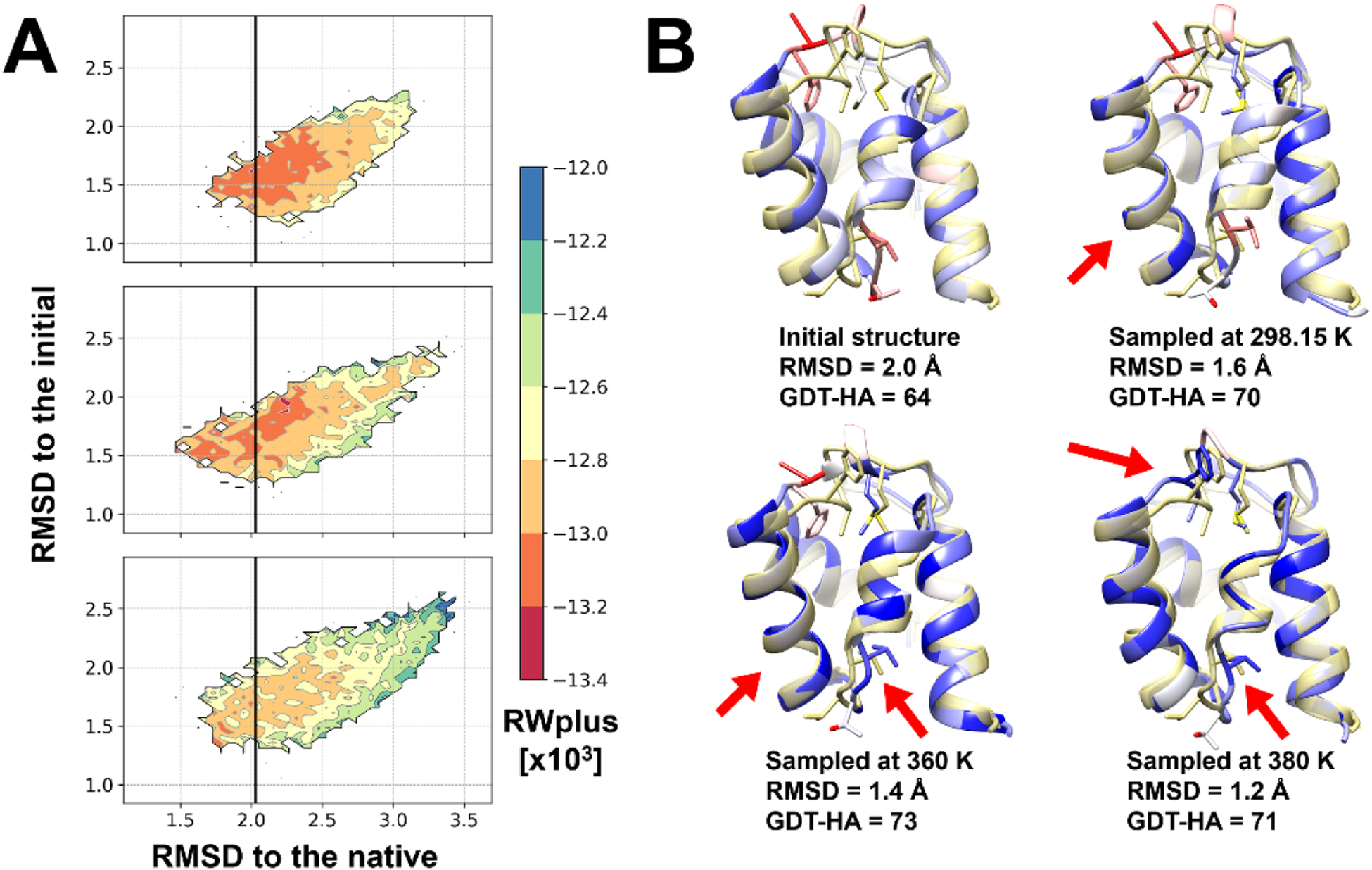
Examples for comparisons of conformational sampling at different temperatures for TR662. Cα-RMSDs with respect to the native and the initial structures are shown as contour maps with the corresponding RWplus scores (A) for the sampled conformations at 298.15 K (top), 360 K (middle), and 380 K (bottom). The initial model qualities are marked with black vertical lines. The best sampled structures are presented (B). The best sampled structures are shown in cartoon diagrams with blue-to-red colors. The colors represent the residue-wise lDDT score; blue and red are for high (> 0.8) and low (< 0.3) scores. The experimental structures are overlaid as a transparent yellow cartoon diagram.

To understand the effect of temperature in more detail, we compared the refinement performance consistency at different temperatures. (Figure S4). Refinement results can vary for independent runs because of stochastic sampling. Sampled conformational space can be different between independent sets of simulations as we use limited sampling for refinement. Based on such an analysis, we find that refinement at higher temperatures is more consistent, meaning that different refinement runs for the same target produce more similar results than at lower temperatures. Presumably, this is because it was easier to escape from local minima at higher temperatures. On the other hand, at lower temperatures, it took more time to get over local minima, so sampled conformational space could be different between independent refinement simulations as they were kinetically trapped in local minima. The consequence of this observation is that fewer refinement runs, at less computational costs, may be sufficient when using elevated temperatures to achieve reliable refinement.

Considering both the performance and the consistency, we concluded that MD simulations at 360 K are the optimal choice for refinement with the combined restraints.

Refinability of alternative initial models via MD simulations

The third aspect we are investigating here involves augmenting refinement using alternative initial models. Before we present results from a refinement protocol that uses multiple initial models, we like to discuss what determines refinability - and why there could be an advantage of using additional initial models.

Perhaps not surprisingly, refinement with alternative initial models that were closer to the native state were more likely to result in better refined models than refinement with the original initial models (Figure S5). Especially, better initial models in terms of Cα-RMSD and SphereGrinder were highly correlated to improvements over the refined models from the original initial models after refinement. However, building better alternative initial model is not trivial for originally accurate models. For example, alternative initial models for CASP targets whose original initial models have GDT-HA scores above 60 had lower GDT-HA scores by −7.4 on average, and only 13% of them were better than the original initial models. Especially in the context of CASP, alternative models are likely inferior to the initial model, because initial models for refinement may have been chosen from the best models that were generated otherwise without refinement. However, in the context of practical structure prediction where the native structure is unknown and initial structures are generated with a preferred method of choice, simply generating alternative initial models with different methods may result in better initial models at least in some cases.

Nevertheless, even if alternative models are worse, they can occasionally result in better refined models than the original initial model. As an example, we consider one of the generated alternative models for TR893 that had a poorer model quality than the original initial model with GDT-HA scores of 70 and 49 for the original and alternative initial model, respectively. However, it turned out that refinement from the alternative model was more successful than refinement from the original initial model (Figure 5). Refinement with the alternative model could resolve more erroneous regions than refinement from the original model. Thus, the initially best model is not always the best starting point for refinement. This raises the more general question of what exactly determines refinability of a model via MD simulations-based refinement.

Figure 5. An example of refinement with an alternative model.

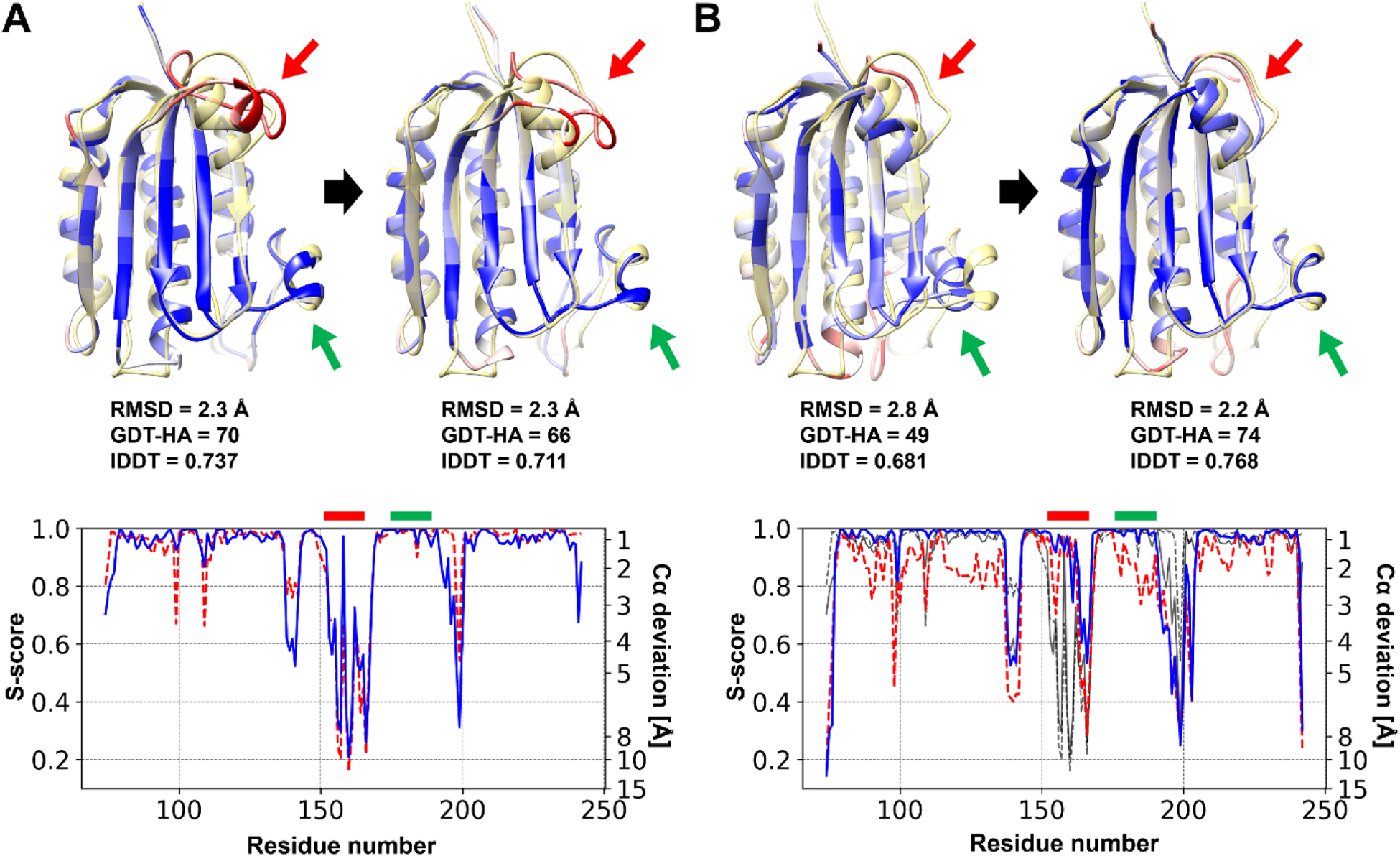
Refinement for TR893 with the original initial model (A) and an alternative initial model (B). Model structures are presented with the figure scheme as in Figure 4. The residue-wise S-score for the initial and refined models are shown as red dashed and blue solid lines, respectively, at the bottom of each panel. In panel B, the values for the original initial models are overlaid as black dashed and solid lines, respectively. Highlighted regions are indicated with red and green arrows on the structure diagrams, and they are marked with thick bars above the residue-wise S-score plot.

Applying residue-based analysis metrics (see Methods) we found that moderately incorrect residues were the most likely to be refined. The residues that experienced the most improvements may have RMSD deviations between 2.5 to 5 Å, or S-scores between 0.5 and 0.8 (Figure 6). Similarly, in terms of the residue-wise lDDT score, residues that have values between 0.5 and 0.8 had the highest chance of being refined. There was less gain for residues that were either less or more accurate. Residues already correct in the initial model had less room for improvement so that almost any change would decrease accuracy. On the other hand, residues deviating too much were too far from their correct positions for stochastic sampling via MD to find the correct structure, especially in the presence of restraints.

Figure 6. Residue-wise model quality improvements as a function of initial model quality.

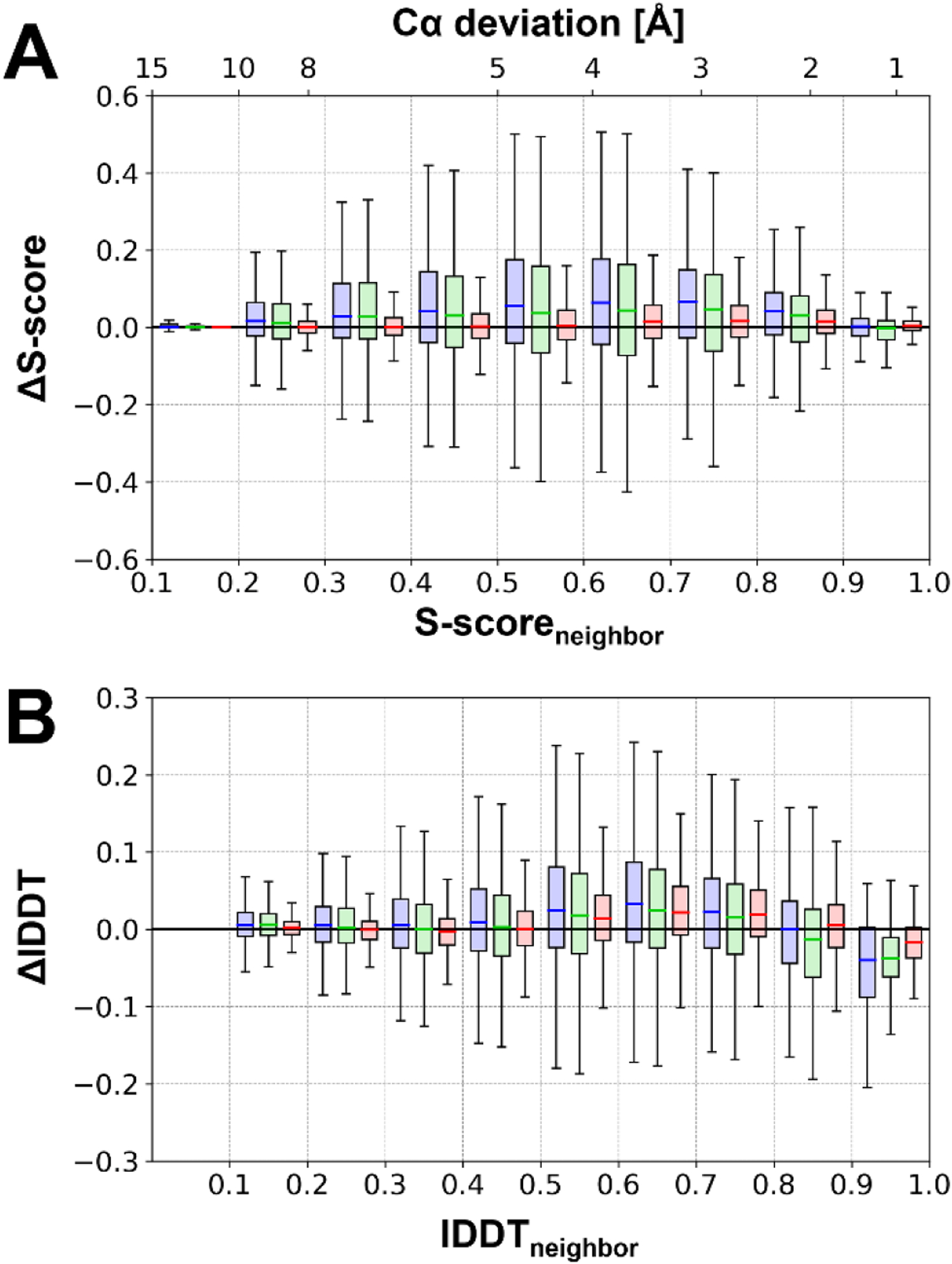
Residue-wise model quality changes after refinement as a function of residue-wise initial model quality in terms of S-score (A) and residue-wise lDDT scores (B). Statistical analysis for each bin is shown as a boxplot for refinement with “CASP14” sampling protocol (blue), “CASP13-simple” (green), and “CASP12-simple” (red).

In the example in Figure 5, residues indicated by the red arrows were roughly reoriented to their correct positions in the alternative initial model. The residues did not perfectly overlap and still deviated from their correct positions, but they came closer to their correct positions after MD refinement as the region became “refinable” via alternative initial model building. On the other hand, this region could not be refined well when starting from the original initial model because the deviations from the native positions were too large. At the same time, residues that deviated more in the alternative model than in the original initial model but were still within the radius of “refinability” could therefore be improved to a similar degree. An example in TR893 is the region indicated by the green arrow that was not as accurate initially in the alternative initial model, but was nevertheless improved close to the native structure after MD refinement. As a net effect, the alternative initial model could be refined more than the original initial model because of the significant improvement of one region (indicated with the red arrow) that could not be improved from the original initial model while still improving other parts of the structure to the same degree, even though they were less accurate in the alternative initial model (such as the region indicated with the green arrow).

Refinement using additional alternative initial models

Motivated by the analysis presented above, we tested a protocol where refinement runs were started from an initial model as well as additional alternative models. The results for the test sets considered here are shown in Table 1, Figure S6 and S7. For comparison, we also report results based on our previous refinement protocols that were used during CASP12³⁷ and CASP13.²⁷ (see Methods) We found refinement to be improved when using multiple initial model regardless of the protocol for ensemble selection. This approach was applied during CASP14 with the additional initial models subjected to the same computational sampling as the original model, i.e. less than 1 GPU day on an RTX-2080Ti card for most targets (Figure S8). Therefore, refinement with additional initial models is higher, proportional to the number of additional models, but since all of the runs are independent, efficient parallelization is possible.

Table 1.

Benchmark results of the tested protocols

Sampling protocol	Ensemble selection	ΔCα-RMSD [Å]1	ΔGDT-HA1	ΔlDDT1	ΔSphGr1
CASP14 (multiple initial models2)	CASP123	−0.311 / −0.524	4.72 / 6.33	0.0365 / 0.0479	3.13 / 4.84
	RWplus	−0.294 / −0.521	4.12 / 6.20	0.0366 / 0.0479	3.28 / 4.85
CASP14 (single initial model)	CASP12	−0.168 / −0.297	4.03 / 5.11	0.0282 / 0.0352	1.63 / 2.77
	RWplus3	−0.214 / −0.308	3.81 / 4.90	0.0289 / 0.0347	1.64 / 2.66
CASP13-simple	CASP12	−0.092 / −0.179	2.74 / 3.84	0.0172 / 0.0236	0.67 / 1.62
	RWplus3	−0.101 / −0.177	2.34 / 3.57	0.0173 / 0.0235	0.64 /1.56
CASP12-simple	CASP123	−0.025 / −0.035	2.34 / 2.72	0.0150 / 0.0173	0.42 / 0.86
	RWplus	−0.034 / −0.039	2.58 / 2.84	0.0162 / 0.0180	0.41 / 0.87

¹Averaged model quality changes for model 1 and best out of 5 models.

²Single initial model-based procedure was used for targets that were not able to generate alternative initial models.

³Selected ensemble selection methods are highlighted in bold characters.

DISCUSSION

We have analyzed here in detail how some of the factors of an MD-based protein structure refinement protocol can affect refinement performance based on benchmark sets consisting of CASP refinement targets. In the end, we arrived at a new sampling protocol, applied during CASP14, that significantly outperformed earlier protocols that were developed for CASP12 and CASP13. The key advances described here are an optimized use of restraints together with moderately elevated temperatures during the simulations. This conclusion was largely independent of the ensemble selection method, either CASP12 or RWplus, suggesting that improvements in conformational sampling are more important than the exact scoring and selection protocol. The increase in temperature allowed us to sample more broadly and increase progress towards the native state. Remarkably, the improvements with the “CASP14” protocol were manifested not only in better global structure metrics, but also in local structure qualities such as the SphereGrinder score, an area where it had been difficult before for us to make significant improvements^{14, 16–17}. The key for improving both global and local structure quality was the combined use of positional and distance restraints during refinement.

We further improved refinement success by considering additional alternative initial models. The additional improvements over refinement based on a single model were quite significant, especially in terms of RMSD and SphereGrinder metrics. Presumably, the improvements from using multiple initial models are due to both alternative model generation and simply the extended sampling via MD simulations. Model quality improvements were tracked step by step (Figure S9). The finding that refinement from additional models led to such significant differences may be surprising given that the CASP refinement targets are largely selected as one of the best initial predictions and most alternative initial models are likely worse in initial accuracy. However, we show that rather than overall initial accuracy, the key quantity for determining refinement success is that the local, per-residue accuracy surpasses a given threshold and it is therefore very possible that structures that are considered overall less accurate may actually be more refinable. Moreover, our ensemble selection and averaging protocol is well-equipped to recognize via scoring which initial models lead to the most refined structures so that it is not necessary to determine beforehand which initial model may be more refinable. As always, there is still room for improvement to achieve better model selection during refinement with multiple initial models since the best out of five model is yet significantly better than the model 1 that was selected (Table 1). However, we note that for many applications such as the generation of initial models for solving crystal structures via molecular replacement, it may be sufficient to generate just one out of five models at very high accuracy even without knowing a priori which one is most accurate, as there may be other criteria such as experimental observables to distinguish between models.

A key aspect of the protocol with multiple initial models relates to the how alternative models are generated. Simple, template-based modeling based on alternative templates, e.g. via MODELLER⁵¹ is not likely to generate alternative models that are competitive initial models subjected to refinement that would likely come from more sophisticated protocols such as Rosetta⁵⁹, I-TASSER⁶⁰, or most recently deep-learning based prediction pipelines. One approach may be to employ competing protocols to generate alternative initial models, e.g., based on different deep-learning protocols. However, this is difficult to implement in practice since not all protocols are fully public and using multiple protocols may incur significant computational cost and complexity. Here, we took a simpler approach of hybridizing between the given initial model and multiple additional template-based models via a modified version of the “Iterative hybridize” protocol of Rosetta. This resulted in sufficiently high-quality alternative models using a compact protocol that is relatively straightforward to apply as a stand-alone refinement procedure, even within an automatic server context. However, other approaches could be taken. For example, our multiple-model refinement protocol could take advantage of multiple models generated initially by any given prediction method, such as the I-TASSER server⁶⁰ that usually gives five models.

The success of refinement via MD is known to depend on protein size - smaller systems are easier to refine - and initial model quality - models that are too far or too close to the native state are more difficult to refine. This remains generally true with the improved protocol (Figures S10 and S11), but as the new sampling protocol extended the range of refinable residues within a given target (Figure 6), we found that refinement success was also generally extended to a wider range of targets with larger sizes and lower initial model quality. Especially, the use of multiple initial models was beneficial in this regard as it allowed a wider range of conformational states to be covered. As a result, the added ability to consistently refine residues with more than 200 residues (Figure S10B and S11B) is a significant advance that is expected to expand the application of protein structure refinement towards high-resolution structure prediction.

As restraints profoundly affects refinement performance, there may be room for improvements in the use of restraints for refinement. For example, an optimized selection of restraint parameters for a target protein may result in a better model. Therefore, we investigated how the selection of restraint parameters affects refinement performance as a function of protein size and initial model quality. (Figures S12 and S13). For accurate initial models, stronger restraints generally worked better as they do not need broader sampling, while moderate strength restraints, the parameters we selected in this work, usually performed well for worse models. In terms of protein size, moderate strength restraints generally worked well for smaller proteins, in contrast, stronger restraints were helpful for bigger proteins. It seems weaker restraints allow broader sampling, but they need much longer simulations to be effective. Hence, the simulation length applied in this work may not be enough for refinement of bigger proteins with weaker restraints. Based on these analyses, the protocol proposed here could be improve further by using a restraint strategy that applies different strength of restraints depending on the initial model. Furthermore, restraints can be applied in a different way for every residue depending on its properties such as predicted residue-wise error. Recently, Hiranuma et al. proposed a new refinement method that utilized residue-residue distance error estimation to guide refinement.⁶¹

The improvements in protein model quality via physics-based refinement promise to enhance the utility of such models for addressing biological questions. To further focus on this aspect, we analyzed specifically ligand binding site accuracy (Table S1) and improvements in structurally diverse regions between homologs (Figure S14). Ligand binding sites are functionally critical for many proteins. Some of the ligand binding sites analyzed in this work were modeled correctly; they had backbone RMSDs of lower than 1 Å and may not need refinement of the model for further analysis of the binding sites (Table S1). On the other hand, some other models had only moderate accuracy in the ligand binding sites which may hinder further applications such as virtual screening or molecular docking. After refinement, many models could be improved even although ligand binding information was not used. We expect that by explicitly incorporating ligand binding site information further improvements could be possible.⁶² Structurally variable local regions between homologous proteins may be especially interesting to understand differences in function between related proteins. However, the accurate modeling of structurally variable regions is more challenging, as native structures may adopt different structures from their homologs. Template-based modeling is often less successful for such regions, and ab initio approaches such as loop modeling may be needed.^63–65 Even although we did not consider structurally variable regions specifically, those regions also became more accurate along with the rest of the structures (Figure S14).

Finally, on a more philosophical note, the use of multiple alternative initial models raises the question of what exactly should be considered structure refinement. Strictly speaking, the classical idea of refinement is to take a given model and improve its accuracy, mostly via orthogonal approaches to how the initial model was generated. We believe that our proposed protocol of generating alternative initial models via hybridization using other structural templates still falls into such a framework as the initial model “drives” the hybridization and is always included in all of the refinement runs. However, one could also view the approach taken by us as a refinement protocol variant where conformational sampling from the initial model is effectively guided by alternative models in order to more effectively restrain conformational space to plausible (sub-)structures. While we did not exactly implement such a protocol here one could imagine a variety of such sampling protocols to fully address the still unresolved challenge of efficiently navigating an extremely high-dimensional landscape with significant kinetic barriers hindering progress towards finding the native state.

CONCLUSIONS

In this work, we systematically analyzed aspects of a previously proposed MD-based protein structure refinement protocol. The main outcome is a new optimized protocol that showed significant improvements over previous MD simulation-based refinement protocols with improved accuracy and a wider range of applicability of structure refinement to targets of larger size and with poorer initial model quality. There are three components that were essential for the improvements: 1) A combined use of Cartesian restraints and inter-residue distances based on Cα atoms led to better balance between preserving and improving both global and local structures; 2) The use of elevated temperatures during simulation (i.e. 360 K) allowed more productive accelerated sampling towards native-like conformation without unfolding due to the presence of restraints; 3) The use of alternative initial models that were generated via hybridization of the initial model with additional template-based models resulted in better refinement performance due to an expanded the conformational space and access to alternative models that may be more refinable in different parts of a given structure compared to the initial model. The new protocol brings refined structures significantly closer to experimental accuracy and expands the practical application of MD-based refinement methods.