Abstract
Brain-computer interface (BCI) system based on motor imagery (MI) usually adopts multichannel Electroencephalograph (EEG) signal recording method. However, EEG signals recorded in multi-channel mode usually contain many redundant and artifact information. Therefore, selecting a few effective channels from whole channels may be a means to improve the performance of MI-based BCI systems. We proposed a channel evaluation parameter called position priori weight-permutation entropy (PPWPE), which include amplitude information and position information of a channel. According to the order of PPWPE values, we initially selected half of the channels with large PPWPE value from all sampling electrode channels. Then, the binary gravitational search algorithm (BGSA) was used in searching a channel combination that will be used in determining an optimal channel combination. The features were extracted by common spatial pattern (CSP) method from the final selected channels, and the classifier was trained by support vector machine. The PPWPE + BGSA + CSP channel selection method is validated on two data sets. Results showed that the PPWPE + BGSA + CSP method obtained better mean classification accuracy (88.0% vs. 57.5% for Data set 1 and 91.1% vs. 79.4% for Data set 2) than All-C + CSP method. The PPWPE + BGSA + CSP method can achieve higher classification in fewer channels selected. This method has great potential to improve the performance of MI-based BCI systems.
Keywords: Channel selection, Motor imagery, PPWPE, BGSA
Introduction
Brain-computer interface is an auxiliary technology that directly provides external technical operations by interpreting brain information (Alcaide-Aguirre and Huggins 2014). It allows the brain to communicate directly with external devices, providing patients with neurologically impaired diseases a new means of communicating with the outside world (Jin et al. 2011; McFarland and Wolpaw 2011). When the brain is carrying out different mental tasks (Gaume et al. 2019; Zeng et al. 2018), its potential activity presents a large amount of distinguished information (Raghu et al. 2017), which can be used as features in EEG-based BCI systems.
Complete BCIs have the following functions: signal acquisition, preprocessing, feature extraction, classification, and controlling application (Ghaemi et al. 2017). Non-invasive electroencephalogram (EEG) is currently a widely used in recording brain activity due to its convenience (Ang et al. 2011; Kevric and Subasi 2017). In the preprocessing step, filtering, dimensionality reduction techniques and blind source separation techniques are widely used in removing artifacts, such as Electromyography (EMG) and Electrooculography (EOG). With regard to feature extraction, the common spatial pattern (CSP) method has a good performance on motor imagery (MI) task (Dong et al. 2017; Kumar and Sharma 2018; Miao et al. 2017; Zhang et al. 2017). Support vector machine (SVM) plays an important role in classification algorithms (Feng et al. 2018; Kumar et al. 2017; Selim et al. 2018). The controlling applications can be a wheel chair (Puanhvuan et al. 2017), robot, speller, or robotic arm (Dokare and Kant 2014).
The performance of the BCI system can be improved by the following aspects: improving the preprocessing algorithm, extracting subject-special feature, and determining the appropriate algorithm for classification.
Multichannel EEG recording can record EEG activity comprehensively, but some channels contain noise and reductant information. The proper selection of channels containing useful information is critical to improving the performance of MI BCI systems (Qiu et al. 2016). Many techniques have been used in channel selection, such as, filtering technique, wrapper technique, embedded technique, hybrid technique, and human-based technique (Alotaiby et al. 2015). Yang et al. applied genetic algorithms to channel selection and achieved relatively significant performance improvements (Yang et al. 2012). Various improved versions of genetic algorithms such as RC-GA (He et al. 2013), NSGA-II (Kee et al. 2015), etc. have also been applied to eliminate redundant channels. Qiu et al. (2016) proposed an improved sequential floating forward selection (ISFFS) algorithm that can select the useful channels and greatly save search time. Miao et al. proposed a correlation-based channel selection (CCS) method that reduces the reductant channels (Jin et al. 2019). Deep belief networks(DBN) was also used to find the optimal channel combination to simplify the BCI system (Jing-Ru et al. 2019).
To shorten the time of channel selection, and increase the effectiveness of the channel selection, a new evaluation parameter for the channels, called the position priori weight permutation entropy (PPWPE) was proposed by this paper. The PPWPE is based on the weight permutation entropy in the information theory and contains amplitude and position information. Useful channels containing large amounts of amplitude information are selected through the quantification of information contained in the channels. The influence of artifacts on useful EEG signals is prevented by considering electrode position information a priori position correction information. The binary gravitational search algorithm (BGSA) has the better performance on binary search problem. Ghaemi et al. (2017) used an improved version of BGSA for channel selection. Using the BGSA method for a wide range of channels requires many iterations and a large amount of memory. To find good channel combinations in few iterations, a novel channel selection method combining PPWPE and BGSA was proposed.
The paper is organized as follows: In Sect. 2, we describe the permutation entropy (PE) and weight permutation. Moreover, we proposed priori position permutation entropy and described other methods we used. Section 3 shows the data sets. Results are discussed in Sect. 4, and conclusion is described in Sect. 5.
Methods
Permutation entropy
EEG signals are a series of complex nonlinear time series. Permutation entropy (PE) is an effective method for measuring the complexity of the time series and compares neighboring values of each point and maps them to ordinal patterns (Bandt and Pompe 2002). The PE method can identify the non-linear patterns in the signals (Nicolaou and Georgiou 2012), reduce a problem space to a limited set of discrete symbols, and increase the robustness to noise. The basic principle of the method consists of transforming the signal into a finite kind of discrete symbol sequence and quantizing the entropy of the signal according to the probability density of these symbols (Acharya et al. 2015).
Given a time series , definite its time-delay embedding representation as follow:
| 1 |
For the parameter determines time delay, determines the sub-vectors’ dimension. Depending on the sort order of every sub-vectors’ amplitudes, each sub-vector is then assigned a unique symbol. For a given sub-vector dimension there are possible orderings. Thus symbols are utilized. For the time series there are sub-vectors are used. These sub-vectors can be represented by distinct symbols . PE is then defined as the Shannon entropy as follows:
| 2 |
is defined as
| 3 |
where trans(·) denotes the map from sub-vector space to symbol space. denotes the cardinality of a set. An alternative way of writing is
| 4 |
where the function defined as if , and if . PE values range . To some extent, a PE value represents how much information a channel contains. The complexity of a signal time series and the information it contains increases with PE. However, PE only can retain the order structure information, and the same order structure may be may be caused by different amplitude differences. In an EEG series, especially the EEG series in an MI task, amplitude information is important.
Weighted permutation entropy
To highlight the amplitude information in the EEG series, Fadlallah et al. (2013) proposed a weight-permutation entropy (WPE). The basic principle of the method is transferring the amplitude information to weight information and combining it with the classical PE values. Sub-vectors with large amplitude changes greatly contribute to the PE value, and the small amplitude changes (possibly due to noise) have small contributions to the PE value (Deng et al. 2017). A WPE value can preserve the useful amplitude information in the EEG series.
The WPE calculation steps are as follows:
| 5 |
| 6 |
when Eqs. (5) and (6) were compared with Eqs. (2) and (4), WPE was the same as PE at a constant weight. Equations 2 and 6 retained the form of Shannon entropy, and WPE was an extension of PE. The weight calculated from the magnitude can also be seen as selecting a feature for each sub-vector. The weight value for the MI EEG signal can be calculated through several methods. The present study uses the variance or energy of each neighbors’ sub-vector (Fadlallah et al. 2013). The weight value can be calculated as follows:
| 7 |
can be calculated as follows:
| 8 |
The weight-permutation entropy consider the amplitude information, but the effects of artifacts generated by nontarget brain activity will be magnified.
Position priori weight-permutation entropy
The influence of artifacts generated by nontarget brain regions on the activity of target brain regions was prevented by considering the active position of an MI. We selected the position of the C3 and C4 channel as the center position and compute the relative distance of the channel to the two center position. The relative distance of the channel was transferred to the priori position information of channel and add to the WPE to constitute the position prior weight permutation entropy (PPWPE). The channel priori position information can be calculated as follows:
| 9 |
| 10 |
where the is the relative distance between the th channel and C3 channel; the is the relative distance between the th channel and C4 channel. is the th channel’s coordinate in the x direction, is the th channel’s coordinate in the y direction. In this paper, the two-dimensional coordinate system for the representation of the electrode position was utilized. The origin coordinate is the position of Fz electrode (for 59 channels in Data set 1) or position of Fpz (for 118 channels in Data set 2).
| 11 |
As seen from the priori position information , if the th channel is close to the C3 or C4 channel, the will be large. If the th channel is far from the channel C3 and C4 channel, the will be small. The PP(C3) and PP(C4) were set to 1 under initial conditions. The range of the PP(m) values was adjusted according to the range of values of the coordinates.
The is the priori position information for one channel. Thus, the PPWPE should be calculated for every channel. The EEG signal series (, = number of trails, = number of channels, and S = number of samples), only include two kinds of imagery task ( trails for class 1, trails for class 2). The PPWPE for all channels can be calculated as follows:
| 12 |
where is the all channels’ priori position information.
| 13 |
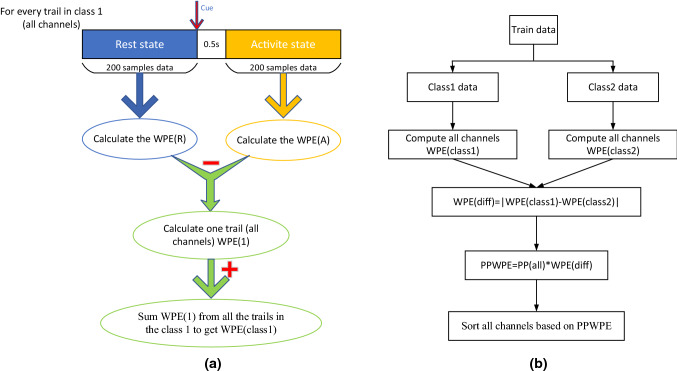
was calculated from the 0.5–2.5 s data after the start of MI in each trail. was calculated from the 200 samples data before the cue showing. Figure 1 describes the process of calculating WPE from one trail, and Fig. 2 describes the process of calculating PPWPE from two class of trail data. The channels were sorted based on the PPWPE value obtained for each channel. The channels, which have high PPWPE value, are important and have more amplitude information than those with low PPWPE value. These channels are close to the motor area in brain. Based on the sorted results obtained, half of the effective channels were filtered out.
Fig. 1.
PPWPE calculation process. The figure a is the process of calculating WPE for class 1, the figure b is the calculation process of PPWPE for all channels
Fig. 2.
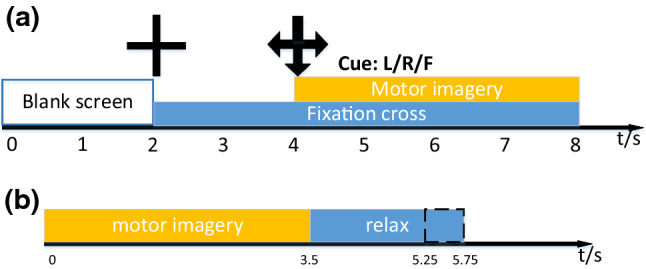
Experiment procedure. The figure a is the timing of single trail of Data set 1. The figure b is the timing of single trail of Data set 2
Binary gravitational search algorithm
Although half of the effective channels were filtered by the sorting result of PPWPE, the binary gravitational search algorithm (BGSA) was used in the selection of effective channels. This algorithm is an extension of the GSA algorithm, and was first proposed by Rashedi et al. (2010). It is a population optimization algorithm based on the law of universal gravitation and Newton’s second law. The algorithm and its improved version have been successfully applied in feature selection and channel selection. The GBSA algorithm is specifically designed for solving binary problems.
Given a system with P agents, the spatial information of the th agent can be expressed as follows:
| 14 |
The parameter represents the dimension of the space in the present study, expressed the combination of the channels, is the size of channels, indicates the th channel, can only be 0 or 1. At a time “t”, the force in th dimension space between th agent and th agent can be calculated as follows:
| 15 |
where and are the masses of the two agents at the time “t”. The th agent is the one that apply gravity, the th agent is the one that accept gravity. The mass of th agent can be updated as follows:
| 16 |
| 17 |
where is the optimization objective function and is called fitness function. It determines the mass of the agent. Over time, agents are expected to be attracted by the heaviest agent, and it represent the optimum solution in the search space. Meanwhile, is a constant that depends on time t and initial value, and is a small constant, and is the Hamming distance between th agent and th agent, can be calculated as follows:
| 18 |
The total force of the th agent in the th dimension can be expressed as follows:
| 19 |
where is a random value between 0 and 1. is a function that gradually decreases linearly with time. This response ensures that all agents apply force at the beginning and only one last agent applies force at the end apply force.
The acceleration of the th agent in the th dimension due to the total force can be calculated as follows:
| 20 |
The next velocity can be updated as follows:
| 21 |
where is a random values between 0 and 1 and provides a randomized characteristic to the search. In the process of solving binary problem, each dimension of the search space only take the value 0 or 1. Then, the position of the agent in the each dimension are changed as a probability according to Eq. (22). The is a function to transfer the to a probability.
| 22 |
The position of the agent can be updated as follows:
| 23 |
Feature extraction
In the BCI applications, the feature extraction also plays an important role in maximizing the performance of the system. In this paper, the common spatial patterns (CSP) to extract the features (Ramoser et al. 2000). The CSP algorithm is widely used in the EEG signals processing in the MI-based BCI systems (Cheng et al. 2017; Zhao et al. 2010). The basic principle of the CSP algorithm is to use the diagonalization of the matrix to find a set of optimal spatial filters for projection (Zuo et al. 2019). Thus, the variance of the difference between the two types of signals is maximized, and the feature vector with higher discrimination is obtained.
For the calculation, the single trail EEG signal can be represented as an matric E, where the is the number of the channels, and S is the number of the sample points of every channel. The spatial covariance of the E can be calculated as follows:
| 24 |
where the is the transpose operator on , and trace() is the calculation of the trace of the matrix. Two kinds of signal distributions, left MI and right MI, can be obtained. The spatial covariance , is calculated by averaging all trails of each kind of EEG signal. The composite spatial covariance of the two kinds of signal can be calculated as follows:
| 25 |
The composite spatial covariance can be expressed as follows:
| 26 |
where is the eigenvalue matrix of the composite spatial covariance , and is the eigenvectors matrix of the . In this process, the eigenvalues are arranged in order from largest to smallest.
The whitening matrix can be calculated as follows:
| 27 |
After the transformation of the composite space covariance matrix with the whitening matrix, the eigenvalues of the new matrix are equal to 1. The and the can be transformed as follows:
| 28 |
Formally, if they contain the common eigenvectors, can be expressed as follows:
| 29 |
Then, can be expressed as follows:
| 30 |
and
| 31 |
where I is the identity matrix. Given that the eigenvalues of the two kinds of EEG signals are always equal to 1, the eigenvectors with smallest eigenvalue of has the largest eigenvalue of . According to this characteristic, a projection matrix can be calculated as follows:
| 32 |
The one trail EEG signal E can be decomposition with the projection matrix as follows:
| 33 |
The features, which can be used for training classifier, are calculated by transforming the EEG according to (33). The feature can be chosen from the () as follows:
| 34 |
Support vector machine
SVM is a widely used machine learning method, the present form of SVM was created by Vapnik (Vapnik and Vapnik 1998). SVM has good performance on two classification problems, and some good results show that the SVM has outstanding performance in BCI systems. The basic principle of SVM is to create a hyperplane between the two types of data and maximize the classification interval. If there is a data set , the aim is to find a weight vector and produce a hyperplane with a threshold b.
| 35 |
The solution of this problem is
| 36 |
In this paper, the LIBSVM was selected to train the classifier (Chang and Lin 2011), and the Radial Basis Function was selected as the kernel function.
Experiment and results
Data descriptions
Data set 1
The first data set comes from the BCI competition IV and provided by the Berlin BCI group (Blankertz et al. 2007). All data were recorded from seven healthy subjects. However, the data of subjects ‘c’, ‘d’, ‘e’ were artificially generated, which was not used in the study. Experimental paradigm was the standard MI paradigm without feedback. The signal was recorded by the Ag/AgCl electrode cap with 59 channels. For every subject, the signal was selected from two kinds of MI task processing. In each run, a fixation cross displayed first at the center of the computer screen for 2 s. Then the fixation cross became the cue (the fixation with arrow) and displayed for 4 s, during which the subject performed a specific MI task. Finally, a blank screen lasting 2 s was shown to let subject rest. Two runs of the experiment were performed. Each run contains 100 trials. Figure 2 shows the timing diagram of the one trail. The data, which was down sampled to 100 Hz, was selected. The data set can be download from the website: http://www.bbci.de/competition/iv/.
Data set 2
The second data set comes from the BCI Competition III, which was recorded from the 5 healthy subject with 118 channels (Dornhege et al. 2004). The visual cue displayed in the screen center for 3.5 s, during which each subject performed an MI task according to the cue. Then the subjects had 1.75–2.25 s to have a rest. Three kinds of cues (left hand, right hand, foot) were provided for the subjects. In total, 280 trails MI task were provided to each subject, and all EEG data was down-sampled to 100 Hz. The data set can be download from the website: http://www.bbci.de/competition/iii/.
Channel selection based on PPWPE
PPWPE + CSP
As an evaluation indicator, the PPWPE mentioned above contains amplitude changes and electrode position information. The train data was used in the computation of the PPWPE of each channel, and all the channels were sorted according to the PPWPE values (details are in the methods section). The resulting channel order was seen as a search order, and the channels were added one by one. In fact, to calculate PPWPE, we first calculated the weight-permutation entropy of each electrode in the resting and active states during the MI tasks and then calculated the increase in WPE value from the resting state to the active state. Afterward, we calculated the difference in WPE value increase between two kinds of motor imagery and the difference in entropy increase between two kinds of MI. Finally, sort all channels based on the size of the difference obtained.
The channels with the higher ranking result were considered rich in amplitude change information and position information, which are needed by the channels. To finalize the number of channels and ensure the simplicity of the algorithm, a sequential addition strategy was adopted. The time complexity of the algorithm was reduced by considering the results searched in half of the channels valid, that is, the number of channels was controlled within half of the total number of channels. The rationality of this setup will be elaborated in the section of discussion. Figure 3 depicts the channel selection processing using PPWPE + CSP for Data Set 1. In the PPWPE + CSP channel selection algorithm, channels were added in order obtained, until the whole channels filtered were added. Finally, the channel number and channel combination were determined according to the classifier performance obtained.
Fig. 3.
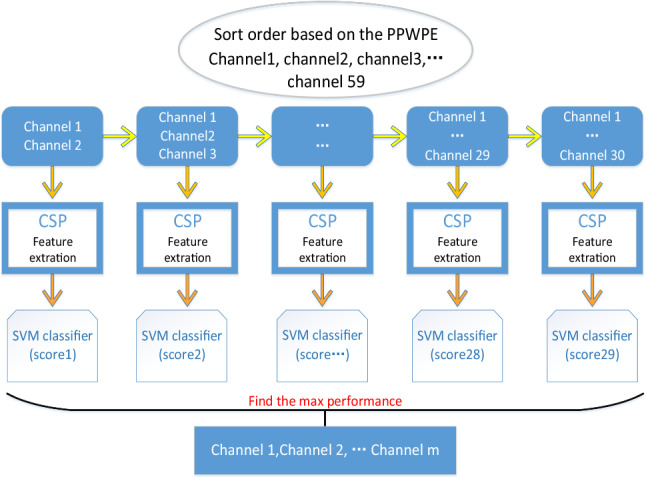
PPWPE + CSP channel selection algorithm. All channels were sorted by PPWPE value, selected half of channels with larger PPWPE value. According to the order of the sorting results, the channels were added one by one until all the selected channels were added. Feature were extracted by CSP algorithm, and fed into SVM classifier. Determine the final channel combination based on the classification accuracy obtained
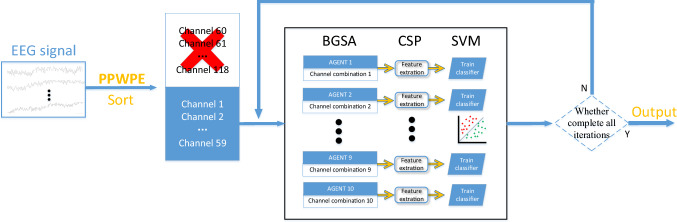
PPWPE + BGSA + CSP
In this method, based on the sort result obtained by calculating PPWPE, the channels in the second half were deleted. The number of channels was reduced, and redundant information was removed by using the BGSA for secondary channel selection. The Fig. 4 depicts PPWPE + BGSA + CSP algorithm in Data set 2. In this study, 10 agents and 50 iterations were used in searching the best selection. The dimension of every agent were 30 in Data set 1 and 59 in Data set 2.
Fig. 4.
PPWPE + BGSA + CSP channel selection algorithm. First, based on the calculated PPWPE value of each channel, half of the channels with larger PPWPE value are selected. Then, used the remaining channels as search space and performed iterative search using BGSA algorithm. Determined the final channel selection scheme based on the obtained classification accuracy
Whole data processing
In this work, in the calculation of PPWPE in the rest state, a signal with a data length of 200 samples (before the cue appears) was used. To ensure uniform data length, we used 200 samples length data in the calculation of the active PPWPE (after the cue appears). However, in the CSP extraction feature phase, different time windows were used (0.5–4.5 s for Data set 1, 0.5–3.5 s for Data set 2). The EEG signal from every trail was filtered between 8 and 30 Hz by a fifth-order butterworth filter.
Experimental results
Performance evaluation on PPWPE + BGSA + CSP
To verify the validity of the proposed channel selection algorithms, we performed experiments on the two data sets mentioned above. PPWPE + BGSA + CSP was compared with several other channel selection strategies. A few notes were made:
All-C + CSP: CSP was used in the extraction of features from all the channels.
PPWPE + CSP: According to the calculated PPWPE, all the channels were sorted, and the larger half of the lead of the PPWPE were selected. The selected channels were added one by one to form channel combinations. The features were extracted from these combinations by CSP.
All-C + BGSA + CSP: the optimal combination in the whole channel range was searched using the BGSA, and features were extracted with CSP algorithm.
PPWPE + BGSA + CSP: All channels were sorted based on the PPWPE obtained, and the channels in the second half were cut. In the remaining channels, the BGSA algorithm was used to search the optimal channel combination, and the feature extraction was performed by CSP.
In this study, we first tested the effects of PPWPE and BGSA methods independently, and then tested the proposed combination of the two. All experimental results were obtained after ten-fold cross validation. We only chose two pairs features extracted by CSP for classification. The experimental results of the above four methods on two data sets are shown in detail in Table 1. Table 1 shows that the proposed PPWPE + BGSA + CSP method had the highest classification performance on all subjects in the two data sets. When All-C + CSP was used as the reference baseline, the other three methods improved in terms of mean accuracy. In Data set 1, the mean accuracies improved by 20.25% (with PPWPE + CSP), 26.63% (with All-C + BGSA + CSP), and 30.50% (with PPWPE + BGSA + CSP) relative to the mean accuracy of the All-C + CSP method. In Data set 2, which had five subjects, the mean classification accuracy improved by 7.73% (with PPWPE + CSP), 12.18% (with All-C + BGSA + CSP) and 14.75% (with PPWPE + BGSA + CSP).
Table 1.
Classification performance in Data set 1 and Data set 2
| Methods | All-C + CSP | PPWPE + CSP | All-C + BGSA + CSP | PPWPE + BGSA + CSP |
|---|---|---|---|---|
| Subject | Acc (%) | Acc (%) | Acc (%) | Acc (%) |
| a | 49.50 | 78.00 | 88.50 | 91.00 |
| b | 47.00 | 62.50 | 68.50 | 73.50 |
| f | 43.00 | 78.00 | 85.50 | 92.50 |
| g | 90.50 | 92.50 | 94.50 | 95.00 |
| Mean ± SD | 57.50 ± 22.16 | 77.75 ± 12.25 | 84.13 ± 11.15 | 88.00 ± 9.81 |
| aa | 80.00 | 82.36 | 82.86 | 85.71 |
| al | 97.86 | 98.57 | 98.93 | 99.29 |
| av | 49.29 | 59.29 | 76.07 | 82.86 |
| aw | 83.21 | 91.07 | 92.14 | 94.29 |
| ay | 86.43 | 89.29 | 92.86 | 93.57 |
| Mean ± SD | 79.36 ± 18.11 | 84.12 ± 15.03 | 88.57 ± 9.05 | 91.14 ± 6.71 |
| p value | – | 0.023 | 0.013 | 0.010 |
Except for the last row of data, the maximum value of each row of data is bold
The PPWPE + BGSA + CSP method showed the best performance when applied to the subjects individually. The results obtained from the data set verification showed that the PPWPE + BGSA + CSP method proposed in this paper is effective, and the combined method is better than PPWPE or BGSA alone.
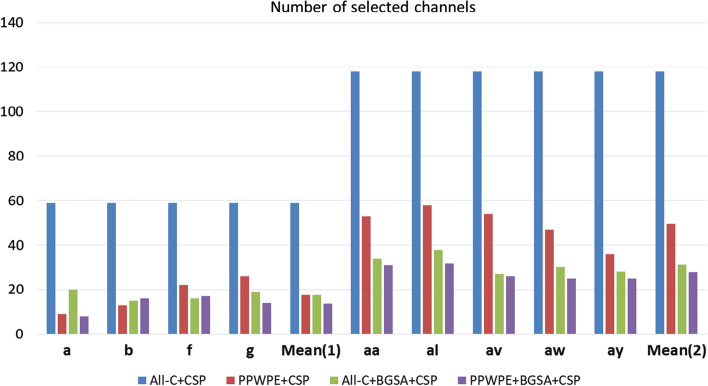
The number of channels selected in the four kinds of channel selection methods were recorded. The histogram of Fig. 5 shows the number of channels ultimately selected for Data set 1 and Data set 2 under the four channel selection methods. In the Data set 1 (Fig. 5 left side), the least channels were selected by PPWPE + CSP method for subject “b”, the least channels were selected by All-C + BGSA + CSP method for subject “f”, and the PPWPE + BGSA + CSP method had the best performance for subject “a” and “g”. In the Data set 2 (Fig. 5 right side), the PPWPE + BGSA + CSP method showed the best results in all subjects. In term of mean number of channels selected, the least channels were selected by PPWPE + BGSA + CSP algorithm in both Data sets.
Fig. 5.
Number of selected channels in Data set 1 and Data set 2. Mean (1) and Mean (2) represent the average number of selected channels in Data set 1 and Data set 2
Effect of feature number
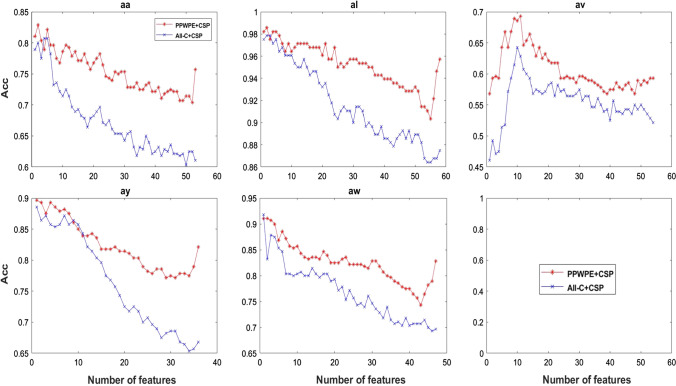
The number of features extracted by CSP method is a key factor for the performance of classifier trained by SVM. The effect of increasing the number of features extracted by the CSP method under the conditions of All-C + CSP and the channel selected by PPWPE + CSP in the Data set 2 were analyzed. In the CSP algorithm, the number of features was at most equal to the number of channels. Given that the number of channels selected in the PPWPE + CSP algorithm is different (detail of number of channels selected by PPWPE + CSP method can be seen from Fig. 5), the maximum number of features differ from subject to subject. Figure 6 shows that, as the number of features increases, the classification accuracy of the classifier decreases in the form of fluctuations, except in subject ‘av’. For the subject ‘av’, when the number of features is less than 10, the trend of accuracy increased. When the number of features is greater than 10, the accuracy seemed to decline. Overall, the accuracy of the classifier after channel selection by PPWPE + CSP method was always higher than that of the classifier trained under the whole channel condition. This result indicates that PPWPE has certain robustness to the selection of feature numbers.
Fig. 6.
Accuracy with respect to different number of features for 5 subjects from Data set 2
To better illustrate the generalization performance of the proposed method, we have added a set of experiments with full features, that is, the number of channels was equal to the number of the features extracted by CSP. Under the full features condition, the highest accuracy achieved under several methods is recorded in Table 2. In the Half (PPWPE) method, a half channel was selected after sorting according to the PPWPE value. Under the all features condition, for all subjects from both Data sets, the method PPWPE + BGSA + CSP still had the best performance in terms of mean accuracy in all the subjects from both data sets.
Table 2.
Performance under all features condition
| Methods | All-C + CSP | Half (PPWPE) + CSP | PPWPE + CSP | All-C + BGSA + CSP | PPWPE + BGSA + CSP | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Subject | Acc (%) | Acc (%) | Acc (%) | Acc (%) | Acc (%) | |||||
| a | 59 | 53.50 | 30 | 74.00 | 9 | 81.00 | 16 | 90.50 | 13 | 93.50 |
| b | 59 | 48.00 | 30 | 52.00 | 4 | 59.50 | 28 | 52.00 | 11 | 69.50 |
| f | 59 | 51.50 | 30 | 55.00 | 8 | 76.50 | 17 | 86.50 | 12 | 87.00 |
| g | 59 | 72.50 | 30 | 82.00 | 25 | 87.50 | 27 | 90.50 | 14 | 93.00 |
| Average | 59 | 56.38 | 30 | 65.75 | 11.5 | 76.13 | 22 | 79.88 | 12.5 | 85.75 |
| aa | 118 | 63.57 | 59 | 71.79 | 11 | 76.07 | 44 | 81.97 | 31 | 85.00 |
| al | 118 | 86.79 | 59 | 94.64 | 50 | 96.07 | 45 | 98.93 | 30 | 98.57 |
| av | 118 | 51.79 | 59 | 56.43 | 49 | 63.57 | 54 | 73.93 | 21 | 77.50 |
| aw | 118 | 66.43 | 59 | 80.71 | 29 | 87.14 | 44 | 93.93 | 21 | 93.93 |
| ay | 118 | 66.79 | 59 | 77.86 | 13 | 86.79 | 40 | 90.71 | 20 | 94.64 |
| Average | 118 | 67.07 | 59 | 76.29 | 30.4 | 81.93 | 45.4 | 87.86 | 24.6 | 89.93 |
| p-value | 9.4846e−04 | 4.9761e−05 | 2.3211e−04 | 1.586e−05 | ||||||
For data whose column label is Acc, bold the maximum Acc of each row, and for data whose column label is Nsc bold the minimum Nsc of each row
By comparing the classification accuracy obtained under the All-C + CSP and Half(PPWPE) + CSP methods, half of the channels selected from all the channels based on PPWPE values significantly improved classification accuracy, and the PPWPE standard was effective. By comparing the last column of accuracy in Tables 1 and 2, subjects ‘a’ and ‘ay’ can achieve higher accuracy under all-feature conditions. This observation showed that different subjects had different level of sensitivity to the selection of the number of features. However, overall, under the new channel selection method proposed, selecting two pairs of features was reasonable.
Comparison of channel selection
Classification accuracy using PPWPE + BGSA + CSP method was compared with classification accuracies calculated with other algorithms during channel selection.
The 3C + CSP method just selected three channels (C3, C4 and Cz) from all the channels, which is based on the physiological position of the motor cortex. This method selects the least number of channels among other methods and has relatively little memory usage and computation time in implementation.
The CSP-rank method (Tam et al. 2011) first sorts the absolute values of the filter coefficients in each filter, then sequentially obtains the electrodes with the second largest coefficient from the two spatial filters. However, the calculation time of the CSP-rank method is relatively long.
The RSS-SFSM (Aydemir and Ergun 2019) method was inspired by sequential forward feature selection method, it uses iterative and traversal methods to search, and its search speed is faster. In this paper, features were extracted by CSP.
Table 3 shows the classification accuracy obtained in Data set 2 through different methods. In terms of accuracy, whether for each subject or on average, the highest accuracy was obtained by PPWPE + BGSA + CSP method. The number of channels selected was within acceptable limits. In summary, the channel selection algorithm proposed in this paper is superior to the other three methods.
Table 3.
Accuracy comparison of different methods applied on Data set 2
| Methods | 3C + CSP | CSP-rank | RSS-SFSM + CSP | PPWPE + BGSA + CSP | ||||
|---|---|---|---|---|---|---|---|---|
| Subject | Acc (%) | Acc (%) | Acc (%) | Acc (%) | ||||
| aa | 3 | 56.53 | 46 | 81.43 | 14 | 77.14 | 31 | 85.71 |
| al | 3 | 85.36 | 57 | 98.57 | 11 | 92.14 | 32 | 99.29 |
| av | 3 | 54.64 | 30 | 54.29 | 9 | 75.36 | 26 | 82.86 |
| aw | 3 | 81.07 | 32 | 90.00 | 14 | 89.64 | 25 | 94.29 |
| ay | 3 | 88.93 | 55 | 94.30 | 12 | 92.14 | 25 | 93.57 |
| Average | 3 | 73.31 | 44 | 83.72 | 12 | 85.28 | 27.8 | 91.14 |
For data whose column label is Acc, bold the maximum Acc of each row, and for data whose column label is Nsc bold the minimum Nsc of the last row
Discussion
Rationality of filtering half of channels based PPWPE
In our experiment, all channels were sorted according to the PPWPE value. On the basis of the sorted results, half of the channels were filtered out. To explain the rationality of adopting this method, the influence of the number of channels on the average classification accuracy was tested by adding all the channels one by one to the sorting result. Figure 7 shows the average accuracy of all subjects in the two data sets under different channel numbers. In Data set 1 (left side of Fig. 7), the highest classification accuracy was obtained before the number of channels increased to half the total number of the channels. However, when the number of channels exceeded half the total number of the channels, classification accuracy started to decline. In Data set 2 (right side of Fig. 7), the highest classification accuracy was also obtained before the number of channels increased to half the total number of channels. When the number of channels exceeded half the total number of channels, the average classification accuracy stopped increasing.
Fig. 7.
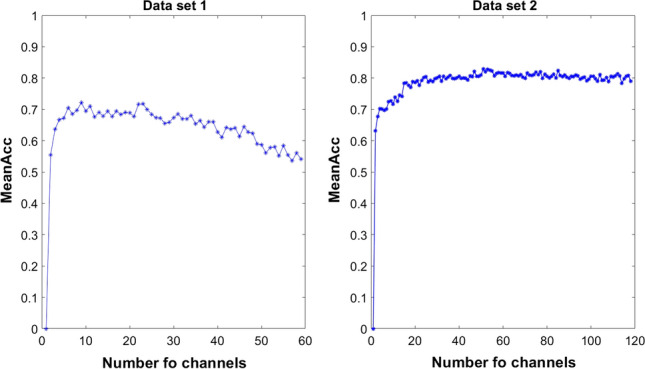
The mean classification accuracy of the two data sets varies with the number of channels. All channels were sorted by PPWPE value, according to the sorting result, increased the channel one by one
Therefore, half of the channels screened according to the PPWPE value contained most of the useful information for classifying MI activities. The information contained in the reserved half of the channel is relatively important, which shows the rationality of the method.
Channels selected distribution
The channels selected by the PPWPE + BGSA + CSP method from two data sets were recorded. The channel distribution of two subjects from each Data set was selected and plotted in Fig. 8.
Fig. 8.
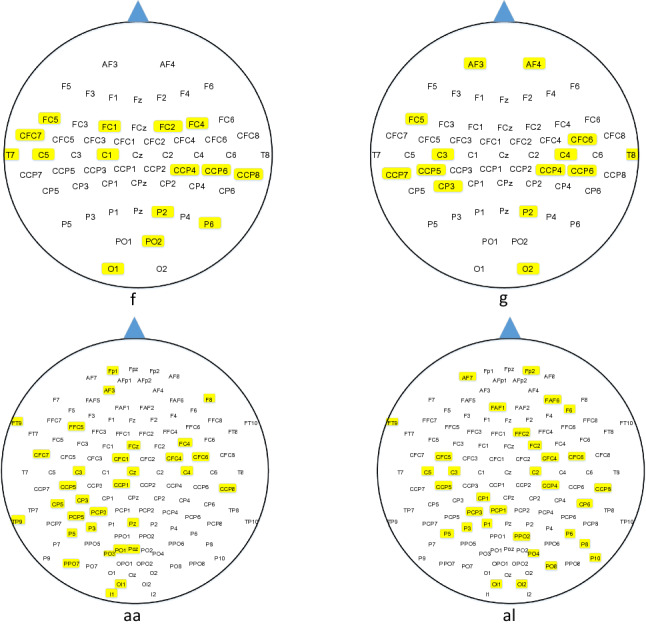
Distribution of channels selected using PPWPE + BGSA + CSP
Figure 8 shows that most of the selected channels were distributed in the vicinity of the motor cortex. Individual differences are the important features of the EEG signal. Thus, a large difference in the location distribution of the selected channels was observed among the subjects. However, the distribution of the selected channels still met the theoretical basis of cognitive neuroscience. Although some channels that were far from the motor cortex were also selected, the amplitude of the artifacts in some areas was extremely large to be avoided, and the subjects required multiple brain areas to work together during the MI tasks.
Features distribution
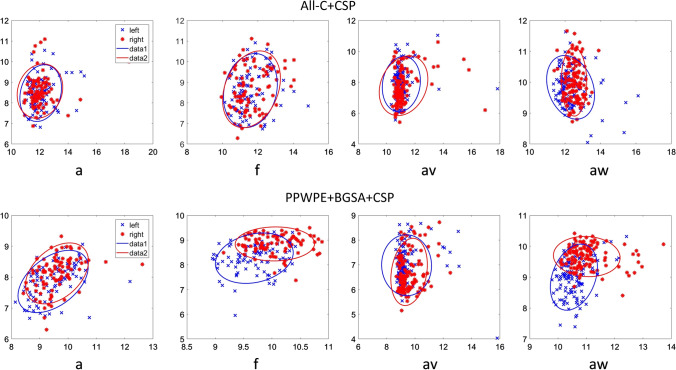
To illustrate the effectiveness of the proposed method, we drew the feature extracted by PPWPE + BGSA + CSP from Data set 1 (subject “a” and “f”) and Data set 2 (subject “av” and “aw”) and compared them with the features extracted by the All-C + CSP method. It can be seen from Fig. 9 shows that the distinguishability of features extracted using the PPWPE + BGSA + CSP method was more obvious than that extracted by the All-C + CSP method. This finding showed that the proposed method can render the obtained features separable and thereby increases classification accuracy.
Fig. 9.
Comparison of feature distribution (Data set 1, subject ‘a’ and ‘f’; Data set 2, subject ‘av’ and ‘aw’). Two subplots in the column show the results of each subject with different methods (All-C + CSP, PPWPE + BGSA + CSP). The horizontal and vertical axes represent two features extracted in each trail. The feature distribution with PPWPE + BGSA + CSP become more discriminative
Advantage of PPWPE
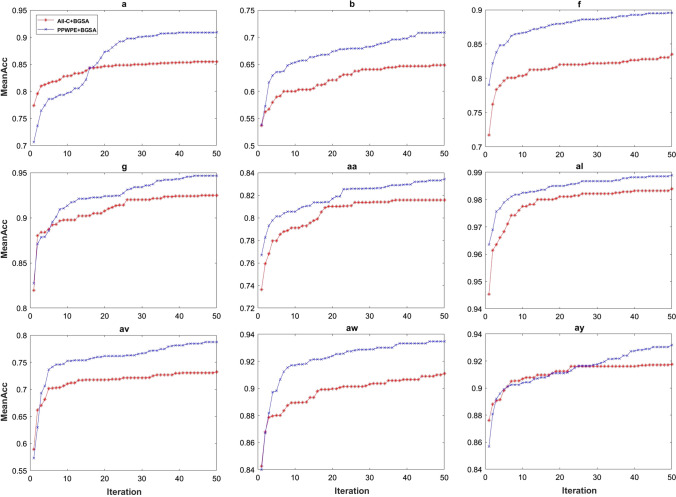
In this study, the PPWPE values of all the channels were calculated. PPWPE value was used as a new performance indicator for measuring channels. It contains the amplitude and position information of the channels. The amplitude variation of the channel increased with the PPWPE value, and the distance to the motor cortex decreased.
According to the sorting result of the PPWPE value, half of the channels were eliminated. Thus, the search space of the BGSA decreased. Figure 10 shows the mean accuracy of agents when BGSA was used under the all-channel condition and half-channel (selected by PPWPE value) condition. Figure 10 shows that the mean accuracy obtained through the PPWPE + BGSA method was higher than mean accuracy obtained through the All-C + BGSA method after a few iterations. In addition, under the all channels condition, the BGSA algorithm quickly finds the local optimum value. Moreover, finding a new solution was difficult when the number of iterations was increasing. However, under the half-channel (selected by the PPWPE value) condition, the agents gradually found good solutions, and the mean accuracy was always higher than that under all-channel condition. This outcome fully demonstrated that using the PPWPE value in channel evaluation is reasonable.
Fig. 10.
Average accuracy for ten agents in every iteration for all subjects from two data sets
Comparison of existing method with our method
To further evaluate the performance of the algorithm proposed in this study, we compared the existing channel selection algorithm with the algorithm proposed in this paper. The results are shown in Tables 4 (dataset 1) and 5 (dataset 2).
Table 4.
Comparison of classification accuracy between existing method and our method (dataset 1)
| Methods | ISFFS (Qiu et al. 2016) | GSFS (Radman et al. 2019) | CCS + RCSP (Jin et al. 2019) | DBN (Jing-Ru et al. 2019) | Our method | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Subject | Acc (%) | Acc (%) | Acc (%) | Acc (%) | Acc (%) | |||||
| a | 6 | 69.00 | 6 | 75.00 | 46 | 85.50 | 16 | 72.50 | 8 | 91.00 |
| b | 15 | 63.00 | 13 | 72.00 | 30 | 67.00 | 16 | 85.00 | 16 | 73.50 |
| f | 8 | 65.00 | 15 | 78.00 | 10 | 79.50 | 16 | 87.50 | 17 | 92.50 |
| g | 22 | 72.00 | 12 | 83.00 | 3 | 94.50 | 16 | 97.50 | 14 | 95.00 |
| Average | 12.75 | 67.25 | 11.5 | 77.00 | 22.5 | 81.6 | 16 | 85.625 | 13.8 | 88.00 |
For data whose column label is Acc, bold the maximum Acc of each row, and for data whose column label is Nsc bold the minimum Nsc of the last row
Table 5.
Comparison of classification accuracy between existing method and our method (dataset 2)
| Methods | RC-GA (He et al. 2013) | NSGA-II (Kee et al. 2015) | ISFFS (Qiu et al. 2016) | CCS-RCSP (Jin et al. 2019) | Our method | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Subject | Acc (%) | Acc (%) | Acc (%) | Acc (%) | Acc (%) | |||||
| aa | 39 | 86.40 | 30 | 74.44 | 27 | 76.40 | 42 | 82.50 | 31 | 85.71 |
| al | 18 | 98.50 | 13 | 98.47 | 47 | 94.30 | 33 | 96.80 | 32 | 99.29 |
| av | 46 | 75.10 | 19.1 | 70.78 | 18 | 65.00 | 52 | 71.10 | 26 | 82.86 |
| aw | 26 | 93.90 | 6 | 90.52 | 27 | 89.50 | 14 | 92.90 | 25 | 94.29 |
| ay | 16 | 87.10 | 4.3 | 83.44 | 35 | 91.40 | 67 | 93.90 | 25 | 93.57 |
| Average | 29 | 88.20 | 14.5 | 83.53 | 30.8 | 83.30 | 42 | 87.40 | 27.8 | 91.14 |
For data whose column label is Acc, bold the maximum Acc of each row, and for data whose column label is Nsc bold the minimum Nsc of the last row
For dataset 1, in terms of classification accuracy, the average classification accuracy obtained by our method is higher than that of the DBN, ISFFS, CCS-RCSP, GSFS method. Although the results in Table 4 show that the GSFS algorithm can obtain a smaller number of channels, the classification accuracy of the GSFS method is lower. This shows that the GSFS method may have lost some important electrodes.
For dataset 2, we compared our method(PPWPE + BGSA) with RC-GA, NSGA-II, ISFFS, CCS-RCSP. It can be seen that the channels selected by PPWPE + BGSA method offer a higher classification accuracy for most subjects (except ‘ay’) as shown in Table 5. The number of channels selected by our method is more than that obtained by NSGA-II, but the classification accuracy obtained by our method is much higher.
By combining Tables 4 and 5, it can be concluded that our method can effectively select a small number of channels containing important information while ensuring a high classification accuracy.
Generalizability of the proposed algorithm
We also used wavelet transform (WT) (Hazarika 2019) as a feature extraction method to test the performance of the proposed algorithm, and the results are presented in Table 6. Considering that the number of features equal to the number of channels when using wavelet transform to extract features, the results of CSP feature extraction presented in Table 6 also use full features. Compared with the full-channel (All-C) condition, using the channel selection method(PPWPE + BGSA) proposed in this paper can improve the classification accuracy and effectively reduce redundant channels under both wavelet transform (WT) and CSP feature extraction. Note that since the parameters of wavelet transform are not specifically optimized for this data set, the obtained accuracy may not be high. It suggests that combining the proposed method with different feature extraction methods can still effectively reduce redundant channels and improve classification accuracy.
Table 6.
Performance of method proposed with different feature extraction
| Method | All-C + WT | PPWPE + BGSA + WT | All-C + CSP | PPWPE + BGSA + CSP | ||||
|---|---|---|---|---|---|---|---|---|
| Subject | Acc (%) | Acc (%) | Acc (%) | Acc (%) | ||||
| aa | 118 | 58.93 | 26 | 64.64 | 118 | 63.57 | 31 | 85.00 |
| al | 118 | 62.50 | 25 | 83.57 | 118 | 86.79 | 30 | 98.57 |
| av | 118 | 52.86 | 26 | 65.36 | 118 | 51.79 | 21 | 77.50 |
| aw | 118 | 62.50 | 31 | 71.07 | 118 | 66.43 | 21 | 93.93 |
| ay | 118 | 78.31 | 26 | 87.50 | 118 | 66.79 | 20 | 94.64 |
| Average | 118 | 63.00 | 26.8 | 74.43 | 118 | 67.07 | 24.6 | 89.93 |
For data whose column label is Acc, bold the maximum Acc of each row, and for data whose column label is Nsc bold the minimum Nsc of the last row
Future work
In this study, a novel channel selection algorithm called PPWPE + BGSA + CSP was proposed. In the calculation of the PPWPE value, the amplitude and position information of the channel were considered and combined. Basing on the PPWPE value obtained, we selected half of the useful channels. Using the BGSA for secondary searches in these channels improved channel combinations. In this study, we did not focus on the information contained in the frequency bands of EEG signals. Given that frequency bands often contain important information, we will consider frequency band information in our future work.
Conclusion
A channel selection algorithm based on PPWPE for MI-based BCI was proposed. The PPWPE is a novel performance indicator for channel measurement. It combines amplitude information and position prior information and selects half of the more important channels according to PPWPE. The BGSA can find the good channel combination from channels selected by PPWPE. High classification accuracy can be obtained by using the SVM method to classify features extracted by CSP from selected channels. The experimental results showed that the PPWPE algorithm can initially select half of the channels reasonably, and the BGSA search algorithm can further select the channel combination. In short, the proposed method has potential in improving the performance of MI-based BCIs.
Acknowledgements
This work was supported by the National Key Research and Development Program 2017YFB13003002. This work was also supported in part by the Grant National Natural Science Foundation of China, under Grant Nos. 61573142, 61773164 and 91420302, the programme of Introducing Talents of Discipline to Universities (the 111 Project) under Grant B17017, and the “ShuGuang” project supported by Shanghai Municipal Education Commission and Shanghai Education Development Foundation under Grant 19SG25.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Jing Jin, Email: jinjingat@gmail.com.
Wanzeng Kong, Email: kongwanzeng@hdu.edu.cn.
References
- Acharya UR, Fujita H, Sudarshan VK, Bhat S, Koh JEW. Application of entropies for automated diagnosis of epilepsy using EEG signals: a review. Knowl Based Syst. 2015;88:85–96. doi: 10.1016/j.knosys.2015.08.004. [DOI] [Google Scholar]
- Alcaide-Aguirre RE, Huggins JE. Novel hold-release functionality in a P300 brain–computer interface. J Neural Eng. 2014;11:066010. doi: 10.1088/1741-2560/11/6/066010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alotaiby T, Abd El-Samie FE, Alshebeili SA, Ahmad I. A review of channel selection algorithms for EEG signal processing. EURASIP J Adv Signal Process. 2015;201:66. doi: 10.1186/s13634-015-0251-9. [DOI] [Google Scholar]
- Ang KK, et al. A large clinical study on the ability of stroke patients to use an EEG-based motor imagery brain–computer interface. Clin EEG Neurosci. 2011;42:253–258. doi: 10.1177/155005941104200411. [DOI] [PubMed] [Google Scholar]
- Aydemir O, Ergun E. A robust and subject-specific sequential forward search method for effective channel selection in brain computer interfaces. J Neurosci Methods. 2019;313:60–67. doi: 10.1016/j.jneumeth.2018.12.004. [DOI] [PubMed] [Google Scholar]
- Bandt C, Pompe B. Permutation entropy: a natural complexity measure for time series. Phys Rev Lett. 2002;88:174102. doi: 10.1103/PhysRevLett.88.174102. [DOI] [PubMed] [Google Scholar]
- Blankertz B, Dornhege G, Krauledat M, Muller KR, Curio G. The non-invasive Berlin brain–computer interface: fast acquisition of effective performance in untrained subjects. Neuroimage. 2007;37:539–550. doi: 10.1016/j.neuroimage.2007.01.051. [DOI] [PubMed] [Google Scholar]
- Chang CC, Lin CJ. LIBSVM: a Library for Support Vector Machines. ACM Trans Intell Syst Technol. 2011;2:1–27. doi: 10.1145/1961189.1961199. [DOI] [Google Scholar]
- Cheng MM, Lu ZH, Wang HX. Regularized common spatial patterns with subject-to-subject transfer of EEG signals. Cogn Neurodyn. 2017;11:173–181. doi: 10.1007/s11571-016-9417-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng B, Cai LH, Li SN, Wang RF, Yu HT, Chen Y, Wang J. Multivariate multi-scale weighted permutation entropy analysis of EEG complexity for Alzheimer’s disease. Cogn Neurodyn. 2017;11:217–231. doi: 10.1007/s11571-016-9418-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dokare I, Kant N. Classification of EEG signal for imagined left and right hand movement for brain computer interface applications. Int J Appl Innov Eng Manag. 2014;2014:291–294. [Google Scholar]
- Dong EZ, Li CH, Li LT, Du SZ, Belkacem AN, Chen C. Classification of multi-class motor imagery with a novel hierarchical SVM algorithm for brain-computer interfaces. Med Biol Eng Comput. 2017;55:1809–1818. doi: 10.1007/s11517-017-1611-4. [DOI] [PubMed] [Google Scholar]
- Dornhege G, Blankertz B, Curio G, Muller K-R. Boosting bit rates in noninvasive EEG single-trial classifications by feature combination and multiclass paradigms. IEEE Trans Biomed Eng. 2004;51:993–1002. doi: 10.1109/TBME.2004.827088. [DOI] [PubMed] [Google Scholar]
- Fadlallah B, Chen BD, Keil A, Principe J. Weighted-permutation entropy: a complexity measure for time series incorporating amplitude information. Phys Rev E. 2013;87:022911. doi: 10.1103/PhysRevE.87.022911. [DOI] [PubMed] [Google Scholar]
- Feng JK, et al. Towards correlation-based time window selection method for motor imagery BCIs. Neural Netw. 2018;102:87–95. doi: 10.1016/j.neunet.2018.02.011. [DOI] [PubMed] [Google Scholar]
- Gaume A, Dreyfus G, Vialatte FB. A cognitive brain-computer interface monitoring sustained attentional variations during a continuous task. Cogn Neurodyn. 2019;13:257–269. doi: 10.1007/s11571-019-09521-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghaemi A, Rashedi E, Pourrahimi AM, Kamandar M, Rahdari F. Automatic channel selection in EEG signals for classification of left or right hand movement in Brain Computer Interfaces using improved binary gravitation search algorithm. Biomed Signal Process Control. 2017;33:109–118. doi: 10.1016/j.bspc.2016.11.018. [DOI] [Google Scholar]
- Hazarika J (2019) Wavelet transform based approach for EEG feature selection of motor imagery data for brain computer interfaces. In: 3rd International conference on inventive systems and control (ICISC 2019)
- He L, Hu Y, Li Y, Li D. Channel selection by Rayleigh coefficient maximization based genetic algorithm for classifying single-trial motor imagery EEG. Neurocomputing. 2013;121:423–433. doi: 10.1016/j.neucom.2013.05.005. [DOI] [Google Scholar]
- Jin J, Allison BZ, Sellers EW, Brunner C, Horki P, Wang XY, Neuper C. An adaptive P300-based control system. J Neural Eng. 2011;8:036006. doi: 10.1088/1741-2560/8/3/036006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin J, Miao YY, Daly I, Zuo CL, Hu DW, Cichocki A. Correlation-based channel selection and regularized feature optimization for MI-based BCI. Neural Netw. 2019;118:262–270. doi: 10.1016/j.neunet.2019.07.008. [DOI] [PubMed] [Google Scholar]
- Jing-Ru S, Jian-Guo W, Zhong-Tao X, Yuan Y, Junjiang L (2019) A method for EEG contributory channel selection based on deep belief network. In: 2019 IEEE 8th data driven control and learning systems conference (DDCLS) proceedings, pp 1247–1252
- Kee C-Y, Ponnambalam SC, Loo C-K. Multi-objective genetic algorithm as channel selection method for P300 and motor imagery data set. Neurocomputing. 2015;161:120–131. doi: 10.1016/j.neucom.2015.02.057. [DOI] [Google Scholar]
- Kevric J, Subasi A. Comparison of signal decomposition methods in classification of EEG signals for motor-imagery BCI system. Biomed Signal Process Control. 2017;31:398–406. doi: 10.1016/j.bspc.2016.09.007. [DOI] [Google Scholar]
- Kumar S, Sharma A. A new parameter tuning approach for enhanced motor imagery EEG signal classification. Med Biol Eng Comput. 2018;56:1861–1874. doi: 10.1007/s11517-018-1821-4. [DOI] [PubMed] [Google Scholar]
- Kumar S, Sharma A, Tsunoda T. An improved discriminative filter bank selection approach for motor imagery EEG signal classification using mutual information. BMC Bioinform. 2017;18:545. doi: 10.1186/s12859-017-1964-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McFarland DJ, Wolpaw JR. Brain–computer interfaces for communication and control. Commun ACM. 2011;54:60–66. doi: 10.1145/1941487.1941506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miao MM, Wang AM, Liu FX. A spatial-frequency-temporal optimized feature sparse representation-based classification method for motor imagery EEG pattern recognition. Med Biol Eng Comput. 2017;55:1589–1603. doi: 10.1007/s11517-017-1622-1. [DOI] [PubMed] [Google Scholar]
- Nicolaou N, Georgiou J. Detection of epileptic electroencephalogram based on permutation entropy and support vector machines. Expert Syst Appl. 2012;39:202–209. doi: 10.1016/j.eswa.2011.07.008. [DOI] [Google Scholar]
- Puanhvuan D, Khemmachotikun S, Wechakarn P, Wijarn B, Wongsawat Y. Navigation-synchronized multimodal control wheelchair from brain to alternative assistive technologies for persons with severe disabilities. Cogn Neurodyn. 2017;11:117–134. doi: 10.1007/s11571-017-9424-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiu ZY, Jin J, Lam HK, Zhang Y, Wang XY, Cichocki A. Improved SFFS method for channel selection in motor imagery based BCI. Neurocomputing. 2016;207:519–527. doi: 10.1016/j.neucom.2016.05.035. [DOI] [Google Scholar]
- Radman M, Chaibakhsh A, Nariman-zadeh N, Huiguang H (2019) Generalized sequential forward selection method for channel selection in EEG signals for classification of left or right hand movement in BCI. In: 2019 9th international conference on computer and knowledge engineering (ICCKE), pp 137–142
- Raghu S, Sriraam N, Kumar GP. Classification of epileptic seizures using wavelet packet log energy and norm entropies with recurrent Elman neural network classifier. Cogn Neurodyn. 2017;11:51–66. doi: 10.1007/s11571-016-9408-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramoser H, Muller-Gerking J, Pfurtscheller G. Optimal spatial filtering of single trial EEG during imagined hand movement. IEEE Trans Rehabil Eng. 2000;8:441–446. doi: 10.1109/86.895946. [DOI] [PubMed] [Google Scholar]
- Rashedi E, Nezamabadi-pour H, Saryazdi S. BGSA: binary gravitational search algorithm. Nat Comput. 2010;9:727–745. doi: 10.1007/s11047-009-9175-3. [DOI] [Google Scholar]
- Selim S, Tantawi MM, Shedeed HA, Badr A. A CSP\AM-BA-SVM approach for motor imagery BCI system. IEEE Access. 2018;6:49192–49208. doi: 10.1109/ACCESS.2018.2868178. [DOI] [Google Scholar]
- Tam W-K, Ke Z, Tong K-Y (2011) Performance of common spatial pattern under a smaller set of EEG electrodes in brain-computer interface on chronic stroke patients: a multi-session dataset study. In: 2011 annual international conference of the IEEE engineering in medicine and biology society. IEEE, pp 6344–6347 [DOI] [PubMed]
- Vapnik V, Vapnik V. Statistical learning theory. New York: Wiley; 1998. [Google Scholar]
- Yang JH, Singh H, Hines EL, Schlaghecken F, Iliescu DD, Leeson MS, Stocks NG. Channel selection and classification of electroencephalogram signals: an artificial neural network and genetic algorithm-based approach. Artif Intell Med. 2012;55:117–126. doi: 10.1016/j.artmed.2012.02.001. [DOI] [PubMed] [Google Scholar]
- Zeng H, Yang C, Dai GJ, Qin FW, Zhang JH, Kong WZ. EEG classification of driver mental states by deep learning. Cogn Neurodyn. 2018;12:597–606. doi: 10.1007/s11571-018-9496-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Wang Y, Jin J, Wang XY. Sparse bayesian learning for obtaining sparsity of EEG frequency bands based feature vectors in motor imagery classification. Int J Neural Syst. 2017;27:1650032. doi: 10.1142/S0129065716500325. [DOI] [PubMed] [Google Scholar]
- Zhao QB, Rutkowski TM, Zhang LQ, Cichocki A. Generalized optimal spatial filtering using a kernel approach with application to EEG classification. Cogn Neurodynamics. 2010;4:355–358. doi: 10.1007/s11571-010-9125-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuo CL, et al. Novel hybrid brain-computer interface system based on motor imagery and P300. Cogn Neurodyn. 2019;14:253–265. doi: 10.1007/s11571-019-09560-x. [DOI] [PMC free article] [PubMed] [Google Scholar]