Key Points
Question
Do contemporary machine learning methods improve prediction of in-hospital death after hospitalization for acute myocardial infarction (AMI)?
Findings
In this cohort study of 755 402 patients with AMI in a nationwide registry, machine learning models that used the same data inputs as logistic regression were not associated with substantially improved prediction of in-hospital mortality after AMI. Two of these models, extreme gradient descent boosting and meta-classifier, however, were associated with improved calibration across the risk spectrum, reclassifying 1 in every 4 patients deemed to be at moderate or high risk for death in logistic regression accurately as low risk, consistent with the actual observed risk.
Meaning
These findings suggest that machine learning models are not associated with substantially better prediction of risk of death after AMI but may offer greater resolution of risk, which can better clarify the individual risk for adverse outcomes.
Abstract
Importance
Accurate prediction of adverse outcomes after acute myocardial infarction (AMI) can guide the triage of care services and shared decision-making, and novel methods hold promise for using existing data to generate additional insights.
Objective
To evaluate whether contemporary machine learning methods can facilitate risk prediction by including a larger number of variables and identifying complex relationships between predictors and outcomes.
Design, Setting, and Participants
This cohort study used the American College of Cardiology Chest Pain-MI Registry to identify all AMI hospitalizations between January 1, 2011, and December 31, 2016. Data analysis was performed from February 1, 2018, to October 22, 2020.
Main Outcomes and Measures
Three machine learning models were developed and validated to predict in-hospital mortality based on patient comorbidities, medical history, presentation characteristics, and initial laboratory values. Models were developed based on extreme gradient descent boosting (XGBoost, an interpretable model), a neural network, and a meta-classifier model. Their accuracy was compared against the current standard developed using a logistic regression model in a validation sample.
Results
A total of 755 402 patients (mean [SD] age, 65 [13] years; 495 202 [65.5%] male) were identified during the study period. In independent validation, 2 machine learning models, gradient descent boosting and meta-classifier (combination including inputs from gradient descent boosting and a neural network), marginally improved discrimination compared with logistic regression (C statistic, 0.90 for best performing machine learning model vs 0.89 for logistic regression). Nearly perfect calibration in independent validation data was found in the XGBoost (slope of predicted to observed events, 1.01; 95% CI, 0.99-1.04) and the meta-classifier model (slope of predicted-to-observed events, 1.01; 95% CI, 0.99-1.02), with more precise classification across the risk spectrum. The XGBoost model reclassified 32 393 of 121 839 individuals (27%) and the meta-classifier model reclassified 30 836 of 121 839 individuals (25%) deemed at moderate to high risk for death in logistic regression as low risk, which were more consistent with the observed event rates.
Conclusions and Relevance
In this cohort study using a large national registry, none of the tested machine learning models were associated with substantive improvement in the discrimination of in-hospital mortality after AMI, limiting their clinical utility. However, compared with logistic regression, XGBoost and meta-classifier models, but not the neural network, offered improved resolution of risk for high-risk individuals.
This cohort study evaluates whether contemporary machine learning methods can facilitate prediction of death from acute myocardial infarction by including a larger number of variables and identifying complex relationships between predictors and outcomes.
Introduction
An assessment of risk of death after an acute myocardial infarction (AMI) is useful for guiding clinical decisions for patients and for assessing hospital performance.1,2,3,4 New analytic approaches may enhance risk prediction with existing data beyond traditional statistical approaches. Existing risk prediction models developed in the prediction of AMI outcomes have been limited by lack of inclusion of nonlinear effects and complex interactions among variables in national samples or have only evaluated these effects in small patient groups.5,6,7,8,9,10,11,12,13,14,15,16 With advances in computation and analytics, however, it may be possible to create models in large and diverse patient groups, which may improve on traditional models with existing information. Specifically, the application of machine learning techniques has the potential to improve on accuracy in the prediction of in-hospital mortality after AMI.17,18,19
Accordingly, using data collected in the Chest Pain–MI Registry (CP-MI Registry; formerly known as the ACTION Registry) of the National Cardiovascular Data Registry (NCDR), a national clinical quality program from the American College of Cardiology, we assessed whether machine learning techniques, compared with logistic regression, could improve prediction of in-hospital AMI mortality. The CP-MI Registry includes information on more than 1 million AMI hospitalizations at 1163 hospitals across the US. We used the most contemporary published model for mortality after AMI, which used logistic regression,8,9 to compare the performance characteristics of our models derived using machine learning.
Methods
This cohort study used the American College of Cardiology CP-MI Registry to identify all AMI hospitalizations between January 1, 2011, and December 31, 2016. Data analysis was performed from February 1, 2018, to October 22, 2020. The Yale University Institutional Review Board reviewed the study and waived the requirement for informed consent given the deidentified data. The study followed the Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) reporting guideline.
The CP-MI Registry
The CP-MI Registry collects data from participating hospitals on patients admitted with AMI, including both ST-elevation myocardial infarction (STEMI) and non-STEMI. Data are collected through retrospective medical record review and submitted using a standardized data collection tool. Collected data include patient demographics, presentation information, pre-hospital vital signs, selected laboratory data from the hospital course, procedures, timing of procedures, and select in-hospital outcomes. The NCDR data quality program enhances data completeness and accuracy through audits and feedback.20
Patient Population
Between January 1, 2011, and December 31, 2016, a total of 993 905 patients with AMI from 1128 hospitals were included. Similar to the approach used in prior studies,21,22 patients transferred to another facility for management (n = 47 308) or missing information on history of percutaneous coronary intervention, a key risk factor included in the current standard for predicting mortality outcomes (n = 191 195), were excluded (eTable 1 in the Supplement). Those patients excluded had age and sex distribution similar to those of patients included in the analysis but slightly higher rates of STEMI and unadjusted mortality (eTable 1 in the Supplement). After the exclusion of these patients, 755 402 patients remained for modeling. We also constructed a secondary cohort in which patients were not excluded for missing variables and covariates with missingness greater than 5% were excluded as predictors in the model (n = 946 597).
Patient Variables and Data Definitions
Patient variables available to a practitioner at the time of presentation were selected for modeling. These variables include patient demographics, medical history, comorbidities, home medications, electrocardiogram findings, and initial medical presentation and laboratory values. The outcome of this study was death from any cause during hospitalization.
The current standard model for AMI mortality built within the NCDR uses 9 variables to predict mortality and was derived from 29 candidate variables using logistic regression by McNamara et al.21 We included 2 sets of variables to build our machine learning models. First, we included the 29 variables used to derive the current NCDR standard.21 Second, we used an expanded variable set with all other variables that would be available to a practitioner at the time of hospital presentation with an AMI (eTable 2 in the Supplement). A priori, we included variables that were available in at least 90% of patients, resulting in 8 candidate continuous variables and 48 categorical variables with a missing variable rate of less than 1%. For these variables, we imputed missing values to the mode for categorical variables and median for continuous variables. In sensitivity analyses, we pursued multiple imputation using the multivariate imputation by chained equations method, which derives predicted values of the missing values using a regression-based approach. These analyses were tested in a 5-fold validation exercise to evaluate the robustness of our strategy. Finally, we evaluated models that included patients who had been excluded from the primary analyses because of missing covariates (threshold ≥5%), thereby excluding key variables that are a part of the current standard.
Modeling Strategies
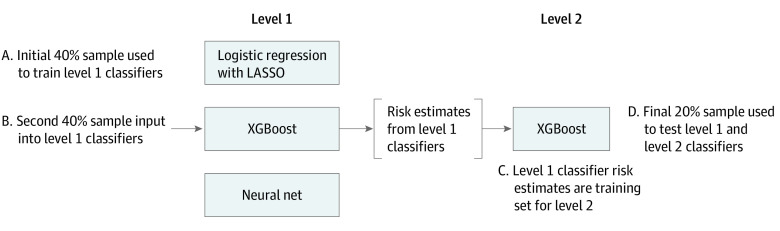
We divided the data into an initial 75% subset (April 1, 2011, through September 30, 2015) for model development and the more recent 25% subset (October 1, 2015, through December 31, 2016) for model testing. The model development period was further divided into 2 equal halves (April 1, 2011, to September 30, 2013, and October 1, 2013, to September 30, 2015) to develop level 1 and level 2 models, respectively (Figure 1).
Figure 1. Design of Machine Learning Algorithms.
The level 1 classifiers consist of 3 independent models each trained on the same initial training sample (sample A), including logistic regression with least absolute shrinkage and selection operator (LASSO), extreme gradient descent boosting (XGBoost), and a neural network. The next training sample (sample B) is then input into the level 1 classifiers, resulting in 3 risk estimates for each observation in sample B, 1 from each level 1 model. These 3 risk estimates are then used to train the level 2 XGBoost classifier (sample C). A final sample (sample D) is input into the level 1 classifiers to obtain risk estimates for input into the level 2 classifier. Performance of the level 1 and level 2 classifiers is assessed using this final training set D.
We compared 3 modeling strategies with logistic regression: (1) gradient descent boosting, (2) a neural network, and (3) a meta-classifier approach that combined logistic regression with least absolute shrinkage and selection operator (LASSO) regularization, a gradient descent boosting, and a neural network. Gradient descent boosting models make predictions using a series of decision trees, representing an interpretable model. Unlike logistic regression, this model can include higher-order interactions and account for complex nonlinear relationships between model variables and outcomes. The method of gradient descent boosting chosen was extreme gradient boosting, or XGBoost.23 XGBoost incorporates a measure of how much model accuracy is improved by the addition of a given variable, with a higher gain value implying greater importance in generating a prediction. Neural networks are a type of machine learning technique that, like the human brain, connects layers of nodes (neurons) to model an output. Finally, the meta-classification approach uses an XGBoost model to combine the outputs of 3 supervised learning models, including LASSO, XGBoost, and a neural network (Figure 1).24 Therefore, the meta-classifier was a level 2 model that was based on the results of prediction models applied directly to patients (level 1 models).
The computational approach is shown in Figure 1. The first half of the derivation cohort was used to train 4 methods; logistic regression, LASSO, XGBoost, and a neural network. The second half of the derivation cohort was then used as a training set for the level 2 meta-classifier. We validated the various approaches with the remaining 25% of the sample.
Statistical Analysis
Model discrimination was measured using the area under the receiver operating characteristic curve (AUROC or C statistic) and its 95% CIs.25 In addition, the positive predictive value (or precision) and the sensitivity (recall) across all possible risk thresholds for predicting mortality were plotted using the precision-recall curve. The precision-recall curve, unlike the AUROC, is not affected by the number of true-negative results. In data sets with small event rates and therefore a large expected true-negative rate, such as the one studied here, the precision-recall curve is well suited for comparing different models. For both the C statistic and area under the precision-recall curve, values closer to 1 correspond to more accurate models.
Because the objective of the models is to address prediction at an individual level, we calculated the mean squared prediction error for each model, which represents the mean probability of an inaccurate prediction for a patient. A lower value suggests more accurate prediction. We also calculated the F score, sensitivity, specificity, positive predictive value, and negative predictive value. In addition, we calculated a Brier score for each model as a measure of model accuracy. The score represents the reliability of the model minus the resolution plus an error term and represents the mean squared error between the observed and predicted risk.26,27 Further details are included in the eMethods and eFigure 1 in the Supplement.
Model calibration was measured using (1) the calibration slope, which was calculated as the regression slope of the observed mortality rates across the deciles of predicted mortality rates; (2) the reliability component of the Brier score; and (3) shift tables, in which we classified patients in the validation cohort into prespecified categories of low (<1%), moderate (1%-5%), or high risk (>5%) of death based on logistic regression and one of the machine learning models, creating a 9-way matrix of patients that included risk profiles assigned by the 2 models (low-low, low-moderate, and so on). We then calculated the actual rate of events in these groups, focusing on discordant categories, and compared them against the observed rates of mortality. We conducted sensitivity analyses with risk thresholds set at less than 1.5%, 1.5% to 3%, and greater than 3%.
All analyses were conducted using open-source Python, version 3.8.0 (Python Software Foundation) and R software, version 3.6 (R Foundation for Statistical Computing). The level of significance was set at a 2-sided P < .05.
Results
Characteristics of Study Population
A total of 755 402 patients (mean [SD] age, 65 [13] years; 495 202 [65.5%] male) were identified during the study period. Among the 755 402 patients in the primary study cohort, the overall in-hospital mortality rate was 4.4%. The derivation cohort consisted of 281 997 patients used to derive the level 1 classifiers, 282 921 to train the meta-classifier model (level 2 model), and the remaining 190 484 patients for the test cohort. Table 1 includes characteristics for the derivation and validation cohorts. A total of 562 423 patients (74%) had hypertension, 257 072 (34%) had diabetes, 188 297 (25%) had experienced a prior myocardial infarction, and 94 897 (13%) had a diagnosis of heart failure. In addition, 292 784 (39%) presented with a STEMI, 95 240 (13%) with heart failure, 28 783 (4%) with cardiogenic shock, and 29 458 (4%) after cardiac arrest (Table 1).
Table 1. Baseline Characteristics of the Derivation and Validation Cohortsa.
| Characteristic | Derivation cohort (n = 564 918) | Validation cohort (n = 190 484) |
|---|---|---|
| Demographic characteristics | ||
| Age, mean (SD), y | 65 (14) | 65 (13) |
| Weight, mean (SD), kg | 87 (22) | 88 (22) |
| Male sex | 369 455 (65) | 125 747 (66) |
| Race | ||
| White | 479 428 (85) | 161 567 (85) |
| Black | 65 726 (12) | 21 363 (11) |
| Medical history | ||
| History of diabetes | 190 280 (34) | 66 792 (35) |
| History of hypertension | 419 803 (74) | 142 620 (75) |
| History of dyslipidemia | 344 758 (61) | 116 511 (61) |
| Current or recent smoker | 191 638 (34) | 62 191 (33) |
| History of chronic lung disease | 67 370 (14) | 716 (11) |
| Current dialysis | 14 153 (3) | 4902 (3) |
| History of MI | 140 878 (25) | 47 419 (25) |
| History of HF | 70 925 (13) | 23 972 (13) |
| Prior PCI | 142 900 (25) | 50 279 (26) |
| Prior CABG | 76 462 (14) | 24 435 (13) |
| History of atrial fibrillation | 44 164 (8) | 18 148 (10) |
| Prior cerebrovascular disease | 68 891 (12) | 22 832 (12) |
| Prior peripheral arterial disease | 52 660 (9) | 15 167 (8) |
| Presentation | ||
| Presentation after cardiac arrest | 22 368 (4) | 7090 (4) |
| In cardiogenic shock | 22 095 (4) | 6688 (4) |
| In HF | 72 621 (13) | 22 619 (12) |
| Heart rate, mean (SD), beats/min | 84 (24) | 84 (24) |
| SBP at presentation, mean (SD), mm Hg | 146 (35) | 148 (36) |
| Presentation ECG findings | ||
| STEMI | 117 078 (39) | 73 136 (38) |
| New or presumed new | ||
| ST depressions | 219 648 (39) | 19 261 (10) |
| T-wave inversions | 64 294 (11) | 12 918 (7) |
| Transient ST-segment elevation lasting <20 min | 43 873 (8) | 1667 (1) |
| Initial laboratory values | ||
| Troponin ratio, mean (IQR) | 2.5 (0.50-16.3) | 3.5 (0.78-20.0) |
| Creatinine, mean (SD), mg/dL | 1.3 (1.2) | 1.3 (1.2) |
| Creatinine clearance, mean (SD), mL/min | 85 (43) | 85 (42) |
| Hemoglobin, mean (SD), g/dL | 14 (2) | 14 (2) |
Abbreviations: CABG, coronary artery bypass graft; ECG, electrocardiography; HF, heart failure; IQR, interquartile range; MI, myocardial infarction; PCI, percutaneous coronary intervention; SBP, systolic blood pressure; STEMI, ST-elevation myocardial infarction.
SI conversion factors: To convert creatinine to micromoles per liter, multiply by 88.4; to convert creatinine clearance to mL/s/m2, multiply by 0.0167; to convert hemoglobin to grams per liter, multiply by 10.
Data are presented as number (percentage) of patients unless otherwise indicated.
Model Discrimination
The current NCDR model with 9 variables had good discrimination (AUROC, 0.867) using β coefficients in the original model applied to the data. In models that used the 29-variable set that was used to derive the NCDR standard, machine learning models achieved modest improvements in discrimination over logistic regression using the same data inputs (Table 2). The AUROC for all 3 models was numerically higher than logistic regression in both the limited variable set and the expanded variable set, with corresponding improvements in the area under the precision-recall curve (Table 2; eFigures 2-5 in the Supplement). The XGBoost and meta-classifier models achieved a discrimination of 0.898 (95% CI, 0.894-0.902) and 0.899 (95% CI, 0.895-0.903), respectively, applied to the expanded set of variables compared with 0.888 (95% CI, 0.884-0.892) with the logistic regression model. The XGBoost and meta-classifier models had more accurate predictions at an individual level than logistic regression models, with a lower mean squared prediction error across both sets of variables, but this effect was not observed with the neural network (eFigure 6 in the Supplement).
Table 2. Performance Characteristics of Models for Predicting In-Hospital Mortality in Acute Myocardial Infarction.
| Characteristic | Logistic regression | LASSO | Neural network | XGBoost | Meta-classifier |
|---|---|---|---|---|---|
| Variables included in the model of McNamara et al21 | |||||
| Model performance metrics | |||||
| AUROC (95% CI) | 0.878 (0.875-0.881) | 0.874 (0.870-0.879) | 0.874 (0.870-0.878) | 0.886 (0.882-0.890) | 0.886 (0.882-0.890) |
| Precision-recall AUC | 0.372 | 0.367 | 0.371 | 0.395 | 0.398 |
| F score | 0.415 | 0.408 | 0.411 | 0.432 | 0.432 |
| Sensitivity | 0.42 (0.41-0.43) | 0.43 (0.42-0.45) | 0.41 (0.40-0.42) | 0.44 (0.43-0.45) | 0.43 (0.42-0.44) |
| Specificity | 0.97 (0.97-0.97) | 0.97 (0.97-0.97) | 0.97 (0.97-0.97) | 0.97 (0.97-0.97) | 0.98 (0.97-0.98) |
| PPV | 0.41 (0.40-0.42) | 0.38 (0.37-0.39) | 0.41 (0.40-0.42) | 0.42 (0.41-0.43) | 0.44 (0.43-0.45) |
| NPV | 0.97 (0.97-0.97) | 0.97 (0.97-0.98) | 0.97 (0.97-0.97) | 0.98 (0.97-0.98) | 0.97 (0.97-0.98) |
| Brier score | |||||
| Reliability, mean (SD), ×10−6 | 28.4 (9.2) | 96.3 (16.5) | 224.0 (26.1) | 9.5 (3.8) | 2.3 (2.1) |
| Resolution, mean (SD), ×10−3 | 5.6 (0.1) | 5.5 (0.1) | 5.4 (0.1) | 5.8 (0.1) | 5.9 (0.1) |
| Uncertainty | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 |
| Overall, ×10−2 | 3.52 | 3.54 | 3.56 | 3.49 | 3.48 |
| Expanded variables included from the CP-MI Registry | |||||
| Model performance metrics | |||||
| AUROC (95% CI) | 0.888 (0.884-0.892) | 0.886 (0.882-0.890) | 0.885 (0.881-0.889) | 0.898 (0.894-0.902) | 0.899 (0.895-0.903) |
| Precision-recall AUC | 0.421 | 0.415 | 0.406 | 0.451 | 0.453 |
| F score | 0.436 | 0.436 | 0.428 | 0.458 | 0.459 |
| Sensitivity | 0.47 (0.45-0.48) | 0.42 (0.41-0.43) | 0.43 (0.42-0.44) | 0.45 (0.44-0.47) | 0.43 (0.42-0.44) |
| Specificity | 0.97 (0.97-0.97) | 0.98 (0.98-0.98) | 0.97 (0.97-0.98) | 0.98 (0.98-0.98) | 0.98 (0.98-0.98) |
| PPV | 0.41 (0.40-0.42) | 0.45 (0.44-0.46) | 0.43 (0.42-0.44) | 0.46 (0.45-0.47) | 0.49 (0.48-0.50) |
| NPV | 0.98 (0.98-0.98) | 0.97 (0.97-0.98) | 0.97 (0.97-0.98) | 0.98 (0.98-0.98) | 0.97 (0.97-0.98) |
| Brier score | |||||
| Reliability, mean (SD), ×10−6 | 229.4 (25.6) | 40.6 (10.3) | 55.7 (11.2) | 6.5 (3.5) | 4.3 (2.6) |
| Resolution, mean (SD), ×10−3 | 6.0 (0.1) | 5.9 (0.1) | 5.8 (0.1) | 6.4 (0.2) | 6.5 (0.2) |
| Uncertainty | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 |
| Overall, ×10−2 | 3.50 | 3.49 | 3.50 | 3.43 | 3.42 |
Abbreviations: AUROC, area under the receiver operator characteristic curve; AUC, area under curve; CP-MI Registry, National Cardiovascular Data Registry’s Chest Pain–MI Registry; LASSO, least absolute shrinkage and selection operator; NPV, negative predictive value; PPV, positive predictive value.
Model Calibration
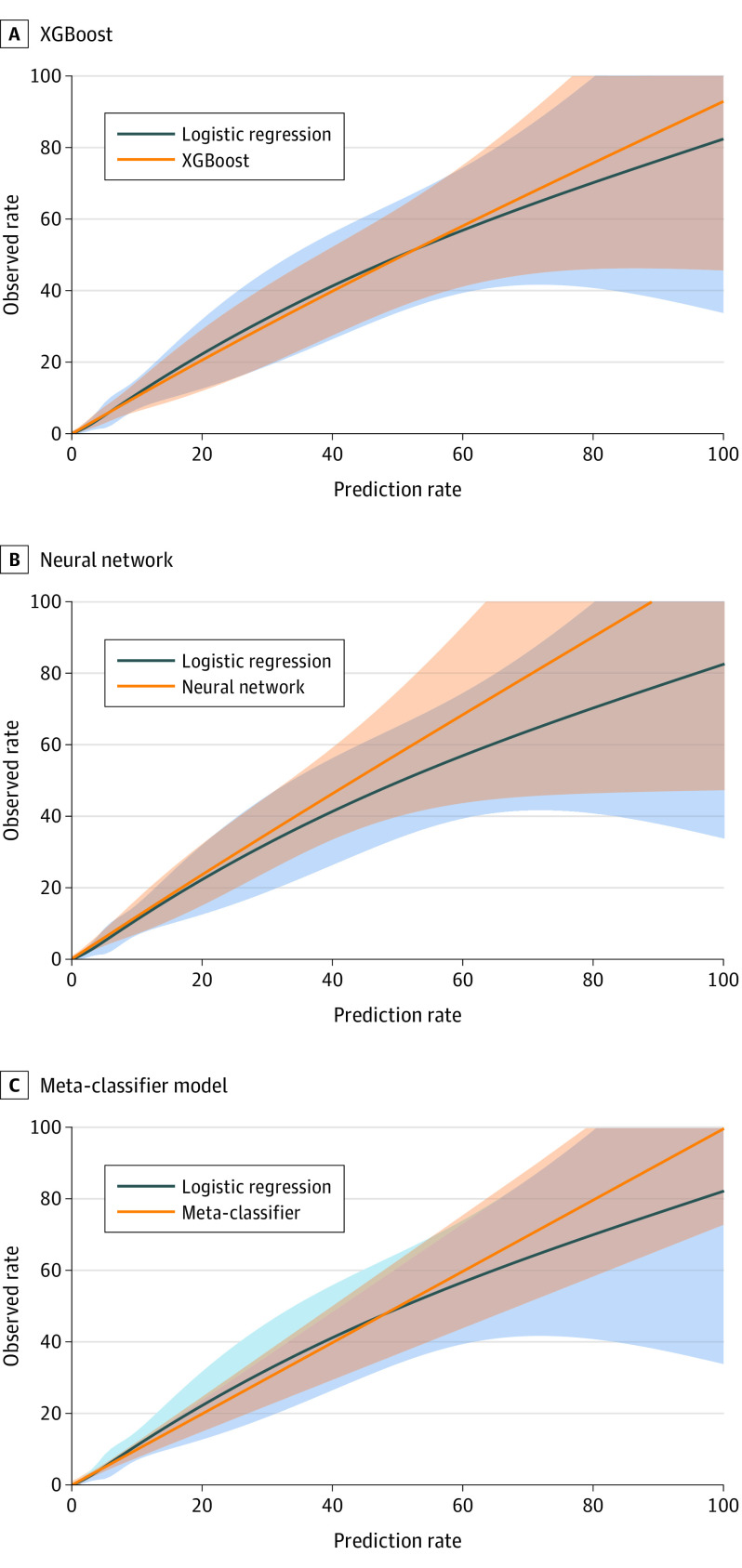
Of the 3 machine learning models, the XGBoost and the meta-classifier models but not neural network had improvements in calibration slopes compared with logistic regression, when they were applied to a limited or an expanded set of variables (Figure 2; eFigures 7 and 8 in the Supplement). The components and overall Brier score for the different models are included in Table 2. Models with lower values of reliability indicate higher agreement between predicted and observed risk and therefore have better performance. Even with the limited set of model variables, the mean (SD) reliability measure of the meta-classifier (2.3 [2.1] × 10−6) and XGBoost models (9.5 [3.8] × 10−6) but not the neural network (224.0 [26.1] × 10−6) were smaller (and therefore more accurate) compared with the logistic regression model (28.4 [9.2] × 10−6). The machine learning models also had significantly greater resolution (higher range of accurate prediction across the spectrum of risk) than the model based on logistic regression. The highest mean (SD) resolution was found in the meta-classifier (5.9 [0.1] × 10−3) and XGBoost (5.8 [0.1] × 10−3) models followed by the logistic regression model (5.6 [0.1] × 10−3) and the neural network (5.4 [0.1] × 10−3).
Figure 2. Predicted Risk of In-Hospital Mortality by Machine Learning and Logistic Regression Models.
Extreme gradient boosting model (XGBoost) (A), neural network (B), and meta-classifier model (C), using the 29-variable input used in the development of the model by McNamara et al.21 The shaded areas denote standard error of the calibration.
All 3 machine models more accurately classified patients in clinically relevant categories of risk. In shift tables (eTable 3 in the Supplement), predicted risk across each of the machine learning models (<1%, 1%-5%, and >5%) were individually compared against the predicted risk categories across logistic regression models. In these analyses, individuals with a predicted risk that was discordant between 1 of the machine learning methods and logistic regression was evaluated against the actual rate of observed events in the group. Each of the 3 machine learning models more accurately identified the actual rate of mortality for a group of patients when discordance was found. For example, among patients predicted to be at low risk based on the meta-classifier or XGBoost models and low, moderate, or high risk based on logistic regression, a negligible difference was found in the mortality rate among those also predicted to be at low risk by logistic regression (mortality rate, 0.3%) or moderate or high risk (mortality rate, 0.5%), despite predicted mortality risk of greater than 1% by logistic regression. In contrast, patients who were at low risk based on logistic regression had an observed mortality rate of 2.2% if at moderate or high risk based on the meta-classifier model. A similar pattern was observed for all, compared with logistic regression models applied to the same data.
Notably, 30 836 of 121 839 individuals (25%) deemed to be at moderate or high risk by logistic regression were more appropriately classified as being at low risk by the meta-classifier, consistent with their actual observed rates of mortality after AMI, even with models using the same model inputs. Moreover, 2951 of 68 645 individuals (4%) who were deemed to be at low risk by logistic regression were reclassified as moderate to high risk (Table 3). There was a similar reclassification of risk in the XGBoost model, which reclassified 32 393 medium-high risk individuals (27%) based on logistic regression to low risk, which is more consistent with the observed rates. Furthermore, 3452 patients (5%) classified as low risk by logistic regression were reclassified as medium-high risk by XGBoost (Table 3). The reclassification of low-risk individuals to moderate-high risk was also not consistent with observed events with machine learning models. The models based on expanded variables more accurately categorized patient risk than the limited set of variables, with machine learning models offering additional calibration of risk for the same set of variables. The observations on reclassification were consistent in sensitivity analyses using different risk thresholds (<1.5%, 1.5%-3%, and >3%), wherein patients reclassified by XGBoost and meta-classifier but not neural networks had observed event rates consistent with the classified groups (eTable 4 in the Supplement).
Table 3. Performance of the XGBoost and Meta-Classifier Models Compared With Logistic Regressiona.
| Model | Expanded LR, No. of patients (% observed mortality) | |||
|---|---|---|---|---|
| <1% | 1%-5% | >5% | All | |
| XGBoost vs LR | ||||
| Expanded XGBoost | ||||
| <1% | 65 193 (0.27) | 31 971 (0.65) | 422 (1.18) | 97 586 (0.40) |
| 1%-5% | 3384 (0.95) | 44 486 (2.21) | 13 155 (3.91) | 61 025 (2.51) |
| >5% | 68 (2.94) | 2899 (6.21) | 28 906 (20.79) | 31 873 (19.42) |
| All | 68 645 (0.30) | 79 356 (1.73) | 42 483 (15.37) | 190 484 (4.26) |
| Meta-classifier vs LR | ||||
| Expanded meta-classifier | ||||
| <1% | 65 694 (0.27) | 30 661 (0.65) | 175 (0.00) | 96 530 (0.39) |
| 1%-5% | 2930 (1.06) | 45 726 (2.17) | 9033 (3.55) | 57 689 (2.33) |
| >5% | 21 (0.00) | 2969 (6.03) | 33 275 (18.66) | 36 265 (17.61) |
| All | 68 645 (0.30) | 79 356 (1.73) | 42 483 (15.37) | 190 484 (4.26) |
Abbreviation: LR, logistic regression.
Pairwise comparisons of the same patients classified into low (<1%), medium (1-5%), and high (>5%) risk of death based on logistic regression and XGBoost (top) and meta-classifier (bottom).
The improvements in calibration were consistent across imputation strategies for missing variables, including the mode imputation and 5-fold multiple imputation strategies (eTable 5 in the Supplement). Furthermore, in an additional sensitivity analysis that included most patients by using a smaller number of features, XGBoost achieved an AUROC of 0.899 (95% CI, 0.895-0.904) and meta-classifier achieved an AUROC of 0.901 (95% CI, 0.896-0.905), largely similar to logistic regression (AUROC, 0.890; 95% CI, 0.886-0.895).
Subgroup Analyses
In assessments of subgroups of age, sex, and race, logistic regression models were less well calibrated in patients who were younger and White compared with older (calibration slope, 0.90; 95% CI, 0.87-0.93 in those 18-44 years of age vs 0.94; 95% CI, 0.91-0.97 in ≥65 years of age) and Black patients (calibration slope, 0.93; 95% CI, 0.92-0.95 in White patients vs 0.95; 95% CI, 0.89-1.00 in Black patients). In contrast, the meta-classifier model was well calibrated across patient groups. Of the other models, XGBoost, but not the neural network, was better calibrated in patient subgroups relative to logistic regression (eTable 6 in the Supplement).
Discussion
In this cohort study, in a large national registry of patients with AMI, machine learning models did not substantively improve discrimination of in-hospital mortality compared with models based on logistic regression. However, 2 of these models were associated with improvement in the resolution of risk over logistic regression and with improved classification of patients across risk strata, particularly among those at greatest risk for adverse outcomes. One of these models, XGBoost, is interpretable and represents the collection of individualized decision trees that address complex relationships among variables. The second model, meta-classifier, which aggregated information from multiple machine learning models, also had better model calibration than logistic regression. Despite almost no improvements in discrimination, these models led to reclassification of 1 in every 4 patients deemed moderate or high risk for death with logistic regression as low risk, which was more consistent with their observed event rates. However, machine learning models were not uniformly superior to logistic regression, and a neural network model had worse performance characteristics than a logistic regression model based on the same inputs.
The study builds on prior studies5,6,7,8,9,10,11,12,13,15 that used machine learning in predicting AMI outcomes. Most of these studies5,6,7,8,9,10,11,12,13,15 found improved prediction with applications of classification algorithms of varying complexity. However, they were limited by smaller patient groups, with limited generalizability in the absence of standard data collection.5,6,7,8,9,10,11,12,13,15 In a large national registry with standardized data collection across more than 1000 hospitals, improvements in risk prediction for in-hospital mortality with machine learning models were small and likely do not meet the threshold to be relevant for clinical practice.
However, there are notable aspects of the new models. Without the cost of collecting additional data or a reliance on literature review or expert opinion for variable selection, the models achieved similar model performance characteristics as logistic regression, which is relevant for predictive modeling in clinical areas where disease mechanisms are not well defined. Moreover, 2 of the 3 models were much better calibrated across patient groups based on age, sex, race, and mortality risk and were therefore better suited for risk prediction despite only modest improvement in overall accuracy. Notably, this improvement in predictive range occurred in critical areas by accurately reclassifying individuals at high risk to categories more accurately reflecting their risk. A focus on traditional measures of accuracy underperform in capturing the scale of these improvements because the events are rare and model discrimination is driven by patients not experiencing the mortality event.28,29 In this respect, the Brier score offers a more comprehensive assessment of model performance, combining model discrimination and calibration. The Brier score represents the mean squared difference between the predictions and the observed outcome. A perfect model has a Brier score of 0, and when 2 models are compared, a smaller Brier score indicates better model performance. Both XGBoost and meta-classifier models had scores that were lower than the logistic models by several multiples of the SDs of the score. Given the only marginal improvements in model discrimination, the lower Brier scores reflect the improved calibration noted in the calibration slope and shift tables.
Of note, 1 of the models that performs well is interpretable because it represents a collection of decision trees, thereby ensuring transparency in its application that specifically addresses the concerns with black-box machine learning models. Furthermore, although their development is computationally intensive, their eventual deployment at an individual patient level does not require substantial computational resources. Therefore, the clinical adoption of these models likely depends on whether their gains in prediction accuracy are worth their computationally intensive development and lack of interpretability. Some machine learning models may, therefore, have greater clinical utility in higher-dimensional data where they can uncover complex relationships among variables30,31,32 and of variables with outcomes but only provide limited gains in relatively low-dimension registry data. Furthermore, not all machine learning performed well. The neural network model developed using all available variables in the registry was inferior to the logistic regression based on similar inputs, indicating that not all machine learning models are uniformly superior to traditional methods of risk prediction.
Limitations
This study has limitations. First, although the CP-MI registry captures granular clinical data on patients with AMI, relevant information, such as duration of comorbidities and control of chronic diseases (besides diabetes), was not captured in the registry and is, therefore, not included in the assessment. Furthermore, certain prognostic characteristics of the patients’ general health are not included.33,34 Second, although models are based on sound mathematical principles, the study does not identify whether the excess risk identified with the models is modifiable. Third, shift tables judge classification across risk thresholds but may overemphasize small effects around thresholds. However, other calibration metrics also suggest more precise risk estimation by XGBoost and the meta-classifier among patients classified as being at high risk by logistic regression. Fourth, the study was not externally validated. Therefore, although the observations may be generalizable to the data in the NCDR CP-MI Registry, they may not apply to patients not included or hospitals not participating in the registry. However, because the data are collected as a part of routine clinical care at a diverse set of hospitals, other hospitals that collect similar data could likely apply these modeling strategies.
Conclusions
In a large national registry, machine learning models were not associated with substantive improvement in the discrimination of in-hospital mortality after AMI, limiting their clinical utility. However, compared with logistic regression, the models offered improved resolution of risk for high-risk individuals.
eMethods. Supplementary Methods
eTable 1. Differences in Characteristics of Patients Excluded vs Included in the Analyses
eTable 2. List of Patient Variables Used in Modeling
eTable 3. Shift Table Representing Actual Observed Event Rates for Pairs of Models
eTable 4. Shift Tables for Sensitivity Analysis With Risk Thresholds for Shift Tables Set at Risk <1.5%, 1.5-3%, >3%, Each Model Trained With Expanded Variables From the Chest Pain-MI Registry
eTable 5. Area Under the Receiver Operator Characteristic Curve for the 5-Fold Multiple Imputation
eTable 6. Model Calibration Slopes in Patient Subgroups
eFigure 1. Derivation of Brier Score Components Based on Calibration Curve
eFigure 2. Receiver Operator Characteristic for Logistic Regression, Neural Network (NN), XGBoost, and Meta-Classifier Models, Developed Using Variables Included in the Current Model for In-hospital Mortality by McNamara et al
eFigure 3. Precision-Recall Curves for Logistic Regression, Neural Network (NN), XGBoost, and Meta-Classifier Models, Developed Using Variables Included in the Current Model for In-hospital Mortality by McNamara et al
eFigure 4. Receiver Operator Characteristic for Logistic Regression, Neural Network (NN), XGBoost, and Meta-Classifier Models, Developed Using the Expanded Set of Variables in the Chest Pain-MI Registry
eFigure 5. Precision-Recall Curves for Logistic Regression, Neural Network (NN), XGBoost, and Meta-Classifier Models, Developed Using the Expanded Set of Variables in the Chest Pain-MI Registry
eFigure 6. Mean Squared Prediction Error of Machine Learning Models Compared With Logistic Regression
eFigure 7. Calibration of Models Developed Using Limited Number of Variables Included in the Current Standard (McNamara et al)
eFigure 8. Calibration of Models Developed Using Expanded Number of Variables Included in the Chest Pain-MI Registry
References
- 1.Fox KA, Dabbous OH, Goldberg RJ, et al. Prediction of risk of death and myocardial infarction in the six months after presentation with acute coronary syndrome: prospective multinational observational study (GRACE). BMJ. 2006;333(7578):1091. doi: 10.1136/bmj.38985.646481.55 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Granger CB, Goldberg RJ, Dabbous O, et al. ; Global Registry of Acute Coronary Events Investigators . Predictors of hospital mortality in the global registry of acute coronary events. Arch Intern Med. 2003;163(19):2345-2353. doi: 10.1001/archinte.163.19.2345 [DOI] [PubMed] [Google Scholar]
- 3.Antman EM, Cohen M, Bernink PJ, et al. The TIMI risk score for unstable angina/non-ST elevation MI: a method for prognostication and therapeutic decision making. JAMA. 2000;284(7):835-842. doi: 10.1001/jama.284.7.835 [DOI] [PubMed] [Google Scholar]
- 4.Fox KA, Poole-Wilson P, Clayton TC, et al. 5-year outcome of an interventional strategy in non-ST-elevation acute coronary syndrome: the British Heart Foundation RITA 3 randomised trial. Lancet. 2005;366(9489):914-920. doi: 10.1016/S0140-6736(05)67222-4 [DOI] [PubMed] [Google Scholar]
- 5.Souza AD, Migon HS. Bayesian binary regression model: an application to in-hospital death after AMI prediction. Pesquisa Operacional. 2004;24(2):253-267. doi: 10.1590/S0101-74382004000200003 [DOI] [Google Scholar]
- 6.Zoni-Berisso M, Molini D, Viani S, Mela GS, Delfino L. Noninvasive prediction of sudden death and sustained ventricular tachycardia after acute myocardial infarction using a neural network algorithm. Ital Heart J. 2001;2(8):612-620. [PubMed] [Google Scholar]
- 7.Li X, Liu H, Yang J, Xie G, Xu M, Yang Y. Using machine learning models to predict in-hospital mortality for ST-elevation myocardial infarction patients. Stud Health Technol Inform. 2017;245:476-480. [PubMed] [Google Scholar]
- 8.Samad MD, Ulloa A, Wehner GJ, et al. Predicting survival from large echocardiography and electronic health record datasets: optimization with machine learning. JACC Cardiovasc Imaging. 2019;12(4):681-689. doi: 10.1016/j.jcmg.2018.04.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yosefian I, Farkhani EM, Baneshi MR. Application of random forest survival models to increase generalizability of decision trees: a case study in acute myocardial infarction. Comput Math Methods Med. 2015;2015:576413. doi: 10.1155/2015/576413 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Myers PD, Scirica BM, Stultz CM. Machine learning improves risk stratification after acute coronary syndrome. Sci Rep. 2017;7(1):12692. doi: 10.1038/s41598-017-12951-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mansoor H, Elgendy IY, Segal R, Bavry AA, Bian J. Risk prediction model for in-hospital mortality in women with ST-elevation myocardial infarction: a machine learning approach. Heart Lung. 2017;46(6):405-411. doi: 10.1016/j.hrtlng.2017.09.003 [DOI] [PubMed] [Google Scholar]
- 12.Austin PC. A comparison of regression trees, logistic regression, generalized additive models, and multivariate adaptive regression splines for predicting AMI mortality. Stat Med. 2007;26(15):2937-2957. doi: 10.1002/sim.2770 [DOI] [PubMed] [Google Scholar]
- 13.Shouval R, Hadanny A, Shlomo N, et al. Machine learning for prediction of 30-day mortality after ST elevation myocardial infraction: an Acute Coronary Syndrome Israeli Survey data mining study. Int J Cardiol. 2017;246:7-13. doi: 10.1016/j.ijcard.2017.05.067 [DOI] [PubMed] [Google Scholar]
- 14.Bigi R, Mafrici A, Colombo P, et al. Relation of terminal QRS distortion to left ventricular functional recovery and remodeling in acute myocardial infarction treated with primary angioplasty. Am J Cardiol. 2005;96(9):1233-1236. doi: 10.1016/j.amjcard.2005.06.062 [DOI] [PubMed] [Google Scholar]
- 15.Bigi R, Gregori D, Cortigiani L, Desideri A, Chiarotto FA, Toffolo GM. Artificial neural networks and robust Bayesian classifiers for risk stratification following uncomplicated myocardial infarction. Int J Cardiol. 2005;101(3):481-487. doi: 10.1016/j.ijcard.2004.07.008 [DOI] [PubMed] [Google Scholar]
- 16.Zhang D, Song X, Lv S, Li D, Yan S, Zhang M. Predicting coronary no-reflow in patients with acute ST-segment elevation myocardial infarction using Bayesian approaches. Coron Artery Dis. 2014;25(7):582-588. doi: 10.1097/MCA.0000000000000135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mortazavi BJ, Downing NS, Bucholz EM, et al. Analysis of machine learning techniques for heart failure readmissions. Circ Cardiovasc Qual Outcomes. 2016;9(6):629-640. doi: 10.1161/CIRCOUTCOMES.116.003039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Breiman L. Statistical modeling: the two cultures. Stat Sci. 2001;16(3):199-231. doi: 10.1214/ss/1009213726 [DOI] [Google Scholar]
- 19.Shouval R, Bondi O, Mishan H, Shimoni A, Unger R, Nagler A. Application of machine learning algorithms for clinical predictive modeling: a data-mining approach in SCT. Bone Marrow Transplant. 2014;49(3):332-337. doi: 10.1038/bmt.2013.146 [DOI] [PubMed] [Google Scholar]
- 20.Messenger JC, Ho KK, Young CH, et al. ; NCDR Science and Quality Oversight Committee Data Quality Workgroup . The National Cardiovascular Data Registry (NCDR) Data quality brief: the NCDR Data Quality Program in 2012. J Am Coll Cardiol. 2012;60(16):1484-1488. doi: 10.1016/j.jacc.2012.07.020 [DOI] [PubMed] [Google Scholar]
- 21.McNamara RL, Kennedy KF, Cohen DJ, et al. Predicting in-hospital mortality in patients with acute myocardial infarction. J Am Coll Cardiol. 2016;68(6):626-635. doi: 10.1016/j.jacc.2016.05.049 [DOI] [PubMed] [Google Scholar]
- 22.Peterson ED, Dai D, DeLong ER, et al. Contemporary mortality risk prediction for percutaneous coronary intervention: results from 588,398 procedures in the National Cardiovascular Data Registry. J Am Coll Cardiol. 2010;55(18):1923-1932. doi: 10.1016/j.jacc.2010.02.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chen T BM, Khotilovich V, Tang Y. xgboost: eXtreme Gradient Boosting: R package version 0.6-4 [software]. R Foundation for Statistical Computing; 2018.
- 24.Pedregosa F VG, Gramfort A, Duchesnay E. Scikit-learn: machine learning in Python. J Machine Learning Res. 2011;12:2825-2830. [Google Scholar]
- 25.Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143(1):29-36. doi: 10.1148/radiology.143.1.7063747 [DOI] [PubMed] [Google Scholar]
- 26.Brier GW. Verification of forecasts expressed in terms of probability. Monthly Weather Rev. 1950;78:1-3. doi: [DOI] [Google Scholar]
- 27.Siegert S. Forecast verification routines for ensemble forecasts of weather and climate: R package version 0.5-2 [software]. R Foundation for Statistical Computing; 2017. Accessed December 10, 2019. https://CRAN.R-project.org/package=SpecsVerification.
- 28.Walsh CG, Sharman K, Hripcsak G. Beyond discrimination: a comparison of calibration methods and clinical usefulness of predictive models of readmission risk. J Biomed Inform. 2017;76:9-18. doi: 10.1016/j.jbi.2017.10.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Leisman DE. Rare events in the ICU: an emerging challenge in classification and prediction. Crit Care Med. 2018;46(3):418-424. doi: 10.1097/CCM.0000000000002943 [DOI] [PubMed] [Google Scholar]
- 30.Galloway CD, Valys AV, Shreibati JB, et al. Development and validation of a deep-learning model to screen for hyperkalemia from the electrocardiogram. JAMA Cardiol. 2019;4(5):428-436. doi: 10.1001/jamacardio.2019.0640 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Attia ZI, Noseworthy PA, Lopez-Jimenez F, et al. An artificial intelligence-enabled ECG algorithm for the identification of patients with atrial fibrillation during sinus rhythm: a retrospective analysis of outcome prediction. Lancet. 2019;394(10201):861-867. doi: 10.1016/S0140-6736(19)31721-0 [DOI] [PubMed] [Google Scholar]
- 32.Attia ZI, Kapa S, Lopez-Jimenez F, et al. Screening for cardiac contractile dysfunction using an artificial intelligence-enabled electrocardiogram. Nat Med. 2019;25(1):70-74. doi: 10.1038/s41591-018-0240-2 [DOI] [PubMed] [Google Scholar]
- 33.Kazi DS, Bibbins-Domingo K. Accurately predicting cardiovascular risk-and acting on it. Ann Intern Med. 2020;172(1):61-62. doi: 10.7326/M19-3662 [DOI] [PubMed] [Google Scholar]
- 34.Dodson JA, Hajduk AM, Geda M, et al. Predicting 6-month mortality for older adults hospitalized with acute myocardial infarction: a cohort study. Ann Intern Med. 2020;172(1):12-21. doi: 10.7326/M19-0974 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
eMethods. Supplementary Methods
eTable 1. Differences in Characteristics of Patients Excluded vs Included in the Analyses
eTable 2. List of Patient Variables Used in Modeling
eTable 3. Shift Table Representing Actual Observed Event Rates for Pairs of Models
eTable 4. Shift Tables for Sensitivity Analysis With Risk Thresholds for Shift Tables Set at Risk <1.5%, 1.5-3%, >3%, Each Model Trained With Expanded Variables From the Chest Pain-MI Registry
eTable 5. Area Under the Receiver Operator Characteristic Curve for the 5-Fold Multiple Imputation
eTable 6. Model Calibration Slopes in Patient Subgroups
eFigure 1. Derivation of Brier Score Components Based on Calibration Curve
eFigure 2. Receiver Operator Characteristic for Logistic Regression, Neural Network (NN), XGBoost, and Meta-Classifier Models, Developed Using Variables Included in the Current Model for In-hospital Mortality by McNamara et al
eFigure 3. Precision-Recall Curves for Logistic Regression, Neural Network (NN), XGBoost, and Meta-Classifier Models, Developed Using Variables Included in the Current Model for In-hospital Mortality by McNamara et al
eFigure 4. Receiver Operator Characteristic for Logistic Regression, Neural Network (NN), XGBoost, and Meta-Classifier Models, Developed Using the Expanded Set of Variables in the Chest Pain-MI Registry
eFigure 5. Precision-Recall Curves for Logistic Regression, Neural Network (NN), XGBoost, and Meta-Classifier Models, Developed Using the Expanded Set of Variables in the Chest Pain-MI Registry
eFigure 6. Mean Squared Prediction Error of Machine Learning Models Compared With Logistic Regression
eFigure 7. Calibration of Models Developed Using Limited Number of Variables Included in the Current Standard (McNamara et al)
eFigure 8. Calibration of Models Developed Using Expanded Number of Variables Included in the Chest Pain-MI Registry