JUE Insight: Understanding spatial variation in COVID-19 across the United States

Abstract

What factors explain spatial variation in the severity of COVID-19 across the United States? To answer this question, we analyze the correlates of COVID-19 cases and deaths across US counties. We document four sets of facts. First, effective density is an important and persistent determinant of COVID-19 severity. Second, counties with more nursing home residents, lower income, higher poverty rates, and a greater presence of African Americans and Hispanics are disproportionately impacted, and these effects show no sign of disappearing over time. Third, the effect of certain characteristics, such as the distance to major international airports and the share of elderly individuals, dies out over time. Fourth, Trump-leaning counties are less severely affected early on, but later suffer from a large severity penalty.

“Look at us today (...) We are your future (...) New York is the canary in the coal mine (...) New York is going first. What happens to New York is going to wind up happening to California and Washington state and Illinois. It’s just a matter of time.”

—Andrew Cuomo, March 24, 2020

1. Introduction

While COVID-19 has reached even the remotest corners of the United States, there remains tremendous heterogeneity in the severity of the pandemic across US counties. As of November 30, 2020, a county at the 75th percentile of COVID-19 deaths per capita had triple the deaths of a county at the 25th percentile. Similarly, a county at the 75th percentile of COVID-19 cases per capita had twice as many cases as a county at the 25th percentile. What is the source of this heterogeneity in cases and deaths across US counties? Should policies be sensitive to such spatial variation? There are, we think, two legitimate views on these questions.

Under the first view, spatial variation in disease severity only reflects differences in timing, as epitomized by Andrew Cuomo’s statement quoted above. As the disease spreads, ultimately every location in the US will have similar infection rates, similar death rates, and similar rates of hospitalization. If this is the case, policy need not be responsive to local characteristics.

Under the second view, spatial variation in cases and deaths reflects underlying fundamental differences across locations - population density, modes of transportation, housing arrangements, the age distribution of the population, its health conditions, etc. At any point in time, locations will continue to differ according to these characteristics, and these differences will persist. This provides a foundation for policies that are sensitive to local specificities.

This paper aims to adjudicate between these two views, by examining a broad set of potential correlates of COVID-19 severity. We pay particular attention to various dimensions of population density: we consider the average density experienced by a random individual in the square kilometer around her, as well as the role of public transportation, living arrangements, and housing density. We also assess the importance of a variety of indicators of socio-economic vulnerability: the share of the elderly, the presence of minorities, the prevalence of underlying health conditions, educational attainment, and measures of poverty and inequality. Finally, local political orientation is likely to affect both policies and the behavioral response to COVID-19, so we explore the association between Donald Trump’s county vote share in the 2016 election and disease severity. A strength of our approach is that we consider many potential correlates all at once.1

Our analysis examines the role of these factors at various points in time, starting on March 15, 2020 and ending on November 30, 2020. We examine variation in COVID-19 cases and deaths on a daily basis using two approaches. The first approach looks at the cross-section of US counties at a given date, providing snapshots of the correlates of disease severity at particular moments in time. The second approach looks at the cross-section putting all counties at the same stage in terms of days since cases and deaths reached a certain threshold per capita. This allows us to correct for differences in the timing of disease onset, to better assess if spatial variation reflects the differential timing of disease onset or fundamental differences between locations.

Our paper delivers four key takeaways. First, density is an important and persistent determinant of COVID-19 severity. Identifying this persistent effect requires going beyond simple density to measure the effective density experienced by individuals in their daily lives – either by taking a high-resolution view of population density or by considering the space people occupy at home or in public transit. Second, we identify several vulnerable groups whose presence has a large and persistent effect on how hard a location is hit by the pandemic. Counties with more nursing home residents, lower income, higher poverty rates, and a greater presence of African Americans and Hispanics are disproportionately impacted, and these effects show no sign of disappearing. Third, certain characteristics are important early on in the pandemic, and die out over time. In the case of the distance to major international airports, this reveals a sequencing pattern: the virus initially appeared in locations that are well connected with the rest of the world, and then spread to the rest of the country. In the case of age, this may reveal a behavioral response: early on counties with a high proportion of elderly experienced more deaths, but later in the pandemic this pattern reversed, as the at-risk population adjusted its behavior. Fourth, in the early stages of the pandemic, Trump-leaning counties were less severely affected, but later on, they experience a large and persistent severity penalty. It is possible that Republican-voting counties acquired lax attitudes toward mask-wearing and lockdown measures when COVID-19 was less severe in their areas, leaving them unwilling to respond more decisively when the pandemic caught up with them.

Where does this leave us in terms of the two views? On balance, the evidence is consistent with the second view: there are fundamental differences across locations that persistently explain the spatial variation in disease severity. Counties with higher effective density or a bigger proportion of vulnerable populations suffer disproportionately from COVID-19 cases and deaths. Our results therefore suggest that policies addressing the pandemic should be sensitive to these local specificities. The allocation of scarce resources, such as protective equipment, medical treatments, and vaccines, should prioritize areas where local conditions are persistently associated with worse disease severity.

2. Specification and data

In this section, we relate our empirical specification to standard epidemiological models and provide a brief overview of the data.

2.1. Specification

A specification consistent with the SIRD model. Standard epidemiological models, such as the SIRD model, posit laws of motion of the number of susceptible, infectious, recovered and deceased people for a given population and a given infectious disease. These laws of motion are governed by a few key parameters: the rate of infection, the rate of recovery and the rate of mortality. Together, these determine, for a given population, the evolution of the number of cases and deaths over time.

To fix ideas, denote by $C_{it}$ the cumulative number of cases and by $D_{it}$ the cumulative number of deaths from COVID-19 in county $i$ at time $t$. The rate of infection, ${\beta }_i,$ and the rate of death, ${\delta }_i$, are likely to be, to an extent, county-specific. For example, we would expect counties with higher population density, where individuals are more likely to run into each other, to have a higher rate of infection ${\beta }_i$. Similarly, we would expect counties with a larger share of elderly to experience higher death rates ${\delta }_i$. Differences in these parameter values across counties imply differences in the paths of $C_{it}$ and $D_{it}$ across counties. For example, a county with a higher ${\beta }_i$ will have higher cumulative cases and deaths at any point time, compared to a similar county with a lower ${\beta }_i$. This is related to the well-known result that a higher expected number of infections from an infected individual (i.e., a higher basic reproduction number $R_0$) generates in the limit more cumulative cases and more cumulative deaths. Some of these insights are illustrated with simulations in the recent work by Fernández-Villaverde and Jones (2020).

The objective of this paper is to explore the importance of county-specific factors that affect ${\beta }_i$ and ${\delta }_i$. These parameters affect the dynamic paths of cases and deaths, and hence their levels at every point in time. We are interested in accounting for differences in levels of cumulative cases and deaths in the cross-section of counties. Hence we run, for each time period $t,$ county-level regressions of cases or deaths on a set of potential determinants of ${\beta }_i$ and ${\delta }_i$:

$${\tilde{C}}_i={\alpha }_0+\sum _{j=1}^k{\alpha }_j{x}_{ij}+{\epsilon }_i$$ (1)

and

$${\tilde{D}}_i={\gamma }_0+\sum _{j=1}^k{\gamma }_j{x}_{ij}+{\nu }_i$$ (2)

where $x_{ij}$ are county-level regressors that potentially affect ${\beta }_i$ and ${\delta }_i,$ ${\epsilon }_i$ and ${\nu }_i$ are county-level disturbance terms, and ${\tilde{C}}_i$ and ${\tilde{D}}_i$ are measures of, respectively, the cumulative number of cases and deaths in county $i$. We return to the precise definition of ${\tilde{C}}_i$ and ${\tilde{D}}_i$ in the next subsection.

These period-by-period regressions can capture any functional form for the path of the number of cumulative cases and deaths over time. As such, they are consistent with the functional forms generated by standard epidemiological models. Indeed, to allow for maximum flexibility in the changing relation between county-level dterminants and disease severity, we choose a parsimonious period-by-period cross-sectional regression framework over a more structural empirical model that explicitly estimates the SIRD model.

The standard SIRD model assumes that individuals have equal probabilities of interacting with each other. In that sense, it does not really capture spatial features that make some individuals (or groups) more or less likely to interact with others. Bisin and Moro (2020) introduce a spatial SIR model with behavioral responses that explicitly incorporates these spatial concerns. When people are no longer matched randomly with the entire population, but are more likely to interact with people in their vicinity, local herd immunity becomes a possibility. In this model, spatial heterogeneity in disease severity can be magnified due to differences in modes of interaction and the spatial scale of interaction. This is why our empirical analysis seeks to capture dimensions of density that reflect the extend of local interactions, as experienced by people in their daily lives.

Sample based on daily cross-sections. We take two approaches to define the sample used in the cross-county analysis. The first approach is to carry out the analysis date by date. In this case, a time period $t$ refers to a calendar date $d,$ and we simply run regressions (1) and (2) on daily cross-sections, from March 15, 2020 to November 30, 2020. Early in the sample period, counties with zero cases and zero deaths are more prevalent. In order not to ignore the extensive margin, we use the inverse hyperbolic sine transformation (henceforth IHS – see Bellemare and Wichman, 2020), so:2

$$\begin{array}{ccc}\hfill {\tilde{C}}_i& =& \log (C_i+\sqrt{C_i^2+1})\hfill \\ \hfill {\tilde{D}}_i& =& \log (D_i+\sqrt{D_i^2+1})\hfill \end{array}$$

When defining a time period as a calendar date, a potential issue is that part of the cross-county variation in disease severity may be related to timing factors. For example, if low-density counties are hit later by COVID-19 than high-density counties, then their cumulative cases or deaths will tend to be lower on any given date. To address this concern, we control for certain factors that could affect the timing of the arrival of COVID-19 to a particular county. For instance, we control for the distance to an airport with direct international flights to high-severity countries.

Sample accounting for the differential timing of onset. The second approach more directly addresses differential timing of onset by considering each county at the same time elapsed since onset. Here we refer to onset as the day when a county reached a certain threshold, either in terms of cumulative cases or deaths per capita. To formally define days elapsed since onset, start by denoting, for each county $i,$ an indicator variable $I_{id}^C$ that takes a value of 1 if county $i$ has reached at least 1 case per 100,000 population on day $d$. For each county $i$ and day $d,$ the number of days since it reached that threshold is then:

$$s_{id}^C=\sum _{v=1}^d{I}_{iv}^C.$$

For the choice of each cross-county sample, we then set $s_{id}^C$ to a fixed number $t$.3 That is, the first sample consists of all counties one day after reaching the threshold, the second sample consists of all counties two days after reaching the threshold, and so on. Since each regression compares counties that have all passed the same threshold of per capita cases a fixed number of days before, this limits the effect of differential timing of onset across locations.

Similarly, we define the time elapsed since reaching the threshold of 0.5 deaths per 100,000 population. For each county $i$ and day $d,$ the number of days since it reached that threshold is $s_{id}^D={\sum }_{v=1}^d{I}_{iv}^D,$ where $I_{id}^D$ is an indicator variable taking a value of 1 if county $i$ has reached at least 0.5 deaths per $100,000$ population on day $d$. Here as well, each regression compares counties that have passed the deaths per capita threshold a fixed number of days before.

When defining a time period as the time elapsed since reaching a positive threshold in either cases or deaths, by construction there remains no county with zero cases or deaths in the sample. In this case, we simply define:

$$\begin{array}{ccc}\hfill {\tilde{C}}_i& =& \log \left(C_i\right)\hfill \\ \hfill {\tilde{D}}_i& =& \log \left(D_i\right)\hfill \end{array}$$

Summary of specifications. To summarize, we have four baseline specifications. There are two outcomes: cases and deaths. There are two ways to construct the sample: by calendar date, using the IHS of cases or deaths as dependent variables; or placing each county at the same time since onset, using the log of cases and deaths as dependent variables.4

2.2. Data

We use daily data on COVID-19 reported cases and deaths collected at the county level by the New York Times. Online Appendix Table A1 (Panel A) contains summary statistics for various metrics of cases and deaths constructed from these data, revealing substantial variation across counties. To our knowledge these are the best data available at the county level, yet it is important to acknowledge several possible data challenges. These are particularly acute for cases, and early in the period, since reported cases depend on testing, and testing was initially far from uniformly and widely prevalent. Data issues are not absent from deaths data either, as reporting standards vary across jurisdictions and deciding whether a death was caused by COVID-19 involves an element of judgment. An alternative would be to use data based on excess mortality, but these are not available at the county level on a daily basis.5

Regarding measurement error, we note the following. First, if errors are random, they will raise the standard error of the regression without creating bias. However, if both testing and the reporting of deaths are systematically correlated with the included explanatory variables, we will need to interpret the corresponding estimates carefully as reflecting effects on both underlying severity and on reporting of cases and deaths. Second, to the extent that testing capacity varies at the state level, including state fixed effects may in part correct for systematic measurement error due to uneven testing intensity. Third, testing may also be more strongly targeted toward individuals showing symptoms, resulting in artificially high case fatality rates (CFR=deaths/cases). However, this is less of a concern at more advanced stages of the pandemic.6 Fourth, as locations ramped up testing and fine tuned the reporting of deaths, measurement error in cases and deaths have become less relevant.

We also gathered a wide range of county-level indicators to be used as independent variables. Variable definitions and sources are provided in the Online Data Appendix, summary statistics are in Online Appendix Table A1 (Panel B) and these variables are displayed in map form in Online Appendix Fig. A1.

3. Baseline results

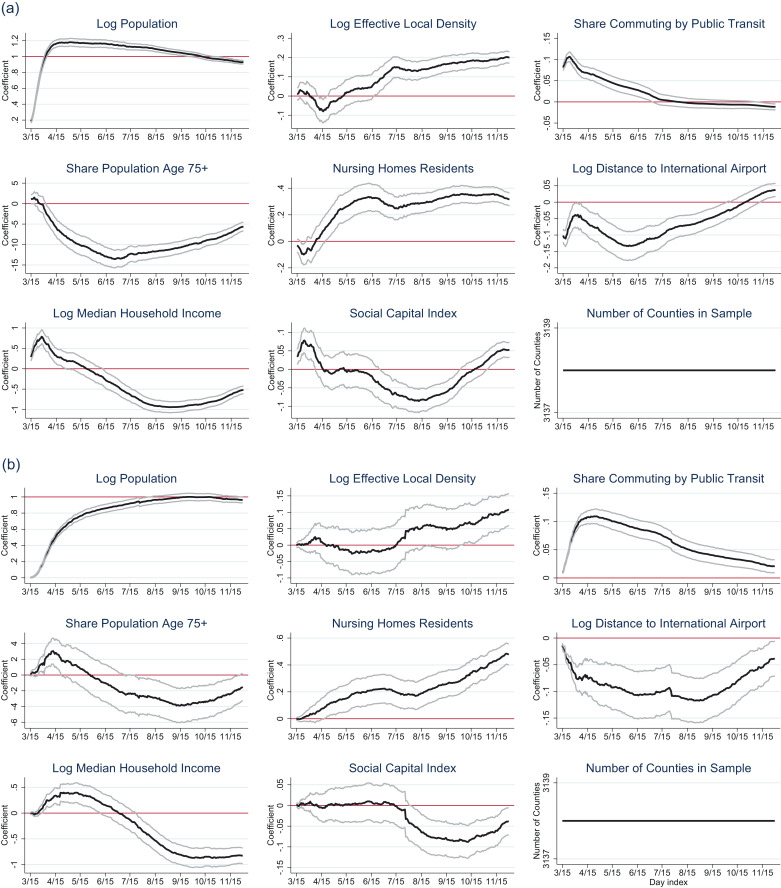
Table 1 and Fig. 1 present the baseline results of this paper. Table 1 presents estimates for the four main specifications described in the previous subsection: columns (1) and (3) consider cases and deaths for the cross-section of counties as of November 30, 2020, whereas columns (2) and (4) report estimates for the synchronized sample of counties 225 days since onset (for cases) and 215 days since onset (for deaths).7 Fig. 1 displays the day-by-day evolution of the coefficients for each correlate of disease severity, from March 15 to November 30, 2020.

Table 1.

OLS Regressions for Cases and Deaths (Dependent variable listed in second row).

	(1)	(2)	(3)	(4)
	Log Cases, IHS, Nov. 30	Log Cases, 225 days post-onset	Log Deaths, IHS, Nov. 30	Log Deaths, 215 days post-onset
Log population	0.931	0.860	0.963	0.971
	(0.011)***	(0.015)***	(0.018)***	(0.027)***
	[0.892]	[0.829]	[0.832]	[0.870]
Log effective local density	0.201	0.198	0.109	0.062
	(0.015)***	(0.019)***	(0.025)***	(0.036)*
	[0.128]	[0.135]	[0.063]	[0.040]
% people who commute by public transportation	−0.012	−0.005	0.020	0.027
	(0.004)***	(0.004)	(0.006)***	(0.005)***
	[−0.023]	[−0.010]	[0.036]	[0.079]
Share of people aged 75 & above	−5.595	−7.886	−1.503	−1.680
	(0.541)***	(0.695)***	(0.885)*	(1.158)
	[−0.084]	[−0.119]	[−0.020]	[−0.023]
% nursing home residents in pop.	0.317	0.360	0.477	0.775
	(0.024)***	(0.035)***	(0.040)***	(0.077)***
	[0.091]	[0.100]	[0.124]	[0.158]
Log km to closest airport w/flights from top 5 COVID countries	0.038	0.0001	−0.038	−0.054
	(0.010)***	(0.012)	(0.017)**	(0.016)***
	[0.028]	[0.000]	[−0.025]	[−0.053]
Log household median income	−0.518	−0.727	−0.829	−0.983
	(0.047)***	(0.058)***	(0.078)***	(0.096)***
	[−0.081]	[−0.127]	[−0.116]	[−0.174]
Social Capital Index, 2014	0.053	−0.009	−0.038	−0.092
	(0.010)***	(0.013)	(0.017)**	(0.024)***
	[0.043]	[−0.007]	[−0.028]	[−0.058]
Constant	2.681	4.916	1.898	2.955
	(0.512)***	(0.621)***	(0.836)**	(1.010)***
$R^2$	0.88	0.81	0.74	0.73
$R^2$ (per capita specification)	0.17	0.17	0.11	0.20
$N$	3,138	2,756	3,138	1,445

* $p<0.1$; ** $p<0.05$; *** $p<0.01$. Standard errors in parentheses and standardized betas in brackets.

- Onset day is defined as the day at which the number of cases reaches 1 per 100,000 (for cases) and 0.5 per 100,000 (for deaths).

- We report two $R^2$ values: one from the specification with log population on the right-hand side, and another from an alternative specification where we instead subtract log population from the dependent variable as described in the first row. The latter allows an assessment of the joint importance of all regressors except log population.

Fig. 1.

(a) Effects on Log Cases (IHS), by Date. (b) Effects on Log Deaths (IHS), by Date.

We consider a set of eight baseline correlates. The first is log population, which acts as a scaling variable. Its inclusion implies that the seven other estimates can be interpreted as the determinants of cases and deaths in per capita terms.8 We now turn to these other determinants.

3.1. The persistent role of density

Defining effective density. A first set of regressors relates to population density, since living in closer proximity is likely to imply a higher infection rate $\beta$. A simple measure of population density is the county’s population divided by its land area. However, this may not adequately capture effective density, since some counties may have extensive land areas, in spite of most people living in fairly dense areas (think for instance of Clark County NV, where most of the population is tightly clustered in and around Las Vegas). Theoretically, what matters should not be average density over a whole county, but a measure that reflects the frequency and closeness of interactions between people. We therefore calculate the average density that a random individual of a county experiences in the square kilometer around her. We refer to this variable as a county’s “effective local density”. To further capture effective density, we also consider the share of people who commute using public transportation, a factor that has been argued to be an important spreader of the virus (Harris, 2020). The correlation between local effective density and the public transportation variable is $37.5\%,$ so they capture different dimensions of density.

Baseline results on density.Table 1 shows the importance of density as a determinant of severity. For cases, log effective local density is statistically significant at the $1\%$ level and positively associated with the outcome. The magnitude of the effect on cases is large (the standardized betas are respectively $12.8\%$ or $13.5\%$ in columns (1) and (2)). Density also positively predicts deaths, but with a smaller standardized magnitude (respectively $6.3\%$ and $4\%$ in columns (3) and (4)). Turning to the use of public transportation, we find a negative effect on cases (though insignificant in column (2)), but a positive, large and highly significant effect on deaths. Taken together, these results suggest that density continues to be an important predictor of disease severity, even in the later stages of the pandemic.

Fig. 1 examines the evolution of these effects over calendar dates. It displays coefficient estimates from the specifications of Eqs. (1) and (2), with $95\%$ confidence intervals, estimated separately for each day between March 15 and November 30, using a common sample of 3138 counties.9 We find that the effect of local effective density rises over time. In contrast, the effect of public transportation follows the opposite pattern - it starts out strongly positive in the early weeks of the pandemic, but converges toward zero later. A possible interpretation is that behavioral adaptations to the disease led people to exercise more caution over time when using public transportation, or that working from home substituted for the use of public transit in later phases of the pandemic, weakening the effect of this variable on disease severity.

Further measures of density. The results above suggest that a parsimonious definition of density, captured by two variables, can explain a substantial share of the spatial variation in COVID-19 severity. However, there are many other possibly relevant dimensions of density. Table 2 conducts a more in-depth analysis of these dimensions, by considering five additional measures. These include two dummy variables for urban status (respectively, large central or large fringe metro county, and medium metro and small metro county, as defined by the National Center for Health Statistics), two variables capturing the density of living arrangements (the percentage of dwellings that are in multi-unit structures, and the average number of persons per household), and the conventional measure of density (the log of population per square mile).10

Table 2.

A Further Investigation of the Effect of Density (Dependent variable listed in second row).

	(1)	(2)	(3)	(4)
	Log Cases, IHS, Nov. 30	Log Cases, 225 days post-onset	Log Deaths, IHS, Nov. 30	Log Deaths, 215 days post-onset
Log effective local density	0.203	0.199	0.125	0.068
	(0.017)***	(0.021)***	(0.027)***	(0.040)*
	[0.129]	[0.136]	[0.072]	[0.044]
% people who commute by public transportation	−0.005	0.002	0.032	0.034
	(0.004)	(0.005)	(0.007)***	(0.006)***
	[−0.010]	[0.005]	[0.057]	[0.101]
Log population density	0.009	0.025	0.034	0.090
	(0.012)	(0.015)*	(0.019)*	(0.027)***
	[0.010]	[0.028]	[0.035]	[0.091]
Large central metro county or large fringe metro county	−0.011	0.049	0.228	0.234
	(0.039)	(0.045)	(0.063)***	(0.073)***
	[−0.003]	[0.013]	[0.046]	[0.068]
Medium metro county or small metro county	0.010	0.058	0.130	0.104
	(0.027)	(0.032)*	(0.044)***	(0.054)*
	[0.003]	[0.018]	[0.032]	[0.033]
Housing units in multi-unit structures, percent, 2009–2013	−0.004	−0.004	−0.009	−0.007
	(0.002)**	(0.002)	(0.003)***	(0.004)*
	[−0.022]	[−0.025]	[−0.047]	[-0.049]
Persons per household, 2009–2013	0.465	0.719	0.863	1.154
	(0.054)***	(0.070)***	(0.088)***	(0.124)***
	[0.073]	[0.118]	[0.122]	[0.170]
$R^2$	0.88	0.82	0.75	0.76
$R^2$ (per capita specification)	0.20	0.22	0.15	0.27
$N$	3138	2756	3138	1,445
F test (7 density variables)	39.18	35.68	27.77	26.38
p-value	0.000	0.000	0.000	0.000

* $p<0.1$; ** $p<0.05$; *** $p<0.01$. Standard errors in parentheses and standardized betas in brackets.

- All specifications contain an intercept and controls for log population, the share of people aged 75 and above, the percentage of nursing home residents in the population, log kilometers to the closest airport with flights from top 5 COVID countries, log household median income and the social capital index for 2014.

- Onset day is defined as the day at which the number of cases reaches 1 per 100,000 (for cases) and 0.5 per 100,000 (for deaths).

- We report two $R^2$ values: one from the specification with log population on the right-hand side, and another from an alternative specification where we instead subtract log population from the dependent variable as described in the first row. The latter allows an assessment of the joint importance of all regressors except log population.

Among the additional measures of density, persons per household tends to be significant for both cases and deaths. We also find that simple population density and residing in a metro area are not significantly related to cases when other measures of density (especially log effective local density) are controlled for, but these variables tend to predict deaths (columns (3) and (4) of Table 2). Conditional on all density measures, the share of housing units that are in multi-unit structures has a negative effect on both cases and deaths, though this effect is sometimes insignificant.

Summary. Density is a persistently important determinant of disease severity across space. This should come as no surprise: as with any other infectious disease, contact between susceptible and infected individuals is a key determinant of the spread of the disease. However, the actual degree of contact between people is not straightforward to measure. Our findings highlight the importance of using measures of effective density rather than a simple measure of population divided by land area. The finding of a persistent impact of effective density contrasts with recent narratives that suggest the death of density by highlighting the spread of COVID-19 to rural areas.

3.2. Other correlates

Age and nursing homes. A second group of regressors relates to the age structure of the population. Given the much higher mortality rate among the elderly, in Table 1 we control for the share of the population aged 75 and above. We also include a county-level measure of nursery home residents divided by population, as this group may be particularly susceptible (Barnett and Grabowski, 2020).

We find interesting results. Both cases and deaths are negatively associated with the percentage of people aged 75 and older. Fig. 1 reveals that the effect of cases has been negative virtually from the onset of the pandemic. This negative effect may reflect differences in lifestyles between counties with different age structures. For instance, places with a large share of retired individuals may feature fewer places (bars, stadiums) where the disease spreads rapidly. On the other hand, the effect of the share of the elderly on deaths starts out being positive, and remains so until the beginning of June. This initial period may reflect the higher death rate from COVID-19 among the elderly. Later in the pandemic, as more at-risk individuals adjust their behavior, the effect of the share of the elderly switches and remains persistently negative.

When it comes to the share of the population in nursing homes, we find positive partial correlations for both cases and deaths, with large magnitudes ranging from $9.1\%$ to $15.8\%$. Figs. 1 and A2 reveal that these effects are persistent and even increasing over time. These findings are consistent with the idea that once a county is affected by the pandemic, its nursing homes can quickly become powder kegs, and account for large shares of county-wide deaths.

Proximity to international airports. The onset of the pandemic in specific locations in the US may have been related to connectivity with high-severity countries (Wells et al., 2020). We construct a measure of the distance to any airport with direct flights to one of the top-5 countries with coronavirus cases on March 15, 2020 (China, South Korea, Iran, Italy and Spain). This variable bears an initially negative relationship with cases and deaths, but the magnitude of this relationship diminishes over time (Figs. 1 and (A2). The reason is straightforward: the initial condition (where the virus initially appears) loses potency as the disease spreads spatially to locations with fundamentals conducive to its prevalence.

Median income and social capital. Among the remaining correlates, we consider median household income, a standard metric to capture differences in economic well-being across counties. Figs. 1 and A2 reveal that the effect of log median income is initially positive, but then turns negative - for both cases and deaths. One interpretation is that the initial positive effect could be related to the emergence of the disease in well-connected, high-income urban locations like New York. Later, counties with higher income were in a better position to mitigate the severity of the pandemic – either through individual behavioral responses from wealthier households, or through better policy capacity, and the effect of median income turned negative. We will return to the issue of income, poverty and social vulnerability in Section 4.

Finally, our baseline specification includes a measure of social capital from Rupasingha et al. (2006). Theoretically, this measure could exert either a positive influence on disease severity, if social capital is associated with more contact, or it could bear a negative effect, if social capital improves the ability to mobilize communities against the disease. We do not find a very consistent pattern: the effect started out close to zero, turned negative around June 2020, and moved back toward zero at later dates.11

Model fit. An assessment of model fit is hampered by the inclusion of log population as a scaling variable on the right hand side of our specification, which explains a lot of the variation in cases and deaths. To address this issue, Table 1 reports the $R^2$ obtained from a regression where log population is subtracted from the dependent variable, and no longer included as a regressor. We find that the remaining regressors of Table 1 jointly account for $11\%$ to $20\%$ of the observed variation in disease severity.

3.3. State fixed-effects

Table A2 reports results with state fixed effects. The results are broadly similar to those of Table 1 in terms of the signs and magnitudes of the coefficients on the eight main regressors. Online Appendix Figs. A3 and A4 graphically display estimates on the state fixed effects, ordered by size, for the specifications of columns (1) and (3) of Table A2. These plots reveal that, after controlling for the eight baseline correlates of disease severity, some states have lower or higher cases or deaths as of November 30, 2020. We find that counties in Hawaii, Vermont and Maine, for instance, have lower severity, while counties in North and South Dakota, the Midwest and the South tend to have higher severity. These differences could reveal idiosyncrasies that are hard to capture using additional regressors varying at the county level (for instance, Hawaii is an island). They could also capture some omitted factors excluded from our parsimonious specification, such as state-level policies.

4. Socioeconomic status, race and human capital

Race.Table 3 Panel A explores the possible role of race. It reports four different specifications: columns (1) and (3) report regressions for cases and deaths, based on a cross-section of counties as of November 30, whereas columns (2) and (4) report regressions based on a cross-section of counties 225 days after onset (for cases) and 215 days after onset (for deaths). To the baseline regressors, we add measures of the racial composition of a county by controlling for the shares of African Americans, Hispanics, American Indians and Asians, with the excluded category being the share of Whites and others. The shares of African Americans and of Native Americans are positively and significantly associated with both the number of cases and the number of deaths. The association with the share of Hispanics is also positive, albeit significant in only three of the four specifications. Finally the share of Asians displays a significant negative association with COVID-19 severity in all four columns. In terms of magnitudes, the share of African Americans stands out with large standardized beta coefficients, especially for deaths ($19.3\%$ and $27.3\%$ in columns (3) and (4)). Overall these results support concerns that the COVID-19 pandemic has a disproportionate effect on different racial groups, even after controlling for a broad set of county-specific variables such as median income, density, etc.

Table 3.

An Investigation of Race and Education (Dependent variable listed in second row).

	(1)	(2)	(3)	(4)
	Log Cases, IHS, November 30	Log Cases, 225 days since onset	Log Deaths, IHS, November 30	Log Deaths, 215 days since onset
Panel A: Baseline specification plus race share variables
% Black or African American	0.003	0.010	0.023	0.024
	(0.001)***	(0.001)***	(0.001)***	(0.001)***
	[0.025]	[0.109]	[0.193]	[0.273]
% Hispanic or Latino	0.001	0.007	0.014	0.016
	(0.001)	(0.001)***	(0.001)***	(0.002)***
	[0.008]	[0.061]	[0.107]	[0.136]
% American Indian and Alaska Native	0.007	0.010	0.013	0.018
	(0.001)***	(0.002)***	(0.002)***	(0.004)***
	[0.031]	[0.045]	[0.056]	[0.057]
% Asian	−0.030	−0.014	−0.039	−0.021
	(0.004)***	(0.006)**	(0.007)***	(0.008)***
	[−0.053]	[−0.027]	[−0.062]	[−0.048]
$R^2$	0.88	0.82	0.77	0.79
$R^2$ (per capita specification)	0.19	0.22	0.22	0.36
$N$	3,138	2,756	3,138	1,445
Panel B: Baseline specification plus education variables
High school graduate or higher, percent of persons age 25+	−0.006	−0.029	−0.041	−0.065
	(0.002)***	(0.003)***	(0.003)***	(0.005)***
	[−0.026]	[−0.140]	[−0.165]	[−0.288]
Bachelor’s degree or higher, percent of persons age 25+	−0.014	−0.007	−0.010	0.004
	(0.002)***	(0.002)***	(0.003)***	(0.003)
	[−0.081]	[−0.045]	[−0.050]	[0.029]
$R^2$	0.88	0.82	0.76	0.77
$R^2$ (per capita specification)	0.20	0.23	0.16	0.30
$N$	3,138	2,756	3,138	1,445

* $p<0.1$; ** $p<0.05$; *** $p<0.01$. Standard errors in parentheses and standardized betas in brackets.

- Onset is defined as the day at which the number of cases reaches 1 per 100,000 (for cases) and 0.5 per 100,000 (for deaths).

- All specifications contain an intercept and controls for the baseline set of 8 variables in Table 1.

- We report two R² values: one from the specification with log population on the right-hand side, and another from an alternative specification where we instead subtract log population from the dependent variable as described in the first row. The latter allows an assessment of the joint importance of all regressors except log population.

Education.Table 3 Panel B analyzes whether the level of education may be a source of heterogeneity in disease severity across counties. We take the same four specifications as in the previous table with the same baseline regressors, and add two controls for the level of education: the share of a county’s population that has a high school degree or more, and the share of a county’s population that has a bachelor’s degree or more (the excluded variable is the share of people with less than a high school degree). We find a negative gradient of disease severity with respect to educational attainment: counties with large proportions of college graduates fare best, followed by counties with a large share of individuals with a high school degree. Hence, we find evidence that more disadvantaged locations (measured by education) fare worse.

Inequality and Poverty. Table A3 reports results of an in-depth investigation of the role of inequality and poverty. In the baseline regressions we already included median household income. We add two measures that capture inequality and poverty: the Gini index within the bottom $99\%$ and the poverty rate. We find that both poverty and inequality positively predict disease severity in columns (2)-(4) but not in the first specification, where most of the effect of local prosperity loads on log median income. The results are quantitatively meaningful: for example, the poverty rate shows standardized coefficients in the range of 10.6–19.8% when considering its impact on deaths.12

Health. Table A4 investigates whether underlying health conditions or the quality of health care have an impact on outcomes. As measures of underlying health issues, we take the share of the population that smokes and the share of the population that is obese. As measures of quality of health care, we take the risk-adjusted 30-day mortality rates for heart attacks, heart failure and pneumonia. The share of obese people is positively associated with COVID-19 severity, while there is no statistically significant association with smoking. Turning to risk-adjusted mortality rates, we find some evidence that risk-adjusted mortality from pneumonia is positively correlated with deaths (on the other hand, the signs of the correlations on risk-adjusted mortality from heart failures often have the opposite signs from what is expected). These results tend to be sensitive to the inclusion of more controls. In sum, with the exception of obesity, we do not find much evidence that health conditions or the quality of health care are first-order determinants of cross-county variation in cases and deaths.

Summary. This section documented a general pattern that low educational attainment, a large share of African American and Hispanic minorities, a high poverty rate, low median income - i.e. having a large share of economically or socially disadvantaged individuals – is positively associated with COVID-19 severity.

5. Political patterns in the spread of COVID-19

Many commentators have observed that there exists a political divide over attitudes toward the COVID-19 pandemic (see for instance Pew Research Center, 2020). In turn, these disagreements may reflect underlying differences in disease severity across locations with different political orientations. Weniger and Ou (2020) and Kolko, 2020a, Kolko, 2020b observe that, in its early stages, the disease was more severe in Democratic-leaning states and counties than in Republican-leaning locations. Does severity indeed vary according to local political orientation? In this subsection, we try to better understand the political divide in disease severity.

We start by examining the effect of the vote share obtained by Donald Trump in the 2016 general election on cases and deaths. We do so for two specifications and two time periods. The first specification only controls for log population and the Trump vote share. The second specification is a comprehensive specification controlling for all of the putative determinants of disease severity discussed in the previous sections.13 We consider a cross-section early in the pandemic (June 29, 2020) and one later (November 30, 2020). The four columns of Table A5 report the four resulting sets of estimates - Panel A for cases and Panel B for deaths.14

We uncover interesting patterns. First, in the early stages of the pandemic, the short specification shows a negative association between Trump vote share and disease severity: Trump counties were not as severely affected as Democratic-leaning counties (column (1)). The standardized beta on Trump vote share is large: $10.7\%$ for cases and $14.5\%$ for cases.

Second, when adding controls for the local determinants of disease severity, the negative relationship between Trump vote share and disease severity disappears (for cases) or flips signs (for deaths) – as seen in column (3). Thus, factors like population density, demographic composition, etc. entirely account for the apparent Trump advantage in disease severity even early on in the pandemic.

Third, in more recent times, we see a severity penalty for Trump-leaning counties in both the short and the comprehensive specifications. This shows that as the pandemic has spread, the initial advantage derived from local specificities (population density, demographics) disappeared, and a meaningful disadvantage appeared: the standardized beta on Trump vote share in the comprehensive specification is now $15.2\%$ (for cases) and $18.5\%$ (for deaths).15

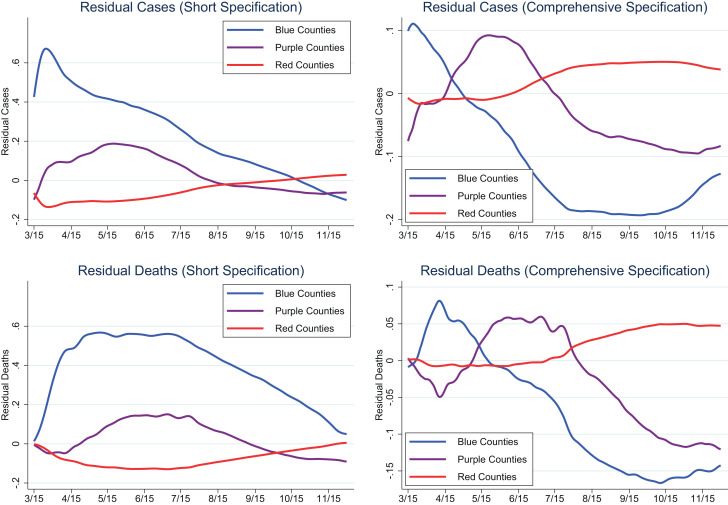
Fig. 2 illustrates these three patterns graphically over time. For each day between March 15 and November 30, we run regressions of log cases and log deaths using either the short or the comprehensive specification in Table A5, excluding the Trump vote share. Fig. 2 then plots how the average residuals evolve over time for three groups of counties: red, blue and purple.16 For the residuals from the short specification (left panels), we see a large initial political divide between blue and red counties, for both cases and deaths. For cases, this divide starts to narrow almost from the beginning, and persists until about mid-October 2020. For deaths, the political divide in severity starts to narrow substantially in mid-July and all but disappears by the end of November. A similar picture emerges when looking at residuals from the comprehensive specification (right panels), but the political divide disappears much earlier, by May. It then reverses itself strongly, to the point that there is now a large and persistent penalty to being a red county (purple counties stand in between the red and blue counties, but closer to the latter).

Fig. 2.

The Political Divide in COVID-19 Severity.

How can we interpret these partisan patterns in disease severity? Early on in the pandemic, Republican-leaning areas were less hard hit by COVID-19. This may have led to the early development of politically patterned policy and behavioral preferences, resulting in lax attitudes toward mask-wearing, social distancing and lock-down measures.17 Under this view, as the pandemic spread to Trump-leaning counties, their preferences and attitudes had already been formed, preventing them from responding more decisively to worsening local conditions. Ultimately, this resulted in greater disease severity in Trump-leaning areas of the country.18

6. Conclusion

Many observers have argued that COVID-19 would eventually spread to all corners of the United States. This view is epitomized by this paper’s opening quote by Andrew Cuomo. There remains, however, considerable spatial variation in the severity of the disease across space. Does this variation merely reflect the legacy of initial conditions and differential timing of the disease onset, or does it instead reflect fundamental underlying differences between locations? In this paper, we seek to shed light on this question by exploring a wide range of correlates of COVID-19 severity across US counties. We show that spatial variation is significantly and persistently associated with a wide range of observable county characteristics.

We find a persistent role for population density as a correlate of cases and deaths. We argue that it is important to measure the effective density experienced by people in their daily lives. We do so by considering the density people encounter in their living arrangements and in local transit. We also develop a measure of the average density an individual faces in a square kilometer around her. Besides density, other factors persistently affect COVID-19 severity across counties: having more nursing home residents, greater poverty rates, or a larger presence of African Americans or Hispanics. Time will tell whether this persistence will persist.

While many determinants show persistent effects through time, others display changing patterns. Proximity to major international airports is an important predictor early on, because these are the locations where the virus first appeared. Over time, it spread to the rest of the country, so the effect of initial conditions vanished. Having a greater proportion of elderly individuals was associated with more deaths in the early stages of the pandemic, but as this at-risk population adjusted its behavior, this pattern reversed. Counties with a high Trump vote share in the general election of 2016 fared better early on, but later experienced more cumulative deaths and cases per capita. Partisan preferences about policy and behavioral responses to the pandemic may have formed in early stages, leading Trump counties to respond less forcefully when they got hit by COVID-19 at later stages of the pandemic.

Overall, our results suggests that spatial heterogeneity in COVID-19 is not just about timing: many local characteristics, such as density, have large and persistent effects on disease severity. Policymakers should therefore be sensitive to the specificities of different locations when designing responses to the spread of COVID-19. Even when local characteristics do not exhibit persistent effects, they often display systematic time paths. If so, these time patterns are also informative for policymakers interested in spatially allocating resources over the life-cycle of the pandemic.

Credit author statement

Both authors contributed equally to the paper.

Appendix A. Supplementary materials

Supplementary Data S1

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/