A simple estimate of axon size with diffusion MRI

Abstract

Noninvasive estimation of mean axon diameter presents a new opportunity to explore white matter plasticity, development, and pathology. Several diffusion-weighted MRI (DW-MRI) methods have been proposed to measure the average axon diameter in white matter, but they typically require many diffusion encoding measurements and complicated mathematical models to fit the signal to multiple tissue compartments, including intra- and extra-axonal spaces. Here, Monte Carlo simulations uncovered a straightforward DW-MRI metric of axon diameter: the change in radial apparent diffusion coefficient estimated at different effective diffusion times, ΔD_⊥. Simulations indicated that this metric increases monotonically within a relevant range of effective mean axon diameter while being insensitive to changes in extra-axonal volume fraction, axon diameter distribution, g-ratio, and influence of myelin water. Also, a monotonic relationship was found to exist for signals coming from both intra- and extra-axonal compartments. The slope in ΔD_⊥ with effective axon diameter increased with the difference in diffusion time of both oscillating and pulsed gradient diffusion sequences.

1. Introduction

Axon diameter is one important characteristic of white matter, as it correlates with the conduction velocity of action potentials—a regulated process that is important for brain function (Seidl, 2014) and potentially a source of white matter plasticity (Sampaio-Baptista and Johansen-Berg, 2017). A number of diffusion-weighted MRI (DWI) techniques have been proposed to measure axon diameter in vivo (Alexander et al., 2010; Assaf et al., 2008; Veraart et al., 2020; Xu et al., 2014). In these methods, the estimate of axon diameter relies primarily on sensitivity to time dependent changes of water diffusion in the direction orthogonal to the axon orientation. As the diffusion time increases, water interacts with lipid bilayers and other barriers, reducing the radial diffusion coefficient (D_⊥), which is an apparent measure of water diffusion orthogonal to axon orientation provided by diffusion tensor analysis.

A variety of temporally varying gradient waveforms may be used to encode water diffusion, which differ in their sensitivities to the effects of restriction. Pulsed-gradient or bipolar waveforms (Stejskal and Tanner, 1965) are used most commonly; however, the minimum diffusion time that can be probed with commonly available hardware is long compared to the time water diffuses across axons in the brain. Oscillating-gradient waveforms (Schachter et al., 2000; Stepinik, 1981) can achieve shorter diffusion times, but also require strong, fast switching gradients. Optimization of diffusion-encoding gradient waveforms for axon diameter measurement remains an active area of investigation (Drobnjak et al., 2016; Nilsson et al., 2017).

There are also open questions on how water diffusion in white matter should be modeled mathematically. In most current models, the diffusion-weighted signal originates from multiple compartments (Panagiotaki et al., 2012), primarily intra-axonal and extra-axonal spaces. Whereas several analytic models are available to approximate intra-axonal water diffusion in terms of axon diameter, extra-axonal water diffusivity is less well characterized. Many models have assumed that extra-axonal water diffusion is approximately constant with diffusion time, and that diffusion-time dependent changes in D_⊥ result from only intra-axonal water, although this assumption has been subsequently challenged (Burcaw et al., 2015; Grussu et al., 2019; Lam et al., 2014; Novikov and Kiselev, 2010; Veraart et al., 2019; Xu et al., 2014).

A recent imaging study reported sex and age differences between radial diffusivity values measured with oscillating gradient vs pulsed-gradient DWI acquisitions (Tétreault et al., 2020). These results were interpreted through a limited set of simulations of water diffusion, which suggested that the changes in D_⊥ correlated strongly with axon diameter, and were primarily due to diffusion-time dependent changes in extra-axonal water. Here we report findings from a more comprehensive set of Monte Carlo simulations, aimed at more closely examining these findings. Diffusion-weighted signals were simulated in arenas of axons covering extremes in extra-axonal volume fraction, axon g-ratio, compartmental water exchange, the free diffusion coefficient of water, and axon packing heterogeneity. The findings showed that while D_⊥ strongly depends upon several tissue characteristics, the change in D_⊥ with diffusion time (ΔD_⊥) robustly correlates with axon diameter, and the slope of ΔD_⊥ vs. axon diameter increases with a difference in diffusion times probed by the diffusion-weighted gradient waveforms.

2. Methods

Similar to previous work (Harkins and Does, 2016; Tétreault et al., 2020), Monte Carlo simulations of water diffusion were used to compute D_⊥ for various tissue characteristics and experimental parameters. Simulations were performed in periodic 2D arenas of axons, where concentric circles defined the spatial boundary between intra-axonal space, myelin, and extra-axonal space. Individual axons were parameterized with an inner diameter, d, and g-ratio, g. Individual axon diameters were randomly drawn from a log-normal probability density (Buzsáki and Mizuseki, 2014), which was characterized by the arithmetic mean axon diameter, $\overline{d}$, and standard deviation of the log-spaced diameters, σ. (The common log-normal parameter, μ, was related to $\overline{d}$ and σ as $\mu =\text{ln}\left(\overline{d}/\mu \text{m}\right)-{\sigma }^2/2$, where ln(·) indicates the natural logarithm). For each simulation, a square arena was randomly filled with 500 non-overlapping axons using a previously-described procedure (Hall and Alexander, 2009) at a prescribed extra-axonal volume fraction, v_e. The length of the square arena was $L=\sqrt{{\sum }_n\pi {\left(d_n/g\right)}^2/\left(4v_{\text{e}}\right)}$. Four example arenas are given in Fig. 1, with: v_e = 0.3, g = 0.7, and σ = 0.0, 0.3, 0.5, & 0.7.

Fig. 1.

(top) Axon diameter distributions with σ = 0.0, 0.3 0.5, and 0.7, and (bottom) corresponding example simulation geometries for v_e = 0.5. The effective mean axon diameter, 〈d〉_eff (defined in Section 2.1), is larger than the arithmetic mean axon diameter $\overline{d}$ and varies with the heterogeneity of axon diameter.

For all simulations, a total of 125000 spin particles were placed into intra-axonal space, extra-axonal space, and—when not being neglected—myelin. Particle diffusion was simulated from excitation (t = 0) to the echo time (t = 100ms) with a constant time step of Δt = 0.01ms. Diffusion-weighted signals were calculated from the accumulated phases of the diffusing spins imparted by the diffusion-weighted gradient waveform. Both pulsed gradient (with gradient duration δ, gradient separation Δ, and effective diffusion time, t_eff = Δ − δ/3) and cosine modulated oscillating gradient (with duration T, N cycles, t_eff = T/4 N, and frequency f₀ = N/T) waveforms were evaluated. D_⊥ was calculated from signals simulated with b-values of 0 and 0.3ms/μm². D_⊥ was also independently calculated from spins residing in intra-axonal and extra-axonal compartments, resulting in D_i⊥ and D_e⊥, respectively. ΔD_⊥ was defined as the difference in D_⊥ resulting from diffusion waveforms with different t_eff, including oscillating gradient and pulse gradient diffusion encoding. Simulations were implemented in CUDA, wrapped into MATLAB, and performed on a Linux workstation with a GeForce GTX Titan GPU. As previously published (Harkins and Does, 2016), the simulation framework has been validated with tests to the physics of particle interactions (including jump tests for permeable & impermeable geometries, and stability of particle density over time) as well as comparison to models with known solution (including free diffusion, T₂ relaxation, and low b-value approximated solutions to diffusion inside impermeable cylinders Vangelderen et al. (1994)). The software used to perform these simulations is available from the corresponding author upon direct request.

2.1. The effective inner axon diameter

Given a distribution of axon sizes, several scalar measures of the average axon diameter have been published as relevant for water diffusion in white matter. Considering these measures, a family of possible effective inner axon diameters (〈d〉_eff) has been previously defined (Burcaw et al., 2015) as

$${\langle d\rangle }_{\text{eff}}\triangleq {\left(\frac{{\sum }_n{d}_n^p}{{\sum }_n{d}_n^q}\right)}^{1/(p-q)},$$ (1)

where p and q are natural numbers, and p ≥ q + 1. For water diffusion inside axons, some previous works have used the area-weighted mean axon diameter (p = 3 & q = 2)(Alexander et al., 2010; Harkins et al., 2012), while others have proposed sequence-dependent measures, using p = 4 & q = 2 for narrow pulsed gradient DWI and p = 6 & q = 2 for both wide pulsed gradient and oscillating gradient DWI (Burcaw et al., 2015; Novikov et al., 2019). Note that our previous study (Tétreault et al., 2020) defined d as the outer diameter. Here, 〈d〉_eff was defined as the inner diameter with p = 4 and q = 2, but different measures are considered in Appendix A. As shown in Fig. 1, 〈d〉_eff increases with σ, since it is weighted towards larger axon diameters.

2.2. Simulation sets

Seven independent sets of simulations were performed to investigate how tissue characteristics and experimental parameters affect D_⊥ and ΔD_⊥. Unless otherwise specified, each simulation set was repeated with mean inner axon diameters, $\overline{d}=0.5$, 1.0, 1.5, 2.0, 3.0, & 4.0 μm and axon diameter distributions, σ = 0.3, 0.5, & 0.7. Default tissue characteristics were as follows: axons were uniformly placed in the simulation arena; v_e = 0.3; g = 0.7 (constant for all axons); myelin water was neglected (i.e. no water in myelin, and no exchange of water between compartments); intra- & extra-axonal spaces used equal values for water density; the free water diffusion coefficient was the same in both intra-axonal and extra-axonal space (D_0,ie = 3.0 μm²/ms); and the transverse relaxation time-constant was the same in both intra-axonal and extra-axonal space (T_2,ie = 80 ms). Unless otherwise specified, diffusion weighting was imparted with both a cosine modulated oscillating gradient (OG: N = 4, T = 40ms, t_eff = 2.5ms, G_max = 207mT/m) and a pulsed gradient pair (PG: Δ = 62ms, δ = 6ms, t_eff = 60ms, G_max = 44mT/m).

Set I: Exploring D_⊥ and ΔD_⊥ The first set of simulations evaluated D_⊥ and ΔD_⊥ in geometries with uniform axon diameter, σ = 0, and v_e = 0.5 over an extreme range of axon diameter, $\overline{d}=0.2$, 0.5, 0.75, 1.0, 1.5, 2.0, 3.0, 4.0, 6.0, 8.0, 10, 12, 15, 20, 30, 40, 50, 80, & 100 μm.

Set II: simulation precision Simulations over a limited set of $\overline{d}\left(=0.5,1.0,\text{ and }2.0\mu \text{m}\right)$ were repeated 4× to evaluate the run-to-run variations in D_⊥, ΔD_⊥, and 〈d〉_eff due to selecting a finite number of axons from the distribution (500) from a given axon diameter distribution and a finite number of spin particles (125000). ΔD_⊥ vs. 〈d〉_eff was fitted to a 2nd order polynomial, and the standard deviation of the simulation measures of ΔD_⊥ was estimated as the root-mean-squared residual.

Set III: extra-axonal volume fraction Simulations were performed to investigate how D_⊥ and ΔD_⊥ change over a wide range of extra-axonal volume fractions, v_e = 0.3, 0.4, 0.5, 0.6, & 0.7. Additional simulations were included with σ = 0; however, due to limitations in packing density, v_e was limited to 0.5, 0.6, & 0.7.

Set IV: myelin This set of simulations aimed to test the influence of myelin and myelin water. Simulations were performed over a wide range of g-ratios, g = 0.6, 0.7, 0.8, 0.9, 0.99, where g remained constant for all axons within a simulation arena. Also, since g-ratio is known to vary with axon diameter, an additional simulation was performed with g = 0.5 + 0.02d (Berthold et al., 1983). To test if myelin water would influence the simulation results,each simulation was performed twice—once neglecting myelin water, and again incorporating myelin water and myelin water exchange. Here we defined myelin water as having one-half the density of intra- and extra-axonal spaces (p_m/p_ie = 0.5) (van der Knaap and Valk, 2005), T_2,m = 15ms (MacKay et al., 1994; Stewart et al., 1993); and D_0,m = 0.001μm²/ms (Harkins et al., 2012). Water exchange was governed by the the difference in radial diffusivities and water densities across a compartment boundary, such that intra- or extra-axonal water crossed into myelin with a probability, $P=\sqrt{D_{0,\text{m}}/D_{0,\text{ie}}}\cdot p_{\text{m}}/p_{\text{ie}}$. For an example axon with d = 1 μm and g = 0.7, this is equivalent to a myelin water lifetime of ≈ 25 ms.

Set V: diffusion time In addition to the PG (t_eff = 60ms) and OG (t_eff = 2.5ms) diffusion weighting schemes defined above, simulation set I was repeated with 3 additional short t_eff schemes. The OG waveform was repeated with N = 8 (t_eff = 1.25ms, G_max = 410mT/m) and N = 2 (t_eff = 5ms, G_max = 105mT/m), and the PG gradients were repeated with Δ = 12ms (t_eff = 10ms, G_max = 108mT/m).

Set VI: D_0,ie This simulation set aimed at testing the influence of the free diffusion coefficient of intra- and extra-axonal water. Simulations were performed with σ = 0.5, and D_0,ie = 0.5, 1.0, 1.5, 2.0, 2.5, & 3.0μm²/ms.

Set VII: heterogeneous axon packing Finally, simulations were run to test how variations in axon packing affect the observed relationship between ΔD_⊥ and 〈d〉_eff. The approach was to vary the axon density between v_e = 0.3 in the center of the arena and v_e = 1.0 at the extremes of the arena, with a linear transition in axon density between the two extremes, creating a trapezoid-like distribution of axons spatially. The length of the transition was given by ΔL. For ΔL = 0, the all the axons were packed into the center half of the arena, with axon density resembling a rectangle function, while if ΔL = L/2, axon density was triangular. To achieve such distributions, a simulation arena was initially seeded with 1500 axons at v_e = 0.3, σ = 0.5, and $\overline{d}=1.0\mu \text{m}$. Then, axons were selectively pruned from the arena, where the probability of pruning was calculated from the spatial trapezoidal density based upon the location of the axon in both x and y, and evaluated with a random number generator (rand in MATLAB). Simulations were run in arenas with 11 linear spaced values of ΔL between 0 and L/2.

3. Results

Set I: D_⊥ and ΔD_⊥ Fig. 2 shows D_⊥ and ΔD_⊥ from intra-axonal, extra-axonal, and total water signal over a broad range in axon diameter. Note that since σ = 0, ${\langle d\rangle }_{\text{eff}}=\overline{d}$. The top panel shows D_⊥ from oscillating gradient diffusion encoding, the top middle from pulsed-gradient diffusion, and the bottom middle is the difference in D_⊥ from the two encoding methods. While D_⊥ increases monotonically with 〈d〉_eff for both the oscillating and pulsed gradient diffusion waveforms, ΔD_⊥ peaks at 〈d〉_eff between 10 and 20 μm. The exact shape and range of ΔD_⊥ will depend upon the diffusion gradient waveforms being used. Since axons in the brain are relatively small compared to the range explored in this simulation set, the black box highlights the range in 〈d〉_eff explored in the elaborated simulation sets given below. This range of axon diameter is expanded in the bottom panel of the figure.

Fig. 2.

Simulation set I. D_⊥ and ΔD_⊥ from oscillating (OG) and pulsed-gradient (PG) diffusion encoding in axon geometries with v_e = 0.5 and σ = 0. Intra-axonal water (red), extra-axonal water (yellow), and total water (blue) D_⊥ increase monotonically with 〈d〉_eff, while ΔD_⊥ peaks between 10 and 20 μm. The black box outlines the range in 〈d〉_eff investigated for the remainder of the simulations, which is highlighted in the bottom panel. Over this subset of axon diameters, ΔD_⊥ monotonically increases with 〈d〉_eff.

Set II: simulation precision Fig. 3 shows simulation results from nine different axon diameter distributions, each repeated four times with an independently generated collection of 500 axons. The OG and PG D_⊥ measures and the corresponding ΔD_⊥ values are plotted vs 〈d〉_eff. These results show some variations in D_⊥ and ΔD_⊥ for a given 〈d〉_eff, particularly at low values of 〈d〉_eff (square blue markers, for example), but the variations are small compared to the observed trends with 〈d〉_eff, particularly for ΔD_⊥. The gray line shows a second order polynomial fit of ΔD_⊥ vs 〈d〉_eff. From this regression, the standard deviation of ΔD_⊥ was estimated to be 0.007 μm²/ms, which is much smaller than the range in ΔD_⊥ observed. Thus, we concluded that the number of axons and the number of spin particles used in the simulation was sufficient for the evaluations of ΔD_⊥ as a measure of 〈d〉_eff.

Fig. 3.

Simulation set II. Simulations were repeated 4× for each combination of mean inner axon diameter ($\overline{d}=0.5$, 1.0, and 2.0 μm) and axon diameter distributions (σ = 0.3, 0.5, and 0.7). The left and middle column show the simulated radial apparent diffusion coefficient (D_⊥) for oscillating gradient and pulsed gradient diffusion experiments respectively. The right panel shows the difference in D_⊥ measured by the two sequences (ΔD_⊥). The standard deviation of ΔD_⊥ with 〈d〉_eff was estimated from the residual of a second order polynomial fit.

Set III: extra-axonal volume fraction Simulation results from a large set of axon diameter distributions and extra-axonal volume fractions are summarized in Fig. 4. The top row shows example simulation arenas with varying v_e. The middle row shows OG (t_eff = 2.5ms) and PG (t_eff = 60ms) measures of D_⊥ for different distributions and v_e. In all cases, OG measures of D_⊥, but not the PG measures, are noticeably sensitive to 〈d〉_eff, but looking from left (v_e = 0.3) to right (v_e = 0.7) it is also clear that for both OG and PG D_⊥ is heavily influenced by v_e. Interestingly though, the dispersion between OG and PG measures of D_⊥ with 〈d〉_eff was similar for each case of v_e and apparently independent of distribution shape, σ. This is made more clear in the lower panel, which shows that ΔD_⊥ increases monotonically over this range in 〈d〉_eff, while roughly independent of v_e and σ. These observations are consistent with the recently presented preliminary studies (Tétreault et al., 2020).

Fig. 4.

Simulation set III. (top row) Example simulation arenas with identical axon diameter distributions but varied extra-axonal volume fraction. Red bars = 10 μm. (middle) Apparent radial diffusion coefficients (D_⊥) calculated with different tissue and experimental parameters, demonstrating the dominant effect of v_e on D_⊥. (bottom) In contrast, the difference between D_⊥ acquired with oscillating- and pulsed-gradients (ΔD_⊥) is relatively independent of v_e and increases with the effective inner axon diameter.

To investigate the intra- and extra-axonal contributions to ΔD_⊥, Fig. 5 shows ΔD_i⊥ and ΔD_e⊥ vs 〈d〉_eff from simulation set III. Here and below, results from all distribution shapes (i.e. σ = 0.3, 0.5, 0.7) were plotted identically as dots. Note that ΔD_e⊥ ≈ ΔD_i⊥ near 〈d〉_eff = 4 μm. Below this diameter, ΔD_e⊥ > ΔD_i⊥, and extra-axonal water dominates the relationship between ΔD_⊥ with 〈d〉_eff. Above this diameter, ΔD_e⊥ < ΔD_i⊥, and intra-axonal water dominates the trend between ΔD_⊥ with 〈d〉_eff. Regardless of the domain, both ΔD_i⊥ and ΔD_e⊥ increase monotonically with 〈d〉_eff, and, therefore, an increase in ΔD_⊥ can be interpreted as an increase in axon size, independent of the underlying compartmental contribution.

Fig. 5.

Intra- (top) and extra-axonal (bottom) contributions to ΔD_⊥ with 〈d〉_eff, taken from simulation set III. For smaller axon diameters, ΔD_e⊥ > ΔD_i⊥. For larger axon diameters, ΔD_e⊥ < ΔD_i⊥.

Set IV: myelin The evaluations of the role of myelin on ΔD_⊥ are summarized in Fig. 6. These data show that the trend in ΔD_⊥ with 〈d〉_eff is largely independent of the presence and relative thickness of myelin, including when g varies as a function of axon size. Also, comparing the left and right panels, inclusion of myelin water and diffusion of water between compartments has little effect on ΔD_⊥.

Fig. 6.

Simulation set IV. ΔD_⊥ simulated over a wide range in myelination and myelin water. All distribution shapes (i.e. σ = 0.3, 0.5, and 0.7) are plotted as dots. The trend in ΔD_⊥ with 〈d〉_eff is consistent over a wide range in g-ratio, and is not impacted by the inclusion of myelin water and water exchange between compartments.

Set V: t_eff Results from simulations using various OG and PG diffusion encoding waveforms is shown in Fig. 7. In all cases, the relationship between ΔD_⊥ and 〈d〉_eff remains, but the slope at any 〈d〉_eff increases with the difference in t_eff.

Fig. 7.

Simulation set V. The magnitude of the slope in ΔD_⊥ with 〈d〉_eff increases with difference in effective diffusion time of the diffusion encoding waveforms.

Set VI: D_0,ie Results from simulations varying D_0,ie is shown in Fig. 8. The relationship between ΔD_⊥ and 〈d〉_eff is mostly independent of D_0,ie, except at D_0,ie = 0.5 μm²/ms, where ΔD_⊥ values are lower at larger axon sizes.

Fig. 8.

Simulation set VI. The value of the free diffusion coefficient of intra- and extra-axonal water, D_0,ie, significantly impacts the radial diffusivity simulated with oscillating gradient (OG, top) and pulsed gradient (PG, middle) diffusion waveforms. However, the relationship between ΔD_⊥ and 〈d〉_eff (bottom) is consistent over a wide range in D_0,ie. Only in the lowest value of D_0,ie are the values of ΔD_⊥ reduced for large axon sizes.

Set VII: heterogeneous axon packing Results from simulations with variations in axon packing axons are shown in Fig. 9. The top row shows three example spatial distributions of axon density with ΔL = 0, L/4, and L/2, while the middle row shows axon distributions after pruning based upon the spatial distribution. In the bottom panel, simulations over a wide of ΔL indicated that ΔD_⊥ was sensitive to variations in axon packing heterogeneity, which may bias measurements of axon diameter based upon this metric.

Fig. 9.

Simulation set VII: To create spatial variations in axon packing density, axons within a simulation arena generated with v_e = 0.3, σ = 0.5 and $\overline{d}=1$ μm were selectively pruned based upon a trapezoid packing density with a variable transition width, given by ΔL. Example distributions are shown in the top row, and resulting simulation arenas are shown in the middle row. Simulations indicate that variations in packing density do influence ΔD_⊥, and could bias estimates of axon diameter.

4. Discussion

This work suggests a robust metric of axon diameter can be obtained from relatively simple diffusion measurements: the difference in the radial apparent diffusion, ΔD_⊥, collected at two different, appropriate diffusion times. Simulations demonstrated that ΔD_⊥, for our selected gradient waveforms, depends primarily on effective inner axon diameter, 〈d〉_eff, and is largely independent of extra-axonal volume fraction, axon diameter distribution, free diffusion coefficient, and myelin characteristics. The magnitude of ΔD_⊥ with 〈d〉_eff increases with the difference in diffusion time between the DW-MRI acquisitions, at least over the range of times investigated. Further, the relationship between ΔD_⊥ and 〈d〉_eff has contributions from both intra- and extra-axonal water signals, allowing it to be sensitive to smaller axons than could be probed with an intra-axonal contrast alone.

This study builds upon several recent studies. One recent study involving pulsed- and oscillating-gradient experiments and numerical simulations interpreted differences in D_⊥ with diffusion time to be roughly proportional to axon diameter (Tétreault et al., 2020). Whereas the simulations in that work were limited to investigating changes with v_e with the specific diffusion waveforms that were performed experimentally, the present work provides a more complete evaluation of ΔD_⊥, including sensitivity over several tissue characteristics and diffusion weighting waveforms. Two other recent in vivo human brain studies each reported a diffusion-time difference measure, similar to ΔD_⊥, noting that it highlighted white matter tracts known to have larger diameter axons (Dell’Acqua et al., 2019; Padron et al., 2019), which is consistent with the simulation results here. Another study looked at the difference in D_⊥ between PG and OG as reporting on microstructure, but not specifically axon diameter (Arbabi et al., 2020). That study also noted that ΔD_⊥ can be calculated from only two acquisitions when the b-value is the same between two acquisitions, removing the need to acquire a separate b=0 scan. Also, one prior study proposed the diffusion dispersion rate with OG frequency (essentially ΔD_⊥ divided by frequency difference between two OG measures) as a measure of axon diameter (Xu et al., 2016). In that case, as in other prior axon diameter mapping methods, the relationship between D_⊥ and axon diameter was based on the intra-axonal water signal only.

While ΔD_⊥ increases monotonically with axon diameter, intra- and extra-axonal water contribute differently to this relationship. In regions with small axons, ΔD_⊥ depends primarily on extra-axonal water and increases approximately linear with 〈d〉_eff. With larger axons, intra-axonal water contributes more to ΔD_⊥ and results in a more quadratic increase with 〈d〉_eff. Also, note that where extra-axonal water signal dominates, it makes sense that ΔD_app is reporting on outer axon diameters (i.e., outside the myelin) rather than inner-axon diameter. Here, 〈d〉_eff was defined as the inner diameter, and Appendix A provides more discussion how the definition of 〈d〉_eff affects the relationship with ΔD_app.

Of course, several studies have noted that extra-axonal water significantly contributes to diffusion measured in the brain (Lam et al., 2014; Novikov and Kiselev, 2010; Veraart et al., 2019). Some studies have even noted a relationship between diffusion characteristics of extra-axonal space and axon diameter. One study found differences in the radial diffusion and kurtosis coefficients of extra-axonal water with diffusion time and axon diameter (Grussu et al., 2019). Another study, found a relationship between the correlation time of extra-axonal water and axon diameter (Burcaw et al., 2015), and subsequent studies have reported correlation lengths that compare with axon diameter (Fieremans et al., 2016; Lee et al., 2018).

An interesting consequence of finding that extra-axonal space can also report on axon diameter is that this may in fact have influenced prior axon diameter mapping studies. In some studies involving tissues with large axons and/or using systems with strong gradients, it may be that much of the sensitivity to axon diameter was derived primarily from intra-axonal water diffusion characteristics (Assaf et al., 2008; Barazany et al., 2009; Huang et al., 2020; Ong and Wehrli, 2010; Stanisz et al., 1997; Veraart et al., 2020; Xu et al., 2014). However, for the majority of in vivo human brain studies, gradient strength will only be sufficient to attenuate intra-axonal signals from the largest axons, and so axon diameter measures will tend to be high (Alexander et al., 2010; Huang et al., 2015). In these cases, axon diameters may also be overestimated because the contribution from extra-axonal space is neglected in the analysis. It is likely that inclusion of extra-axonal water signal in such models could improve the sensitivity to smaller axon diameters.

The ΔD_⊥ presented in this work was sensitive to a single metric of axon diameter, 〈d〉_eff, even while the underlying distribution of axon sizes may be somewhat broad. Since 〈d〉_eff is weighted towards larger diameters in the distribution, it includes contribution both from the mean and the variance of the diameter distribution. Still, it might be possible for advanced diffusion encoding schemes to estimate more complex characteristics of axons in tissue. Some recent studies have also characterized the distribution of axon diameter as a single representative value (Veraart et al., 2020), while other recent studies have looked to estimate the distribution of axon diameters (Anaby et al., 2019; Romascano et al., 2020). Since intra- and extra-axonal water diffusion is sensitive to different measures of axon diameter (see the Appendix), and given the near linear dependence of ΔD_e⊥ on axon size and the near quadratic dependence of ΔD_i⊥, it may be possible to incorporate multiple oscillating gradient, pulsed gradient and/or double diffusion encoding schemes to estimate parameters like the variance of the axon diameter distribution, extra-axonal volume fraction, and/or g-ratio, (Ianu et al., 2017; Kakkar et al., 2018; Shemesh, 2018). We note that, in some regions of white matter, the distribution of axon diameter may not be well represented by the log-normal distribution used in this and previous studies, and the single-parameter measure for diameter may break down in tissues with axon diameter distributions that are multimodal.

There are several limitations to this study. First, while the simple 2D geometry allows simulation of water diffusion over such a broad range of tissue properties in a reasonable computation time, the model of white matter consists of only axons within the arena, and neglects signal from other possible compartments (glial cell bodies, blood, CSF, etc.) that could influence D_⊥. Further, the simulation ignores potential dispersion of axons along white matter fiber bundles, which is also present in white matter (Zhang et al., 2012). Future studies can explore these relationships in more realistic geometries of white matter, such as recently developed methods using synthetic (Ginsburger et al., 2019; 2018; Palombo et al., 2019) and histology based geometries (Lee et al., 2020; 2019).

Second, the diffusion experiments simulated in this work were not optimally designed for either human or small animal imaging systems. Sensitivity of ΔD_⊥ to axon diameter depends on the difference in diffusion times (as illustrated in Fig. 7) but also on the image signal-to-noise ratio (SNR). For D_⊥ = 0.5μm²/ms and b = 0.3ms/μm², we used a z-score threshold method (Nilsson et al., 2017) to compute the number of voxels needed within a region of interest (ROI) to detect a given ΔD_⊥ for a given SNR—see Table 1. For example, to detect ΔD_⊥ = 0.1μm²/ms, which corresponds to 〈d〉_eff ≈3μm, 11 voxels are required when SNR = 20 and only 2 voxels are needed when SNR = 50. In practice, gradient strength and slew rate will affect both diffusion time and SNR (through its effect on echo time). Similar to previous work (Drobnjak et al., 2016; Nilsson et al., 2017), gradient waveforms can be optimized by considering contributions of both intra- and extra-axonal water, including effects of transverse relaxation. Also, instead of sinusoidal oscillating gradients, trapezoid-based oscillating gradient gradient waveform and tensor encoding using 2 gradient channels simultaneously can provide more efficient diffusion encoding (Baron and Beaulieu, 2014). Ultimately, the practical limits of using ΔD_⊥ to measure axon diameter in the presence of noise remains to be determined.

Table 1.

Number of voxels in an ROI necessary to detect ΔD_⊥ for a given signal-to-noise ratio (SNR), using the z-score threshold method outlined in Nilsson et al. (2017).

		ΔD⊥ (μm2/ms)
		0.05	0.10	0.20
SNR	20	41	11	3
	50	7	2	1

Lastly, the trends in ΔD(t) with 〈d〉_eff, g and v_e have not been validated. Future studies should be aimed at validating these studies in animal models. Further, studies should be aimed at bridging the gap between the simple metrics outlined here and previously published theoretical studies of diffusion in extra-axonal water.

5. Conclusion

In this work, Monte Carlo simulations were used to show that the difference in the radial diffusivity measured at multiple diffusion times can be used as a metric of axon diameter in white matter, being relatively independent of extra-axonal volume fraction, g-ratio, heterogeneity of axon size, and water exchange.

Appendix A. Effective diameters of intra- and extra-axonal water

Data from the simulation sets in this manuscript were used to analyze the appropriate effective measure of axon diameter for intra- and extra-axonal compartments individually and collectively for the trend in ΔD_⊥. Considering the effective diameter defined in Eq. (1), all relevant values of p ≤ 6 were analyzed.

Fig. A1.

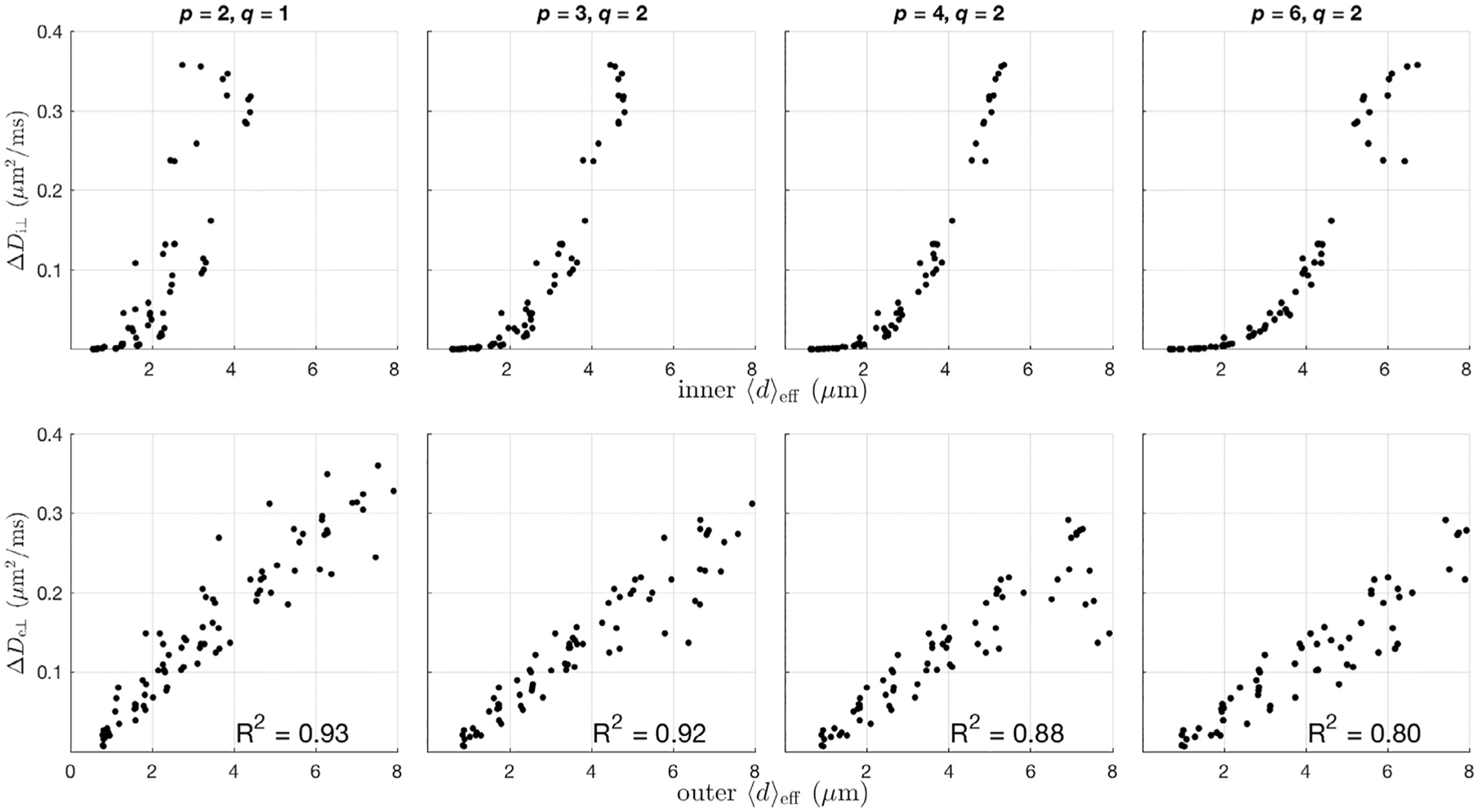
Data from simulation set III was used to investigate the appropriate index of axon diameter appropriate for diffusion in intra- and extra-axonal water diffusion. Top: ΔD_i⊥ vs inner 〈d〉_eff for notable combinations of p, and q as defined in Eq. (1). Bottom: ΔD_e⊥ vs outer 〈d〉_eff. Intra-axonal water best corresponds to 〈d〉_eff defined with p =4 & q = 2, while extra-axonal water best corresponds to an outer effective diameter with p = 2 & q = 1.

Fig. A2.

Data from simulation set IV was used to investigate the best index of axon diameter of the simulated ΔD_⊥, plotted as a function of inner 〈d〉_eff (top) and outer 〈d〉_eff (bottom). Note that at larger axon diameters, the variance of ΔD_⊥ is smaller when defining 〈d〉_eff as the inner diameter compared to the outer diameter. Similarly, at smaller axon diameters, the variance of ΔD_⊥ is smaller when defining 〈d〉_eff as the outer diameter compared to the inner diameter.

Simulation set III was used to analyze the relationship between intra- and extra-axonal compartmental diffusion with 〈d〉_eff, as this simulation set provides both a wide variety for the extra-axonal volume fraction, and intra-axonal size and size distribution. Fig. A1 shows ΔD_i⊥ vs inner 〈d〉_eff (top) and ΔD_e⊥ vs outer 〈d〉_eff (bottom) for notable combinations of p and q. Note that the variance in ΔD_i⊥ appears to be minimized with p = 4 & q = 2—a value that has previously been used as an axon diameter index for diffusion imaging (Burcaw et al., 2015). For extra-axonal diffusion, the linear correlation coefficient is highest for ΔD_e⊥ when p = 2 & q = 1, although the trend is similar for all cases shown.

Simulation set IV was used to analyze the relationship between total water diffusion with 〈d〉_eff because the variation in g-ratio uncouples the inner and outer axon diameters. From simulation set IV, Fig. A2 shows ΔD_⊥ vs inner 〈d〉_eff (top) and outer 〈d〉_eff (bottom). Note that when axon diameters are small, there is less variation in ΔD_⊥ when plotted vs outer 〈d〉_eff, while at larger axon diameters, there is less variation in ΔD_⊥ when plotted vs inner 〈d〉_eff. Therefore, the appropriate definition of d—being inner vs outer diameter—in the calculation of 〈d〉_eff may depend upon the axon size being probed. Throughout this work, 〈d〉_eff was defined as the inner diameter with p = 4 and q = 2, as that provided the clearest relationship with ΔD_⊥ over the entire range of axon diameters studied.