Effects of ambient conditions on the risk of pressure injuries in bedridden patients—multi‐physics modelling of microclimate

Abstract

Scientific evidence regarding microclimate and its effects on the risk of pressure ulcers (PU) remains sparse. It is known that elevated skin temperatures and moisture may affect metabolic demand as well as the mechanical behaviour of the tissue. In this study, we incorporated these microclimate factors into a novel, 3‐dimensional multi‐physics coupled model of the human buttocks, which simultaneously determines the biothermal and biomechanical behaviours of the buttocks in supine lying on different support surfaces. We compared 3 simulated thermally controlled mattresses with 2 reference foam mattresses. A tissue damage score was numerically calculated in a relevant volume of the model, and the cooling effect of each 1°C decrease of tissue temperature was deduced. Damage scores of tissues were substantially lower for the non‐foam mattresses compared with the foams. The percentage tissue volume at risk within the volume of interest was found to grow exponentially as the average tissue temperature increased. The resultant average sacral skin temperature was concluded to be a good predictor for an increased risk of PU/injuries. Each 1°C increase contributes approximately 14 times as much to the risk with respect to an increase of 1 mmHg of pressure. These findings highlight the advantages of using thermally controlled support surfaces as well as the need to further assess the potential damage that may be caused by uncontrolled microclimate conditions on inadequate support surfaces in at‐risk patients.

1. INTRODUCTION

Health care facilities worldwide are burdened by pressure ulcers (PU) and, throughout the years, have increased their focus on PU prevention. However, there are insufficient data to determine if the actions taken and the increased focus have reduced the PU prevalence in these facilities.1, 2, 3

PU prevalence surveys have shown that the sacrum is the most commonly reported anatomic location of all PUs (28.3%). Most patients (78%) were 61 years or older. Despite the efforts invested in PU monitoring and prevention, PU prevalence rates remain relatively unchanged.4

Although there is abundant literature regarding PU, the complex interactions of the different factors causing these wounds are not fully understood. Specifically, the extent of the contribution associated with microclimate as a factor in PU causation and its interaction with sustained tissue deformations have yet to be quantified.5, 6, 7, 8, 9, 10 Microclimate was defined in 1976 and included skin temperature, humidity, and air movement.11 Regarding PUs, microclimate is used to mainly describe the skin surface temperature and skin moisture.10, 12

The effect of moisture on skin mechanical properties has long been investigated.13, 14, 15, 16 Stratum corneum cells are composed largely of the fibrous protein keratin. When exposed to different levels of relative humidity (RH), the mechanical properties of keratin change. Specifically, when the RH is 98%, the stratum corneum breaking strength is 25% of the breaking strength at RH of 32%.13 Breaking strength declines almost linearly as the RH rises. Rotaru et al.17 measured the coefficient of friction (COF) between the forearm of 3 subjects and different hospital sheets in wet and dry conditions. COF for the wet condition ranged from 0.5 to 0.95, while COF of the dry condition ranged from 0.2 to 0.4. Derler and Gerhardt16 obtained similar results; in addition, they found that the hydration effect on skin COF is more prominent in women than in men.

Physiologically, elevated skin temperature results in an increase of tissue metabolic demand, an approximate 10% increase in metabolic demand per 1°C of skin temperature elevation.18, 19 The skin‐to‐mattress interface, where heat is trapped, is prone to elevated skin temperature, especially in standard foam mattresses. Elevated sacral skin temperature has been previously shown to increase the risk of PU formation. Sae‐Sia et al.20 showed in their study that, regardless of the reclining position, the mean sacral skin temperature in subjects who developed a PU was ~37.2°C, while in those who did not develop PUs, it was ~36.0°C.

Patel et al.21 demonstrated the effects of temperature elevation on surface pressure‐induced changes in rat skin blood perfusion (SBP). Their findings showed that mean SBP increases by 14% to 20% for an 8°C skin elevation (from 28°C to 36°C) at low pressures of up to 18 mmHg. Under increased pressure, SBP declines significantly for both heated (36°C) and non‐heated (28°C) skin. Moreover, heated skin deformed differently under increasing pressure, resulting in 2 different force‐displacement curves for heated and non‐heated skin. They concluded that increased temperature stiffened the rat's skin in response to increased surface pressure, possibly as a result of heat‐induced changes in tissue permeability of the interstitial matrix. This conclusion should not be taken for granted. The skin is an anisotropic composite material,22 with collagen and elastin fibre reinforcement, oriented differently at the various skin sites. The mechanical properties of the skin have been studied both in vivo and in vitro, showing the skin's behaviour under compression loading23, 24 and tensile loading.23, 24, 25 Xu et al.23 also tested the temperature‐related changes in the compression and tensile loading methods. Their data for large strains showed that while the tensile stiffness of the skin decreases as the temperature rises, the compressive stiffness increases. One possible explanation for this is that in the compressive test, the load is applied through the matrix of the skin tissue, perpendicular to the orientation of the collagen fibres, whereas in tensile loading, the collagen fibres carry most of the load, and their reaction to the temperature change is immediately apparent in the results (dehydration and denaturation of the collagen fibres at high temperatures).

Because the SBP baseline requirements are greater for warmed skin, blood flow deficit and consequent ischaemia would be much more severe at higher skin temperature for any pressure greater than approximately 25 mmHg. Lachenbruch et al.25, 26 estimated the magnitude of the skin‐cooling protective effect based on Patel's work. He determined the baseline SBP for heated and non‐heated skin. Based on the SBP reduction relative to the baseline value, an estimation of equivalent surface pressure reduction was made.

Kokate et al.27, 28 developed a porcine model experiment to investigate the relationship between applied temperature, pressure, and time of application in the formation of PUs in superficial and deep tissues. Using their extensive experimental data, injury threshold graphs were constructed, combining all 3 parameters to a probability of wound formation per tissue. Despite the limitations of this study, the aforementioned damage score threshold equations provided a convenient predictive tool for injuries resulting from combinations of temperature, pressure, and time parameters. Results showed that for lower applied temperatures, the injury threshold increased for all tissues. The operating temperature of various support surfaces aimed to prevent PU formation is 30°C to 36°C;29 hence, some of these mattresses may improve pressure distributions over bony prominences but may also promote PU formation due to higher temperatures.

Finite element (FE) modelling has been used in evaluating stress and strain distribution in both deep and superficial tissues under changing support mattresses and/or tissue conditions. Several studies have been conducted on different types of mattresses and patient positions.30, 31, 32, 33, 34, 35, 36 However, the performance of the variety of microclimate control support surfaces, such as air‐fluidised, low‐air‐loss, and gel mattresses, in PU prevention has not yet been evaluated through FE methods. To the best of our knowledge, an FE model that couples the mechanical behaviour of the mattress and the thermal effects of the microclimate control system into a realistic anatomical geometry does not yet exist. Accordingly, such an innovative coupled multi‐physics model of the buttocks is presented here.

2. METHODS

2.1. Geometry and mesh

The geometry of the model was based on an MRI scan of a female volunteer (age 28, height 1·66 [m]). The scan was conducted twice, in a supine lying position, on a rigid board and on a rigid board with no support for the buttocks, resulting in 2 different scans: deformed and undeformed buttocks. The 3‐dimensional (3D) MRI scan was then imported to the Scan‐IP module of Simpleware^® Ltd37; the mattress was added to the model later. The size of the buttocks model was 23 × 38.2 × 22.3 cm (length × width × height, maximal length in each axis). The dimensions of the mattress were 23 × 42 × 6 cm (length × width × height). Using Scan‐IP, the buttocks MRI scan slices were segmented to 4 different tissue types: bone, muscle, fat, and skin (Figure 1A).

Figure 1.

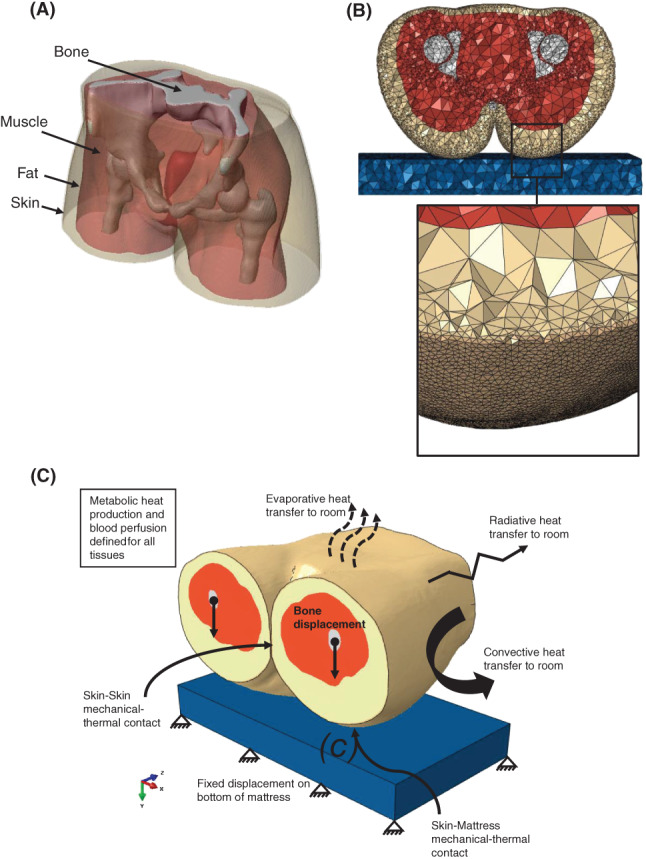
The 3‐dimensional (3D) finite element model of the buttocks: (A) Resultant 3D model of the buttocks from the MRI scan, depicting the tissue layers. (B) Axial cross‐section of the mesh with an enlarged tilted view showing the elements distribution at the skin and fat tissue layers closest to the mattress. (C) A 3D isometric view of the model, demonstrating the interfaces and boundary condition relationships in the model

We used Scan‐IP for FE meshing as well (Figure 1B). A mesh refinement was defined on the bottom side of the skin that comes in contact with the mattress during simulations. Element lengths at the refinement area were 2 mm or smaller. This resulted in a mesh of 753 269 elements, which were all 4 nodes thermally coupled tetrahedron elements (C3D4T) for both the mattress and the buttocks. Mesh sensitivity tests showed that higher mesh densities did not affect the numerical convergence or results accuracy (results of denser meshes stayed below the 2% difference relative to the chosen mesh).

2.2. Finite element modelling

Our FE model needed to facilitate coupled physics calculations, that is, thermal‐structural coupling, in order for the model to be useful for microclimate investigations. We therefore chose ABAQUS v6.14^® 38 as our FE solver as, after evaluating several options, we found that this software package was the most suitable for the above purpose. The thermal model and the structural model are each computationally challenging and require considerable computer power for managing the numerical processes. Hence, some assumptions and simplifications were made for the modelling framework to allow feasible solutions of the thermal‐structural problem. The coupled model schematic boundary conditions and loads are shown in Figure 1C.

2.2.1. The biothermal model of the supine buttocks

The Fiala thermoregulation models of passive39 and active40 systems were chosen to represent the human thermoregulation system. Our subject is assumed to lie on a hospital mattress (mattresses with different properties were tested) in a thermally controlled hospital environment. Given the controlled ambient conditions, some of the thermoregulatory elements of the active thermoregulation system in the Fiala model could be omitted. The mattresses chosen for modelling were 2 foam mattresses of different stiffness of 5 kPa and 15 kPa and 3 additional 5 kPa mattresses with different thermal properties: water mattress, low‐air‐loss (LAL) mattress, and high‐air‐loss (HAL) mattress. The thermal properties of the different mattresses are shown in Table 1. The thermal boundary conditions used for foam mattresses and water mattress are constant ambient temperature and convection heat loss at all exposed areas of the mattress. In the case of the air‐loss (LAL and HAL) mattresses, simplification of a constant upper surface temperature was introduced. It was set based on the results of Reger et al.41 for the average temperature reduction at the air‐loss mattress to human body (equivalent) interface. This simplification enables accounting for the steady‐state temperature reduction expected in air‐loss mattresses while avoiding the complex modelling and simulation of the full function of air flow and temperature distribution in those mattresses (which is beyond the scope of the present study).

Table 1.

Thermal properties of the tissues and the different mattress technologies simulated in the modelling

Material	$\mathit{k}\left[\frac{\mathit{W}}{\mathit{mK}}\right]$	${\mathit{C}}_{\mathit{p}}\left[\frac{\mathit{J}}{\mathit{kgK}}\right]$	$\mathit{\rho }\left[\frac{\mathit{kg}}{{\mathit{m}}^3}\right]$	${\mathit{q}}_{\mathit{m},0}\left[\frac{\mathit{W}}{{\mathit{m}}^3}\right]$	${\mathit{w}}_{\mathit{bl},0}\left[\frac{1}{\mathit{s}}\right]$
Skina	0.47	3680	1085	368	1.05E‐03
Fata	0.16	2300	850	58	3.60E‐06
Musclea	0.42	3768	1085	684	5.38E‐04
Bonea	0.75	1700	1357	0	0
Foamb	0.026	1000	40	‐	‐
Waterc	0.6154	4178	995.7	‐	‐
LAL/HALd	0.026	1005	1.16	‐	‐

Abbreviations: HAL, high air loss; k, thermal conductivity; LAL, low air loss; C _p, specific heat; ρ, density; w _{bl, 0} and q _{m, 0}, basal values for blood perfusion and metabolic rates in thermal neutrality.

^aData adopted from literature.25

^bData adopted from literature.31

^cWater thermal properties at 30 (°C).

^dThermal properties of air at 30 (°C) were taken for LAL/HAL.

Pennes42 formulated the fundamental balance of heat transfer within biological tissues:

$$k{\nabla }^{2}T+q_m+{\rho }_{\mathit{bl}}{w}_{\mathit{bl}}{c}_{\mathit{bl}}\left(T_{\mathit{bl},a}-T\right)=\mathit{\rho c}\frac{\partial T}{\partial t}$$ (1)

where k is the thermal conductivity of the tissue; T is the tissue temperature; q _m is the metabolic heat rate of the tissue; ρ _bl, w _bl and c _bl are the blood density, perfusion rate, and heat capacity, respectively; and T _{bl, a} is the arterial blood temperature. As a steady state is assumed, the right side is considered to be 0.

The expressions for the metabolic heat rate, q _m, and the blood perfusion rate, w _bl, are built so that at thermal neutrality conditions, the heat rate and perfusion rate of the specific tissue are at their basal levels. As the tissue temperature differs from its neutral state, their values change as a function of that temperature difference. The equations that were adopted from Fiala's passive model39 are detailed below and were implemented in the computational model using Fortran subroutines. The metabolic heat rate is given by:

$$q_m=q_{m,0}+{\mathit{\Delta q}}_m$$ (2)

where q _{m, 0} is the basal metabolic heat rate of a specific tissue material, and Δq _m is the additional heat rate due to possible local autonomic thermoregulation:

$${\mathit{\Delta q}}_m={\mathit{\Delta q}}_{m,\mathit{bas}}+q_{m,\mathit{sh}}+q_{m,w}$$ (3)

where q _{m, sh} and q _{m, w} are the additional heat produced by shivering and by exercise, respectively, and Δq _{m, bas} is the difference between the actual basal rate and the basal rate corresponding to neutral thermal conditions. Assuming no additional heat rate due to exercise or shivering, the expression for Δq _m is reduced to:

$${\mathit{\Delta q}}_m={\mathit{\Delta q}}_{m,\mathit{bas}}=q_{m,0}·\left[2^{\left(T-T_0\right)/10}-1\right]$$ (4)

where T ₀ is the tissue temperature at its setpoint.

The blood perfusion rate (units of [1/s]) at non‐neutral conditions varies with changes in the local metabolic heat rate, q _m.:

$$w_{\mathit{bl}}=w_{\mathit{bl},0}+{\Delta w}_{\mathit{bl}}$$ (5)

where w _{bl, 0} is the basal blood perfusion rate, and Δw _blis the change in demand for oxygen as a function of the change in metabolic heat rate:

$$w_{\mathit{bl}}=w_{\mathit{bl},0}+\frac{{\mu }_{\mathit{bl}}·\Delta q_m}{{\rho }_{\mathit{bl}}{c}_{\mathit{bl}}}$$ (6)

where μ _bl is a proportionality constant (units of [1/K]).

The passive blood circulation was assumed to be in equilibrium, that is, the blood pool temperature was assumed to be equal to the venous temperature, and no counter‐current heat exchange between blood vessels was incorporated into the model; hence, T _{bl, a}is constant. The buttocks were modelled without clothing, and therefore, no clothing insulation was taken into consideration. The heat loss to the environment by respiration in the Fiala model is distributed within several body elements of the pulmonary tract and was thus assumed to be 0 for our buttocks model.

The buttocks model was assumed to exchange heat with the environment through radiation, convection, and evaporation. All 3 heat loss equations were adopted from Fiala's passive model.39 The convective heat exchange with the environment is given by.

$$q_c=h_{c,\mathit{mix}}·\left(T_{\mathit{sk}}-T_{\mathit{amb}}\right)$$ (7)

where T _sk is the skin surface temperature, T _amb is the ambient temperature, and h _{c, mix} is the local convection coefficient, determined as a function of the local skin temperature:

$$h_{c,\mathit{mix}}=\sqrt{a_{\mathit{nat}}\sqrt{T_{\mathit{sk}}-T_{\mathit{amb}}}+a_{\mathit{frc}}{v}_{\mathit{air}}+a_{\mathit{mix}}}$$ (8)

where v _air is air velocity, and a _nat, a _frc, a _mix are regression coefficients (nat = natural, frc = forced, and mix = absolute term).

The resultant mean natural convection coefficient in neutral conditions was calculated for verification and was compared with results of other thermoregulation models:

$$h_{c,\mathit{\text{mean}}}=\frac{\int q_c{\mathit{dA}}_{\mathit{sk}}}{A_{\mathit{sk}}\left(T_{\mathit{sk},m}-T_{\mathit{amb}}\right)}=3.51\left[\frac{W}{m^{2}K}\right]$$ (9)

where q _c is the local convective heat flux, dA _sk is the corresponding skin surface section, A _sk = 0.2332[m ²] is the total skin surface of the model, T _{sk, m} = 33.5^° C is the area‐weighted mean skin temperature, and T _amb = 28^° C; thus, ΔT = 5.5^° C.

The resultant mean convection coefficient is in good agreement with previous published simulation results39, 43, 44, 45, 46; see Table 2 for the reference values of the mean convective heat transfer coefficient.

Table 2.

Mean convective heat transfer coefficients of a naked human body in natural convection conditions, as reported in the up‐to‐date literature

Reference	Fanger 43	Rapp 44	Murakami et al.45	Fiala et al.39	Pan et al. 46	Present study
${\mathit{h}}_{\mathit{c},\mathit{\text{mean}}}\left[\frac{\mathit{W}}{{\mathit{m}}^2\mathit{K}}\right]$	3.7a	4.0a	3.9	2.9a	3.0b	3.5

^aResults derived from Figure 2 of Fiala et al.39 at ΔT ≅ 5.5^° C.

^bResult is for ΔT ≅ 6.5^° C.

The radiation heat exchange with the environment is given by:

$$q_r=h_r·\left(T_{\mathit{sk}}-T_{\mathit{amb}}\right)$$ (10)

where h _r is radiative heat transfer coefficient, expressed as:

$$h_r=\sigma {\varepsilon }_{\mathit{sf}}{\varepsilon }_{\mathit{sr}}{\psi }_{\mathit{sf}-\mathit{sr}}·\left(T_{\mathit{sk}}^{*2}+T_{\mathit{amb}}^{*2}\right)\left(T_{\mathit{sk}}^{*}+T_{\mathit{amb}}^{*}\right)$$ (11)

where σ = 5.67 ∙ 10⁻⁸[W/m ² K ⁴] is the Bolzmann constant; ɛ _sf = 0.99 and ɛ _sr = 0.93 are the emission coefficients of the legs and of the surrounding surfaces, respectively; ψ _{sf − sr} = 0.9 is the corresponding view factor; and $T_{\mathit{sk}}^{*}$and $T_{\mathit{amb}}^{*}$ are the absolute temperatures of the local skin sector and of the surrounding surfaces, respectively.

Under steady‐state conditions, in which no sweat is secreted because of thermoregulatory control mechanism, the evaporative heat transfer expression from Fiala's passive thermoregulation system is reduced to the heat transport by moisture diffusion through the skin and is given by:

$$q_{\mathit{ev}}=\frac{P_{\mathit{osk},\mathit{sat}}-P_{\mathit{sk}}}{R_{e,\mathit{sk}}}$$ (12)

where P _{osk, sat} is the saturated vapour pressure within the outer skin layer, P _sk is the actual vapour pressure at the skin surface, and 1/R _{e, sk} = 0.003[W/m ² Pa] is the skin moisture permeability. The expression for P _{osk, sat} assumes the following form:

$$P_{\mathit{osk},\mathit{sat}}=100·\exp \left(18.956-\frac{4030}{T_{\mathit{sk}}+235}\right)$$ (13)

and the expression for P _sk is:

$$P_{\mathit{sk}}=\frac{\frac{P_{\mathit{osk},\mathit{sat}}}{R_{e,\mathit{sk}}}+U_{e,\mathit{cl}}{P}_{\mathit{air}}}{U_{e,\mathit{cl}}+\frac{1}{R_{e,\mathit{sk}}}}$$ (14)

where U _{e, cl} is the resultant evaporation coefficient of clothing over the skin, and P _air is the vapour pressure in the ambient air at relative humidity of 40% (neutral ambient conditions).

As our modelling assumes no clothing to this end, the expression for U _{e, cl} is obtained as:

$$U_{e,\mathit{cl}}=L_{\mathit{air}}{h}_{c,\mathit{mix}}$$ (15)

where L _air = 0.0165[K/Pa] is the Lewis constant for air, and h _{c, mix} is the local convection coefficient.

The heat loss to the environment due to vasomotion was calculated iteratively as the residual heat loss needed for changes of skin temperature and rectal temperature (as a function of the ambient temperature) to be in good agreement with the Fiala model.39 These relationships are shown in Figure 2A: The maximal skin temperature deviation relative to Fiala model results was 0·37%, and the maximal rectal temperature deviation was 1.17%. The heat flux distribution from the skin to the environment was also in good agreement with other thermoregulation models46, 47 (Figure 2B).

Figure 2.

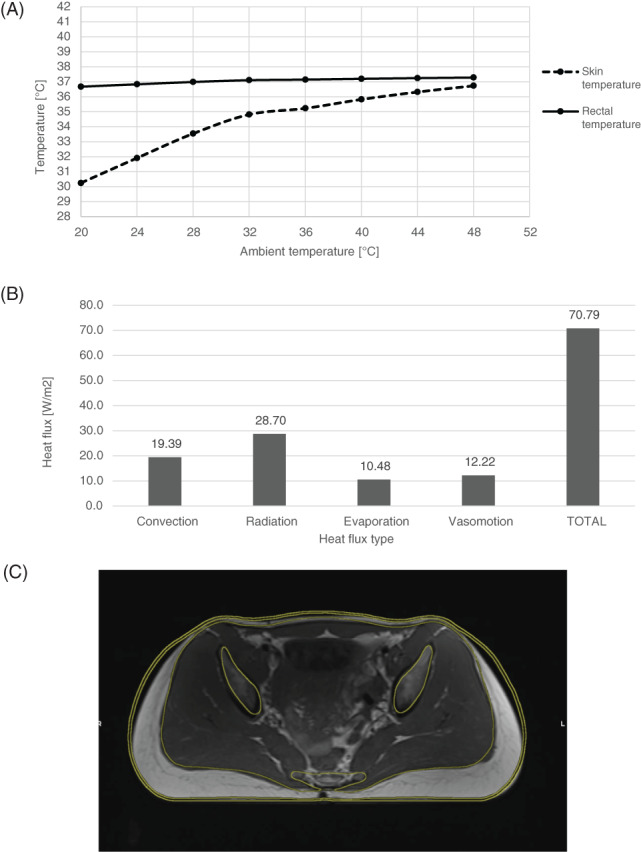
Thermal model and mechanical model verification results: (A) The steady‐state skin and rectal temperatures of the undeformed model as a function of the ambient temperature. (B) The contribution of the various heat transfer mechanisms to the average heat flux from the skin at thermal neutrality. (C) The achieved optimal contour fitting of the buttocks model on a rigid board with the corresponding MRI scan of the buttocks on a rigid support surface

For the caudal and cephalad surfaces of the model, a boundary condition of equal heat flux was defined. All thermal properties of the biothermal model are specified in Table 1.

2.2.2. The biomechanical model of the supine buttocks

The skin, subcutaneous fat, and skeletal muscle tissues were assumed to behave as homogenous‐isotropic‐hyperelastic materials that follow a large strain elasticity behaviour through the Neo‐Hookean form of strain energy potential,34, 38, 48 with a strain energy density function W:

$$W=C_{10}\left(\overline{I_1}-3\right)+\frac{1}{D_1}\left(J_{\mathit{el}}-1\right)$$ (16)

where $\overline{I_1}$ is the first invariant of the right Cauchy‐Green deformation tensor, C ₁₀ is a material parameter, J _el is the determinant of the deformation gradient tensor, and D ₁ is:

$$D_1=\frac{2}{K_0}$$ (17)

where K ₀ is the initial bulk modulus of the material.

Validation of the biomechanical model of the buttocks was achieved by matching the resulting deformed contours of tissues with their real deformed shape, recorded in the deformed MRI scans. The tissues were assumed to be incompressible. Initial values of the material parameter, C ₁₀, for each tissue was adopted from Oomens et al.34 To fit the material parameters to the model, incremental changes in the parameters were made iteratively on several structural analysis runs simulating lying on a rigid board until an optimal fitting of tissue layers contour was obtained. The best contour‐matching results of the final run on a rigid board are shown in Figure 2C, and the corresponding final material parameters are listed in Table 3.

Table 3.

Mechanical properties of the tissues and different mattresses simulated in the modelling and corresponding characteristics of finite element mesh

Material	C10 [kPa]	K0 [kPa]	υ	E [kPa]	# of mesh elementsd
Skina	4	666.67	0.494	‐	237 638
Fata	0.4	66.67	0.494	‐	314 740
Musclea	0.225	37.5	0.494	‐	125 215
Boneb	‐	‐	0.3	7e6	43 240
Foam	‐	‐	0.3	5/15	32 436
Waterc	‐	‐	0.3	5	32 436
LAL/HALc	‐	‐	0.3	5	32 436

Abbreviations: C10, material parameter (temperature dependent for Skin tissue); K₀, initial bulk modulus; υ, Poisson's ratio; E, linear elastic modulus.

^aData adopted from literature.32

^bData adopted from literature.33

^cWater, LAL, and HAL mattresses elastic modulus and Poisson's ratio were chosen as 5 kPa and 0·3 for comparison.

^dAll mesh elements are C3D4T—4 node thermally coupled tetrahedron.

In addition, the physical weight of the buttocks was verified. The thighs and buttocks weigh approximately 14.8% of the total body mass.49 The total body mass of our subject was 61 kg, and therefore, the buttocks and thighs should weigh approximately 9 kg (≈88.5 N). The integral reaction force was hence calculated on all the fixed FE nodes located at the bottom of the mattress, and the result was 88.3 N, which is in very good agreement with the approximate weight of our buttocks model.

Bone tissues (sacrum and femurs) were modelled as linear‐elastic materials with a modulus of elasticity of 7 GPa.30, 48 All mattresses were assumed to be linear‐elastic as well, with elastic moduli of 5 or15 kPa.

2.2.3. Coupled boundary conditions and loads acting on the buttocks model

Surface‐to‐surface contact was set between the refined mesh part of the skin and the mattress. Friction was determined between skin and the support surface, with a coefficient of friction (COF) ranging from 0.4 to 0.9 depending on the mattress type and its permeability to sweat. Foam mattresses characterised by poor heat clearance were assumed to accumulate sweat at a steady‐state condition, and therefore, their COF with the skin was defined as 0.9. The COF for a water mattress was defined as 0·7, and for low‐air‐loss (LAL) and high‐air‐loss (HAL) mattresses, it was set to 0.4. Self‐contact was set between the skin on each side of both thighs, and this contact was defined as frictionless.

The skin material parameter C ₁₀ was defined as a function of skin temperature according to the results and conclusions from Patel et al.24 As skin temperature rises from 28°C to 36°C, the skin stiffness increases by 25%, approximately more than 3% per 1°C. Given the expected temperature range of our cases, this change in stiffness of the skin is not expected to have a meaningful influence on the entire model or on the resultant risk for PU development, but it represents the potential worst‐case result and should contribute to the results of the comparative study.

The model surfaces at both ends of the MRI scan (towards the torso in 1 direction and towards the legs on the other) was fixed for displacements on the z‐axis (along the body axis). The upper part of the sacrum was set to move 0.07 m in the y‐axis, towards the mattress, and no other displacements in the x‐axis or z‐axis were allowed. The bottom surface of the mattress was fixed in all directions.

The thermal model was solved separately to obtain the temperature field of the undeformed buttocks in thermal neutrality conditions, as detailed in Table 4 (no tissue displacements). This solution was used as the initial condition for the buttocks temperature in the thermal‐structural coupled model. Convection, radiation, and evaporation to the environment were set between the skin surface and the surroundings, and these heat loss equations were programmed into the FE code using the Fortran subroutines FILM and DFLUX, which were designated to sync with ABAQUS CAE.

Table 4.

The assumed thermal neutrality conditions

T amb(° C)	${\mathit{v}}_{\mathit{air}}\left(\frac{m}{s}\right)$	RH(%)	ɛ w
28.0	0.05	40.0	0.93

Abbreviations: T _amb, ambient temperature; v _air, air velocity; RH, relative humidity; ɛ _w, surrounding walls emissivity.

The metabolic heat rate was modelled using the Fortran subroutine HETVAL, which allows the setting of volumetric heat production per material (ie, per tissue type) as a function of the current tissue temperature and tissue location relative to the mattress (ie, in contact with the mattress or not).

Thermal conductance was set between the mattress and the skin that comes in contact with the mattress during the solution of the contact problem. This was achieved by using another Fortran subroutine GAPCON, which allows detection of the clearance between each node on the skin surface to the mattress for each iteration during the simulations. Once the clearance decreases below a predetermined distance of 0.1 mm, thermal conductance at the specific node turns active, and heat loss by convection, radiation, and evaporation is disabled (ie, there is no exposure to the environment).

At the end of each such increment, a damage score in the relevant tissues was evaluated. This damage score was calculated using the UVARM subroutine. It was programmed to store temperature and pressure values in all the elements that are in contact with the mattress and assign these values to the relevant tissues. Then, the damage score was calculated using the equations developed by Kokate et al.28 (Figure 3).

Figure 3.

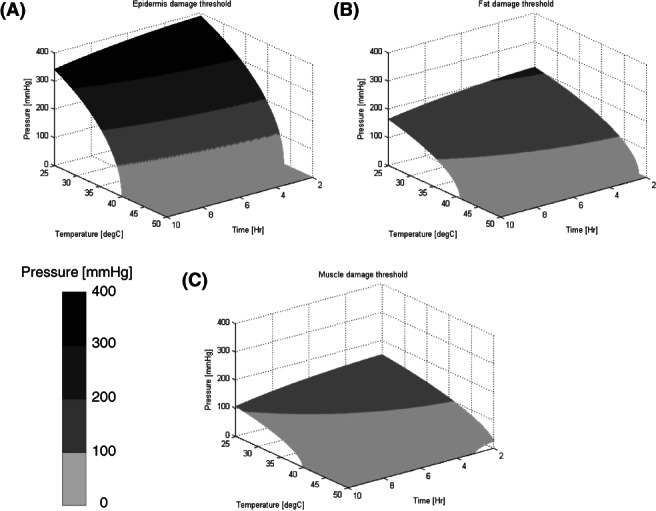
Damage score threshold 3D plots for (A) Epidermis, (B) Fat, and (C) Muscle tissue, caused by applied pressure and temperature for varying durations, reconstructed using the equations developed by Kokate et al.28 The plotted surface represents a unity damage score, a value that was determined by the original authors as the damage threshold

For each simulation case (simulations were distinct by the mattress type), the simulation criterion was said to be met successfully when achieving the desirable physical weight of the buttocks, as detailed above. This was achieved by calculating the integral reaction force at the bottom of the mattress at the end of each increment until reaching the desired force. The flowchart of the coupled model simulations is depicted in Figure 4.

Figure 4.

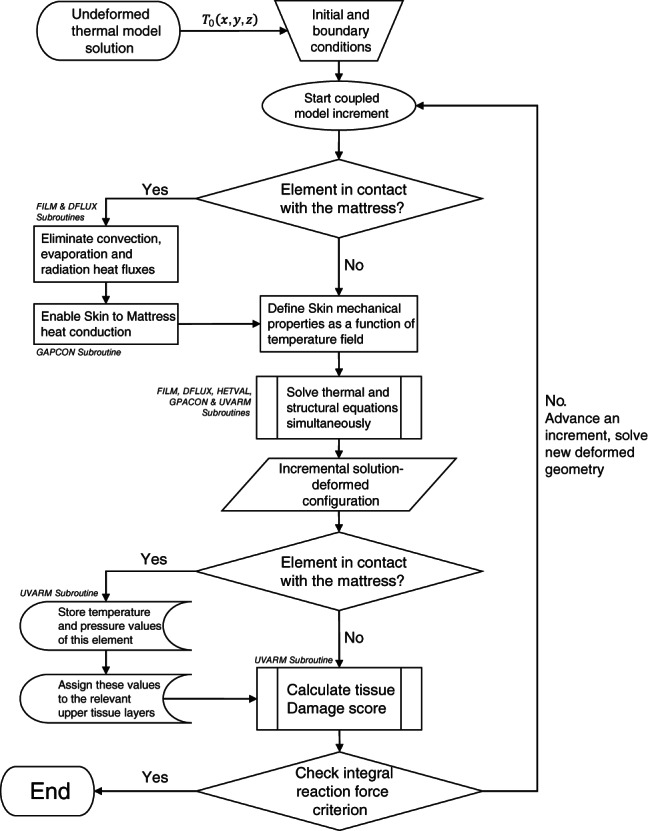
A schematic flowchart for the finite element‐based coupled model

Simulations were conducted using an Intel Core i7‐4930 K CPU @ 3.40GHz processor with 64.0 GB installed RAM and Windows 7 Enterprise SP1 64‐bit operation system. Despite the computer power of the aforementioned workstation, given the complexity of this multi‐physics real‐geometry modelling, the approximate time duration required for solution of each simulation case was approximately 72 h.

3. RESULTS

As with the verification of the biomechanical FE model, we chose the slice of the MRI scan demonstrating the largest tissue deformations near bony prominences to focus our analyses on the regions at the greatest risk for injury. A small box at the central coccyx area was chosen as the volume of interest (VOI). See Figure 5A.

Figure 5.

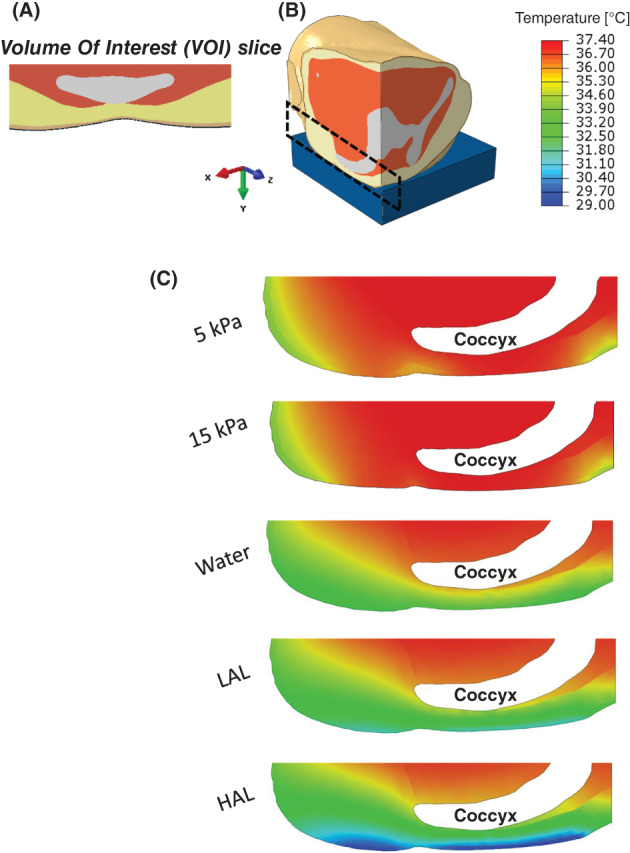
Temperature distributions in the tissues of the buttocks on different support surfaces: (A) Axial view of the deformed volume of interest (VOI) in the supine buttocks. (B) Location of the examined area for the temperature distribution. (C) Temperature distribution on a sagittal cross‐section of the buttocks for each of the simulated mattresses

Examining the effect of the different support surfaces on the average tissue temperature in the chosen VOI showed significant changes in average temperatures, not only for the outer skin layer but also for the fat and muscle tissue layers. Figure 5 depicts temperature distributions on a sagittal cross‐section of the buttocks for each of the simulated mattresses. The average VOI skin temperature was 33.4°C, 31.8°C, and 29.4°C for the water, LAL, and HAL mattresses, respectively, whereas the average VOI skin temperature for foam mattresses was 37·1 ^° C. Using the foam mattress results as the baseline, the HAL mattress doubled the skin temperature reduction compared with the water mattress (ratio of 2.07). This ratio was similar for fat (ratio of 2.03) and the muscle (ratio of 2.11) tissues. The ratio between the temperature reductions in tissues for the LAL mattress compared with the water mattress was also consistent across the different tissue types, with an average of 1.43. The trend of the average temperature per tissue type across the different mattresses and the percentage temperature reduction achieved by the different mattresses with respect to the foam mattress are shown in Figure 6 (in panels A and B, respectively). As expected, due to the (active) thermoregulation system of the body, the deeper the tissue is, the less its temperature could be affected by the different mattress technologies (Figure 6A). For example, the average temperature of skeletal muscle tissue, when the body is resting on a foam mattress, was 37.3 ^° C, whereas for the HAL mattress, it was 36.1 ^° C, that is, only 1.2 ^° C lower. Conducting these comparisons for the more superficial skin and fat tissues resulted in more considerable temperature differences, of 7.6 ^°C and 4.4 ^° C, respectively. We found that the differences in skin temperatures between the foam mattresses with the 2 differing stiffness characteristics (15 and 5 kPa) were negligible. Hence, given that these 2 stiffness values reflect the range of product stiffness values for this type of mattresses, the results indicate that stiffness of the foam (in foam mattresses) does not contribute to temperature build‐up under the body of the user. Referring to the temperature distributions in the different mattresses, the LAL and HAL mattresses, which were defined with a constant upper surface temperature, had a more uniform and lower temperature distribution compared with the water and foam mattresses. This emphasises the differences in heat evacuation capabilities across the mattress designs and, eventually, is a factor in the overall risk of injury (which increases in higher temperatures).

Figure 6.

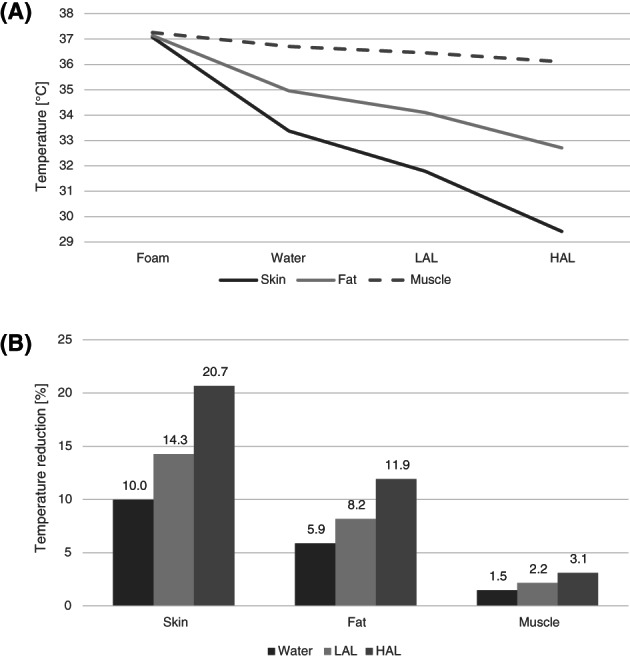
Temperature distributions in the volume of interest (VOI) in the supine buttocks: (A) The trend of the average temperature in VOI per tissue type across the different support surfaces. (B) The percentage tissue temperature reduction in the VOI associated with use of the different support surfaces relative to the foam mattress

Peak tissue strains were localised at the soft tissues surrounding the coccyx and were distributed similarly across the different mattresses, with the exception of the 15 kPa (stiffer) foam mattress, for which greater strains were developed in all the tissue layers beneath the coccyx. The strains, temperature, and tissue damage scores calculated for the transverse plane of the body, at the VOI, are shown in Figure 7. The average damage scores of the tissues were substantially lower for the non‐foam mattresses compared with the foams. With specific regards to the water, LAL, and HAL mattresses, the average damage score for skin tissue after 3 h of simulated lying was 74%, 92%, and 98% lower than for the 15 kPa foam mattress, respectively. Conducting the same comparison for skin tissue at durations of 7 and then 10 h of simulated motionless lying resulted in lower reductions of the damage score by the non‐foams, 58%–97% after 7 h and 45%–82% after 10 h. This phenomenon, of the non‐foam mattresses providing less protection for increasing durations of supine lying as manifested in calculated damage scores, has been shown to be consistent for all tissue types. This points to the (already known) fact—which is supported clinically and by international guidelines for pressure injury prevention—that no existing mattress technology can deliver tissue protection for an unlimited time period where there is no repositioning. Comparing the 5 kPa foam mattress with the 15 kPa foam mattress with regards to damage scores, the average damage score for skin when the body is resting on the 5 kPa mattress was mildly reduced, by 7.1%, 9.4%, and 12.3% for 10, 7, and 3 h of lying, respectively. These moderate reductions in damage scores can be attributed to the slightly better envelopment provided by the softer foam, which allows better pressure distribution at the skin‐to‐surface interface and allows heat to better dissipate. The average damage scores per tissue type and for all the mattress technologies studied here are summarised in Figure 8 for lying durations of 3, 7, and 10 h.

Figure 7.

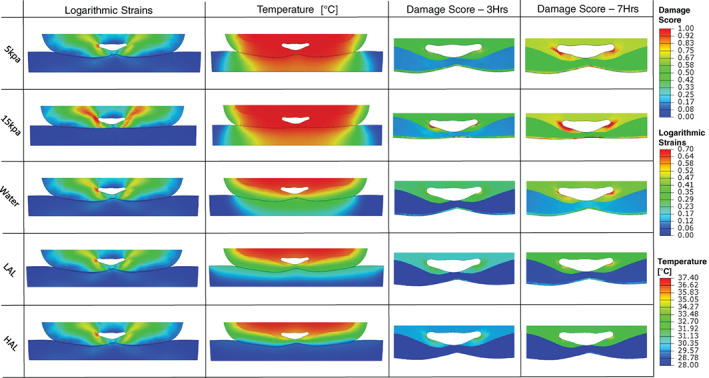
Contours of logarithmic strain and temperature distribution in tissues and in the support surface are depicted on the most injury‐prone axial cross‐section of the buttocks, across the different support surface types. Damage score for durations of 3 and 7 h are depicted on the same axial cross‐section, zoomed in to the VOI

Figure 8.

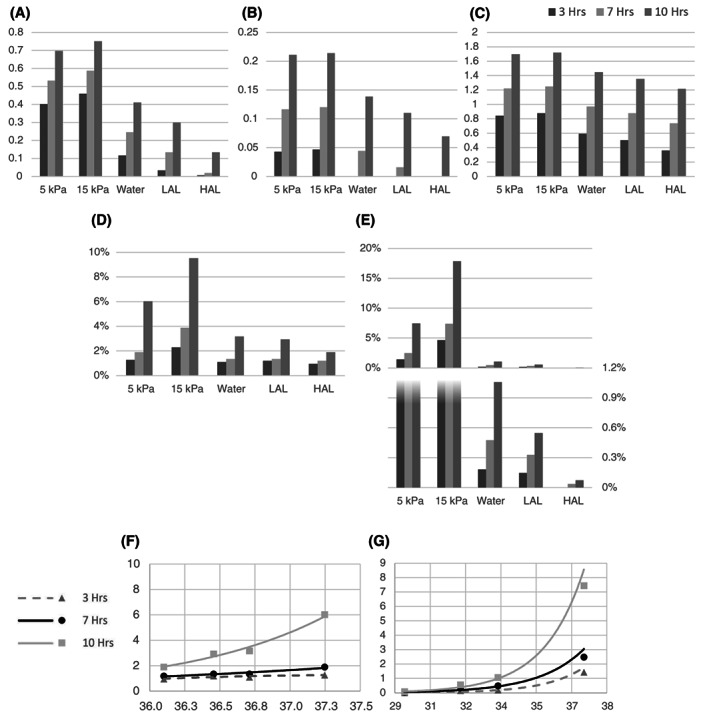
Summary of the damage score data for: (A) skin, (B) fat, and (C) muscle tissues. The average damage scores in the volume of interest (VOI) are compared across the different support surfaces for durations of 3, 7, and 10 h. The resultant percentages of (D) muscle and (E) skin tissues at risk in the VOI are shown for durations of 3, 7, and 10 h. The relation between the average tissue temperature and percentage of tissue at risk of damage are shown for (F) muscle and (G) muscle for durations of 3, 7, and 10 h

The calculated damage scores ranged from 0 to 2. Although there were considerable variations in tissue strain and temperature magnitudes and distributions across the different mattress conditions, muscle tissue in the VOI consistently showed the highest average damage score for all mattress technologies, ranging from 0.87 for the 15 kPa foam to 0.36 in HAL mattress after 3 h of motionless lying, and from 1.71 in 15 kPa foam to 1.21 in HAL mattress after 10 h of lying. Skin tissue showed high damage scores for the foam mattresses, with substantial reductions for the water, LAL, and HAL mattresses, which are more effective in heat dissipation from the skin with respect to foams. For example, after 10 h of static lying at a supine posture, the average damage score for skin was 0.75 for the 15 kPa foam but only 0.41, 0.30, and 0.13 for the water, LAL, and HAL mattresses, respectively.

We further examined the volumetric percentage of tissues in the VOI, which crossed a damage score of unity, which was at the fifth quintile of damage score values calculated across our present set of simulations, and was therefore considered to indicate a high risk of potential tissue damage. For the skin, the %‐volumes of tissue at risk after 10 h of lying were orders of magnitude lower for the water, LAL, and HAL mattresses compared with the foams, but the differences were less for muscle tissue (Figure 8). For the 2 foam mattress stiffnesses, and again consistent with the above‐described data, the skin volume exceeding a damage score of unity was strongly influenced by the stiffness of the mattress, with the stiff (15 kPa) mattress resulting in a greater skin volume at risk (Figure 8). However, the at‐risk tissue volumes in the deep tissues (muscle and fat) were nearly unaffected by the stiffness of the foam mattress (Figure 8).

We used the results of the above analyses of at‐risk tissue conditions at the VOI from all the simulation cases and lying durations in order to create a plot of the resultant %‐volume of tissue at risk as a function of the average tissue temperature, regardless of the chosen mattress (Figure 8F, G). This plot indicates that the at‐risk tissue volume grows exponentially with the average tissue temperature (Figure 8F, G).

4. DISCUSSION

The literature discussing PU causes of formation and prevention methods is diverse. Many studies focus on the biomechanical aspects, which contribute to PU formation, for example, pressure distribution, support surface stiffness, etc.,30, 31, 32, 33, 34 and on the biomechanical actions and solutions for PU prevention, for example, repositioning, motionless lying durations, nursing crew guidelines etc.50 Microclimate, although increasingly discussed and referred to as a fundamental element in PU formation,14, 16, 24, 25, 26, 27, 28 is still missing from quantitative studies. Computational modelling is extremely useful for comparing biomechanical performances of different support surfaces, particularly regarding deep tissue loads demonstration, which cannot be measured using pressure mats. Despite that, the complexity of the physiological relationship between tissue temperature, skin moisture, skin coefficient of friction, and their effects on PU formation at different tissue depths (skin, fat, and muscle)16, 20, 27, 28, 29 has made computational modelling much more challenging for this cause. To our knowledge, no FE model that couples the biothermal and biomechanical physics and compares different mattress technologies, including microclimate control mattress, exists.

In this study, we used an MRI‐based buttocks FE model and incorporated several predictive tools from previous studies to simulate, for the first time, how microclimate control support surfaces perform biomechanically and biothermally with respect to standard foam mattresses of different stiffnesses. The results are temperature, strain, and damage score maps of the 3D buttocks model under the changing conditions, which are further discussed below.

Referring to the thermal results of the coupled model, the steady‐state average sacral skin surface temperature in the foam mattress cases was in good agreement with previous experimental studies on hospital beds.51, 52, 53 Furthermore, the contribution of the various heat transfer mechanisms to the average heat flux from the skin to the surroundings at thermal neutrality was also in good agreement with other thermoregulation models46, 47 (Figure 2B).

The resulting deep tissue temperature reduction in the water, LAL, and HAL mattresses relative to the foam mattresses (shown in Figure 6B) was noticeable, lowering muscle tissue temperature near bony prominences by 1.5°C to 3°C. These results, along with the skin temperature results for the different mattresses, correlate with the experimental finding from the porcine study28 of the potential for ischaemic tissue damage.

While the results from our model were in a wide range of temperatures, pressures, and damage scores for the different tissues, the porcine study was conducted with specific temperature increments of 5°C and specific applied pressures with variable sample sizes. In addition, the anatomy, thickness, and composition of the tissue layers (and hence, biophysical, biomechanical, and biothermal properties) are not similar in the modelled buttocks and studied porcine model, which limits direct comparisons. Nevertheless, a qualitative comparison between the results shows good correlation of potential damage severity and location. For example, when comparing the porcine study case of 35°C and pressures of 10 and 50 mmHg with the water mattress, for short durations, the porcine study28 case showed 0 to mild tissue damage in all tissues, and our water mattress model predicted the same. For medium durations, the porcine study case showed mild damage in all tissue layers, while our model predicted mild damage for skin and fat and moderate damage for the muscle tissue. This difference can be attributed to the different durations of the comparison as other cases from the porcine study showed increased muscle damage severity relative to fat and skin tissues for longer durations (10 h). Comparing the 35°C case from the porcine study with our 15 kPa mattress, for medium durations, both the porcine study results and our 15 kPa foam model showed moderate damage for skin and fat tissues and severe damage for muscle. For longer durations, the porcine study showed severe damage throughout all tissue layers, and our 15 kPa foam model resulted in severe damage to the skin and muscle tissues and moderate (but increased) damage to the fat tissue. This trend reconfirms, from both biothermal and biomechanical perspectives, that pathological changes in pressure injuries for bedridden patients in supine lying position begin at the deep tissue and progress to the subcutaneous and cutaneous layers as the duration of exposure to sustained deformations increases.8, 23, 24, 49

The average sacral skin temperature results of the different mattress models can be used as a predictor for increased risk of pressure injuries. For similar mattress stiffnesses and durations, raised sacral skin temperature in the range of 29.4°C to 37.1°C correlates with increased skin, fat, and muscle tissue damage score (except in the fat tissue, where the correlation with increased damage score starts at ~33.4°C). These results are supported by a study by Sae‐Sia et al.,47 who measured the PU incidence and sacral skin temperature in hospitalised neurologically impaired patients and found that, regardless of the reclining position, the mean sacral skin temperature in subjects who developed a PU was ~37.2°C, while in those who did not develop a PU, it was ~36.0°C. Our study may also support the work by Newman and Davis54 who found that 45% of subjects who had increased sacral temperature measured by thermography developed a PU within 10 days of admission in a geriatric unit.

Generally, a 1°C increase of skin temperature results in approximately 10% increase in tissue metabolism. As a result, tissue blood perfusion increases to minimise accumulation of tissue waste, reducing the tissue tolerance to ischaemia, making it more susceptible to injury at lower pressure levels. Our results further demonstrate how this phenomenon can affect subcutaneous and deep tissues for several different cases of support surfaces, with different resulting sacral skin temperatures.

The protective effect of cooling the skin on the formation of pressure injuries was tested by Patel et al.21 and was further discussed by Lachenbruch et al.25 They established a skin blood perfusion (SBP) baseline value, with which they could quantify the protective effect of cooling the skin from 36°C to 28°C, equivalent to reducing the interface pressure from 56 to 40 mmHg (ie, approximately 2 mmHg pressure reduction per 1°C reduction). Lachenbruch et al.26 conducted an additional study with 10 volunteers and concluded that 1°C contributes 8.0 to 14.1 times as much to ischaemia as 1 mmHg and that differences in reactive hyperaemia caused by a 4°C increase were more profound between 32°C and 36°C than between 28°C and 32°C.

We estimated the same cooling effect contribution from our model results. By normalising the effect of the increased sacral pressure between the 5 kPa foam mattress and the 15 kPa foam mattress (both with the same sacral skin temperature of 37°C) on the damage score at the skin, we obtained the contribution of 1 mmHg to the average damage score of the skin. By normalising the effect of the increased sacral temperature between the 5 kPa and the water mattress (both with a negligible difference of sacral skin pressure) on the damage score at the skin, we obtained the contribution of 1°C to the average damage score of the skin. The resultant ratio is that each 1°C contributes 13.0 to 14.9 times as much to the damage score as 1 mmHg for supine lying durations of 3, 7, and 10 h. Furthermore, our results also showed that in the temperature range of 33.5°C to 37°C, the skin damage score increased at a rate of 0.078 (damage score/1°C) relative to 0.028 (damage score/1°C) for the range of 29.4°C to 33.5°C. These results are all in good agreement with the abovementioned study.26

FE modelling always involves limitations. The possible implications of our model limitations should not to be overlooked. Mechanical properties were taken from previous computational studies, as detailed in Table 3. However, these properties differ from 1 patient to another and from different areas of the model. Similar to several previous FE models, the skin was assumed to behave as an isotropic hyperelastic soft tissue and was modelled using the Neo‐Hookean strain energy function. This modelling method, although simpler, does not represent the skin's directional mechanical properties accurately as the skin is an anisotropic material. Furthermore, the mechanical property of the skin was defined as temperature‐dependent, but (as a simplification) thermal properties were not defined as mechanical loading‐dependent. In real‐world scenarios, temperature effects may differ under compression and tensile loading conditions, which again highlight the complex structural‐thermal interactions in the living body. The finalisation of properties was verified on a specific slice of interest, located on the sacrum cross‐section, where the tissue deformation was the largest. An optimisation of these properties along several cross‐sections would reduce the accuracy of our results at the VOI, and thus was not conducted. The mechanical properties of the water, LAL, and HAL mattresses were assumed to be equal because we wanted to have the ability to isolate the structural effects resulting purely from the mattress resistance, making the comparison between the thermal mattress and the 5 kPa foam mattress simpler. The LAL and HAL mattresses were not modelled or verified with an appropriate CFD model; for simplicity, we assumed a constant upper surface temperature of both of these mattresses based on previous studies, as mentioned in the Methods section. The damage score equations were adopted from a previous porcine study.24 Differences in anatomical structure and tissues properties are potential reasons for possible inaccuracies of our model. Specifically, differences in tissue layers thickness make the comparison of the contact pressure effect on deep tissues risk for injury more challenging. The strength of our model is its ability to enable a comparative study, rather than an absolute investigation of each mattress’ results.

This coupled physics model can be further developed and improved for future work and the better understanding of the thermal and mechanical effects of different mattresses and conditions on the risk for pressure injuries formation. Studies considering different patients, such as diabetic, dehydrated, inflamed tissues, increased core temperature, and different pathoanatomies, are worth investigation. The environmental conditions can be improved and varied, for example, increased or reduced room temperature, different relative humidity conditions, accumulated urine or sweat on the mattress, varying positions, and clothing of the patient. In spite of the 3D modelling advantages, a 2D model will have the advantage of a simpler and less time‐consuming model.

In conclusion, we have developed an innovative coupled physics model based on previous studies’ results and model equations. The model results show good correlation with previous experiments in the field of microclimate and its effects on the risks for pressure injuries formation. The damage score parameter, despite the mentioned model limitations, has been proven as a strong tool for comparison of different case studies. This model can definitely benefit research activity both in the biomedical engineering field, for thermal control support surfaces evaluation and development, and in the nursing field, for demonstration of the performance advantages of different industrial support surfaces, both thermal‐controlled and regular foam mattresses.

Zeevi T, Levy A, Brauner N, Gefen A. Effects of ambient conditions on the risk of pressure injuries in bedridden patients—multi‐physics modelling of microclimate. Int Wound J. 2018;15:402–416. 10.1111/iwj.12877