Probing in vivo cortical myeloarchitecture in humans via line-scan diffusion acquisitions at 7T with 250–500 micron radial resolution

Abstract

Purpose:

The goal of this study was to measure diffusion signals within cerebral cortex using the line-scan technique to achieve extremely high resolution in the radial direction (i.e., perpendicular to the cortical surface) and to demonstrate the utility of these measurements for investigating laminar architecture in the living human brain.

Methods:

Line-scan diffusion data with 250–500 micron radial resolution were acquired at 7T on eight healthy volunteers, with each line prescribed perpendicularly to primary somatosensory cortex (S1) and primary motor cortex (M1). Apparent diffusion coefficients (ADCs), fractional anisotropy (FA) values and radiality indices were measured as a function of cortical depth.

Results:

In the deep layers of S1, we found evidence for high anisotropy and predominantly tangential diffusion, with low anisotropy observed in superficial S1. In M1, moderate anisotropy and predominantly radial diffusion was seen at almost all cortical depths. These patterns were consistent across subjects and were conspicuous without averaging data across different locations on the cortical sheet.

Conclusion:

Our results are in accord with the myeloarchitecture of S1 and M1, known from prior histology studies: in S1, dense bands of tangential myelinated fibers run through the deep layers but not the superficial ones, and in M1, radial myelinated fibers are prominent at most cortical depths. This work therefore provides support for the idea that high-resolution diffusion signals, measured with the line-scan technique and receiving a boost in signal-to-noise ratio at 7T, may serve as a sensitive probe of in vivo laminar architecture.

Introduction

A key characteristic of cerebral cortex is the variation of structural properties with cortical depth—in particular, the variation of cell morphology and density (i.e., cytoarchitecture) and the variation of myelination patterns (i.e., myeloarchitecture). Since cortical areas with different cyto- or myeloarchitecture typically serve different functional roles, the ability to study the depth-dependent structure of cortex, noninvasively and in vivo, could provide an unprecedented opportunity to investigate structure-function relationships in the living human brain.

While MRI is an obvious candidate for noninvasive, in vivo studies, a major challenge for the investigation of MR signals as a function of cortical depth, often referred to as “laminar MRI” (1), lies in the fact that cortex has a thickness on the order of a couple of millimeters, not much larger than the size of the isotropic voxels typically used for in vivo acquisitions—on the order of a millimeter or so. As illustrated in Figure 1A, this can lead not only to partial-volume contamination from the adjacent white matter and cerebrospinal fluid (CSF), but also to the mixing of signals across different cortical layers. Substantially lowering the isotropic voxel size would reduce these partial-volume effects, but at the cost of a huge decrease in signal-to-noise ratio (SNR), which scales linearly with voxel volume. By noting, however, that structural properties in cortex vary quite rapidly in the radial direction (i.e., perpendicular to the cortical surface) but rather slowly in the tangential directions (i.e., parallel to the cortical surface), the use of a highly anisotropic voxel geometry suggests itself as a solution to this problem. As long as these anisotropic voxels are prescribed appropriately, as illustrated in Figure 1B, one receives both the benefit of high resolution in the radial direction and that of high SNR via the large voxel size in the tangential directions. As discussed later, line-scan techniques (2–4) quite naturally give rise to such anisotropic voxel geometries, making them arguably the method of choice for laminar MRI studies.

FIG. 1.

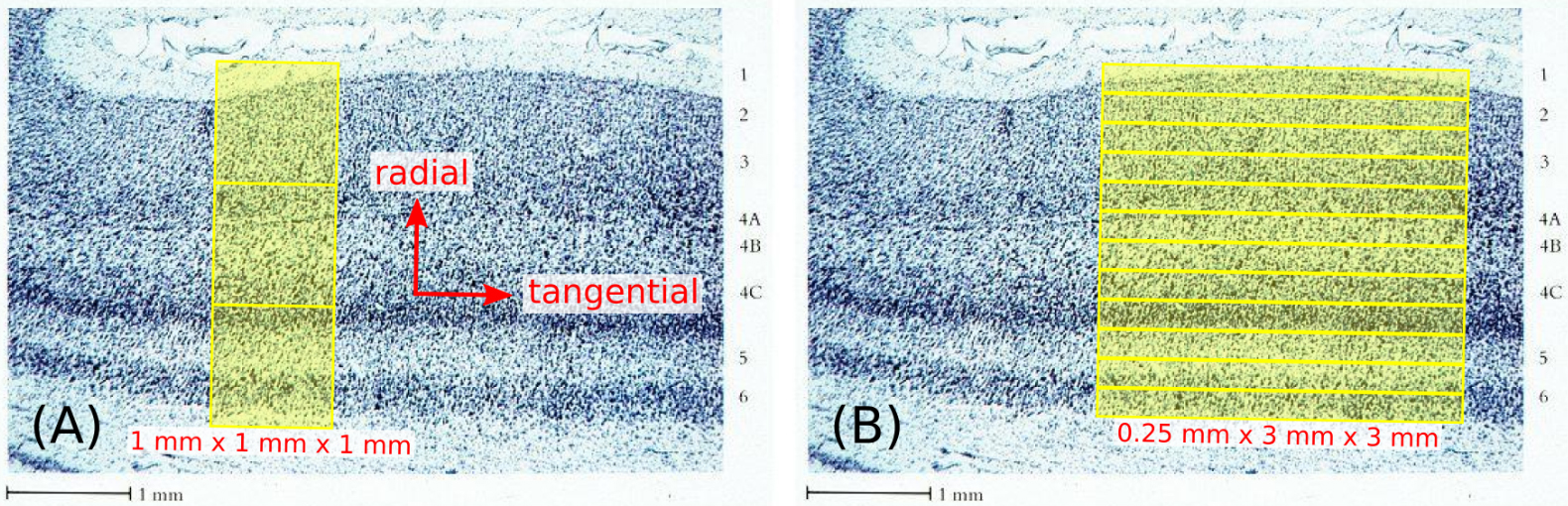
Nissl stain of primary visual cortex (reproduced from ref. #77), illustrating the cytoarchitecture of cortical gray matter. The use of 1 mm isotropic voxels shown in (A) inevitably leads to substantial mixing of signals from different cortical layers, as well as a high likelihood of partial-volume contamination from the adjacent white matter and CSF. On the other hand, the use of highly anisotropic voxels, as shown in (B) for the example of 0.25×3×3 mm voxels, can greatly reduce these partial-volume effects without sacrificing SNR, as long as the voxels are suitably positioned and oriented with respect to the radial and tangential directions of the cortical surface, indicated in (A). Although the points above are illustrated on primary visual cortex (V1) in this figure, they are applicable to any cortical area, e.g., primary somatosensory cortex (S1) and primary motor cortex (M1), which are the focus of this study.

As an application of this idea, we chose to study laminar diffusion signals in human primary somatosensory cortex (S1) and primary motor cortex (M1). Previous studies consistently reported that the principal diffusion direction was mostly tangential in S1 and mostly radial in M1; the use of 1–1.5 mm (5–8) isotropic voxels in these studies is, however, of concern for the reasons given above, especially since S1 is one of the thinnest cortical areas in humans—approximately 1.5 mm in thickness (6). The goal of this study was therefore to acquire line-scan diffusion data in S1 and M1 with very high radial resolution (250–500 μm), not only in an attempt to reproduce the findings of the aforementioned studies but with reduced concerns of partial-volume effects, but also to go beyond those studies to investigate the detailed depth dependence of the diffusion signals, and to compare these results with the known myeloarchitecture of S1 and M1 from classical histology studies (9).

Methods

Data acquisition

Eight healthy volunteers (6F/2M; ages 22–30 years), having provided informed consent under the auspices of the local institutional review board, were scanned on a Siemens 7T whole-body system (Siemens Healthineers, Erlangen, Germany) using custom-built radiofrequency (RF) coils for the head—a birdcage transmit coil and a 32-channel receive coil (10). These subjects had all participated in previous MRI studies, with their prior anatomical scans exhibiting very little head motion artifact. The whole-brain anatomical scan used in this study was a T₁-weighted dual-echo 3D MPRAGE scan (11) with FOCI adiabatic inversion pulses, acquired in ~8 minutes with the following parameters: TE₁/TE₂/TI/TR = 1.8/3.7/1100/2530 ms, readout bandwidth = 651 Hz/px, FA = 7°, GRAPPA PE acceleration factor = 2 and 0.75×0.75×0.75 mm³ voxel size (12).

The MPRAGE images, generated from the root-mean-square of the echoes, were used as an anatomical localizer for prescribing the subsequent line-scan diffusion acquisitions: the central sulcus was first identified on each hemisphere and then M1 and S1 (which lie respectively on the anterior and posterior banks of this sulcus) were inspected in search of cortical patches that were flat on the scale of a few millimeters or more. For each of the eight volunteers in this study, it was possible to find at least one such location. A single line was then prescribed, centered approximately on the central sulcus and oriented perpendicularly to M1 and S1 at this location (see Figure 2).

FIG. 2.

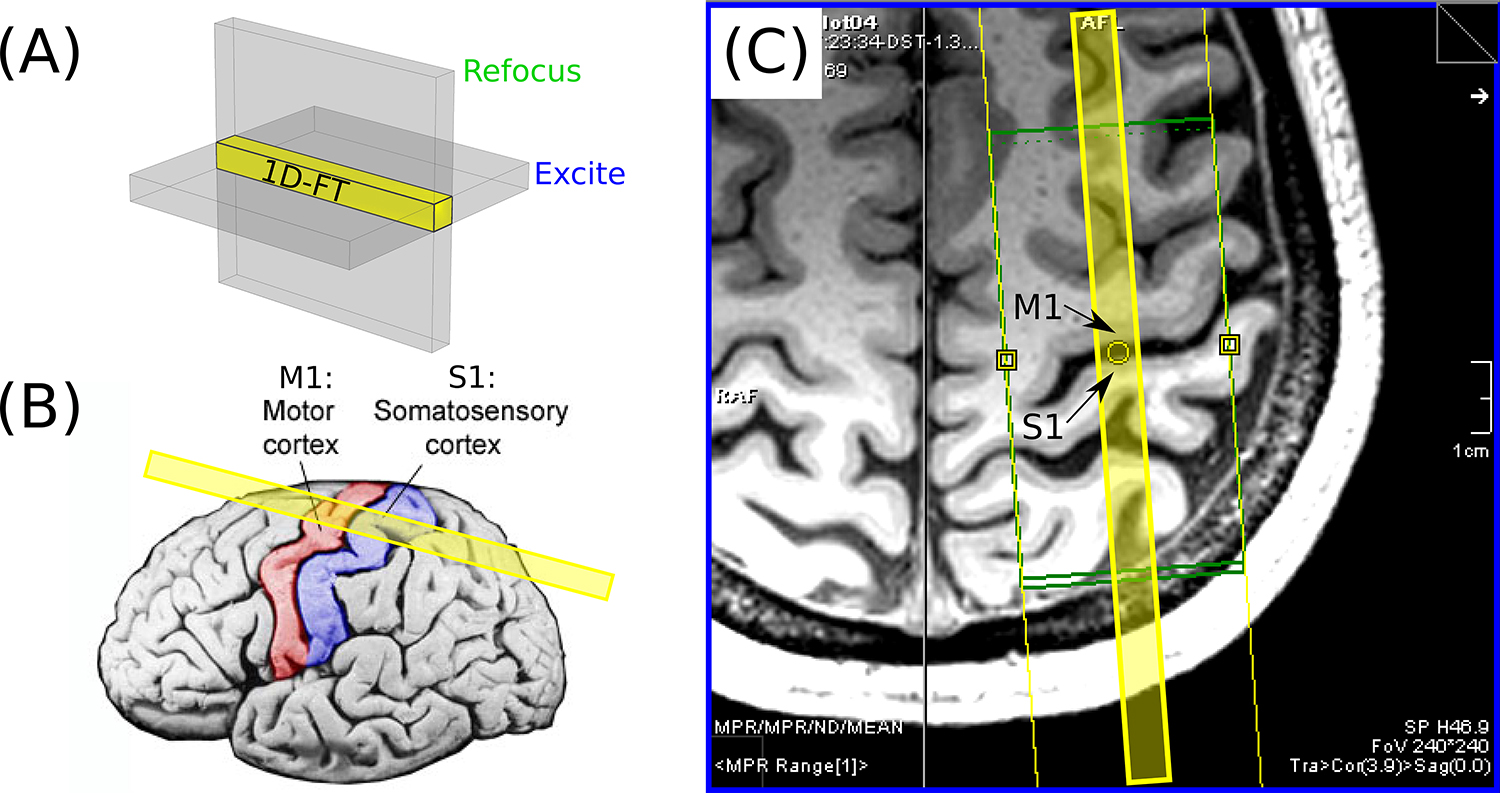
(A) An illustration of the concept underlying the spin-echo line-scan technique (2–4): by applying the slice-select gradients for the RF excitation and refocusing pulses orthogonally to one another, the MR signal arises from the column of spins within the intersection of the two slices, shown in yellow. This “line” only requires Fourier encoding in one direction and can thus be reconstructed via a 1D Fourier Transform (FT), with no need for phase encoding. (B) The prescription of the line shown with respect to a surface rendering of cortex, with M1 and S1 colored red and blue, respectively. (C) A slice through the 3D MPRAGE data of volunteer 1, as seen on the scanner console. Note the relatively flat patch of M1 and S1 adjacent to the yellow circle; the line (shown in yellow overlay) was prescribed to be as perpendicular as possible to cortex at this location.

To address the well-known spatial nonuniformity of the B₁⁺ transmit field in the adult-sized head at 7T (13,14), we employed the following calibration strategy in order to improve the accuracy of the flip angles (and thus maximize the SNR) for the line-scan diffusion acquisitions in the M1/S1 region of interest. By default, the scanner system sets the transmit reference voltage via a calibration measurement taken at isocenter, which could potentially introduce variability across subjects due to the variability in head positioning relative to isocenter. We therefore acquired a B₁⁺ map (15) for each volunteer and determined the reference voltage required for the region of interest at the beginning of each experimental session. For B₀ shimming, a ~5 cm shim box was centered on the region of interest and the Siemens “3DShim” procedure was performed 2–3 times in succession prior to the diffusion scans.

For the diffusion acquisitions, we used a custom implementation of the line-scan diffusion pulse sequence first described by Chenevert et al. (16). This is a single-line technique, with the slice-select gradients for the RF excitation and refocusing pulses applied orthogonally to one another—the line is then defined by the intersection of the two slices, as shown in Figure 2A, with the excitation slice selection roughly in the axial plane and the refocusing slice selection roughly in the sagittal plane. Trapezoidal diffusion-encoding gradients were placed on either side of the crushers bracketing the refocusing pulse (see Supporting Information Figure S–1 for the pulse sequence diagram and Supporting Information Figure S–2 for crushing considerations), making this a pulsed-gradient spin-echo (PGSE) diffusion sequence (17). The following parameters were common to all the line-scan diffusion acquisitions used in this study: TR/TE = 2000/50 ms, readout bandwidth = ~100 Hz/px, excitation/refocusing RF pulse duration = 2.0/2.5 ms with nominal FA = 90/180° and time-bandwidth product = 2.7/2.7, diffusion gradient duration/separation δ/Δ = 16.8/21.8 ms, and with the diffusion gradient amplitude G varied from 0 to 54.6 mT/m in order to achieve 21 b-values equally spaced from ~0 to 1000 s/mm². The voxel size along the line was either 250 or 500 μm with a 256 mm readout field of view and nominal line thickness of 3 mm, yielding voxel dimensions of either 0.25×3×3 or 0.5×3×3 mm³.

The number of diffusion gradient directions employed was either 3 (volunteers 1–7) or 13 (volunteers 3–6, 8). For the “3-dir” acquisitions, the first direction was chosen to be along the line, i.e., in the radial direction of cortex for a properly prescribed line. This was approximately in the anterior/posterior (A/P) direction for the patch of M1/S1 targeted for each volunteer in this study. The other two directions were chosen to be perpendicular to the first and to one another; these two tangential directions were approximately in the medial/lateral (M/L) and superior/inferior (S/I) directions. For the 500 μm scans, a single repetition was acquired in ~2 minutes, whereas for the 250 μm scans, four repetitions were acquired (~8 minutes) in order to match the SNR of the 500 μm scans. For the “13-dir” data, an additional 10 diffusion gradient directions were employed, distributed approximately uniformly on the unit hemisphere. For the 500 μm scans, a single repetition was acquired in ~9 minutes; for the 250 μm scans, it was typically only possible to acquire three repetitions (~27 minutes) within each session.

Data analysis

The line-scan signals were reconstructed and analyzed offline in MATLAB (MathWorks, Natick, MA, USA), given raw multi-coil data as input. A 1D FT was applied to transform the data from k-space into physical space (i.e., the “image” domain), using the fft function in MATLAB. For the 500 μm data, where a single repetition was acquired, a root-sum-of-squares (rSoS) operation was then applied in order to combine signals across receive-coil channels. For the 250 μm data, where multiple repetitions were acquired, complex-valued signal averaging was performed prior to coil combination. Before averaging across repetitions, however, it was necessary to account for the well-known shot-to-shot (i.e., TR-to-TR) phase variations in diffusion-weighted signals (18). The following phase-correction strategy was therefore implemented, exploiting the fact that the (within-TR) phase varies somewhat slowly across space (19–21): for each voxel, the complex-valued line-scan signal was first spatially averaged over a 33-voxel window (~8 mm in extent) centered on the voxel, and the phase of this average was subtracted from the phase of the voxel. This was done not only for each voxel and TR (and hence for each diffusion gradient direction and b-value), but also on a per-channel basis, thus removing any phase offsets between coil channels. Complex-valued averaging across repetitions was then performed on the phase-corrected data (22), followed by rSoS coil combination, resulting in a signal magnitude S for each voxel, direction and b-value.

For the 3-dir data, per-voxel apparent diffusion coefficients (ADCs) were derived for each direction individually. This was done by first fitting a straight line to the logarithm of the magnitude signal ln(S) versus b-value using linear regression (regress function in MATLAB); the resulting slope and intercept were then used to initialize nonlinear fitting to a monoexponential function via the Levenberg-Marquardt algorithm (lsqnonlin function in MATLAB), yielding the final estimate of the ADC for each voxel and direction. For the 13-dir data, the above MATLAB functions were used again, but now to fit the diffusion tensor (23,24) simultaneously to signals from all diffusion gradient directions. Linear fitting of ln(S) versus b-value and direction was used to derive an initial estimate of the diffusion tensor; this linear estimate was then used to initialize the Levenberg-Marquardt algorithm, yielding the final estimate of the diffusion tensor for each voxel. In all of the fits above, only the 19 b-values from 100 to 1000 s/mm² were used, in order to minimize potential contamination from perfusion effects (i.e., intravoxel incoherent motion, IVIM) at low b-values (25). Two metrics were derived from the diffusion tensor: (i) the fractional anisotropy or FA (26) and (ii) the radiality index $\left|\overrightarrow{\epsilon }\bullet \widehat{n}\right|$, defined only for gray matter voxels with FA ≥ 0.05 (5,6), where $\overrightarrow{\epsilon }$ is the principal eigenvector of the diffusion tensor and $\widehat{n}$ is the unit vector normal to the cortical surface—thus a radiality index of zero is indicative of a principal diffusion direction tangential to the cortical surface, whereas a value of one indicates a radial diffusion direction, perpendicular to the cortical surface.

Results

Figure 3 shows plots of ADC versus location for the 3-dir acquisitions from volunteer 1, at 500 and 250 μm radial resolution. The following observations hold at both resolutions but are more convincing at 250 μm resolution, for which eight voxels lie within S1, versus only three voxels at 500 μm: (i) In the upper or “superficial” part of S1, the ADCs are very similar for the three directions (standard deviation: 0.02 μm²/ms), suggestive of isotropic diffusion here. (ii) In deep S1, on the other hand, the ADCs are very different for the three directions (standard deviation: 0.24 μm²/ms), taking on the lowest value in the radial direction (along the line, roughly in the A/P direction, and shown in red). Although the (tensor-based) principal diffusion direction cannot be determined from the use of only three diffusion gradient directions, we can at least say that this observation of non-radial diffusion is consistent with the diffusion direction being primarily tangential in deep S1. (iii) Non-radial diffusion is also seen in the white matter adjacent to S1 and M1. (iv) Non-radial diffusion is not, however, observed in deep M1, allaying concerns that the results in deep S1 may simply be due to partial voluming of the adjacent white matter. (v) In this regard, note also the steep increase in ADCs as one goes from S1 to CSF, or from M1 to CSF, with values in CSF of ~2.5 μm²/ms (outside the range of the plots). The steepness of these curves suggests that very little partial voluming has occurred between gray matter and the adjacent CSF.

FIG. 3.

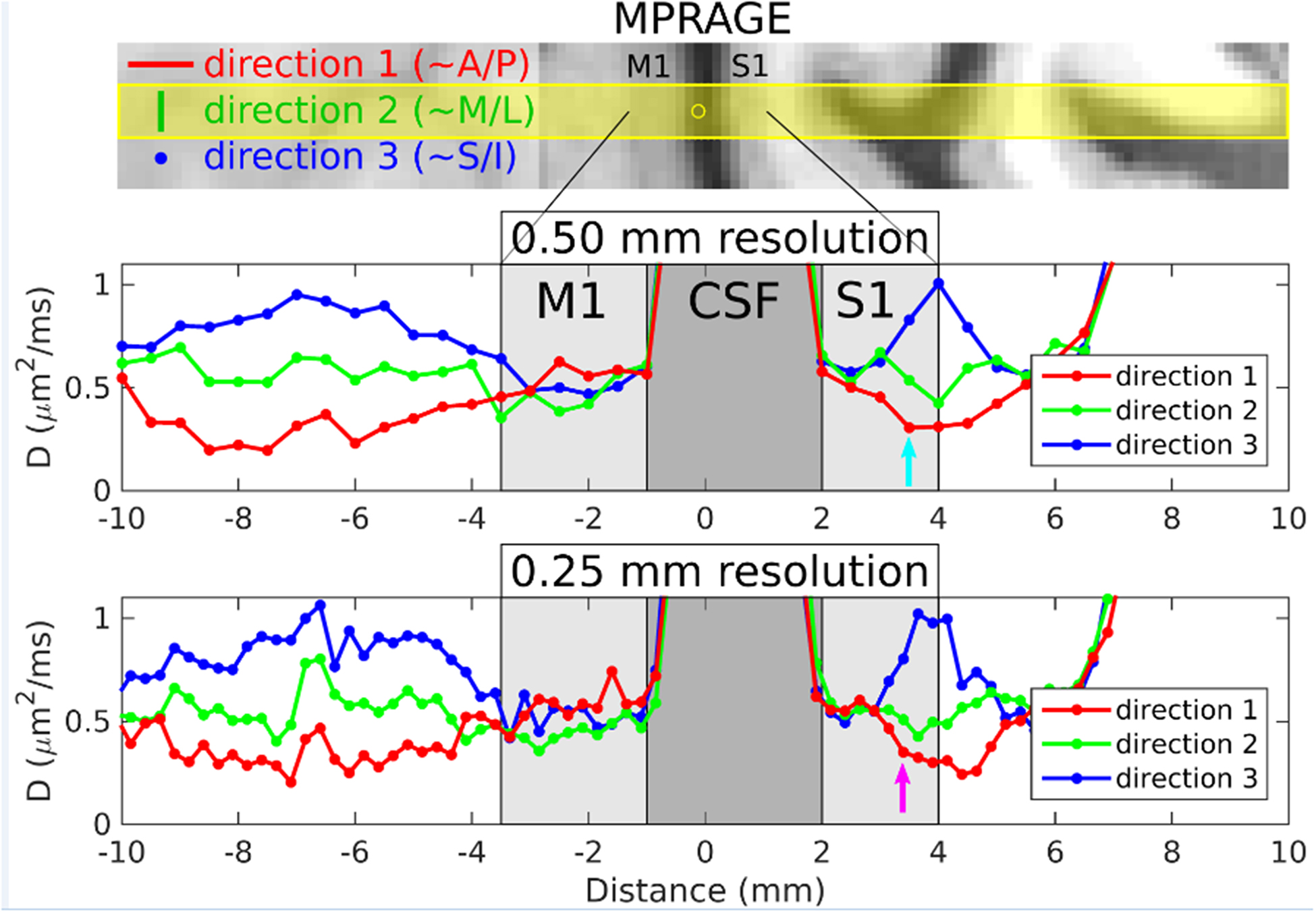
Results from volunteer 1 for the 3-dir acquisitions at 500 and 250 μm radial resolution. The top panel shows MPRAGE data resampled into the same orientation as the line-scan acquisitions. The prescribed line location and thickness are overlaid in yellow, with the yellow circle indicating the center point of the line (i.e., the origin in the plots below). For the three directions indicated (direction 1: ~A/P=anterior/posterior and radial to M1/S1 at this location, direction 2: ~M/L=medial/lateral and tangential to M1/S1 at this location, direction 3: ~S/I=superior/inferior and also tangential to M1/S1 at this location), plots of apparent diffusion coefficient D versus position along the line are shown in the middle and bottom panels for the 500 and 250 μm radial resolution acquisitions, respectively. M1 and S1 (light gray shaded regions) and central sulcus CSF (dark gray shaded region) were delineated based on the MPRAGE image in the top panel.

Figure 4 presents plots of signal magnitude versus b-value for both a 500 μm voxel and a 250 μm voxel in deep S1 in volunteer 1, confirming that the data are fit well with a monoexponential function, as would be expected given the b-value range of 100 to 1000 s/mm². Similar SNRs (of ~25) were seen in S1 and M1 at both 500 μm (one repetition) and 250 μm resolution (four repetitions), which we take as evidence of a successful strategy of phase correction and complex-valued averaging across repetitions (see Methods and Supporting Information Table S–1). Monte Carlo simulations reveal that this level of SNR results in a precision of ~10% in the estimation of ADCs (see Supporting Information Table S–2).

FIG. 4.

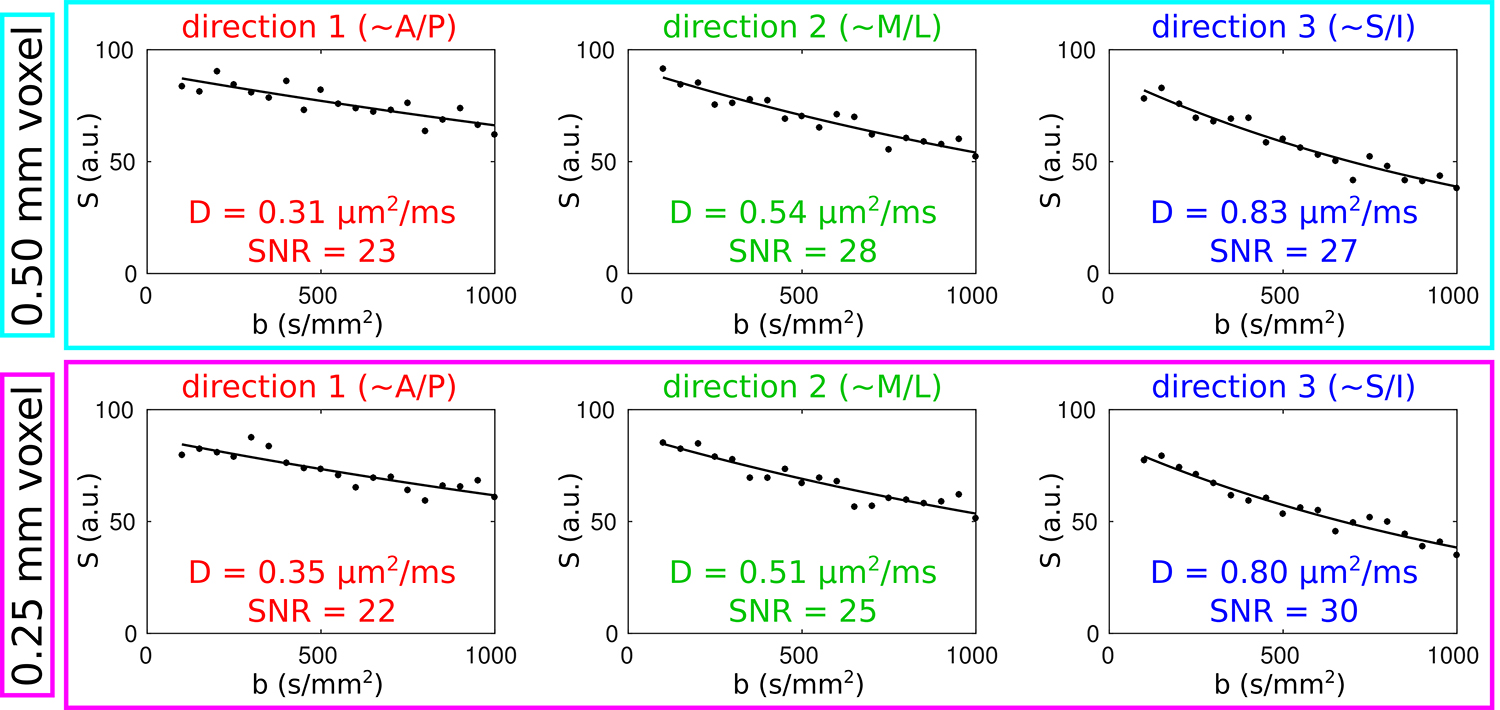
For the 500 μm voxel (in deep S1) indicated by the cyan arrow in Figure 3, the upper panel shows plots of signal magnitude versus b-value for each of the directions in the 3-dir acquisitions (dots=data points, curves=monoexponential fits) and the lower panel shows the corresponding plots for the 250 μm voxel indicated by the purple arrow in Figure 3. Along with the apparent diffusion coefficients D derived from the fits, SNR estimates are also shown; these were calculated by dividing the y-intercept of the fitted curves by the standard deviation of the residuals.

Figure 5 shows results from volunteers 2–7 for the 3-dir acquisitions at 250 μm radial resolution. In S1, the same overall pattern seen in volunteer 1 is also visible in each of these individuals: namely, very little evidence for anisotropy in superficial S1 and high anisotropy consistent with tangential diffusion in deep S1. We remark that this pattern can be readily appreciated without resorting to averaging across individuals or extensive averaging across different locations on the cortical sheet for a given individual.

FIG. 5.

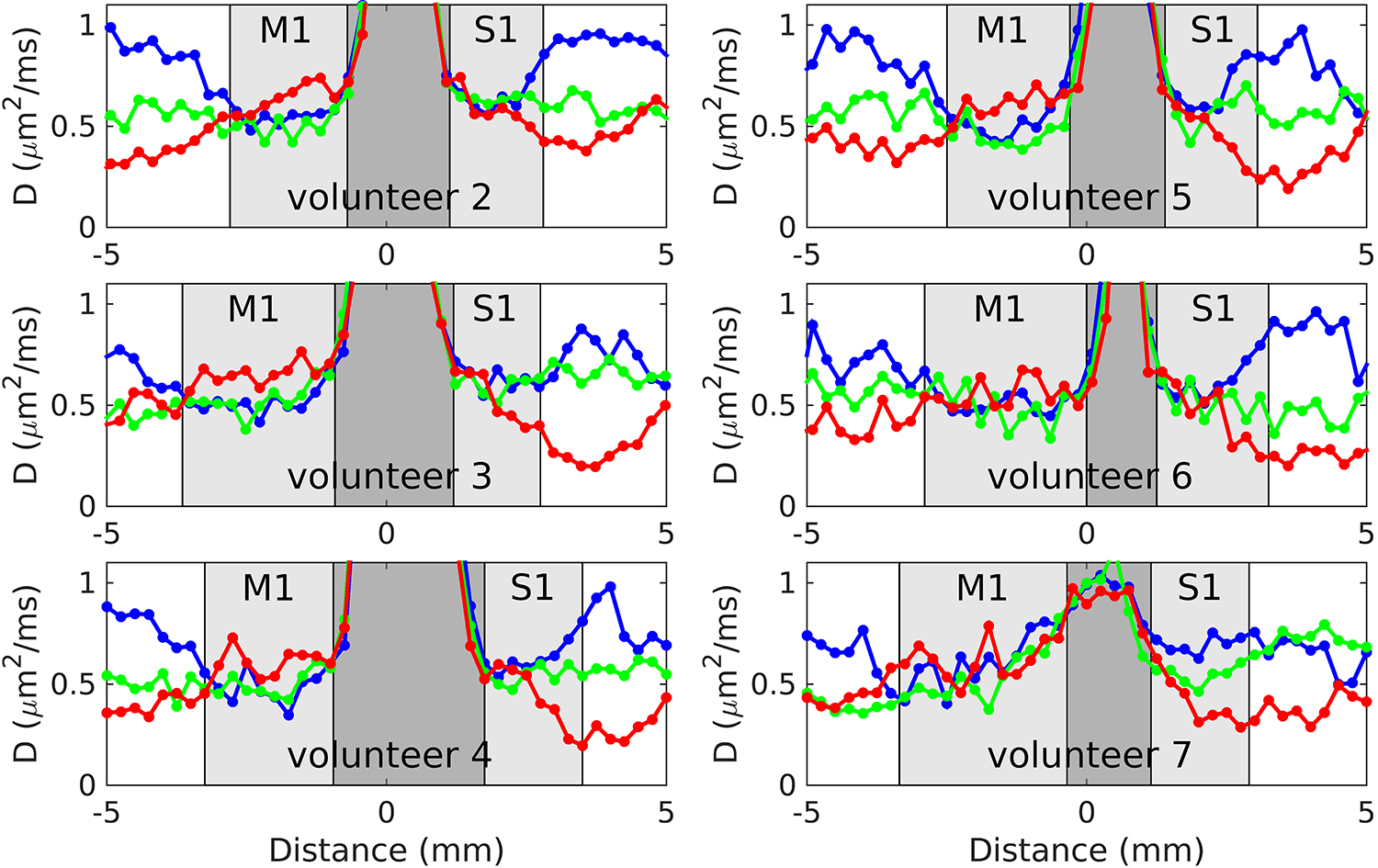
Plots of ADC versus location for volunteers 2–7, for the 3-dir acquisitions at 250 μm radial resolution. As in Figure 3, the red curves correspond to the diffusion gradient direction being in the radial direction, along the line and in roughly the A/P direction, whereas the green and blue curves correspond to two orthogonal diffusion gradient directions, tangent to cortex, in roughly the M/L and S/I directions, respectively.

Figure 6 shows plots of FA and radiality index versus location for volunteer 6, derived from the 13-dir acquisitions at 500 and 250 μm radial resolution. Note the rather low FA values (~0.1) in superficial S1 versus the much higher values (~0.4) in deep S1, where low values of the radiality index are seen, indicating a principal diffusion direction that is predominantly tangential. These results confirm what was qualitatively surmised from the 3-dir results above, which lacked the quantitative measures of anisotropy (i.e., FA) and directionality with respect to cortex (i.e., radiality index) now available. In M1, moderate FA values (~0.2) are seen, with high values of the radiality index at almost all cortical depths except near the boundaries, indicating a principal diffusion direction that is predominantly radial. Evidence for radial diffusion in M1 is much clearer here than in the 3-dir results, where it was somewhat harder to appreciate (see Figure 5), likely on account of M1 not having very high FA values, unlike deep S1, resulting in less striking differences in ADC across diffusion gradient directions. Similar results for FA and radiality index in M1 and S1 were obtained on the four other individuals for whom 13-dir data were acquired, as shown in Figure 7.

FIG. 6.

Results from volunteer 6 for the 13-dir acquisitions at 500 and 250 μm radial resolution. The top panel shows MPRAGE data resampled into the same orientation as the line-scan acquisitions, with the prescribed line overlaid in yellow and the yellow circle indicating the origin in the plots below. Plots of FA and radiality index versus position along the line are shown in black and purple, respectively, for the 500 μm (middle panel) and 250 μm (bottom panel) acquisitions. Note that the radiality index is only defined for gray matter voxels with FA ≥ 0.05.

FIG. 7.

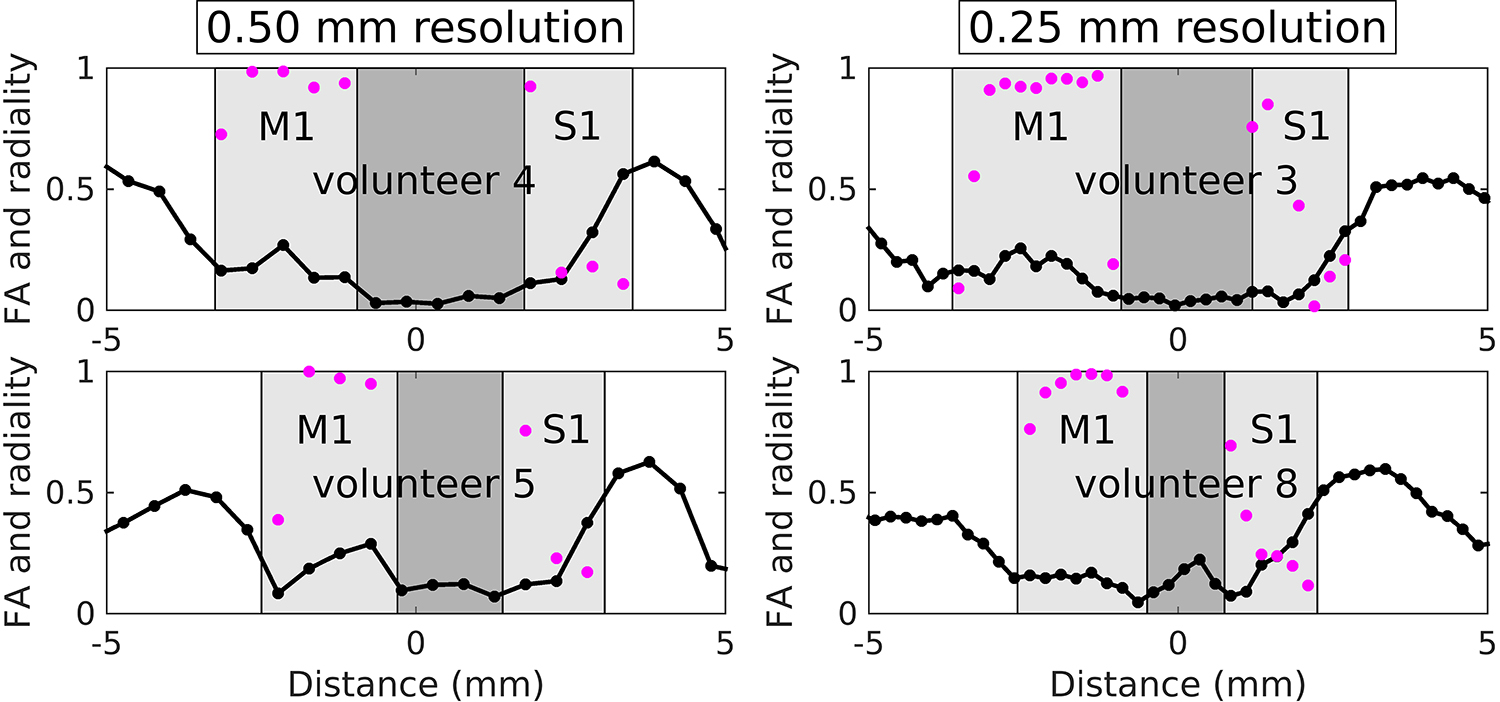
Plots of FA (black) and radiality index (purple) versus location, derived from the 13-dir acquisitions, for volunteers 4 and 5 (500 μm radial resolution) and volunteers 3 and 8 (250 μm radial resolution).

If we identify superficial cortical layers with the upper half of cortex and deep layers with the lower half, a statistical comparison between the two can be performed, as shown in Tables 1 and 2 for S1 and M1, respectively. Highly significant differences in FA and radiality were found for superficial versus deep S1 (Table 1), but not for superficial versus deep M1 (Table 2). While these statistics serve to reinforce the findings described in the previous paragraph, we caution against general use of the assumption that the superficial and deep layers strictly correspond to the upper and lower halves of cortex, since layer positions are known to vary with the cortical folding pattern (and possibly other factors), a point we return to in the Discussion.

TABLE 1.

Mean ± standard deviation of FA and radiality for superficial and deep S1 along with the p-values resulting from t-test comparisons of superficial versus deep FA and radiality. Data are from all 13-dir acquisitions at 500 and 250 μm radial resolution (volunteers 3–6 and 8).

	FA	radiality
superficial S1	0.11 ± 0.04	0.45 ± 0.28
deep S1	0.36 ± 0.16	0.12 ± 0.07
p-value	< 0.001	< 0.001

TABLE 2.

Mean ± standard deviation of FA and radiality for superficial and deep M1 along with the p-values resulting from t-test comparisons of superficial versus deep FA and radiality. Data are from all 13-dir acquisitions at 500 and 250 μm radial resolution (volunteers 3–6 and 8).

	FA	radiality
superficial M1	0.16 ± 0.06	0.87 ± 0.23
deep M1	0.17 ± 0.05	0.82 ± 0.23
p-value	0.56	0.52

Discussion

Our results are in agreement with prior in vivo studies reporting mostly tangential diffusion in S1 and mostly radial diffusion in M1 (5–8), but with far less concern that these observations may be attributed to partial-volume effects, given the high radial resolution (250–500 μm) used here. Going further than those studies, we show that the tangential diffusion in S1 originates from the deeper layers, with very little evidence of diffusion-tensor anisotropy in the superficial layers. These results are also in good agreement with the myelination patterns in S1 and M1 known from histology: in S1, dense bands of tangential myelinated fibers run through the deep layers but not the superficial ones, and in M1, radial myelinated fibers are prominent at most cortical depths (see Figure 8). We remark that diffusion-weighted signals are not specific to myelinated fibers—unmyelinated axon bundles have also been shown to result in robust diffusion anisotropy (27,28) and non-axonal processes such as those from dendrites and glia are further contributors to gray matter diffusion signals (29–31). Nonetheless, the agreement between our results and histology supports the idea that high-resolution diffusion signals may serve as a sensitive probe of in vivo cortical myeloarchitecture.

FIG. 8.

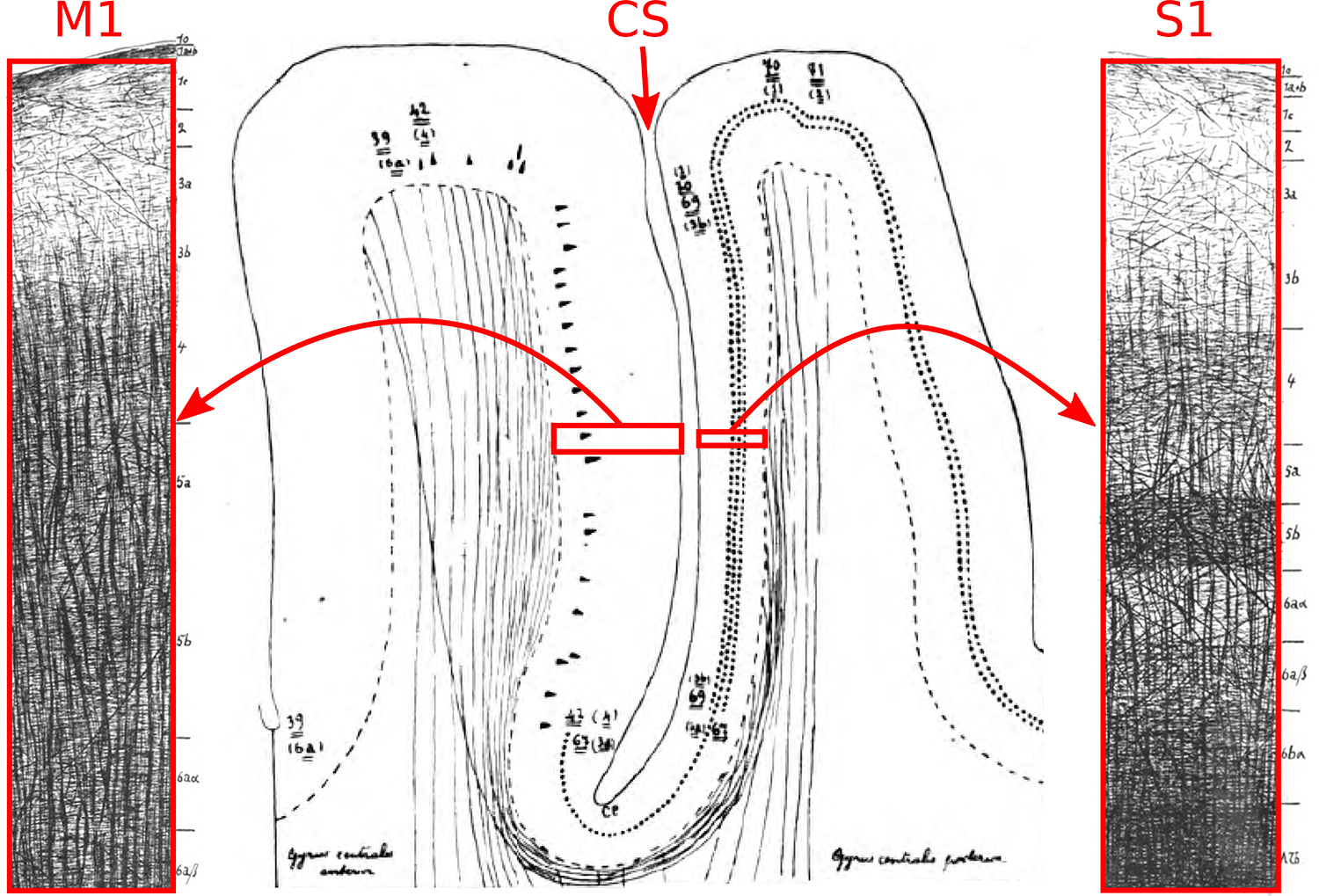
Myeloarchitecture of M1 and S1, adapted from the seminal monograph of Vogt and Vogt (9). In M1, note the dominance of radial myelinated fibers at most cortical depths, and in S1, note the pronounced tangential myelinated fibers in the deep layers. CS=central sulcus.

The benefits of high resolution might suggest the investigation of laminar MRI signals via ex vivo studies, since the extremely long scan durations that are possible here enable the acquisition of small voxels with adequate SNR, achieved primarily through the use of extensive signal averaging. Ex vivo diffusion studies are challenging, however, since the fixation process can lead to a substantial reduction in both (i) T₂ (32,33), leading to a loss of signal relative to the use of the same TE in vivo, and (ii) ADC (32,34), requiring the use of much higher b-values than in vivo, which typically means a significant increase in TE to accommodate the increase in diffusion weighting, and thus a further loss of SNR. Interestingly, ex vivo studies of S1 have shown either an absence of tangential diffusion (35) or much less tangential diffusion than in vivo (6), contradicting the general belief that diffusion directionality is preserved well between ex vivo and in vivo studies. Previously, this discrepancy could perhaps have been dismissed as being due to partial voluming of the white matter adjacent to S1 in low-resolution in vivo data, but we see very little to suggest significant partial-volume effects in our high-resolution data, given the steep ADC transition from cortex to CSF (see Figure 3 and accompanying text) and the lack of evidence for tangential diffusion in deep M1 (see radiality index plots in Figure 6).

In the developing brain, cortex typically exhibits radial diffusion (36,37), as do the majority of cortical areas in the adult brain (6). Thus it is interesting to highlight the rare instances when this “rule” is violated, as it seems to be in deep S1. We note that the diffusion direction here appears to be approximately in the S/I direction (see Figures 3 and 5). This direction is roughly orthogonal to the head-foot axis of the somatotopic representation of the body (i.e., the “homunculus”) in S1, consistent with an interpretation of high connectivity within body part (e.g., within the somatotopic representation of the hands). This particular pattern of deep-layer connectivity likely has implications for the neural computations executed within this cortical area, the elucidation of which could ultimately lead to a better understanding of the functionality of S1 and its role in the perception of touch.

We now return to a point raised in the Introduction, namely that line-scan techniques might be the method of choice for laminar MRI studies. One apparent limitation of this technique is that it is difficult to achieve very thin lines, just as it is difficult to achieve thin slices in 2D acquisitions, since doing so while attempting to maintain slice-selection profiles typically requires the use of very long RF pulses, which are undesirable due to the possibility of significant spin relaxation effects during the pulses. However, if the line is prescribed such that it is perpendicular to the cortex in the region of interest, this limitation becomes inconsequential since it is not just acceptable, but in fact desirable (from an SNR perspective), to have large voxel size in the tangential directions, along which cortical architecture varies quite slowly. In the radial direction, along which cortical architecture varies rather rapidly, the requirement of small voxel size is met by simply increasing the readout gradient area to a suitably high value. Thus line-scan acquisitions naturally lend themselves to the anisotropic voxel geometry best suited for laminar MRI (see Figure 1). Furthermore, by virtue of being a single-shot technique, relatively simple phase-correction schemes can be employed for line-scan diffusion acquisitions, as performed here prior to complex-valued signal averaging across repetitions (see Methods), versus the far more complicated schemes required for multi-shot methods (18,38). We also note that although the most traditional line-scan methodology involves the use of perpendicular excitation and refocusing slice-select gradients (2–4), line scanning may also be performed through the use of other techniques such as outer volume suppression (39,40), where saturation bands are added to 2D slice selection in an attempt to null signal from spins outside the desired line. Indeed, despite the difficulty of completely suppressing unwanted signal with this strategy, line-scan techniques based on outer volume suppression have found use in laminar fMRI studies of rodents in small-bore scanners (41–43).

EPI has largely superseded line scanning in modern diffusion studies, given its much higher spatial coverage per unit scan time^†. However, even if it were feasible to acquire EPI data with comparable resolution to our line scans (0.25×3×3 mm³) without making the TE prohibitively long, it is highly improbable that multiple lines of these EPI voxels would intersect cortical patches orthogonally—a requirement if one is to minimize partial-volume effects in laminar studies—given the substantial curvature and folding pattern of human cerebral cortex. Thus it is unclear that the increased spatial coverage provided by EPI would actually be of any real benefit for laminar MRI at high radial resolution—a point that also applies to any other Cartesian sampling/reconstruction scheme such as the use of anisotropic 3D FLASH voxels for laminar fMRI (46) or even the use of multiple, parallel lines within the line-scan framework (47–49). One could, however, envision an extension of our approach employing multiple, non-parallel lines, with each line independently prescribed with respect to a separate patch of cortex. This could substantially increase the efficiency of our acquisition scheme, but would likely require considerable offline planning on a previously-acquired anatomical scan, with care taken to avoid having any lines intersect at a location of interest, disrupting the magnetization there. Moreover, incidental magnetization transfer effects (50–52) would also have to be assessed.

Field strengths of 7T and above are not necessarily seen as being advantageous for in vivo diffusion MRI of the human brain from an SNR perspective, given the combination of shorter T₂ values at higher field and the long TEs typical of EPI-based diffusion acquisitions (53). These long TEs result not only from the time required to accommodate diffusion-encoding gradients, but also from the time required for the EPI readout. The readout time for a comparable line-scan acquisition can be considerably shorter, however, allowing a substantial reduction in TE for the same diffusion encoding. For the 50 ms TE (and 2 s TR) used here, we estimate a doubling of SNR at 7T versus 3T, based on the simulations of Uğurbil et al. (see ref. #54, Figure 20). This can be translated into a doubling of the radial resolution per unit scan time at 7T versus 3T, for a fixed SNR. These simulations assume similar gradient and RF coil performance at the two field strengths, however—an assumption that may not hold in practice.

The laminar diffusion patterns observed in this study were consistent across subjects and were conspicuous without averaging data across different locations on the cortical sheet—a common practice in studies of the cortical depth dependence of MR signals (55,56). This practice can be problematic, however, since layer positions are known to vary with the cortical folding pattern, with the granular layer shifted towards the pia mater in gyral crowns and towards the white matter (i.e., in the opposite direction) in sulcal fundi (57); averaging across cortical locations could therefore lead to the undesired mixing of signals across layers. Even after accounting for this shift (58), Hinds et al. (59) have reported a systematic, residual variation in the depth of the stria of Gennari in human V1 in the direction of the eccentricity coordinate of the retinotopic representation (roughly the anterior-to-posterior direction). This suggests that factors other than cortical folding may influence the positions of layers, complicating the prediction of the layer positions from cortical geometry alone. By avoiding averaging across cortical locations, the above issues—which are not only rather complicated but also not fully understood—can be sidestepped.

The astute reader may have noticed that, with the 250 μm results in hand, one can often go back and look at the 500 μm results and identify many of the features seen in the higher-resolution data. Why then should one go through all the effort needed to acquire the higher-resolution data? The problem here is the implicit expectation that an anatomical feature will go from being barely visible at 500 μm to clearly visible at 250 μm—a rather unrealistic expectation even for a two-fold improvement in resolution. In our opinion, the true benefit of going to higher resolution comes not from the sudden appearance of a feature, but rather from an increased confidence that the observed feature is real and not attributable to the various sources of noise or artifact inherent to MR data. In our case, if we just had data at 500 μm radial resolution, where only about three data points lie clearly within S1 in volunteer 1 (see Figure 3) and volunteer 6 (see Figure 6), it is not clear how confidently we could have made statements regarding the depth dependence of diffusion signals in this cortical area; at 250 μm radial resolution, we lacked no such confidence. Indeed, one wonders if there are other, perhaps quite subtle, features in our 250 μm data that we are failing to appreciate as being real without the benefit of data with 125 μm radial resolution.

Subject motion can of course be a concern for any in vivo, high-resolution scans with restricted field of view, such as the line-scan acquisitions described here. For the present study, our strategy with regard to head motion was simply to recruit experienced volunteers whose prior scans had shown very little motion artifact. A strategy such as this, while feasible for preliminary investigations (see also Supporting Information Figure S–3), is obviously quite restrictive and limits the ability to draw upon volunteers from the population at large. It is our hope that techniques for prospective motion correction (60), such as those using external trackers (61–63) or MR-based navigators (64,65), will ultimately prove useful in this setting.

In this study, we did not use b-values above 1000 s/mm², keeping us in the regime of validity for both monoexponential fits of signal versus b-value and diffusion-tensor fits of signal versus b-value and diffusion gradient direction. At higher b-values, kurtosis (66,67) or biexponential (68,69) signal models may be more appropriate and the laminar variation of quantities derived from fits to these models would likely be of interest, if such data could be acquired with adequate SNR. Increasing the number of diffusion gradient directions to thirty or more would also enable the measurement of orientation distribution functions (ODFs) with more angular detail than that provided by the single tensor model, e.g., via the use of spherical deconvolution (70) or persistent angular structure (PAS) algorithms (71). This additional detail comes at the cost of increased scan time, but may help clarify the situation in places where radial and tangential fibers cross and are in equal abundance, as may be the case in superficial S1, where we observed very low diffusion-tensor anisotropy. The signal models, or representations (72), above stand in contrast to biophysical models, which explicitly reference some specific aspect of tissue microstructure, e.g., axon diameter in the AxCaliber framework (73). However, any potential increase in specificity often comes at the expense of sensitivity.

Although the argument for anisotropic voxel geometry was made with cortical gray matter in mind, similar considerations may also hold for superficial white matter, which lies immediately below the cortical surface. Inspection of Figures 6 and 7 reveals consistently higher FA values for the white matter adjacent to S1 compared to the white matter adjacent to M1, perhaps reflecting differences in the ratio of tangential U-fibers (74) to radial fibers entering or exiting cortex. Again, the high-angular-resolution methods referenced in the previous paragraph may be required in order to better understand the fiber crossings here.

In closing, we have demonstrated the utility of line-scan acquisitions for investigating the depth dependence of in vivo diffusion signals in human cerebral cortex. Although our focus was on S1 and M1, this technique could be applied to any cortical area containing a sufficiently flat patch, and perhaps to the adjacent white matter as well. The method could also be modified to be sensitive to other MR contrast mechanisms such as longitudinal or transverse relaxation, e.g., through the use of multiple TRs or TEs to enable the measurement of laminar T₁ or T₂ values, respectively. Given the sensitivity of these relaxometry measures to myelin and iron content, combining them with diffusion-based metrics may ultimately provide a more complete MR-based description of laminar architecture, which could aid the noninvasive delineation of cortical layers and areas (75,76). The ability to study the internal structure of cortex in the living human brain would also open up opportunities to study changes over time, due to development, plasticity or aging, in health or in disease.

Supplementary Material

supp info

SUPPORTING INFORMATION FIG. S-1. Pulse sequence diagram for the line-scan diffusion acquisitions used in this study, generated by the sequence simulator in “POET”, a part of the Siemens “IDEA” pulse sequence programming environment. Note in particular that the slice-select gradient for the RF excitation pulse is orthogonal to that for the refocusing pulse (in the z- and y-directions, respectively, in this example), with the “line” then defined by the intersection of these two slices. Note also the absence of phase-encoding gradients, since frequency encoding in the readout direction (the x-direction in this example) suffices to spatially encode signals for such 1D acquisitions. See Methods for pulse sequence parameter values.

SUPPORTING INFORMATION FIG. S-2. Although phase-encoding (PE) gradients are not typically employed in line-scan acquisitions, they can be incorporated in order to generate a 2D-encoded image, which can help characterize certain aspects of signal behavior. For example, a 2D-encoded version of the line-scan sequence was used here to help calibrate the setting of crusher gradients. (A) When the area of the crusher gradients is too small and the PE gradients are played out between the excitation and refocusing pulses, an artifact can be seen at PE isocenter (note that the PE isocenter, indicated by the labeled axes shown on the right, does not in general correspond to the center of the image). This artifact is caused by the refocusing pulse undesirably tipping some longitudinal magnetization into the transverse plane—an effect that becomes increasingly pronounced the further the excitation and refocusing flip angles are from their ideal values of 90° and 180°, respectively (as a result of either RF transmit voltages being set inappropriately or non-rectangular slice-selection profiles, or both). Since the PE gradients occur prior to the refocusing pulse, this artifactual transverse magnetization is not phase-encoded, and thus manifests as a line at PE isocenter. On the other hand, the non-artifactual transverse magnetization directly following the excitation pulse is phase-encoded and manifests as signal at the desired location, at the center of the image. (B) When the crusher gradient area is set to an appropriately high value, the artifact is “crushed” away but the desired signal remains. The pulse sequence parameters used here were mostly the same as those described in the Methods, but with the diffusion gradients turned off, 32 PE steps employed and 2×2 mm² in-plane voxel size (256×64 mm² field of view). The crusher gradient area was set to either (A) 31.3 or (B) 62.6 ms·mT/m. The latter value was chosen for all line-scan diffusion acquisitions in this study, since it was found empirically to largely eliminate the above artifact in each volunteer while only making a small contribution of ~1 s/mm² to the overall b-factor. (C) Same as (B), but windowed normally, whereas the window levels in (A) and (B) were chosen with artifact conspicuity in mind. Note that practically no signal is seen in the regions above and below the prescribed line—this is not always the case with line-scan methods that attempt to suppress the signal outside the line via the use of saturation bands (i.e., “outer volume suppression”), as opposed to the technique of orthogonal excitation and refocusing slice selection used here.

SUPPORTING INFORMATION TABLE S-1. As a validation of our strategy of phase correction and complex-valued averaging across repetitions (see Methods), a comparison of SNR at 500 versus 250 μm radial resolution was sought, with and without averaging and phase correction at the latter resolution. Note that only one repetition was acquired for the 500 μm resolution data, and thus averaging across repetitions was obviously not applicable for this data. Phase correction was therefore also unnecessary here since a root-sum-of-squares (rSoS) coil combination was performed, which discards phase. For gray matter voxels in volunteer 1, this resulted in an SNR of ~23 (first row of the table below). For the 250 μm resolution data, although four repetitions were acquired, when only one repetition was analyzed (with no averaging or phase correction, as with the 500 μm data), the SNR was approximately halved (second row), as would be expected given that SNR scales linearly with voxel volume (recall that the voxel size in the radial direction is proportional to voxel volume here since the same line width of 3 mm was used for both radial resolutions). Complex-valued averaging of the 250 μm resolution data across the four repetitions should in principle yield the same SNR as the 500 μm resolution data with one repetition, since SNR also scales with the square root of the data acquisition time. Without phase correction prior to complex-valued averaging, however, the SNR drops further (third row), due to the well-known shot-to-shot phase variations in diffusion-weighted signals. With phase correction, on the other hand, the expected recovery of SNR is realized, with similar levels in the four-repetition 250 μm data (fourth row) and the single-repetition 500 μm data (first row). The SNR means and standard deviations reported below are across all M1 and S1 voxels in volunteer 1, and across all diffusion gradient directions in the 3-dir acquisition scheme.

SUPPORTING INFORMATION TABLE S-2. Results from Monte Carlo simulations used to investigate the precision of apparent diffusion coefficient estimates D at various levels of SNR, given the same b-values used in the analyses of our in vivo data (i.e., 19 b-values equally spaced between 100 and 1000 s/mm²). A value of D = 0.6 μm²/ms was taken as ground truth in the simulations, and five different SNR levels ranging from 5 to 80 were studied. For each SNR level, 30,000 trials were performed; in each trial, a different instantiation of Gaussian random noise (with the standard deviation chosen to yield the desired SNR) was added to the noise-free monoexponential decay curve and D was estimated with the same procedure used for the in vivo data (see Methods). The mean and standard deviation across the trials is reported below. Note that for the SNR level of 20 (which is close to the levels observed in our in vivo data), the standard deviation of D is approximately 0.06 μm²/ms, corresponding to a coefficient of variation (and thus precision) of ~10%.

SUPPORTING INFORMATION FIG. S-3. The top panel shows the MPRAGE data for volunteer 1, the middle panel shows the signal intensity (in arbitrary units) at the lowest b-value (~0) for each repetition of the 250 um acquisitions, and the bottom panel shows the signal difference between subsequent repetitions. These plots suggest that very little motion occurred across the repetitions.