Patient-Adaptable Intracranial Pressure Morphology Analysis Using a Probabilistic Model-Based Approach

Abstract

Objective.

We present a framework for analyzing the intracranial pressure (ICP) morphology. Analyzing ICP signals is challenging due to the non-linear and non-Gaussian characteristics of the signal dynamics, inevitable corruption with noise and artifacts, and variations in the ICP pulse morphology among individuals with different neurological conditions. Existing frameworks make unrealistic assumptions regarding ICP dynamics and are not tuned for individual patients.

Approach.

We propose a dynamic Bayesian network (DBN) for automated detection of three major ICP pulsatile components. The proposed model captures the non-linear and non-Gaussian dynamics of the ICP morphology and further adapts to a patient as the individual’s ICP measurements are received. To make the approach more robust, we leverage evidence reversal and present an inference algorithm to obtain the posterior distribution over the locations of pulsatile components.

Results.

We evaluate our approach on a dataset with over 700 hours of recordings from 66 neurological patients, where the pulsatile components have been annotated in prior studies. The algorithm obtains an accuracy of 96.56%, 92.39%, and 94.04% for detecting each pulsatile component on the test set, showing significant improvements over existing approaches.

Significance.

Continuous ICP monitoring is essential in guiding the treatment of neurological conditions such as traumatic brain injuries. An automated approach for ICP morphology analysis takes a step toward enhancing patient care with minimal supervision. Compared to previous methods, our framework offers several advantages. It learns the parameters that model each patient’s ICP in an unsupervised manner, resulting in an accurate morphology analysis. The Bayesian model-based framework provides uncertainty estimates and reveals interesting facts about ICP dynamics. The framework can be readily applied to replace existing morphological analysis methods and support the application of ICP pulse morphological features to aid the monitoring of pathophysiological changes of relevance to the care of patients with acute brain injuries.

1. Introduction

Intracranial pressure (ICP) is one of the most important physiological variables for guiding therapeutic decisions in the care of patients with acute brain injuries. Continuous ICP monitoring is warranted when treating patients with severe brain injuries in acute care settings and it can last several days when a patient’s status is the most fragile and dynamic. ICP signal contains rich information related to a patient’s pathophysiological status. The most straightforward use of such information is to detect and treat extremely high brain pressure to prevent life-threatening conditions such as brain herniation. In fact, this use of ICP monitoring is a prevailing one and well-established. However, considering that the clinically accepted practice of ICP monitoring is still highly invasive requiring surgically drilling the skull to place sensors, ideally more useful information for managing patients should be derived from ICP signals.

Physiologically speaking, ICP results from interactions among multiple physiological systems: cardiovascular, respiratory, cerebral vascular, cerebrospinal fluid, and brain tissues. ICP signal thus has a complex form and contains multiple distinct and interacting components (or sub-peaks). Due to its cardiovascular origin, ICP signal is pulsatile and in sync with heart beats. In addition, an ICP signal contains an oscillatory component that reflects influence from respiratory activities. At an even lower frequency spectrum, an ICP signal can show slow waves that exist in many other neurophysiological signals. Therefore, there is a need for biomedical engineers and data scientists to develop more advanced algorithms to extract additional information to support clinicians make the best use of ICP monitoring in their clinical decisions.

There are many potential routes to analyze an ICP signal as evidenced in published studies (Hornero et al., 2005, 2007; Hu et al., 2007; Holm and Eide, 2008; Hu et al., 2008a; Eide et al., 2012; Santamarta et al., 2012; Calisto et al., 2012; García et al., 2013; Xu et al., 2013; Lee et al., 2015; García et al., 2018; Megjhani et al., 2019; Park et al., 2019; Hüser et al., 2020). Among these approaches, one particular area worth further investigation is characterization of ICP pulse waveform. Our previous works have shown that quantification of ICP pulse waveform morphology can predict ICP elevation (Hu et al., 2010b), detect distal cerebral arterial changes (Hu et al., 2009, 2010a; Asgari et al., 2011a,b,c, 2012, 2013; Connolly et al., 2015; Liu et al., 2019, 2020), recognize false ICP alarms (Scalzo and Hu, 2013; Scalzo et al., 2012c), and determine the external ventricular drain (EVD) weaning outcome (Hu et al., 2012a; Arroyo-Palacios et al., 2016). In these studies, we developed and used an ICP pulse morphological analysis algorithm – called morphological clustering and analysis of intracranial pressure (MOCAIP) (Hu et al., 2008c; Scalzo et al., 2009, 2010, 2012a).

MOCAIP proceeds by first detecting individual ICP pulses, clustering them to find a representative pulse from the largest cluster, detecting a combination of landmarks of this representative ICP pulse (local optima and inflection points), and then designating the locations of up to three sub-peaks. Through this process, metrics that quantify the morphology of the pulse can be systematically computed. However, our experience has revealed weaknesses of the algorithm that result in sometime excessive needs of manually correcting the positions as returned by MOCAIP. To further translate the past discoveries enabled by MOCAIP through a more automated process to enable its practice in a real-world setting, it is imperative to address weaknesses of MOCAIP and this is the objective of this study.

In this work, we propose a framework based on dynamic Bayesian networks (DBNs) for ICP morphology analysis. Our framework adopts the first stages of MOCAIP as the data preprocessing step and offers several improvements: (1) it uses a principled way for modeling the distribution of ICP components based on data instead of simply making a Gaussian assumption, (2) it models the dynamics and temporal changes of ICP which were not considered in the MOCAIP framework, (3) it allows the ICP components not to necessarily be in the major ICP pulse landmarks, improving over possible missed detections, (4) it deploys a statistically principled optimization objective for finding the maximum a posteriori locations of ICP components, and (5) it allows the framework parameters to adapt for individual patients.

The paper is organized as follows. We begin by reviewing some preliminary concepts and notation in Section 2 on dynamic Bayesian networks and inference of state variables in DBNs using particle filtering and motivate the use of evidence reversal for the problem considered in this work. In Section 2, the modules of the proposed framework including data pre-processing steps and development of the temporal model are described. The framework is then tested on more than 700 hours of data and the performance is compared with MOCAIP as well as a clustering approach inspired by the work of (Lee et al., 2015). The experimental results are presented in Section 4, followed by careful evaluation of the advantages and shortcomings of the proposed approach. We conclude the paper by summarizing the framework and discussing several directions for future work.

2. Preliminaries

2.1. Dynamic Bayesian networks

A dynamic Bayesian network, or DBN, is a temporal probabilistic model that is used to represent a complex model of sequential data. DBNs are used in a wide range of applications such as finance (Giudici and Spelta, 2016), seismic monitoring (Riggelsen et al., 2007; Moore and Russell, 2017), and physiological monitoring (Yang et al., 2010). To construct a DBN, one must specify a set of variables, the conditional dependencies between them, and their evolution over time. In particular, a DBN models a partially observed Markov process with hidden variables {X_n}_n≥1, observed variables {Y_n}_n≥1, and parameters θ across steps n using a probabilistic model defined as follows

$$X_1~p(X_1;\theta ),$$

$$X_n|X_{n-1}~p(X_n|X_{n-1};\theta ),$$

$$Y_n|X_n~p(Y_n|X_n;\theta ),$$

where p(X₁; θ ) is the prior distribution over the hidden (state) variables, p(X_n|X_n−1; θ) is the transition (propagation) model, and p(Y_n|X_n; θ) is the sensor (observation) model.¹ The transition model represents the temporal evolution of hidden variables by specifying the conditional dependencies between hidden variables across time steps. The sensor model defines the conditional probability of receiving a particular observation given a certain hidden variable.

The success of probabilistic model-based approaches has been established in several areas of healthcare (Williams et al., 2006; Heldt et al., 2006). Model-based methods have shown to be more robust in the presence of noise and artifacts, which are common in physiological applications, compared to model-free methods (Aleks et al., 2009; Chen et al., 2016). Furthermore, model-based methods are generally more data-efficient making them well-suited for physiological applications where data are often scarce.

In this work, we use a DBN to specify a dynamical model of the ICP pulsatile components that captures the uncertainty due to temporal evolution and observation noise and adapts the model for individuals through learning the static variables in an unsupervised manner. We choose a DBN since it can represent non-linear and non-Gaussian dynamics compared to alternative dynamical models such as linear dynamical systems with Gaussian noise. After specifying the model, the three major pulsatile components are identified by solving a statistical inference problem described in the following section. The experimental results presented in Section 4 demonstrate improved performance compared to previous model-free methods.

2.2. Latent variable inference via particle filtering

We are interested in computing the filtering distribution p(X_n|Y_1:n), i.e. the posterior distribution of the current hidden variables given all the information provided by the observed variables up to the present. Exact filtering in complex systems with non-linear and non-Gaussian dynamics is generally intractable. Particle filtering methods, introduced by Gordon et al. 1993, are a popular class of algorithms used to obtain a numerical approximation of the posterior distribution using weighted samples, or particles. More specifically, particle filter first samples K particles ${\{x_1^k\}}_{k=1}^K$ from the prior distribution and initiates particle weights to be identical. Then the following update cycle is repeated for each time step:

1. Particle propagation: Each particle k is propagated to the following time step by sampling the next particle $x_{n+1}^k$ conditioned on the current particle $x_n^k$ using the transition model, i.e. $x_{n+1}^k~p(.|x_n^k;\theta )$.²

2. Weight assignment: Each particle k is weighted by the likelihood it assigns to the new evidence $p(y_n|x_n^k;\theta )$.

3. Resampling: Particles are resampled proportional to their weights and new particles with identical weights are generated.

Without the resampling step, particle filter will generate a set of particles where only a few retain significant weights. As a result, the effective sample size (ESS) for representing the posterior distribution dramatically drops. Conventionally, particles are resampled proportional to their weights only at time steps where ESS falls below a certain threshold. Subsequently, samples with negligible weights are likely to be discarded and particles with large weights are likely to be duplicated, resulting in more samples in high probability regions. More advanced resampling techniques have been extensively researched, see (Li et al., 2015) for an overview.

2.3. Evidence reversal

Although sequential Monte Carlo algorithms such as particle filtering often provide accurate approximations to the posterior distribution, if the DBN has certain characteristics the samples may diverge from the reality as more observations are received. For example, consider the case where the observation model p(Y_n|X_n) is fairly accurate, i.e. any realized observation Y_n = y_n has high probabilities for some values of X_n and very low probabilities for the others. If the transition model is fairly inaccurate, the weighting process assigns extremely low weights to most particles which are incompatible with the observations. In this scenario, only a few samples approximate the posterior distribution approximation resulting in large approximation error. This happens despite the fact the sensor is accurately providing observations (Figure 1(a)).

Figure 1:

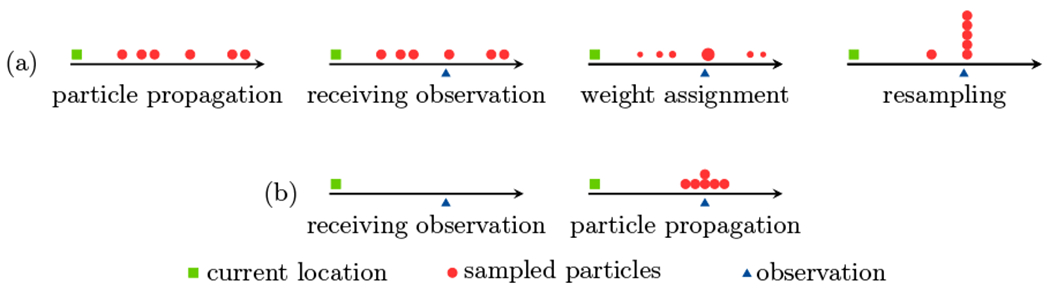
An example demonstrating sample impoverishment when the transition model exhibits high uncertainty but the observation model is fairly accurate. The particle filtering steps of propagation, weight assignment, and resampling, applied to a standard DBN, are shown in (a). As a result of the inaccurate transition model, most particles are far from the observation and are assigned small weights. During resampling, the particles with small weights are naturally eliminated resulting in a reduction in sample diversity. Particle filtering applied to a DBN with evidence reversal is shown in (b). Here, particles are sampled after the observation is received and therefore, more diverse particles compatible with the observation are generated.

Evidence reversal (ER), proposed by Kanazawa et al. 1995, addresses this problem by reconstructing the DBN so that the observation Y_n becomes the ancestor of X_n. ER ensures samples to be compatible with the observations in every time step. Figure 2 illustrates an schematic diagram of the ER transformation on a DBN. We can easily see that the two networks are equivalent by writing the joint distribution of X_n and Y_n conditioned on X_n−1 in both networks:

$$p(X_n,Y_n|X_{n-1})=p(X_n|X_{n-1})p(Y_n|X_n)=p(Y_n|X_{n-1})p(X_n|X_{n-1},Y_n).$$

Under ER, the particle filtering assigns weights according to p(Y_n|X_n−1) and propagates samples by sampling from p(X_n|X_n−1, Y_n). Figure 1(b) illustrates an example where evidence reversal overcomes sample impoverishment.

Figure 2:

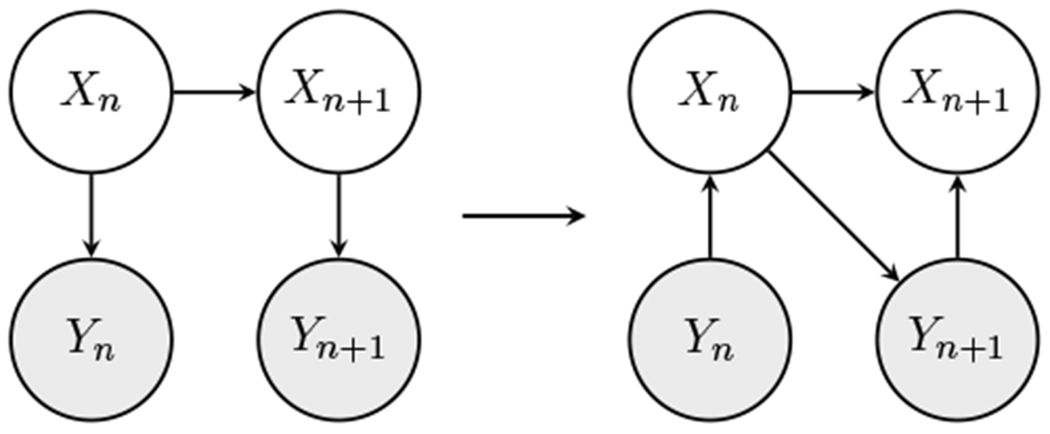
The left figure shows the standard DBN and the right figure shows the ER transformation. The shaded nodes represent the observations.

3. Intracranial pressure morphology analysis framework

Figure 3 illustrates the block diagram of the ICP monitoring framework. This framework includes three major components: (1) a pre-processing block that cleans the ICP signals and extracts a set of candidate locations for pulsatile components, (2) a training block that computes the model parameters, and (3) a dynamic Bayesian network that returns the three major pulsatile components.

Figure 3:

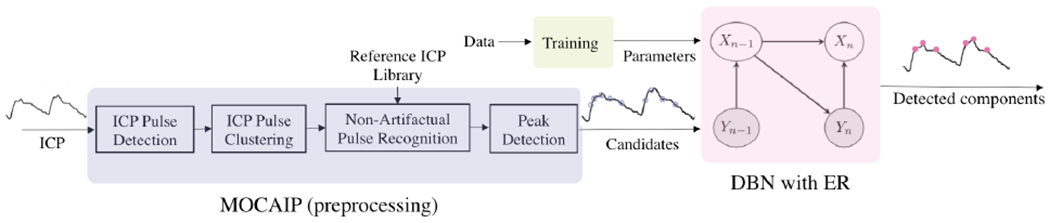
Flow chart of the proposed framework for ICP morphology analysis which includes data pre-processing, training, and inference over a dynamic Bayesian model. In the model, the latent variables are the ICP major pulsatile components $X_n=\{X_n^1,X_n^2,X_n^3\}$ and observed variables are the candidate locations $Y_n=\{Y_n^1,\dots ,Y_n^{C_n}\}$, where C_n is a random variable representing the number of candidates obtained for pulse n.

3.1. Dataset

The dataset includes ICP and ECG signals acquired from 66 patients who were admitted to the UCLA Adult Hydrocephalus Center for assessment of normal pressure hydrocephalus (NPH) using the overnight ICP monitoring technique. ICP of these patients was continuously monitored for up to 24 hours using Codman intraparenchymal microsensors (Codman and Schurtleff, Raynaud, MA) placed in the right frontal lobe. Simultaneously, ECGs of the patients were continuously measured using GE bedside monitors. The signals were recorded either using a data acquisition system placed on a wheel (PowerLab TM SP-16) or using an enterprise-wide data acquisition software solution (BedMasterTM ) at a sampling frequency of 400Hz and 240Hz, respectively. The use of this dataset to develop a set of rules to predict the outcome of cerebrospinal fluid shunt procedures for these NPH patients was reported in a prior work (Hu et al., 2012b). These rules were based on MOCAIP metrics that were obtained by first applying the MOCAIP algorithm to analyze 30-second of ICP and then by manual review and correction of any incorrectly designated ICP sub-peaks. For the purpose of the present study, the manually corrected detections of ICP sub-peaks are then used as ground truth to assess the accuracy of the proposed algorithm.

3.2. Data pre-processing

We adopt similar data pre-processing steps as the MOCAIP framework, which is briefly described here. We refer the reader to the original MOCAIP paper for a more detailed explanation (Hu et al., 2008c). The data pre-processing block admits a raw ICP signal, obtains a sequence of dominant pulses, and extracts a set of candidate points for each dominant ICP pulse according to the following steps.

1. ICP pulse detection: The ICP signals are first segmented into a sequence of pulses using the ICP pulse detection method presented in our previous work (Hu et al., 2008b). This algorithm leverages a robust ECG beat detection as well as interval constrains to aid ICP pulse segmentation.

2. ICP pulse clustering: ICP signals can be contaminated by various types of noise and artifacts including high-frequency noise from the measurement devices, movement artifacts, and sensor detachments. To obtain clean pulses, a hierarchical clustering algorithm is used to cluster sub-sequences of raw ICP pulses and the average pulse of the largest cluster is taken as the representative (dominant) pulse of each sub-sequence.

3. Non-artifactual pulse recognition: Occasionally when large signal segments are corrupted with noise, dominant pulses obtained from pulse clustering become artifactual. The non-artifactual pulses are identified using a reference library of validated pulses created during training.

4. Candidate detection: Candidate locations for major pulsatile components are identified by obtaining certain landmarks on each ICP pulse. These landmarks are identified by merging the intersections of concave and convex regions and maximum curvature points.

3.3. Detection of major pulsatile components

Our framework relies on constructing a DBN that corresponds to a simplified model of the ICP evolution over time. The latent and observed variables of this model are listed below.

1. Latent variables X_n = {X_n(1), X_n(2), X_n(3)} denote the arrival time of three major components of pulse n with respect to the arrival time of the most recent heartbeat. $X_n^i$ takes values in ${\mathbb{R}}^{+}\cup \{m\}$, with $X_n^i=m$ when component i is not recognizable (missing). A sub-peak can be missing because of poor signal quality or pathological reasons. Based on our experience, the likelihood of missing a sub-peak is less than 10%. The fact that any of the three target sub-peaks can be missing in a given ICP pulse makes the process of sub-peak designation more challenging.

2. Observed variables Y_n = {Y_n(1), …, Y_n(C_n)} are candidate locations for major components of pulse n that are extracted during the pre-processing stage. C_n is a random variable denoting the number of candidates the algorithm has detected for pulse n.

Transition model.

First, we specify the transition model for the instances where all three components are present. We model the evolution of ICP pulsatile components as a Markov process according to the following:

$$\begin{gathered} p(X_n|X_{1:n-1}=p(X_n|X_{n-1})=p(X_n(1),X_n(2),X_n(3)|X_{n-1}(1),X_{n-1}(2),X_{n-1}(3)) \\ =p(X_n(1)|X_{n-1}(1))p(X_n(2)|X_{n-1}(2),X_n(2)>X_n(1)) \\ \times p(X_n(3)|X_{n-1}(3),X_n(3)>X_n(2)). \end{gathered}$$

Motivated by the histograms of the locations of major pulsatile components in the training data, we adopt the following model for evolution of X_n(i)

$$X_n(i)=X_{n-1}(i)+{\eta }_n(i)\text{for}i=\{1,2,3\},$$ (1)

where η_n(i) ~ Laplace(0, b(i)), where b(i) is the Laplace distribution scale parameter. Figure 4 presents the histogram of η_n(i) for three patients demonstrating that the concentration of η_n(i) around zero is not well-described by a Gaussian distribution. Due the symmetry and high concentration of histograms around zero, we choose to model η_n(i) according to a Laplace distribution. Furthermore, the histograms suggest that the scale parameters b(i) vary across patients. Thus, We take b(i) to be a static hidden variable, i.e. b_n(i) = b_n−1(i) = b(i), and infer it as the ICP observations are received for each patient. Taking b(i) as a latent variable as opposed to a constant parameter allows the model to adapt for an individual patient’s physiology and neurological condition.

Figure 4:

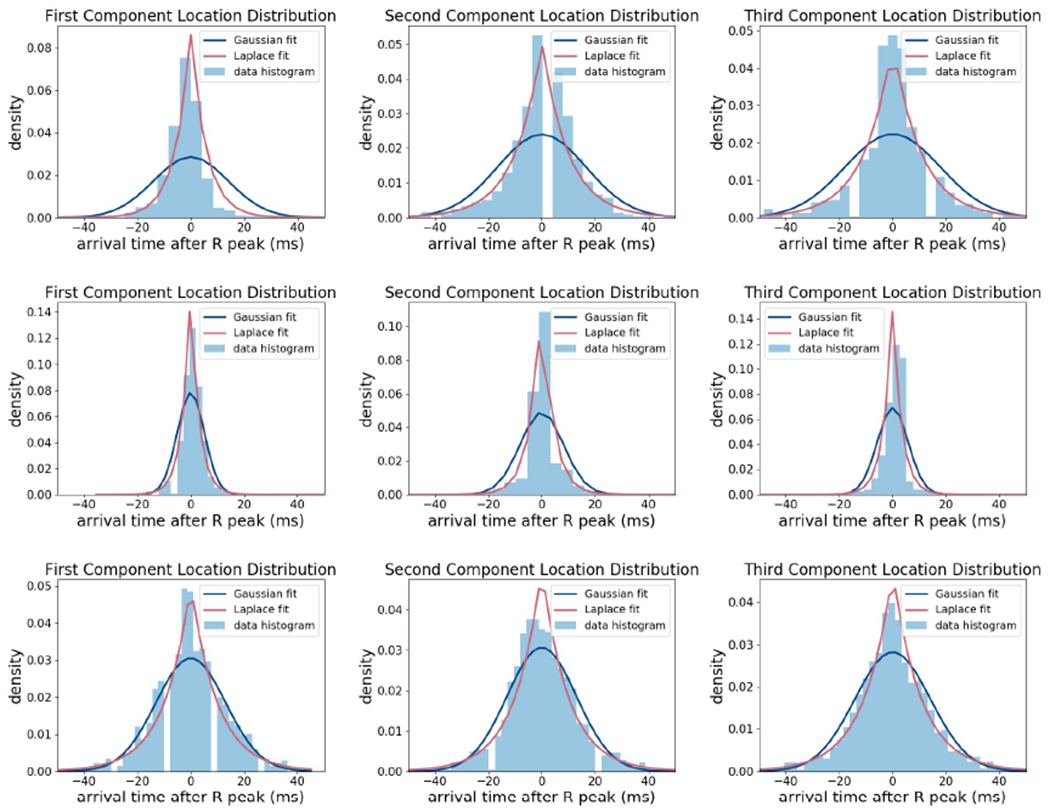
Histogram of η_n(i) = X_n(i) − X_n−1(i) for three different patients and fitted Laplace and Gaussian distributions.

We allow X_n(i) to be missing with a constant probability p_m(i) that is learned during training. For the cases where X_n−1(i) is missing, we take the temporal evolution of X_n(i) to be

$$X_n(i)=X_{n-k}(i)+\sum _{j=n-k+1}^n\eta j(i),$$ (2)

where n − k is the last pulse whose component i was present. Note that Equation (2) is equivalent to Equation (1) when k = 1.

Prior distribution.

We specify prior distributions for the latent variables b(i) and X_n(i). Since b(i) is a scale parameter, we use a wide uniform distribution and we take X₀(i) ~ Laplace(μ(i), b(i)), where μ(i) is computed using a maximum likelihood estimate on training set.

Observation model.

In our setup, since the three major pulsatile components are often visually distinguishable landmarks, they tend to be included in or very close to the candidate points with high probability even though candidate points often include several spurious points as well. Given a set of candidate points Y_n = y_n(1), … y_n(c_n) the observation model p(Y_n|X_n) assigns high weights to some values of X_n and extremely low weights to most values of X_n. Thus, the proposed DBN is an example where the standard particle filtering works poorly due to sample impoverishment as explained in Section 2.3. We address this problem by using evidence reversal.

Model under evidence reversal

Recall from Section 2.3 that for an ER transformation, the transition distribution p(X_n|X_n−1, Y_n) and the likelihood distribution p(Y_n|X_n−1) should be specified. We design p(X_n|X_n−1, Y_n; b) to be a hybrid —mixture of discrete and continuous— distribution where X_n takes values in Y_n with high probability. Denote by p_c(i) the probability that X_n(i) is equal to one of the candidates. Let α_j(i) be the value of the Laplace probability density function at Y_n(j) = y_n(j) with mean x_n−1(i) and scale parameter b(i), i.e.

$${\alpha }_j(k)=\mathrm{Laplace}(y_n(j);x_{n-1}(i),b(i)).$$

Let L(i) = 0 for i = 1 and L(i) = X_n(i – 1) for i = 2, 3, be the minimum value that X_n(i) can take. The transition distribution is defined as

$$p(X_n(i)|X_{n-1}(i),L(i),Y_n)=\{\begin{array}{ll}{X}_n(i)=Y_n(j),\text{for}\{j:Y_n(j)>L(i)\}& \text{w}.\text{p}.p_c(i)\frac{{\alpha }_j(i)}{{\sum }_j{\alpha }_j(i)}\\ X_n(i)=m& \text{w}.\text{p}.p_m(i)\\ X_n(i)~\mathrm{Laplace}(X_{n-1}(i-1),b(i)|X_n(i)>L(i))& \text{w}.\text{p}.1-p_c(i)-p_m(i)\end{array}$$

The above distribution states that X_n(i) is equal to candidate Y_n(j) with probability $p_c(i)\frac{{\alpha }_j(i)}{{\sum }_j{\alpha }_j(i)}$ if Y_n(j) > L(i). The total probability that X_n(i) is one of the candidates is p_c(i) and the probability that X_n(i) is missing is p_m(i). Finally, with probability 1 − p_c(i) − p_m(i), X_n(i) is present but is not equal to any of the candidate points. In this case, X_n(i) has a (truncated) Laplace distribution satisfying X_n(i) > L(i). Using lower bounds L(i) ensure that 0 < X_n(1) < X_n(2) < X_n(3). In Figure 5, the left plot illustrates an example on the probabilities assigned to each candidate points. The right plot presents the hybrid transition distribution.

Figure 5:

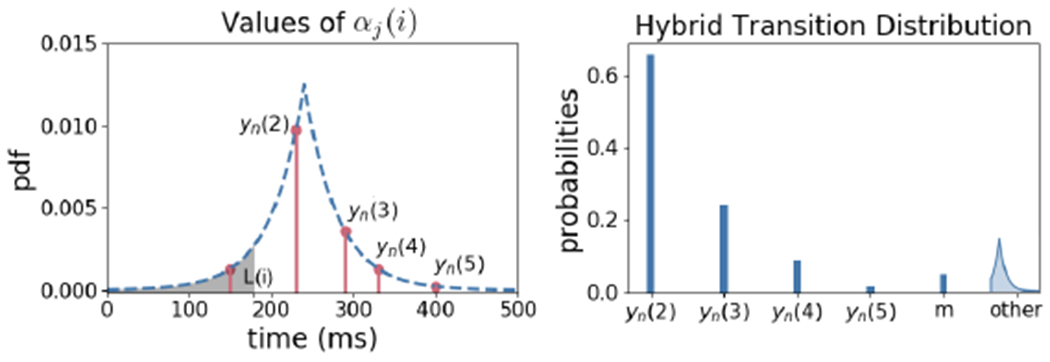
Left: The probability density function (pdf) of Laplace(X_n−1(i), b(i)) at candidate locations. X_n(i) can take values only in the candidates that are greater than L(i). Right: Hybrid probability distribution of X_n(i) over the candidates, missing value, and a truncated Laplace distribution.

The likelihood distribution p(Y_n|X_n−1) is computed by considering all valid assignments of candidates to ICP components. In particular, candidates Y_n can be assigned to either of the three components or none of them. An assignment is considered valid if it satisfies X_n(1) < X_n(2) < X_n(3). For example, for candidates Y_n = {150, 200, 230, 320, 500}, assignments {1, none, 2, 3, none} and {none, 1, none, 3, none} are valid which are equivalent to {X_n(1) = 150, X_n(2) = 230, X_n(3) = 320} and {X_n(1) = 200, X_n(2) = m, X_n(3) = 320}, respectively. Let $\mathcal{A}$ be the set of all valid assignments. The likelihood distribution can be written as

$$p(Y_n|X_{n-1})=\sum _{a\in \mathcal{A}}p(a)p(Y_n|X_{n-1},a).$$

Probability of each assignment p(a) is computed using p_c(i). For instance, if the assignment only selects components two and three from the candidates, p(a) = (1 − p_c(1))p_c(2)p_c(3), which is th probability that component one is not in the candidates but components two and three are. Conditioned on an assignment, the likelihood p(Y_n|X_n−1, a) using the Laplace pdfs with expected values X_n−1(1), X_n−1(2), X_n−1(3) assuming that spurious observations can appear anywhere in the ICP pulse uniformly at random. For example, for the assignment a = {1, none, 2, 3, none}, we have the following likelihood

$$p(Y_n|X_{n-1},a)=\mathrm{Laplace}(Y_n(1)|X_{n-1}(1))\mathrm{Uniform}(Y_n(2))\mathrm{Laplace}(Y_n(3)|X_{n-1}(2))\times \mathrm{Laplace}(Y_n(4)|X_{n-1}(3))\mathrm{Uniform}(Y_n(5)).$$

Computing this likelihood is essential for tuning parameters b(i).

4. Results

We implement the ER transformation of the proposed DBN and use particle filtering with 1000 samples as the inference algorithm. We run the framework on more than 700 hours of data collected from 66 patients and measure the performance of the algorithm for detecting sub-peaks against expert reviewed and corrected sub-peak annotations. A sub-peak detected by the algorithm is accepted as correct if it is within 50ms of the annotations.

We compare the performance of our framework to the MOCAIP framework. The MOCAIP framework has a similar pre-processing method as explained earlier but uses a different method for designating the three major components given the candidates. In particular, MOCAIP models the locations of each three components as a Gaussian distribution $X_n(i)~\mathcal{N}(\mu (i),{\sigma }^2(i))$ for i ∈ {1, 2, 3}. Note that the component location distributions in MOCAIP are the same for every pulse whereas in this work the distributions change dynamically for different pulses. The parameters of the three Gaussian distributions are computed by fitting the training data that were used in the original publication (Hu et al., 2008c). The distributions thus learned using this approach remain the same for all patients. Then, the following score function is computed for all valid assignments J(i₁, i₂, i₃) = p(X_n(1) = Y_n(i₁))+p(X_n(2) = Y_n(i₂))+p(X_n(3) = Y_n(i₃)). Furthermore, component i is considered missing if p(X_n(j) ≥ Y_n(i_j)) < ρ, for a pre-specified value ρ.

Advantages of an individualized framework.

Figure 6 compares the performance of DBN with ER transformation (DBN-ER) with the MOCAIP framework for a patient. In Figure 6(b), the MOCAIP framework uses component location densities obtained from a group of patients in for the component designation process. As a result, MOCAIP is prone to errors for patients whose component locations are not described well by the location densities computed during training. This is despite the fact that all three major components are included in the candidates. The DBN-ER framework, however, has the advantage of adapting component location distribution to each individual patients by: (I) modeling the evolution of X_n(i) − X_n−1(i) resulting in a lower variance distribution, and (II) adapting distribution parameters as more data is received for each patient.

Figure 6:

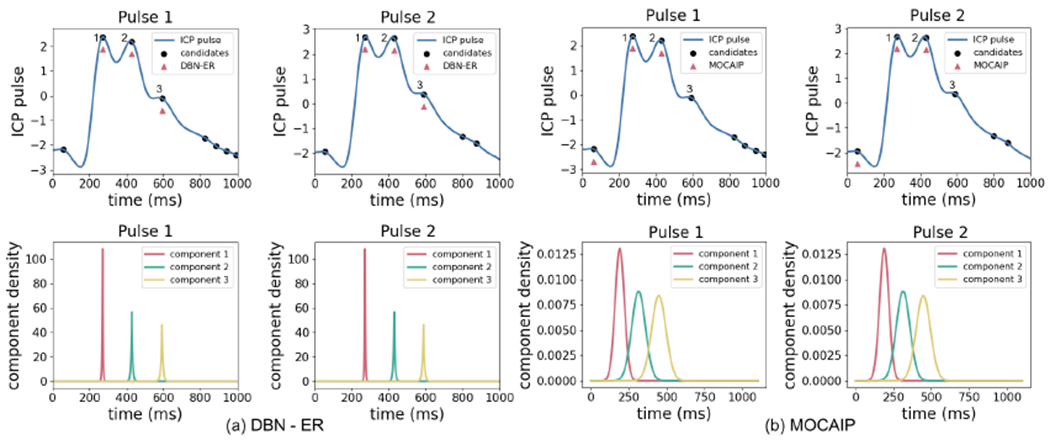
The top plots show two consecutive ICP pulses for a patient and the performance of DBN-ER (left) and MOCAIP (right). The expert annotations are denoted by 1, 2, and 3. The bottom plots show the distributions over the locations of each components which are modeled by Laplace distributions X_n(i) = Laplace(X_n−1(i), b(i)) in DBN-ER and Gaussian distributions X_n(i) = Normal(μ(i), σ²(i)) in MOCAIP.

Advantages of a dynamical model.

Another advantage of the DBN-ER framework is that the dynamical model allows for the correction of potential errors occurred during candidate detection step. Figure 7 shows an example where the first component location is missing in the candidates. Since the MOCAIP framework only allows the components to be selected from the candidates or be declared as missing, it does not detect the first component. On the other hand, in DBN-ER, components can take values that are not necessarily equal to candidates. In addition, DBN-ER leverages the dynamic model to reliably estimate the location of X_n(1) given X_n−1(1).

Figure 7:

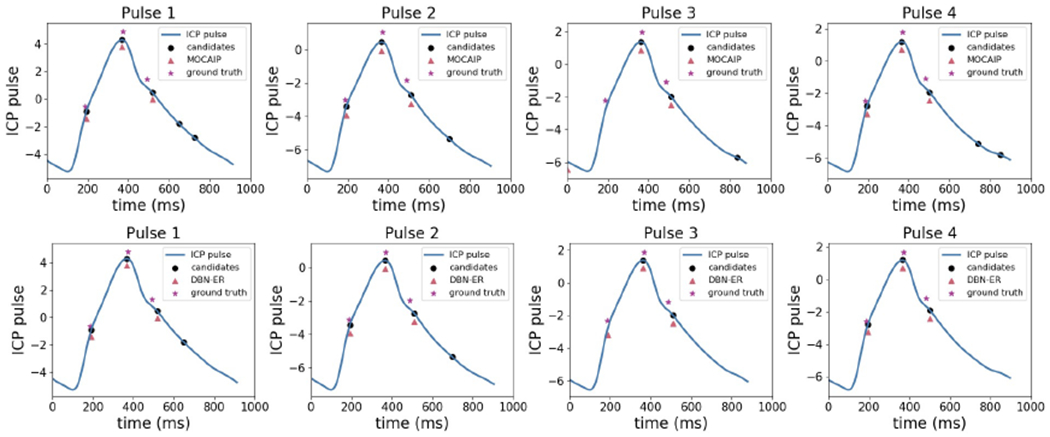
Performance of MOCAIP (top) compared to DBN-ER (bottom) where a candidate is missing. The ability of DBN-ER to use the information from previous pulses and to detect components outside candidates reduces missed detections.

Failure cases.

We present two cases where the proposed method fails to identify the components correctly. Figure 8 shows a corrupted ICP pulse that was not correctly classified during the pre-processing step of non-artifactual pulse recognition. An ICP pulse is considered corrupted when an expert classifies it as too noisy that reliable sub-peak assignment is not possible. Despite the fact that this pulse is visually corrupted, the algorithm detects one component. Although the proposed method improves over MOCAIP by not heavily relying on the candidate detections, the quality of the pulse and candidates still affect the performance. This issue can be addressed by improving the non-artifactual pulse detection and candidate point detection modules.

Figure 8:

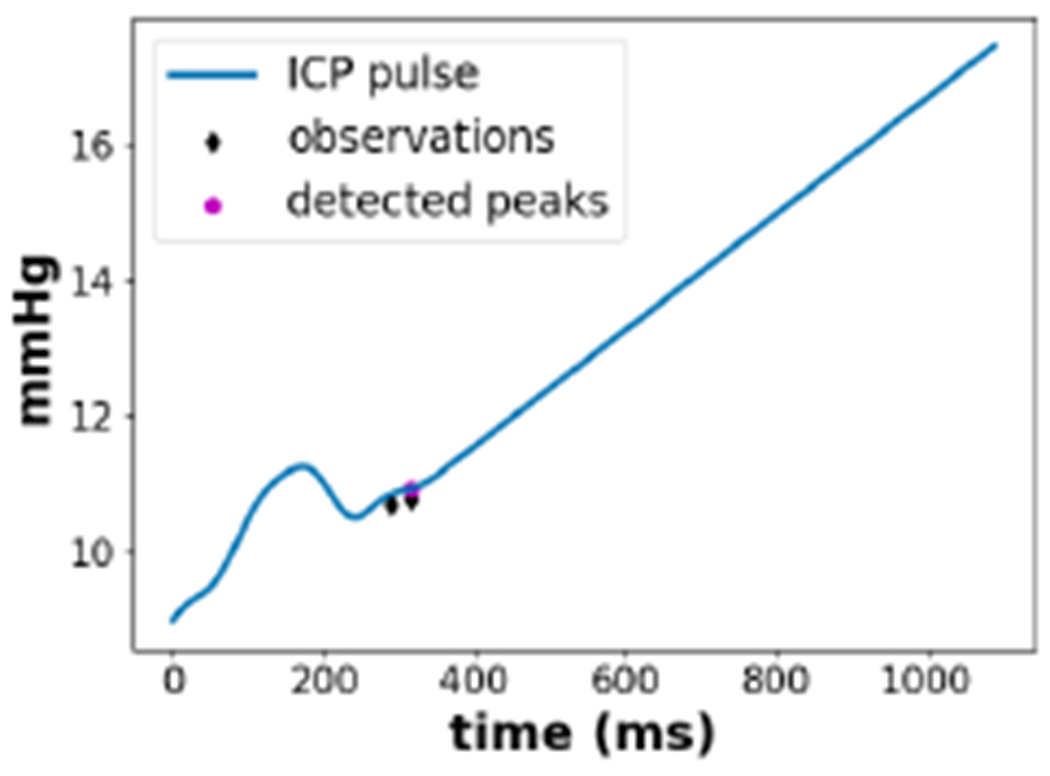
An example where the DBN-ER algorithm fails to detect a corrupted ICP pulse.

Figure 9 shows an example where the algorithm correctly detects the third components in the first three pulses despite the fact that they are not included in the candidate peaks. However, after receiving observations for a few pulses, the algorithm wrongly concludes that the third component is not present as it is not detected in the candidate peaks for a while. This example shows that the algorithm is somewhat vulnerable to persistent errors in the observations. This problem can be addressed by improving the quality of component detection step. In addition, including more information from the ICP pulse besides the component location such as curvature and amplitude alleviates this problem and is left for future work.

Figure 9:

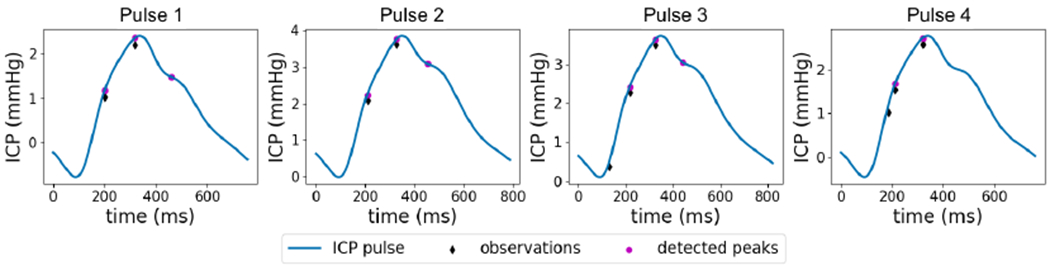
An example where existence of a persistent error in the observations results in missing the third component.

Overall performance.

We compare the overall performance of our framework to the MOCAIP framework as well as another method based on clustering inspired by (Lee et al., 2015). For the clustering approach, we use the same pre-processing and candidate detection steps as in MOCAIP and apply the clustering method described in (Lee et al., 2015) for the final step of designating the three major components. Table 1 compares the accuracy of algorithms in detecting the three components over the test set in addition to the standard deviation of detection accuracy among the patients. DBN-ER significantly improves the detection accuracy of each component and obtains a more robust performance across patients owing to parameter adaptation.

Table 1:

Accuracy of detecting three major ICP pulsatile components and the standard deviation of the detection accuracy among patients.

	Component 1		Component 2		Component 3
	accuracy	s.d.	accuracy	s.d.	accuracy	s.d.
Clustering	71.57%	0.36	89.76%	0.16	83.41%	0.21
MOCAIP	90.17%	0.17	87.56%	0.25	86.53%	0.24
DBN-ER (ours)	96.56%	0.07	92.39%	0.18	94.04%	0.12

As an additional performance measure, we compute a displacement error: the averaged difference between the detected sub-peaks $\{{\widehat{x}}_n(1),{\widehat{x}}_n(2),{\widehat{x}}_n(3)\}$ and the expert labels $\{x_n^{*}(1),x_n^{*}(2),x_n^{*}(3)\}$

$${\Delta }_i=\frac{1}{{\widehat{n}}_i}\sum _{n=1}^{{\widehat{n}}_i}|{\widehat{x}}_n(i)-x_n^{*}(i)|,$$

where ${\widehat{n}}_i$ denotes the number of true detections of component i. Table 2 shows that DBN-ER achieves a smaller average displacement error. As discussed before, in some ICP pulses one or more components may be missing. In Table 2, we also compare the performance of the algorithms in their ability to correctly detect a missing sub-peak by obtaining true negative rate (TNR). Overall, DBN-ER performs well in identifying missing sub-peaks. The clustering method yields the best TNR for component 1. However, this score is due to the interval constraints of the clustering method that results in assigning missing value to many first sub-peaks despite their existence. Note that since the chance of missing sub-peaks is relatively small, true positive rates are close to the accuracies reported in Table 1.

Table 2:

Average displacement errors Δ_i and true negative rates of difference algorithms.

	Component 1		Component 2		Component 3
	Δ1(ms)	TNR	Δ2(ms)	TNR	Δ3(ms)	TNR
Clustering	21.6	0.954	15.4	0.844	29.3	0.912
MOCAIP	24.8	0.876	12.9	0.877	24.8	0.835
DBN-ER (ours)	19.0	0.912	10.8	0.908	19.7	0.923

5. Discussion

In this paper, we presented a fully automated and patient-adaptable framework based on a probabilistic dynamic model for the identification of pulsatile components from continuous ICP signals. The efficacy of the proposed framework was evaluated by conducting experiments over more than 700 hours of ICP recordings. We compared our results with those yielded by the MOCAIP framework (Hu et al., 2008c) as well as a clustering approach inspired by (Lee et al., 2015), demonstrating significant improvements. The temporal feature of our framework enables recalling necessary information regarding the locations of components from previous pulses. This information in addition to the observations results in making more confident and robust decisions during the component designation step. The proposed framework deploys a probabilistic generative model which can also be used to make predictions on the arrival times of upcoming pulsatile components and provide uncertainty estimates for the predictions. We included static hidden variables in the DBN that are tuned for each patient as more data are received in an unsupervised manner, which allows for improved performance by making the detection mechanism individualized. The approach presented here is theoretically guaranteed, data-efficient, and interpretable.

In addition to MOCAIP, several other approaches are proposed for ICP sub-peak detection such as (Lee et al., 2015; Calisto et al., 2012). Since the implementation and specific details of these approaches are not publicly available, we implemented an algorithm inspired by the clustering approach of Lee et al. 2015 and compared the performance to our approach in the previous section. We now highlight the algorithmic and conceptual differences between these works and our work.

The method presented by Calisto et al. 2012 is not fully automated and cannot be used for real-time patient monitoring. For each patient, this method requires an expert to annotate the three pulsatile components of ten randomly-selected pulses and the annotations are later used for component identification. Furthermore, the non-artifactual pulses are recognized by comparing the current pulse with three preceding and three succeeding pulses, which performs poorly in case of a relatively persistent artifact. Similar to MOCAIP, Lee et al. 2015 also first finds a set of candidate locations. It then applies k-means on the candidates to assign three pulsatile components, unlike the method presented in this paper which finds the most likely location of pulsatile components using a Bayesian model-based approach. A main limitation of (Lee et al., 2015) is the preliminary step of manual removal of artifactual recordings by an expert which limits the use of the framework for fully automated patient monitoring. The above frameworks do not consider the dynamics of pulsatile components, the uncertain nature of the problem, and adaptability to individual patients, which are addressed in this paper. Our framework based on DBN-ER offers additional advantages such as flexibility in admitting more complex models and providing insights on the temporal model of the ICP.

6. Future work

The model-based framework for ICP morphology analysis elicits several interesting extensions and directions for future work. Possible directions for technical improvements are described below.

The transition model.

The dynamical model presented in this paper is developed by analyzing the dynamics of ICP sub-peaks from annotated data and a simple understanding of human physiology. This results in a relatively simple model that admits only a few parameters, making it less prone to overfitting in clinical applications when data are relatively scarce. However, if more data are available, using a more complex model of the dynamics would greatly improve the performance. This goal can be achieved in several ways. For example, while we only considered the arrival time of ICP components, one can increase the modeling power by considering both the arrival time and signal amplitude of each component. Introducing hierarchical structures and incorporating the temporal and static effects of different neurological conditions on the pulsatile components are other ways of improving the model. Alternatively, one can deploy expert knowledge for designing a more complex model; an example of such a method is the recent work of Wang et al. 2019 that presents a lumped parameter network for modeling the ICP signal by leveraging mechanistic understanding of physiology. Finally, the current model only considers short-term temporal dependencies. Designing a framework that handles a long-term memory, a difficult challenge in machine learning, is a direction worth pursuing.

The pre-processing step.

We used MOCAIP’s pre-processing approach to obtain a sequence of dominant ICP pulses and eliminate noise followed by a candidate detection step. Improving non-artifactual pulse recognition and candidate detection modules is expected to increase the final accuracy. Furthermore, in the current implementation, the dominant pulse represents a short segment of the ICP recording. An interesting future direction is analyzing the morphology of individual pulses by combining the proposed DBN with alternative methods of handling noise and artifacts.

The observations.

In the current framework, we only considered candidate locations as DBN observations. Including more observations could improve the performance of the framework at the cost of making the system more complex and perhaps, adding a requirement for using more advanced inference techniques. For instance, to alleviate the problem with detecting ICP components in corrupted pulses that are not removed in the pre-processing step, additional observations such as signal quality indices can be considered. Recent works demonstrated that DBNs that include raw signals as observations without a pre-processing or feature extraction step are highly effective. An example is a signal-based DBN presented in (Moore and Russell, 2017) where raw seismic signals are used as observations to achieve state-of-the-art performance in seismic monitoring.

In addition to technical improvements, research venues that have demonstrated the potential clinical values of quantitative ICP pulse morphological analysis (Hu et al., 2010b,a; Kasprowicz et al., 2010; Asgari et al., 2012; Scalzo et al., 2012b,c; Scalzo and Hu, 2013; Hu et al., 2012a; Liu et al., 2019, 2020) can readily benefit from a more accurate delineation of ICP pulse morphological features.