A new extended rayleigh distribution with applications of COVID-19 data

Abstract

This paper aims to model the COVID-19 mortality rates in Italy, Mexico, and the Netherlands, by specifying an optimal statistical model to analyze the mortality rate of COVID-19. A new lifetime distribution with three-parameter is introduced by a combination of Rayleigh distribution and extended odd Weibull family to produce the extended odd Weibull Rayleigh (EOWR) distribution. This new distribution has many excellent properties as simple linear representation, hazard rate function, and moment generating function. Maximum likelihood, maximum product spacing and Bayesian estimation methods are applied to estimate the unknown parameters of EOWR distribution. MCMC method is used for the Bayesian estimation. A numerical result of the Monte Carlo simulation is obtained to assess the use of estimation methods. Also, data analysis for the real data of mortality rate is considered.

Introduction

One of the main tasks of statistics is to find efficient statistical modeling for natural life events in the form of known probability distributions. Probability distributions are used to model natural life phenomena that are characterized by uncertainty and riskiness. Many probability distributions have been derived because the natural life phenomena are complex and very hard to model by traditional distributions. However, known probability distributions remain unable to represent data for some natural phenomena accurately. These lead to the expansion and modification of generalized probability distributions. The addition of some new parameters to the known probability distributions improved the quality of suitability for the natural phenomena data and higher accuracy of describing the shape of the distribution’s tail.

Most of the Rayleigh probability distribution extensions have been derived because of their great importance in describing many natural life phenomena. The Rayleigh probability density function, attributed to Lord Rayleigh (1842–1919), is concerned with describing skewed data see Rayleigh [1] Many researchers consider one scale parameter Rayleigh, like Robert C.P. Diebolt and Robert [2] discussed deviation and distance measure in economic, which can be applied in another natural phenomena data. The extended probability distribution was originally introduced by Lehmann [3]. Kundu and Raqab [4] provided a generalization of the Rayleigh probability distribution and estimated its unknown parameters using several different methods. Voda [5] used the conservative technique to derive a new generalization of the Rayleigh probability distribution. Dey [6] presented Bayesian estimates of the Rayleigh probability distribution parameters using the linex loss functions and square error loss function. Merovci [7] used the square ordinal transformation method in developing the transmuted Rayleigh probability distribution. Merovci and Elbatal [8] presented a Weibull- Rayleigh probability distribution. Mahmoud and Ghazal [9] discussed the estimation of the exponentiated Rayleigh parameters based on type II censored data. Ateeq et al. [10] derived the Rayleigh-Rayleigh distribution (RRD) using the Transformed Transformer technique. El-Sherpieny and Almetwally [12] introduced Bivariate generalized Rayleigh distribution based on Clayton copula with various applications. Almetwally et al. [11] used the maximum likelihood and maximum product spacing estimates for generalized Rayleigh distribution based on the adaptive type-II progressive censoring schemes. Al-Babtain [13] proposed a new extension of the Rayleigh distribution with a two-parameter called type I half logistic Rayleigh distribution.

Here we study a new model with three parameters, it is called extended odd Weibull Rayleigh (EOWR) distribution. The EOWR distribution is obtained based on the extended odd Weibull-G (EOW-G) family, which was introduced by Alizadeh et al. [14]. Let $\bar{G}\left(x\text{;}\delta \right)=1-G\left(x\text{;}\delta \right)$ and $g\left(x\text{;}\delta \right)=\frac{\mathit{dG}\left(x\text{;}\delta \right)}{\mathit{dx}}$ denote the survival function (SF) and probability density function (PDF) of a baseline model with parameter vector $\delta$ respectively, so the CDF of the EOW-G family is given by:

$$F(x\text{;}\alpha ,\beta ,\delta )=1-{\left\{1+\beta {\left[\frac{G\left(x\text{;}\delta \right)}{\bar{G}\left(x\text{;}\delta \right)}\right]}^{\alpha }\right\}}^{\frac{-1}{\beta }},x\in \mathbb{R}\text{.}$$ (1)

The corresponding PDF of (1) is defined by

$$f(x\text{;}\alpha ,\beta ,\delta )=\frac{\alpha g\left(x\text{;}\delta \right)G{\left(x\text{;}\delta \right)}^{\alpha -1}}{\bar{G}{\left(x\text{;}\delta \right)}^{\alpha +1}}{\left\{1+\beta {\left[\frac{G\left(x\text{;}\delta \right)}{\bar{G}\left(x\text{;}\delta \right)}\right]}^{\alpha }\right\}}^{\frac{-1}{\beta }-1},x\in \mathbb{R},$$ (2)

where $\alpha$and $\beta$are positive shape parameters. The random variable with PDF (2) is denoted by $X~$EOW-G($\alpha ,\beta ,\delta$). Afify and Mohamed [16] introduced a new flexible three-parameter exponential distribution called the extended odd Weibull exponential distribution. Alshenawy et al. [17] used the maximum likelihood estimation and maximum product spacing estimates to estimate the parameters of the extended odd Weibull exponential distribution under the progressive type-II censoring scheme with random removal.

Our goal in this paper is to study point estimation of the unknown parameters of EOWR by using two classical methods of estimation and the Bayes estimation method. A statistical comparison between these methods is conducted via simulation to assess these method’s performance and to study how these estimators behave for several sample sizes and parameter values.

The rest of this paper is organized as follows. In Section ‘EOWR distribution’, we define EOWR distribution. Some EOWR statistical properties as a linear representation of its PDF is obtained in Section ‘Statistical properties’. Three methods of point estimation are studied in Section ‘Parameter estimation’. In Section ‘Simulation analysis’, a simulation study is conducted to compare the performance of these estimation methods. Three real data sets of COVID-19 from different life applications are used in Section ‘Applications to COVID-19 data’ to prove the efficiency of the EOWR distribution compared to other distributions. Finally, conclusions and major findings are given in Section ‘Conclusion’.

EOWR distribution

The three-parameter EOWR distribution is a special model of EOW-G family with Rayleigh distribution as a baseline function. The Rayleigh distribution under consideration has respectively PDF and CDF of the form $g\left(x\text{;}\delta \right)=2\delta {\mathit{xe}}^{-\delta x^2}$ and $G\left(x\text{;}\delta \right)=1-e^{-\delta x^2},x>0,\delta >0$. By substituting the CDF and PDF of the Rayleigh model in Eq. (1) and Eq. (2) respectively, we obtain the CDF and PDF of the EOWR distribution respectively as;

$$F(x\text{;}\alpha ,\beta ,\delta )=1-{\left\{1+\beta {\left[e^{\delta x^2}-1\right]}^{\alpha }\right\}}^{\frac{-1}{\beta }},x>0,\alpha ,\beta ,\delta >0\text{.}$$ (3)

$$f(x\text{;}\alpha ,\beta ,\delta )=2\alpha \delta {\mathit{xe}}^{\delta x^2}{\left(e^{\delta x^2}-1\right)}^{\alpha -1}{\left[1+\beta {\left(e^{\delta x^2}-1\right)}^{\alpha }\right]}^{-\frac{1+\beta }{\beta }},x>0,\alpha ,\beta ,\delta >0\text{.}$$ (4)

Therefore, a random variable with PDF (4) is denoted by $X~$EOWR$(\alpha ,\beta ,\delta )$. The EOWR model reduces to the two parameter Weibull Rayleigh model when $\beta \to 0^{+}$.

The hazard rate function (HR) of the EOWR distribution are given by

$$h(x\text{;}\alpha ,\beta ,\delta )=\frac{2\alpha \delta {\mathit{xe}}^{\delta x^2}{\left(e^{\delta x^2}-1\right)}^{\alpha -1}}{1+\beta {\left(e^{\delta x^2}-1\right)}^{\alpha }}$$

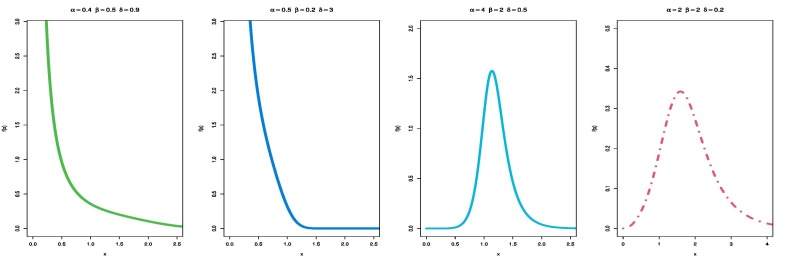
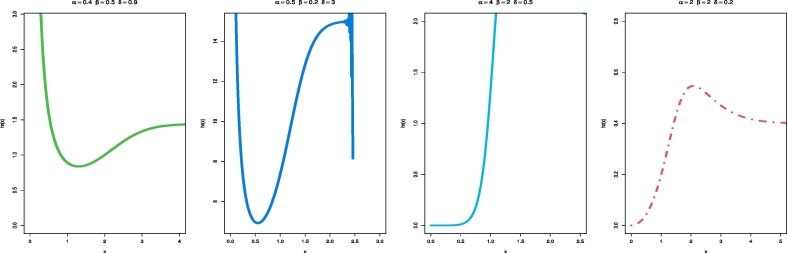
Fig. 1, Fig. 2 are different shapes of the PDF and HR of the EOWR distribution. These figures show that the EOWR distribution PDF can be right-skewed, symmetric, or decreasing curves. The HR of the EOWR distribution has some important shapes, including constant, decreasing, and upside down curve, which are attractive characteristics for any lifetime model. It can be noticed from the application section that the EOWR distribution has great flexibility and can be used to model skewed data, hence being widely applied in different areas such as biomedical studies, biology, reliability, physical engineering, and survival analysis.

Fig. 1.

Plots of the probability density function (PDF) of the EOWR distribution.

Fig. 2.

Plots of the hazard rate function (HR) of the EOWR distribution.

Statistical properties

This section presents some statistical properties of the EOWR distribution, namely, the linear representation of PDF, which is useful in finding the moments and moment generating function (MGF).

Linear representation

Linear representation for the EOWR density using series techniques is useful for finding many statistical values and properties of the distribution Of interest. Alizadeh et al. [14] showed that EOW-G family has the following mixture representation of its density

$$f\left(x\right)={\displaystyle \sum _{j,k=0}^{\infty }}{a}_{j,k}{h}_{\alpha j+k}\left(x\right),$$

where $a_{j,k}=\frac{-{\beta }^j\mathrm{\Gamma }\left(\alpha j+k\right){\left(\frac{-1}{\beta }\right)}_j}{k!j!\mathrm{\Gamma }\left(\alpha j\right)}$, where ${\left(\frac{-1}{\beta }\right)}_j=\frac{-1}{\beta }\left(\frac{-1}{\beta }-1\right)\dots \left(\frac{-1}{\beta }-j+1\right)$, and

$h_{\alpha j+k}\left(x\right)=\left(\alpha j+k\right)g\left(x\right)G{\left(x\right)}^{\alpha j+k-1}$ is the exponential-G density with positive power parameter $\alpha j+k$. Now substituting the PDF and the CDF of the Rayleigh distribution, the above equation can be written as

$$f\left(x\right)={\displaystyle \sum _{j,k=0}^{\infty }}{a}_{j,k}2\delta {\mathit{xe}}^{-\delta x^2}{\left(1-e^{-\delta x^2}\right)}^{\alpha j+k-1}\text{.}$$ (5)

Eq. (5) can be written as

$$f\left(x\right)={\displaystyle \sum _{j,k=0}^{\infty }}{\upsilon }_{j,k}h\left(x\text{;}\alpha j+k,\delta \right),$$ (6)

where ${\upsilon }_{j,k}=\frac{a_{j,k}}{\left(\alpha j+k\right)}$, and $h\left(x\text{;}\alpha j+k,\delta \right)$ denotes generalized Rayleigh density with $\left(\alpha j+k,\delta \right)$ as parameters of generalized Rayleigh distribution. Hence the PDF of EOWR can be expressed as a linear combination of generalized Rayleigh distribution. Let X  be a random variable having generalized Rayleigh distribution with parameter $({\alpha }^{\ast },\delta$). Then, the $r^{\mathit{th}}$ ordinary moment, and MGF of X are

$$\begin{array}{cc}{\mu }_{r,X}({\alpha }^{\ast },\delta )\hfill & =E\left(x^r\right)={\int }_0^{\infty }{x}^{r}h\left(x\text{;}{\alpha }^{\ast },\delta \right)\mathit{dx}\hfill \\ \hfill & ={\alpha }^{\ast }\delta {\displaystyle \sum _{l=0}^{\infty }}\left(\begin{array}{c}{\alpha }^{\ast }-1\hfill \\ l\hfill \end{array}\right){(-1)}^l\mathrm{\Gamma }\left(\frac{r}{2}+1\right){\left(\delta (l+1)\right)}^{\frac{-r-2}{2}},\hfill \end{array}$$ (7)

and

$$\begin{array}{cc}{M}_X\left(t,{\alpha }^{\ast },\delta \right)\hfill & =E\left(e^{\mathit{xt}}\right)={\int }_0^{\infty }{e}^{\mathit{xt}}h\left(x\text{;}{\alpha }^{\ast },\delta \right)\mathit{dx}\hfill \\ \hfill & ={\alpha }^{\ast }\delta {\displaystyle \sum _{l,a=0}^{\infty }}\left(\begin{array}{c}{\alpha }^{\ast }-1\hfill \\ l\hfill \end{array}\right){(-1)}^l\frac{t^a}{a!}\mathrm{\Gamma }\left(\frac{a}{2}+1\right){\left(\delta (l+1)\right)}^{\frac{-a-2}{2}}\text{.}\hfill \end{array}$$ (8)

Moments and moment generating functions

The $r^{\mathit{th}}$ moment of the EOWR distribution follows directly from Eqs. (6), (7)

$${\mu }_r={\displaystyle \sum _{j,k=0}^{\infty }}{\upsilon }_{j,k}{\mu }_{r,X}(\alpha j+k,\delta )\text{.}$$ (9)

Referring to Eq. (6) and Eq. (8), the MGF of the EOWR distribution is given by:

$$M\left(t\right)={\displaystyle \sum _{j,k=0}^{\infty }}{\upsilon }_{j,k}{M}_X\left(t,\alpha j+k,\delta \right)\text{.}$$ (10)

Quantile function and median

The quantile function of EOWR distribution is used in the theoretical aspect of probability theory for this model, like statistical applications, and simulations. Simulation algorithm used quantile function to produce simulated random samples. The quantile function (Q) of the EOWR distribution is given by

$$Q\left(q\right)=\sqrt{\frac{1}{\delta }\log \left\{1+{\left(\frac{1}{\beta }\left[{\left(1-q\right)}^{-\beta }-1\right]\right)}^{\frac{1}{\alpha }}\right\}}$$ (11)

In particular, the median of EOWR distribution can be derived from Eq. (11) by setting q  = 0.5. Then, the median is given by $\mathit{median}=\sqrt{\frac{1}{\delta }\log \left\{1+{\left(\frac{1}{\beta }\left[2^{\beta }-1\right]\right)}^{\frac{1}{\alpha }}\right\}}$.

Parameter estimation

In this section, we use different point estimation methods to estimate the unknown parameters of the EOWR. We use maximum likelihood estimator (MLE), the maximum product of spacing estimator (MPS) and Bayesian estimation methods. In the last few years, parameter estimation using different estimation methods got great attention from many authors such as Almetwally and Almongy [19], Haj Ahmad and Almetwally [20], Basheer et al. [21], and Afify and Mohamed [16].

Maximum likelihood method

Let $x_1,\cdots ,x_n$ be a random sample from the EOWR distribution with parameters $\alpha ,\beta$, and $\delta$. The likelihood function can be written as:

$$L\left(\mathrm{\Theta }\right)=2^n{\alpha }^n{\delta }^n{e}^{\delta {\displaystyle \sum _{i=1}^n}{x}_i^2}{\displaystyle \prod _{i=1}^n}\left\{x_i{\left(e^{\delta x_i^2}-1\right)}^{\alpha -1}{\left[1+\beta {\left(e^{\delta x_i^2}-1\right)}^{\alpha }\right]}^{-\frac{1+\beta }{\beta }}\right\},$$ (12)

and $\mathrm{\Theta }=\left(\alpha ,\beta ,\delta \right)$is a vector of the EOWR parameters, the log-likelihood function is

$$\ell \left(\mathrm{\Theta }\right)\propto n\left[\log \left(\alpha \right)+\log \left(\delta \right)\right]+\delta {\displaystyle \sum _{i=1}^n}{x}_i^2+(\alpha -1){\displaystyle \sum _{i=1}^n}\log \left(e^{\delta x_i^2}-1\right)-\left(\frac{1+\beta }{\beta }\right){\displaystyle \sum _{i=1}^n}\log \left[1+\beta {\left(e^{\delta x_i^2}-1\right)}^{\alpha }\right],$$ (13)

The MLE are obtained by solving the following normal equations,

$$\frac{\partial \ell \left(\mathrm{\Theta }\right)}{\partial \alpha }=\frac{n}{\alpha }+{\displaystyle \sum _{i=1}^n}\log \left(e^{\delta x_i^2}-1\right)-(\beta +1){\displaystyle \sum _{i=1}^n}\frac{{\left(e^{\delta x_i^2}-1\right)}^{\alpha }\log \left(e^{\delta x_i^2}-1\right)}{1+\beta {\left(e^{\delta x_i^2}-1\right)}^{\alpha }},$$ (14)

$$\frac{\partial \ell \left(\mathrm{\Theta }\right)}{\partial \delta }=\frac{n}{\delta }+{\displaystyle \sum _{i=1}^n}{x}_i^2+\left(\alpha -1\right){\displaystyle \sum _{i=1}^n}\frac{e^{\delta x_i^2}{x}_i^2}{e^{\delta x_i^2}-1}-\alpha (\beta +1){\displaystyle \sum _{i=1}^n}\frac{{\left(e^{\delta x_i^2}-1\right)}^{\alpha -1}{x}_i^2{e}^{\delta x_i^2}}{1+\beta {\left(e^{\delta x_i^2}-1\right)}^{\alpha }},$$ (15)

and

$$\frac{\partial \ell \left(\mathrm{\Theta }\right)}{\partial \beta }=\frac{1}{{\beta }^2}{\displaystyle \sum _{i=1}^n}\log \left[1+\beta {\left(e^{\delta x_i^2}-1\right)}^{\alpha }\right]-\frac{\beta +1}{\beta }{\displaystyle \sum _{i=1}^n}\frac{{\left(e^{\delta x_i^2}-1\right)}^{\alpha }}{1+\beta {\left(e^{\delta x_i^2}-1\right)}^{\alpha }}\text{.}$$ (16)

These Eqs. (14), (15), (16)) cannot be solved explicitly. Hence a nonlinear optimization the algorithm as Newton Raphson method is used by equating them to zero.

Maximum product spacing

According to Cheng and Amin [22], the MPS method is an efficient estimation method that have some advantages compared to other point estimation methods. So we use MPS in this section to have point estimation of the unknown parameters of EOWR distribution. This can be obtained by solving the normal equations resulted from taking partial derivatives of logarithm of product spacing function $G\left(\mathrm{\Theta }\right)$ which is written as:

$$\begin{array}{cc}G\left(\mathrm{\Theta }\right)=\hfill & {\left\{\left(1-{\left\{1+\beta \mathrm{\Delta }{\left(x_1\right)}^{\alpha }\right\}}^{\frac{-1}{\beta }}\right)\left(1-{\left\{1+\beta \mathrm{\Delta }{\left(x_n\right)}^{\alpha }\right\}}^{\frac{-1}{\beta }}\right)\right\}}^{\frac{1}{n+1}}\hfill \\ \hfill & {\left\{\underset{i=2}{\overset{n}{\times \prod }}\left[{\left\{1+\beta \mathrm{\Delta }{\left(x_{i-1}\right)}^{\alpha }\right\}}^{\frac{-1}{\beta }}+{\left\{1+\beta \mathrm{\Delta }{\left(x_i\right)}^{\alpha }\right\}}^{\frac{-1}{\beta }}\right]\right\}}^{\frac{1}{n+1}}\text{.}\hfill \end{array}$$

where $\mathrm{\Delta }\left(x_i\right)=\left(e^{\delta x_i^2}-1\right)$ and the logarithmic function of $G\left(\mathrm{\Theta }\right)$

$$\begin{array}{c}\log G\left(\mathrm{\Theta }\right)\propto \frac{1}{n+1}\left(\log \left[1-{\left\{1+\beta \mathrm{\Delta }{\left(x_1\right)}^{\alpha }\right\}}^{\frac{-1}{\beta }}\right]+\log \left[1-{\left\{1+\beta \mathrm{\Delta }{\left(x_n\right)}^{\alpha }\right\}}^{\frac{-1}{\beta }}\right]\right)+\hfill \\ \frac{1}{n+1}{\displaystyle \sum _{i=2}^n}\log \left[{\{1+\beta \mathrm{\Delta }{\left(x_{i-1}\right)}^{\alpha }\}}^{\frac{-1}{\beta }}+{\left\{1+\beta \mathrm{\Delta }{\left(x_i\right)}^{\alpha }\right\}}^{\frac{-1}{\beta }}\right]\text{.}\hfill \end{array}$$ (17)

The MPS estimators of $\mathrm{\Theta }$ are obtained by differentiating the log-product Eq. (17) with respect to each parameter, then we solve the nonlinear system of equations found by using any iterative procedure techniques such as Newton Raphson algorithms. This method was developed in the last few years to estimate parameter of the model under censoring scheme see Ng et al. [23], Basu et al. [24], Almetwally and Almongy [25], Almetwally et al. [19], [26], El-Sherpieny et al. [27], and Alshenawy et al. [18].

Bayesian estimation

Bayesian methods is a statistical inference that depends on the choice of the prior distribution and the loss function. In this method all parameters are considered as random variables with certain distribution called prior distribution. If prior information is not available, we need to select one. Since the selection of prior distribution plays an important role in estimation of the parameters, our choice for the priors are the independent gamma distributions. On the other hand, the loss function is important in Bayesian methods. Most of the Bayesian inference procedures are developed under the symmetric and asymmetric loss functions. One of the most common symmetric loss function is the squared error loss (SEL) function. The independent joint prior density function of $\mathrm{\Theta }$can be written as follows:

$$\pi \left(\mathrm{\Theta }\right)=\frac{h_1^{s_1}}{\mathrm{\Gamma }\left(s_1\right)}\frac{h_2^{s_2}}{\mathrm{\Gamma }\left(s_2\right)}\frac{h_3^{s_3}}{\mathrm{\Gamma }\left(s_3\right)}{\alpha }^{s_1-1}{\beta }^{s_2-1}{\delta }^{s_3-1}{e}^{-(h_1\alpha +h_2\beta +h_3\delta )}\text{.}$$ (18)

The joint posterior density function of $\mathrm{\Theta }$ is obtained from (12) and (18)

$$\pi \left(\mathrm{\Theta }\right|\underset{\_}{x})=\frac{L\left(\underset{\_}{x}\right|\mathrm{\Theta }).\pi (\mathrm{\Theta })}{{\int }_{\mathrm{\Theta }}^{}L\left(\underset{\_}{x}\right|\mathrm{\Theta }).\pi (\mathrm{\Theta })d\mathrm{\Theta }}\text{.}$$ (19)

can be rewritten as follows

$$\pi \left(\mathrm{\Theta }\right|\underset{\_}{x})\propto {\alpha }^{n+s_1-1}{\beta }^{s_2-1}{\delta }^{n+s_3-1}{e}^{-(h_1\alpha +h_2\beta )}{e}^{\delta \left({\displaystyle \sum _{i=1}^n}{x}_i^2-h_3\right)}{\displaystyle \prod _{i=1}^n}{\left(e^{\delta x_i^2}-1\right)}^{\alpha -1}{\left[1+\beta {\left(e^{\delta x_i^2}-1\right)}^{\alpha }\right]}^{-\frac{1+\beta }{\beta }},$$ (20)

The conditional distribution can obtained as follows

$$\pi \left(\alpha \right|\delta ,\beta ,\underset{\_}{x})\propto {\alpha }^{n+s_1-1}{e}^{-h_1\alpha }{\displaystyle \prod _{i=1}^n}{\left(e^{\delta x_i^2}-1\right)}^{\alpha -1}{\left[1+\beta {\left(e^{\delta x_i^2}-1\right)}^{\alpha }\right]}^{-\frac{1+\beta }{\beta }},$$ (21)

$$\pi \left(\delta \right|\alpha ,\beta \underset{\_}{x})\propto {\delta }^{n+s_3-1}{e}^{\delta \left({\displaystyle \sum _{i=1}^n}{x}_i^2-h_3\right)}{\displaystyle \prod _{i=1}^n}{\left(e^{\delta x_i^2}-1\right)}^{\alpha -1}{\left[1+\beta {\left(e^{\delta x_i^2}-1\right)}^{\alpha }\right]}^{-\frac{1+\beta }{\beta }},$$ (22)

and

$$\pi \left(\beta \right|\alpha ,\delta \underset{\_}{x})\propto {\beta }^{s_2-1}{e}^{-h_2\beta }{\displaystyle \prod _{i=1}^n}{\left[1+\beta {\left(e^{\delta x_i^2}-1\right)}^{\alpha }\right]}^{-\frac{1+\beta }{\beta }}\text{.}$$ (23)

The Bayes estimators of $\mathrm{\Theta }$, say $({\widehat{\alpha }}_B,{\widehat{\beta }}_B,{\widehat{\delta }}_B)$ based on SEL function is given by

$${\widehat{\mathrm{\Theta }}}_{B-\mathit{SEL}}(\alpha ,\beta ,\delta )=E_{\left(\mathrm{\Theta }\right|\underset{\_}{x})},$$ (24)

where,

$${\widehat{\alpha }}_{B-\mathit{SEL}}={\int }_0^{\infty }\alpha {\int }_0^{\infty }{\int }_0^{\infty }\pi \left(\mathrm{\Theta }\right|\underset{\_}{x})d\beta d\delta d\alpha ,$$ (25)

$${\widehat{\beta }}_{B-\mathit{SEL}}={\int }_0^{\infty }\beta {\int }_0^{\infty }{\int }_0^{\infty }\pi \left(\mathrm{\Theta }\right|\underset{\_}{x})d\alpha d\delta d\beta ,$$ (26)

and

$${\widehat{\delta }}_{B-\mathit{SEL}}={\int }_0^{\infty }\delta {\int }_0^{\infty }{\int }_0^{\infty }\pi \left(\mathrm{\Theta }\right|\underset{\_}{x})d\alpha d\beta d\delta \text{.}$$ (27)

It is noticed that the integrals given by Eqs. (24), (25), (26), (27) can’t be obtained explicitly. Because of that, we use the MCMC to find an approximate value of integrals in (24), (25), (26), (27). Many authors used the MCMC technique, such as [19], [26], [37], [38], [39], [41], [42], [43], [15]. The MH algorithm produces a series of draws from EOWR distribution as follows:

Algorithm 1 The MCMC Algorithm
1: Initiate with ${\alpha }^{\left(0\right)}={\widehat{\alpha }}_{\mathit{MLE}},{\beta }^{\left(0\right)}={\widehat{\beta }}_{\mathit{MLE}},{\delta }^{\left(0\right)}={\widehat{\delta }}_{\mathit{MLE}}$.
2: Set $i=1$.
3: Generate ${\alpha }^{\ast \ast }$ from proposal distribution $\mathbf{N}({\alpha }^{(i-1)},\mathit{var}({\alpha }^{(i-1)}\left)\right)$.
4: Evaluate the acceptance probability
$A\left({\alpha }^{\left(i-1\right)}|{\alpha }^{\ast \ast }\right)=\min \left[1,\frac{\pi \left({\alpha }^{\ast }|{\beta }^{\left(i-1\right)},{\delta }^{\left(i-1\right)}\right)}{\pi \left({\alpha }^{\left(i-1\right)}|{\beta }^{\left(i-1\right)},{\delta }^{\left(i-1\right)}\right)}\right]$.
5: Generate $U~U(0,1)$.
6: If $U⩽A\left({\alpha }^{\left(i-1\right)}|{\alpha }^{\ast \ast }\right)$, put ${\alpha }^{\left(i\right)}={\alpha }^{\ast }$, else put ${\alpha }^{\left(i\right)}={\alpha }^{(i-1)}$.
7: Do the steps from ((2)-(6)) for $\beta$ and $\delta$.
8: Put $i=i+1$.
9: Repeat steps ((3)-(8)), N times to obtain $({\alpha }^{\left(1\right)},{\beta }^{\left(1\right)},{\delta }^{\left(1\right)})$,…, $({\alpha }^{\left(N\right)},{\beta }^{\left(N\right)},{\delta }^{\left(N\right)})$.

Then, the BEs of $u(\alpha ,\beta ,\delta )$ using MCMC under SE loss function

$${\tilde{u}}_{\mathit{SEL}}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}u({\alpha }^{\left(i\right)},{\beta }^{\left(i\right)},{\delta }^{\left(i\right)})\text{.}$$

Simulation analysis

In this section, the Monte-Carlo simulation procedure is performed to compare the classical estimation methods: MLE, MPS, with Bayesian estimation method under square error loss function based on MCMC, for estimating parameters of EOWR distribution by R programming language. Monte-Carlo experiments are carried out based on data generated from the distribution. Ten thousand random samples from EOWR distribution were generated, where X has EOWR lifetime for different actual values of parameters and different sample sizes n=(50, 100, and 200). We could define the best estimator methods as which minimizes the bias and root mean squared error (RMSE) of estimators.

Table 1, Table 2 summarizes the simulation results of point estimation methods proposed in this paper. We consider the bias and the RMSE values in order to perform the needed comparison between different point estimation methods. The following remarks can be noted from these tables:

Table 1.

Bias and RMSE of EOWR distribution for MLE, MPS, and Bayesian when $\alpha =0.5$.

$\alpha =0.5$				MLE		MPS		Bayesian
$\beta$	$\delta$	n		Bias	RMSE	Bias	RMSE	Bias	RMSE
0.5	0.5	50	$\alpha$	0.0183	0.1240	−0.0059	0.0087	0.0062	0.0414
			$\beta$	0.0105	0.8714	0.1152	0.3386	0.1075	0.2227
			$\delta$	0.0269	0.3340	0.0587	0.0665	0.0907	0.1791
		100	$\alpha$	0.0025	0.0683	−0.0062	0.0040	0.0048	0.0371
			$\beta$	−0.0189	0.6002	0.0741	0.1938	0.1272	0.2294
			$\delta$	0.0177	0.2677	0.0422	0.0348	0.0732	0.1392
		200	$\alpha$	0.0042	0.0460	−0.0030	0.0020	0.0043	0.0318
			$\beta$	0.0413	0.3988	0.0685	0.1171	0.1079	0.2137
			$\delta$	0.0289	0.1856	0.0342	0.0203	0.0608	0.1189
	2	50	$\alpha$	0.0095	0.1031	−0.0155	0.0078	0.0078	0.0418
			$\beta$	−0.0498	0.5912	−0.0046	0.1853	0.0772	0.1711
			$\delta$	−0.0202	0.7408	0.0011	0.3149	0.1607	0.3494
		100	$\alpha$	0.0020	0.0632	−0.0057	0.0035	0.0078	0.0373
			$\beta$	−0.0483	0.5419	0.0356	0.1069	0.0751	0.1651
			$\delta$	0.0008	0.9164	0.0654	0.2222	0.1581	0.3380
		200	$\alpha$	0.0017	0.0467	−0.0028	0.0019	0.0050	0.0325
			$\beta$	0.0017	0.3634	0.0485	0.0559	0.0745	0.1608
			$\delta$	0.0411	0.6169	0.0772	0.1242	0.1478	0.3097
2	0.5	50	$\alpha$	0.0179	0.0883	−0.0225	0.0065	0.0034	0.0402
			$\beta$	0.1007	0.6120	−0.0195	0.1984	0.0508	0.0853
			$\delta$	0.0381	0.1775	0.0150	0.0288	0.0561	0.1332
		100	$\alpha$	0.0137	0.0667	−0.0102	0.0035	0.0045	0.0384
			$\beta$	0.2856	1.3758	−0.0040	0.0876	0.0482	0.0834
			$\delta$	0.0718	0.3392	0.0045	0.0112	0.0342	0.0912
		200	$\alpha$	0.0034	0.0425	−0.0093	0.0017	0.0013	0.0320
			$\beta$	0.0785	0.5627	−0.0209	0.0384	0.0454	0.0819
			$\delta$	0.0217	0.1403	−0.0016	0.0052	0.0251	0.0706
	2	50	$\alpha$	0.0176	0.1017	−0.0213	0.0073	0.0062	0.0382
			$\beta$	0.1072	1.0997	−0.0480	0.1761	0.0400	0.0757
			$\delta$	0.0687	0.7861	−0.0452	0.1742	0.0940	0.3061
		100	$\alpha$	0.0109	0.0658	−0.0111	0.0038	0.0053	0.0376
			$\beta$	0.0967	0.8821	−0.0236	0.0966	0.0394	0.0748
			$\delta$	0.1147	0.9710	−0.0105	0.0960	0.0968	0.2719
		200	$\alpha$	0.0025	0.0470	−0.0094	0.0018	0.0017	0.0307
			$\beta$	0.0254	0.5610	−0.0232	0.0602	0.0365	0.0719
			$\delta$	0.0346	0.4849	−0.0115	0.0543	0.0841	0.2240

Table 2.

Bias and RMSE of EOWR distribution for MLE, MPS, and Bayesian when $\alpha =2$

$\alpha =2$				MLE		MPS		Bayesian
$\beta$	$\delta$	n		Bias	RMSE	Bias	RMSE	Bias	RMSE
0.5	0.5	50	$\alpha$	0.0763	0.4108	−0.0188	0.1031	0.0037	0.0208
			$\beta$	−0.0087	0.4392	0.0655	0.1490	0.0605	0.1722
			$\delta$	−0.0024	0.0589	0.0063	0.0034	0.0116	0.0454
		100	$\alpha$	0.0250	0.2283	−0.0174	0.0449	0.0036	0.0265
			$\beta$	−0.0189	0.2722	0.0337	0.0669	0.0336	0.1440
			$\delta$	−0.0014	0.0390	0.0043	0.0015	0.0067	0.0312
		200	$\alpha$	0.0238	0.1901	−0.0031	0.0208	0.0048	0.0325
			$\beta$	0.0055	0.1994	0.0347	0.0280	0.0299	0.1179
			$\delta$	0.0005	0.0268	0.0040	0.0007	0.0047	0.0231
	2	50	$\alpha$	0.0848	0.4883	0.0110	0.1802	0.0040	0.0220
			$\beta$	−0.0053	0.5195	0.0884	0.2352	0.0557	0.1710
			$\delta$	−0.0185	0.2605	0.0229	0.0624	0.0372	0.1659
		100	$\alpha$	0.0360	0.3164	0.0031	0.0869	0.0022	0.0273
			$\beta$	0.0009	0.3449	0.0647	0.1137	0.0381	0.1486
			$\delta$	−0.0052	0.1806	0.0222	0.0309	0.0235	0.1232
		200	$\alpha$	0.0119	0.2015	−0.0014	0.0383	0.0015	0.0326
			$\beta$	−0.0078	0.2116	0.0351	0.0445	0.0183	0.1150
			$\delta$	−0.0067	0.1138	0.0116	0.0126	0.0094	0.0881
2	0.5	50	$\alpha$	0.0933	0.4091	−0.0698	0.1299	0.0010	0.0210
			$\beta$	0.0935	0.8778	0.0208	0.4735	0.0448	0.1068
			$\delta$	0.0078	0.0917	0.0005	0.0060	0.0190	0.0621
		100	$\alpha$	0.0665	0.3711	−0.0348	0.0763	0.0024	0.0265
			$\beta$	0.0732	0.7833	0.0243	0.3001	0.0392	0.1178
			$\delta$	0.0027	0.0625	−0.0007	0.0033	0.0101	0.0416
		200	$\alpha$	0.0450	0.2147	−0.0192	0.0342	0.0032	0.0295
			$\beta$	0.0751	0.4542	0.0291	0.1509	0.0410	0.1219
			$\delta$	0.0045	0.0433	0.0006	0.0017	0.0066	0.0293
	2	50	$\alpha$	0.3318	0.9574	−0.0362	0.1857	0.0013	0.0214
			$\beta$	0.7134	2.4516	0.1022	0.7926	0.0379	0.1031
			$\delta$	0.1614	0.6438	0.0328	0.1295	0.0745	0.2226
		100	$\alpha$	0.1235	0.4749	−0.0302	0.0936	0.0025	0.0257
			$\beta$	0.2302	1.1271	0.0382	0.4345	0.0353	0.1108
			$\delta$	0.0471	0.3434	−0.0017	0.0659	0.0369	0.1543
		200	$\alpha$	0.0427	0.2836	−0.0292	0.0532	0.0020	0.0291
			$\beta$	0.0653	0.6103	−0.0026	0.2270	0.0297	0.1154
			$\delta$	0.0138	0.2215	−0.0075	0.0362	0.0270	0.1238

Concluding remarks on simulation

.

• 1.By increasing the sample size the values of the parameters tend to the true values of the parameters.
• 2.By increasing the sample size the RMSE of the parameters decreases.
• 3.Bayesian estimation method under squared error loss function has the least RMSE among all estimation methods.
• 4.The MPS provides better estimation values compared with the MLE referring to the value of the RMSE.

Applications to COVID-19 data

In this section, three real data of COVID-19 mortality rates from Italy, Mexico, and the Netherlands [see https://covid19.who.int/] are given to test the EOWR distribution’s goodness of fit. The EOWR model is compared with other related models such as Rayleigh (R), Marshall-Olkin Rayleigh (MOR) [28], Kumaraswamy exponentiated Rayleigh (KER) Rashwan [29] and extended odd Weibull exponential (EOWE) distribution see Afify et.al. [16]. Table 3, Table 4, Table 5 provide values of Crammer-von Mises (W*), Anderson–Darling (A*), and Kolmogorov- Smirnov (KS) statistic and its P-value for all models fitted based on three real data sets. For more information about Covid-19 data see, Abdel-Rahman [31], [32], [33], [34], [35], [36], [40], [30].

Table 3.

MLE estimates, SE, KS test, P-values, W*, and A* for COVID-19 data of Italy.

Italy	$\alpha$	$\beta$	$\delta$	$\lambda$	W*	A*	KS	P-value
EOWR	2.9019	15.8688	0.0551		0.0653	0.3685	0.0828	0.7819
	1.0417	9.3609	0.0170
R	6.5829				0.1328	0.8044	0.1360	0.2056
	0.4285
MOR	0.7578	7.0444			0.1343	0.7990	0.1137	0.4004
	0.3509	0.9770
KER	0.0131	1.6751	1.8468	0.5114	0.1325	0.8022	0.1219	0.3184
	0.0172	2.1649	3.1031	0.8593
EOWE	1.4103	0.0356	0.0710		0.1324	0.8023	0.1239	0.3004
	0.2710	0.1753	0.0116

Table 4.

MLE estimates, SE, KS test, P-values, W*, and A* for COVID-19 data of Mexico.

Mexico	$\alpha$	$\beta$	$\delta$	$\lambda$	W*	A*	KS	P-value
EOWR	1.9711	6.6509	0.0633		0.0293	0.1777	0.0449	0.9815
	0.5438	3.8516	0.0227
R	4.6719				0.1185	0.7626	0.0934	0.3027
	0.2248
MOR	0.6115	5.3157			0.0822	0.5155	0.0602	0.8283
	0.2121	0.6052
KER	0.2670	0.1734	0.9477	1.3805	0.0955	0.6087	0.1227	0.0773
	0.0021	0.0169	0.0663	0.0680
EOWE	2.1998	1.1979	0.1406		0.0908	0.5128	0.0736	0.6017
	0.4146	0.6327	0.0180

Table 5.

MLE estimates, SE, KS test, P-values, W*, and A* for COVID-19 data of Netherlands.

Netherlands	$\alpha$	$\beta$	$\delta$	$\lambda$	W*	A*	KS	P-value
EOWR	1.3172	2.7624	0.0335		0.0262	0.1807	0.0734	0.9932
	0.4285	2.2505	0.0170
R	4.9985				0.0520	0.3158	0.1167	0.7655
	0.4563
MOR	0.6136	5.6754			0.0359	0.2301	0.0832	0.9746
	0.3955	1.1974
KER	0.0115	3.2253	2.3294	0.4031	0.0506	0.3084	0.1046	0.8646
	0.0203	5.5682	7.5032	1.2984
EOWE	2.0538	1.0192	0.1274		0.0272	0.1873	0.0827	0.9758
	0.6509	0.9289	0.0267

The first data represents a COVID-19 mortality rates data belongs to Italy of 59 days, that is recorded from 27 February to 27 April 2020. The data are as follows: 4.571 7.201 3.606 8.479 11.410 8.961 10.919 10.908 6.503 18.474 11.010 17.337 16.561 13.226 15.137 8.697 15.787 13.333 11.822 14.242 11.273 14.330 16.046 11.950 10.282 11.775 10.138 9.037 12.396 10.644 8.646 8.905 8.906 7.407 7.445 7.214 6.194 4.640 5.452 5.073 4.416 4.859 4.408 4.639 3.148 4.040 4.253 4.011 3.564 3.827 3.134 2.780 2.881 3.341 2.686 2.814 2.508 2.450 1.518.

The second data represents a COVID-19 mortality rate data belongs to Mexico of 108 days, that is recorded from 4 March to 20 July 2020. This data formed of rough mortality rate. The data are as follows: 8.826 6.105 10.383 7.267 13.220 6.015 10.855 6.122 10.685 10.035 5.242 7.630 14.604 7.903 6.327 9.391 14.962 4.730 3.215 16.498 11.665 9.284 12.878 6.656 3.440 5.854 8.813 10.043 7.260 5.985 4.424 4.344 5.143 9.935 7.840 9.550 6.968 6.370 3.537 3.286 10.158 8.108 6.697 7.151 6.560 2.988 3.336 6.814 8.325 7.854 8.551 3.228 3.499 3.751 7.486 6.625 6.140 4.909 4.661 1.867 2.838 5.392 12.042 8.696 6.412 3.395 1.815 3.327 5.406 6.182 4.949 4.089 3.359 2.070 3.298 5.317 5.442 4.557 4.292 2.500 6.535 4.648 4.697 5.459 4.120 3.922 3.219 1.402 2.438 3.257 3.632 3.233 3.027 2.352 1.205 2.077 3.778 3.218 2.926 2.601 2.065 1.041 1.800 3.029 2.058 2.326 2.506 1.923.

The third data represents a COVID-19 data belonging to the Netherlands of 30 days, which recorded from 31 March to 30 April 2020. This data formed of rough mortality rate. The data are as follows: 14.918 10.656 12.274 10.289 10.832 7.099 5.928 13.211 7.968 7.584 5.555 6.027 4.097 3.611 4.960 7.498 6.940 5.307 5.048 2.857 2.254 5.431 4.462 3.883 3.461 3.647 1.974 1.273 1.416 4.235.

Concluding remarks on real data

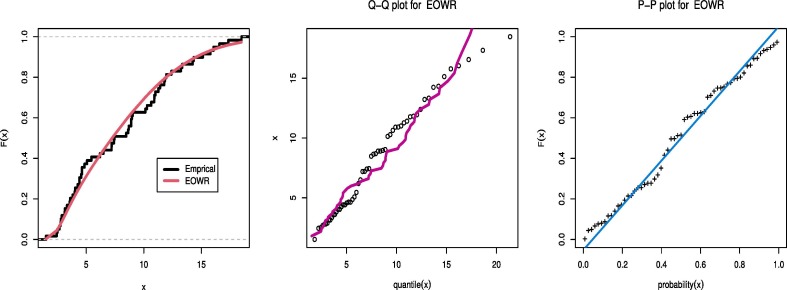
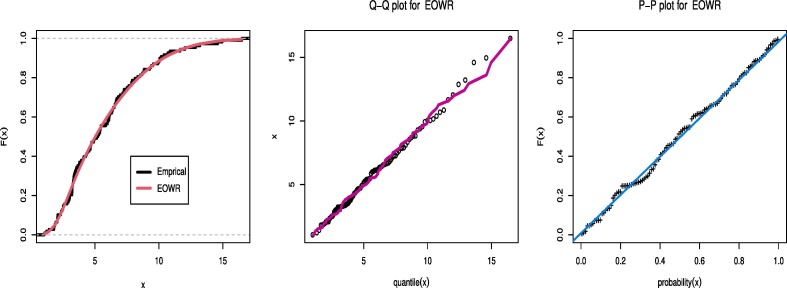
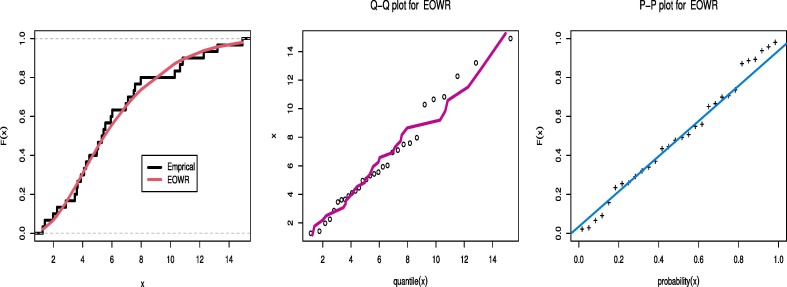
From Table 3, Table 4, Table 5 it is obvious that EOWR distribution has minimum values of all information criteria as W*, A*, and KS compared with other competitive distributions. Also the P-value for KS has the highest value. This leads us to conclude that EOWR is the best fit for the three real data sets. Empirical, Q-Q and P-P plots are shown in Fig. 3, Fig. 4, Fig. 5 , indicate that our distribution is a superior model for modeling the above real data.

Fig. 3.

Estimated PDF, PP-plot and QQ-plot of EOWR for COVID-19 data of Italy.

Fig. 4.

Estimated PDF, PP-plot and QQ-plot of EOWR for COVID-19 data of Mexico.

Fig. 5.

Estimated PDF, PP-plot and QQ-plot of EOWR for COVID-19 data of the Netherlands.

Conclusion

In this paper, we presented a new generalization of Rayleigh and Weibull distributions called EOWR distribution. We studied its statistical properties and obtained a linear representation for its pdf, which was efficient in finding moments, generating function. Different classical and Bayes estimation methods were considered to find point estimation of EOWR unknown parameters $\alpha ,\beta$ and $\delta$. A comparison was conducted via simulation analysis using the R package to distinguish the performance of different estimation methods. MCMC method was used for that purpose, and the Bayesian estimation method was better than classical estimation methods referring to the value of RMSE. Also, three real data sets of COVID-19 mortality rates were considered, and they showed that EOWR provides the best fit for these kinds of data compared with other competitive distributions.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.