Associations of 3-year-olds’ block-building complexity with later spatial and mathematical skills

Abstract

Block-building skills at age 3 are related to spatial skills at age 5 and spatial skills in grade school are linked to later success in science, technology, engineering, and mathematics (STEM) fields (Wai, Lubinski, & Benbow, 2009; Wai, Lubinski, Benbow, & Steiger, 2010). Though studies have focused on block-building behaviors and design complexity, few have examined these variables in relation to future spatial and mathematical skills or have considered how children go about copying the model in detail. This study coded 3-year-olds’ (N = 102) block-building behaviors and structural complexity on 3-D trials of the Test of Spatial Assembly (TOSA; Verdine, Golinkoff, Hirsh-Pasek, & Newcombe, 2017). It explored whether individual differences in children’s building behaviors and the complexity of their designs related to accuracy in copying the model block structures or their spatial and mathematical skills at ages 4 and 5. Our findings reveal that block-building behaviors were associated with concurrent and later spatial skills while structural complexity was associated with concurrent and later spatial skills as well as concurrent mathematics skills. Future work might teach children to engage in the apparently successful block-building strategies examined in this research to evaluate a potential causal mechanism.

Research on block play supports a strong relation between building skill and spatial and mathematical skills (Caldera et al., 1999; Verdine, Golinkoff, Hirsh-Pasek, & Newcombe, 2017). Most prior research has focused on measuring building skill by, for example, coding children’s accuracy in copying models (Stiles & Stern, 2001); coding the strategies used to generate block constructions (e.g., forming a reiterative relation in one direction, Stiles & Stern, 2001); or examining children’s ability to use blocks flexibly (Kamii, Miyakawa, & Kato, 2004). Although some studies have focused only on the accuracy of the end product in block building and its relation to later mathematical skills (Verdine et al., 2017; Wolfgang, Stannard, & Jones, 2001), the process of creating block designs may provide additional information about spatial skills that is not accessible by only scoring their accuracy. Prior work examining the complexity of children’s constructions and the process by which the constructions were built (e.g., Stiles & Stern, 2001; Kamii et al., 2004; Ramani, Zippert, Schweitzer, & Pan, 2014) suggests that there are differences in the approach children use, but these studies did not explore whether the differences predict spatial or mathematical outcomes in subsequent years. The current study extended this prior work by not only exploring the process by which children build their constructions during structured block play, but also by examining how the process relates to later spatial and mathematical outcomes. Specifically, the current study examined whether 3-year-olds’ block-building behaviors and structural complexity during structured block play 1) related to overall accuracy on the building task, and 2) predicted spatial or mathematical skills at ages 4 and 5 above-and-beyond accuracy on the block-building task.

Block Play and Spatial and Mathematical Skills

Structured and unstructured play with blocks and similar puzzles is related to a wide variety of skills including mathematical skills (e.g., Schmitt, Korucu, Napoli, Bryant, & Purpura, 2018; Wolfgang et al., 2001), divergent thinking and problem solving (Pepler & Ross, 1981), and social skills (Owens, Granader, Humphrey, & Baron-Cohen, 2008; Legoff & Sherman, 2006). Yet, structured block play has garnered the most attention for its role in spatial development (Caldera et al., 1999; Verdine et al., 2017). During structured block play, children may be asked to create their own block construction based on a model construction. So why might block-building behaviors and accuracy of constructions during structured block play relate to spatial skills? Children’s ability to copy a model likely taps into the four broad categories of spatial skills as conceptualized by Chatterjee (2008) and later expanded upon by Newcombe and Shipley (2015). Encoding the model to be copied requires an understanding of the intrinsic-static properties of the model (e.g., size and arrangement of blocks). Imagining how the orientations of blocks relate to each other to copy the design may require extrinsic-static skills. Rearranging the blocks to match the model may require extrinsic-dynamic skills, such as perspective taking. Finally, visualizing changes that may improve a child’s construction may require intrinsic-dynamic skills, such as mental rotation. Still, the long-term implications of these relations between block building and spatial skills are unclear.

A few studies have examined the relation between certain block-building behaviors and building success. For instance, in a constructive block play study with 1- to 4-year-olds, participants were asked to create the tallest building possible from 20 blocks (Kamii et al., 2004). Researchers observed their strategies and coded certain behaviors that were later found to relate to building success, which the authors argued reflected a strong grasp of certain spatial concepts. The behaviors included: (1) aligning horizontal edges of blocks, (2) using flat blocks vertically, (3) and combining triangular blocks to create a square base. Additionally, Ramani and colleagues (2014) examined 4- to 5-year-olds’ block constructions during a block-building task and found that vertical block placements were associated with overall complexity of children’s completed block structures indicating a stronger grasp on certain spatial concepts. While describing the structural complexity of block constructions provides some insight into children’s spatial concepts, other spatial assessments were not administered in these prior studies to examine the explicit association between the block-building behaviors, complexity of structures, and other spatial skills.

Other studies have linked the nature of play with blocks to a variety of spatial skills such as spatial visualization (Casey et al., 2008), transformation (Casey & Bobb, 2003), and measurement (Cross, Woods, & Schweingruber, 2009). One study (Verdine, Troseth, Hodapp, & Dykens, 2008) found children with higher spatial visualization scores looked more to the model during a structured jigsaw puzzle task. However, this behavior was not compared to actual block-building performance. Caldera and colleagues (1999) examined the complexity of block play and how it related to children’s performance on a variety of spatial tasks (e.g., WPPSI and WISC Block Design, Embedded Figures, and Copying Blocks). They defined complexity of block play by 1) placing two complementary blocks together (e.g., two ramps to form a rectangle), 2) rotating and flipping blocks before placing them in a structure; and 3) symmetrical placement of blocks. More complex block play during free play was related to better performance on the spatial tasks.

Blocks and mathematics

Using a skill-building framework, block building activities may provide children with opportunities to gain skills that are both directly related to mathematics (e.g., counting blocks) and indirectly related. Perhaps block building facilitates more complex spatial reasoning that is employed during later mathematics learning. Prior correlational studies support links between children’s mathematical skills and spatial construction skills, such as accuracy of copying block models (Verdine et al., 2017); complexity of block play (e.g., stacking blocks to form small towns; Trawick-Smith, Swaminathan, Baton, Danieluk, Marsh, & Szarwacki, 2017); and parent reports of the frequency of children’s constructive activities (Oostermeijer, Boonen, & Jolles, 2014). Moreover, spatial skills, such as mental imagery, may help mediate the concurrent association between block building accuracy and mathematical skills (Pirrone, Nicolosi, Passanisi, & Di Nuovo, 2015).

An experimental study by Schmitt and colleagues (2018) found that providing preschoolers with a play-based, semi-structured block-building intervention marginally helped improve their numeracy, shape recognition, and mathematical language skills. The researchers speculated that during block-building experiences, children need to count the number of blocks and visualize where blocks go in the structure before placing them. Thus, block building may provide children with direct mathematical experiences, such as counting, sorting, measuring, and classifying (e.g., Park, Chae, & Boyd, 2008; Wolfgang et al., 2001; Yelland, 2011).

In addition to providing direct experiences for mathematical reasoning, block building may provide indirect benefits. Prior work suggests that children decompose an already-built structure into units as evidenced by the presence and distinction of rotation and translation errors of certain block placements when trying to build a replica (Verdine et al., 2017). Therefore, we can reason from this prior work that children encode smaller complex units and relations within the structure rather than encoding structures holistically. As such, understanding units with blocks may prepare children for learning that numbers can also be decomposed into smaller units (Clements & Sarama, 2007). Although the mechanisms of the space-math link are a little unclear, prior work suggests several explanations. For example, placing numbers on a number line, an inherently spatial task, reflects an understanding of magnitude (e.g., de Hevia & Spelke, 2009; Gunderson, Ramirez, Beilock, & Levine, 2012) and may be facilitated by dynamic spatial imagery (e.g., Möhring, Frick, & Newcombe, 2018). For comprehensive reviews on the relation between spatial and mathematics skills see Mix (2019); Mix and Cheng (2012); Newcombe, Levine, and Mix (2015); and Lourenco, Cheung, and Aulet (2018).

Even with the established link between spatial and mathematics skills, almost no studies have demonstrated longitudinal associations between early block play and later mathematics skills. However, one study by Wolfgang, Stannard, and Jones (2003) assessed how 4-year-olds’ used LEGOS during unstructured block play using the Lunzer Five-Point Play Scale (1955), which ranged from not using the LEGOS according to the blocks’ “physical or representational properties” to using the LEGOS in a “highly insightful manner, adapted to a concept that clearly transcends it” (Wolfgang et al, 2003, p. 469). Block play scores correlated with several measures of later mathematical skills or interest in middle school and high school. According to the authors, perhaps preschoolers who scored higher on the block play rating were developing the cognitive capabilities that would permit them to perform well in later, higher abstract mathematics (e.g., geometry and trigonometry). However, because the Lunzer scale used broad, subjective terms that are difficult to define (e.g., “highly insightful”), it is impossible to conjecture specific mechanistic relations between block play and later mathematics skills. Overall, this longitudinal study along with the other studies that find links between block play and mathematics skills suggest a skill-building framework; mastering block-building skills may facilitate children’s more complex spatial reasoning that is employed during later mathematics learning.

In all, prior studies examined direct building behaviors on the blocks themselves, such as aligning horizontal edges of blocks (Kamii et al., 2004); placing vertical and horizontal blocks, creating bridges, and block matching (Ramani et al., 2014); and rotating blocks before placing them (Caldera et al., 1999). However, because replicating block designs requires careful building, recognition of errors, and ensuring that additional attempts fix problems, there are other behaviors that could be examined to provide more insight into the block-building process. An additional behavior includes the number of different block reattachments made in attempt to fix errors. Behaviors that do not involve direct action on the blocks may also provide additional insight, such as gazing more to the model to help guide placement of blocks or time for completion. Additionally, prior studies coded the complexity of children’s construction in a multitude of ways, including symmetrical placement of blocks (Caldera et al., 1999); forming small towns (Trawick-Smith et al., 2017); and using blocks according to their physical properties (Wolfgang et al., 2003). The current study examines the 1) different types of building behaviors and structural complexity not previously explored and 2) associations between these building behaviors, structural complexity, and concurrent or later spatial and mathematics skills.

Development of Block-Building Skills Between Ages 3 and 4

Due to rapid development in block-building skills between ages 3 and 4, this timeframe may be fruitful for exploring block-building behaviors and relations to future spatial skills. The ability to construct complex multi-relational designs typically emerges between ages 3 and 4 (Stiles-Davis, 1988; Kamii et al., 2004). Before age 3, block designs are typically restricted to simple, repetitive patterns such as stacks or single lines (Bayley, 1969; Forman, 1982; Gesell, 1925; Stiles-Davis, 1988). However, by age 4 “children produce multicomponent structures with multiple spatial relations, extending in multiple directions in space with multiple points of contact between components” (Stiles & Stern, 2001, p. 159). These developmental changes in early spatial skills may be generated from complex interactions between the child and their environment, which may also leave long-term influences on the child’s spatial development trajectory (Bronfenbrenner & Morris, 2006). Perhaps as 3-year-olds change their environments to daycare or preschool, they are being provided with spatial activities they may not have received in their home environments (e.g., playing with puzzles, learning shapes and their properties, arts and crafts that require spatial visualization skills). In turn, these spatial interactions may boost children’s spatial skills and interest in spatial activities, including block building and spatially-involved domains such as mathematics.

Individual Differences

This boost in block building skill is the trend for most children, but there are important group and individual differences that suggest an influence of early experiences. For example, a study by Verdine et al. (2014) found significant differences in 3-year-olds’ structured block building, specifically on complex designs, such that children from low-socioeconomic status (SES) backgrounds were already lagging behind their higher-SES peers. Early spatial language production and skill are also heavily associated with environmental factors and spatial experiences (Levine, Ratliff, Huttenlocher, & Cannon, 2012; Pruden, Levine, & Huttenlocher, 2011; Levine, Huttenlocher, Taylor, & Langrock, 1999). For example, lower-SES parents report using significantly fewer spatial words with their children compared to higher-SES parents (Verdine, Golinkoff, Hirsh-Pasek, Newcombe, et al., 2014). A similar difference is also found with mathematical school-readiness, such that by preschool many children from low-SES homes are lagging behind their middle-SES peers (Child Trends Databank, 2015).

Environmental differences may perpetuate these early SES differences in spatial and mathematics skills. For instance, lower-SES children may have restricted access to toys that are beneficial for children’s spatial development, including building blocks (Jirout & Newcombe, 2015; Levine et al., 2012). However, one study found no significant difference in the amount of spatial play between SES groups (Jirout & Newcombe, 2015). Even if frequency of spatial play does not relate to SES differences in spatial performance, the quality of spatial play (e.g., the processes and structural complexity in block building) may. Thus, toddlerhood presents a great opportunity for exploring early spatial development from both normative and individual differences perspectives. But, do differences in the acquisition of block skills from age 3 to 4 have meaningful long-term relations to spatial or mathematical outcomes? The few existing studies would suggest they do, though most studies have focused on construction accuracy with no long-term follow-up.

The Current Study

Using the Test of Spatial Assembly (TOSA, Verdine et al., 2017), 3-year-olds’ spatial assembly skills were measured through a series of model reconstruction tasks with flat foam cutout shapes (2-D) and interlocking construction blocks (3-D) (see Figure 1A). The TOSA was selected because 3-year-olds’ overall accuracy predicts approximately 35% of the variability in spatial skills at age 5 (Verdine et al., 2017). A coding system for the 3-D trials of the TOSA was used to explore children’s building behaviors and structural complexity while the 2-D trials were included to broaden the types of spatial skills assessed. The current study explored specific block-building behaviors and types of structural complexity that were not examined in prior work, but are hypothesized to be important for not only accuracy of final block constructions, but for spatial problem-solving skills more generally. Replicating designs requires careful building, recognizing errors, and ensuring that additional attempts fix problems. Thus, children need to look at the model to guide placements (‘Number of Gazes’) and attempt to fix inaccuracies by reattaching pieces in different configurations (‘Number of Reattachments’). Even if an attempt is ultimately incorrect, looking at the design, trying novel arrangements, and spending more time (‘Trial Time’) should be indicative of spatial problem-solving skills not evident from the final accuracy of the product. Coding for these three moment-to-moment building behaviors (number of gazes; number of reattachments; and trial time) offers an opportunity to deeply analyze how children approach these problems. If children who gaze more at the model, have a higher number of reattachments, and have longer trial times have better concurrent and later spatial and mathematics skills, then this could be an area for intervention to explore the suspected causal mechanisms.

Figure 1.

A. The construction models used for each of the 12 TOSA trials. B. Example of a model (top) with a child’s copy (bottom). The model contains two partial overlaps: the red (3×2) and green (2×2) blocks in the top construction cover half of the width of the yellow (4×2) base block. The model also contains one perpendicular arrangement: the red (3×2) block is perpendicular to the yellow (4×2) base block. The child’s copy would receive no partial overlap points but would receive a point for perpendicular arrangement as the child’s copy includes the perpendicular relationship of the red to the yellow block.

In addition to block-building behaviors, the complexity of the block structures is related to concurrent spatial skills (Caldera et al., 1999). Prior work characterized complex arrangements of blocks as involving multiple blocks intersecting through multiple spatial planes (Kamii et al., 2004; Stiles & Stern, 2001). In the current study, some constructions in the 3D TOSA require certain complex arrangements and so, children’s completed block structures were coded on two dimensions of complexity that have not been previously examined: 1) using only half of the width of one of the blocks (‘partial overlap’) and 2) placing blocks perpendicular to one another (Figure 1B). The ability to understand units and the spatial relations between blocks, in addition to accurately composing and decomposing items from their constituent parts, may be indicative of children’s underlying spatial concepts. Even if the block arrangements may not be 100% accurate, children who attempt to build these complex arrangements may have more advanced spatial concepts than children who do not attempt them. Thus, overall construction accuracy alone may not provide a comprehensive assessment of children’s spatial concepts. In combination with the current study’s design to investigate the longitudinal implications of block building processes, exploring children’s use of these behaviors and structural complexity can add significantly to our knowledge of the acquisition of early spatial and mathematical skills.

Research aims and hypotheses

Three specific research questions were addressed: 1) Are block-building behaviors (number of gazes to the model, number of reattachments, and trial time) and structural complexity (number of overlapping pieces and number of perpendicular arrangements) associated with concurrent spatial skills as measured by accuracy on the TOSA?; 2) Do these behavior and structural complexity variables predict future spatial skills over-and-above accuracy on the task?; and 3) Do these behavior and structural complexity variables also predict concurrent and later mathematics skills? An additional aim was to explore if longitudinal relations between initial block-building behaviors or structural complexity and concurrent and later spatial and math skills differ by children’s SES.

We expected the block-building behaviors and structural complexity to be indicative of spatial competence broadly and therefore predictive of scores on other markedly different construction tasks like the 2-D TOSA trials and the non-construction-related spatial tasks administered in subsequent years. Specifically, at age 3, we expected building behaviors (number of looks to the model; number of rearrangements; trial time) to have the strongest associations with TOSA scores since they have obvious links to accuracy. For instance, a child cannot correctly copy something they do not reference or take time to carefully copy. We also expected that the structural complexity variables would relate to other spatial skills assessed at ages 4 and 5. The ability to use complex solutions at age 3 would suggest those children are already ahead in spatial development and more likely to continue to acquire spatial competencies. Given the findings that suggest a relationship between spatial and mathematical skills (e.g., Verdine et al., 2017), we also expected block-building behaviors and structural complexity to have concurrent and long-term associations with mathematics performance. In regards to the exploratory aim of examining SES-group level differences, we expected that building behaviors would be more predictive of later spatial and math skills for low-SES children and that the more advanced block-building process of structural complexity would be more predictive of later spatial and math skills for high-SES children.

Method

Participants

This study was reviewed and approved by the Internal Review Board at the University of Delaware. Participants were 3-year-olds (N = 102; 55 males, 47 females) between the ages of 37.8 and 47.8 months (M = 43.60 months; SD = 2.54) recruited from private preschools and Head Start programs in neighborhoods with mixed socioeconomic status (SES) around a medium-sized mid-Atlantic city. Here we use “SES” as shorthand for the education level of the mother, as Hoff (2013) argued. Those whose mothers received a 4-year college degree or higher were in the higher-SES group and all others were in the lower-SES group (51 higher-SES; 51 lower-SES). Participants were native English speakers with no identifiable speech, vision, or hearing impairments. Testing occurred in preschools in areas with minimal distraction.

Measures – Age 3

Test of Spatial Assembly (TOSA)

Each trial of the TOSA (Verdine et al., 2017; see Figure 1A) involved the experimenter placing a model in front of the child with only the pieces needed to complete the design. While the focus of the current study is on block-building behaviors and structural complexity during the 3D TOSA, the 2D TOSA was included during the age 3 assessments to 1) broaden the types of spatial skills assessed and 2) examine if block-building behaviors and structural complexity would predict to 2-D performance. In both 2- and 3-D trials, the model was left in plain sight for the duration of a trial and participants indicated when they were finished. The 2-D trials required children to copy a printed image of arranged geometric shapes using foam cut-outs of the shapes. For 3-D trials, children used interlocking MegaBloks® to duplicate block arrangements. Videos of children completing these 3-D trials and photographs of the final constructions were taken for coding. The behavior variables, coded from video, are indicative of how children completed designs. Construction complexity variables were coded from still images of completed trials. Krippendorff’s alpha (Hayes & Krippendorff, 2007) is used for reliability, which can be calculated across any numbers of coders or metrics and with unequal sample sizes, providing a single statistic for each variable. Alpha levels above .8 are acceptable with those from .667 to .8 recommended for tentative conclusions (Krippendorff, 2004).

Behavior variables

Three behavior variables were coded. Reattachments counted the number of times per trial a child separated a block and reattached it in a new position; they were not counted if replaced in the same position. Reliability coding on 20% of the sample yielded an acceptable alpha of .85.

Gazes coded the average number of times a child looked at the model for each trial. Initial reliability on 20% of the sample was .65, a little below the traditional acceptable level. Most discrepancies were due to testing locations that made it hard to capture both the child’s eyes and hands on camera, so all participant videos were double-coded. Trials were deemed not codable if the child’s eyes were off screen for more than 15 seconds (52 of 440 total trials). Participants with 3 or more missing trials were removed (N = 12). Trials with discrepancies of more than 4 gazes (15 trials) were coded again by a third coder. If that coder’s count was within 4 of an initial coder, their value replaced the discrepant coder (N = 11). The remaining trials were dropped (N = 4). After policing, the average discrepancy was .81 gazes per trial; all discrepancies were 4 or less and only 18% of trials (69 out of 384) had a discrepancy greater than one. Because the sample was fully double-coded, the average from both coders was used, minimizing any single coder’s influence.

Trial Time recorded how long, in seconds, the child took to complete each trial starting once the child touched the blocks and ending immediately after the child was no longer touching them. Initial reliability coding on 20% of the sample yielded an alpha of .91. Although this was an acceptable level, where there were discrepancies they were large. Therefore, we double-coded the entire sample, finding discrepancies of greater than 15 seconds on 33 trials. These initial discrepancies occurred because of the difficulty in deciding when to start and end the timing of the trial. For example, should the start of a trial be when the child first touches the pieces or starts looking at the model? And should the end be when the child last touches the model or when they attach the last piece? The decision was made to start timing when the child first touched the blocks and stop timing when the child stopped touching the blocks. However, even this simple rule could be complicated by “grabby” children who would touch things as the experimenter was trying to transition between trials, which was almost always the source of discrepancies larger than a second or two. Therefore, a third coder timed the discrepant trials to resolve disputes. After the third coder coded the discrepant times, the largest discrepancy was 9 seconds and alpha was .96.

Because the three behavior variables (number of reattachments, number of gazes, and trial time) were all significantly, positively correlated with one another, a composite “behavior” variable was created. First, each of the three variables were z-scored and then the composite variable was created by averaging these three z-scored variables.

Complexity variables

Two variables coded children’s use of complex block relationships from images of the completed designs: (1) Partial Overlap, which captured the number of times a child attached one block to another using only half of the width of one of the blocks and (2) Perpendicular Arrangement, which captured how often the child attached one block perpendicular to an underlying block if these arrangements were present in the model (only Trials 4 through 6). See Figure 1B for examples of each. These specific configurations seemed to contribute heavily to the difficulty of the designs and children varied in producing them. For instance, some children never tried these arrangements while other children were accurate or inaccurate in producing them. If the children formed accurate partial overlaps then the child’s complex arrangements matched the complex arrangements of the model. If the children formed inaccurate partial overlaps then the two blocks were incorrectly oriented to one another while still forming a partial-overlap. Thus, it is possible that children could have these two types of complex arrangements in their constructions without being accurate. Across all trials, each of five possible partial overlaps and three possible perpendicular arrangements were coded as either 0 (not created) or 1 (created). Thus, the maximum possible score was five for partial overlaps and three for perpendicular arrangements. Reliability coding of 20% of the sample yielded acceptable alpha levels of .88 for partial overlap and .90 for perpendicular arrangement.

Because the two complexity variables (number of partial overlaps and number of perpendicular arrangements) were significantly, positively correlated with each other, a composite “complexity” variable was created. First, each of the two variables were z-scored and then the composite variable was created by averaging these two z-scored variables.

Spatial skill (TOSA accuracy)

The TOSA yielded accuracy scores for the 2-D and 3-D trials (see Verdine et al., 2017 for coding details), which were also combined to create an overall TOSA score. The 2-D trials have markedly different task demands; for example, there is no possibility of a 2-D equivalent to the complexity variables because the 2-D shapes do not interlock and are not placed on top of one another. Because the behavior and structural complexity variables were coded from the 3-D trials, the 2-D trials along with other measures used in the study provide an opportunity to assess the specificity of these block-building variables as indicators of spatial skill. The overall score is the average of the z-scores from the accuracy totals for the 2-D and 3-D trials. Reliability coding of 20% of the sample yielded acceptable levels (alpha = .75).

Mathematical measures

The Early Mathematics Assessment System for Age 3: Number and Operations Subtest (EMAS-3; Ginsburg, Lee, Pappas, & Rosenfeld, 2010) was given as the mathematics measure. The EMAS-3 tests a range of early mathematics skills, such as highest count, number order, and nonverbal addition and subtraction. Alpha for the EMAS-3 subtest is reported as .86 with a test-retest reliability of .79 (Ginsburg et al., 2010). The alpha for the current sample was .74. The highest count was a verbal free counting measure given with the EMAS-3, but because it is a scale variable it was not incorporated in the EMAS total. Thus, the math skills score at Age 3 used in the current analysis was an average of the z-scores from separate highest count and EMAS-3 results.

General vocabulary measure

The 4^th Edition of the Peabody Picture Vocabulary Test (PPVT; Dunn & Dunn, 2007) was administered at age 3 to assess receptive vocabulary. The test asks children to point to the image representing a word from among one target image and three distractors. Administration stops after children answer a block of consecutive items incorrectly. Split-half and alpha reliability for 3-year-olds are ≥0.93 and alternate form and test-retest correlations are ≥0.90. This measure was used as a covariate in the analyses to help control for language skills and general intelligence (Hodapp & Gerken, 1999).

Measures – Age 4

Spatial measures

Age 4 spatial assessments included the Wechsler Preschool and Primary Scales of Intelligence III: Block Design Subtest (WPPSI; Wechsler, 2002) and the Woodcock-Johnson III: Spatial Relations Subtest (WJ-III; Woodcock, McGrew, & Mather, 2001). The WPPSI was administered as per the standardized instructions; children use red and white blocks with various surface patterns to generate a target design. The WJ-III was also administered as per the standardized instructions and consisted of 33 trials with a total possible score of 81 points. Children saw a design on the left side of a page with possible component pieces to the right. A point was awarded for each correctly identified component. A Rasch analysis determined the median reliability for the subtest to be r₁₁ = .81. Scores from each of these tests were z-scored and averaged to create an age 4 spatial skills score.

Mathematical measures

The EMAS: Number and Operations Subtest for Age 4 (EMAS-4; Ginsburg et al., 2010) and Wechsler Individual Achievement Test: Math Problem Solving Subtest (WIAT; Wechsler, 2009) were given. The EMAS-4 assessed skills such as highest count, number comparison, number order, and addition and subtraction. The reported alpha for this EMAS-4 subtest is .93 with a test-retest reliability of .82 (Ginsburg et al., 2010) and .85 with the current sample. The WIAT is a common and widely available assessment of mathematics ability appropriate for 4-year-olds that assessed overall number knowledge including counting, number identification, number magnitude, and children’s understanding of number words such as “more, “less”, “equal”, and “second”. The Math Problem Solving Subtest has an internal reliability of .93 for preschoolers. Scores from EMAS-4 and WIAT were z-scored and averaged to create an Age 4 mathematics skills score.

Measures – Age 5

Spatial measures

The Children’s Mental Transformation Task (CMTT; Levine et al., 1999) and the WJ-III were given at Age 5. The WJ-III was given in identical fashion as the Age 4 administration. The CMTT was included because it has been shown to be a reliable and valid measure of spatial skills related to early childhood spatial activities like puzzle building (Levine et al., 2012). On the CMTT, children were shown an array of four shapes and two target pieces and instructed to (mentally) put the two target pieces together to make one shape. The child was then instructed to point to one of the four shapes to indicate what the shape would look like. The CMTT consists of 32 problems with 8 problems from each of 4 different categories (horizontal translation, diagonal translation, horizontal rotation, and diagonal rotation). Scores from each of these tests were z-scored and averaged to create an Age 5 spatial skills score.

Mathematical measures

At age 5, children were again administered the WIAT and the Jordan Number Sense Brief (NSB; Jordan, Glutting, Ramineni, & Watkins, 2010). The NSB tests a variety of math skills including counting skills, number recognition, number comparison, nonverbal calculation, story problems, and number combinations. The NSB was in the latter stages of its development with an item pool similar to that used in Hassinger-Das, Jordan, Glutting, Irwin, and Dyson (2014). Scores from each test were z-scored and averaged to create an Age 5 mathematics skills score.

Results

A cross-lagged path model, controlling for PPVT, was used to explore all three research aims (see Supplemental Information for detailed information about the analysis and attrition). The power estimates of the significant pathways of interest (i.e., pathways that included block-building behaviors and structural complexity as predictors) ranged from .66 to .99 (M = .78). Although not a main aim of the study, the first section briefly describes the stability and cross-lagged longitudinal relations between spatial and mathematics performance from ages 3, 4, and 5. The following sections describe the results of the cross-lagged path model (see Figure 2) broken down by the three main aims: 1) concurrent associations between building behaviors and structural complexity, and spatial skills as measured by accuracy on the TOSA, 2) longitudinal associations between building behaviors and structural complexity at age 3 with spatial skills at ages 4 and 5, and 3) concurrent and longitudinal associations between block-building behaviors and structural complexity and mathematical skills at ages 3, 4, and 5. The final section describes the results of cross-lagged path model split by low- and high-SES groups to address the exploratory aim of examining if these concurrent and longitudinal associations differ by SES (see Figure S1 in Supplemental Information). See the Appendix for descriptive statistics and partial-correlations (controlling for age 3 general vocabulary) for all variables used in the model.

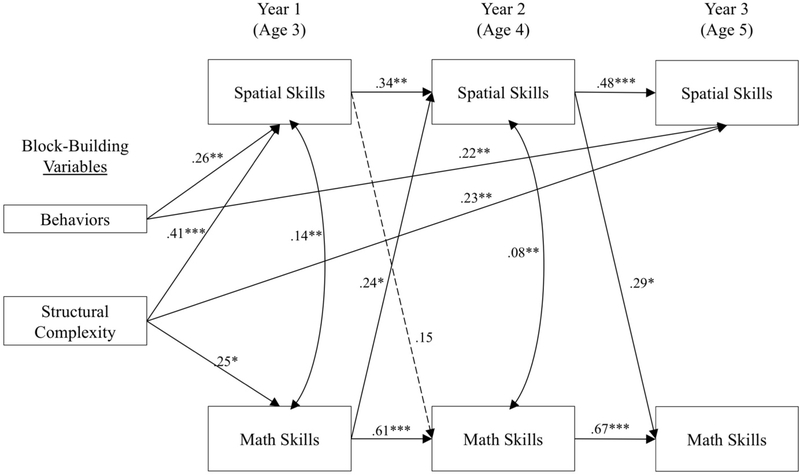
Figure 2.

Cross-lagged path model of associations between block-building behaviors and structural complexity and spatial and math skills over time, including the Age 3 general vocabulary covariate. For simplicity, the covariate and its significant paths are not displayed. Single-headed arrows represent significant regression pathways, whereas double-headed arrows represent significant covariances. Non-significant paths and covariances are also not displayed for simplicity. Path estimates are shown on each arrow. Overall, the model has good fit, robust χ²(4) = 0.96, p = .917.

*p < .05; **p < .01; ***p < .001. Dotted lines indicate marginally-significant paths (p < .07)

Longitudinal Relations Between Spatial and Mathematics Skills

Autoregressive paths

Even though the spatial and mathematics composite performance variables at each year were comprised of various developmentally-appropriate tasks, there were still significant and stable relations between Age 3, 4, and 5 spatial skills as well as relations between Age 3, 4, and 5 mathematics skills.

Cross-lagged paths

Spatial skills at Age 3 marginally predicted mathematics skills at Age 4 (β = 0.14, p = .064), but because this is a marginal path, it will not be interpreted in the Discussion. Additionally, spatial skills at Age 4 predicted mathematics skills at Age 5 (β = 0.29, p = .013). Interestingly, mathematics skills at Age 3 predicted spatial skills at Age 4 (β = 0.24, p = .034).

Aim 1: Concurrent Relations Between Spatial Skills and Block-Building Variables

Both children’s block-building behaviors (β = 0.26, p = .005, power = .83) and complexity of the constructed models (β = 0.41, p < .001, power = .99) were significantly associated with concurrent spatial skills’ accuracy.

Aim 2: Longitudinal Relations Between Spatial Skills and Block-Building Variables

Neither children’s block-building behaviors (p = .736) nor structural complexity (p = .833) predicted Age 4 spatial skills’ accuracy. However, both block-building behaviors (β = 0.22, p = .001, power = .65) and structural complexity (β = 0.23, p = .001, power = .67) significantly predicted Age 5 spatial skills’ accuracy.

Aim 3: Relations Between Mathematics Skills and Block-Building Variables

Concurrent Age 3 Relations

Only children’s structural complexity (β = 0.25, p = .040, power = .70) was significantly associated with concurrent mathematics skills. Block-building behaviors was not significantly associated with concurrent mathematics skills (p = .605).

Longitudinal Age 4 and 5 Relations

Children’s block-building behaviors did not significantly predict Age 4 (p = .649) or Age 5 (p = .107) mathematics skills. Structural complexity also did not significantly predict Age 4 (p = .591) or Age 5 (p = .673) mathematics skills.

Exploratory SES Group Differences

Longitudinal relations between spatial and mathematics skills

For low-SES children, there was no longitudinal stability in spatial skills and little stability in mathematics skills between ages 3, 4, and 5. However, there were significant cross-lagged paths between spatial and mathematics skills over the three years. For high-SES children, there was stability in both spatial and mathematics skills over the three years. However, there were minimal cross-lagged paths between spatial and math skills over the three years.

Relations between block-building variables, spatial skill, and mathematics skills

For the low-SES group, block-building behaviors significantly predicted Age 5 spatial (β = 0.37, p < .001) and mathematics (β = 0.29, p = .007) skills. However, there were no concurrent or longitudinal associations between structural complexity and spatial and mathematics skills. For the high-SES group, block-building behaviors were only significantly associated with concurrent spatial skills (β = 0.29, p = .008). Structural complexity was significantly associated with concurrent spatial (β = 0.51, p < .001) and mathematics (β = 0.35, p = .034) skills as well as later Age 5 spatial skills (β = 0.28, p < .001). Although a marginally significant path, structural complexity was negatively associated with Age 5 mathematics skills (β = −0.15, p = .054). However, given the marginal significance of this negative parameter, it will not be interpreted in the Discussion. See Figure S1 in Supplemental Information for the model split by SES.

Discussion

Here we explored 3-year-old’s block-building behaviors and complexity of built structures in completing the 3-D trials of the TOSA (Verdine et al., 2017) and how they related to concurrent and later spatial and mathematics skills. The processes children use to copy block structures has barely been explored – especially given the established role of blocks in early spatial development (e.g., Casey et al., 2008; Jirout & Newcombe, 2015; Verdine et al., 2017). Though these variables, in some cases, necessarily relate to block building accuracy, focusing on accuracy alone neglects several key elements of how children create designs. Therefore, this work built on prior studies of 3-year-olds’ spatial assembly skills by Verdine et al., (2017) and research suggesting that block-building skills are indicative of their grasp of important spatial concepts (e.g., Caldera et al., 1999; Casey et al., 2008; Kamii et al., 2004; Ramani et al., 2014; Stiles & Stern, 2001). An affordance of the current cross-lagged path model is to explore longitudinal relations between spatial and mathematics skills. In all, spatial and mathematics skills both had separate stable relations from age 3 through age 5. Furthermore, mathematics skills at age 3 predicted spatial skills at age 4 and spatial skills at age 4 predicted mathematics skills at age 5. There were also significant covariances between spatial and mathematics skills at ages 3 and 4. However, given that some of the significant associations were underpowered, the current analysis suggests a space-math link during these early years, but encourages future work to further examine these early associations. The three current research questions are sequentially described below.

Aim 1: Concurrent Relations Between Spatial Skills and Block-Building Variables

Our first question was to examine if block-building behaviors and structural complexity were strongly associated with concurrent spatial skills. Because children were asked to copy block designs during the TOSA, certain behaviors performed during construction and structural complexity (e.g., partial-overlapping and perpendicular arrangements) might relate to their success on the task. The current study focused on three behaviors: 1) number of times children looked to the model, 2) average time spent per trial, and 3) number of times pieces were reattached to different locations on the construction. Block-building behaviors and structural complexity were positively associated with concurrent spatial skills.

We know from prior work on jigsaw puzzles that individuals with higher spatial skills look more to the guiding picture (Verdine et al., 2008). Thus, those who look more to the physical model may gather more of the needed spatial information using their intrinsic- and extrinsic-static spatial skills to add to visuospatial working memory, whereas children who look to the model infrequently likely create a less rich mental representation. When it comes to developing spatial skills, a child who recognizes that looking often is a useful strategy may be a step ahead of another child who looks less, even if they make the same mistakes. However, this association should be taken lightly for two reasons: 1) the reliability of the coding of eye gaze in the current study can only be considered acceptable and 2) there were also missing data points during children’s trials. Regardless, the current evidence provides a foundation for future work to use other methods to examine this behavior of looking at the model for reference and its possible relations with concurrent and later spatial and math skills. In regards to the other two coded behaviors, a longer average trial time and attempting to correct placement of pieces with number of reattachments may both be indicative of children being careful and attempting to construct more accurate structures. In doing so, children may employ intrinsic-dynamic (e.g., mental rotation of blocks) and extrinsic-dynamic (e.g., imagining the structure from various perspectives) spatial skills. Thus, a larger composite ‘behavior’ score indicates a higher frequency of productive behaviors.

Examining structural complexity included coding of complex block arrangements (e.g., partially overlapping blocks and perpendicular arrangements) as characterized as involving multiple blocks intersecting through multiple spatial planes (Kamii et al., 2004; Stiles & Stern, 2001). In the current study, structural complexity was significantly associated with task accuracy. Children who perceive the complex arrangements in the model and actively construct complex arrangements in their own structures have more advanced spatial concepts. When specifically considering partially-overlapping arrangements, though the difference between a complete overlap and a partial overlap was only one set of studs, producing a partial overlap required the use of extrinsic-static spatial skills by imagining how the orientations of blocks relate to each other. Some children never seemed to consider building partially-overlapping arrangements in their structures. Creating partial overlap requires children to conceptualize each individual row or column of studs as unique interlocking points for other blocks. Children who do not segment this way or who, perhaps, can only conceptualize units of equal length and width (i.e., 2 by 2) may only consider a limited number of solutions. Because half of the models in the 3-D TOSA (1–3) do not require this arrangement and the error often results in only a small shift of one set of studs, a failure to think about the blocks as having smaller units will not result in errors on many trials and would not look very obviously wrong to an adult observer of the final construction. Not creating partial overlap, therefore, would not tend to strongly influence scores for most accuracy coding systems. It was only through careful observation of children actively working that we noted some children tended to consistently avoid partial overlap arrangements. Similarly, with perpendicular arrangements, children who perceived the perpendicular arrangement of a set of two blocks and then reconstructed a perpendicular arrangement in their own construction may have more advanced spatial concepts. Some children seemed to notice that two pieces were adjacent to one another in the perpendicular arrangement in the model, however, they were unable to construct the perpendicular relation. Instead, these children placed the two adjacent pieces side-by-side in a parallel relation. Ultimately, the ability to understand units and the spatial relations between blocks, in addition to accurately composing and decomposing items from their constituent parts, may be an underlying skill that is helpful in completing the TOSA. Even more domain-general processes, such as attention, could help contribute to the detection and configuration of these complex arrangements. Overall, this finding of structural complexity relating to block-building accuracy supports prior work (Caldera et al., 1999).

Aim 2: Longitudinal Relations Between Spatial Skills and Block-Building Variables

The second question we addressed was whether block-building behaviors and structural complexity predict future spatial skills over-and-above spatial assembly accuracy. There were no significant relations between the age 3 composite behavior score and structural complexity score and age 4 spatial skills. However, the age 3 composite behavior and structural complexity scores both predicted age 5 spatial skills. The appearance of a correlation two years later may be for several reasons. First, a single year between assessments may have been insufficient to see changes in spatial skills. Second, these findings could be a function of the measures themselves. For example, the CMTT (Levine et al., 1999) by age 5 may require more spatial visualization skills than the age 4 spatial assessment (the WPPSI Block Design subtest), making it easier for correlations to be revealed. The apparent strength of this prediction from behaviors and structural complexity to age 5 spatial skills is noteworthy not only because of the length of time between the initial measurement and the outcome (age 3 to age 5) but also because the spatial tests given at age 5 were quite different. For example, the age 5 spatial tests that assessed mental spatial transformations, like mental rotation (Wiedenbauer & Jansen-Osmann, 2008) or mental folding (Harris, Newcombe, & Hirsh-Pasek, 2013), do not require physical manipulation of materials.

It is important to note that these significant longitudinal associations of the block-building (TOSA) behaviors and structural complexity with later spatial skills hold even when controlling for accuracy on the TOSA. Thus, 3-year-olds who produced these behaviors and perceived and constructed complex arrangements—even if they were not 100% accurate—may have more advanced early spatial concepts that develop overtime and can be useful in future spatial problem-solving tasks. It is also important to acknowledge that the composite variables of block-building behavior and structural complexity may measure additional processes that play a role in later spatial reasoning. For example, behaviors such as referencing the model could be indicative of domain-general processes, such as the use of strategies to help reduce cognitive load or working memory or perseverance. In sum, certain behaviors and the production of complex block arrangements at young ages appear to be indicators of spatial understanding and may prove to be additional indices of spatial competence.

Aim 3: Relations Between Mathematical Skills and Block-Building Variables

The final question we addressed was whether block-building behaviors and structural complexity relate to concurrent and later skills in other domains such as mathematics. Spatial and mathematical skills have been well established as being linked (e.g., Mix & Cheng, 2012), even in young children (Verdine et al., 2017). There are a number of theories about why spatial and mathematical skills may be related (see Mix, 2019 for a short review), including neuroscientific evidence suggesting that the brain regions responsible for some spatial and numerical processing overlap (Ansari, 2008; Dehaene, Piazza, Pinel, & Cohen; 2003; Göbel, Walsh, & Rushworth, 2001). Behavioral work provides additional evidence consistent with a deep connection (Bachot, Gevers, Fias, & Roeyers, 2005; Zorzi, Priftis, & Umiltà, 2002).

Concurrent relations

Structural complexity—but not block-building behaviors—related to children’s mathematics performance at age 3. Although the mechanisms to explain this link are not established, prior work suggests that block-building may require mathematical reasoning, such as counting, sorting, measuring, and classifying (e.g., Park et al., 2008; Wolfgang et al., 2001; Schmitt et al., 2018; Yelland, 2011). Verdine and colleagues (2014) also suggest that building block structures with LEGOs may require an understanding of discrete units and thus, invoke measurement concepts such as counting the pips or studs. This may be why structural complexity and not building behaviors per se relates to children’s concurrent mathematics performance.

Longitudinal relations

Though TOSA accuracy scores appear to tap spatial skills that predict later mathematics performance (Verdine et al., 2017), the block-building behaviors and structural complexity coded in the current study did not significantly relate to later mathematics performance assessed at ages 4 and 5. It is possible the behaviors and complexity variables do not measure the specific aspects of spatial skills that relate strongly with more advanced mathematics skills in this age group, whereas TOSA accuracy does. As Mix et al. (2016) noted, not all components of spatial skills relate to all mathematical skills or vice versa. For young children, specifically, one of the driving forces behind the link may be intertwined mechanisms for understanding magnitude representations (Gunderson et al., 2012; Simms, Clayton, Cragg, Gilmore, & Johnson, 2016) and the variables assessed here may simply not be strongly related to that skill.

Exploratory SES Differences

Verdine et al. (2014) found that children’s performance accuracy on the 3-D trials of the TOSA differed by SES. Here we explored whether the concurrent and longitudinal relations between block-building behaviors or structural complexity and spatial and mathematical skills varied by SES. For high-SES children, it appears that structural complexity at age 3 was related to concurrent and later spatial skills whereas for low-SES children, behaviors were related to later spatial and mathematical skills. These relations were found while controlling for general vocabulary or general intelligence (Hodapp & Gerken, 1999) and thus, it could be that the less spatial block-building behaviors, such as referencing the model, were facilitative for low-SES children whereas more spatial structural complexity was facilitative for high-SES children. Again, due to the small sample size, these exploratory findings of SES differences indicate possible group-level differences. Because lower-SES children fall behind their higher-SES peers in spatial and mathematical skills (e.g., Arnold & Doctoroff, 2003; Verdine et al., 2017), these SES-differentiated pathways between block-building behaviors and structural complexity may provide insight into this achievement gap. Future research should further examine possible SES differences. If these differences are supported, this could imply areas for future spatial interventions. Not all children rely on or produce the same block-building behaviors and structural complexity and some children may benefit more from certain processes.

Limitations and Future Directions

This work demonstrates that understanding how children assemble block design structures during structured block play can be as important in predicting spatial development as the accuracy of their final product. A strength of this work is the longitudinal design with the inclusion of a more comprehensive cross-lagged path model. Yet, this longitudinal design also limited the number of participants and measures that could realistically be collected. In future research, for example, a visuospatial working memory task might be included. Likewise, this work is admittedly exploratory, especially when analyzing possible SES differences. We noted some patterns in children’s block-building behaviors and structural complexity seemed to portend their success on the TOSA and other spatial tasks more broadly, but additional confirmatory work is necessary.

Nonetheless, this study provides strong motivation for doing that work; some of these variables may provide easier ways of coding spatial skills from block constructions and may add predictive power to typical construction accuracy measures. For instance, structural complexity was highly predictive of later spatial skills and could have been easily coded from the pictures of the child’s design when accuracy scoring the TOSA. Understanding when these block-building behaviors and use of complex arrangements emerge and whether any of them are predictive at even younger ages, could also be fruitful. At young ages, most spatial assessments cannot be easily administered and block building accuracy measures are not easily collected. Future work should examine if these behavior and complexity variables are useful as a spatial measure at ages when children’s block playing is more free-form and it is difficult to get them to purposefully copy a specific design.

Conclusion

Block-building behaviors and structural complexity that children demonstrate while engaging in structured block play are strong indicators of children’s overall performance and, more importantly, predict spatial skills across time and beyond the realm of spatial construction accuracy. It is essential to understand how differences in these processes develop because that knowledge could help generate teaching strategies for promoting spatial assembly skills and broader problem-solving approaches. Indeed, block-building interventions marginally supported preschoolers’ mathematics learning (Schmitt et al., 2018), especially those from underserved communities (Bower et al., 2020). Moreover, work by Borriello and Liben (2017) demonstrates that encouragement can positively influence maternal spatial behaviors during block play. Therefore, a safe first step in improving spatial development is to encourage parents and educators to participate in more structured block play with their children and to inform them of the importance of behaviors (e.g., referencing the model) and highlighting spatial relations and the complex ways that blocks can be arranged.

Appendix.

Descriptive statistics and partial-correlations

	N	M	SD	1	2	3	4	5	6	7
1. Complexity	96	0	.95
2. Behavior	66	0	.91	.294**
3. Y1 Spatial	100	0	.84	.560***	.420***
4. Y1 Math	97	−.01	.85	.280**	.021	.376***
5. Y2 Spatial	81	0	.85	.299**	.220	.477***	.372**
6. Y2 Math	81	0	.85	.325**	.129	.474***	.728***	.537***
7. Y3 Spatial	59	0	.87	.499***	.404**	.545***	.366**	.637***	.401**
8. Y3 Math	60	.01	.96	.291*	.269	.515***	.530***	.568***	.682***	.511***
PPVT	97	65.65	20.76
Age	102	43.59	2.54
Reattachment	78	.99	1.14
Gazes	66	3.63	2.30
Trial Time (s)	78	33.43	18.62
Partial Overlap	96	.91	1.33
Perpendicular	96	.63	.84

^*<.05

^**<.01

^***<.001

The table includes partial correlations controlling for PPVT. Variables 1–8 are z-score composite variables, so means were set at 0. Y1, Y2, and Y3 represent year 1, year 2, and year 3 respectively.