Multi-stage adaptive enrichment trial design with subgroup estimation

Abstract

We consider the problem of estimating the best subgroup and testing for treatment effect in a clinical trial. We define the best subgroup as the subgroup that maximizes a utility function that reflects the trade-off between the subgroup size and the treatment effect. For moderate effect sizes and sample sizes, simpler methods for subgroup estimation worked better than more complex tree- based regression approaches. We propose a three-stage design with a weighted inverse normal combination test to test the hypothesis of no treatment effect across the three stages.

1. Introduction

Adaptive enrichment trials adapt the entry criteria based on data observed in the trial so far to restrict enrollment to subjects in whom the experimental treatment is believed to work. Enriching the subject population in the trial can increase statistical power to detect a treatment effect if a new therapy only works in a subgroup of subjects. Additionally, it reduces the number of subjects in the trial who have no apparent benefit from the drug therefore not exposing them to potentially harmful side-effects. Adaptive enrichment literature can be divided into two categories: methods that adaptively enrich based on already pre-specified subgroups and methods where the subgroup is estimated during the trial. Most methods with predefined subgroups specify a single subgroup (Jenkins et al. 2011; Ondra et al. 2016), while some allow predefining several candidate subgroups, usually up to three (Wang et al. 2009; Lai et al. 2014; Liu et al. 2010; Wassmer and Dragalin 2015). A number of publications describe clinical trial designs where the subgroup is estimated and the treatment effect is tested in the same trial (Friedlin and Simon 2005; Jiang et al. 2007, 2010; Simon and Simon 2013, 2017; Zhang et al. 2017, 2018; Diao et al. 2019).

Lipkovich et al. (2017) recently reviewed methods for subgroup estimation. They categorized trials with subgroup estimation into two classes based on the objectives in enrichment. The first class is the enrichment trials where the goal is to find the ‘best subject’ for a given treatment. Subgroup in these methods is usually estimated by fitting a model with interaction. The second class is trials with the goal of finding the optimal treatment rules for a given subject. The goal of our paper is the former, that is, to find the best subjects for a given treatment and to demonstrate that the treatment is better than a control. For subgroup estimation, when dealing with multiple biomarkers, non-parametric tree-based regression methods may be more suited to deal with higher order interactions or unknown forms of relationship between covariates and response (Loh et al. 2014).

In publications with methods where the subgroup is being estimated during the trial, several of these (Simon and Simon 2013, 2017; Zhang et al. 2017; Diao et al. 2019) considered a trial with adaptive enrichment. Simon and Simon (2013) described a multi-stage design with a single biomarker. The best cut-off for the single biomarker was defined as the one maximizing the interaction term. At each stage the best subgroup is estimated and the next stage enrolls subjects from the best subgroup only. Zhang et al. (2018) considered a two-stage adaptive enrichment design with up to two predictive biomarkers where the second stage enrolls subjects in the subgroup estimated using the first stage data. Diao et al. (2019) described a two-stage adaptive enrichment design with a single continuous predictive biomarker and time-to-event endpoint.

The best subgroup is generally defined in one of two ways. The first way is to define the best subgroup as subjects within the biomarker subset where the treatment effect is equal to or higher than a minimally clinically relevant treatment effect (Friedlin and Simon 2005; Renfro et al. 2014). The other way to define the best subgroup is through a utility function (Lai et al. 2014; Graf et al. 2015; Zhang et al. 2017; Graf et al. 2019; Joshi et al. 2019). The utility function specifies the trade-off between the size of the subgroup and the treatment effect in the subgroup. An example of a utility function is the function equal to the square root of subgroup prevalence multiplied by the treatment effect in the subgroup (Lai et al. 2014). Under the assumption of equal variances of the treatment effect in all subgroups, maximizing this utility is the same as maximizing the square root of the prevalence of the subgroup multiplied by the treatment effect in the subgroup and is the same as maximizing the power of the treatment comparison. The subgroup defined this way yields good power of treatment comparison in a post-hoc analysis of an unenriched population when the subgroup is estimated and tested (Joshi et al. 2019). The advantage of the utility function approach is that there is no need to pre-specify the minimum treatment effect.

In this paper, we evaluate a number of methods to estimate the subgroup in an adaptive enrichment trial with the goal of establishing an initial efficacy of a new treatment in any subgroup. We propose a three-stage design where the best subgroup is estimated after stage 1 and refined after stage 2. In Section 2, we give the definition of the best subgroup and illustrate it on several true models for response to treatment as a function of biomarker and treatment. Testing for the treatment effect and the design of the trial is discussed in Section 3. In Section 4 we compare several methods of subgroup estimation via simulations. Conclusions are presented in Section 5.

2. Subgroup estimation methods

Let $X=(X_1,X_2,\mathrm{...},X_M)$ be a vector of continuous biomarkers measured at baseline. We work with $X_m$ in [0,1], m = 1,…,M, as biomarkers can be always rescaled. Subjects are randomized between active treatments. Let T be the treatment indicator, T = 1 for “Active” and T = 0 for “Control”. Let $Y$ be a continuous response variable such that higher values indicate improvement in the well-being of the subject. Let, ${\mu }_T(x)=E(Y|X=x,T=1)$ and ${\mu }_C(x)=E(Y|X=x,$ $T=0)$ be the expected responses of a subject at observed biomarker values, $x$, randomized to the active treatment and the control respectively. For the ith randomized subject with i = 1…, n, $(x_{i1},\mathrm{...},x_{iM},y_i,t_i)$ represents the observed data, where $x_{i1}\mathrm{...}{x}_{iM}$ are the observed values of continuous biomarkers, some or none of which are associated with response to treatment.

To identify the best subgroup, i.e., a subset of the full population that is not too small and shows response to the treatment, we use a utility function to quantify the trade-off between the size of the subgroup and the magnitude of the treatment effect (Lai et al. 2014; Zhang et al. 2017). Let $S\equiv S(X)$ be a subgroup based on the biomarker vector $X.$ A natural form of the utility is,

$$U(S,\gamma )=\pi {(S)}^{\gamma }\left[{\mu }_T(S)-{\mu }_C(S)\right],$$

where $\pi (S)=P(X\in S)$ is the prevalence of the subgroup and $\gamma \in [0,1]$ denotes the corresponding weight. Here ${\mu }_T(S)$ and ${\mu }_C(S)$ are the expected responses to the treatment and the control in the subgroup. For a given value of γ, the best subgroup is then defined as $S^{*}$ where $S^{*}=\arg \max \left\{\pi {(S)}^{\gamma }\left[{\mu }_T(S)-{\mu }_C(S)\right]\right\}$. Lai et al. (2014) considered $U_1=U(S,\gamma =0.5)=$ $\pi {(S)}^{0.5}\left[{\mu }_T(S)-{\mu }_C(S)\right]$. This function is proportional to the power of treatment comparison or, equivalently, the non-centrality parameter in the test for the treatment effect. Joshi et al. (2019) showed that for weights larger than 1, the best subgroup always coincides with the whole population under the assumption that the treatment response in the experimental treatment group is no worse than the response in the control arm. Joshi et al. (2019) considered the utility $U_2=U(S,\gamma =0.75)=\pi {(S)}^{0.75}[{\mu }_T(S)-{\mu }_C(S)]$ that favors larger subgroups compared to U₁.

Defining the subgroup through maximizing a utility allows comparing methods of estimation of the best subgroup using a single measure. We introduce a measure we refer to as $\%U$. It is computed by taking the ratio of the value of the utility corresponding to the estimated subgroup to the value of the utility of the best theoretical subgroup for a given true model and then multiplying by 100%. If the best subgroup is estimated perfectly, the %U is equal to 100%. Methods for subgroup estimation are usually compared using the sensitivity and specificity. Since methods with higher sensitivity usually have lower specificity, one needs to look at both measures to compare estimation methods. We evaluate methods for subgroup estimation using a single measure, %U.

We evaluate several subgroup estimation methods that have been discussed in the literature (Lipkovich et al. 2017). Let $T^{*}$ be the treatment indicator with $T^{*}=1$ for subjects randomized to treatment and $T^{*}=-1$ for subjects on control, in the estimation models. We use T* here to distinguish it from the treatment indicator T = 1 or 0 more commonly used. We will use T = 1 or 0 later to define true models. We use a linear model (LM) as an example to describe our approach that we apply to each of the methods we investigated. Consider a linear model with first and second order main effects for biomarker and all pairwise interaction terms between all available biomarkers and treatment

$$E\left(Y|\mathit{X},T^{\mathrm{*}}\right)=\alpha +\beta T^{\mathrm{*}}+\sum _{m=1}^M{\gamma }_m{X}_m+\sum _{m=1}^M{\rho }_m{X}_m^2+\sum _{m=1}^M{\delta }_m{X}_m{T}^{\mathrm{*}}+\sum _{m=1}^M{\phi }_m{X}_m^2{T}^{\mathrm{*}}+\sum _{l=1}^{M-1}\mathrm{ }\sum _{m=l+1}^M{\lambda }_{lm}{X}_l{X}_m{T}^{\mathrm{*}}.$$

Following Tian et. al (2014), consider a model where the outcome is modified by multiplying the responses of subjects on control by −1 i.e. $E\left(T^{*}Y|\mathit{X},T^{*}\right)$. Since T* = {−1, 1} with probability 0.5 and does not depend on covariates due to randomization, we have

$$E\left(T^{\mathrm{*}}Y|\mathit{X},T^{\mathrm{*}}\right)=\beta +\sum _{m=1}^M{\delta }_m{X}_m^2+\sum _{m=1}^M{\phi }_m{X}_m^2{T}^{\mathrm{*}}+\sum _{l=1}^{M-1}\mathrm{ }\sum _{m=l+1}^M{\lambda }_{lm}{X}_l{X}_m$$ (1)

For a given Δ define an estimated subgroup S(Δ) as $S(\Delta )=\left\{x_i:E(T^{*}Y|x_i)>\Delta \right\}$. Let ${\Delta }^{*}=\arg {\max }_{\Delta }\left\{U(S(\Delta ))\right\}$. The estimated best subgroup, S^*, depends on a specific method of estimating $E(T^{*}Y|x_i)$. We use this approach for all subgroup estimation methods we consider. Let ${\Delta }_i\equiv \Delta (x_i)=E(T^{*}Y|x_i)$ be the expected treatment effect for a biomarker vector $x_i$, that is, the expected treatment effect of subject i, i = 1,…, n. There are at most n candidate subgroups, each indexed by ${\Delta }_i$ in a clinical trial with n subjects. For each expected treatment effect ${\Delta }_i$, i, i = 1,…, n, we can define a corresponding subgroup of subjects with expected treatment effect larger than S(Δ_i). The estimated utility U₁ for this subgroup is a product of the average estimated treatment effect in the subgroup and the square root of the estimated prevalence. Denote the expected treatment effect for which the estimated utility is maximized by ${\Delta }^{*}$, ${\Delta }^{*}={\Delta }_i$, for some i, i = 1,…,n. The best subgroup $\{x:E(T^{*}Y|x)>{\Delta }^{*}\}$ includes subjects with the biomarker vector $x$ such that the estimated treatment effect for that vector is higher than ${\Delta }^{*}$.

Least Absolute Shrinkage and Selection Operator or LASSO (Tibshirani 1996) is a shrinkage and variable selection method based on linear regression. The coefficients in a linear model (1) with covariates $\{X_1,X_2,\mathrm{...},X_M\}$ are estimated by minimizing the sum of squared residuals, with a bound on the sum of absolute value of the coefficients. Alternatively, we minimize the sum of squared residuals plus a penalty term equal to the sum of with absolute values of the coefficients multiplied by $\tau$> 0

$$min\sum _{i=1}^n\mathrm{ }\left(T_i^{\mathrm{*}}{Y}_i-\beta -\sum _{m=1}^M\mathrm{ }{\delta }_m{X}_{im}-\sum _{m=1}^M\mathrm{ }{\phi }_m{X}_{im}^2-\sum _{l=1}^{m-1}\mathrm{ }\sum _{m=l+1}^M\mathrm{ }{\lambda }_{lm}{X}_{il}{X}_{im}\right)+\tau \left(\sum _{m=1}^M\mathrm{ }\left[\left|{\delta }_m\right|+\left|{\phi }_m\right|\right]+\sum _{l=1}^{m-1}\mathrm{ }\sum _{m=l+1}^M\mathrm{ }\left|{\lambda }_{lm}\right|\right)\mathrm{ }.$$

Large values of $\tau$ put a higher penalty and shrinks most coefficients to zero and lead to under-fitting. Smaller values of $\tau$ result in LASSO shrinking coefficients of some covariates (if not considered important) to zero and can thus can help with variable selection by removing covariates that are not associated with the outcome. Yuan and Lin (2006) developed a group LASSO method where the covariates are considered together in non-overlapping groups. If a specific group is selected, then the coefficient estimates of all those in the group will be non-zero and zero if they belong to a group not selected. An advantage of forming groups is that we avoid choosing the interaction term if the corresponding main effects are not selected. A disadvantage of using just grouped LASSO is that it prevents model variables from belonging to multiple groups. Zeng and Breheny (2016) improved upon the group LASSO by adding an overlap condition allowing for a model variable to belong to more than one group and thus have a non-zero coefficient if any of the groups it belongs to is selected. To illustrate, suppose that covariates $X_1$ and $X_2$ are the only two covariates associated with the treatment effect and, therefore, the group with three elements G₁ = $\left\{X_1,X_2,X_1{X}_2\right\}$ is the group that is related to treatment effect. If we do not use overlapping group LASSO, then if G₂ = $\{X_1,X_3,X_1{X}_3\}$ is not selected, the coefficient for $X_1$ is set to 0, even though it is present in G_1. We used the overlapping group LASSO (OGLASSO) method of Zeng and Breheny (2016) in the simulations. The linear model is re-formulated in terms of the group coefficients that are obtained by minimizing,

$$min{\left(T^{*}Y-\tilde{X}\theta \right)}^T\left(T^{*}Y-\tilde{X}\theta \right)+\tau \left(\sum _{g=1}^G\sqrt{K_g}\left|\right|{\theta }^g\left|\right|\right)$$

Here, ${\theta }^g=({\theta }_1^g,\mathrm{...},{\theta }_M^g)$ is the $M\text{x}1$ vector of coefficients corresponding to each original predictor in the $g^{th}$ group with $\sum _{\mathbf{g}=1}^{\mathbf{G}} {\mathit{\theta }}^{\mathbf{g}}=\left({\delta }_1,...,{\delta }_m,{\varphi }_1,...,{\varphi }_m,{\lambda }_1,...,{\lambda }_{\left(M-1\right)m}\right)\prime$, $\theta$ is the vector of all ${\theta }^g$, $\tilde{X}$ is the new design matrix corresponding to $\theta$, G is the number of groups and $K_g$ is the number of elements in the $g^{th}$ group. When ${\theta }^g$ is selected, all model variables in this group are selected, irrespective of whether they are present in another group. Once the model coefficients are estimated, we define ${\Delta }_i$= $E(T^{*}Y|x_i)$ and estimate the best subgroup as before.

A tree-based method, Classification And Regression Trees (CART) (Breiman et al. 1984), recursively partitions the data into two disjoint subsets by minimizing the heterogeneity of the outcome in each partition. The resulting prediction model can be illustrated by a single decision tree and the terminal nodes of the tree can be interpreted as subgroups. For a continuous outcome, the partitioning is based on minimizing the residual sum of squares. We perform post-pruning based on the complexity parameter of 0.01.

In the tree-based method of Random Forests (RF) (Breiman 2001), the predicted value is an average over a collection of trees rather than a single tree as in CART. We use 500 trees while implementing this method. Unlike a single decision tree in CART, random forests prediction model cannot be described as a set of rules as the CART model, making it a ‘black box’ type prediction model.

Support Vector Machine (SVM) introduced by Cortes and Vapnik (1995) is used for both classification and regression problems. In case of a continuous outcome, it fits a hyperplane or a function such that all points on either side of this function are within a certain pre-defined distance from the function and there is a penalty for points falling outside the range. The regression method seeks to find a linear function which can be used to predict the outcome for each subject. We compare these four methods in the simulation study in Section 4 to give recommendations on the method to be used for subgroup estimation in a clinical trial.

3. Adaptive design with enrichment

We propose a three-stage enrichment design for a randomized trial comparing a new treatment with a control. We enroll a total of n subjects, n₁ + n₂ + n₃ = n, with n_k subjects enrolled in the kth stage, k = 1, 2, 3. At each stage, the subjects are equally likely to be randomized to the experimental treatment arm or the control arm. The dual objective of the trial is to demonstrate the efficacy of a new therapy in any subgroup and to estimate the best subgroup. The best subgroup is defined as the subgroup that maximizes the utility U₁. We propose the following three-stage design:

• (1)In stage 1, n₁ subjects are enrolled from the full population, n_1//2 receive active treatment and n_1//2 receive the control. At the first interim analysis, using data from stage 1, the best subgroup is estimated based on maximizing utility U₂.
• (2)In stage 2, subject population is fully enriched. That is only subjects from the subgroup estimated at the end of stage 1 are enrolled. At the second interim analysis, we use data from n₁ + n₂ subjects enrolled so far to estimate the subgroup based on maximizing a utility U₁.
• (3)In stage 3, only subjects from the subgroup estimated at the end of stage 2 are enrolled.
• (4)At the end of the trial, let Z_k be the test statistic to test $H_0$ based on stage k data, defined as

$$Z_k=\frac{{\widehat{\mu }}_{T,k}-{\widehat{\mu }}_{C,k}}{{\widehat{\sigma }}_k\sqrt{\frac{1}{0.5n_k}+\frac{1}{0.5n_k}}},$$

where ${\widehat{\mu }}_{T,k}$and ${\widehat{\mu }}_{C,k}$ are the estimated mean responses in treatment and control arms respectively and ${\widehat{\sigma }}^2{}_k$ is the estimated common variance for treatment and control groups at stage k, k = 1,2,3.

Consider the test statistic:

$$\tilde{Z}=\sqrt{n_1/n}{Z}_1+\sqrt{n_2/n}{Z}_2+\sqrt{n_3/n}{Z}_3$$

A test based on $\tilde{Z}$ preserves the type I error rate since, conditional on the enrollment decision taken at the end of stages 1 and 2, the components Z_k are independent. A similar approach for testing the hypothesis of no treatment effect was used in Simon and Simon (2013). Assuming that the response to the new treatment is not worse than the control for any set of biomarkers, the test $\tilde{Z}$ is the test for any treatment effect $H_0:{\mu }_T-{\mu }_C=0$. We maximize U₂ to estimate the best subgroup at stage 1 in order to estimate a larger subgroup, and then at stage 2, using U₁, we can narrow down to the correct subgroup. We maximize U₂ after stage 1 since the U₂–defined subgroup is the same or larger than the U₁–defined subgroup and contains the U₁–defined subgroup. After stage 2, we narrow down the estimated subgroup but considering the U₁-defined subgroup.

In stage 2, only subjects from the estimated best subgroup are enrolled. This leads to oversampling of subjects in the best estimated subgroup in the combined stage 1 and stage 2 sample. Hence, we need to use inverse probability weighting when working with the combined stage 1 and 2 sample, for example, when maximizing utility U₁. Each subject in the estimated best subgroup, stage 2 population, regardless of the stage of enrollment, is assigned a weight of ${\widehat{\pi }}_1/(1+{\widehat{\pi }}_1)$ where ${\widehat{\pi }}_1$ is the estimated prevalence of the best estimated subgroup from stage 1 that was used to sample stage 2 population. Otherwise, the weight is 1. The weights are used after the model is fitted at the utility maximization step described in Section 2.

To adjust the mean response, the set of subjects with predicted response less than the predicted cutoff after stage 1 is weighted by the corresponding ‘true’ proportion.

Since a new therapy might not work, we consider a possibility of stopping for futility at the end of stage 2. If the new therapy only works in a small subgroup of subjects, the observed treatment effect might be low after stage 1 when the new therapy is investigated in the full population. Therefore, stopping for futility is considered at the end of stage 2. At the end of stage 2, we compute the test statistic ${\tilde{Z}}_2=\sqrt{n_1/(n_1+n_2)}{Z}_1+\sqrt{n_2/(n_1+n_2)}{Z}_2$. The trial is stopped for futility if ${\tilde{Z}}_2<b$. The cut-off b is computed based on a desired probability of stopping for futility under the alternative hypothesis.

Placing futility analysis earlier in a trial leads to more savings in the expected sample size in a trial (Chang et al., 2020). However, in our set-up, if there is a relatively small subgroup of patients with a sizable treatment effect with low or no treatment effect in other patients, there is a danger of stopping for futility when futility is tested in an unenriched population. That is why we propose to test for futility after stage 2, after the population was enriched. If accrual is slow and the outcome is observed relatively quickly, more stages than three should be considered with futility assessment and prospective enrichment at each interim analysis.

4. Simulation Study

4.1. Comparison of subgroup estimation methods

First, we compare the performance of the five subgroup estimation methods described in Section 2 for several true models via simulations. The best subgroup is defined as the subgroup that maximizes the utility U₁. In the change-point models below, the best subgroup either includes everyone or is defined by the function of biomarkers in the indicator function of the model. To find whether it is the former or the latter, we compute U₁ on both of these candidate subgroups and select the one with the larger value of U₁. In more complex cases, for example, in model 5, one can find the best subgroup by generating a large set of biomarker vectors, e.g., 100,000. The expected treatment effect values are then computed for each of the vectors and the values are ordered to find the value of the treatment effect such that the utility U₁ is maximized for all the biomarker vectors that yield the values of the treatment effect larger than the specified.

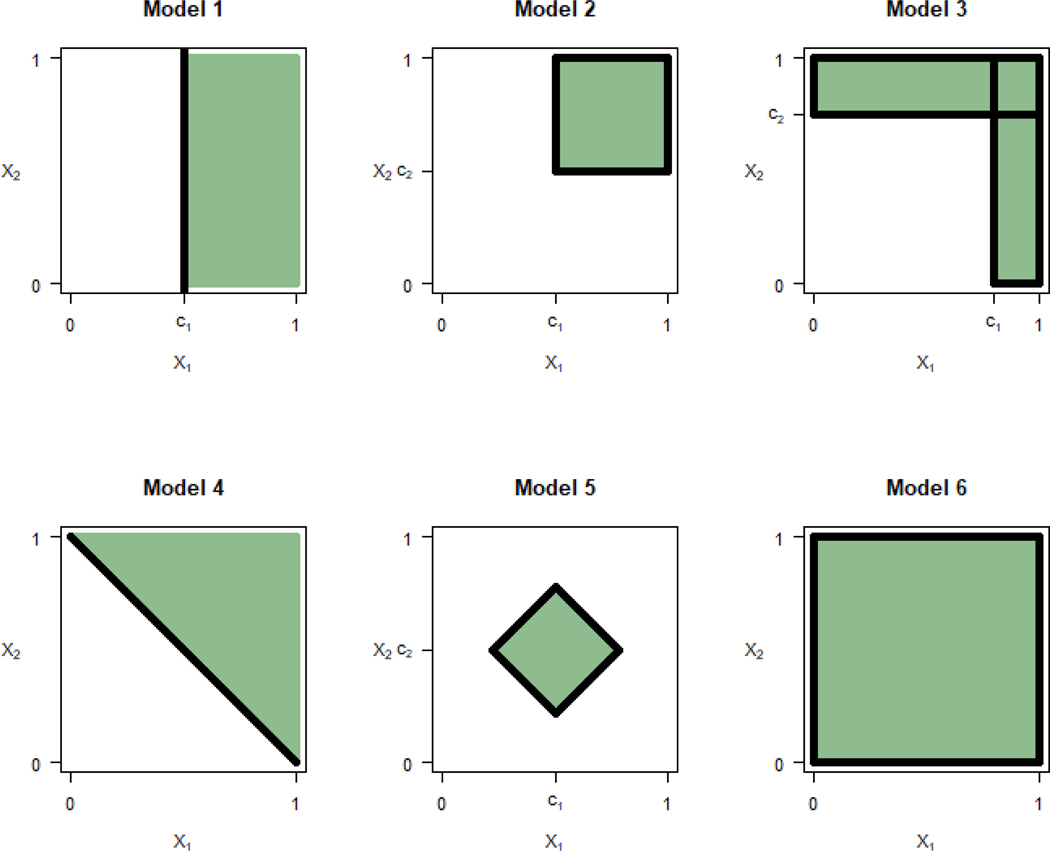
In the models below $X_m~U(0,1)$, m = 1,2, and $Y~N(E[Y|X,T],1)$. The treatment indicator variable T is defined as T = 1 for an active treatment and T = 0 for a control. Figure 1 shows the best subgroup for each of the examples.

Figure 1:

Best subgroup for models 1–6

Model 1. Change-point model with a single biomarker with

$$E\left[Y|X,T\right]=\mu T+\theta I\left(X_1>c_1\right)T$$

When $\mu =0,$ $\theta =0.4$ and c₁ = 0.5, the subgroup that maximizes U₁ for this model is $S^{*}=\{X_1>0.5\}.$ For this best subgroup, the treatment effect is $\delta =0.4$, the prevalence is ${\pi }_{U_1}=P\left[X\in S^{*}\right]=0.5$ and the utility is $U_1=\delta \sqrt{{\pi }_{U_1}}=\mathrm{0.28.}$ Note that another candidate for the best subgroup is the subgroup that includes all subjects. The corresponding utility is 0.2, lower than the utility for S*.

Model 2. Change-point model with two biomarkers with

$$E\left[Y|X,T\right]=\mu T+\theta I(X_1>c_1\text{ and }{X}_2>c_2)T$$

When $\mu =0,$ $\theta =0.4$, c₁ = c₂ = 0.5, the subgroup that maximizes U₁ for this model is $S^{*}=\{X_1>0.5\text{ and }{X}_2>0.5\}.$ For this best subgroup, the treatment effect is , the prevalence is ${\pi }_{U_1}=P\left[X\in S^{*}\right]=0.25$ and the utility is $U_1=\delta \sqrt{{\pi }_{U_1}}=0.20$.

Model 3. Change-point model with two biomarkers with

$E\left[Y|X,T\right]=\theta \text{ [}I(X_1>c_1)(X_2<c_2)+I(X_1<c_1)(X_2>c_2)+I(X_1>c_1)(X_2>c_2)]T$.

When $\theta =0.3$, c₁ = 0.8 and c₂ = 0.75, the best subgroup that maximizes U₁ is $S^{*}=S_1\cup S_2$ where $S_1=\{X_1>0.8\text{ and }{X}_2<0.75\}$, $S_2=\{X_1<0.8\text{ and }{X}_2>0.75\}$. For the best subgroup, the treatment effect is , the prevalence is ${\pi }_{U_1}=P[X\in S^{*}]=0.40$ and the utility is $U_1=\delta \sqrt{{\pi }_{U_1}}=\mathrm{0.19.}$

Model 4. Change-point model with two biomarkers with

$$E\left[Y|X,T\right]=\mu T+\theta I((X_1+X_2)>c)T$$

When $\mu =0,$ $\theta =0.38$, and c = 1, the best subgroup that maximizes U₁ for this model is For the best subgroup, the treatment difference is $\delta =0.38$, the prevalence is ${\pi }_{U_1}=P\left[X\in S^{*}\right]=0.5$ and the utility is $U_1=\delta \sqrt{{\pi }_{U_1}}=0.27$.

Model 5. A model with two biomarkers with

$$E\left[Y|X,T\right]=\mu e^{-\theta (|X_1-c_1|+|X_2-c_2|)}T$$

The best subgroup $S^{*}$ when $\mu =1.5$, $\theta =6.5,$ c₁ = 0.5 and c₂ = 0.5 is shown in Figure 1. The average treatment effect in the best subgroup is $\delta =0.5$, the prevalence is ${\pi }_{U_1}=0.15$ and the utility is $U_1=\delta \sqrt{{\pi }_{U_1}}=\mathrm{0.19.}$

Model 6. A model with $E\left[Y|X,T\right]=\mu T$. When $\mu =0.5$, the subgroup includes everyone, ${\pi }_{U_1}=1$, with the treatment effect of $\delta =0.5$ and utility of $U_1=\delta \sqrt{{\pi }_{U_1}}=\mathrm{0.5.}$

We compared the performance of the five methods, LM, OGLASSO, CART, RF and SVM, applied to data generated from models 1–6 and considering four biomarkers X₁, X₂, X₃, X₄. Predictions for LM, OGLASSO, CART, RF and SVM were obtained by using functions lm, grpreg Overlap, rpart, randomForest, and svm in R with default parameters for all, except we used OGLASSO with $\tau =0.05$. We used a fixed value of $\tau =0.05$ rather than getting $\tau$ via cross-validation (Tibshirani and Tibshirani 2009) because a fixed value had better performance in the simulations with normally distributed outcome.

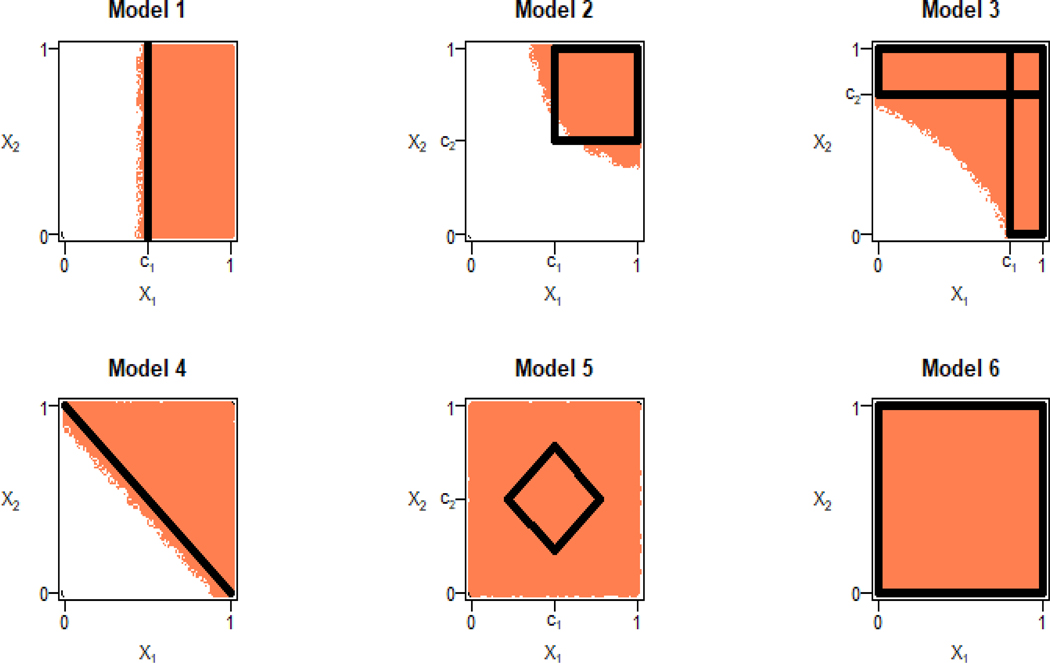
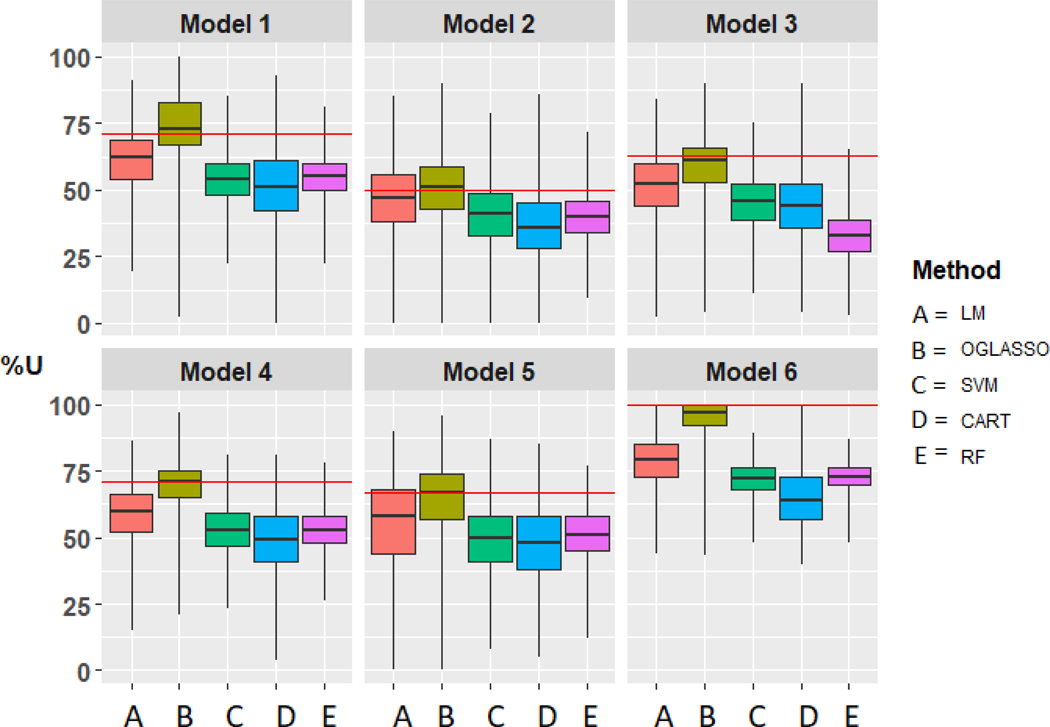
Figure 2 shows the subgroups estimated using LM with two biomarkers, X₁ and X₂, and unlimited sample size. The same figure corresponds to subgroup estimation by applying OGLASSO to X₁ and X₂ and additional noise biomarkers with unlimited sample size when OGLASSO provides perfect variable selection. We simulated data from the models 1–6 above with n = 400 subjects, 200 in the active treatment and 200 in the control arm. We added two noise biomarkers, X₃ and X₄, to evaluate variable selection performance of the methods. Figure 3 shows the box plots for the distribution of %U based on 3000 simulation runs for methods LM, OGLASSO, SVM, CART and RF. For all models, OGLASSO performs the best, followed by LM, SVM, CART and RF. As far as variable selection by OGLASSO, we computed the proportion of times the right set of biomarkers, X₁ in model 1, X₁ and X₂ in models 2–5 were selected. The right set of biomarkers was selected 8% of the time in models 1–5. In model 6, no biomarkers are associated with the treatment response and OGLASSO made this conclusion in 3% of the runs. In about 3% of the trials for models 1–5 OGLASSO incorrectly concluded that no biomarkers were associated with the treatment response.

Figure 2:

Large sample subgroup estimation for models 1–6 using linear model applied to two biomarkers.

Figure 3:

Comparison of the Linear Model (LM), Overlapping Group LASSO (OGLASSO), Support Vector Machines (SVM), Classification and Regression Trees (CART) and Random Forests (RF) for subgroup estimation in a clinical trial with 400 subjects with four biomarkers using box plots for the distribution of %U. Horizontal line represents %U in all subjects.

We conclude that linear model-based methods are the best to use for estimation of the subgroup based on four biomarkers, one or two of which are associated with treatment response. To serve as a reference for results presented in Figure 3, the %U in all subjects generated from Models 1–6 are 71, 50, 63, 71, 67 and 100 respectively.

4.2. Enrichment design

We consider a design that estimates the subgroup by maximizing U₂ after stage 1, and enrolls only subjects from the estimated subgroup in stage 2. Stage 3 is enriched based on the subgroup estimated at the second interim analysis that maximizes U₁. The total sample size in the trial is n = 360 subjects with stage-wise sample sizes of $n_1=n_2=n_3=360/3=120$.

We used models 1, 2, and 4 from Section 4.1 to simulate the outcomes in the trial, models D1-D5 below. In change-point models we use ${\pi }_0$ to denote the prevalence of the biomarker space where the treatment effect is higher, then the average treatment effect in all comers, Δ, can be computed as $\Delta =\mu +\theta {\pi }_0$. The prevalence of the best subgroup for U₁ and U₂ is shown in Table 1.

Table 1:

Adaptive three-stage design with the total sample size of n = 360 with data generated from models D1-D5. Columns ${\widehat{\pi }}_{U_1}$and $\%U$show the median, 25th and 75th percentiles.

Model	Prevalence of true subgroups	Prevalence of estimated subgroup, ${\widehat{\pi }}_{U_1}$	$\%U$ of estimated subgroup	Power without enrichment	Power with enrichment	Power with enrichment and futility	Probability to stop for futility
D1	${\pi }_{U_2}=0.60$ ${\pi }_{U_1}=0.60$	0.72 (0.60, 0.85)	80 (73, 85)	0.78	0.84	0.84	0.05
D2	${\pi }_{U_2}=0.64$ ${\pi }_{U_1}=0.64$	0.72 (0.59, 0.85)	90 (81, 96)	0.73	0.77	0.77	0.07
D3	${\pi }_{U_2}=1.00$ ${\pi }_{U_1}=0.21$	0.63 (0.50, 0.78)	70 (62, 73)	0.53	0.60	0.60	0.14
D4	${\pi }_{U_2}=0.46$ ${\pi }_{U_1}=0.46$	0.67 (0.56, 0.79)	70 (64, 75)	0.66	0.80	0.79	0.07
D5	${\pi }_{U_2}=1.00$ ${\pi }_{U_1}=1.00$	0.77 (0.63, 0.91)	87 (79, 95)	0.81	0.82	0.81	0.05

Model D1: Model 1 with $\mu =0.05,$ $\theta =0.4$, c₁ = 0.4, yielding ${\pi }_0=0.6$ and Δ = 0.29.

Model D2: Model 4 with $\mu =0.05,$ $\theta =0.35$, c = 0.85, yielding ${\pi }_0=0.64$ and Δ = 0.28.

Model D3: Model 2 with $\mu =0.10,$ $\theta =0.55$, c₁ = 0.65, c₂ = 0.4, yielding ${\pi }_0=0.21$ and Δ = 0.21.

Model D4: Model 2 with $\mu =0$, $\theta =0.55$, c₁ = 0.32, c₂ = 0.32, yielding ${\pi }_0=0.46$ and Δ = 0.25.

Model D5: Model 2 with $\mu =0,$ $\theta =0.30$, c₁ = 0 and c₂ = 0, yielding ${\pi }_0=1.00$ and Δ = 0.30.

We used OGLASSO described in Section 2 to estimate the subgroup as it performed better than other methods (Section 4.1). As before, the methods were applied to four biomarkers such that either one or two of them were effect modifying in all true models considered and the other three or two were noise biomarkers. The total sample size, n = 360, was chosen to yield 60% – 80% power in the simulated trials. This corresponds to the average effect size, averaging effect sizes before and after enrichment, of about 0.3. Because of enrichment, the average effect size in the patient population in our trial is higher than the average effect size in all patients. Futility stopping was implemented at the second interim analysis. The futility boundary b = 1.0356 was computed to yield the probability of stopping for futility of γ = 0.10 if the true effect size is 0.3. The treatment effect of 0.3 yields power of 1 – β = 0.81 when the total sample size is 360 and the type I error rate is two-sided α = 0.05. The formula for the futility stopping cut-off b is $b=\left[{\Phi }^{-1}(1-\alpha /2)+{\Phi }^{-1}(1-\beta )\right]\sqrt{240/360}+{\Phi }^{-1}(\gamma )$. Here Φ⁻¹( ) is an inverse of the standard normal cumulative distribution function.

Table 1 shows the results for $\%U$ and power for testing for the treatment effect in an enriched population for the design using OGLASSO with $\tau =0.075$ in the first interim analysis and $\tau =0.05$ in the second interim analysis. Using $\tau =0.075$ in OGLASSO drops more biomarkers compared to $\tau =0.05$. If a biomarker is dropped after stage 1, sampling in stage 2 is continued across the full range of the biomarker providing information for OGLASSO analysis after stage 2. This is the reason for using a larger value of τ in the first interim analysis.

To understand what the %U metric means, we computed %U for the subgroup that includes all subjects. That is, what %U do we have if we do not estimate the subgroup. These are 83%, 85%, 72%, 68% and 100% for models D1-D5 correspondingly. %U is 100% for model D5 because the treatment effect is constant across all values of all biomarkers and, hence, the best subgroup coincides with the overall population. The median %U of the estimated subgroup after stage 2 (Table 1) was close to above %U values. That is, if improving %U was our main focus, we would have been better off including everyone in the best subgroup rather than estimating the subgroup. The prevalence of the estimated subgroup was much higher than the prevalence of the true subgroup in models D1-D4. Even the 25th percentile of the prevalence of the estimated subgroups was higher than the true prevalence in models D1-D4. In model D5, where there is no subgroup and the treatment effect is the same everywhere yielding the prevalence of the true subgroup of 100%, the median prevalence of the estimated subgroup was 87%. We conclude that we cannot achieve perfect subgroup estimation with 240 subjects, 120 per arm, given effect sizes in models D1-D5.

The power in partially enriched population was higher by 5%−13%, however, compared to a non-enriched trial for models D1-D4. For example, for model D4, power without enrichment was 66% compared to 79% with enrichment. In the null model, not shown in Table 1, the type I error rate was preserved, as expected, because subgroups were estimated prospectively. With a futility look added at the second interim analysis, power decreased by about 1%. The probability of stopping for futility was in the range 0.05 – 0.14 under the alternative hypothesis, while it was about 0.75 under the null hypothesis (not shown in Table 1). We conclude that the proposed design can be useful for evaluation of treatments that might not work in all subjects as it increases power through prospective patient population enrichment, though subgroup estimation is not perfect.

Two variations of the design were also considered – in the first variation we maximized $U_1$ at interim 1 and in the second variation we did not estimate a subgroup at interim 1 and enrolled everyone in stage 2. These designs did not perform better (results are available from the authors) compared to the design illustrated in Table 1.

4. Discussion

We considered the problem of estimating the best subgroup and testing for treatment effect in a clinical trial. The best subgroup was defined through maximizing the non-centrality parameter, utility $U(c,\gamma )=\pi {(c)}^{\gamma }\left[{\mu }_T(c)-{\mu }_C(c)\right]$. We introduced a metric $\%U$ to measure the quality of estimation of the subgroup. It is the % of the ratio of the utility in the estimated subgroup to the true utility of the underlying model. For several true models of response as a function of treatment and biomarkers, we compared four methods of estimation of the best subgroup, linear model, RF, CART and SVM. For moderate sample sizes, fitting a linear model-based method with main effect and first order pairwise interaction terms performed better than more complex methods such as RF, CART and SVM.

We propose a three-stage enrichment design where the subgroup is estimated at both interims 1 and 2. At the first interim analysis the subgroup is estimated by maximizing the utility U₂. The three-stage design we proposed can be used for initial assessment of efficacy of treatment that is not believed to be efficacious in all patients, but might be efficacious in a subgroup of patients. If such a treatment is investigated in a trial with all comers, the efficacy signal will be diluted and might be missed. Adaptive enrichment allows the signal detection even when the subgroups of patients for whom the treatment is working has a rather small prevalence.