Estimating publication bias in meta-analyses of peer-reviewed studies: A meta-meta-analysis across disciplines and journal tiers

Abstract

Selective publication and reporting in individual papers compromise the scientific record, but are meta-analyses as compromised as their constituent studies? We systematically sampled 63 meta-analyses (each comprising at least 40 studies) in PLoS One, top medical journals, top psychology journals, and Metalab, an online, open-data database of developmental psychology meta-analyses. We empirically estimated publication bias in each, including only the peer-reviewed studies. Across all meta-analyses, we estimated that “statistically significant” results in the expected direction were only 1.17 times more likely to be published than “nonsignificant” results or those in the unexpected direction (95% CI: [0.93, 1.47]), with a confidence interval substantially overlapping the null. Comparable estimates were 0.83 for meta-analyses in PLoS One, 1.02 for top medical journals, 1.54 for top psychology journals, and 4.70 for Metalab. The severity of publication bias did differ across individual meta-analyses; in a small minority (10%; 95% CI: [2%, 21%]), publication bias appeared to favor “significant” results in the expected direction by more than threefold. We estimated that for 89% of meta-analyses, the amount of publication bias that would be required to attenuate the point estimate to the null exceeded the amount of publication bias estimated to be actually present in the vast majority of meta-analyses from the relevant scientific discipline (exceeding the 95th percentile of publication bias). Study-level measures (“statistical significance” with a point estimate in the expected direction and point estimate size) did not indicate more publication bias in higher-tier versus lower-tier journals, nor in the earliest studies published on a topic versus later studies. Overall, we conclude that the mere act of performing a meta-analysis with a large number of studies (at least 40) and that includes non-headline results may largely mitigate publication bias in meta-analyses, suggesting optimism about the validity of meta-analytic results.

1 ∣. INTRODUCTION

Publication bias—that is, the selective publication of “statistically significant” results¹—has compromised the integrity of the scientific record.² Empirical results often replicate at lower than expected rates (e.g., References ^3-7), “p-hacking” (i.e., intentionally or unintentionally rerunning analyses to attain “statistically significant” results) appears widespread,^8,9 and results in some top social sciences journals exhibit severe publication bias.^10,11 Most attention on publication bias and scientific credibility to date has focused on individual published papers, often those in higher-tier journals. In contrast, meta-analyses represent an arguably higher standard of scientific evidence, and the implications of publication bias in individual papers on meta-analyses are not clear. Are meta-analyses of biased literatures simply “garbage in, garbage out”, or are meta-analyses more robust to publication bias than are their constituent studies?

Some existing work has investigated the prevalence of “small-study effects” (i.e., systematically different point estimates in small vs. large studies) in meta-analyses by testing for funnel plot asymmetry^12,13 and estimating the percentage of systematically sampled meta-analyses with “statistically significant” funnel plot asymmetry; these estimates include 7% to 18% among Cochrane Database meta-analyses,¹⁴ 13% among meta-analyses in Psychological Bulletin and the Cochrane Database,¹⁵ and 27% among medical meta-analyses.¹⁶ However, the purpose of these existing studies was not to provide a pure assessment of publication bias, as many of the asymmetry tests they used detect small-study effects that can reflect heterogeneity in addition to publication bias.^13,16 Other investigators have reported strong publication bias in meta-analyses by applying the excess significance test,^17,18 but this method may substantially overestimate publication bias if population effects are heterogeneous,^19,20 which is the case in many meta-analyses.²¹ Other methods that have been used to empirically assess publication bias often require population effects to be homogeneous.¹⁵

We built upon prior work by conducting a new meta-analysis of meta-analyses that we systematically collected from four sources, which spanned a range of journals and disciplines. We used a selection model^22,23 to estimate publication bias severity across all the meta-analyses, within sources, and within disciplines. Additionally, to explore hypothesized study-level contributors to publication bias, we assessed whether studies published in higher-tier journals exhibit more publication bias than those in lower-tier journals^24,25 and whether the chronologically first few studies published on a topic exhibit more publication bias than later studies (the “Proteus effect”^26,27).

2 ∣. METHODS

2.1 ∣. Systematic search methods

We systematically searched for meta-analyses from four sources: (1) PLoS One; (2) four top medical journals:ⁱ New England Journal of Medicine, Journal of the American Medical Association, Annals of Internal Medicine, and Lancet; (3) three top psychology journals: Psychological Bulletin, Psychological Science, and Perspectives on Psychological Science; and (4) Metalab, an online, unpublished repository of meta-analyses on developmental psychology. Metalab is a database of meta-analyses on developmental psychology whose datasets are made publicly available and are continuously updated; these meta-analyses are often released online prior to publication in peer-reviewed journals.^28,29 We selected these sources in order to represent a range of disciplines, particularly via the inclusion of PLoS One meta-analyses. Additionally, because selection pressures on meta-analyses themselves may differ by journal tier, we chose sources representing higher-tier journals, a middle-tier journal with an explicit focus on publishing all methodologically sound papers regardless of results (PLoS One), and a source that is not a standard peer-reviewed journal (Metalab). We chose these specific medical and psychology journals because they are among the highest-impact journals in these disciplines that publish original research, including meta-analyses.

For the three published sources, we reverse-chronologically reviewed each meta-analysis published after 2013 until we had obtained data suitable for reanalysis to fulfill or surpass prespecified sample sizes (Supporting Information). We considered meta-analyses published after 2013 because we had first searched PLoS One reverse-chronologically until we reached prespecified sample sizes, which resulted in meta-analyses published after 2013. Then, when searching the other sources, we also considered only meta-analyses published after 2013 for consistency with the PLoS One sample. Our inclusion criteria were: (1) the meta-analysis comprised at least 40 studies to enable reasonable power and asymptotic properties to estimate publication bias;^22,23 (2) the meta-analyzed studies tested hypotheses (e.g., they were not purely descriptive); and (3) we could obtain study-level point estimates and standard errors as described in Section 2.2. Regarding the 40-study criterion for articles that reported on more than one meta-analysis (e.g., because they performed meta-analyses by subgroup), we considered only the meta-analysis with the largest number of studies. For PLoS One, we defined three disciplinary categories (social sciences, natural sciences, and medicine) and searched until we had obtained at least 10 usable meta-analytic estimates per discipline.

Because relatively few meta-analyses were published in the top medical and top psychology journals, we included all eligible meta-analyses published after 2013.ⁱⁱ For the unpublished source, Metalab, we used publicly available data to include the meta-analyses^30-34 meeting the above inclusion criteria. We conducted the searches on December 20, 2018 (PLoS One), May 13, 2019 (the top medical journals), May 4, 2019 (the top psychology journals), and May 26, 2019 (Metalab). For PLoS One, we used PubMed to search “meta analysis[Title] AND ‘PLoS One’[Journal],” restricting the search to 2013 onward. For the top medical and top psychology journals, we either used comparable PubMed search strings provided online (https://osf.io/cz8tr/) or we directly searched the journal's website for papers with “meta-analysis” in the title or abstract. For Metalab, we used Table 1 from Tsuji et al.³⁵ to screen 10 existing Metalab meta-analyses using our inclusion criterion for the number of point estimates.

TABLE 1.

Overall and within-group estimates of the selection ratio ($\mathrm{S}\widehat{\mathrm{R}}$) from robust meta-analyses

Group	k	$\mathit{S}\widehat{\mathit{R}}$ [95% CI]	max $\mathit{S}\widehat{\mathit{R}}$	q95	$\widehat{\tau }$	p-value versus PLOS
Overall	58	1.17 [0.93, 1.47]	54.77	3.51	0.63
PLoS One	30	0.83 [0.62, 1.11]	2.95	1.70	0.52	Ref.
Medical	9	0.97 [0.58, 1.63]	2.12	1.37	0.26
Natural sciences	11	0.59 [0.32, 1.06]	2.81	1.55	0.63
Social sciences	10	1.07 [0.66, 1.73]	2.95	1.75	0.40
Top medical	6	1.02 [0.52, 1.98]	2.39	1.62	0.39	0.50
Top psychology	17	1.54 [1.02, 2.34]	7.80	4.84	0.63	0.01
Metalab	5	4.70 [1.94, 11.34]	54.77	9.94	0.43	0.005

Note: k: number of analyzed meta-analyses; max $S\widehat{R}$: maximum estimated selection ratio among the group's meta-analyses; q₉₅: estimated 95th quantile of true selection ratios among the group's meta-analyses; $\widehat{\tau }$: meta-analytic estimate of the standard deviation of log-selection ratios; p-value: meta-regressive inference for the difference in publication bias severity versus all PLOS One meta-analyses.

2.2 ∣. Data extraction

We extracted study-level data using publicly available datasets, datasets we obtained by contacting authors, or data we manually extracted from published forest plots or tables. We also excluded studies from the grey literature, which we defined as those that were not published in a peer-reviewed journal or peer-reviewed conference proceeding. Grey literature therefore included, for example, dissertations, book chapters, and statistical estimates that the meta-analysts obtained by contacting other investigators. We excluded grey literature for several reasons. First, we were primarily interested in the specific selection pressures that shape the peer-reviewed literature, the cornerstone of the scientific canon. The selection pressures affecting the grey literature may differ from those affecting the peer-reviewed literature, for example, if the preferences of peer reviewers and journal editors contribute strongly to publication bias. If we had included grey literature, this could give an impression of less publication bias than actually affects the canonical, peer-reviewed literature. Additionally, we speculated that disciplinary norms regarding the inclusion of grey literature in meta-analyses may differ substantially, potentially complicating our comparisons of publication bias severity across disciplines. For example, as of the year 2000, the majority of medical meta-analyses did not include grey literature,³⁶ and this seemed to remain true in our more recent sample of medical meta-analyses. On the other hand, our impression is that recent meta-analyses in experimental psychology usually do involve grey literature searches, perhaps reflecting recently heightened attention within this discipline to publication bias and the “replication crisis.”³

To minimize data entry errors, we used independent dual coding by a team of six research assistants (Acknowledgments) and the first author, and we used stringent quality checks to verify data entry. Details of the data extraction process appear in the Supporting Information, and the final corpus of meta-analyses is publicly available (excluding those for which we could obtain data only by contacting the authors) and is documented for use in future research (https://osf.io/cz8tr/). For each meta-analysis in the top medical and top psychology groups, we coded each meta-analyzed study by journal, publication year, and the journal's Scimago impact rating.³⁷ Scimago ratings are conceptually similar to impact factors, but weight a journal's citations by the impact of the citing articles rather than treating all citations equally. Additionally, unlike impact factors, Scimago ratings are available in a single, standardized online database.³⁷ We coded each study by its journal's Scimago rating in 2019 or the most recent available rating regardless of the study's publication year in order to avoid conflating overall secular trends in scientific citations with relative journal rankings. We defined “higher-tier” journals as those surpassing a Scimago rating of 3.09 for psychology (chosen such that the lowest-ranked “higher-tier” journal was Journal of Experimental Psychology: General and all specialty journals were considered “lower-tier”) or 7.33 for medicine (chosen such that the lowest-ranked “higher-tier” journal was Annals of Internal Medicine).ⁱⁱⁱ All other journals were defined as “lower-tier.”

To assess whether publication bias was more severe for the first few studies published on a topic compared to later studies, we coded studies as being published “early” vs “later” as follows. For each meta-analysis, we considered the first chronological year in which any study was published; if multiple studies were published that year, then all point estimates from those studies were coded as “early.” If instead only one study was published during the first year, then all point estimates from all studies published during the chronologically first 2 years were coded as “early.” All point estimates not coded as “early” were coded as “later.”

2.3 ∣. Primary statistical analyses

2.3.1 ∣. Estimates of publication bias severity

We estimated publication bias using selection models (e.g., References^22,23,38), a class of statistical methods that assume that publication bias selects for studies with statistically “significant” results in the expected direction, such that these results (which we term “affirmative”) are more likely to be published than statistically “nonsignificant” results or results in the unexpected direction (which we term “nonaffirmative”) by an unknown ratio. This selection ratio represents the severity of publication bias: for example, a ratio of 30 would indicate severe publication bias in which affirmative results are 30 times more likely to be published than nonaffirmative results, whereas a ratio of 1 would indicate no publication bias, in which affirmative results are no more likely to be published than nonaffirmative results. This operationalization of publication bias, in which “statistically significant” results are more likely to be published, conforms well to empirical evidence regarding how publication bias operates in practice^8,39 and provides an intuitively tractable estimate of the actual severity of publication bias itself. Selection models essentially detect the presence of non-affirmative results arising from analyses that were conducted but not reported; these results are therefore missing from the published and meta-analyzed studies. Specifically, we used a selection model that specifies a normal distribution for the population effect sizes, weights each study's contribution to the likelihood by its inverse-probability of publication based on its affirmative or nonaffirmative status, and uses maximum likelihood to estimate the selection ratio.^22,23 The normal distribution of population effects could reflect heterogeneity arising because, for example, studies recruit different populations or use different doses of a treatment; even if these moderators are not measured, selection models can still unbiasedly estimate the severity of publication bias as long as the type of heterogeneity that is present produces approximately normal population effects.^22,23

As in standard meta-analysis, selection models assume that studies' point estimates are independent, but this assumption may be violated when some studies contribute multiple point estimates to a meta-analysis (e.g., estimates of a single intervention's effect on different subject populations). To minimize the possibility of non-independence, we randomly selected one point estimate per study within each meta-analysis and then fit the selection model to only these independent estimates. Because the “expected” effect direction differed across meta-analyses, we first synchronized the signs of all point estimates so that positive effects represented the expected effect direction. To this end, we first reanalyzed all point estimates using restricted maximum likelihood estimation and the R package metafor and, treating the sign of the resulting pooled point estimate as the expected effect direction, reversed the sign of all point estimates for any meta-analysis with a negative pooled point estimate. We fit a selection model to estimate the inverse of the selection ratio and its standard error.^22,23 We then used robust methods⁴⁰ to meta-analyze the log-transformed estimates of the selection ratio, approximating their variances via the delta method. We used the R packages weightr⁴¹ and robumeta,⁴² respectively, to fit the selection model and robust meta-analysis.

To characterize variability across individual meta-analyses in publication bias severity, we calculated non-parametric calibrated estimates of the true selection ratio in each meta-analysis.⁴³ Intuitively, the calibrated estimates account for statistical uncertainty in the selection ratio estimates by shrinking the estimate in each meta-analysis toward the overall meta-analytic average selection ratio, such that the least precisely estimated selection ratios receive the strongest shrinkage toward the meta-analytic average.⁴³ As a post hoc analysis, we estimated^44,45 the percentage of meta-analyses with selection ratios greater than 1 (indicating any amount of publication bias in the expected direction, regardless of severity), greater than 1.5, and greater than 3. Likewise, we estimated the percentage of meta-analyses with selection ratios smaller than symmetric thresholds on the opposite side of the null (i.e., 1/1.5 ≈ 0.67 and 1/3 ≈ 0.33), representing “publication bias” that unexpectedly favors nonaffirmative results. To characterize the upper limit of publication bias that might be expected in our sample of meta-analyses, we calculated the maximum estimate of the selection ratio; however, this is a crude, upward-biased measure because sampling error introduces more variation in the study-level estimates than in the underlying population effects.⁴³ Therefore, we additionally estimated the 95th quantile of the true selection ratios using the calibrated estimates [43]. We did this using the R package MetaUtility.⁴⁶ We conducted the latter analyses across all meta-analyses as well as by group and, within the PLoS One group, by discipline. We conducted a number of sensitivity analyses to assess the impacts of possible violations of modeling assumptions, all of which yielded similar results (Supporting Information).

2.3.2 ∣. Study-level indicators of publication bias

For the top medical and top psychology meta-analyses, but not those in PLoS One or Metalab,^iv we assessed the association of the tier of the individual study's journal with two study-level measures of publication bias: whether the study was affirmative^v per Section 2.3 and the size of its point estimate. To characterize the size of each study's point estimate relative to those of other studies on the same topic, we computed within-meta-analysis percentiles of point estimates. We used percentiles rather than raw effect sizes to provide a metric that is comparable across meta-analyses regardless of their differing numbers of studies, mean effect sizes, and measures of effect size. We estimated the percentages of affirmative results and mean point estimate percentiles by journal tier (higher-tier vs. lower-tier), and by study chronology (early vs. later publication date). As a post hoc analysis, we estimated the overall risk ratio of an affirmative result comparing higher-tier to lower-tier journals (i.e., the relative probability of an affirmative result in higher-tier vs. lower-tier journals) using log-binomial generalized estimating equations models with robust inference to account for correlation of point estimates within studies and meta-analyses.^47,48 We also conducted a comparable set of descriptive and regression analyses regarding a study's chronology, including all four groups of meta-analyses.

3 ∣. PRIMARY RESULTS

3.1 ∣. Corpus of meta-analyses

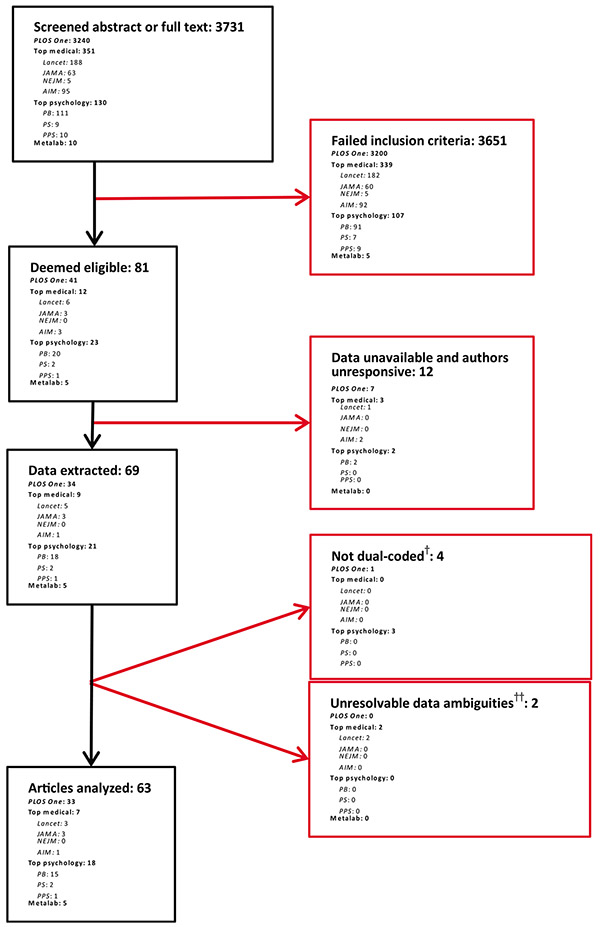
Figure 1 is a PRISMA flowchart depicting the inclusion and exclusion of meta-analyses. Our ultimate dataset comprised 63 meta-analyses: 33 in PLoS One, 7 in top medical journals, 18 in top psychology journals, and 5 in Metalab. A spreadsheet describing the scientific topics of each meta-analysis and our methods of data extraction for each is available online (https://osf.io/cz8tr/). Of the PLoS One meta-analyses, 10 were categorized as medical, 11 were social sciences, and 12 were natural sciences. We obtained study-level data from publicly available datasets for 27 meta-analyses, by scraping published figures or tables for 23 meta-analyses, and by contacting authors for the remaining 13 meta-analyses. The total number of point estimates after the removal of studies from the grey literature^vi was 12 494, and the meta-analyses comprised a median of n= 80 point estimates each. The total numbers of point estimates within each group are provided in Tables 2 and 3. When we reanalyzed the peer-reviewed studies within each meta-analysis using robust meta-analysis to accommodate clustering of point estimates within studies,⁴⁰ the mean magnitude of pooled point estimates after synchronizing their directions as described in Section 2.3 and without correction for publication bias was 0.52 for standardized mean differences (k=29 meta-analyses), 1.33 for ratio measures, including odds ratios, hazard ratios, risk ratios, and mean ratios (k=13), and 0.22 for Pearson's correlations (k=15). An additional six meta-analyses used other, less common types of effect size.^vii

FIGURE 1.

PRISMA flowchart depicting article screening and exclusion process. Black boxes on the left indicate meta-analyses that remained in the pool of assessed articles at each step; red boxes on the right indicate meta-analyses excluded at each step of assessment. ^†Meta-analyses not dual-coded due to data collection time constraints. Metalab is omitted because these meta-analyses were intentionally single-coded. ^††Meta-analyses that were excluded due to unresolvable ambiguities in their datasets; see Supporting Information for details

TABLE 2.

Probabilities of affirmative results overall, by journal tier, and by a study's chronology as one of the first few published (“early”) versus as one of the later studies published (“later”)

Group	n	P(affirm)	P(affirm ∣ top-tier)	P(affirm ∣ lower-tier)	P(affirm ∣ early)	P(affirm ∣ later)
PLoS One	3636	0.36 [0.33, 0.39]			0.50 [0.28, 0.72]	0.32 [0.27, 0.36]
Top medical	558	0.47 [0.37, 0.56]	0.26 [0.04, 0.48]	0.50 [0.39, 0.61]	0.58 [0, 1]	0.46 [0.37, 0.56]
Top psychology	7501	0.59 [0.56, 0.62]	0.56 [0.50, 0.63]	0.59 [0.56, 0.63]	0.53 [0.37, 0.69]	0.59 [0.56, 0.62]
Metalab	799	0.43 [0.38, 0.48]	0.53 [0.29, 0.76]	0.41 [0.36, 0.46]	0.64 [0.37, 0.91]	0.41 [0.36, 0.46]

Note: PLoS One was omitted from journal tier analyses. Cluster-robust confidence intervals are presented, accounting for correlation of p-values within studies. n: number of point estimates in group (which may exceeded number in each analysis due to missing data); P(affirm): probability of an affirmative result.

TABLE 3.

Mean within-meta-analysis percentiles of point estimates ($\overline{Q}$) overall, by journal tier, and by a study's status as one of the first three (“early”) published versus as one of the later studies published

Group	n	${\overline{\mathit{Q}}}_{\text{higher}-\text{tier}}$	${\overline{\mathit{Q}}}_{\text{lower}-\text{tier}}$	${\overline{\mathit{Q}}}_{\text{early}}$	${\overline{\mathit{Q}}}_{\text{later}}$
PLoS One	3636			0.46 [0.35, 0.58]	0.51 [0.49, 0.54]
Top medical	558	0.40 [0.26, 0.55]	0.52 [0.46, 0.58]	0.40 [0.08, 0.72]	0.52 [0.47, 0.57]
Top psychology	7501	0.50 [0.47, 0.54]	0.51 [0.49, 0.52]	0.56 [0.44, 0.69]	0.51 [0.49, 0.52]
Metalab	799	0.61 [0.52, 0.71]	0.49 [0.46, 0.52]	0.62 [0.43, 0.80]	0.49 [0.46, 0.52]

Note: PLoS One was omitted from journal tier analyses. n: number of point estimates in group (which may exceeded number analyzed due to missing data).

Among top medical and top psychology meta-analyses (those used in journal tier analyses), 18% of point estimates were published in higher-tier journals. Among the meta-analyses that were published in top medical journals, 4% of estimates were in higher-tier journals. Among the meta-analyses in top psychology journals, 18% of estimates were in higher-tier journals. We extracted journal tier data for 95% of point estimates in top medical and top psychology meta-analyses; some data were missing because the study's journal had apparently not received a Scimago ranking, and we excluded these point estimates in journal tier analyses. We manually coded journal year data for a convenience sample of all meta-analyses, including 75% of all point estimates; 3% of these point estimates were published early (ranging from 3% to 5% within the four groups). To obtain this convenience sample, we assigned the manual coding of each meta-analysis to two of our six research assistants in a manner that would equalize their workloads given meta-analyses' differing sizes; the research assistants then worked on coding their assigned meta-analyses until the end of their summer positions.

3.2 ∣. Estimates of publication bias severity

We estimated the selection ratio using a total of 58 meta-analyses; we excluded estimates from meta-analyses with fewer than three affirmative studies or fewer than three nonaffirmative studies to minimize problems of statistical instability.^22,23 The analyzed meta-analyses had a median of n=49 independent point estimates per meta-analysis, with an overall total of 3,960 estimates. Via meta-meta-analysis, we estimated that affirmative results were 1.17 times more likely to be published than nonaffirmative results (95% CI: [0.93, 1.47]). Table 1 and Figure 2 display estimates by disciplinary group and by individual meta-analysis, respectively. In PLoS One meta-analyses, affirmative results were an estimated 0.83 (95% CI: [0.62, 1.11]) times as likely to be published than nonaffirmative results, which is in fact in the direction opposite what would be expected with publication bias favoring affirmative results (albeit with a wide confidence interval that overlaps the null). Meta-analyses in top medical journals (selection ratio estimate: 1.02; 95% CI: [0.52, 1.98]; p = 0.50 vs. PLoS One) exhibited very little publication bias, and those in top psychology journals (estimate: 1.54; 95% CI: [1.02, 2.34]; p = 0.01 vs. PLoS One) exhibited some, though not extreme, publication bias in the expected direction. In contrast, in Metalab, affirmative results were an estimated 4.70 times more likely to be published than nonaffirmative results (95% CI: [1.94, 11.34]; p = 0.005 vs. PLoS One), though the wide confidence interval indicated considerable uncertainty. A post hoc F-test for overall differences between groups yielded p = 0.048.

FIGURE 2.

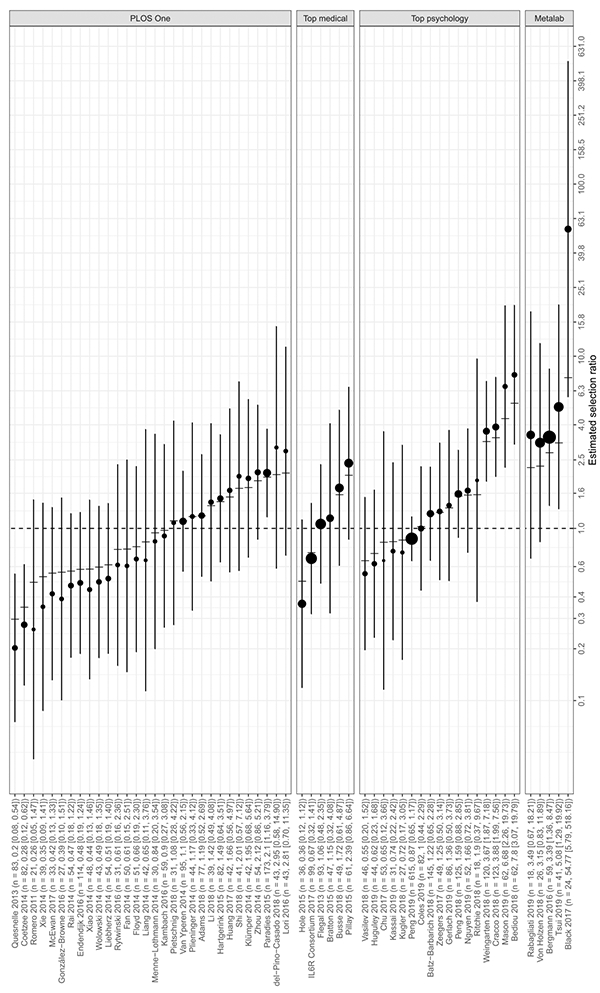
Selection ratio estimate for each meta-analysis, ordered by group and by the calibrated estimate of the meta-analysis' true selection ratio (vertical tick marks). The label for each meta-analysis shows n, the number of analyzed (i.e., independent) point estimates in the meta-analysis, and the estimated selection ratio with a 95% confidence interval. Colored circles represent point estimates of the selection ratio in each meta-analysis, with areas proportional to the meta-analysis' relative weight in the within-group meta-analyses of selection ratios. The x-axis is presented on the log scale. Error bars represent 95% confidence intervals. The vertical dashed line represents the null (no publication bias)

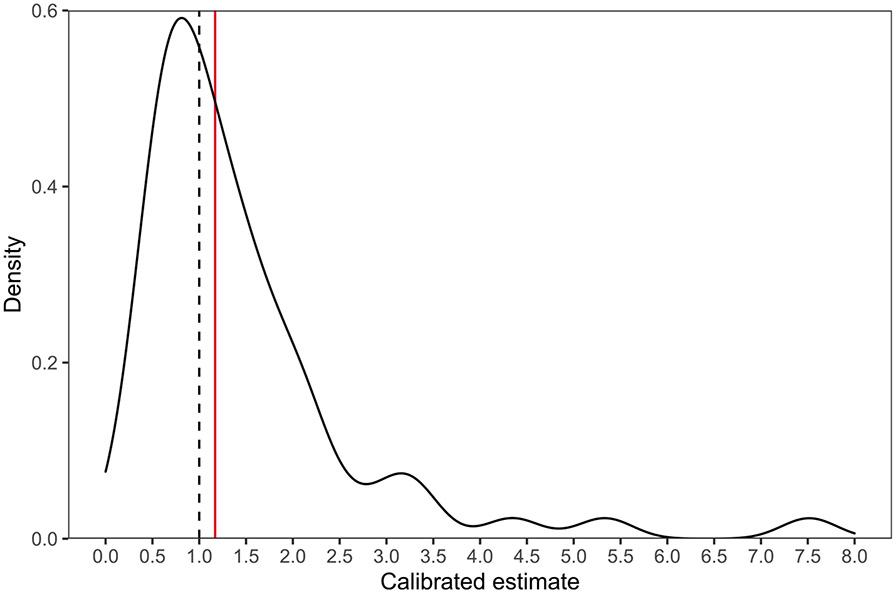
Regarding the variability of publication bias severity across individual meta-analyses, Figure 3 displays the estimated density of selection ratios across all groups of meta-analyses, suggesting that most meta-analyses exhibited little publication bias, but that there was considerable right skew. Accordingly, we estimated that only 53% (95% CI: [34%, 67%]) of meta-analyses had selection ratios greater than 1 (the null), but that a considerable minority (36%; 95% CI: [16%, 48%]) had selection ratios greater than 1.5, and a small number (10%; 95% CI: [2%, 21%]) had selection ratios greater than 3. The estimated 95th quantile of the true selection ratios was 3.51. Regarding selection ratios in the unexpected direction, a minority of meta-analyses had selection ratios smaller than 1/1.5 ≈ 0.67 (22%; 95% CI: [9%, 34%]) and almost none had selection ratios smaller than 1/3 (2%; 95% CI: [0%, 9%]).

FIGURE 3.

Estimated density of selection ratios across all groups of meta-analyses. Black dashed line: null (no publication bias). Red solid line: estimate of overall average selection ratio

3.3 ∣. Percentages of affirmative results

Across all four groups of meta-analyses, 50% of point estimates (95% CI: [48%, 53%])^viii were affirmative, and 55% of point estimates (95% CI: [53%, 57%]) were “significant” regardless of point estimate sign. Regarding journal tier, the percentage of affirmative results in top medical and top psychology meta-analyses (n=7,622 point estimates) was nearly identical for higher-tier journals (56%, 95% CI: [49%, 62%]) and lower-tier journals (58%, 95% CI: [55%, 62%]); see Table 2. Overall, results in higher-tier journals were an estimated 0.99 times as likely to be affirmative as those in lower-tier journals (95% CI: [0.90, 1.09]; p=0.83).

Regarding studies' chronological ordering, the percentage of affirmative results was almost exactly the same for early results (54%; 95% CI: [42%, 67%]) as for later results (55%; 95% CI: [53%, 58%]), though this pattern appeared to vary somewhat across the four major groups of meta-analyses (see final two columns of Table 2). Overall, early results were an estimated 1.03 times as likely to be affirmative than later results (95% CI: [0.84, 1.26]; p= 0.79). Risk ratio estimates for each meta-analysis for both journal tier and study chronology are presented in Figures S2 and S3. We conducted sensitivity analyses in which we considered publication in terms of two-tailed “significance” (i.e., a two-tailed p < 0.05 regardless of point estimate sign) rather than “affirmative” status. Similar to primary analyses, this sensitivity analysis estimated that higher-tier journals were 1.03 (95% CI: [0.84, 1.26]; p= 0.79) times as likely to be “significant” as results in lower-tier journals and estimated that early results were 1.03 (95% CI: [0.86, 1.23]; p= 0.76) times as likely to be “significant” as later results. We also conducted a sensitivity analysis in which we excluded from the “higher-tier” designation a single journal (Journal of Educational Psychology) that had contributed 47% of the higher-tier point estimates. After excluding this journal, higher-tier point estimates appeared less likely than lower-tier point estimates to be affirmative (Supporting Information).

3.4 ∣. Size of point estimates

Combining all four groups of meta-analyses, the mean within-meta-analysis percentile of point estimates in higher-tier journals (0.51; 95% CI: [0.48, 0.54]) was identical to that in lower-tier journals (0.51; 95% CI: [0.49, 0.52]). There was almost no difference in mean percentiles comparing studies in higher- versus lower-tier journals (estimate: 0.01; 95% CI: [−0.02, 0.05]; p= 0.37). Within groups, results were mixed, with meta-analyses from top medical journals perhaps showing somewhat smaller point estimates in early studies, Metalab showing the opposite pattern, and the remaining two groups showing little difference (Table 3, final two columns). Considering studies' chronological ordering, the mean percentile in early studies (0.55; 95% CI: [0.45, 0.64]) was also similar to that in later studies (0.51; 95% CI: [0.49, 0.52]); the estimated difference was 0 (95% CI: [−0.05, 0.05]; p= 0.92).

4 ∣. EXPLORATORY RESULTS

4.1 ∣. Sensitivity to varying amounts of publication bias

As an alternative method of considering the possible impact of publication bias on meta-analysis results, we conducted post hoc sensitivity analyses to assess the severity of hypothetical publication bias that would be required to “explain away” the results of each meta-analysis,⁴⁹ rather than to estimate the actual amount of publication bias in each meta-analysis as we did in the main analyses. The sensitivity analysis methods assess: (1) the minimum selection ratio that would be required to attenuate a meta-analytic pooled point estimate to the null and (2) the minimum selection ratio that would be required to shift the confidence interval to include the null. They also allow estimation of a “worst-case” pooled point estimate and confidence interval under maximal publication bias in which affirmative studies are almost infinitely more likely to be published than nonaffirmative studies; these worst-case estimates are obtained by simply meta-analyzing only the nonaffirmative studies.⁴⁹ These methods obviate the distributional and independence assumptions required for our main analysis models, providing a form of sensitivity analysis for the main results.

For these analyses, we retained all point estimates from each meta-analysis and used a robust sensitivity analysis model to account for clustering and non-normality,⁴⁹ which we fit using the R package PublicationBias.⁵⁰ Worst-case pooled point estimates remained in the same direction as the pooled point estimate for 66% of meta-analyses, indicating that no amount of publication bias under the assumed model would suffice to shift the point estimate to the null for this majority of meta-analysis. Among these meta-analyses, the worst-case point estimate was on average 28% as large as the pooled point estimate. Considering all meta-analyses, the worst-case 95% confidence interval limit excluded the null for 25% of meta-analyses, indicating that no amount of publication bias under the assumed model would suffice to shift the confidence interval to include the null. The estimated 5th and 10th percentiles of the true selection ratios indicated that for 95% of meta-analyses, affirmative results would need to be at least 1.46 times more likely to be published than nonaffirmative results in order to attenuate the pooled point estimate to the null; and for 90% of meta-analysis, this ratio would need to be at least 3.36. In fact, for 89% of meta-analyses, the amount of publication bias required to attenuate the pooled point estimate to the null exceeded our previous empirical estimate of the actual amount of publication bias in 95% of meta-analyses from the relevant group (c.f. Table 1, column “q₉₅”). Additionally, for 74% of meta-analyses, the amount of publication bias required to shift the confidence interval to include the null exceeded this 95th percentile empirical estimate of actual publication bias severity.^ix

4.2 ∣. Selection ratios by additional meta-analysis characteristics

The severity of publication bias might be associated with other characteristics of meta-analyses in addition to their disciplinary group. This exploratory analysis considered two additional covariates defined at the level of meta-analyses: (1) the designs of the meta-analyzed studies (all observational, all randomized, or a combination of both designs; see Supporting Information for details) and (2) the median publication year of the meta-analyzed studies. We considered the latter because publication bias severity might be affected by secular trends in conventional publication criteria or in the stringency of top-tier journals. Alternatively, publication bias might differ for meta-analyses of large, well-established literatures (those with earlier median publication years) than for meta-analyses of smaller, more nascent literatures (those with later median publication years).

We analyzed 29 meta-analyses with complete data on these covariates (i.e., for which we had coded studies' years and whose reported inclusion criteria allowed us to determine study designs). These meta-analyses' median study publication years ranged from 1999 to 2015, with a median of 2010. Fourteen meta-analyses (48%) contained only observational studies, 12 (41%) contained only randomized studies, and 3 (10%) contained both designs. We meta-regressed their estimated log-selection ratios on study design, median publication year, and group. Compared to meta-analyses comprising only observational studies, we estimated that selection ratios in meta-analyses comprising only randomized studies were 1.11-fold (95% CI: [0.47, 2.60]; p= 0.79) larger on average (holding constant group and median publication year), and selection ratios in meta-analyses comprising both designs were an estimated 0.89-fold (95% CI: [0.34, 2.33]; p= 0.77) as large on average. These findings did not suggest substantial differences in publication bias severity by study design. We also estimated that a 1-year increase in median publication year was associated with a 1.07-fold (95% CI: [1.01, 1.13]; p= 0.02) increase in a meta-analysis' selection ratio, holding constant group and study design (see also Figure S2), suggesting that meta-analyses of studies published later may have had somewhat more severe publication bias.

4.3 ∣. Effect of including studies from the grey literature in Metalab

As discussed above, publication bias appeared more severe in Metalab than in the published sources of meta-analyses, though the small sample size in Metalab precludes strong conclusions. We speculate that particularly small sample sizes in developmental psychology research (averaging 18 subjects, though often collecting many observations per subject²⁸) may contribute to publication bias in this group. We additionally investigated the effect of including studies from the grey literature on publication bias estimates in Metalab; these studies constituted on average 14% of the independent point estimates included in the selection models. When fit to datasets that include studies from the grey literature, selection models detect the presence of nonaffirmative results arising from analyses that were conducted, but not reported in any published or unpublished source that was available for inclusion in the meta-analysis. Across the five meta-analyses, estimates of publication bias typically increased upon inclusion of the studies from the grey literature; selection ratios increased by on average 1.96-fold, and the ratios of change ranged from 0.76-fold to 4.76-fold. This is consistent with previous findings suggesting that the inclusion of studies from the grey literature did not consistently reduce publication bias in these meta-analyses.³⁵

4.4 ∣. Selection ratios stratified by study-level predictors

Our primary analyses regarding study-level predictors of publication bias severity used as outcomes study-level proxies of publication bias severity, namely point estimate size and affirmative status. It would be informative to additionally include such study-level predictors in the selection models themselves, but the relevant statistical methods are a work in progress and are not yet implemented in code.⁵¹ Instead, in the following exploratory analyses, we fit selection models to two strata of studies within each meta-analysis, where the strata represented the presence or absence of a study-level predictor.³⁸ We analyzed only meta-analyses for which each stratum had ≥40 studies and ≥3 affirmative and non-affirmative studies. When we could analyze more than three meta-analyses, we meta-analyzed the resulting stratum-specific selection ratio estimates, such that each analyzed meta-analysis contributed one estimated selection ratio to each stratum-specific analysis. When we could analyze only three or fewer meta-analyses, we instead reported results for each meta-analysis individually.

4.4.1 ∣. Peer-reviewed studies versus studies in the grey literature

The large majority of meta-analyses in our sample contained very few, if any, studies from the grey literature, but four meta-analyses did have enough studies to perform the stratified analyses.^x For one meta-analysis, the selection model did not converge for the grey literature studies, leaving three analyzed meta-analyses (Table 4). For all three meta-analyses, confidence intervals for the stratum-specific selection ratio estimates substantially overlapped one another and also substantially overlapped the null. For the first meta-analysis, a meta-analysis in PLoS One on hand cross-pollination versus natural pollination of plants,⁵² the selection ratio estimates were <1 (i.e., in the unexpected direction) for both publication categories. For the second, a meta-analysis in PLoS One on perceived racism and mental health,⁵³ the estimated selection ratios were comparable between publication categories. For the third, a meta-analysis in the top psychology group on facial feedback and affect,⁵⁴ the estimated selection ratio was in fact larger in the grey literature studies than in the peer-reviewed studies, but was estimated with substantial uncertainty. Overall, in this small, exploratory analysis of three meta-analyses, none suggested more severe publication bias in peer-reviewed studies. However, it is important to note that these meta-analyses necessarily contained an unusually large number of grey literature studies; scientific topics for which a large grey literature exists and is available to meta-analysts might have different norms shaping publication bias than fields in which, much more typically, little grey literature is available to meta-analysts.

TABLE 4.

Estimated selection ratios with 95% confidence intervals in three meta-analyses

Meta-analysis	Group	Discipline	Study publication status	$\mathrm{S}\widehat{\mathrm{R}}$
Wolowski52	PLoS One	Natural sciences	Peer-reviewed	0.46 [0.17, 1.27]
			Grey literature	0.33 [0.08, 1.45]
Paradies53	PLoS One	Social sciences	Peer-reviewed	2.10 [1.16, 3.79]
			Grey literature	2.39 [0.91, 6.27]
Coles54	Top psychology	–	Peer-reviewed	0.66 [0.34, 1.29]
			Grey literature	2.80 [0.41, 19.25]

4.4.2 ∣. Studies in higher- versus lower-tier journals

As a counterpart to the primary analyses regarding journal tier, we fit selection models to the studies in higher-tier journals and to those in lower-tier journals for the two meta-analyses containing enough studies to do so. Both meta-analyses were in the top psychology group and were published in Psychological Bulletin. For the first,⁵⁵ which addressed a technical question regarding meta-cognition, the estimated selection ratio among the lower-tier estimates was 3.77 (95% CI: [1.49, 9.54]) and among the higher-tier estimates was 3.77 (95% CI: [1.17, 8.74]). For the second,⁵⁶ on the association between fluid intelligence and performance at reading and mathematics, the estimated selection ratio among the lower-tier estimates was 0.76 (95% CI: [0.56, 1.05]) and among the higher-tier estimates was 5.92 (95% CI: [1.59, 22.04]). Thus, in the first meta-analysis, given the fairly wide confidence intervals, there appeared heuristically to be little difference between journal tiers in publication bias severity. However, in the second, the publication bias appeared considerably more severe in the higher-tier journals.

These differing results might reflect heterogeneity in publication bias severity across individual journals, even within each journal tier category. In both meta-analyses, a majority of higher-tier results were published in just one or two journals. For the first meta-analysis, 66% of higher-tier results were published in Journal of Consumer Research and Journal of Personality and Social Psychology combined. For the second, 64% of higher-tier results were published in Journal of Educational Psychology, the same journal whose exclusion in an aforementioned sensitivity analysis had reduced the estimated risk ratio of an affirmative result in higher- versus lower-tier journals from 0.99 to 0.82 (Section 3.3). However, these results are merely exploratory and do not allow us to parse potential differences in publication bias across individual journals into effects of, for example, the journals' subdisciplines, their editorial practices, and authors' submission practices.

4.4.3 ∣. Studies among the earlier 50% to be published versus the later 50%

We estimated selection ratios in the earlier 50% of studies to be published relative to all studies in the corresponding meta-analysis versus in the later 50%. In contrast to the primary analyses in which we more stringently defined “early” studies as only the first few published (Section 2.2), the present analysis split studies by the median publication year within their corresponding meta-analysis, a decision we made to maximize within-stratum sample sizes. We thus analyzed nine meta-analyses, including two in top medical journals and seven in top psychology journals. We estimated average selection ratios of 1.51 (95% CI: [0.85, 2.70]) for the earlier 50% of studies within each meta-analysis and 1.29 (95% CI: [0.73, 2.26]) for the later 50% of studies; heuristically, this small exploratory analysis did not suggest that publication bias was considerably more or less severe in the earlier versus later 50% of studies.

4.4.4 ∣. More versus less precise studies

We investigated whether the severity of publication bias might have differed for more precise versus less precise studies. We pursued this analysis because we speculated that the relatively more severe publication bias seen in Metalab might reflect the studies' typically very small sample sizes. For this analysis, we defined “more precise” studies as those whose estimated standard errors were less than the median for their corresponding meta-analysis, and inversely for “less precise” studies. We analyzed nine meta-analyses (two in PLoS One, two in top medical journals, and five in top psychology journals), estimating average selection ratios of 1.15 (95% CI: [0.69, 1.93]) for the less precise 50% of studies and 1.66 (95% CI: [0.75, 3.70]) for the more precise 50% of studies. Again, given the wide confidence intervals, this exploratory analysis did not strongly support differential publication bias by study precision, though the point estimates were consistent with somewhat more severe publication bias in more precise studies.

5 ∣. DISCUSSION

Our systematic analysis of meta-analyses spanning several disciplines suggested that publication bias is perhaps milder than expected in meta-analyses published in PLoS One, top medical journals, and top psychology journals. Study-level measures of publication bias, namely the percentage of affirmative results and the size of point estimates, indicated that publication bias did not differ meaningfully for original studies published in higher-tier versus lower-tier journals, nor for the first few studies published on a topic versus for later studies. An exploratory, post hoc analysis did suggest, however, that publication bias might have been more severe in meta-analyses of studies whose median publication year was later. In contrast to the main analysis regarding the first few studies within each meta-analysis, which could capture effects of changing publication pressures as a scientific field develops, the post hoc analysis using absolute median publication years could capture effects of secular trends in scientific norms as well as of differing publication bias in meta-analyses of well-established versus nascent literatures. Secondary analyses that assessed the sensitivity of meta-analyses' findings to varying amounts of hypothetical publication bias, rather than estimating the amount of publication bias itself, corroborated primary findings and suggested that the major conclusions of most meta-analyses are robust to plausible amounts of publication bias. However, the severity of publication bias did differ across individual meta-analyses; we estimated that a considerable minority (36%; 95% CI: [16%, 48%]) had selection ratios greater than 1.5, and that a few (10%; 95% CI: [2%, 21%]) had selection ratios greater than 3. The estimated 95th quantile of the true selection ratios was 3.51.

Our estimates of publication bias were lower than we expected. For comparison, previous work examining social sciences lab experiments estimated selection ratios from 10 to 48 (Tables 1 and 2 in Andrews and Kasy¹⁰), which are an order of magnitude larger than our estimates. Others have estimated publication bias by prospectively or retrospectively following cohorts of study protocols submitted to specific ethics committees or funded by specific granting agencies. In a systematic review of such cohort studies (typically within the medical domain), eight estimates of parameters qualitatively similar to the selection ratio ranged from approximately 0.73 to 3.51 (Table 5 in Dwan et al⁵⁷).^xi A cohort study⁵⁹ published since that review followed social sciences experiments funded through a certain granting agency, estimating a selection ratio of approximately 2.95. Our research question and methodology differed in an important manner from those of these previous studies: rather than estimating publication bias in original studies themselves, we estimated publication bias in the published results that were included in meta-analyses. It is plausible that meta-analyzed results exhibited relatively little publication bias compared to original papers' results because meta-analyses deliberately attempt to include all results on a topic, including replication studies and null results published in lower-tier journals. However, casting doubt on these explanations, we also found little evidence of increased publication bias in higher-tier journals or in early studies.

We instead speculate that the key alleviator of publication bias in meta-analyses is their inclusion of “non-headline” results, by which we mean results that are reported in published papers but that are de-emphasized (e.g., reported only in secondary or supplemental analyses) and those that meta-analysts obtain through manual calculation or by contacting authors. In contrast, we describe as “headline” results those that are particularly emphasized in published (e.g., those that are included in abstracts or otherwise treated as primary). For comparison, among a semi-systematic sample of headline results^xii (n=100) from studies published in three top psychology journals, 97% were “statistically significant” regardless of the sign of the point estimate,³ compared to only 54% of results from the same three journals in our own corpus but that had been included in some meta-analysis (n=238). Similarly, among headline results (i.e., p-values reported in the abstracts) sampled from papers in four top medical and one top epidemiology journal,⁶⁰ 78% were “significant” (n=15,653), which appears higher than our 50% for all results in meta-analyses in top medical journals (n=576) and our 32% for PLOS One meta-analyses on medical topics (n= 576)^xiii About 90% of headline findings in both medicine and psychology papers were qualitatively described as supporting the investigated hypothesis,⁶¹ an estimate that again appears considerably higher than our own. Considering instead non-headline results, the percentages of “significant” p-values in top psychology journals⁶² and in an interdisciplinary corpus⁶³ were 64% and 57%, respectively.^xiv Among all results in our own meta-analysis corpus, 55% were “significant,” which is much closer to the estimates in non-headline results than to estimates in headline results. Holistically, these findings provide preliminary support for the possibility that meta-analyses mitigate publication bias largely through their inclusion of non-headline results, which may be less prone to publication pressures than are headline results.

We sampled meta-analyses across disciplines and journals, yielding findings that we believe generalize to a fairly diverse range of meta-analyses and scientific topics. Nevertheless, we restricted our sample to large meta-analyses (those with at least 40 point estimates in original analyses) for statistical reasons described in Section 2.3. It is plausible that bias could operate differently in large meta-analyses, which might be conducted on well-established rather than nascent literatures (e.g., Reference⁶⁶) or which might have used particularly exhaustive search strategies. Last, although our corpus of meta-analyses represented a wide range of scientific topics, it did not represent topics that are not amenable to meta-analysis (e.g., because they use qualitative methods or use statistical methods that do not readily yield simple study-level point estimates). Publication bias may operate differently in such realms of scientific inquiry.

Our research has some limitations. The relatively small number of meta-analyses within each group precludes strong conclusions about differences in publication bias across the groups. As in all analyses of publication bias, our estimates of publication bias relied on statistical assumptions, namely that population effect sizes are approximately normal prior to selection due to of publication bias, that point estimates are independent, and that publication bias favors affirmative results over nonaffirmative results. To determine which results were “affirmative,” we assigned a positive sign to point estimates that agreed in direction with a naïve meta-analytic pooled point estimate that was not corrected for publication bias; this approach effectively assumes that publication bias favors effects in the majority direction. However, we also conducted analyses using sensitivity analysis techniques that obviated the assumptions regarding normality and independence; these findings heuristically corroborated the primary results (Section 4). Additional analyses suggested that the final assumption regarding the mechanism of publication bias was plausible (Supporting Information). We excluded studies from the grey literature from all meta-analyses, potentially limiting generalizability to meta-analyses that include a substantial number of grey literature studies. For example, publication bias might have been yet milder had we included these results, as discussed in Section 2.2. However, exploratory findings (Sections 4.3-4.4.1) cast some doubt on this possibility.

Overall, our results suggest relatively mild publication bias on average in meta-analyses in the interdisciplinary journal PLOS One and in top psychology and medical journals. Critically, the threat of publication bias must not be universally dismissed on these grounds, as the severity of publication bias did differ across individual meta-analyses, as noted above. Publication bias may in fact have been more severe in an unpublished corpus of developmental psychology meta-analyses, though the sample size was small. Our results suggest that the primary drivers of publication bias in meta-analyses are neither the publication process itself, nor the pressures of publishing individual studies or meta-analyses in higher-tier journals, nor the pressure to publish one of the first studies on a topic. The prioritization of findings within published papers as headline versus non-headline results may contribute more to publication bias than these influences. Thus, the mere act of performing a high-quality meta-analysis that includes non-headline results may itself largely mitigate publication bias, suggesting optimism about the validity of most meta-analytic estimates. Nevertheless, it remains critical to design and analyze meta-analyses with careful attention to publication bias.