Abstract
In December 2019, first case of the COVID-19 was reported in Wuhan, Hubei province in China. Soon world health organization has declared contagious coronavirus disease (a.k.a. COVID-19) as a global pandemic in the month of March 2020. Over the span of eleven months, it has rapidly spread out all over the world with total confirmed cases of ~ 41.39 M and causing a total fatality of ~1.13 M. At present, the entire mankind is facing serious threat and it is believed that COVID-19 may have been around for quite some time. Therefore, it has become imperative to forecast the global impact of COVID-19 in the near future. The present work proposes state-of-art deep learning Recurrent Neural Networks (RNN) models to predict the country-wise cumulative confirmed cases, cumulative recovered cases and the cumulative fatalities. The Gated Recurrent Units (GRUs) and Long Short-Term Memory (LSTM) cells along with Recurrent Neural Networks (RNN) were developed to predict the future trends of the COVID-19. We have used publicly available data from John Hopkins University's COVID-19 database. In this work, we emphasize the importance of various factors such as age, preventive measures, and healthcare facilities, population density, etc. that play vital role in rapid spread of COVID-19 pandemic. Therefore, our forecasted results are very helpful for countries to better prepare themselves to control the pandemic.
Keywords: Forecasting COVID-19 pandemic, Time series analysis, Gated Recurrent Units (GRUs), Long Short-Term Memory (LSTM), Recurrent Neural Networks (RNNs)
1. Introduction
Coronavirus disease (COVID-19) is a respiratory illness caused by severe acute respiratory syndrome coronavirus-2 (SARS -CoV-2), which is a strain of coronaviruses. It was first identified in December 2019 when a group of patients demonstrated novel form of viral pneumonia with similar history of visiting wet market in Wuhan China. On March 11th, 2020, World Health Organization (WHO), declared novel coronavirus (2019-nCoV) outbreak as global pandemic [1]. Since then, several preventive measures such as lockdowns, rapid testing, wearing masks, self-quarantine, social distancing are being applied by the countries to stop the spread of COVID-19 pandemic. Despite these measures, COVID-19 is propagating rapidly and affecting both human health and global economy, due to various reasons such aspopulation density, total population, lifestyle, worldwide travel, and precautionary measures etc. As of today (June 11th, 2020), there have been about a total confirmed case of 7.37 M and about 0.41 M total fatalities across the world. Most of these 7.37 M confirmed cases are concentrated in top 10 countries [2] such as USA, Brazil, India, Russia, South Africa, Mexico, Peru, Chile, United Kingdom (UK) and Iran. Firstly, the major concern of the people and the government authorities is to get an estimate about what would be the daily new cases, recovery rate, total fatalities, total number of confirmed cases by forecasting the reported data. Secondly, how long it would take to stop the spread of pandemic COVID-19, ultimately helping the governments and healthcare systems to prepare in-advance for the forecasted number of cases. Recently, machine learning, and deep learning techniques have gained immense interest due to the availability of abundant data. These techniques are very helpful for obtaining the relationships from the data without defining them priori [3]. Further these techniques are also capable of forecasting the trends based on the reported time-series data over a known period of time. Several researchers have used the machine learning and deep learning models to predict short-term forecast of COVID-19 pandemic. The following paragraph very briefly summarizes the literature reported on the machine learning-based forecast of COVID-19 cases.
Ghoshal et al. [4] have used the linear regression and multiple linear regression to predict the number of deaths in India for upcoming six weeks. Authors have predicted that the total deaths in India will be doubled if the COVID-19 preventive measures are unchanged or not implemented strictly. Parbat and Chakraborty [5] have used the Support Vector Regression (SVR) for predicting the COVID-19 cases in India for 60 days based on the time series data reported for the period of ~ 60 days (1st March 2020 to 30th April 2020). Their model has ~ 97% accuracyin predicting the cumulative confirmed cases, total recovered, total fatalities, and has 87% accuracy in predicting the daily new cases. Maleki et al. [6] have employed Autoregressive time-series models based on two-piece scale mixture normal distributions to forecast the confirmed and recovered COVID-19 cases. Their model performed well in forecasting the confirmed and recovered COVID-19 global cases. Benvenuto et al. [7] have reported very briefly about the application of Autoregressive Integrated Moving Average (ARIMA) model to predict the future trends of prevalence and incidence of COVID-19 data. Fotios et al. [8] have used non-seasonal exponential smoothing models to forecast cumulative cases of COVID-19 until 21st march 2020. In another study, Ram Kumar Singh et al. [9] applied holt-winter models and Susceptible, Infected and Recovered (SIR) model on COVID-19 data of India. They reported that COVID-19 cases in India will be highest during the first week of November 2020 and India will return to normalcy by last week of February 2021. Similarly, in another studyShaobo He et al., used SEIR (Susceptible-Exposure-Infective-Recovered) model on COVID-19 data of Hubei province of China. They used particle spam optimization to estimate the parameters of the SEIR model. Moreover, their model considered quarantine and treatment for forecasting the COVID-19 cases [10]. Further details on the SIR and SEIR model can be found elsewhere [9], [10], [11], [12], [13]. Ribeiro et al. [14] have used ARIMA, Cubist Regression, Random Forest, Ridge Regression, SVR, and Stacking-ensemble learning for short-term forecasting of COVID-19 confirmed cases in Brazilian states. Their paper reveals the order of best to worst performing models, the best performing models are found to be SVR and ARIMA. Kumar et al. [15] have used ARIMA model with machine learning approach to forecast the trajectories of COVID-19 pandemic in top 15 countries in the month of April 2020. Their ARIMA model was successfully able to predict the COVID-19 trends in countries such as Iran, Italy, Spain and France. Ardabili et al. [16] have used the machine learning techniques for predicting the COVID-19 outbreak, they found that the multi-layer perceptron model and adaptive network-based fuzzy interface system are found to give promising results. Their study has recommended that individual machine learning models are needed for each country due to the presence of fundamental differences between the countries. The following paragraph briefly summarizes the reported work on the deep learning-based forecast of COVID-19 cases.
Chimmula and Zhang [17] have used the state-of-art deep learning model using Long Short-Term Memory (LSTM) networkto predict the possible ending time of the COVID-19 pandemic in CANADA. Based on their LSTM model, they estimated that the time required for ending the pandemic is about three months. Salgotra et al. [18] have developed models based on the genetic programming for forecasting the total confirmed cases and total fatalities in highly affected states of India and as well as for total India. Authors have reported that their model is less sensitive to the variables and highly reliable in predicting the confirmed cases and deaths. Qi et al. [19] have used the generalized adaptive model to understand the associations of daily average temperature and relative humidity with the daily COVID-19 cases in different provinces in China. Their model found that the increase in the daily average temperature and with increase in the average relative humidity decreases the COVID-19 cases. However, there is no clear trends for the COVID-19 cases throughout main land China. In a study, Ismail et al. [20] conducted a comparative study based on ARIMA, LSTM, Non-linear Autoregressive Neural Networks (NARNN) models toforecast the COVID-19 cases in Denmark, Belgium, Germany, France, United Kingdom, Finland, Switzerland, and Turkey. They found that the LSTM offers lowest Root Mean Square Error (RMSE) compared to other models. Shawni Dutta et al. [21] have used LSTM, Grated Recurrent Unit (GRU), Recurrent Neural Networks (RNN) to predict the confirmed, released, negative, death cases of COVID-19 pandemic. Their study revealed that the combined LSTM based (RNN) model provided a better prediction when compared to the individual models. Anuradha Tomar et al. [22] have used LSTM and curve fitting for the prediction of the number of COVID-19 cases in India for 30 days ahead and effect of preventive measures such as lockdowns and social distancing on COVID-19 spread. Their results shed light on the importance of social distancing and implementation of lockdowns. The actual number of daily cases decreased as estimated by the LSTM and curve fitting methods. Mehdi et al. [23] have used RNN, LSTM, Seasonal Autoregressive Integrated Moving Average (SARIMA) and Holt winter's exponential smoothing and moving average methods to forecast COVID-19 cases of Iran. Their comparative study on these methods showed that LSTM model outperformed other models in terms of less error values for infection development in Iran.
Based on the aforementioned reports, all the models proposed in the literature are confined to very less data points, few countries, or few states in a country or for a very short forecast time. Therefore, there is still room to develop country specific deep learning models to predict the 60-day forecast of the COVID-19 trends in top 10-countries that are highly impacted by COVID-19. Hence, the aim of the present work is to predict the future trends of the cumulative confirmed cases, cumulative recovered cases and cumulative fatalities of the top 10 countries using RNN along with Gated Recurrent Units (GRUs) andLong Short-Term Memory (LSTM) cells. These models were trained on the training data and tested on the testing data, ultimately, the validated models have used to forecast the trend of COVID-19 cases for 60 daysin top-10 highly affected countries. These models were developed in Python based open source PyTorchdeep learning library and simulations were performed on Graphical Processing Units (GPUs) of the Google COLAB cloud computing platform. These models have trained and tested on the John Hopkin's publicly available COVID-19 datasets [24].
2. Recurrent neural networks
The methods for forecasting the time-series data can be mainly classified into two types, machine learning and deep learning methods. Deep learning models are superior over the statistical machine learning models for forecasting the non-linear applications such as prediction of weather, stock prices [25], electro cardiogram (ECG) recordings [26] and crude oil prices [27] etc. Feed Forward Neural Networks (FFNNs) and Recurrent Neural Networks (RNNS) are two types of widely used deep learning techniques but FFNNs are not suitable for forecasting as they are not capable of considering the trends in the time-series data. Whereas RNNs are powerful and robust type of artificial neural networks that uses existing time-series data to predict the future data over a specified length of time. RNNs are very promising techniques due to the internal memory that can remember the important features of the input sequential data which allows them to accurately predict the future. Unlike FFNNs, where the information flows strictly in one direction from layer to layer, in RNNs, the output from the previous time stamp along within put from the present time stamp will be fed into RNN cell, so that the current state of the model is influenced by its previous states. The following equation explains the function of the single RNN cell:
| (1) |
Where, is the weight matrix, is the bias matrix, and are hidden state at current time-step and previous time-step, respectively. RNNs perform computations, very similar to FFNN, using the weights, biases, and activation functions for each element of the input sequence (Fig. 1 A). Essentially a neuron in RNN has a single hyperbolic tangent function in which and are combined and multiplied by some weight matrix and then adding a bias to it followed by passing it through the hyperbolic tangent function which gives back . Hyperbolic tan function is used to scale the actual values so that the values fall in between the range of -1 to +1. At each time step, the output of the RNN cell is updated using a sigmoid function, which is a widely used non-linear activation function in artificial neural networks. The following equation is a mathematical representation of the sigmoid function:
| (2) |
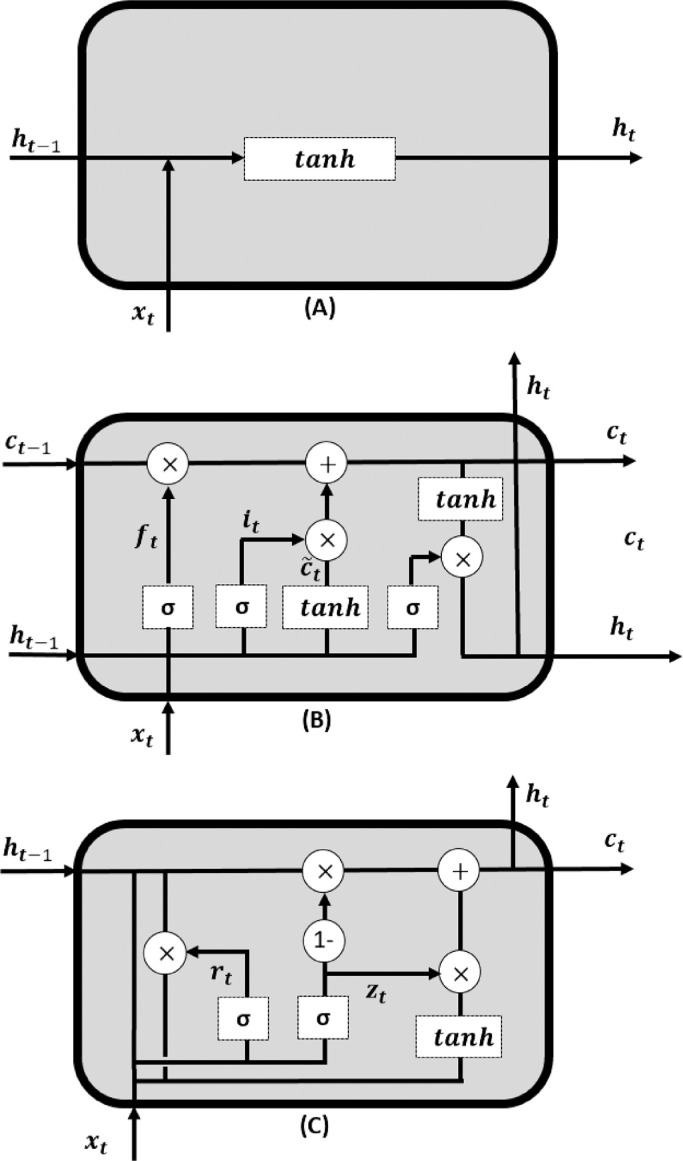
Fig. 1.
Schematic representation of (A) simple Recurrent Neural Network (RNN) cell (B) Long-Short Term Memory (LSTM) cell (C) Gated Recurrent Unit (GRU) cell.
RNN can only recollect the recent information but cannot recollect the earlier information. Though the RNNs can be trained by back-propagation, it will be very difficult to train them for long input sequences due to vanishing gradients. Hence, the main drawback of the RNN architecture is its shorter memory to remember the features, vanishing and exploding gradients. Hence, we have used the combination of RNN with GRU cells and LSTM cells to overcome these drawbacks.
2.1. Long short-term memory (LSTM)
Hochreiter and Schmidhuber [28] have proposed LSTM to overcome the vanishing and exploding gradients problem. The memory of LSTM cell will be stored and converted from input to output in cell state. The general architecture of the LSTM cell can be found in the Fig. 1B. LSTM cell is comprised of the forget gate, output gate, input gate and update gates. As the name indicates, forget gate decides what to forget from the previous memory units, the input gate decides what to accept into the neuron, the update gate updates the cell, and the output gate generates the new long-term memory. These four main components of LSTM will work and interact in a special manner, as it accepts long-term memory, short-term memory, input sequence at a given time step and generates new long-term memory, new short-term memory and output sequence at a given time step. The input gate decides which information must be transferred to the cell; the input gateis mathematically represented as following:
| (3) |
The operator ‘*’ represents the element-wise multiplication of the vectors.
The information to be neglected from the previous memory is controlled by forget gate which is mathematically defined as following:
| (4) |
The cell state is updated by the update gate, expressed mathematically by the following equations:
| (5) |
| (6) |
The hidden layer of the previous time step is updated by the output gate which is also responsible for the updating the output as it is given by:
| (7) |
| (8) |
2.2. Gated recurrent unit (GRU)
Gated Recurrent Units were proposed by Chung et al. [29] which is a simplified version of LSTM and requiresless training time with improved network performance. The operation of a GRU cell is similar to the operation of LSTM cell but GRU cell usesone hidden state that merges the forget gate and the input gate into a single update gate. Further, it combines the cell state and hidden state into one state and hence the total number of gates in GRU is half (update and reset gates) of the total number of gates in LSTM. Hence, it is popular and simplified variant of LSTM cell. The hidden state of the GRU cell is updated by the following equation:
| (9) |
The update gate is computed by the following equation, which decides how much of the GRU unit get updated:
| (10) |
The reset gate is computed very similar to the update gate, it is given by the following equation:
| (11) |
The new remember gate is generated by applying hyperbolic tan function to the reset gate, which is described by the following function.
| (12) |
2.3. Simulation methodology
Scripts were written in PyTorch package of Python (Ver. 3.7) programming language and the simulations were performed on a Google COLAB cloud computing platform. Optimizing the set of hyper parameters, such as number of nodes in each layer (10,100,200,300), number of hidden layers (1,2,3,4,5) and the learning rate (0.1, 0.01, 0.001, 0.0001, 0.00001), is very important for achieving the best sequential prediction. The values in the parenthes is shows the range of the respective variables we have tested for proposing an optimized model. We have proposed customized deep learning models for country specific time-series data by finding the best combination of hyper parameters. Adam optimizer is used for iteratively optimizing the network weights with the mean squared error (MSE) function as loss function. As the RNNs are very sensitive to the fluctuations in the time series data and to capturing the trends in the time series data, the data has to be normalized before feeding it to the neural network. We have used the MinMaxscaler to normalize the data and the following equation (Eq. 13) is a mathematical representation of MinMaxscaler:
| (13) |
Where , , , and represents the original time-series data, the normalized time-series data, minimum and maximum value of the time series data, respectively. MinMaxscaler translates each observation within the feature such that the minimum and maximum values of the observations lie between 0 and 1. The advantages of using MinMaxscaler is that after transforming the data, MinMaxscaler retains the shape of original distribution of the data and does not alter the information that is embedded within the original data. The normalized data is split into testing and training datasets, testing dataset is comprised of last 14 data points of the time-series dataset and the training dataset is comprised of entire time series data excluding the last 14 data points. The training time-series data is divided into several data sequences each of length 30. Each sequential data is fed to the RNN (i.e., the data from day 1 to day 30) to predict the 31st data point (data belongs to 31st day). In the consequent step, the next sequence of the data (day 2- day 31) is fed to RNN to predict the 32nd day data point. Similarly, all the sequences were fed to RNN to complete one set of predictions and which also completesone epoch. Simulations were running for ~ 5000 epochs and the best epoch was considered for the final forecast which corresponds to the global minimum of the loss function. Initially, the RNN models were trained on the training data set and the model's prediction was validated against the testing data. This process was repeated for each country and for each of the three time-series datasets (cumulative cases, recovered cases and total fatalities) to propose a customized RNN models. Then each optimized and validated model was used to forecast the trends. Mean Square Error (MSE) and Root Mean Square Error (RMSE) were used to evaluate the performance of the proposed models, the following equations represents the MSE (Eq. 14) and RMSE (Eq. 15) functions:
| (14) |
| (15) |
Where, is model predicted value, is actual value.
3. Results and discussion
This section describes the forecasted trends of cumulative confirmed, cumulative recovered and cumulative fatalities of the COVID-19 cases in top -10 countries using RNN-LSTM and RNN-GRU models. The top-10 countries based on cumulative confirmed cases, as of August 3rd, 2020, are USA, Brazil, India, Russia, South Africa, Mexico, Peru, Chile, United Kingdom (UK) and Iran. The dataset for each country comprises of three time-series data sets: cumulative confirmed cases, cumulative recovered cases, and cumulative fatalities. The forecast was done for each of the three time-series data of individual country by independently feeding the time-series data into the optimized LSTM and GRU based RNN networks, i.e., a total of 30 simulations were performed.
3.1. Cumulative confirmed cases
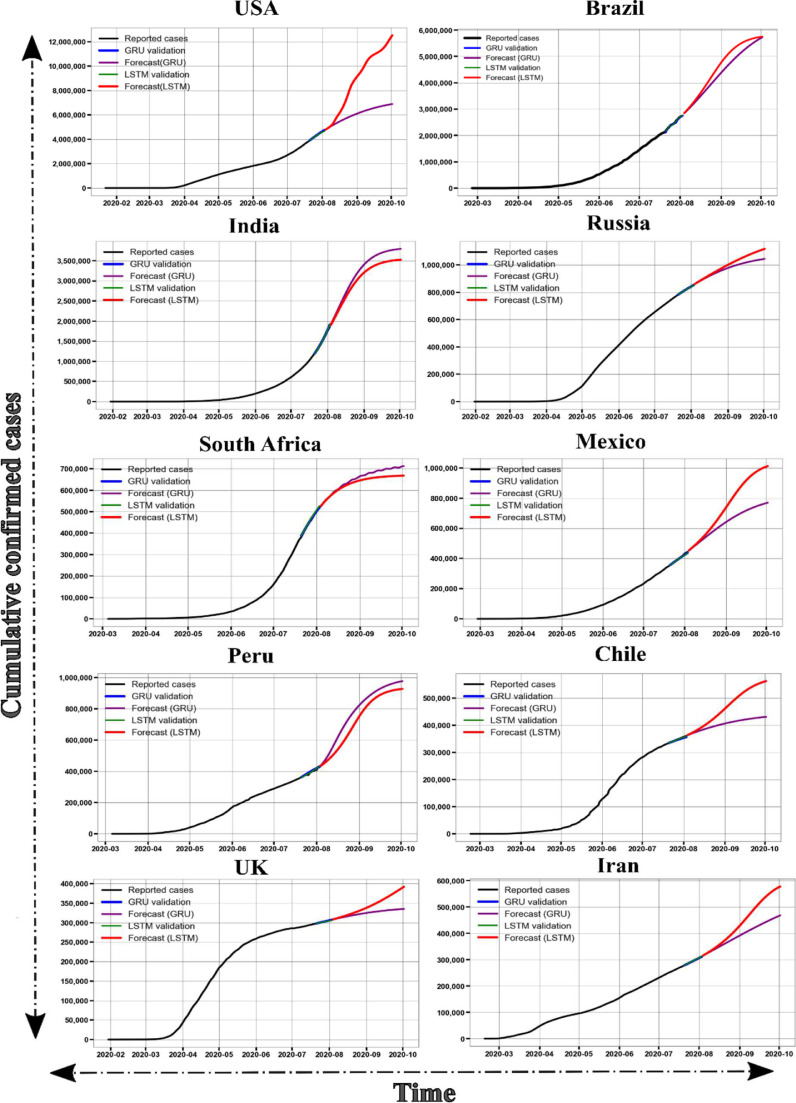
We have presented the 60-day forecast of the cumulative confirmed cases obtained from the RNN-LSTM and RNN-GRU models for top-10 countries. For each country, we have proposed customized models and compared the forecast of RNN-GRU model against the forecast of RNN-LSTM model. In the process of model development for achieving an optimized forecasting model, RNN-GRU and RNN-LSTM models were trained and tested for each of the time-series data of USA, Brazil, India, Russia, South Africa, Mexico, Peru, Chile, UK, and Iran. The optimization of hyper parameters such as number of epochs, hidden size, number of layers and learning rate used for developing RNN-GRU and RNN-LSTM models is done for each country. The details of the optimized hyper parameters, and evaluation metrics (MSE and RMSE) of the proposed models for forecasting the cumulative confirmed cases of each country were given in the Table 1 . The well-trained models with optimized parameters were selected to forecast the cumulative confirmed cases until October 1st, 2020. The 60-day forecast of the cumulative confirmed cases of the top-10 countries as a function of time (i.e., number of days) is shown in Fig. 2 . The reported cases were represented by black line, the LSTM predictions of the test data is represented by green line, the GRU prediction of the test data was represented by blue line, similarly, the LSTM and GRU model's forecasts were represented by red and purple color lines respectively. Even though countries such as India, USA, UK have implemented moderate to stringent preventive measures such as social distancing, lockdowns, the forecast of these countries have continuous growth. It is clear from the results that the forecast of the cumulative confirmed cases in most of the top 10 countries have shown a steady increasing trend.
Table 1.
Models used for forecasting cumulative confirmed cases and their parameters.
| No. | Country | RNN model | Epochs | Hidden size | Number of layers | Learning rate | MSE | RMSE |
|---|---|---|---|---|---|---|---|---|
| 1 | USA | GRU | 5.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 2.96E+12 | 1.72E+06 |
| LSTM | 1.69E+03 | 3.00E+02 | 3.00E+00 | 1.00E-05 | 2.87E+12 | 1.69E+06 | ||
| 2 | Brazil | GRU | 3.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.86E+10 | 1.36E+05 |
| LSTM | 1.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.76E+10 | 1.33E+05 | ||
| 3 | India | GRU | 1.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 4.58E+08 | 2.14E+04 |
| LSTM | 1.80E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 5.57E+08 | 2.36E+04 | ||
| 4 | Russia | GRU | 1.00E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 8.79E+05 | 9.37E+02 |
| LSTM | 2.56E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.10E+06 | 1.05E+03 | ||
| 5 | South Africa | GRU | 1.52E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.08E+07 | 3.29E+03 |
| LSTM | 2.00E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 3.64E+07 | 6.03E+03 | ||
| 6 | Mexico | GRU | 5.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.60E+07 | 4.00E+03 |
| LSTM | 1.50E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 2.36E+07 | 4.86E+03 | ||
| 7 | Peru | GRU | 6.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 5.37E+07 | 7.33E+03 |
| LSTM | 7.00E+01 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.97E+07 | 4.44E+03 | ||
| 8 | Chile | GRU | 3.00E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 6.52E+06 | 2.55E+03 |
| LSTM | 1.30E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.49E+06 | 1.22E+03 | ||
| 9 | UK | GRU | 2.50E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.77E+05 | 4.21E+02 |
| LSTM | 3.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 3.84E+05 | 6.91E+02 | ||
| 10 | Iran | GRU | 4.50E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 3.06E+05 | 5.52E+02 |
| LSTM | 7.05E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.78E+04 | 1.33E+02 |
Fig. 2.
60-day ahead forecast of cumulative confirmed cases for top-10 countries based on RNN-GRU and RNN-LSTM models.
For the forecast of USA’ confirmed cases, it is evident (Fig. 2) that both LSTM and GRU models performed reasonably well in the validation phase of the model development. Though the predictions of the LSTM and GRU models did not varied much from the test data, LSTM has lesser MSE and RMSE (Table 1). The LSTM model required 1694 epochs to converge, whereas GRU model required only 500 epochs. This could be because of the lesser number of parameters in the GRU model when compared to that of the LSTM model's parameters, along with the intrinsic data trends. The USA's LSTM model required 3 hidden layers with 300 neurons per each layer whereas, GRU required 2 hidden layers with 300 neurons in each layer. The 60-day ahead forecast of USA follows an exponential growth (as per LSTM model) and gradual steady increase (as per GRU model) in the number of cumulative confirmed cases in USA. Therefore, there will be ≈7 M confirmed cases according to GRU by the end of September 2020. However, the LSTM model predicted ≈12 M total number of cumulative confirmed cases, by the end of September 2020 in USA which will be much higher than the GRU based forecast. For forecasting the Brazil's cumulative confirmed cases, the predictions from the LSTM and GRU models are almost same with the projection of 5.75 M cases by the end of September 2020. The LSTM model of Brazil required 200 lesser epochs to converge, whereas the other parameters -learning rate, number of hidden layers, hidden size remained the same for both GRU and LSTM models of Brazil. Interestingly, both LSTM and GRU models have very similar values of MSE and RMSE. LSTM forecasted that the confirmed cases would approach a plateau in contrast to the GRU model's linear increasing trend.
The number of cumulative confirmed cases in India are on raise to 3.5 M according to the LSTM model, GRU model for India has forecasted that cumulative confirmed cases would reach a total of 3.7 M by the end of September 2020. Both LSTM and GRU models shows that cumulative cases are approaching plateau by the first week of September 2020. For the same combination of hyper parameters, the GRU model for India has lesser RMSE and MSE values when compared to that of the LSTM model. The GRU and LSTM models of Russia did reasonably well in terms of predictions, with small difference in the RMSE and MSE values. However, as we have seen the performance of the models varied from country to country according to information embedded in the data. In case of Russia, GRU performed well with lesser RMSE than that of the LSTM and the cumulative confirmed cases forecasted by LSTM were ≈90,000 greater than the GRU forecast. From Fig. 2, it is evident that according to LSTM model the maximum number of cumulative confirmed cases in Russia will be ≈1,200,000 by the end of September.
According to Fig. 2, number of cumulative confirmed cases in South Africa are increases at a faster pace as the trend is following an exponential growth phase since April 2020. Both LSTM and GRU models predicted an approaching plateau by the end of September 2020. The LSTM and GRU models predicted that there will be ≈675,000 and ≈710,000 confirmed cases in South Africa by the end of September 2020. For the Mexico's data, the GRU model out performed LSTM model with lower values of MSE and RMSE. The forecasted number of cumulative confirmed cases by GRU model of Mexico are ≈300,000 lesser than the LSTM based predictions.
For the Peru's forecast, both LSTM and GRU models have shown the similar trend, but GRU's predictions are higher than the LSTM predictions (Fig. 2). Both models show that cumulative confirmed cases reach a steady value (plateau) by the end of September 2020. For the same combination of hyper parameters, the LSTM model has lesser MSE and RMSE values when compared to the evaluation metrics of GRU model. For the rest of the countries such as Mexico, Chile, UK and Iran, GRU model predicted a gradual increment but LSTM model predicted a sharp rise in the cumulative confirmed cases for next 60 days. According to the LSTM model, the maximum number of confirmed cases for countries Mexico, Chile, UK, and Iran will reach ≈1 M, ≈0.7 M ≈0.4 M ≈0.57M, respectively. Similarly, GRU's model predicted maximum number of cases ≈0.8 M, ≈0.42 M ≈0.34 M ≈0.47M for countries Mexico, Chile, UK and Iran respectively. The MSE and RMSE of GRU model are lower than that of the LSTM model for countries Mexico, UK (Table 1). However, for Chile and Iran, LSTM model has lesser MSE and RMSE values.
3.1.1. Factors contribute to the surge in the confirmed cases
From the above-mentioned results, it is evident that the forecasted number of cumulative confirmed cases of top 10 countries is alarmingly increasing. Our forecasted trends and values give these top 10 countries, a good picture of the upcoming surge in the number of cumulative confirmed cases to review their precautionary measures, healthcare policies and interpositions. Moreover, the results of cumulative confirmed cases provide the information of the upcoming number of cases there by helping governments to prepare the long term and short-term response to the ongoing COVID-19 crisis. For example, according to the forecast of the cumulative confirmed cases of USA there will be 12M new cumulative confirmed cases by the end of September 2020. By knowing the upcoming number of cases, USA can avoid or cutdown the forecasted number of confirmed cases by implementing social distancing practices, curtailing the travel, and limiting the social gathering at local businesses such as restaurants etc. Our forecasted results can also assist countries that are implementing or implemented strict lockdowns. One such country is India, as it went into lockdown for 3 months during early April 2020. By considering our forecasted cumulative confirmed cases, India can plan for economic recovery by opening borders, local businesses, public schools etc. to new normalcy, while planning a better preventive measure thereby decreasing the potential number of forecasted cumulative confirmed cases. Our forecast results of cumulative confirmed cases not only alert these top 10 countries but also help rest of the world to prepare for the ongoing COVID-19 crisis.
To control the escalation of the number of the COVID-19 cases, along with the government's involvement there must be a proper response from the public as well, because there are many factors at the personal level which are in control of the citizens rather than the government. Some of those factors include social habits, quality (hygiene) of the homes, choice of mobility and the use of masks. According to a Germany's data-based case study on relationship between social habits and odds ratio for wearing masks published by Cornelia et al., people who avoid handshaking are more likely to wear masks to protect themselves and others. However, as of 12th of May 2020, there are 60% of the sample population think these policies are exaggerated [30]. In such scenario it is important to monitor the adherence to the compulsory infection control measures in the public places. Deep learning and artificial intelligence can help monitor control measures. In a study published by Shashi Yadav [31], he proposed a deep learning algorithm based on MobileNetV2 architecture and Convolutional Neural Networks (CNN) which can differentiate people wearing masks from the population. Their model detected the face masks with a precision score of 91.7% and 0.7 confidence score. Such automation is useful in highly populated regions where the risk of infection is high for security personals. The COVID-19 infection rate is directly proportional to the population density as the probability of the exposure increases as the population density increases [32]. The mortality rate is higher in extremely populated areas as the health care facilities are insufficient to meet the demand of increasing new cases [33]. However, in a study, the R2 value of the relation between infection rate and population density was found to be moderate (0.67) [34]. This indicates only a fraction of the infection rate is described by population density meaning other factors contribute to the increase in new daily cases of COVID-19. Mobility restriction is another factor that plays a key role in the spread of the infection. After implementing mobility controls, UK [35] and China has seen decline in the association between the fatalities and social mobility [36].
3.2. Cumulative recovered cases
To propose the best model for each country, we have developed and validated GRU and LSTM models for forecasting the cumulative recovered cases in top-10 countries that are severely affected by the COVID-19 pandemic. For countries USA, Brazil, Russia, Mexico and Peru, GRU performed better than LSTM according to the values of evaluation metrics - RMSE and MSE. The RMSE values of GRU models of these countries are lesser 6.01E+05 (USA), 9.24E+04 (Brazil) 1.08E+03 (Russia), 1.27E+03 (Mexico), and 2.56E+03 (Peru) in comparison to that of the RMSE values of LSTM models of these countries 6.10E+05 (USA), 1.20E+06 (Brazil), 2.77E+03 (Russia), 1.32E+04 (Mexico), 4.61E+03 (Peru). For rest of the top-10 countries, India, South Africa, Chile, U.K. and Iran, LSTM model performed better than GRU model. The LSTM models of these countries (India, South Africa, Chile, U.K., and Iran) have RMSE values of 2.57E+02, 4.05E+03, 8.74E+02, 3.03E+00 and 4.25E+02 respectively. Whereas, the GRU models have RMSE values of 2.76E+02, 4.08E+03, 1.15E+03, 3.40E+00 and 1.04E+03, respectively (Table 2). Fig. 3 shows the number of reported recovered cases and 60 day forecast from the latest date of reported recovered cases in top-10 countries. It is clear from Fig. 3, according to GRU based model the number of recovered cases in USA, Brazil, India, Russia, South Africa, Mexico, Peru, Chile, UK and Iran by the end of September 2020 will be ≈2,650,000, ≈3,250,000, ≈3,000,000, ≈1,000,000, ≈850,000, ≈810,000, ≈510,000, ≈370,000, ≈1,500 and ≈350,000 respectively. According to LSTM models of USA, Brazil, India, Russia, South Africa, Mexico, Peru, Chile, UK, and Iran the cumulative recovered cases will be ≈2,100,000, ≈3,770,000, ≈2,500,000, ≈1,000,000, ≈700,000, ≈870,000, ≈510,000, ≈,380,000 ≈1,500, and ≈470,000 respectively. It is found that there are two different trends that can be observed, one with continuous increase in the recovered cases and the other with reaching a stagnant value of the recovered cases (plateau).
Table 2.
Models used for forecasting recovered cases and their parameters.
| No. | Country | RNN model | Epochs | Hidden size | Number of layers | Learning rate | MSE | RMSE |
|---|---|---|---|---|---|---|---|---|
| 1 | USA | GRU | 2.50E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 3.61E+11 | 6.01E+05 |
| LSTM | 2.30E+01 | 3.00E+02 | 3.00E+00 | 1.00E-05 | 3.72E+11 | 6.10E+05 | ||
| 2 | Brazil | GRU | 6.56E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 8.53E+09 | 9.24E+04 |
| LSTM | 4.02E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.44E+12 | 1.20E+06 | ||
| 3 | India | GRU | 1.52E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 7.67E+04 | 2.76E+02 |
| LSTM | 1.26E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 6.62E+04 | 2.57E+02 | ||
| 4 | Russia | GRU | 3.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.17E+06 | 1.08E+03 |
| LSTM | 1.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 7.65E+06 | 2.77E+03 | ||
| 5 | South Africa | GRU | 2.70E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.67E+07 | 4.08E+03 |
| LSTM | 2.00E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 2.15E+06 | 4.05E+03 | ||
| 6 | Mexico | GRU | 6.50E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.61E+08 | 1.27E+04 |
| LSTM | 1.65E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.73E+08 | 1.32E+04 | ||
| 7 | Peru | GRU | 2.66E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 6.56E+06 | 2.56E+03 |
| LSTM | 7.50E+01 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 2.13E+07 | 4.61E+03 | ||
| 8 | Chile | GRU | 3.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.32E+06 | 1.15E+03 |
| LSTM | 2.60E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 7.65E+05 | 8.74E+02 | ||
| 9 | UK | GRU | 3.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.19E+01 | 3.40E+00 |
| LSTM | 6.46E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 9.20E+00 | 3.03E+00 | ||
| 10 | Iran | GRU | 7.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.09E+06 | 1.04E+03 |
Fig. 3.
60-day ahead forecast of cumulative recovered cases for top-10 countries based on RNN-GRU and RNN-LSTM models.
For countries Russia, Peru, Mexico, Chile, and UK, both the models have shown very similar trend and similar predictions. For USA, India, Brazil, South Africa, and Iran both the models have predicted similar values for the initial couple of weeks and after that starts deviating from eachother. For countries UK, Chile, India, and South Africa both GRU and LSTM models are showing an approaching plateau. Approaching a plateau in recovered cases can only be possible if there is an implementation of stringent measure to control the spread of COVID-19. Further, in countries such as UK and Chile there is very negligible number of recovered cases forecasted. This could be explained by observing the Fig. 3, during the period between March and July 2020 very few recovered cases were reported. In contrast to this observation, when we examine the data of the USA, it is evident that the reported recovered cases during the same period (March to July 2020) has an exponential trend.
3.2.1. Factors contribute to the variation in reported recovered cases
The above discussed contradiction in the observations from country to country implies that the definition of recovered case and the process of reporting the cumulative recovered cases is different from country to country. For example, in USA [37], there are 16 states that have no definition for recovered case and do not report or document the recovered cases. Another 8 states of USA count the number of hospital discharges as recovered case. In states such as South Dakota the recovered case is defined as day-based meaning the infected individual is free from any symptoms for 3 – 42 days. According to John Hopkins, a COVID-19 patientis considered recovered only if the patient is appearing symptom free for 10 days since the occurrence of the first symptom and no fever for 24 hours without using fever reducing medication. Whereas, the loss of smell and taste for weeks cannot be considered in defining the recovered cases [38]. However, the reverse transcription polymerase chain reaction (RT-PCR) test conducted on the four patients who met the criteria for hospital discharge were tested positive after 10 days of the hospital discharge [39], [40]. In a study, [8] Fotios presented a brief insight on the importance of recovered cases, They reported the recovered cases are increasing exponentially as the number of days in the pandemic increase. However, their study was restricted to short time-series data. Whereas in India few tests are conducted per 1,000 population [41] therefore the reported cumulative cases do not represent the actual number of cumulative recovered cases.
Despite the above-mentioned results and limitations, from Fig. 3, it is evident that the recovery rate is increasing in most of the countries. The increase in number of recovered cases depends not only on the definition of recovered case, on the process of the recording the recovered cases but also on various factors such as age, underlying health conditions, preventive measures, and local weather conditions. The recovery statistics [42] show that 60% patients between the age group 20-40 years have recovered. The percentage of patients recovered decreased to 56% for the age groups 50-59 and > 60 years. Moreover, the susceptibility to the COVID-19 and rate of transmission of the disease was varied based on the age of the person. In a case study [43], it is reported that the percentage of manifestation of the clinical symptoms in age group over 70 years is 69% and in individuals under 20 years of age have only 11% chance of manifestation of clinical symptoms. In this scenario, our results based on LSTM and GRU models not only provide information about the number of recovered cases of the near future but alsoshed light on the importance of factors that control the number of recovered cases and the importance in consistency of the process of record keeping of the recovered cases all over the world.
3.3. Cumulative fatalities
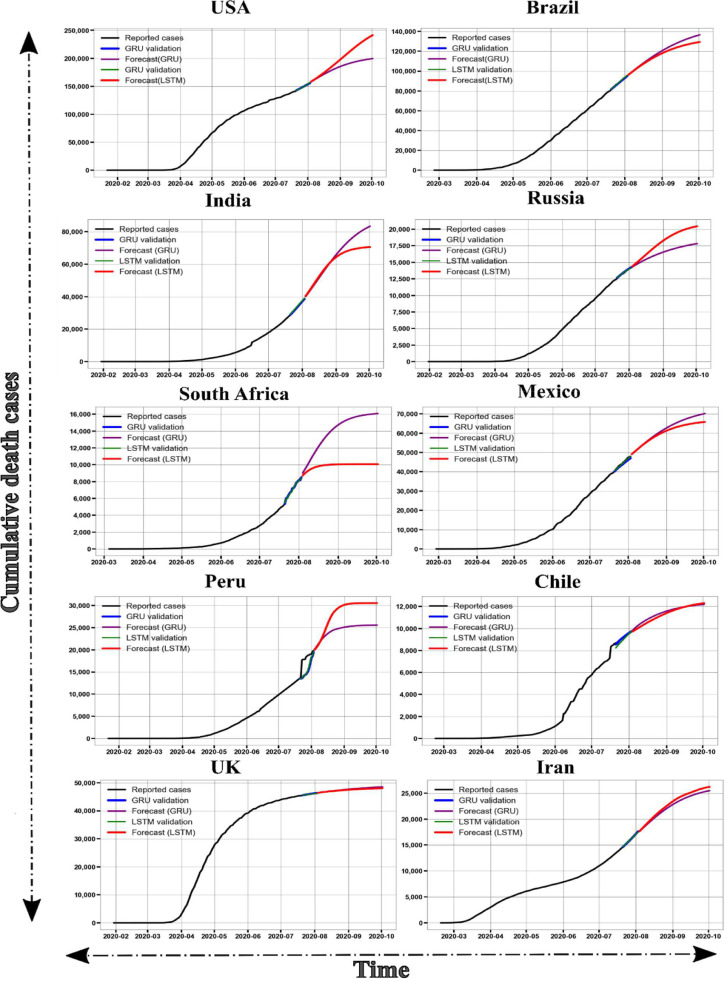
The forecast of the cumulative fatalities for top-10 countries were presented in this section. Fig. 4 depicts the forecasted trends of cumulative fatalities and the corresponding simulation details of both the models for each country are given in Table 3 . From the Fig. 4, it is evident that the number of cumulative fatalities in USA will be in between 200,000 and 240,000 according to forecasts of the GRU and LSTM based models, respectively. As per both the models, the fatalities are continuously increasing as the number of days into the pandemic is increasing. For the number of cumulative fatalities in USA, Peru, Chile, and UK, GRU based model performed better than the LSTM model which is evident from the Table 3. The MSE and RMSE values of the GRU based models for countries USA, Peru, Chile, and UK are lesser than the MSE and RMSE values of their respective LSTM models, The RMSE values of GRU models of the USA, Peru, Chile, and UK, are 4.57E+02, 5.89E+03, 6.64E+01, and 4.40E+01, respectively. The RMSE value of LSTM model of these countries is greater than the RMSE value of GRU models as described in Table 3. From the Fig. 4 and based on GRU model of the countries - Peru, Chile, and UK there will be ≈26,000, ≈12,100, ≈49,000, cumulative fatalities, respectively. Whereas the LSTM model of these countries predicted that there will be ≈31,000, ≈12,100, ≈49,000 cumulative death cases by the end of September 2020. Whereas for fatalities in other countries – Brazil, India, Russia, South Africa, Mexico and Iran, LSTM model performed better than the respective GRU models. The RMSE value of the LSTM models of these countries are 3.66E+04, 2.57E+02, 7.20E+01, 8.74E+02, 3.04E+02, and 5.20E+01 respectively. The number of cumulative fatalities predicted by LSTM models of Brazil, India, Russia, South Africa, Mexico, and Iran are ≈130,000, ≈70,000, ≈21,000, ≈10,000, ≈65,000, ≈27,000, respectively. Similarly, the RMSE values of the GRU models of the countries are described in the Table 3. The number of cumulative fatalities forecasted by the GRU models of Brazil, India, Russia, South Africa, Mexico, and Iran are ≈139,000, ≈81,000, ≈17,650, ≈16,000, ≈70,000 and ≈26,000, respectively. The forecasted trends for Mexico, Chile, UK and Iran are almost same for both LSTM and GRU models and both models show that the cumulative fatalities will reach a plateau by the end of September 2020. Fatalities in Peru, South Africa, Russia also followed a plateau but the agreement between the models is not good. Similar deviation between the models were observed for countries USA, Brazil and India, but the fatalities found to continuously increasing as the pandemic is increasing. According to Fig. 4, the number of cumulative death cases are either increasing (USA, Brazil, India Russia, Mexico, Chile and Iran) or reaching a steady value (South Africa, Peru and UK) as the pandemic period is increasing.
Fig. 4.
60-day ahead forecast of cumulative fatalties for top-10 countries based on RNN-GRU and RNN-LSTM models.
Table 3.
Models used for forecasting cumulative death and their parameters.
| No. | Country | RNN model | Epochs | Hidden size | Number of layers | Learning rate | MSE | RMSE |
|---|---|---|---|---|---|---|---|---|
| 1 | USA | GRU | 5.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 2.09E+05 | 4.57E+02 |
| LSTM | 2.01E+02 | 3.00E+02 | 3.00E+00 | 1.00E-05 | 2.91E+05 | 5.39E+02 | ||
| 2 | Brazil | GRU | 6.00E+01 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.47E+05 | 3.83E+02 |
| LSTM | 1.50E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.34E+09 | 3.66E+04 | ||
| 3 | India | GRU | 2.50E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 7.67E+04 | 2.76E+02 |
| LSTM | 2.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 6.62E+04 | 2.57E+02 | ||
| 4 | Russia | GRU | 2.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 5.48E+03 | 7.40E+01 |
| LSTM | 6.40E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 5.27E+03 | 7.20E+01 | ||
| 5 | South Africa | GRU | 3.50E+01 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.71E+06 | 1.31E+03 |
| LSTM | 2.00E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 7.64E+05 | 8.74E+02 | ||
| 6 | Mexico | GRU | 1.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 6.78E+05 | 8.23E+02 |
| LSTM | 7.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 9.29E+04 | 3.04E+02 | ||
| 7 | Peru | GRU | 1.50E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 3.47E+07 | 5.89E+03 |
| LSTM | 1.50E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 4.33E+07 | 6.58E+03 | ||
| 8 | Chile | GRU | 4.00E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 4.42E+03 | 6.64E+01 |
| LSTM | 2.00E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 5.74E+04 | 2.40E+02 | ||
| 9 | UK | GRU | 3.00E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 1.95E+03 | 4.40E+01 |
| LSTM | 3.00E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 5.81E+03 | 7.60E+01 | ||
| 10 | Peru | GRU | 1.75E+02 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 9.43E+03 | 9.71E+01 |
| LSTM | 1.43E+03 | 3.00E+02 | 2.00E+00 | 1.00E-05 | 2.76E+03 | 5.20E+01 |
3.3.1. Factors contribute to the variation of trends in fatalities
The varied trends in the graphs as shown in Fig. 4 could be because of the lesser availability of infrastructure such as number Intensive Care Units (ICU), number of hospital beds [44], available healthcare workers per number of patients [45] in developing countries such as South Africa, Mexico, Peru, Brazil, India etc. But the raise of the number of fatalities in wealthy nations could be not only because of the above-mentioned factors but also due to lack of strict social distancing, and other preventive measures. Moreover, the average age of the nation also determines the number of fatalities caused by COVID-19. For example in USA, there are 54.3 million residents who are 65 years and older [46], to whom COVID-19 can cause severe illness and can be fatal when compared to younger people of the population [47]. The increased risk of hospitalizations of senior citizens is described elsewhere by Center for Disease Control and Prevention (CDC) [47]. The raise of number of cases is directly related to social distance practices and implementation of other preventive measures. This is evident from the reported data of USA until 3rd August 2020 of the Fig. 2. The number of cumulative confirmed cases increased drastically from the first reported case in USA. Similarly, there are other factors that contribute to the higher mortality in some regions of the world and countries. Such factors include, economic status [48], race/ethnicity [49], [50], housing conditions [51]. Moreover, there is a positive correlation between the poor housing conditions and COVID-19 occurrence and mortality. In USA, the deaths related to COVID-19 pandemic were high in the communities with higher percentage of poor housing conditions [52]. Moreover, there is a strong evidence for the positive correlation between the COVID -19 fatalities and ethnicity. In USA, regions with higher population of Black and Latino residents had higher number of COVID-19 cases per 100,000 population [49]. COVID-19 mortality relation with the health at the county level is more pronounced in the non-urban counties. In these counties the people who work on the farms, and who have lower income are at high risk for COVID-19 mortality [53]. Similarly in a country level case study, it is found that higher COVID-19 mortality is associated with lower government effectiveness, fewer hospital beds and lower test number [54]. Based on the discussion it is important to identify the vulnerable communities of the society so that the public health officials can develop strategies specific to such communities. Tiwari et al. [55] reported an innovative COVID-19 impact assessment algorithm based on random forest machine learning modelto identify and map vulnerable counties. In such situation, our results not only provide an information on the upcoming number of fatalities, but also considers the various factors that play curial role in increasing the mortality caused by COVID-19 disease.
4. Conclusion
The present study reported a 60-day forecast of the covid-19 pandemic using RNN-LSTM and RNN-GRU models. Model with less values of MSE and RMSE is believed to be the best model for forecast. For confirmed cases, LSTM model performs better for countries such as USA, Brazil, South Africa, Peru, Chile and Iran, on the other hand, GRU model performed better for India, Russia, Mexico and UK. LSTM model has predicted to report an alarmingly rise in the confirmed cases in the USA, but GRU predicted a gradual rise in the cases. Confirmed cases in Brazil could reach a plateau (LSTM model) or linear increase in counts (GRU). According to both the models, cumulative cases in India, South Africa and Peru could reach a plateau, in contrast, cases in Russia, Mexico, Chile, UK and Iran may continuously increase.
For recovered cases, LSTM model performs better for India, South Africa, Chile, UK and Iran, whereas GRU model performed better for USA, Brazil, Russia, Mexico and Peru. The recovered cases in Mexico, Iran, Peru and Russia will increase according to both the models. Though the GRU model is over predicting, recovered data in USA, India and South Africa will reach a plateau as per both the models. Similarly, Brazil will also reach plateau but with LSTM overpredicting compared to the GRU. Recovered cases in Mexico, Iran, Peru and Russia will continuously increase in near future, according to LSTM and GRU models. The recovered cases in UK and Chile will reach a plateau in upcoming 60 days, which might be not true due to inconsistency in the reported data.
For the forecast of fatalities data, LSTM model outperformed GRU model for Brazil, India, Russia, South Africa, Mexico and Iran. For fatalities data in countries USA, Peru, Chile and UK, GRU models outperformed LSTM model. Shockingly, the fatalities in USA, Brazil, Russia and India will be continuous to increase with respect to both the LSTM and GRU model. Mexico, Chile, UK and Iran have reported to show a plateau with both model's predictions very consistent with each other. Fatalities in South Africa and Peru will reach a plateau but with less agreement between the model's predictions. Based on the results from the present work, it is highly recommended that to develop a deep learning models by feeding all three cumulative data sets (confirmed, recovered and fatalities) simultaneously to predict the pandemic trends. Further, more amount of data and accurate data is needed to develop robust and accurate models to obtained forecasts with less margin of error and to correlate the forecasts with factors that contribute to the COVID-19 rapid spread. Our study also helps countries realize the importance of the various factors that contribute to the spread of COVID-19 thereby helping them better prepare for the upcoming surge.
CRediT authorship contribution statement
K.E. ArunKumar: Conceptualization, Methodology, Software, Validation, Formal analysis, Writing - original draft, Visualization, Data curation, Resources. Dinesh V. Kalaga: Writing - review & editing, Supervision, Data curation, Project administration. Ch. Mohan Sai Kumar: Data curation. Masahiro Kawaji: Data curation, Project administration. Timothy M Brenza: Data curation, Project administration.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
The authors would like to acknowledge the financial aid obtained from the research project the National Science Foundation-Partnerships for International Research and Education (NFS-PIRE) sponsored by the U.S. National Science Foundation under Award Number 1743794.
References
- 1.Cucinotta D., Vanelli M. WHO declares COVID-19 a pandemic. Acta bio-medica: Atenei Parmensis. 2020;91(1):157–160. doi: 10.23750/abm.v91i1.9397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Worldometers.info. 2020 https://www.worldometers.info/.
- 3.rekhaHanumanthu S. Chaos, Solitons& Fractals; 2020. Role of Intelligent Computing in COVID-19 Prognosis: A State-of-the-Art Review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ghosal S., et al. Diabetes & Metabolic Syndrome: Clinical Research & Reviews; 2020. Prediction of the number of deaths in India due to SARS-CoV-2 at 5–6 weeks. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Parbat D. Chaos, Solitons & Fractals; 2020. A Python based Support Vector Regression Model for prediction of Covid 19 cases in India. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Maleki M., et al. Travel Medicine and Infectious Disease; 2020. Time series modelling to forecast the confirmed and recovered cases of COVID-19. [DOI] [PubMed] [Google Scholar]
- 7.Benvenuto D., et al. Data in brief; 2020. Application of the ARIMA model on the COVID-2019 epidemic dataset. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Petropoulos F., Makridakis S. Forecasting the novel coronavirus COVID-19. PloS One. 2020;15(3) doi: 10.1371/journal.pone.0231236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Singh R.K., et al. Short-term statistical forecasts of COVID-19 infections in India. IEEE Access. 2020;8:186932–186938. doi: 10.1109/ACCESS.2020.3029614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.He S., Peng Y., Sun K. SEIR modeling of the COVID-19 and its dynamics. Nonlin Dyn. 2020;101(3):1667–1680. doi: 10.1007/s11071-020-05743-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Thäter M., Chudej K., Pesch H.J. Optimal vaccination strategies for an SEIR model of infectious diseases with logistic growth. Math Biosci Eng. 2018;15(2):485. doi: 10.3934/mbe.2018022. [DOI] [PubMed] [Google Scholar]
- 12.Tolles J., Luong T. Modeling Epidemics With Compartmental Models. JAMA. 2020;323(24):2515–2516. doi: 10.1001/jama.2020.8420. [DOI] [PubMed] [Google Scholar]
- 13.Teles P. A time-dependent SEIR model to analyse the evolution of the SARS-CoV-2 epidemic outbreak in Portugal. 2020. arXiv preprint arXiv:2004.04735. [Google Scholar]
- 14.Ribeiro M.H.D.M., et al. Chaos, Solitons& Fractals; 2020. Short-term forecasting COVID-19 cumulative confirmed cases: Perspectives for Brazil. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kumar P., et al. Forecasting the dynamics of COVID-19 Pandemic in Top 15 countries in April 2020: ARIMA Model with Machine Learning Approach. 2020. medRxiv. [Google Scholar]
- 16.Ardabili S.F., et al. 2020. Covid-19 outbreak prediction with machine learning. Available at SSRN 3580188. [Google Scholar]
- 17.Chimmula V.K.R., Zhang L. Chaos, Solitons & Fractals; 2020. Time series forecasting of covid-19 transmission in canada using lstm networks. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Salgotra R., Gandomi M., Gandomi A.H. Chaos, Solitons & Fractals; 2020. Time Series Analysis and Forecast of the COVID-19 Pandemic in India using Genetic Programming. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Qi H., et al. Science of the Total Environment; 2020. COVID-19 transmission in Mainland China is associated with temperature and humidity: A time-series analysis. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kırbaş İ., et al. Chaos, Solitons & Fractals; 2020. Comperative analysis and forecasting of COVID-19 cases in various European countries with ARIMA, NARNN and LSTM approaches. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bandyopadhyay S.K., Dutta S. Machine learning approach for confirmation of covid-19 cases: Positive, negative, death and release. 2020. medRxiv. [Google Scholar]
- 22.Tomar A., Gupta N. Prediction for the spread of COVID-19 in India and effectiveness of preventive measures. Sci Total Environ. 2020 doi: 10.1016/j.scitotenv.2020.138762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Azarafza M., Azarafza M., Tanha J. COVID-19 Infection Forecasting based on Deep Learning in Iran. 2020. medRxiv. [Google Scholar]
- 24.Hopkins J. Novel Coronavirus (COVID-19) Cases Data. 2020. https://data.humdata.org/dataset/novel-coronavirus-2019-ncov-cases [cited 2020] Available from: [Google Scholar]
- 25.Kang-Lin P., Wu C.-H., Yeong-Jia J.G. The development of a new statistical technique for relating financial information to stock market returns. Int J Manage. 2004;21(4):492. [Google Scholar]
- 26.Chawla M., Verma H., Kumar V. Elsevier; 2008. RETRACTED: A new statistical PCA–ICA algorithm for location of R-peaks in ECG. [DOI] [PubMed] [Google Scholar]
- 27.Li X., Shang W., Wang S. Text-based crude oil price forecasting: A deep learning approach. Int J Forecast. 2019;35(4):1548–1560. [Google Scholar]
- 28.Hochreiter S., Schmidhuber J. Long short-term memory. Neur Comput. 1997;9(8):1735–1780. doi: 10.1162/neco.1997.9.8.1735. [DOI] [PubMed] [Google Scholar]
- 29.Chung, J., et al., Empirical evaluation of gated recurrent neural networks on sequence modeling 2014. arXiv preprint arXiv:1412.3555.
- 30.Betsch C., et al. Social and behavioral consequences of mask policies during the COVID-19 pandemic. Proc Natl Acad Sci. 2020;117(36):21851–21853. doi: 10.1073/pnas.2011674117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yadav S. Deep Learning based Safe Social Distancing and Face Mask Detection in Public Areas for COVID-19 Safety Guidelines Adherence. Int J Res Appl Sci Eng Tech. 2020;8(7):1368–1375. [Google Scholar]
- 32.Hamidi S., Sabouri S., Ewing R. Does density aggravate the COVID-19 pandemic? Early findings and lessons for planners. J Am Plan Assoc. 2020;86(4):495–509. [Google Scholar]
- 33.Miller I.F., et al. Disease and healthcare burden of COVID-19 in the United States. Nat Med. 2020;26(8):1212–1217. doi: 10.1038/s41591-020-0952-y. [DOI] [PubMed] [Google Scholar]
- 34.Bhadra A., Mukherjee A., Sarkar K. Modeling Earth Systems and Environment; 2020. Impact of population density on Covid-19 infected and mortality rate in India; pp. 1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hadjidemetriou G.M., et al. The impact of government measures and human mobility trend on COVID-19 related deaths in the UK. Transp Res Interdisciplin Perspect. 2020;6 doi: 10.1016/j.trip.2020.100167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kraemer M.U., et al. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science. 2020;368(6490):493–497. doi: 10.1126/science.abb4218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dylan Tiger . Reports on “recovered” Covid-19 cases inconsistent and incomplete. Numbers elusive and may mislead on real medical impact of virus. 2020. https://www.cu-citizenaccess.org/2020/07/10/definitions-of-recovered-from-covid-19-vary-widely-across-the-u-s/ Informatics in Medicine Unlocked 2020 [cited 2020 10 july]; Available from. [Google Scholar]
- 38.CDC . Coronavirus Questions and Answers. 2020. https://www.jhsph.edu/covid-19/questions-and-answers/ [cited 2020]; Available from. [Google Scholar]
- 39.Lan L., et al. Positive RT-PCR test results in patients recovered from COVID-19. JAMA. 2020;323(15):1502–1503. doi: 10.1001/jama.2020.2783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.He S., et al. Positive RT-PCR Test Results in 420 Patients Recovered From COVID-19 in Wuhan: An Observational Study. Front Pharmacol. 2020;11 doi: 10.3389/fphar.2020.549117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Tyagi R., Dwivedi L.K., Sanzgiri A. 2020. Estimation of Effective Reproduction Numbers for COVID-19 using Real-Time Bayesian Method for India and its States. Paper. [Google Scholar]
- 42.Voinsky I., Baristaite G., Gurwitz D. Effects of age and sex on recovery from COVID-19: Analysis of 5769 Israeli patients. J Infect. 2020;81(2):e102–e103. doi: 10.1016/j.jinf.2020.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Davies N.G., et al. Age-dependent effects in the transmission and control of COVID-19 epidemics. Nat Med. 2020;26(8):1205–1211. doi: 10.1038/s41591-020-0962-9. [DOI] [PubMed] [Google Scholar]
- 44.Wadhera R.K., et al. Variation in COVID-19 hospitalizations and deaths across New York City boroughs. JAMA. 2020 doi: 10.1001/jama.2020.7197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Organization W.H. Coronavirus disease 2019 (COVID-19): situation report, 82. 2020. [Google Scholar]
- 46.Older Population and Aging. 2019 [cited 2019]; Available from: https://www.census.gov/topics/population/older-aging.html#:~:text=Older%20Population%20in%20the%20U.S.&text=The%20new%20report%20provides%20analysis,of%20the%20older%20African%20population.&text=According%20to%20the%20U.S.%20Census,million%20on%20July%201%2C%202019.
- 47.CDC . Older Adults. 2020. https://www.cdc.gov/coronavirus/2019-ncov/need-extra-precautions/older-adults.html [cited 2020 11 SEPTEMBER]; Available from: [Google Scholar]
- 48.Han Y., et al. Who is more susceptible to Covid-19 infection and mortality in the States? medRxiv. 2020 [Google Scholar]
- 49.Figueroa, J.F., et al. Association of race, ethnicity, and community-level factors with COVID-19 cases and deaths across US counties. in Healthcare. 2021. Elsevier. [DOI] [PMC free article] [PubMed]
- 50.Webb Hooper M., Nápoles A.M., Pérez-Stable E.J. COVID-19 and Racial/Ethnic Disparities. JAMA. 2020;323(24):2466–2467. doi: 10.1001/jama.2020.8598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Alves M.R., Souza R.A.G.d., Caló R.d.S. Poor sanitation and transmission of COVID-19 in Brazil. Sao Paulo Med J. 2021 doi: 10.1590/1516-3180.2020.0442.R1.18112020. (AHEAD) [DOI] [PubMed] [Google Scholar]
- 52.Ahmad K., et al. Association of poor housing conditions with COVID-19 incidence and mortality across US counties. PloS One. 2020;15(11) doi: 10.1371/journal.pone.0241327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Fielding-Miller R.K., Sundaram M.E., Brouwer K. Social determinants of COVID-19 mortality at the county level. PloS One. 2020;15(10) doi: 10.1371/journal.pone.0240151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Liang L.-L., et al. Covid-19 mortality is negatively associated with test number and government effectiveness. Sci Rep. 2020;10(1):12567. doi: 10.1038/s41598-020-68862-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Tiwari A., et al. Science of The Total Environment; 2021. Using Machine Learning to Develop a Novel COVID-19 Vulnerability Index (C19VI) [DOI] [PMC free article] [PubMed] [Google Scholar]