Fast computational optimization of TMS coil placement for individualized electric field targeting

Abstract

Background:

During transcranial magnetic stimulation (TMS) a coil placed on the scalp is used to non-invasively modulate activity of targeted brain networks via a magnetically induced electric field (E-field). Ideally, the E-field induced during TMS is concentrated on a targeted cortical region of interest (ROI). Determination of the coil position and orientation that best achieve this objective presently requires a large computational effort.

Objective:

To improve the accuracy of TMS we have developed a fast computational auxiliary dipole method (ADM) for determining the optimum coil position and orientation. The optimum coil placement maximizes the E-field along a predetermined direction or, alternatively, the overall E-field magnitude in the targeted ROI. Furthermore, ADM can assess E-field uncertainty resulting from precision limitations of TMS coil placement protocols.

Method:

ADM leverages the electromagnetic reciprocity principle to compute rapidly the TMS induced E-field in the ROI by using the E-field generated by a virtual constant current source residing in the ROI. The framework starts by solving for the conduction currents resulting from this ROI current source. Then, it rapidly determines the average E-field induced in the ROI for each coil position by using the conduction currents and a fast-multipole method. To further speed-up the computations, the coil is approximated using auxiliary dipoles enabling it to represent all coil orientations for a given coil position with less than 600 dipoles.

Results:

Using ADM, the E-fields generated in an MRI-derived head model when the coil is placed at 5900 different scalp positions and 360 coil orientations per position (over 2.1 million unique configurations) can be determined in under 15 min on a standard laptop computer. This enables rapid extraction of the optimum coil position and orientation as well as the E-field variation resulting from coil positioning uncertainty. ADM is implemented in SimNIBS 3.2.

Conclusion:

ADM enables the rapid determination of coil placement that maximizes E-field delivery to a specific brain target. This method can find the optimum coil placement in under 15 min enabling its routine use for TMS. Furthermore, it enables the fast quantification of uncertainty in the induced E-field due to limited precision of TMS coil placement protocols, enabling minimization and statistical analysis of the E-field dose variability.

1. Introduction

Transcranial magnetic stimulation (TMS) is a noninvasive brain stimulation technique (Barker et al., 1985; Paulus et al., 2013), where a TMS coil placed on the scalp is used to generate a magnetic field that induces an electric field (E-field) in the head. This, in turn, directly modulates the activity of brain regions and network nodes exposed to a high intensity E-field (Aberra et al., 2020; Bungert et al., 2017). As such, computational E-field dosimetry has been identified by the National Institute of Mental Health as instrumental for determining brain regions stimulated by TMS and for developing rigorous and reproducible TMS paradigms (NIH, 2017). For efficient and focal stimulation, it is important to position and orient the coil to induce a maximal E-field in the targeted cortical region of interest (ROI) (Herwig et al., 2001; Sack et al., 2009). Furthermore, since coil placement protocols have limited precision, it is also important to quantify the variability in the TMS induced ROI E-field due to potential errors in coil placement. This work proposes a novel auxiliary dipole method (ADM) for fast E-field-informed optimal placement of the TMS coil and for quantifying uncertainty in the TMS induced E-field due to possible coil placement errors.

Optimal TMS coil placement is often determined by using scalp landmarks that correlate with targeted cortical ROIs. For example, to stimulate the dorsolateral prefrontal cortex (DLPFC), the coil is often positioned 5 cm anterior to a position that elicits motor evoked potentials in the contralateral hand muscle (George et al., 1995; Pascual-Leone et al., 1996). Alternatively, the coil is centered at a 10–20 coordinate location commonly used for EEG electrode positioning (Gerloff et al., 1997; Herwig et al., 2003). Scalp landmark-based strategies can result in significant misalignments between the coil placement and the targeted cortical ROI (Rusjan et al., 2010). To improve coil placement, MRI imaging data is sometimes used for ‘neuronavigated’ coil positioning. Standard neuronavigated protocols identify the location on the scalp directly over the targeted cortical site’s center of mass (CM) as the optimal coil center position (Herwig et al., 2001; Rusjan et al., 2010; Sack et al., 2009). This is because commonly used TMS coils have a figure-8 winding configuration that generates a primary E-field (E-field in the absence of the subject’s head) that is strongly concentrated underneath its center (Deng et al., 2013). However, the optimum coil placement site on the scalp can be shifted up to 12 mm (5.5 mm on average) away from the scalp location directly above the CM (Gomez-Tames et al., 2018) by the secondary E-field generated inside the subject’s head due to charge build-up on tissue interfaces (Diekhoff et al., 2011; Salinas et al., 2009; Thielscher et al., 2011). Furthermore, the amplitude of motor evoked potentials is reduced 10 fold when the coil is offset by 4–6 mm from the position with largest response and 100 fold when the coil is offset by more than 10 mm (Koponen et al., 2018), illustrating the need for accurate identification of the optimum coil placement site.

The orientation of the TMS coil is sometimes chosen so that the direction of the induced E-field is perpendicular to the sulcal wall closest to the ROI. This orientation is known to maximize the magnitude of the E-field in the ROI (Gomez-Tames et al., 2018; Janssen et al., 2014, 2015) and therefore corresponds to the lowest threshold for cortical activation, which is reinforced by the perpendicular orientation of the main axon of pyramidal neurons relative to the sulcal wall (Aberra et al., 2020). Indeed, E-field directed into the ROI sulcal wall requires, on average, lowest TMS coil currents to evoke a motor potential (Richter et al., 2013) and is close to the optimal orientation for targeting each region of the hand motor cortical area (Balslev et al., 2007; Brasil-Neto et al., 1992; Gomez-Tames et al., 2018; Raffin et al., 2015). Therefore, in the absence of an explicit model of neural activation, choosing a coil position and orientation that maximizes the E-field strength is a suitable objective.

A further limitation of TMS procedures is that they have a limited, and often unquantified, precision and accuracy of determining and maintaining the coil placement. Even with gold-standard neuronavigation and robotic coil placement, coil position error can exceed 5 mm (Goetz et al., 2019; Ruohonen and Karhu, 2010; Sparing et al., 2008). As such, there is an uncertainty in the TMS induced E-field resulting from uncertainty in the coil placement. This may result in variability in the outcomes of TMS interventions and needs to be quantified. Therefore, in addition to linking the external coil placement and current to the E-field induced in the brain, computational models should ideally account for coil placement uncertainty.

The total E-field induced in cortical ROIs can be determined by using MRI-derived subject-specific volume conductor models and the finite element method (FEM) or the boundary element method (BEM) (Dannhauer et al., 2012; Goetz and Deng, 2017; Gomez et al., 2020a, 2018; Huang et al., 2017; Laakso and Hirata, 2012; Makarov et al., 2019; Raffin et al., 2015). Evaluating the TMS induced E-field for a single coil position using a standard resolution head model currently requires 35 s using SimNIBS FEM (SimNIBS Developers, 2020; Thielscher et al., 2015), 5–10 s using SimNIBS with PARDISO direct solver (Schenk and Gärtner, 2004), or 104 s using BEM accelerated with the fast-multipole method (FMM) (Makarov et al., 2020). Presently, E-field-informed optimal coil placement requires iterative execution of such simulations until an optimal coil position and orientation are found out of a large number of possible options (Balderston et al., 2020; Beynel et al., 2019; Weise et al., 2020). This direct method was implemented in SimNIBS 3.1 (SimNIBS Developers, 2020). However, the computational requirements of the direct method limit the routine use of E-field-informed optimization of coil placement. For example, for this reason we restricted the individual model-based dosing in a recent TMS study to selecting only the coil current setting (Beynel et al., 2020).

This paper introduces a computational approach that enables fast E-field-informed optimization of coil placement using high resolution individual head models. Our framework is exceptionally computationally efficient as it can evaluate the E-fields generated in a targeted cortical ROI using a standard MRI-derived head model when the coil is placed at 5900 different scalp positions and 360 coil orientations per position in under 15 min using a laptop computer. This approach is based on the observation that to determine the coil placement on the scalp that maximizes the E-field in the target cortical ROI it is unnecessary to evaluate the E-field induced outside this ROI. This enables the use of the electromagnetic reciprocity principle to compute only the E-field induced in the ROI. Reciprocity has been used previously in the context of BEM simulations of TMS induced E-fields (Nummenmaa et al., 2013; Stenroos and Koponen, 2019). These previous uses of reciprocity have two bottlenecks: First, they require the determination of either the magnetic field or E-field due to many electromagnetic point sources, which limits their use to lower resolution head models than the ones commonly used in FEM TMS simulations. Second, they are limited to isotropic head models, and thus they cannot account for brain tissue conductivity anisotropy. Here we avoid the low-resolution bottleneck by using FMM (Gimbutas and Greengard, 2015), which enables the rapid calculation of fields due to many electromagnetic point sources. Furthermore, to enable the use of anisotropic conductivity head models, we apply reciprocity by using directly conduction currents in the brain (Wolters et al., 2004). These modifications to previous uses of reciprocity for TMS simulations make our E-field-informed coil placement framework compatible with head models from common transcranial brain stimulation simulation pipelines (Huang et al., 2017; Thielscher et al., 2011). Finally, we introduce a method for approximating the coil currents by auxiliary dipoles that can represent all coil orientations for a given coil position with less than 600 dipoles. This enables the rapid generation of maps that quantify the dependence of the E-field on both coil position and orientation. Furthermore, we post-process these maps to quantify the E-field uncertainty due to the limited accuracy and precision of coil placement methods.

The rest of this paper is structured as follows. First, we describe the proposed approach to rapidly and optimally position and orient a TMS coil on the scalp to maximize a specific E-field component or the E-field magnitude in a brain ROI. Second, the approach is benchmarked in terms of accuracy relative to analytical solutions of a spherical head model and in terms of runtime and memory requirement relative to results obtained by using FEM directly to determine the TMS induced E-fields. Third, we use a number of detailed realistic head models and target cortical ROIs from TMS experiments to compare the proposed method to a conventional approach that places the coil to minimize its distance to the cortical ROI. Finally, we use this approach to estimate rapidly the E-field variation related to coil placement errors that inevitably occur with any TMS procedure.

Software implementations of the methods developed in this paper are available on GitHub (Gomez et al., 2020b) and in the latest version (3.2) of SimNIBS (SimNIBS Developers, 2020). The code can also be used in the MATLAB and Python environments, enabling easy integration with other transcranial brain stimulation software packages such as SCIRun (Dannhauer et al., 2012).

2. Methods

TMS coil placement is specified by the position of its center, R, and its orientation, which is defined by a unit vector $\widehat{O}$ that denotes the direction of the primary E-field directly under the coil center (Fig. 1 A). The average E-field along a specified unit vector $\widehat{t}$ (i.e., $\langle E_{TMS}(r)\cdot \widehat{t}\rangle$, where 〈·〉 computes the average over the ROI) and the average E-field magnitude (i.e., 〈∥E_TMS(r)∥〉in the ROI) are both functions of coil position and orientation. We formulate the goal of optimal TMS coil placement to be the determination of a coil position R_opt and orientation ${\widehat{O}}_{opt}$ that maximizes either $\langle E_{TMS}(r)\cdot \widehat{t}\rangle$ or 〈∥E_TMS(r)∥〉. For example, $\langle E_{TMS}(r)\cdot \widehat{t}\rangle$ can be maximized if a preferential field direction $\widehat{t}$ for activating the targeted neural population is known, whereas 〈∥E_TMS(r)∥〉 is maximized whenever this information is missing. For clarity, we sometimes emphasize the dependence of $\langle E_{TMS}(r)\cdot \widehat{t}\rangle$ on coil position and orientation by referring to $\langle E_{TMS}(r)\cdot \widehat{t}\rangle$ as $\langle E_{TMS}(r)\cdot \widehat{t}\rangle \left(R,\widehat{O}\right)$.

Fig. 1.

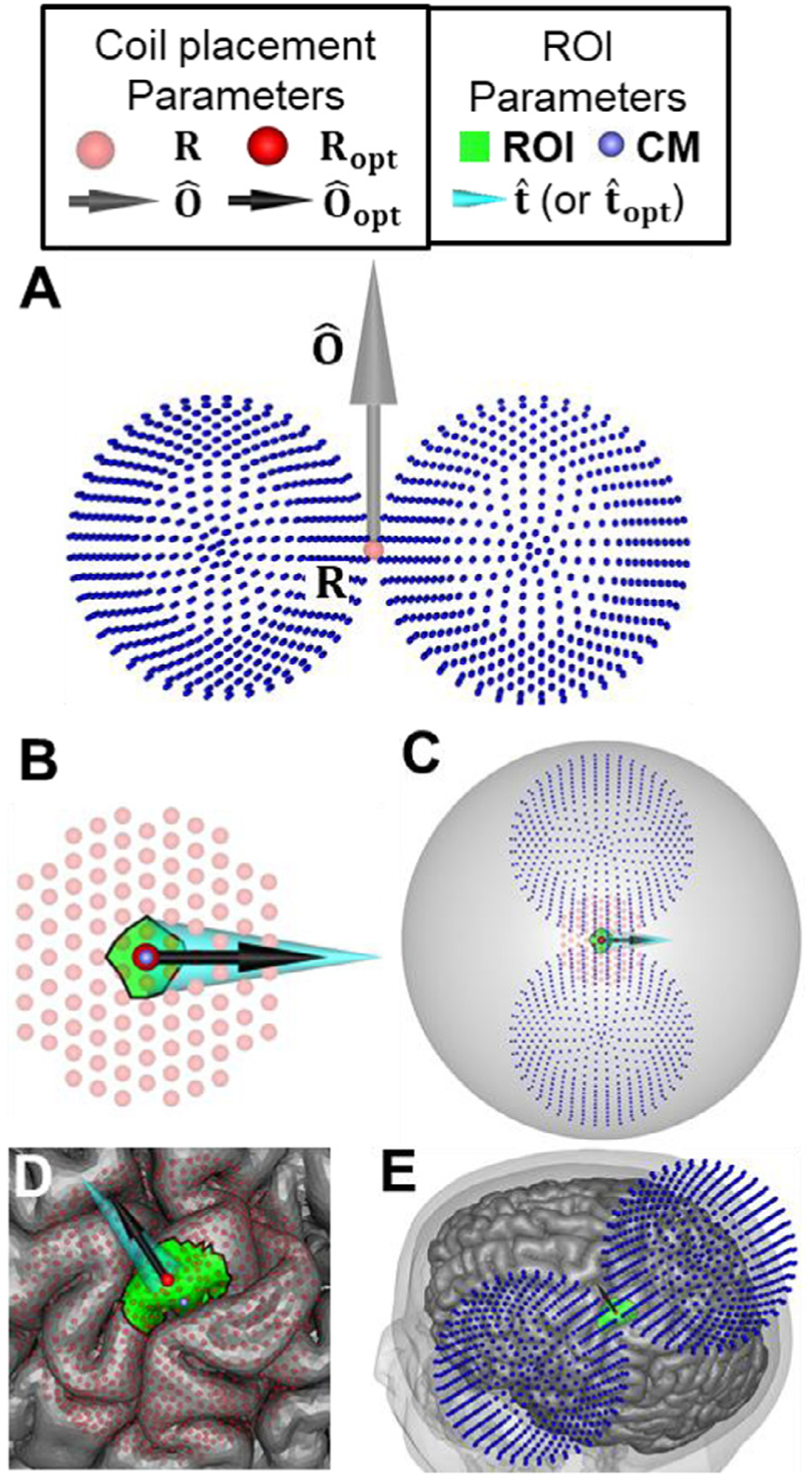
Conventions for describing TMS coil placement in this paper. (A) Figure-8 coil placement is defined by position R and orientation $\widehat{O}$ (the dipoles representing the coil model are shown as small dark blue spheres). (B) Dark and lighter red-colored spheres indicate candidate coil positions above the brain ROI colored in green. The ROI center of mass (CM) is indicated by a small purple sphere. The optimal coil position and orientation are indicated by a red sphere and black arrow, respectively. Wide cyan cone indicates either the preferred E-field direction $\widehat{t}$ in the ROI, if it is specified, or the average E-field direction ${\widehat{t}}_{\text{opt}}$ in the ROI resulting from maximization of the E-field magnitude. (C) For the spherical head model, the optimum coil position is directly above the ROI CM and its orientation is aligned exactly with the specified $\widehat{t}$. (D,E) The same concepts illustrated for an MRI-based head model (Ernie). For such models, the optimum coil position and orientation can differ from CM and $\widehat{t}$ (or ${\widehat{t}}_{\text{opt}}$), respectively.

We describe a fast reciprocity-based method for evaluating $\langle E_{TMS}(r)\cdot \widehat{t}\rangle$. This method is used for rapid determination of R_opt and ${\widehat{O}}_{opt}$ from a large number of candidate coil positions and orientations. Specifically, we define R_opt and ${\widehat{O}}_{opt}$ as the candidate position and orientation that maximize $\langle E_{TMS}(r)\cdot \widehat{t}\rangle$ (Fig. 1 B–E). Furthermore, this method is extended to find R_opt and ${\widehat{O}}_{opt}$ that maximize ∥〈E_TMS(r)〉∥. For typical ROIs, 〈∥E_TMS(r)∥〉 ≈ ∥〈E_TMS(r)〉∥. Therefore, the maximization of ∥〈E_TMS(r)〉∥ also results in the maximization of 〈∥E_TMS(r)∥〉. This enables ADM to maximize the E-field magnitude in an ROI. The average E-field direction in the ROI associated with the optimal coil placement, ${\widehat{t}}_{\text{opt}}$, emerges from this optimization as well.

2.1. Reciprocity method for determining the average E-field along a predetermined direction

Electromagnetic reciprocity is an equivalence relationship between two scenarios (Fig. 2). In one scenario, the TMS coil, modeled as impressed electric current J_TMS (r; t) = p(t) J_TMS(r), generates an E-field E_TMS(r; t) = p′(t)E_TMS(r) inside the head (Fig. 2A). Here t is time, r is a Cartesian location, and p(t) and p′(t) are the temporal variation of the TMS coil current and its time derivative, respectively. In the second scenario, a source J_C(r; t) = p(t) J_C(r) inside the head induces an E-field E_C(r; t) = p′(t) E_C(r) in the TMS coil (Fig. 2B). The reciprocity principle is derived in the supplemental material and has been previously studied in the context of quasi-static magnetic fields (Plonsey, 1972). Reciprocity dictates that the reaction integral between E_TMS(r; t) and J_C(r; t) is equal to the reaction integral between J_TMS(r; t) and E_C(r; t),

$$\int E_{TMS}\text{(}r\text{;t)}\cdot J_C\text{(}r\text{;t)d}r\text{=}\int E_C\text{(}r\text{;t)}\cdot J_{TMS}\text{(}r\text{;t)d}r\text{.}$$ (1)

Fig. 2.

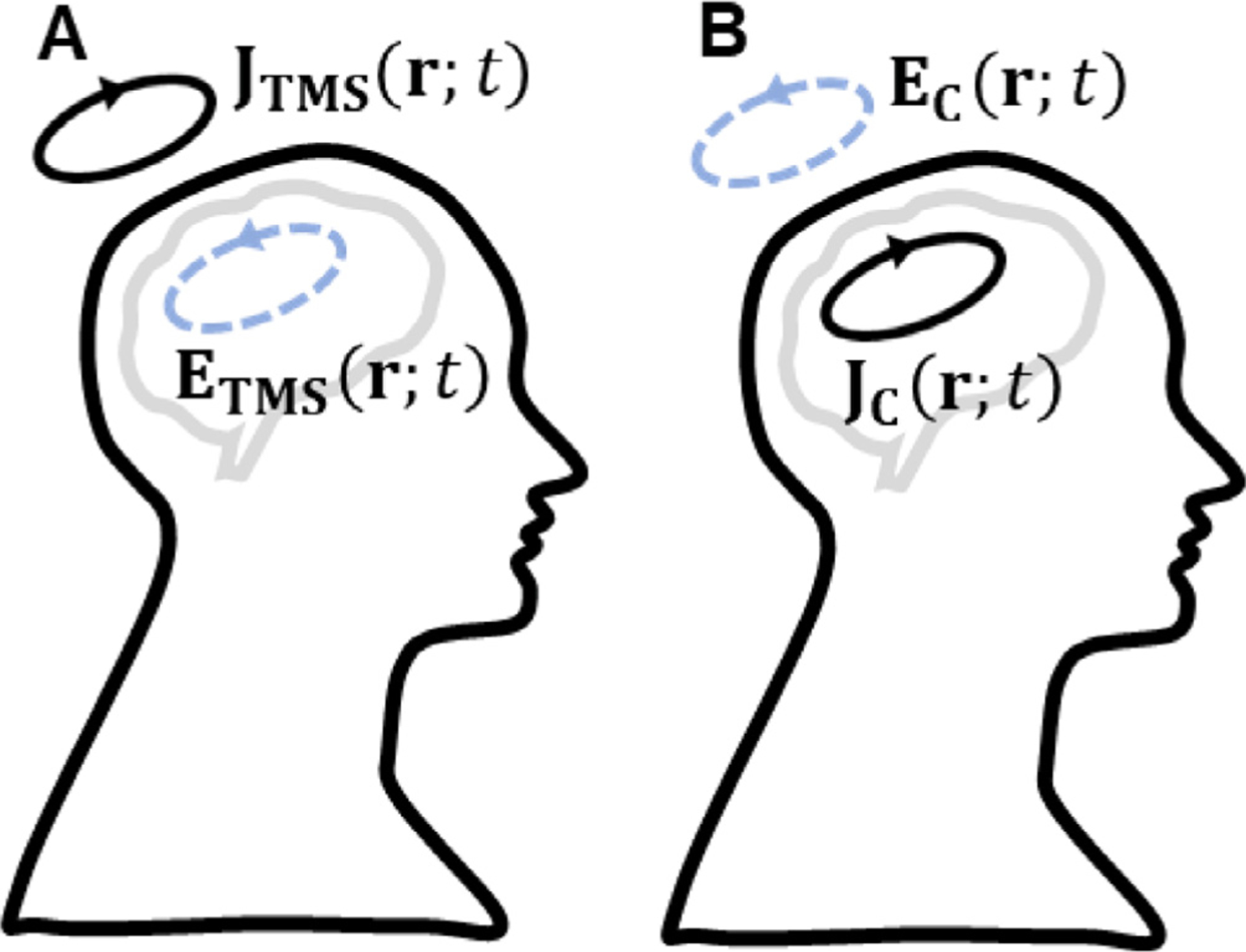
Reciprocal scenarios: (A) The TMS coil current generates an E-field inside the brain. (B) A brain current source generates an E-field where the coil resides.

Here we choose J_C(r; t) = 0 outside of the ROI and $J_C(r;t)=p(t)V_{ROI}^{-1}\widehat{t}$ inside it, where V_ROI is the volume of the ROI. Reciprocity results in the average E-field along $\widehat{t}$ in the ROI being equal to

$$\langle E_{TMS}(r)\cdot \widehat{t}\rangle =V_{ROI}^{-1}\underset{\text{ROI}}{\int }{E}_{TMS}\text{(}r\text{)}\cdot \widehat{t}\text{d}r=\int E_C(r)\cdot J_{TMS}(r)\text{d}r\text{.}$$ (2)

Since for TMS pulse waveform frequencies the E-field spatial and temporal components are separable (quasi-stationary) (Plonsey and Heppner, 1967), the temporal variation of all currents and E-fields—p(t) and p′(t), respectively—is omitted in this and subsequent notation.

Computing $\langle E_{TMS}(r)\cdot \widehat{t}\rangle$ using Eq. (2) requires the evaluation of E_C(r) outside the conductive head. To do this we first need to compute E_C(r) inside the head. Then, the E-field outside the head is computed as a superposition of the E-field due to current J_C(r) and conduction currents $\overline{\overline{\sigma }}(r)E_C(r)$, where $\overline{\overline{\sigma }}(r)$ is the conductivity tensor at position r in the head. Relevant equations for determining E_C(r) are derived in the supplemental material. Specifically, the E-field is

$$E_C(r)=\{\begin{array}{c}{E}_C(r)=-\nabla {\varphi }_C(r)r\in Head\\ -\frac{{\mu }_0}{4\pi }{\int }_{Head}\frac{J_C\left(r^{\prime }\right)+\overline{\overline{\sigma }}\left(r^{\prime }\right)E_C\left(r^{\prime }\right)}{\Vert r-r^{\prime }\Vert }\text{d}{r}^{\prime }r\notin Head\end{array}.$$ (3)

Here μ₀ is the permeability of free space, the integration is done over the head, and ϕ_C(r) is the scalar potential. In the following section, we describe the FEM approach we used to compute E_C(r) inside the head, and numerical integration rules used to estimate Eqs. (2) and (3).

2.2. Discretization of the reaction integral

The E-field inside the head due to J_C(r) satisfies Poisson’s equation, $\nabla \cdot J_C(r)=\nabla \cdot \overline{\overline{\sigma }}(r)\nabla {\varphi }_C(r)$, where E_C(r) = −∇ϕ_C(r). To solve for ϕ_C and ∇ϕ_C we used an in-house 1st order FEM method (Gomez et al., 2020a). First, the head model is discretized into a tetrahedral mesh having P nodes and N tetrahedrons, and each tetrahedron is assigned a constant tissue conductivity tensor. Second, the scalar potential is approximated as a sum of by piece-wise linear nodal elements N_m(r) (where m = 1, 2, … , P) as ${\varphi }_C=\sum _{m=1}^P{(x)}_m{N}_m(r)$. Here x is a P dimensional vector of unknown coefficients that needs to be determined via FEM (Jin, 2014). Third, weak forms of Poisson’s equation are sampled also using piecewise-linear nodal elements as testing functions in a standard Galerkin procedure. This results in a linear system of equations:

$$\begin{gathered} Ax=b, \\ {\left(A\right)}_{m,n}={\int }_{{\text{R}}^3}\overline{\overline{\sigma }}(r)\nabla N_m(r)\cdot \nabla N_n(r)\text{d}r, \\ {\left(b\right)}_m=\frac{V_{ROI}^{-1}}{4\pi }{\int }_{\text{ROI}}\widehat{t}\cdot \nabla N_m(r)\text{d}r, \\ {E}_C(r)=-\sum _{m=1}^P{(x)}_m\nabla N_m(r). \end{gathered}$$ (4)

Entries (A)_m,n are computed analytically using expressions provided in (Jin, 2014) and ROI denotes the support of J_C(r). The system of equations in Eq. (4) is solved using a transpose-free quasi-minimal residual iterative solver (Freund, 1993) to a relative residual of 10⁻¹⁰.

Samples of E_C(r) outside the head are obtained via Eq. (3) and using the FEM solution. The volume cortical and conduction currents are approximated by current dipoles on the centroid of each tetrahedron. The current dipoles are computed as $I_C^{(j)}=\left(\overline{\overline{\sigma }}\left(r_C^{(j)}\right)E_C\left(r_C^{(j)}\right)+J_C\left(r_C^{(j)}\right)\right)V_j$, where $r_C^{(j)}$ is the centroid, and V_j is the volume of the j^th tetrahedron. When the above conduction current approximation is applied to Eq. (3), it yields

$$E_C(r)=-\frac{{\mu }_0}{4\pi }\sum _{j=1}^N\frac{I_C^{(j)}}{\Vert r-r_C^{(j)}\Vert }.$$ (5)

Typically coil models consist of dipoles $I_{\mathbf{\text{coil}}}^{(i)}$ at locations $r_{\mathbf{\text{coil}}}^{(i)}$, where i = 1, 2, … , M. As a result, using a coil dipole model and Eq. (5) to evaluate Eq. (2) results in

$$\langle E_{TMS}(r)\cdot \widehat{t}\rangle =-\frac{{\mu }_0}{4\pi }\sum _{i=1}^M{I}_{\mathbf{\text{coil}}}^{(i)}\cdot \sum _{j=1}^N\frac{I_C^{(j)}}{\Vert r_{\mathbf{\text{coil}}}^{(i)}-r_C^{(j)}\Vert }.$$ (6)

Evaluating Eq. (5) at a single position requires evaluating the sum of N entries (i.e., the number of computations scales with the number of tetrahedrons). Furthermore, computing $\langle E_{TMS}(r)\cdot \widehat{t}\rangle$ using Eq. (6) requires the evaluation of Eq. (5) at M positions (i.e., the number of computations scales with the number of tetrahedrons times the number of coil model dipoles M × N). If one wants to evaluate $\langle E_{TMS}(r)\cdot \widehat{t}\rangle$ for L different coil placements, the number of computations will scale as L × M × N. As a result, there are trade-offs between how large L, M, and N can be while maintaining a tractable number of computations. For example, if the number of tetrahedrons is large we are limited in the number of coil placements for which we can evaluate the E-field. Conversely, if we would like to evaluate the E-field for many coil placements, the resolution of the head model has to be lowered. This is a common limitation of reciprocity-based E-field BEM solvers for TMS (Nummenmaa et al., 2013; Stenroos and Koponen, 2019). To lower the computational cost, we use FMM, which was designed to lower the computational complexity of the calculation of Eq. (6). Specifically, it reduces the total computation from scaling as N × M × L to scaling as the maximum between N and M × L. Using FMM enables us to compute Eq. (6) with both dense head meshes (i.e., large N) and for many coil placements (i.e., large M × L). Moreover, we generate an auxiliary dipole model, described in the following sections, that leverages the same set of dipole locations for multiple coil orientations to speed up our method further. Note that the method as presented here does not work with magnetic dipole TMS coil models. Its extension to magnetic sources requires minor modifications given in the supplemental material. We created software implementations for both electric and magnetic dipole sources, available online (Gomez et al., 2020b).

2.3. Optimizing E-field magnitude

Oftentimes, it is desired to maximize the average E-field magnitude in the ROI

$$\langle \Vert E_{TMS}(r)\Vert \rangle =V_{ROI}^{-1}{\int }_{\text{ROI}}{E}_{TMS}(r)\cdot \left(\frac{E_{TMS}(r)}{\Vert E_{TMS}(r)\Vert }\right)dr.$$ (7)

The E-field generated by the coil in the head does not vary rapidly spatially and has a direction that changes slowly as a function of position. Since typical cortical ROIs are small, the E-field can be well approximated as unidirectional within them. For a given coil position R and $\widehat{O}$ the best possible approximation of 〈∥E_TMS(r)∥〉 that can be obtained while replacing unit vector $\frac{E_{TMS}(r)}{\Vert E_{TMS}(r)\Vert }$ by a constant unit-vector (i.e. unidirectional approximation) is 〈∥E_TMS(r)∥〉 ≈ ∥〈E_TMS(r)〉∥. In other words, instead of computing the magnitude and then taking the average over the ROI, the component-wise average of the vector is first computed and then the magnitude is taken. The unidirectional approximation will be less accurate for larger ROIs relative to smaller ones. To assess the accuracy of the unidirectional approximation as a function of ROI size, we compared results obtained by directly computing 〈∥E_TMS(r)∥〉 with ones for ∥〈E_TMS(r)〉∥ for ROIs of varying sizes. Furthermore, we ran SimNIBS 3.1 (Weise et al., 2020) coil placement optimization to maximize 〈∥E_TMS(r)∥〉 and compared with our results obtained by maximizing ∥〈E_TMS(r)〉∥.

The following explains how we use ADM to compute ∥〈E_TMS(r)〉∥. For each candidate coil position and orientation, the ADM is run three times to compute $\langle E_{TMS}(r)\cdot \widehat{x}\rangle (R,\widehat{O})$, $\langle E_{TMS}(r)\cdot \widehat{y}\rangle (R,\widehat{O})$, and $\langle E_{TMS}(r)\cdot \widehat{z}\rangle (R,\widehat{O})$. From these three principal directions we compute $\Vert \langle E(r)\rangle \Vert =\sqrt{E_{TMS}(r)\cdot {\widehat{x}}^2+{\langle E_{TMS}(r)\cdot \widehat{y}\rangle }^2+{\langle E_{TMS}(r)\cdot \widehat{z}\rangle }^2}$. Note that having the three principal directions also enables us to compute $\langle E_{TMS}(r)\cdot \widehat{t}\rangle (R,\widehat{O})$ for any $\widehat{t}$ rapidly using the linear decomposition $\langle E_{TMS}(r)\cdot \widehat{t}\rangle (R,\widehat{O})=(\widehat{t}\cdot \widehat{x})\langle E_{TMS}(r)\cdot \widehat{x}\rangle (R,\widehat{O})+(\widehat{t}\cdot \widehat{y})\langle E_{TMS}(r)\cdot \widehat{y}\rangle (R,\widehat{O})+(\widehat{t}\cdot \widehat{z})\langle E_{TMS}(r)\cdot \widehat{z}\rangle (R,\widehat{O})$. The linear decomposition indicates that computing ∥〈E(r)〉∥ is equal to computing $\langle E_{TMS}(r)\cdot \widehat{t}\rangle (R,\widehat{O})$ while choosing $\widehat{t}=\frac{\langle E_{TMS}(r)\rangle (R,\widehat{O})}{\Vert \langle E_{TMS}(r)\rangle (R,\widehat{O})\Vert }$. As such, maximizing ∥〈E(r)〉∥ is equal to maximizing $\langle E_{TMS}(r)\cdot {\widehat{t}}_{opt}\rangle$, where ${\widehat{t}}_{opt}=\frac{E_{TMS}(r)\left(R_{opt},{\widehat{O}}_{opt}\right)}{\Vert \langle E_{TMS}(r)\rangle \left(R_{opt},{\widehat{O}}_{opt}\right)\Vert }$. In other words, the E-field magnitude optimization also produces a vector that indicates the direction along which we can generate the maximum average E-field.

2.4. Auxiliary dipole approximation

Here we describe the procedure used to approximate all coil orientations using a few dipoles located at auxiliary nodes (Fig. 3). The dipoles are chosen as Gauss-Legendre tensor product nodes of a rectangular box enclosing the coil (Fig. 3B). Assume that the x–y axis is chosen as the coil plane, and it consists of M dipoles $I_{\mathbf{\text{coil}}}^{(i)}$ at locations $r_{\mathbf{\text{coil}}}^{(i)}$, where i = 1, 2, … M (Fig. 3A). From $I_{\mathbf{\text{coil}}}^{(i)}$ and $r_{\mathbf{\text{coil}}}^{(i)}$, we generate P coil dipole models ${\left(I_{\mathbf{\text{coil}}}^{(i)}\right)}_j$ at locations ${\left(r_{\mathbf{\text{coil}}}^{(i)}\right)}_j$, where j = 1, 2, … P, by rotating $I_{\mathbf{\text{coil}}}^{(i)}$ and $r_{\mathbf{\text{coil}}}^{(i)}$ (Fig. 3B). Assume that all the coil models can be bound by a box Ω_box = [−x_coil, x_coil] × [−y_coil, y_coil] × [−z_coil, z_coil] outside the head. For each coil orientation, we need to compute

$$\frac{1}{4\pi }\sum _{i=1}^M{\left(I_{\mathbf{\text{coil}}}^{(i)}\right)}_j\cdot E_C\left({\left(r_{\mathbf{\text{coil}}}^{(i)}\right)}_j\right).$$ (8)

Fig. 3.

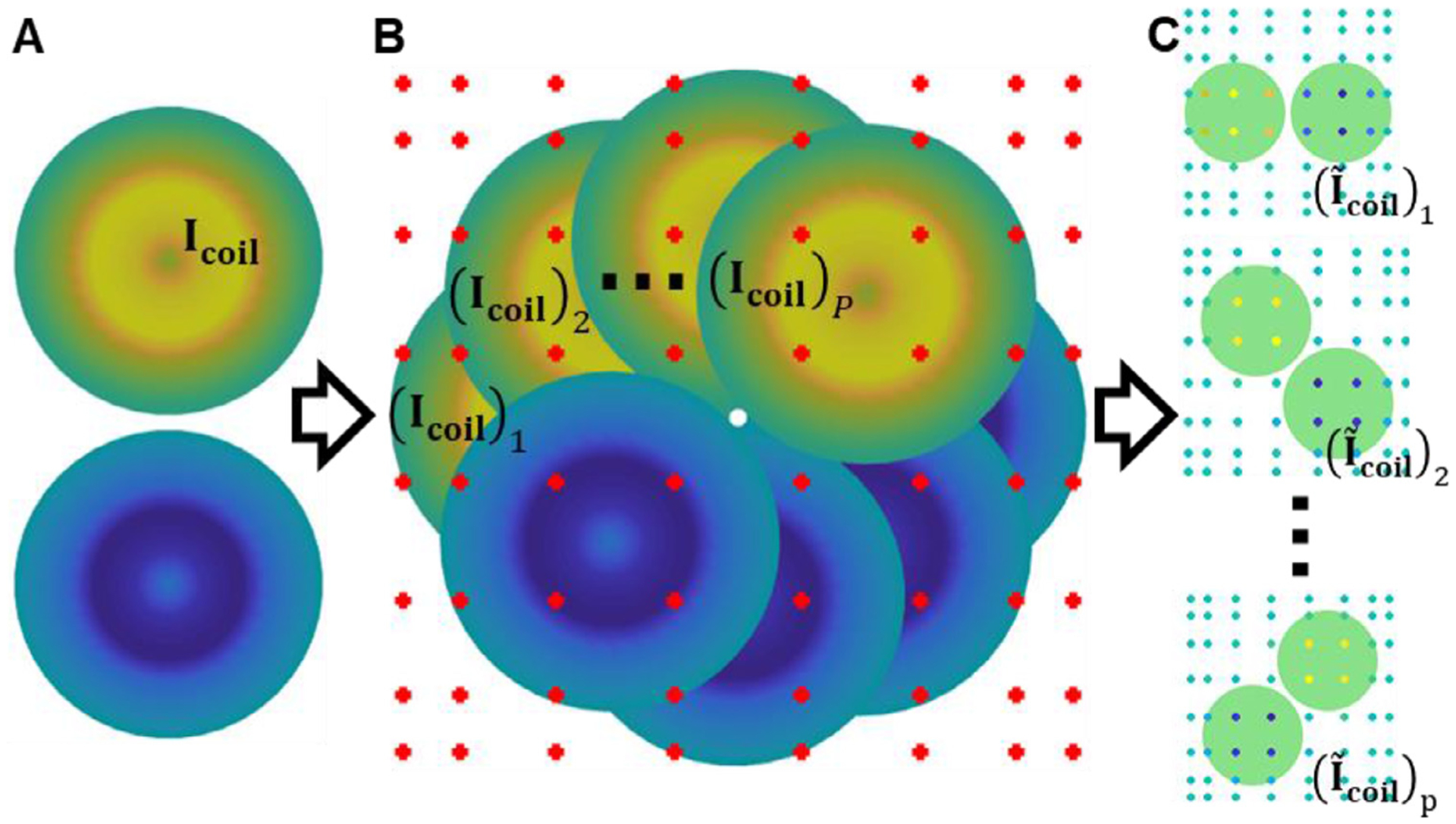
Auxiliary dipole method (ADM) work-flow. (A) TMS coil model consisting of M coil dipoles $I_{\mathbf{\text{coil}}}^{(i)}$ each at location $r_{\mathbf{\text{coil}}}^{(i)}$. (B) P TMS coil models (I_coil)_i each with a different orientation and immersed in a grid of Gauss-Legendre nodes. (C) Magnitude of dipole weights ${\left({\tilde{I}}_{\mathbf{\text{coil}}}\right)}_j$ for P individual coil orientations: warm and cold colors represent positive and negative values, respectively.

Since Ω_box is outside the head, which is a source-free region of space, the E-field can be interpolated as a polynomial with error decreasing exponentially with increasing degree of the polynomial (Gimbutas and Greengard, 2015). The E-field samples $E_C\left({\left(r_{\mathbf{\text{coil}}}^{(i)}\right)}_j\right)$ are determined from a polynomial fit of the E-field defined from auxiliary samples in Ω_box.

Specifically, $E_C\left({\left(r_{\mathbf{\text{coil}}}^{(i)}\right)}_j\right)\approx \sum _{k=1}^L{E}_C\left({\tilde{r}}_{\mathbf{\text{coil}}}^{(k)}\right)L_k\left({\left(r_{\mathbf{\text{coil}}}^{(i)}\right)}_j\right)$, where positions ${\tilde{r}}_{\mathbf{\text{coil}}}^{(k)}$ are chosen from a N_x × N_y × N_z tensor product of 1D Gauss-Legendre quadrature nodes in Ω_box, and L_k are chosen as their corresponding Lagrange polynomials. This choice of points finds a polynomial interpolant that minimizes L² error in a subspace of polynomials with basis consisting of all monomials xⁱy^jz^k, where 0 ≤ i ≤ (N_x − 1), 0 ≤ j ≤ (N_y − 1), and 0 ≤ k ≤ (N_z − 1) (Boyd, 2001), thereby, resulting in a polynomial fit whose error decreases exponentially with increasing number of points. This method is agnostic to the choice of interpolant, as such, a reduced polynomial basis (Yücel et al., 2019) and other spectrally accurate quadrature points (Gimbutas and Greengard, 2015), or a cylindrical bounding box along with a hybrid expansions of cardinal and Lagrange polynomial basis (Boyd, 2001) could potentially be used to generate interpolants that achieve greater accuracy with less points. Furthermore, a curved interpolation domain can be used to generate auxiliary dipoles for non-flat coils; however, this was not explored here and remains a limitation of the method as implemented.

Plugging in our interpolant into Eq. (8) results in the following:

$$\begin{gathered} \frac{1}{4\pi }{\sum }_{i=1}^M{\left(I_{\mathbf{\text{coil}}}^{(i)}\right)}_j\cdot E_C\left({\left(r_{\mathbf{\text{coil}}}^{(i)}\right)}_j\right)\approx \frac{1}{4\pi }{\sum }_{k=1}^L{\left({\tilde{I}}_{\mathbf{\text{coil}}}^{(k)}\right)}_j\cdot E_C\left({\tilde{r}}_{\mathbf{\text{coil}}}^{(k)}\right) \\ {\left({\tilde{I}}_{\mathbf{\text{coil}}}^{(k)}\right)}_{\text{j}}={\sum }_{i=1}^M{\left(I_{\mathbf{\text{coil}}}^{(i)}\right)}_j\cdot L_k\left({\left(r_{\mathbf{\text{coil}}}^{(i)}\right)}_j\right). \end{gathered}$$ (9)

In Eq. (9), all of the coil orientations share the same dipole locations enabling the batch evaluation of E_avg (Fig. 3C). Furthermore, Eq. (9) only incorporates information about the Lagrange interpolating polynomial functions; as such, it remains valid for magnetic dipole models without modification.

2.5. Coil modeling

The 2712 magnetic dipole model of the Magstim 70 mm figure-8 coil (P/N 9790) (Thielscher and Kammer, 2004) included in SimNIBS simulated for dI/dt = 1 A/μs was used for all accuracy comparisons (Fig. 1A). In its native space this coil is flat on the x–y plane, centered about the z axis. To keep computation times as small as possible, for all SimNIBS timing comparisons we used the precomputed magnetic vector potentials in lieu of the coil from the model package (file: ‘Magstim_70mm_Fig8.nii.gz’).

To speed-up computation further, we used the auxiliary dipole approximations of the coil to model each a distinct coil orientation. The dipole locations are the same across different auxiliary coil models, and coil models only differ in terms of their dipole weights. As a result, we can rapidly determine E-fields for many coil orientations each time using the same E-field samples outside of the head. In particular, we generated 360 models by rotating the coil dipole model around the z axis (0° to 359° in steps of 1°). To test the convergence of ADM with respect to increasing number of dipole locations, we used the SimNIBS Ernie example model and evaluated auxiliary coil dipole models consisting of all possible combinations of N_x = N_y varying from 1 to 29, and N_z varying from 1 to 3. For all other simulations, the total number of auxiliary dipoles is 578 and grid parameters were chosen as N_x = N_y = 17 and N_z = 2.

2.6. Head modeling

For numerical validation of the method we employed the SimNIBS example spherical shell and Ernie MRI-derived head model meshes. The spherical head mesh consists of a homogenous compartment with radius of 9.5 cm and conductivity of 0.33 S/m. The SimNIBS 3.1 Ernie head model mesh [18] consists of five homogenous compartments including white matter, gray matter, cerebrospinal fluid, skull, and skin. The scalp, skull, and cerebrospinal fluid conductivities were set to SimNIBS 3.1 default isotropic values of 0.465, 0.010, and 1.654 S/m, respectively. The gray and white matter compartments were assigned anisotropic conductivities to account for the fibered tissue structure. This was accomplished within SimNIBS by co-registering the diffusion-weighted imaging data employing a volume normalization of the brain conductivity tensor, where the geometric mean of the tensor eigenvalues was set to the SimNIBS 3.1 default isotropic conductivities of 0.275 and 0.126 S/m for gray and white matter, respectively.

Additional MRI-based head models—M1, M2, M3, and M4—were borrowed from one of our experimental studies involving E-field-based dosing (Beynel et al., 2020), corresponding to subject ids S262, S263, S266, and S269, respectively. Briefly, the models were constructed using structural T1-weighted (echoplanar sequence: Voxel Size = 1 mm³, TR = 7.148 ms, TE = 2.704 ms, Flip Angle = 12°, FOV = 256 mm², Bandwidth = 127.8 Hz/pixel), T2-weighted (echo-planar sequence with fat saturation: Voxel Size = 0.9375 × 0.9375 × 2.0 mm³, TR = 4 s, TE = 77.23 ms, Flip Angle = 111°, FOV = 240 mm2, Bandwidth = 129.1 Hz/pixel), and diffusion-weighted scans (Single-shot echo-planar: Voxel Size = 2 mm³, TR = 17 s, TE = 91.4 ms, Flip Angle = 90°, FOV = 256 mm², Bandwidth = 127.8 Hz/pixel, Matrix size = 1282, B-value = 2000s/mm², Diffusion directions = 26). Each model was first generated employing the co-registered T1- and T2-weighted MRI data to model major head tissues (scalp, skull, cerebrospinal fluid, and gray and white brain matter) represented as tetrahedral mesh elements. The number of tetrahedral mesh elements and nodes ranged 3.82–3.92 million and 0.679–0.699 million, respectively. Mesh conductivities were assigned following the same procedure as for the SimNIBS Ernie model.

2.7. ROI and grid generation

For the spherical head, we considered a 1 cm diameter ROI centered 1.5 cm directly below the apex of the sphere as shown in Fig. 1C. A number of coil placements were chosen on a 2 cm diameter grid of 3.7–4.2 mm spaced positions and centered 4 mm above the apex of the sphere (Fig. 1C). For each coil placement, the coil was oriented tangentially to the sphere surface and different orientations where chosen by counterclockwise angular displacements of 0°, 45°,90°, and 135° relative to $\widehat{x}\times \widehat{r}$. In other words, candidate orientations $\widehat{O}$ are ${\widehat{v}}_1\text{cos}\left({\theta }_i\right)+{\widehat{v}}_2\text{sin}\left({\theta }_i\right)$, where θ_i is either 0°, 45°,90°, and 135°, ${\widehat{v}}_1=\widehat{r}\times \frac{\widehat{x}}{\Vert \widehat{r}\times \widehat{x}\Vert }$, ${\widehat{v}}_2=\widehat{r}\times {\widehat{v}}_1$, and $\widehat{r}$ is the unit vector in the radial direction.

For the Ernie head model, the ROI was chosen as the gray matter contained in a 1 cm diameter cubic region centered about location (−55.1, −18.0, 96.4) (coordinates are in millimeters) as shown in Fig. 1D and E. Coil placements were chosen by extracting mesh nodes on the scalp that were within a 2 cm diameter of the point on the scalp closest to the centroid of the brain ROI and then projecting the nodes 4 mm outward in direction normal to the scalp surface. For each of the 632 coil placements (Fig. 1D), the coil was placed tangential to the scalp and different orientations where chosen by counterclockwise angular displacements of 0°, 45°, 90°, and 135° relative to ${\widehat{v}}_1=\widehat{X}-\frac{(\widehat{x}\cdot \widehat{n})\widehat{n}}{\Vert \widehat{x}-(\widehat{x}\cdot \widehat{n})\widehat{n}\Vert }$, where $\widehat{n}$ is the unit normal on the scalp directly below the center of the coil. (Additional ROIs and corresponding optimization results are shown in supplemental Fig. S7.)

For each of the four additional models (M1–M4), four ROIs of various sizes where generated using the SimNIBS 3.1 TMS coil placement optimization functionality. Within subject, the center of each ROI was the same and was derived from fMRI-measured brain activity (Beynel et al., 2020). The smallest ROI consisted of a single tetrahedron and had a mean effective diameter (the diameter of a sphere of the same volume) of 1.0 mm across subjects. The three larger ROIs were defined to have effective diameters of 10, 20, and 40 mm. SimNIBS 3.1 was used to generate coil center positions on 3 cm diameter scalp region centered about the scalp position closest to the ROI CM (Beynel et al., 2020). Each coil position was chosen to be approximately 1 mm apart and scalp positions where extruded outward by an amount dependent on the individual hair thickness: 3.26, 2.03, 5.55, and 2.78 mm for models M1–M4, respectively (Beynel et al., 2020). The total number of coil positions was 697, 689, 689, and 697 for models M1-M4, respectively. For each position, we used the direct method with SimNIBS 3.1 and the reciprocity-based ADM to generate, respectively, 72 and 360 coil orientations tangent to the scalp by rotating the coil in 5° and 1° intervals about the scalp normal direction. The coarser discretization of the search space for SimNIBS 3.1 was chosen to make the optimization computationally tractable.

2.8. Visualizations

In this work, all visualizations of anatomical details of the volume conductor models, TMS coil setups and optimizations, and E-field distributions are visualized with SCIRun (version 4.7, R45838; (Dannhauer et al., 2012), Figs. 1 and 9 and parts of Figs. 10 and 11) and MATLAB R2019 (Figs. 3–7, 10, and 11) (MATLAB, 2019).

Fig. 9.

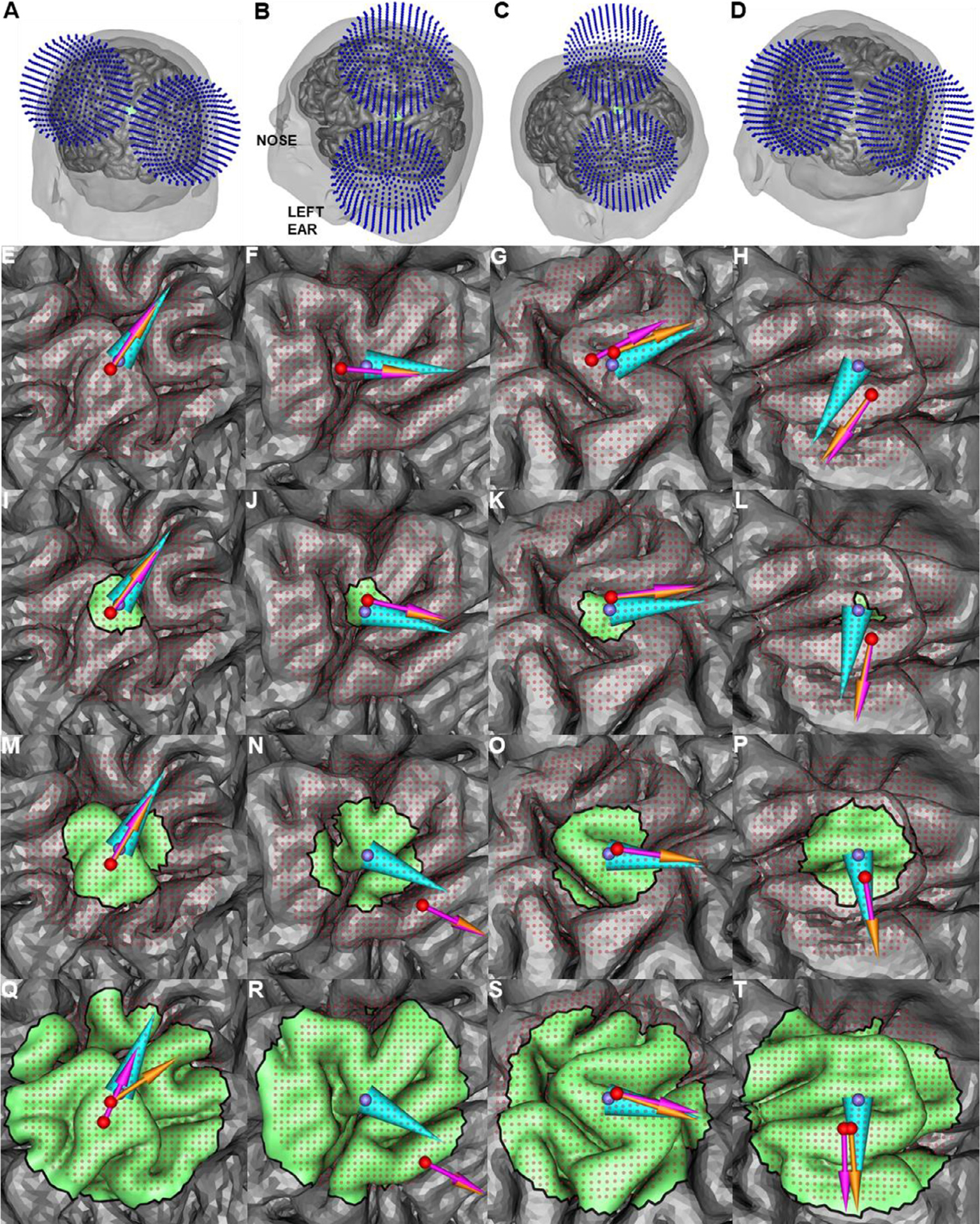
Coil placements maximizing the average E-field magnitude in ROIs of various size in models M1–M4 (left to right columns). (A)–(D): Illustration of the ADM-optimized coil placement for the 10 mm diameter ROI in models M1–M4, respectively. (E)–(T): Position and orientation optimized with the SimNIBS direct method and ADM are represented by pink and orange arrow, respectively, ${\widehat{t}}_{opt}$ and the ROI CM are represented by cyan cone and purple sphere, respectively. Rows, top to bottom, show results for increasing ROI diameter of 1, 10, 20, and 40 mm. In most cases both optimization methods result in the same or similar coil position and orientation.

Fig. 10.

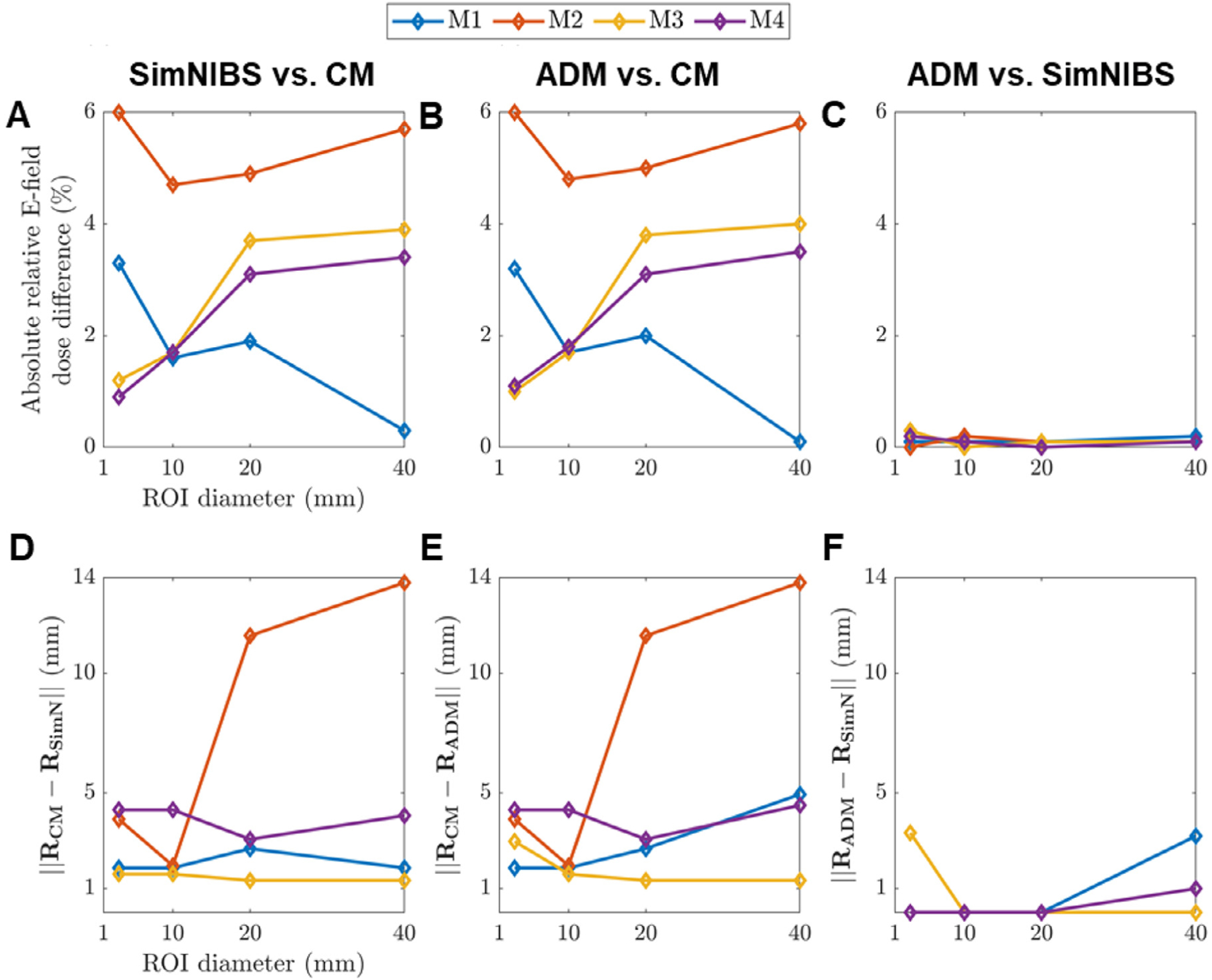
Comparisons of induced average E-field magnitude (A–C) and coil position (D–F) for ROIs of various sizes across different coil positioning strategies: (A,D) SimNIBS 3.1 optimization versus a placement over ROI CM; (B,E) ADM optimization versus ROI CM placement; (C,F) ADM versus SimNIBS 3.1. Additional coil optimization comparisons are given in Tables S1 and S2 in the supplemental material.

Fig. 11.

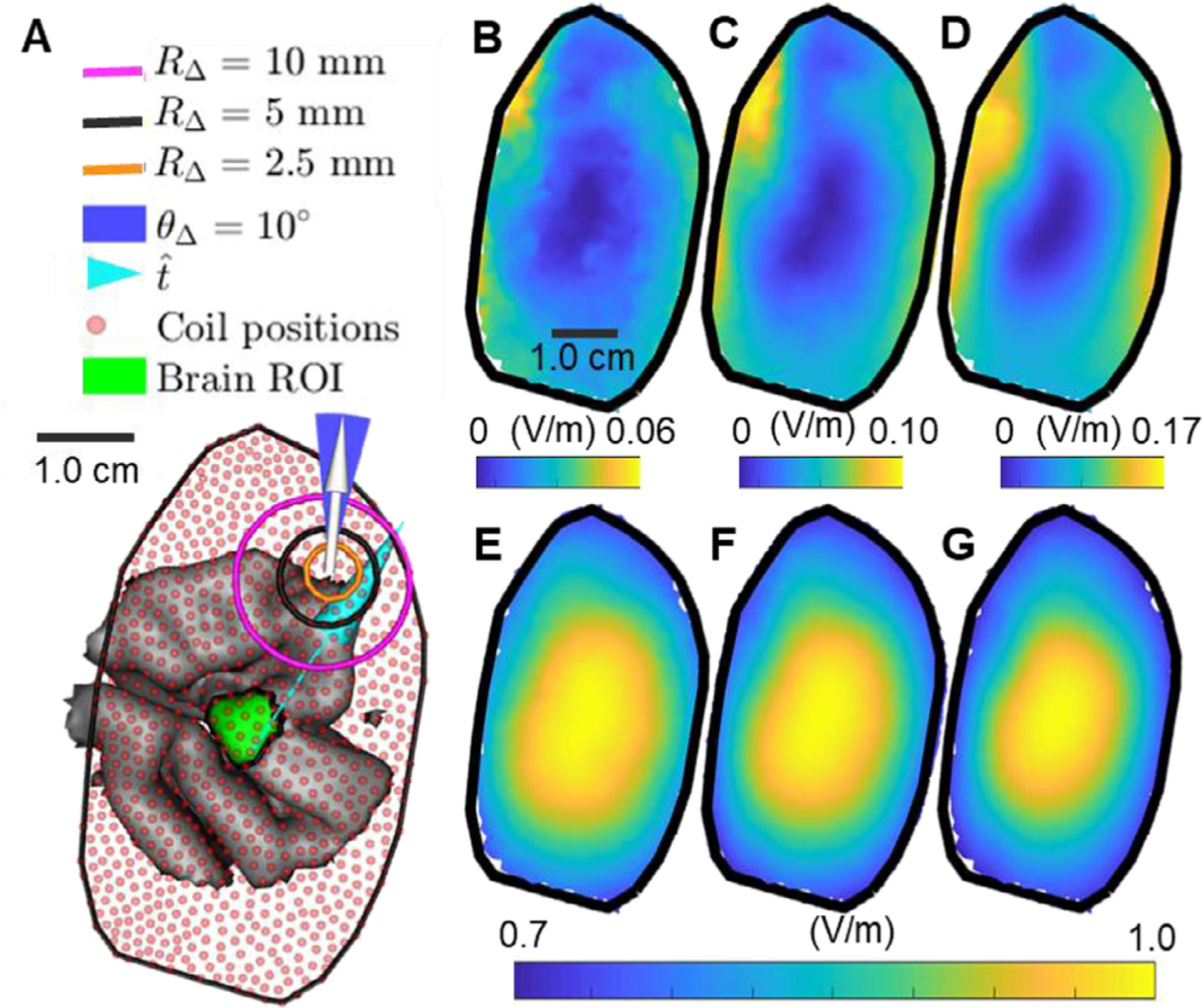
Coil position uncertainty results for model M2 and 10 mm diameter ROI. (A) Coil placements are chosen on the scalp above the brain ROI. The coil is oriented along the white vector and orientation uncertainty is always chosen as θ _Δ = 10°. The support of coil position uncertainty for R_Δ = 2.5 mm, R_Δ = 5.0 mm, and R_Δ = 10 mm is marked by the orange, black, and magenta circles, respectively. The maximum of the expected value and standard deviation for the average E-field along $\widehat{t}$ for each coil position is determined. (B–D) The standard deviation assuming a coil position uncertainty of (B) 2.5 mm, (C) 5 mm, and (D) 10 mm. (E–G) The expected value for the average E-field assuming a coil position uncertainty R_Δ of (E) 2.5 mm, (F) 5 mm, and (G) 10 mm. Results are normalized by the maximum expected average E-field over all coil positions and orientations.

Fig. 7.

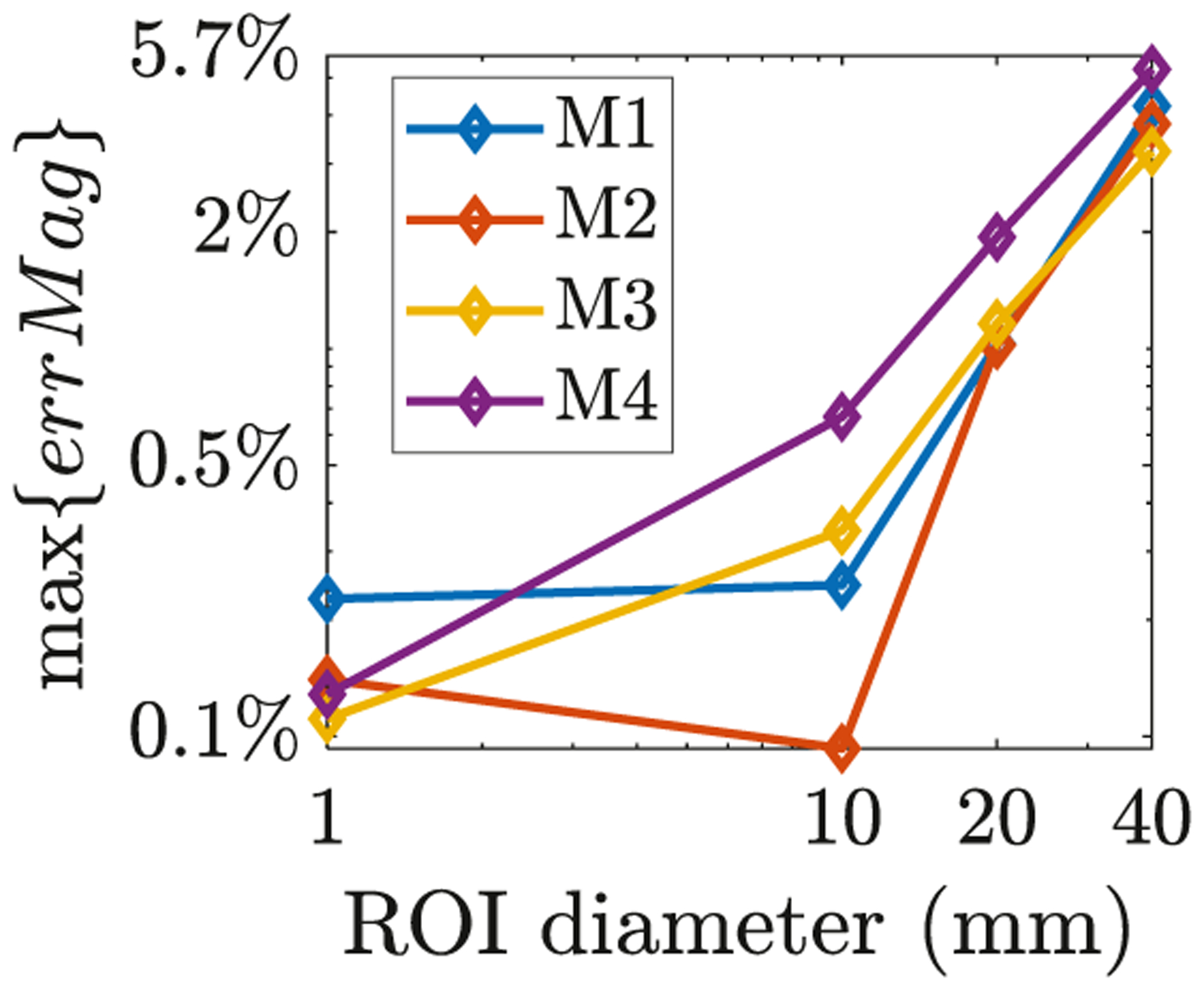
Maximum E-field magnitude estimate error (Eq. (9)) using ADM compared to the reciprocity results as a function of ROI diameter.

2.9. Error metrics

For each optimization setup we consider a normalized absolute error metric, which is normalized to the maximum observed $\langle E_{TMS}(r)\cdot \widehat{t}\rangle$,

$$er{r}_{i,j}=\frac{\left|\langle E_{TMS}(r)\cdot \widehat{t}\rangle \left(R_i,{\widehat{o}}_j\right)-\langle E_{REF}(r)\cdot \widehat{t}\rangle \left(R_i,{\widehat{O}}_j\right)\right|}{\left|\langle E_{REF}(r)\cdot \widehat{t}\rangle \left(R_{opt},{\widehat{O}}_{opt}\right)\right|},$$ (10)

where $\langle E_{TMS}(r)\cdot \widehat{t}\rangle \left(R_i,{\widehat{O}}_j\right)$ and $\langle E_{REF}(r)\cdot \widehat{t}\rangle \left(R_i,{\widehat{O}}_j\right)$ are the average E-field components in direction $\widehat{t}$ computed by one of our proposed methods and a reference method, respectively, for the i^th candidate coil position and j^th orientation. Additionally, we compare the E-field magnitude estimate ∥〈E(r)〉∥ to 〈∥E(r)∥〉 normalized to the maximum observed 〈∥E(r)∥〉,

$$errMa{g}_{i,j}=\frac{\left|\Vert \langle E_{TMS}(r)\rangle \Vert \left(R_i,{\widehat{O}}_j\right)-\langle \Vert E_{TMS}(r)\Vert \rangle \left(R_i,{\widehat{O}}_j\right)\right|}{\langle \Vert E_{TMS}(r)\Vert \rangle \left(R_{opt},{\widehat{O}}_{opt}\right)},$$ (11)

2.10. Coil placement uncertainty quantification

Using the reciprocity technique, we can also compute uncertainty in the E-field resulting from coil placement uncertainty. First, we use the reciprocity method to construct maps indicating the E-field induced for all possible coil positions and orientations on the considered region of the scalp. Second, this map is used to extract uncertainty of the E-field induced during TMS resulting from uncertainty in coil placement.

Uncertainty in coil placement is modeled as a probability distribution describing the likelihood of the coil being placed with a given orientation and location on the scalp. Here we assume that the coil position and orientation are uniformly distributed random variables with distributions centered at the mean scalp position R_μ and coil orientation ${\widehat{O}}_{\mu }$. The support of the distribution comprises the scalp region within a geodesic distance R_Δ from R_μ and all coil orientation deviations up to θ_Δ from ${\widehat{O}}_{\mu }$. For example, during coil placement using a ‘5 cm rule’ the nominal position R_μ of the coil would be exactly 5 cm anterior to a position that elicits motor evoked potentials in the contralateral hand muscle. During the actual TMS procedure there will likely be a small discrepancy in the placement due to limited TMS practitioner error and, as such, the coil will be positioned anywhere up to a distance R_Δ from R_μ on the scalp. Furthermore, the practitioner will have limited precision in orienting the coil. The orientation can be offset from the desired orientation ${\widehat{O}}_{\mu }$ up to θ_Δ. The range of possible coil positions and orientations can be expressed mathematically as

$$\begin{gathered} {\Omega }_{\mathit{\text{coil}}}= \\ \left\{(R,\widehat{O})|{\Vert R-R_{\mu }\Vert }_g\le R_{\Delta };\widehat{O}={\widehat{O}}_{\mu }\text{cos}(\theta )+\widehat{n}\times {\widehat{O}}_{\mu }\text{sin}(\theta ),|\theta |\le {\theta }_{\Delta }\right\}, \end{gathered}$$ (12)

where ∥R − R_μ∥_g is the geodesic distance along the scalp between R and R_μ, and parameters R_Δ and θ_Δ are radii of the positional and angular support of the distribution. The geodesic distance on the scalp is computed using the heat method described in (Crane et al., 2013). The values of R _Δ and θ_Δ are specific to the TMS methods used and should be based on available data (Goetz et al., 2019; Ruohonen and Karhu, 2010; Sparing et al., 2008). Other distributions (e.g., Gaussians) could also be used to discretize the coil position and orientation uncertainty whenever appropriate. To determine the statistical distributions of the E-fields due to coil position and orientation uncertainty we used a Monte Carlo method with 10,000 samples.

3. Results

3.1. Validation

For the spherical head model, we compare the average E-field in the ROI predicted by our in-house direct FEM, reciprocity, and ADM with the analytically computed value. The average E-field computed analytically for each coil placement is shown in Fig. 4. As expected, the maximum occurs when the coil is placed directly above the ROI and oriented to induce a maximum primary E-field along $\widehat{t}$. Fig. 4 also shows the errors normalized to the maximum E-field across all simulations. The maximum error obtained for the direct FEM, reciprocity, and ADM are 0.06%, 0.08%, and 0.46%, respectively. There is a slightly reduced accuracy in the ADM relative to the direct FEM and reciprocity approaches. However, the errors are still very low with the ADM compared to modeling and numerical errors that can exceed 5% in TMS E-field simulations (Gomez et al., 2020a; Saturnino et al., 2019) This indicates that 578 dipoles are sufficient to accurately represent the coil fields for all the test cases. These simulations were also run in SimNIBS 3.1 and we observed maximum error of 0.16%. Additional SimNIBS error figures are given in the supplemental material.

Fig. 4.

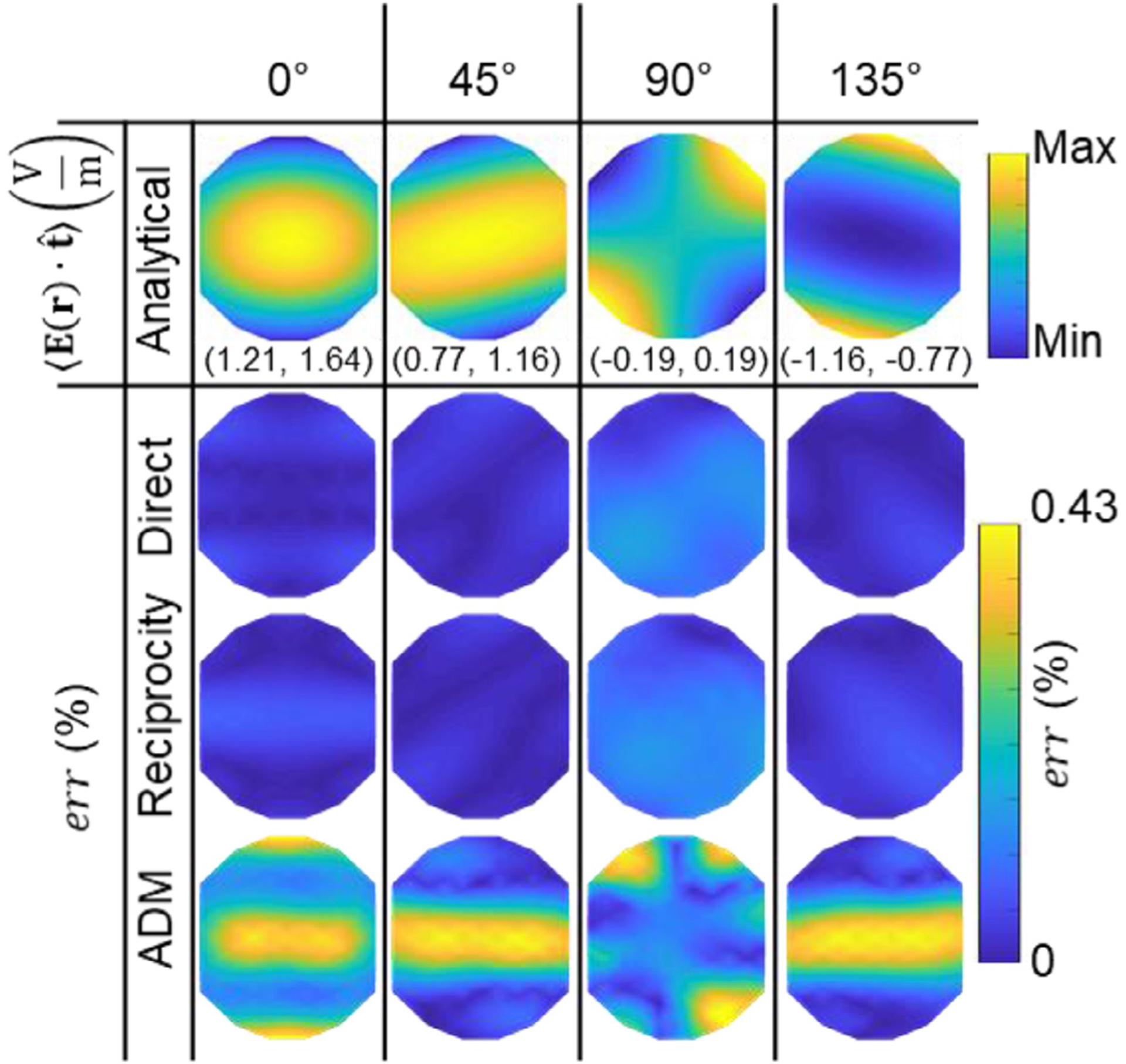
Validation of the computational methods in sphere head model. The 1st row shows, as a reference, the analytically computed average ROI E-field in direction $\widehat{t}$ (oriented horizontally) across TMS coil positions on the scalp. The scalp area spanned by the coil positions has a diameter of 2 cm. Four coil orientations are considered, from left to right: 0°, 45°, 90°, and 135°. The range of observed E-field component values are given in parenthesis below each figure in V/m. The 2nd, 3rd, and 4th row contain the corresponding absolute error relative to the analytical solution, err, for the direct, reciprocity, and ADM methods, respectively.

For the Ernie head model, we compare the average E-field in the ROI predicted by the in-house direct FEM, reciprocity, and ADM. The value of $\widehat{t}$ is chosen (as described above) as (−0.57, −0.72, −0.39) by evaluating the E-field for coil orientations varying from 0° to 359° in 5° intervals at each of the coil positions. The average E-field computed by the direct FEM for each coil position is shown in Fig. 5. A maximum E-field is obtained when the coil is placed 4.5 mm away from the point on the grid closest to the ROI CM. The normalized absolute error of the different approaches, when using direct FEM as reference, is shown in Fig. 5. All approaches agree with the direct FEM and have relative absolute errors below 0.13%. The maximum normalized absolute errors across all simulations of ADM relative to the reciprocity approach is shown in Fig. 6. ADM converges to the reciprocity results exponentially with increasing number of dipoles; an error below 0.5% is observed for the configuration of 578 dipoles used throughout this paper. Additional comparisons with SimNIBS results given in the supplemental material have a maximum relative error below 0.11%.

Fig. 5.

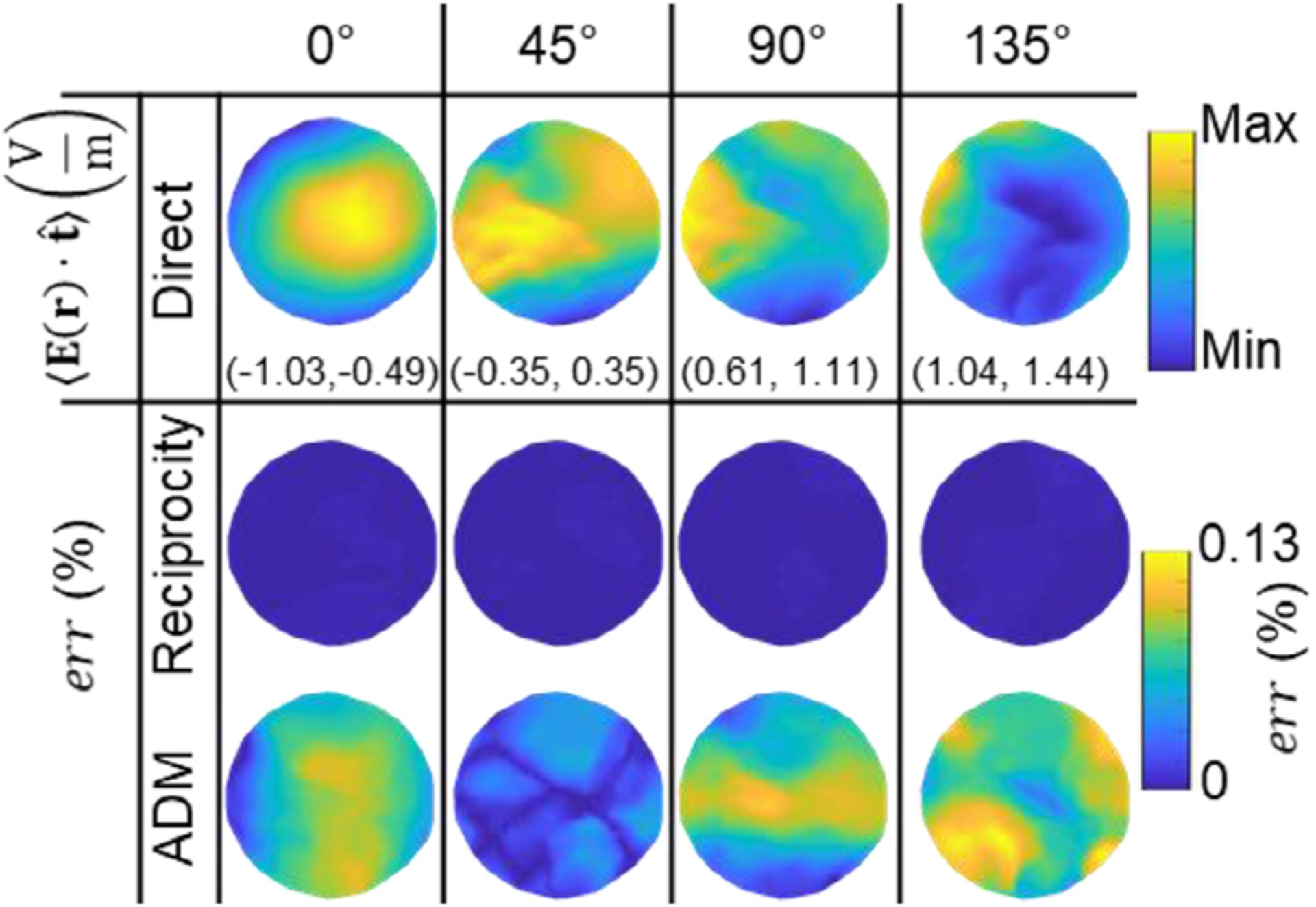
Validation in the Ernie head model, analogous to Fig. 4. The 1st row shows, as a reference, the directly computed average ROI E-field in direction $\widehat{t}$ (oriented horizontally) across TMS coil positions on the scalp. The scalp area spanned by the coil positions has a diameter of 2 cm. Four coil orientations are considered, from left to right: 0°, 45°, 90°, and 135°. The range of observed E-field component values are given in parenthesis below each figure in V/m. The 2nd and 3rd row contain the corresponding error relative to the direct method, err, for the reciprocity and ADM approaches, respectively. The direct method is used as a reference since there is no analytical solution for anatomically-detailed MRI-based head models.

Fig. 6.

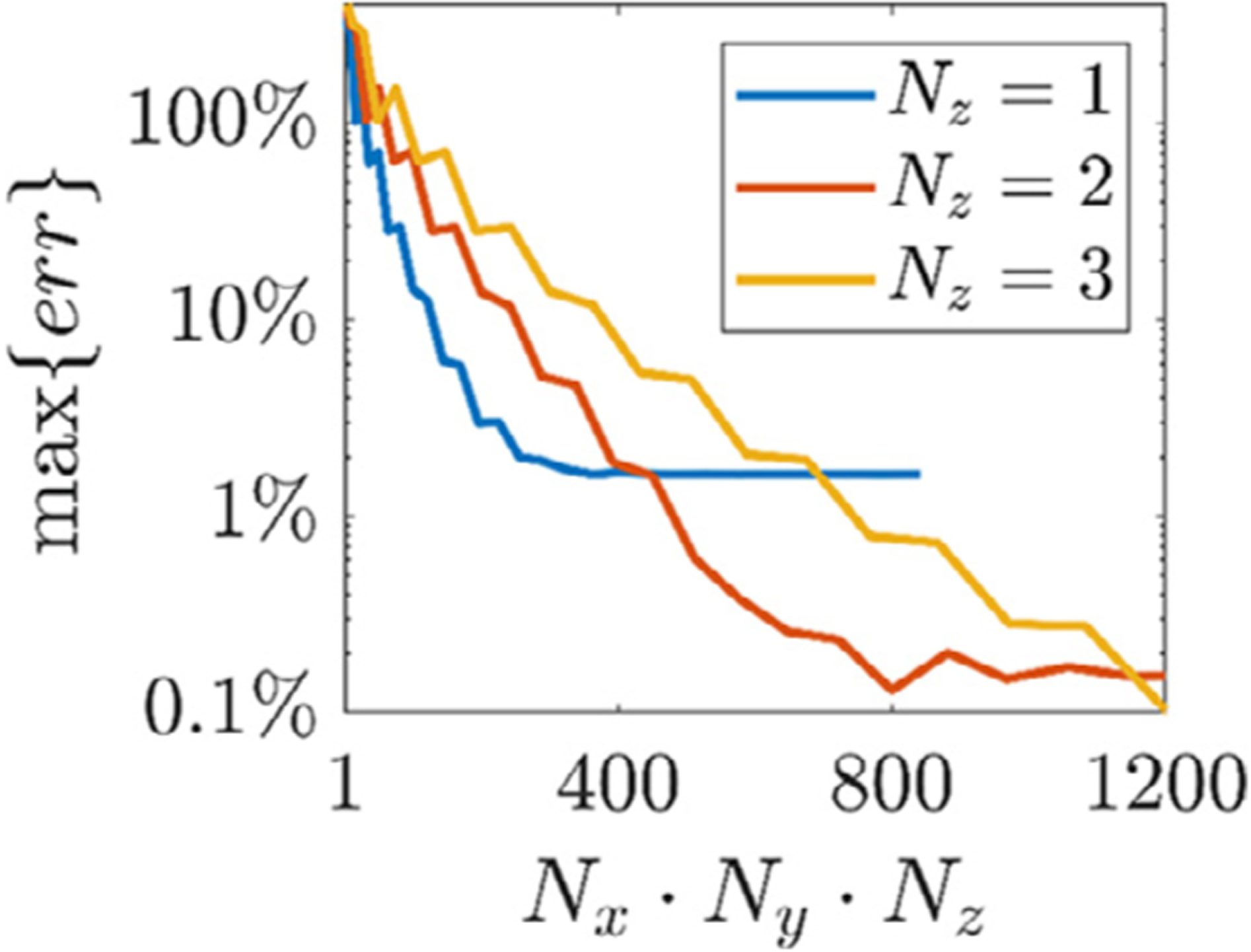
Maximum normalized absolute error for ADM relative to the reciprocity results as a function of number of ADM auxiliary dipoles N_x · N_y · N_z.

For the four models (M1–M4) we compared metric 〈∥E_TMS(r)∥〉 to ∥〈E_TMS(r)〉∥ for ROIs of varying sizes. Fig. 7 shows the maximum magnitude error obtained by comparing ADM to compute ∥〈E(r)〉∥ relative to using direct FEM to compute 〈∥E_TMS(r)∥〉 for ROIs of varying sizes. The maximum error increases with increasing ROI size. Considering the spatial resolution of TMS, the diameter of a typical ROI is below 1 cm diameter, and for these sizes the errors are below 0.5%. For larger ROIs with diameters between 1 cm and 2 cm the error is still below 2.0%, commensurate with the numerical error of good TMS E-field solvers (Gomez et al., 2020a). These results indicate that 〈∥E_TMS(r)∥〉 can be approximated by ∥〈E_TMS(r)〉∥ in many practical TMS settings.

3.2. Computational runtime and memory

Coil placement optimizations were run each time using a different number of candidate position and orientation configurations. The optimizations were run using a high performance computation system that has an Intel(R) Xeon(R) Gold 6154 CPU with a 3.0 GHz 36-core processor and 768 GB of memory as well as a conventional laptop that has an Intel(R) Core(TM) i7–4600 U CPU with a 2.10 GHz dual-core processor and 12 GB of memory. For each model (M1–M4) we ran the SimNIBS 3.1 direct coil position and orientation optimization procedure to maximize 〈∥E_TMS(r)∥〉 and ADM to maximize ∥〈E_TMS(r)〉∥. ADM was recently implemented in SimNIBS 3.2; therefore, the performance comparison effectively contrasts the direct coil placement optimization method in SimNIBS versions 3.1 and 3.2 with ADM available in version 3.2. Fig. 8 shows computational times required as a function of total candidate coil positions and orientations. On the high-performance computation system, the SimNIBS direct coil placement optimization required on average 7 s per candidate configuration, whereas our approach required an average total time of 7 min and 15 s regardless of the number of candidate configurations. As such, a SimNIBS direct optimization with 10,000 candidate coil placements takes 20 h, whereas ADM is 165 times faster, taking a little over 7 min. The ADM runtime includes negligible time finding the Lagrange polynomial expansion (< 1 s) and the rest is split evenly between solving the FEM scenario and a single call to FMM. All of these have to be executed each time ADM is run; as a result, there is no significant setup time in this ADM implementation. The memory required to run the SimNIBS direct optimization ranged 11–11.5 GB, whereas with ADM it was only 6.3–6.5 GB. Note that the memory requirements of the SimNIBS direct method can be lowered to 3.5 GB by using their iterative solver for the optimization (Saturnino et al., 2019), which, however, takes significantly longer. We decided not to use the SimNIBS iterative solver because many current laptop computers have at least 16 GB of memory and, thus, memory requirements do not impede coil position and orientation optimization. ADM computational time starts to increase beyond 100 thousand coil placements (Fig. 8B). The total time to run 1 million coil placements was 15 min, whereas assuming 7 s per simulation, the SimNIBS direct method would have taken approximately 8 days.

Fig. 8.

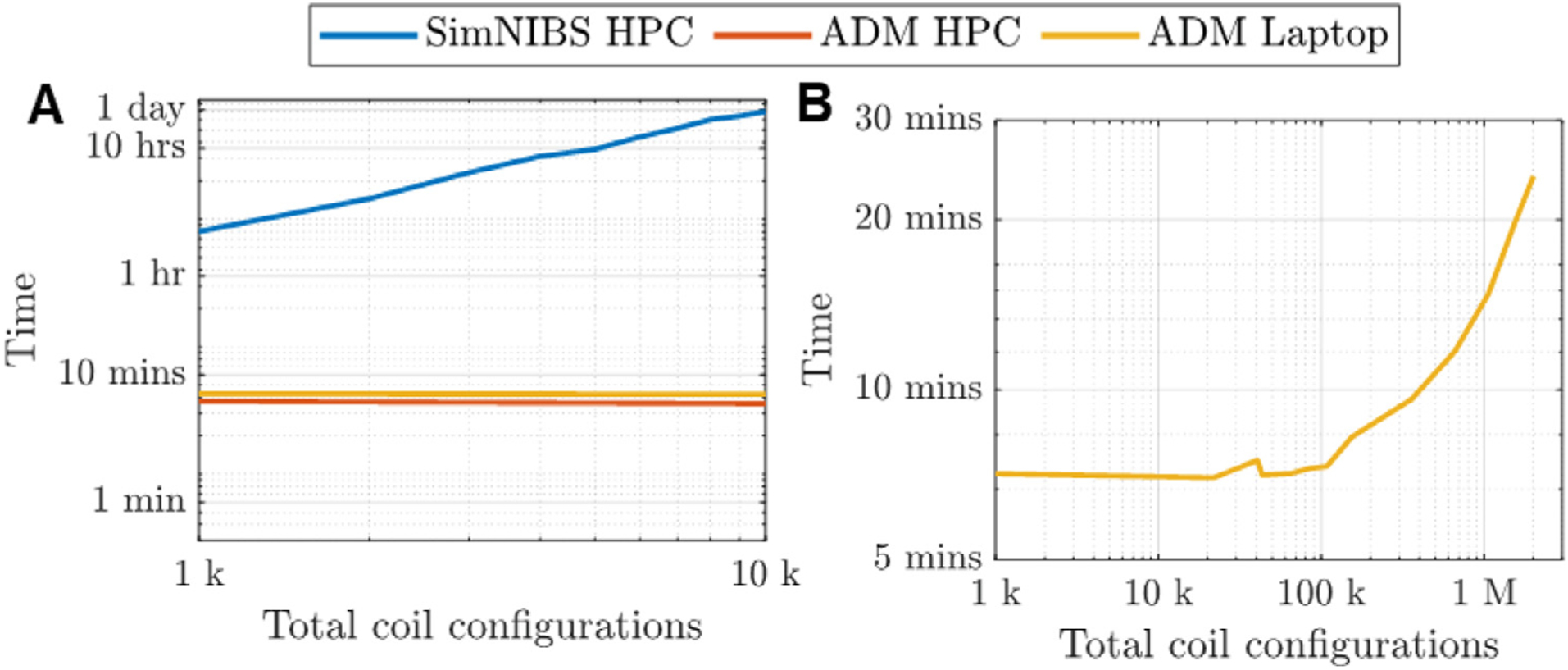
CPU runtime versus number of total coil position and orientation configurations. (A) Results for SimNIBS 3.1 direct method and ADM run on a high performance computation system (HPC) and a laptop (ADM only). (B) Extended results for ADM. CPU runtimes are averaged across models M1–M4.

3.3. Example application of coil position and orientation optimization

Fig. 9 shows results for models M1–M4 using the SimNIBS 3.1 direct method to maximize 〈∥E_TMS(r)∥〉 and ADM to maximize ∥〈E_TMS(r)〉∥. Except for model M3 and its 1 mm (one tetrahedron) diameter ROI, and 40 mm diameter ROI results, all of the coil placement optimizations resulted in the same position and differ in orientation by less than 2° For model M3 and the 1 mm diameter ROI, the optimum coil position computed by our in-house direct method and ADM are identical (supplemental Fig. S5) indicating that the 3.3 mm distance between the optimum of SimNIBS direct method and ADM are likely due to numerical errors. For ROIs with 40 mm diameter, the discrepancy between the ADM and the direct method in SimNIBS optimum TMS coil positions is likely due to inaccuracies in the approximation of the E-field magnitude using ADM. For regions with diameter below 40 mm, the orientation differences are likely because ADM was run with an angular step size of 1°, whereas the SimNIBS direct simulations were run with an angular step size of 5° (due to long computation times). As such, the observed differences in coil orientation between ADM and the direct method in SimNIBS 3.1 are below the resolution of the latter optimization.

Fig. 9 shows the E-field orientation associated with maximum E-field magnitude, ${\widehat{t}}_{opt}$. As is generally the case for TMS, the strongest E-field is approximately tangential to the scalp surface (Ilmoniemi and Sarvas, 2019). Relative to the cortical gyri, ${\widehat{t}}_{opt}$ is typically nearly perpendicular to the nearby sulcal walls. This is consistent with other modeling and experimental results (Gomez-Tames et al., 2018; Janssen et al., 2014, 2015). Whenever there are multiple bends in the ROI, it is difficult to identify the precise normal to the sulcal wall. Our framework helps to disambiguate a specific coil orientation that should be used, although in some cases a range of orientations may yield similar E-field strengths at the target.

In a conventional neuronavigated coil placement protocol, the coil would be placed directly above the CM (R_CM). We compare the optimum coil placements to a placement where the coil is placed above R_CM and oriented along normal to the nearest sulcal wall to the ROI CM (Fig. 9). Fig. 10 compares the coil placement above the CM and the SimNIBS and ADM optimization approaches. The average E-field magnitude in the ROI obtained by placing the coil at R_CM can be up to 6.0% lower than that for the E-field-guided methods (Fig. 10 A and B). The E-fields achieved by each optimum coil placement strategy are almost identical, differing by less than 0.3% (Fig. 10 C). The coil position directly above the ROI CM and the optimization methods can vary as much as 13.8 mm (Fig. 10 D–E), whereas this difference is less than 3.2 mm between ADM and SimNIBS (Fig. 10 F). Thus, the ADM method to optimize ∥〈E_TMS(r)〉∥ results in nearly the same E-field delivery and coil location as using SimNIBS to optimize 〈∥E_TMS(r)∥〉, and both approaches are superior to the coil placement directly above the ROI center.

3.4. Coil placement uncertainty quantification

As an example, we computed the uncertainty in $|\langle E_{TMS}(r)\cdot \widehat{t}\rangle |$ for the 10 mm diameter ROI in head model M2 resulting from coil position and orientation uncertainty. Fig. 11 shows results for various levels of coil position uncertainty. For fixed R_Δ, the minimum of the standard deviation is where the expected value of $|\langle E_{TMS}(r)\cdot \widehat{t}\rangle |$ is highest. The standard deviation for each position increased with R_Δ. For fixed R_Δ, the expected value decreased monotonically away from its optimum, and this decrease accelerated with increasing R_Δ. Fig. 12 plots the 90% confidence interval and expected value for $|\langle E_{TMS}(r)\cdot \widehat{t}\rangle |$ for various levels of position and orientation uncertainty. The expected value of $|\langle E_{TMS}(r)\cdot \widehat{t}\rangle |$ decreased with increasing R_Δ. The range of the 90% confidence interval of $|\langle E_{TMS}(r)\cdot \widehat{t}\rangle |$ nearly doubled if the coil was placed 5 mm away from its optimal position (Fig. 12 A–E). Furthermore, coil orientation uncertainty did not contribute significantly to the total uncertainty (Fig. 12 F). These results indicate that errors in identifying the optimum coil position both decrease effectiveness of TMS and also increase uncertainty in the TMS induced E-field due possible coil positioning errors. Furthermore, it is more critical to identify the optimum coil positioning whenever there are large coil positioning uncertainties associated with the TMS coil placement protocol.

Fig. 12.

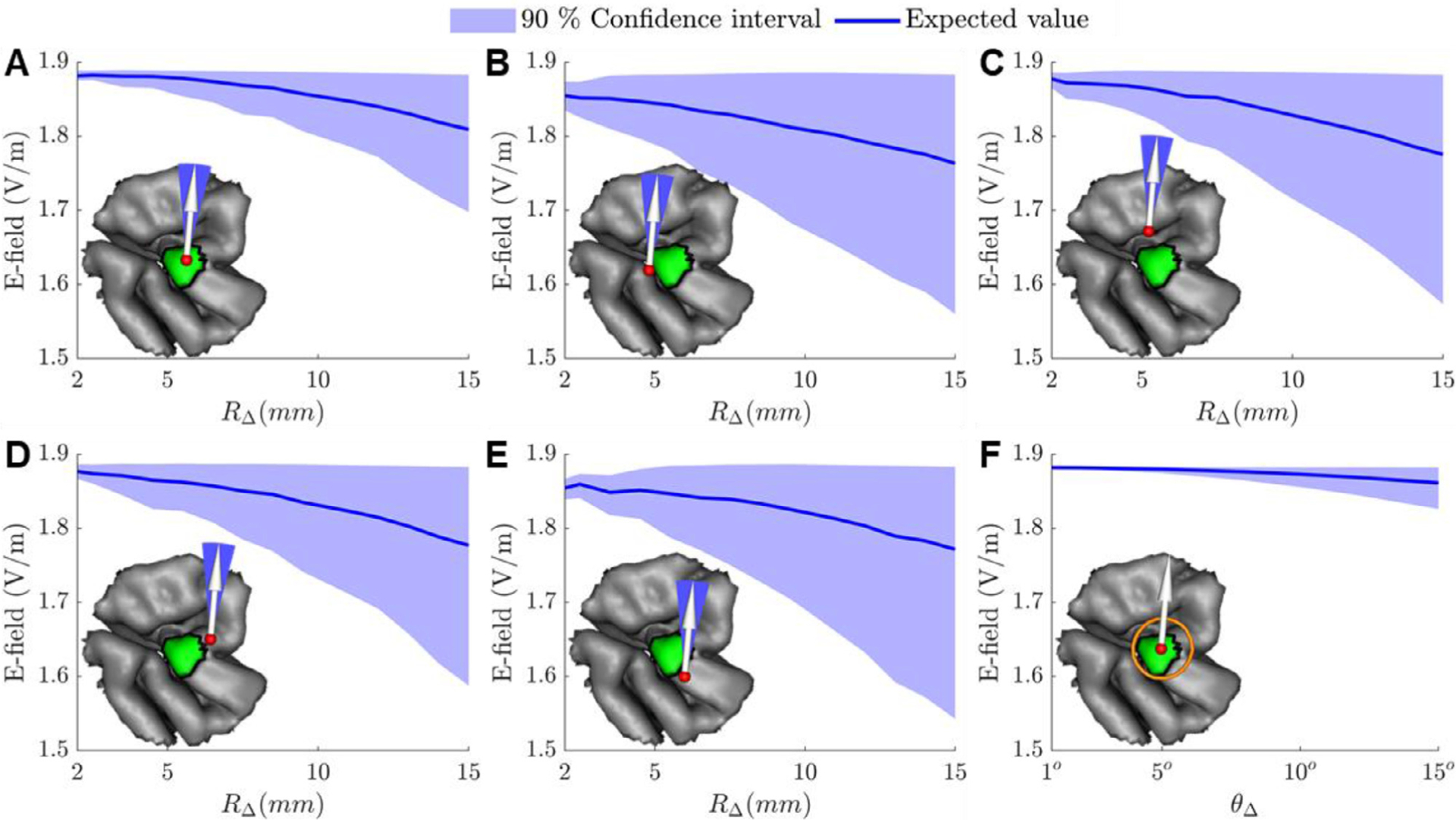
90% confidence region of marginal distributions and expected value of the average E-field along $\widehat{t}$ in the ROI as a function of coil position and orientation uncertainty. (A–E) Results for θ _Δ = 10° and the coil positioned (A) centered or (B–E) 5 mm off-center relative to the ROI. (F) Results for R _Δ = 5 mm and the coil centered above the ROI.

4. Discussion and conclusion

ADM, which uses auxiliary dipoles along with electromagnetic reciprocity, enables rapid extraction of optimal coil position and orientation to target the TMS E-field to specific brain regions. Furthermore, ADM enables the rapid quantification of uncertainty of TMS induced ROI E-fields resulting from uncertainty in the coil position and orientation. The validation results indicate that the average E-field along a given direction in an ROI can be computed with a numerical error below 1% using ADM with 578 dipoles. For ROIs with diameter below 2 cm, the average magnitude of the E-field can be estimated to an error below 2% by executing ADM only three times, corresponding to three orthogonal spatial directions of the E-field. As such, ADM can accurately determine the optimal coil placement based on maximization of either the E-field along a given direction or the total E-field magnitude for typical cortical ROIs. The optimal coil positions and orientations determined via ADM and the direct FEM approach for maximizing the average E-field are virtually identical for ROIs with diameter below 2 cm. However, ADM runs in under 15 min on a laptop to optimize the coil placement, whereas the direct FEM computations take over two days (assuming more than 50,000 coil configurations). Note that the precise number of coil configurations required to determine the optimum coil placement depend on the optimization method and resolution. We did not explore additional optimization methodologies because ADM is able to run up to 1,000,000 coil configurations in under 15 min, which already enables the calculation of the optimum coil placement via an exhaustive search on a grid. Thus, ADM is an accurate and rapid method for E-field-informed coil placement that can be used on a standard laptop.

Supporting the value of coil placement optimization, the difference between the location on the scalp closest to the targeted ROI CM, which represents conventional neuronavigated targeting, and the E-field-informed optimum coil position is 1–14 mm. This is consistent with prior results using direct simulations that observed an average distance of 5.5 mm and as high as 12 mm for ROIs on the temporal brain region (Gomez-Tames et al., 2018). The discrepancy between the ROI CM and E-field-optimized coil placement is driven by the ROI size, cortical geometry, and the scalp-to-cortex distance across different parts of the ROI; for further analysis of large (over 1 cm) discrepancies see the supplemental material and Fig. S6.

The ADM method can be used with a pre-specified optimal E-field direction, if such is known or hypothesized based on a directional specificity of the activation of the targeted neural elements (Aberra et al., 2020). When the objective is to maximize the E-field magnitude in the ROI, the optimal E-field direction is typically close to perpendicular relative to the sulcal wall, consistent with prior studies using the direct method (Gomez-Tames et al., 2018; Janssen et al., 2014, 2015). In certain situations, however, the objectives of maximizing the E-field magnitude versus a directional component of the E-field can lead to significantly different optimal coil placements. For example, if the ROI is split across two neighboring gyri separated highly conductive cerebrospinal fluid, the optimal coil position and orientation may differ markedly, as seen in supplemental Fig. S7I,L. Further, the optimal coil orientation is ambiguous for target ROIs containing highly curved sulcal walls, which means that a range of coil orientations can produce similar E-field magnitude in the ROI.

In this work we assume that the coil is tangential to the scalp. Tangential coil planes were chosen directly above each scalp mesh node with normal direction equal to the average normal of the mesh triangles surrounding the node. To ensure a properly oriented tangential coil plane the scalp surface of the head model should be devoid of spurious step discontinuities arising, for example, from the discretization of the head MRI scans and tissue segmentation. Therefore, smoothing of the scalp mesh may be necessary for a reliable determination of the tangential plane.

The quantification of E-field uncertainty shows how errors in coil positioning both decrease the E-field strength at the target and increase its variability. If there are significant coil positioning uncertainties associated with the TMS protocol, the importance of determining the optimum nominal coil position increases since it can prevent excessive variability in the E-field delivered to the target. Finally, the estimated E-field variation due to procedural uncertainty can enable statistical analysis involving the E-field dose.