Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Feb 9;125(9):2372–2379. doi: 10.1021/acs.jpcb.0c10873

How Hydrogen Bonding Amplifies Isomeric Differences in Pyridones toward Strong Changes in Acidity and Tautomerism

Robby Büchner †,*, Mattis Fondell ‡, Eric J Mascarenhas †,‡, Annette Pietzsch ‡, Vinícius Vaz da Cruz ‡,*, Alexander Föhlisch †,‡
PMCID: PMC7957858  PMID: 33562959

Abstract

graphic file with name jp0c10873_0006.jpg

Steric hindrance of hydration and hydrogen bond enhancement by localized charges have been identified as key factors for the massive chemical differences between the hydroxypyridine/pyridone isomers in aqueous solution. While all isomers occur mainly in the hydroxypyridine form in the gas phase, they differ by more than 3 orders of magnitude both in their acidity and tautomeric equilibrium constants upon hydration. By monitoring the electronic and solvation structures as a function of the protonation state and the O– substitution position on the pyridine ring, the amplification of the isomeric differences in aqueous solution has been investigated. Near-edge X-ray absorption fine structure (NEXAFS) measurements at the N K-edge served as the probe of the chemical state. The combination of molecular dynamics simulations, complete active space self-consistent field (CASSCF), and time-dependent density functional theory (TD-DFT) spectral calculations contributes to unraveling the principles of tautomerism and acidity in multiple biochemical systems based on tautomerism.

Introduction

The proton transfer connecting the enolic hydroxypyridines (HPs) and ketonic pyridones (POs) is prototypical for tautomerism in biological systems.1,2 As seen in Figure 1, both HP and PO occur in three isomeric structures of varying distances between the nitrogen and oxygen functional sites, ranging from ortho (2HP/2PO) to meta (3HP/3PO) to para (4HP/4PO). Due to these geometric differences, the oxygen substituent is conjugated with the pyridine ring in the keto forms of the ortho and para isomers (2PO and 4PO), whereas the meta isomer has no conjugate carbon–oxygen path neither in the 3HP nor the 3PO form.

Figure 1.

Figure 1

Open in a new tab

Equilibrium structures in aqueous solution of the hydroxypyridine/pyridone (HP/PO) tautomers for the ortho, meta, and para isomers and their fully deprotonated states. They vary in oxygen conjugation, tautomeric equilibrium (KT = [PO]/[HP]3,4), and acidity (pKa5,6). Resonance structures are given in the Supporting Information.

Independent of these structural variations, the enol form (HP) is favored over the keto tautomer (PO) in the gas phase by all isomers.1 Upon aqueous solvation, massive differences between the equilibration of the ortho and para versus the meta isomers occur with regard to their tautomeric equilibrium, acidity, and photoreactive properties, with significant implications to their functionalities.

In aqueous solution at room temperature, the ortho and para isomers shift equilibrium away from the gas phase 2HP and 4HP forms to the 2PO and 4PO forms, whereas the meta isomer equilibrates as an equal mixture of the 3HP and 3PO tautomers3,4 (see Figure 1). These local configurations in aqueous solution are accompanied by a similar acidity of the ortho (mainly 2PO) and para (mainly 4PO) isomers in contrast to the mixed (3HP/3PO) meta isomer. In addition, the meta isomer in aqueous solution contains with its 3HP form an efficient UV chromophore, whereas the ortho 2PO and para 4PO isomers do not act as such.

Since 3HP/3PO constitutes inter alia the core moiety of vitamin B6,7,8 i.e., increased photosensitivity is caused upon vitamin B6 overdosing in humans, related to the enolic 3HP tautomer in aqueous solution.9

The ortho tautomer is directly related to multiple nucleobases of DNA and RNA,10 where tautomerism and acidity can lead to mutations and diseases, i.e., by altering the hydrogen bond patterns in DNA.11,12 Nevertheless, biological processes such as the removal of damaged nucleobases2 or the versatile catalysis by RNA enzymes13 depend on the acidity and tautomerism of nucleobases. Understanding the principles of the HP/PO protonation states sheds light on the evolution of nucleobases as storage for genetic information in all living organisms13 and helps to design active substances for new medical treatments (e.g., viral lethal mutagenesis14).

In this work, it is established, as a function of the protonation state and the position of the O– substituent on the pyridine ring, how charge differences and the steric hindrance of hydrogen bond coordination to the first aqueous solvation shell drive, on a microscopic level, the amplification of the initially small molecular differences of the three HP/PO isomers, causing, macroscopically, 3 orders of magnitude variation in tautomeric constants and acidity among the ortho, meta, and para isomers in aqueous solution. The findings are based on the element-specific orbital state populations, chemical sensitivity of near-edge X-ray absorption fine structure (NEXAFS) combined with molecular dynamics (MD) simulations connected to the ab initio X-ray spectrum calculations at the level of complete active space self-consistent field (CASSCF) and time-dependent density functional theory (TD-DFT). In this effort, the ortho, meta, and para pyridone isomers; their fully deprotonated forms, respectively; and the protonated and deprotonated pyridine precursor are investigated in aqueous solution.

Methods

Experimental Details

All samples were purchased from Sigma-Aldrich with a minimum purity of 95% and dissolved in deionized water to obtain 0.1 M solutions. The protonation (of pyridine) and deprotonation (of pyridones) were established by a 1.2-fold molar excess of HCl and KOH, respectively.

The nmTransmission NEXAFS endstation facilitates the spectroscopic investigation of dissolved organic compounds in the soft X-ray regime.15 The sample enters the experimental chamber through two nozzles leading to liquid jets, which form a leaf-shaped surface upon collision. The thickness of the liquid sheet can be varied in the region of the penetration depth of soft X-rays so that transmission measurements become feasible. At the same time, radiation-induced sample damage is prevented through continuous sample replenishment. For the present investigation, a flow rate of 2.5–3.0 mL/min was used in combination with 46 μm sized nozzles.

Photons were provided by Bessy II (Helmholtz-Zentrum Berlin) beamlines UE49-SGM16 for prestudies and UE52-SGM17 for the quantitative absorption measurements. Bandwidths of 0.16 eV (in the case of 2PO) and 0.11 eV (otherwise) were used. The presented spectra were recorded in 0.05 eV steps with an average acquisition time of 6s per point.

The extinction coefficient (ϵ) was obtained from transmittance (T) and concentration (c) according to Beer–Lambert’s law.

graphic file with name jp0c10873_m001.jpg

The sample thickness (l) was estimated using tabulated values18 of the water transmittance at 396 eV yielding 9.2 ± 0.9 μm for 2PO and 5.6 ± 0.6 μm for the other samples.

Since the first region of the spectrum is predominantly independent of the dissolved sample, it is not only used for the calculation of the thickness but also to remove the background of the water transmittance by a linear fit.

For the energy calibration of the experimental results, the signature of co-dissolved N2 at 400.84 eV19,20 was used. A fit of these features in the spectrum of the pristine solvent was subtracted from the spectra of deprotonated samples to yield the pure NEXAFS of the investigated substances.

Computational Details

All electronic structure calculations were carried out with the Orca package.21 All geometries were optimized at the RI-MP2 level with the aug-cc-pVTZ using the aug-cc-pVTZ/C auxiliary basis. The RI-JK approximation was used with the aug-cc-pVTZ/JK fitting basis set.

The MD simulations were performed with the Gromacs package. The OPLS-aa force field has been used for parameterization except for the charges for the intermolecular Coulomb interactions, which were derived by the chelpg22 procedure (based on the relaxed RI-MP2 density). The water molecules were described by the SPC/Fw23 model. Additional details regarding the MD simulations are available in the Supporting Information.

From the MD simulations, minimally solvated models were constructed, including only the hydrogen bonding interactions with the N:, N–H, O–H, and C=O functional groups. These minimally solvated models were used for the subsequent spectral calculations at the CASSCF and TD-DFT levels of theory.

To model the behavior of the lowest π* resonance across the systematic series, CASSCF calculations were carried out in the gas phase, as well as explicitly solvated. The aug-cc-pCVTZ basis set was used for all atoms except for the nitrogen, which was described by the larger aug-cc-pCVQZ. In the solvated cases, the explicit water molecules were described by the smaller cc-pCVDZ basis. The bulk-liquid effects were modeled by the conductor-like polarizable continuum model24 (CPCM). The CASSCF calculations used RI-MP2 natural orbitals as a starting point. The π orbitals of the conjugated ring were included in active space, namely, six active electrons in six orbitals, henceforth called CAS(6,6). This setup excludes only the oxygen lone pair orbital, which is usually poorly correlated in CASSCF calculations. Using this active space, a state-averaged (SA) calculation was carried out for the ground state and the lowest valence-excited state. The valence CASSCF solution was then used as a starting point for the core-state calculation. The N(1s) orbital was rotated into the active space leading to CAS(8,7); then, an SA-CASSCF calculation was carried out including only the ground state and the lowest core-excited state. This setup is expected to recover the majority of static and dynamic correlations for the π* transitions.

For Figure 4, the CASSCF transition moments were shifted by −0.75 eV and convoluted with a Voigt profile of 0.13 eV lifetime broadening25 and 0.51 eV (deprotonated nitrogen) or 0.80 eV (protonated nitrogen) experimental broadening to match the experimental results.

Figure 4.

Figure 4

Open in a new tab

(a) Linear trend of the protonation shift (Δhνπ*) and the pyridone acidity (pKa6,7). (b) Comparison of the experimental NEXAFS with the CASSCF spectra for the gas phase and with explicit solvation (details are given in the Methods section) demonstrating that the magnitude of this shift is governed by solvent–solute interactions.

TD-DFT calculations were performed to study the remaining resonances of the X-ray absorption spectra. The PBE026 hybrid functional was used in all calculations. Additional details are available in the Supporting Information.

Results and Discussion

General Protonation Shift

Near-edge X-ray absorption fine structure (NEXAFS) at the nitrogen K-edge allows us to distinguish and quantify the protonation state at the nitrogen atom. Both the directly coordinated hydrogen atom and the hydrogen bond toward coordinated water molecules in the first solvation shell are monitored in this approach.

In Figure 2b,e, the N K-edge NEXAFS of the ortho, meta, and para isomers are presented, as well as their fully deprotonated states in direct comparison to the (pyridine/Py) precursor and its conjugated acid (pyridinium/PyH+). A characteristic blue shift of the lowest unoccupied molecular orbital (LUMO) π* state is observed for all molecules upon protonation (depicted in Figure 2b,e) via the one-electron transition (≥72%) of the N(1s) electron elevated to the lowest unoccupied π* orbital.

Figure 2.

Figure 2

Open in a new tab

N K-edge NEXAFS spectra of the pyridine precursor (b) and the ortho, meta, para pyridone isomers from top to bottom (e). A protonation shift of the N(1s) → π* resonance is observed across the series. The energies of these transitions are influenced by the competition for charges between nitrogen and oxygen in the core-excited state, as illustrated by the π* orbital plots of the fully deprotonated (a, d) and protonated species (c, f).

The photon energy range of 402–406 eV monitors excitations into higher unoccupied molecular orbitals, mostly of σ* character. In the region of 403.4–403.8 eV, a shoulder (≈0.01 M–1 μm–1) is observed, which is only present in the protonated state. This feature originates from a transition that is mostly localized at the N–H bond. Consequently, it is missing in the spectra of deprotonated species.

The N K-edge spectra of the pyridones (see Figure 2e) largely resemble the NEXAFS of Py(H+). Only the meta isomer exhibits a second π* resonance closely below the feature of 3PO– due to the presence of the HP tautomer. No indication of the presence of 2HP and 4HP has been found, in agreement with the tautomeric equilibrium constants (see Figure 1).

The shape resonances above 406 eV differ both between the pyridone isomers and in comparison with Py(H+). These quasi-bound transitions are known to provide information on interatomic distances.27 The shape resonances are most pronounced in the spectra of PyH+ and 4PO, where the nitrogen atom has an equal distance to both neighboring carbon atoms. The position of this feature is in qualitative agreement with the calculated C–N bond distances: 408.2 eV for 4PO (1.351 Å) and 409.3 eV for pyridinium (1.342 Å). For 3HP/3PO with 1.341–1.346 Å C–N bond distances, the resonance position is intermediate (409.1 eV) and in 2PO the distances differ so widely (1.356, 1.369 Å) that the shape resonance position cannot be assigned unambiguously.

The shape resonance of the deprotonated species seems to be red-shifted similar to the other features. This effect is not caused by the minor changes of the C–N bond distance upon deprotonation but by a general adjustment of the electronic and solvation structures, as discussed in the following sections.

Isomer Specific Charge Distribution

Even though all pyridones show a protonation shift similar to that of Py(H+), the exact peak positions differ depending on the position of the O– substituent. This becomes particularly clear from a comparison of the π* resonances, which also have been used to investigate tautomerism in the past.28

Besides the peak position, the width of the π* resonance depends on the protonation state (of the nitrogen atom in the respective molecule). The broadening (full width at half-maximum (FWHM) + 0.29 eV) for pyridinium/pyridones results mainly from Franck–Condon vibrational excitations29 of the N–H bond during the X-ray absorption process, which are absent in the deprotonated species.

The interspecies shift of the π* resonance, first, depends on the initial electron density at the (nitrogen) atom, which is excited during the X-ray absorption process.30 The better the core charge is screened, the lower is the ionization energy of N(1s) electrons. As far as resonant absorption features are considered, the core electron is excited into a bound state. Since the transition energy depends, inter alia, on the energy of the initial orbital of this electron, excitation and ionization energies are linked by Koopmans’ theorem. Therefore, the NEXAFS peak position contains information on the chemical state of nitrogen in the samples.

2PO– has the highest charge density at the nitrogen site and the smallest ionization potential, followed by 4PO– where the charge is more distributed over the whole molecule. In 3PO–, the electron density is shifted to the oxygen, and in Py, the charge at the nitrogen site is even lower, since the molecule is formally neutral. The same argumentation holds for the protonated case, even though the screening capacity is lower for all species (see Figure 1).

Second, the relaxation of the final state due to the Coulomb attraction between the excited electron and the core-hole influences the excitation energy, especially of the lowest NEXAFS feature. As known from benzene,31 the higher the contribution of the atomic orbital at the excited atom to the relaxed molecular orbital, the more the red shift of π* resonances. In other words, the π* resonance is lowered, if the lowest unoccupied molecular orbital (LUMO) is centered at the nitrogen atom after its relaxation.

The relaxed π* orbitals are depicted in Figure 2a,c,d,f for the fully deprotonated and protonated Py(H+) and pyridones. It can be seen that in the PyH+ case, the probability of the excited electrons to be close to the carbon atoms in the meta position is nearly zero. Oppositely, in 4PO, the LUMO is distributed over all carbon atoms and has a strong contribution from the oxygen. Consequently, the excitation energy (hνπ*) of PyH+ is expected to be strongly red-shifted, whereas only slight deviations are expected for 4PO. The shift of 3PO and 2PO, due to the described final state effect, is intermediate. If single molecules are compared between their protonation states, it is observed that the deprotonated entity has a LUMO, which is more localized at the nitrogen site. Consequently, the blue shift upon protonation is increased by final state effects.

Taking these relaxation effects into account, it can be understood that the initially expected state order hνπ*(2PO–) < hνπ*(4PO–) < hνπ*(3PO–) < hνπ*(Py) is disturbed by the creation of the core-hole leading to hνπ*(2PO–)< hνπ*(PyH) < hνπ*(3PO–) < hνπ*(4PO–). In the protonated case, the excitation energy of PyH+ is lowered to beneath that of hνπ*(2PO) due to final state effects. This order of resonance energies is observed both experimentally and in the calculations (see Table 1).

Table 1. Experimental and Calculated (CASSCF) N K-Edge π* Resonance Positions in eV.

  deprotonated
 protonated
molecule calcd gas calcd aq. exptl calcd gas calcd aq. exptl
Py(H+) 399.68 399.78 399.03 401.78 401.21 400.52
2PO(−) 399.34 399.87 399.00 402.10 401.54 400.72
3PO(−) 400.04 399.91 399.14 402.14 401.41 400.72
4PO(−) 400.25 400.09 399.37 403.15 401.67 401.07
Open in a new tab

By causing the characteristic π* shifts, the core-hole effect provides detailed information on the isomeric differences in charge distribution. In Py(H+), nitrogen is the most electronegative element and the excited electron, therefore, remains in close proximity. In the pyridones, nitrogen competes for electron density with oxygen. This effect increases from 3PO(−) to 2PO(−) to 4PO(−). In 3PO(−), the oxygen is not part of the conjugated system and is already in a charged state. In 2PO(−), both the oxygen and nitrogen atoms are part of the aromatic structure but pull charge in similar directions. In contrast, the conjugated oxygen in 4PO(−) withdraws charge from the nitrogen site, as they lie in opposite sites of the ring.

In short, the constitutional differences between the pyridone isomers cause considerable differences in the electronic structure and charge distribution. These variations are already present in the gas phase, as the CASSCF calculations show (see Table 1). Nevertheless, without an aqueous environment, the electronic differences are not mirrored by macroscopic properties, i.e., the tautomeric equilibrium constants. To gain an insight into the microscopic amplification of the isomeric differences by solvent–solute effects, the solvation structure is analyzed in the following section.

Hydrogen Bonding Interactions

Figure 3 shows how the heteroatoms govern the solvent–solute interactions of Py and the pyridone isomers. In Py, the nitrogen atom accepts on average 0.9 hydrogen bonds (HBs) from water, whereby the bonds are mostly localized out of plane.32,33 If the nitrogen atom is protonated, it naturally cannot accept HBs and, instead, the NH group donates approximately 0.7 HB to the solvent.

Figure 3.

Figure 3

Open in a new tab

Competition of hydrogen bond coordination to the first aqueous solvation shell between the nitrogen and oxygen heteroatom as a function of distance between these functional sites. Solvent O and H densities are depicted for isovalues of 0.68 and 0.09, respectively. The additional heteroatom of the pyridones (compared to pyridine) enhances the total coordination number, even though the hydration of the nitrogen site is sterically hindered if the heteroatoms are in close proximity. The nonconjugate O– substituent in 3PO(−) leads to additional coordination.

The second heteroatom in PO/HP leads to an increase of solvent density in the first solvation shell compared to Py(H+). The solvent structure around the oxygen has the same donutlike shape for all pyridones, and the solvent arrangement at the nitrogen site is similar to that of Py(H+). The coordination numbersa and hydrogen bonding properties, however, differ drastically between the isomers and their protonation states. The comparison of protonated and deprotonated species demonstrates that higher charges always lead to stronger hydrogen bonding interactions.

Within the deprotonated pyridones, the averaged number of accepted hydrogen bonds at the nitrogen site increases with the distance to the oxygen atom, thus from 2PO– (1.6 HB) to 3PO– (1.9 HB) to 4PO– (2.1 HB). The N···H distance is almost constant at 1.8 Å. These observations reveal that the hydration is sterically hindered in the case of close proximity of the two heteroatoms. This finding is in agreement with the enhanced hydration of the oxygen site in 4PO– compared to that in 2PO–. The coordination number at the oxygen site reaches its maximum for 3PO– due to the concentration of charge at the O– substituent, which is not conjugated to the aromatic ring in this isomer. The localized charge enhances hydrogen bond acceptance (3.1 HB) compared to the para (2.9 HB) and the sterically disadvantaged ortho isomers (2.8 HB).

Steric hindrance between the two hydrogen bonding sites and the lack of oxygen conjugation in 3PO are the dominating factors for the hydration of the protonated pyridones as well. 3PO exhibits the highest coordination number both at the oxygen and nitrogen sites, followed by 4PO and 2PO. While hydrogen bond donation by the protonated nitrogen site is similar for all isomers (0.6 HB, 1.9 Å; see the Supporting Information), the number of hydrogen bonds that are accepted by the oxygen atom increase from 2PO (1.6) to 4PO (1.7) to 3PO (2.0) with a common distance of 1.7 Å.

Due to the positive charge of PyH+, HBs are more likely (0.7 HB) and contracted (1.8 Å) at the nitrogen site of this molecule. Analogously, HB acceptance by the deprotonated nitrogen atom is reduced in 3HP and Py (0.9 HB, 1.9 Å) compared to that in the anions.

For 3HP, the probability of accepting HBs at the oxygen is reduced to 0.7 due to the bound proton. The hydrogen atom, however, donates approximately 1.5 HBs to water (1.8 Å). The reason for the additionally donated hydrogen bond compared to the N–H case is the more polar O–H bond, as a result of the higher electronegativity of oxygen. The combination of HB donation and acceptance leads to a coordination number at the oxygen site similar to that at 3PO.

The intensity of the solvent–solute interaction as a function of the O– substitution position can be summarized as follows: the steric hindrance of the solvation increases from the para to the meta to the ortho isomer. 3PO(−) forms additional hydrogen bonds as a result of the nonconjugate C–O– bond. Thereby, the solvation structure underlines the special significance of 3PO, whose acidity and tautomeric equilibrium differ largely from those of the other isomers.

Solvent Influence on Acidity and Tautomerism

Based on the observations of HB formation and the arrangement of water molecules around the pyridones and Py(H+), information on the interactions of hydration and the electronic structure can be gained from the NEXAFS. As seen in the CASSCF calculations (see Figure 4b), the π* resonance position can shift by up to 1.48 eV in the presence of a protic solvent like water.

As it is known from the sulfur derivative of 2PO (2-thiopyridone),34 the core-excitation distorts the solvent–solute interactions, which explains the solvation shifts. According to the equivalent core principle, the effect of a core-hole can be approximated by an increase of the nuclear charge by 1; e.g., core-excited nitrogen (N*) largely behaves like oxygen. Consequently, the polarity of the N*–H bond is increased compared to that of N–H, which strengthens the HB in N–H···OH2. Therefore, the excitation energy is lowered for the protonated species. The magnitude of the red shift is the smallest for 2PO and the largest for 4PO. These differences are mainly caused by the steric hindrance of hydration if NHδ+ and Oδ− are close together, as observed in the MD simulation of the ground state.

The solvation shifts of the deprotonated species are comparatively small, because the solvent–solute interactions are already strong in the ground state. The additional charge in the excited state destabilizes the hydrogen bonding structure, especially in 2PO–, where the LUMO has large contributions at the close-lying Nδ− and Oδ− sites.

Taken together, the response of the solvent–solute interaction to the core-excitation leads to a reduction of the protonation shift Δhνπ* for all species. This shift correlates (within the errors of the measurement) entirely with the acidity of the keto tautomersb. The experimentally observed trend is well reproduced by the CASSCF calculations with explicit solvation. Thereby, the computational findings support the abovementioned reasoning that the smaller Δhνπ* is, the stronger the solvent–solute interactions are. Based on the general relation of hydrogen bonding and acidity,35 it can be stated that the stronger the stabilization of the pyridones by the solvent, the weaker the N–H bond.

It is known from the MD simulations that 3PO has the largest coordination number of all keto forms and that this species also shows a −0.73 eV calculated π* shift upon solvation (see Figure 4). From this, it becomes apparent why 3PO(−) has the lowest Δhνπ* gap of all pyridones. The strong stabilization of 3PO by the solvent is in agreement with the general assumption that the more polar (keto) tautomer is energetically preferable in aqueous solutions.36 However, this effect is not only mediated by the macroscopic dielectricity of water, as initially assumed in multiple studies,7,8,37 but also by hydrogen bonding interactions. Since these interactions diminish for higher temperatures, it can be expected that the equilibrium shifts to the enol form upon heating as observed for 3HP/3PO.38

For 2HP/2PO and 4HP/4PO, the higher polarity of the keto form explains why the tautomeric equilibrium is inverted between the gas phase and aqueous solution. In contrast, 3PO does not seem to obey this rule, as it is the most polar form, but coexists with its enol tautomer in water. In fact, due to missing resonance stabilization of the charges in 3PO, it is severely disadvantaged to the point of not being energetically preferable in an aqueous solution even though it is highly stabilized. This interpretation is in agreement with the rule of Zilberg and Dick that the less stable tautomer receives higher stabilization by the aqueous environment.39 Additionally, the instability of the zwitterionic 3PO explains the higher acidity of 3HP/3PO compared to the other pyridones.

The acidity difference between 2PO and 4PO can be understood, now, as a result of the higher interaction of 4PO with water. The additional stabilization of 4PO agrees with the inverted order of equilibrium constants between vapor 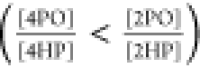Inline graphic and aqueous solution 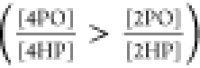Inline graphic.36 Analogous to the 3PO case, the more intense 4PO water interactions stabilize this tautomer but cause its protonation state to be more dependent on the solvent. In other words, the abovementioned finding applies: the higher the stabilization by the solvent, the weaker the N–H bond. Since the solvation, in turn, is dependent on the steric hindrance of the hydration and its enhancement by localized charges, it can be stated that these factors control the acidity and tautomerism of pyridones at the same time.

Conclusions

The amplification of isomeric differences of HP/PO by aqueous hydrogen bonding has been investigated using N K-edge NEXAFS spectroscopy accompanied by systematic CASSCF calculations, distinguishing inherent molecular properties and solvation effects: the dominance of the enol form for all HP/PO isomers in the gas phase is mirrored by minor differences in the electronic structure, especially of the ortho and para isomers in the ground state. The core-excited state reveals first differences dependent on the O– substitution position and conjugation to the pyridine ring. In aqueous solution, the keto tautomers of 2HP/2PO and 4HP/4PO have been spectroscopically identified as dominating entities, whereas 3PO coexists with the enol form. This is consistent with previous studies in the ultraviolet range of light.

The HP/PO solvation structure has been investigated in detail by MD simulations. The common theme among all molecules considered in this study is their ability to form strong hydrogen bonds with the solvent, both by donating a hydrogen bond to water or by accepting it, and thus stabilizing the molecule. However, in 2PO, a steric hindrance of the hydration reduces the solvent stabilization. In contrast, 3PO receives the highest stabilization due to its zwitterionic character.

The strong interaction between the electronic structure of the pyridones and the surrounding water molecules shows that the increase of solvent stabilization of the keto tautomer from 2PO to 4PO to 3PO, being expressed by the N(1s) → π* protonation shift, directly correlates with an increase in acidity. It also explains that the tautomeric equilibrium is not only inverted but that the HP form exists as a miniscule fraction for 2HP/2PO and 4HP/4PO upon solvation. 3PO, which does not contain a neutral resonance structure, is energetically so unfavorable that solvent stabilization, even though it is comparatively high, only increases the share of 3PO in aqueous solution to 50%.

The water environment amplifies the tautomeric differences of the pyridone isomers because the intensity of the HB interaction depends both on the localization of charges as a result of the oxygen conjugation and the proximity of the heteroatoms leading to sterical hindrance. Hydrogen bonding not only stabilizes the keto tautomers but also weakens the covalent bond of the proton at the nitrogen site by the same ratio.

These findings clarify the principles of the HP/PO tautomerism and acidity, which have been under investigation for more than 100 years now,40 and they help to unravel the biological function of nucleobases, vitamin B6, and the pathways of the natural remediation of pyridine.41

Acknowledgments

R.B. and A.F. acknowledge funding from the ERC-ADG-2014, Advanced Investigator Grant No. 669531 EDAX under the Horizon 2020 EU Framework Program for Research and Innovation. The authors thank the Helmholtz-Zentrum Berlin for the allocation of synchrotron radiation beamtime. V.V.C acknowledges Sebastian Eckert for fruitful discussions.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.0c10873.

  • Resonance structures of the pyridone isomers; details of the molecular dynamics simulation (including radial distribution functions, chelpg charges, and hydrogen bonding properties); and TD-DFT calculations (PDF)

  • Optimized geometries of all discussed species in the gas phase and with explicit solvation in Cartesian coordinates (ZIP)

The authors declare no competing financial interest.

Footnotes

a

The coordination numbers are given with respect to the oxygen atoms of water. The underlying radial distribution functions and more details of the MD simulation (including hydrogen bonding analysis) are provided in the Supporting Information.

b

Since the π* shift was calculated for the keto tautomers, the pKa value of the keto tautomers only has been chosen as a measure for the acidity.

Supplementary Material

jp0c10873_si_001.pdf (585.7KB, pdf)
jp0c10873_si_002.zip (10.2KB, zip)

References

  1. Stanovnik B.; Tišler M.; Katritzky A. R.; Denisko O. V.. Advances in Heterocyclic Chemistry, Katritzky A. R., Ed.; Academic Press: New York, 2006; Vol. 91, pp 1–134. [Google Scholar]
  2. Michelson A. Z.; Petronico A.; Lee J. K. 2-Pyridone and derivatives: Gas-phase acidity, proton affinity, tautomer preference, and leaving group ability. J. Org. Chem. 2012, 77, 1623–1631. 10.1021/jo201991y. [DOI] [PubMed] [Google Scholar]
  3. Karelson M. M.; Katritzky A. R.; Szafran M.; Zerner M. C. Quantitative predictions of tautomeric equilibria for 2-, 3-, and 4-substituted Pyridines in both the gas phase and aqueous solution: Combination of AM1 with reaction field theory. J. Org. Chem. 1989, 54, 6030–6034. 10.1021/jo00287a012. [DOI] [Google Scholar]
  4. Beak P. Energies and alkylations of tautomeric heterocyclic compounds: Old problems–new answers. Acc. Chem. Res. 1977, 10, 186–192. 10.1021/ar50113a006. [DOI] [Google Scholar]
  5. Albert A.; Phillips J. N. 264. Ionization constants of heterocyclic substances. Part II. Hydroxy-derivatives of nitrogenous six-membered ring-compounds. J. Chem. Soc. 1956, 1294–1304. 10.1039/jr9560001294. [DOI] [Google Scholar]
  6. Barlin G. B.; Pfleiderer W. Ionization constants of heterocyclic substances. Part IX. Protonation of aminopyridones and aminopyrimidones. J. Chem. Soc. B 1971, 1425–1432. 10.1039/j29710001425. [DOI] [Google Scholar]
  7. Metzler D. E.; Snell E. E. Spectra and ionization constants of the vitamin B6 group and related 3-Hydroxypyridine derivatives. J. Am. Chem. Soc. 1955, 77, 2431–2437. 10.1021/ja01614a022. [DOI] [Google Scholar]
  8. Sánchez-Ruiz J. M.; Llor J.; Cortijo M. Thermodynamic constants for tautomerism and ionization of pyridoxine and 3-Hydroxypyridine in water–dioxane. J. Chem. Soc., Perkin Trans. 2 1984, 2047–2051. 10.1039/P29840002047. [DOI] [Google Scholar]
  9. Wondrak G. T.; Roberts M. J.; Jacobson M. K.; Jacobson E. L. 3-Hydroxypyridine chromophores are endogenous sensitizers of photooxidative stress in human skin cells. J. Biol. Chem. 2004, 279, 30009–30020. 10.1074/jbc.M404379200. [DOI] [PubMed] [Google Scholar]
  10. Kwiatkowski J.; Pullman B.. Advances in Heterocyclic Chemistry, Katritzky A.; Boulton A., Eds.; Academic Press: New York, 1975; Vol. 18, pp 199–335. [Google Scholar]
  11. Pullman B.; Pullman A.. Advances in Heterocyclic Chemistry, Katritzky A.; Boulton A., Eds.; Academic Press: New York, 1971; Vol. 13, pp 77–159. [Google Scholar]
  12. Löwdin P.-O. Proton tunneling in DNA and its biological implications. Rev. Mod. Phys. 1963, 35, 724–732. 10.1103/RevModPhys.35.724. [DOI] [Google Scholar]
  13. Singh V.; Fedeles B. I.; Essigmann J. M. Role of tautomerism in RNA biochemistry. RNA 2015, 21, 1–13. 10.1261/rna.048371.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Li D.; Fedeles B. I.; Singh V.; Peng C. S.; Silvestre K. J.; Simi A. K.; Simpson J. H.; Tokmakoff A.; Essigmann J. M. Tautomerism provides a molecular explanation for the mutagenic properties of the anti-HIV nucleoside 5-aza-5,6-dihydro-2’-deoxycytidine. Proc. Natl. Acad. Sci. U.S.A. 2014, 111, E3252–E3259. 10.1073/pnas.1405635111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Fondell M.; Eckert S.; Jay R. M.; Weniger C.; Quevedo W.; Niskanen J.; Kennedy B.; Sorgenfrei F.; Schick D.; Giangrisostomi E.; et al. Time-resolved soft X-ray absorption spectroscopy in transmission mode on liquids at MHz repetition rates. Struct. Dyn. 2017, 4, 054902 10.1063/1.4993755. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Pietzsch A.; Eisebitt S. The UE49 SGM RICXS beamline at BESSY II. J. Large-Scale Res. Facil. 2016, 2, A54. 10.17815/jlsrf-2-78. [DOI] [Google Scholar]
  17. Miedema P. S.; Quevedo W.; Fondell M. The variable polarization undulator beamline UE52 SGM at BESSY II. J. Large-Scale Res. Facil. 2016, 2, A27. 10.17815/jlsrf-2-79. [DOI] [Google Scholar]
  18. Henke B. L.; Gullikson E. M.; Davis J. C. X-ray interactions: Photoabsorption, scattering, transmission, and reflection at E = 50-30, 000 eV, Z = 1-92. At. Data Nucl. Data Tables 1993, 54, 181–342. 10.1006/adnd.1993.1013. [DOI] [Google Scholar]
  19. Flesch R.; Pavlychev A. A.; Neville J. J.; Blumberg J.; Kuhlmann M.; Tappe W.; Senf F.; Schwarzkopf O.; Hitchcock A. P.; Rühl E. Dynamic stabilization in 1σu→1πg excited nitrogen clusters. Phys. Rev. Lett. 2001, 86, 3767–3770. 10.1103/PhysRevLett.86.3767. [DOI] [PubMed] [Google Scholar]
  20. Gillespie A. W.; Walley F. L.; Farrell R. E.; Regier T. Z.; Blyth R. I. R. Calibration method at the N K-edge using interstitial nitrogen gas in solid-state nitrogen-containing inorganic compounds. J. Synchrotron Radiat. 2008, 15, 532–534. 10.1107/S0909049508014283. [DOI] [PubMed] [Google Scholar]
  21. Neese F. The ORCA program system. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 73–78. 10.1002/wcms.81. [DOI] [Google Scholar]
  22. Breneman C. M.; Wiberg K. B. Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis. J. Comput. Chem. 1990, 11, 361–373. 10.1002/jcc.540110311. [DOI] [Google Scholar]
  23. Wu Y.; Tepper H. L.; Voth G. A. Flexible simple point-charge water model with improved liquid-state properties. J. Chem. Phys. 2006, 124, 024503 10.1063/1.2136877. [DOI] [PubMed] [Google Scholar]
  24. Barone V.; Cossi M. Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. J. Phys. Chem. A 1998, 102, 1995–2001. 10.1021/jp9716997. [DOI] [Google Scholar]
  25. Nicolas C.; Miron C. Lifetime broadening of core-excited and -ionized states. J. Electron Spectrosc. Relat. Phenom. 2012, 185, 267–272. 10.1016/j.elspec.2012.05.008. [DOI] [Google Scholar]
  26. Adamo C.; Barone V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. 10.1063/1.478522. [DOI] [Google Scholar]
  27. Sette F.; Stöhr J.; Hitchcock A. P. Determination of intramolecular bond lengths in gas phase molecules from K shell shape resonances. J. Chem. Phys. 1984, 81, 4906–4914. 10.1063/1.447528. [DOI] [Google Scholar]
  28. Ito E.; Oji H.; Araki T.; Oichi K.; Ishii H.; Ouchi Y.; Ohta T.; Kosugi N.; Maruyama Y.; Naito T.; et al. Soft X-ray absorption and X-ray photoelectron spectroscopic study of tautomerism in intramolecular hydrogen bonds of n-Salicylideneaniline derivatives. J. Am. Chem. Soc. 1997, 119, 6336–6344. 10.1021/ja9641362. [DOI] [Google Scholar]
  29. Vaz da Cruz V.; Ignatova N.; Couto R. C.; Fedotov D. A.; Rehn D. R.; Savchenko V.; Norman P.; Ågren H.; Polyutov S.; Niskanen J.; et al. Nuclear dynamics in resonant inelastic X-ray scattering and X-ray absorption of methanol. J. Chem. Phys. 2019, 150, 234301 10.1063/1.5092174. [DOI] [PubMed] [Google Scholar]
  30. Oji H.; Mitsumoto R.; Ito E.; Ishii H.; Ouchi Y.; Seki K.; Yokoyama T.; Ohta T.; Kosugi N. Core hole effect in NEXAFS spectroscopy of polycyclic aromatic hydrocarbons: Benzene, chrysene, perylene, and coronene. J. Chem. Phys. 1998, 109, 10409–10418. 10.1063/1.477696. [DOI] [Google Scholar]
  31. Klues M.; Hermann K.; Witte G. Analysis of the near-edge X-ray-absorption fine-structure of anthracene: A combined theoretical and experimental study. J. Chem. Phys. 2014, 140, 014302 10.1063/1.4855215. [DOI] [PubMed] [Google Scholar]
  32. Pagliai M.; Mancini G.; Carnimeo I.; De Mitri N.; Barone V. Electronic absorption spectra of pyridine and nicotine in aqueous solution with a combined molecular dynamics and polarizable QM/MM approach. J. Comput. Chem. 2017, 38, 319–335. 10.1002/jcc.24683. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Fileti E. E.; Coutinho K.; Malaspina T.; Canuto S. Electronic changes due to thermal disorder of hydrogen bonds in liquids: Pyridine in an aqueous environment. Phys. Rev. E 2003, 67, 061504 10.1103/PhysRevE.67.061504. [DOI] [PubMed] [Google Scholar]
  34. Norell J.; Eckert S.; Van Kuiken B. E.; Föhlisch A.; Odelius M. Ab initio simulations of complementary K-edges and solvatization effects for detection of proton transfer in aqueous 2-thiopyridone. J. Chem. Phys. 2019, 151, 114117 10.1063/1.5109840. [DOI] [PubMed] [Google Scholar]
  35. Reichardt C.Solvents and Solvent Effects in Organic Chemistry; John Wiley & Sons, Ltd: Weinheim, 2004; pp 5–56; Chapter 2. [Google Scholar]
  36. Beak P.; Fry F. S.; Lee J.; Steele F. Equilibration studies. Protomeric equilibria of 2- and 4-hydroxypyridines, 2- and 4-hydroxypyrimidines, 2- and 4-mercaptopyridines, and structurally related compounds in the gas phase. J. Am. Chem. Soc 1976, 98, 171–179. 10.1021/ja00417a027. [DOI] [Google Scholar]
  37. Wang J.; Boyd R. J. Tautomeric equilibria of Hydroxypyridines in different solvents: An ab initio study. J. Phys. Chem. A 1996, 100, 16141–16146. 10.1021/jp961295z. [DOI] [Google Scholar]
  38. Llor J.; Asensio S. B. Thermodynamics of the solution equilibria of 3-hydroxypyridine and pyridoxine in water-dioxane mixtures. J. Solution Chem. 1995, 24, 1293–1305. 10.1007/BF00972834. [DOI] [Google Scholar]
  39. Zilberg S.; Dick B. Less stable tautomers form stronger hydrogen bonds: the case of water complexes. Phys. Chem. Chem. Phys. 2017, 19, 25086–25094. 10.1039/C7CP04105E. [DOI] [PubMed] [Google Scholar]
  40. Baker F.; Baly E. C. C. CVI.—The relation between absorption spectra and chemical constitution. Part VII. Pyridine and some of its derivatives. J. Chem. Soc., Trans. 1907, 91, 1122–1132. 10.1039/CT9079101122. [DOI] [Google Scholar]
  41. Gupta N.; O’Loughlin E. J.; Sims G. K.. Microbial Metabolism of Xenobiotic Compounds, Arora P. K., Ed.; Springer: Singapore, 2019; pp 1–31. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp0c10873_si_001.pdf (585.7KB, pdf)
jp0c10873_si_002.zip (10.2KB, zip)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES