Dynamics of hydraulic and contractile wave-mediated fluid transport during Drosophila oogenesis

Significance

Fluid flow plays an important role during oogenesis. From insects to mice, oocytes mature by acquiring cytoplasm from sister germ cells, yet the biological and physical mechanisms underlying this transport process remain poorly understood. To study the dynamics of “nurse cell dumping” in fruit flies, we combined direct imaging with flow-network modeling and found that the intercellular pattern and time scale of transport are in accordance with a fundamental hydraulic pressure law. Changes in actomyosin contractility are observed only in the second phase of nurse cell dumping as surface waves that drive transport to completion. These results show that tandem physical and biological mechanisms are required for complete and directional cytoplasmic transport into the egg cell.

Abstract

From insects to mice, oocytes develop within cysts alongside nurse-like sister germ cells. Prior to fertilization, the nurse cells’ cytoplasmic contents are transported into the oocyte, which grows as its sister cells regress and die. Although critical for fertility, the biological and physical mechanisms underlying this transport process are poorly understood. Here, we combined live imaging of germline cysts, genetic perturbations, and mathematical modeling to investigate the dynamics and mechanisms that enable directional and complete cytoplasmic transport in Drosophila melanogaster egg chambers. We discovered that during “nurse cell (NC) dumping” most cytoplasm is transported into the oocyte independently of changes in myosin-II contractility, with dynamics instead explained by an effective Young–Laplace law, suggesting hydraulic transport induced by baseline cell-surface tension. A minimal flow-network model inspired by the famous two-balloon experiment and motivated by genetic analysis of a myosin mutant correctly predicts the directionality, intercellular pattern, and time scale of transport. Long thought to trigger transport through “squeezing,” changes in actomyosin contractility are required only once NC volume has become comparable to nuclear volume, in the form of surface contractile waves that drive NC dumping to completion. Our work thus demonstrates how biological and physical mechanisms cooperate to enable a critical developmental process that, until now, was thought to be mainly biochemically regulated.

Fluid flows play an important role in biological development, from the definition of an organism’s body plan (1) and vertebrate organogenesis (2) to cytoplasmic streaming (3) and tissue morphogenesis (4). A robust biofluid transport process whose dynamics have yet to be uncovered and explained occurs during the development and growth of the egg cell. Across diverse species, oocytes develop within germline cysts alongside nurse-like sister germ cells (5, 6); a key juncture in oogenesis occurs when these sister cells transport their cytoplasm to the oocyte prior to fertilization. As a result, the oocyte grows as its sister cells regress and die (5–8). Although critical for fertility and early embryonic life, the biological and physical mechanisms underlying this transport process are poorly understood.

In Drosophila melanogaster, the oocyte develops within an egg chamber, a multicellular structure comprising a germline cyst that is covered by an epithelium; the germline cyst itself is composed of an oocyte and 15 nurse cells (NCs) that are interconnected through intercellular bridges called ring canals (Fig. 1A) (9–11). Once the oocyte grows to $\sim$50% of the egg chamber’s volume, the NCs transport their cytoplasm into the oocyte in a process called NC dumping; with a diameter of $\sim$10 $\mathrm{\mu }$m, the ring canals are large enough to permit passage of most cytoplasmic contents (Fig. 1B, SI Appendix, Fig. S1A, and Movie S1) (12). It has been proposed that NC dumping is driven by global cortical contractile forces generated through interactions of nonmuscle myosin-II with actin filaments (henceforth actomyosin). According to this hypothesis, the increased contractility brings about an increase in pressure, causing cytoplasm to be “squeezed” out of the NCs and into the oocyte (13–15). Indeed, mutants in the myosin regulatory light chain (RLC), encoded for by the spaghetti squash (sqh) gene, do not complete NC dumping (16, 17), suggesting a critical role for actomyosin dynamics in this process. However, in the absence of time-resolved quantitative data, actomyosin’s role in promoting the complete and directional transport of cytoplasm has remained unclear.

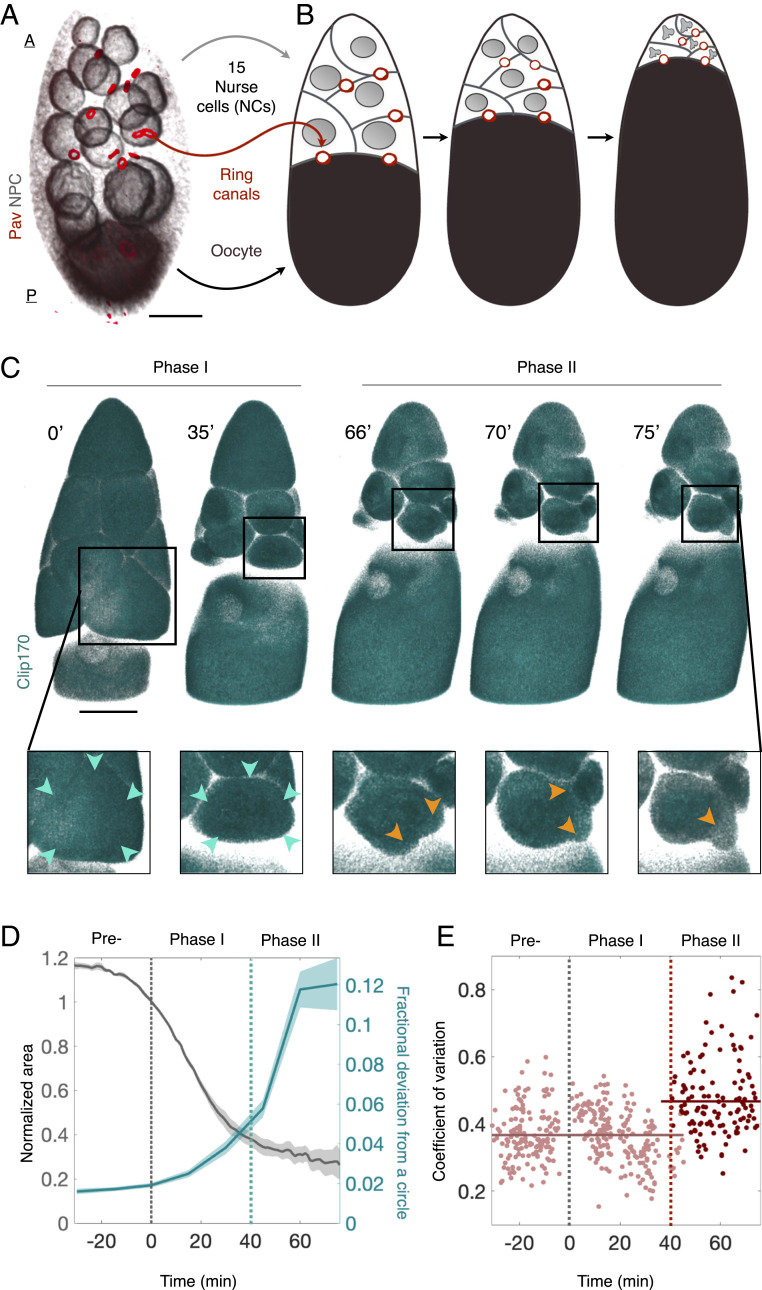
Fig. 1.

NC dumping occurs in two phases. (A) Three-dimensionally rendered confocal image of an egg chamber showing 15 anterior (A) NCs (gray: nuclear pore complex, NPC) and one posterior (P) oocyte (black: NPC) connected through ring canals (red: Pavarotti, Pav). (B) Schematic illustration of NC dumping: NCs shrink as their cytoplasm flows into the oocyte through ring canals. (C) Three-dimensionally rendered time-lapse confocal images of an egg chamber expressing Clip170::GFP undergoing NC dumping. Blowups show an NC first shrinking uniformly (cyan arrowheads; Phase I) before undergoing spatially nonuniform shape deformations and bleb-like protrusions (orange arrowheads; Phase II) that imply increased actomyosin contractility. (Scale bar in A and C: 40 $\mathrm{\mu }$m.) (D) Quantification of changes in cell size (gray) and shape (i.e., fractional deviation from a circle; SI Appendix, Fig. S2 C and D) prior to NC dumping (Pre-) and during Phases I and II. Onset of nonuniform deformations (dashed cyan line) occurs $\sim$40 min into NC dumping (n = 4). (E) Coefficient of variation of cortical Sqh intensity during NC dumping, showing a transition (dashed red line) from uniform (n = 412; Phase I) to nonuniform (n = 122; Phase II) distribution at $\sim$40 min, concomitant with the onset of dynamic cell shape deformations.

To investigate this process, we used live imaging of egg chambers to reconstruct the intercellular transport pattern within the 16-cell germline cluster and corresponding actomyosin activity during NC dumping. We found that our experimental observations, namely the intercellular directional transport pattern and time scale of this transport phenomenon, in both wild type (WT) and mutants, are best captured by a tension-driven networked flow model inspired by the famous two-balloon problem. Our results also reveal a role for actomyosin dynamics during NC dumping: Appearing as surface contraction waves, which have been observed in a variety of biological systems (18–20), changes in actomyosin activity in the latter phase of NC dumping are required for enabling continuous, pressure-driven flow and complete transport. Combined with other recent studies (21), our results demonstrate the importance of both hydraulic transport and biological mechanisms in regulating multicellular collective behavior during oocyte development in higher organisms.

Results

NC Dumping Proceeds in Two Distinct Phases.

Using ex vivo live imaging of egg chambers with simultaneously labeled membranes (Ecad::GFP or Resille::GFP), myosin-II (sqh::mCh), and cytoplasm (Clip170::GFP), we determined the dynamics of NC dumping and corresponding patterns of actomyosin activity. First, through size measurements of the oocyte and the 15 NCs (SI Appendix, Fig. S1), we found that NC dumping unfolds over the course of $\sim$100 min, a period approximately threefold longer than previously reported through indirect estimates (22, 23). We also determined that NCs empty $\sim$75% of their volume into the oocyte through spatially uniform shrinkage of the cells, in the absence of nonuniform cell shape changes and membrane blebbing that imply contractile force generation (Phase I) (24, 25). In contrast, transport of the remaining cytoplasm (Phase II) is accompanied by dynamic and persistent deformations of NC shape along with blebbing (Fig. 1 C and D, SI Appendix, Fig. S2, and Movie S2).

Similarly, we found that NC dumping onset occurs without changes to the level and localization pattern of cortical myosin as compared to the previous developmental stage. NCs’ cortical myosin reorganizes from a uniform to a nonuniform dynamic cortical pattern only $\sim$40 min into NC dumping, coincident with the onset of dynamic NC shape deformations (Fig. 1E, Movies S2 and S3, and SI Appendix, Fig. S3 A and B). Importantly, no such changes in cortical distribution were observed in control membrane markers (SI Appendix, Fig. S3C). NC dumping, therefore, occurs in two distinct phases, only the latter of which coincides with changes in actomyosin distribution and hallmarks of increased contractility.

Phase I Dynamics Are Captured by a Flow-Network Model.

We therefore explored mechanisms whereby directional intercellular fluid flow can occur in the absence of increased contractility and peristalsis-like cell deformations in the NCs. To that end, we first determined the spatiotemporal pattern of intercellular cytoplasmic transport in the 16-cell network. We found that NC dumping unfolds in a hierarchical manner that mirrors the cells’ size and spatial arrangement. While the oocyte is the largest cell in the egg chamber, the NCs, which are arranged in four layers (L1 to L4, Fig. 2A), also exhibit a descending cell-size order according to their distance from the oocyte (26–28). Our data show that NCs directly connected to the oocyte (L1 cells) are first to transport their contents into the oocyte, followed in order by smaller NCs in layers L2 to L4 (Fig. 2 B and C). Therefore, smaller cells in the network empty their contents into larger ones prior to changes in myosin localization and corresponding cell shape deformations.

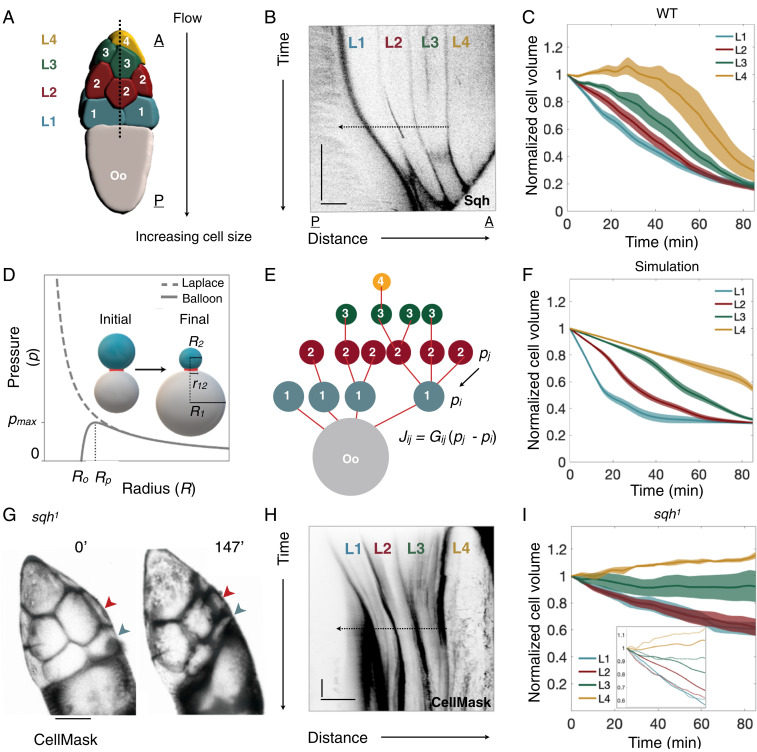
Fig. 2.

NC dumping dynamics are explained by a pressure-driven networked-flow model. (A) Three-dimensional reconstruction of a germline cyst showing the NCs’ arrangement into four layers relative to the oocyte (Oo). During NC dumping, cytoplasm flows in the direction of increasing cell size, from anterior (A) to posterior (P). (B) Kymograph of Sqh intensity in WT along the dashed line shown in A, illustrating hierarchical onset of NC dumping across the four NC layers (L1 to L4); arrow indicates direction of flow. (Scale bars: 30 min, 50 $\mathrm{\mu }$m; black indicates highest intensity.) (C) Plot of normalized NC volumes ($V/V_0$) during NC dumping for each layer from live imaging; $t=0$ is onset of NC dumping; solid line indicates average; envelopes show standard error (n = 15, 12, 9, and 5 cells for layers 1, 2, 3, and 4, respectively). (D) Plots of Young–Laplace’s law and the corrected pressure law for elastic balloons. Pressure is at its maximum, $p_{\text{max}}$, at radius $R_p$; $R_0$ is the uninflated balloon radius; $r_{12}$ is the radius of the pipe connecting balloons 1 and 2. Schematic illustrates the two-balloon problem, where the smaller balloon (cyan) empties into the larger balloon (gray). (E) Network representation of the germline cyst in A showing cells’ relative sizes and connections; cells are shown as nodes and ring canals as edges. (F) Plot of normalized NC volumes from simulations of fluid flow in the germline cyst using the best fit parameter set (solid line); envelopes show standard error constructed from the 10 nearest sets in parameter space (n = 11). Time is scaled by the physical constants of the model. (G) sqh${}^1$ germline mutant showing NCs in the first (blue arrowhead) and second (red arrowhead) layers emptying into the oocyte. (H) Kymograph of intensity of CellMask (a membrane marker) in sqh${}^1$ mutants, showing transport of cytoplasm from the first two layers. (Scale bars: 30 min, 70 $\mathrm{\mu }$m.) (I) Plot as in C of normalized NC volumes over time in sqh${}^1$ germline clones; n = 14, 17, 7, and 6 cells for layers 1, 2, 3, and 4, respectively. (Inset) WT cell volume trajectories from C (solid lines), rescaled in time and overlaid with sqh${}^1$ mutant data (dashed lines), demonstrating slower yet hierarchical intercellular transport.

Driven by these experimental observations, we developed a networked fluid flow model that was inspired by the two-balloon problem: If two identical balloons inflated to different volumes are allowed to exchange air, the smaller balloon will empty its contents into the larger balloon (Fig. 2D). This seemingly counterintuitive phenomenon can be explained by the Young–Laplace law, which states an inverse relationship between pressure $p$ and radius $R$ for a sufficiently large balloon. Taking into account the hyperelastic behavior of rubber, the pressure inside the inflated balloon is then given by

$$p=\frac{2\gamma }{R}\left(1-{\left(\frac{R_0}{R}\right)}^6\right),$$ [1]

where $R_0$ is the radius of the uninflated balloon and $\gamma$ is its surface tension (Fig. 2D) (29, 30).

To investigate whether an analogous model can explain the hierarchical transport observed in Phase I, we approximated each cell by a sphere (31) with time-dependent radius $R_i\left(t\right)$. The actomyosin cortex was assumed to be incompressible and described as an effective neo-Hookean material under static loading (SI Appendix). In this phenomenological description, the effective cell-surface tension $\gamma$ arises from the contributions of both in-plane tension of the plasma membrane and actomyosin cortical tension (32). Extending the two-balloon model to the 16-cell network in the germline cyst (Fig. 2E), the pressure-driven flux $J_{ij}$ from cell $j$ to $i$ through an approximately cylindrical ring canal with hydraulic conductance $G_{ij}$ is

$$J_{ij}=G_{ij}\left(p_j-p_i\right).$$ [2]

Using experimentally determined cell sizes at onset of NC dumping as initial conditions (27), we numerically solved the transport equations for the evolution of cell volumes $V_i$ in the 16-cell tree,

$$\frac{\mathrm{d}{V}_i}{\mathrm{d}t}=\sum _{⟨i,j⟩}{J}_{ij}=\sum _{⟨i,j⟩}{G}_{ij}\left(p_j-p_i\right),$$ [3]

where the sum runs over connected cell neighbors $i$ and $j$.

In the simulations, we used for all 16 cells the same effective tension value $\gamma =4\hspace{0.17em}$ pN/$\mathrm{\mu }$m, estimated from earlier measurements of cytoplasmic viscosity (33) and our own measurements of ring canal radii and volume flux (SI Appendix). This estimate is consistent with previously reported cortical tension values (34). The equilibrium radius $R_0$ in Eq. 1 was chosen proportional to the initial cell radius, $R_{0i}=\rho R_i\left(0\right)$, using the same proportionality constant $\rho$ for all $i=1,\dots ,16$ cells (SI Appendix). Since the initial NC volume is also approximately proportional to the NC nuclear volume (27), this choice is consistent with the fact that the nucleus sets a lower bound on the NC membrane area at the end of Phase I transport. By comparing simulations and experiment, we determined a best-fit parameter $\rho \approx 0.60$; smaller values of $\rho$ favor backflow between adjacent cell layers, in which more posterior NCs transport their cytoplasm into more anterior ones, whereas larger values suppress such backflow. The best-fit value for $\rho$ yielded values $R_{0i}$ no more than 10% larger than the directly measured nuclear radii (SI Appendix), suggesting that the presence of nuclei limits pressure-driven flow once NC volumes become comparable to nuclear volumes. Finally, an initial guess for the hydraulic conductances $G_{ij}$ was obtained by assuming $G_{ij}=\pi r_{ij}^4/\left(8\mu L\right)$ for Poiseuille-type flow (35), where $r_{ij}$ and $L$ are the measured ring canal radii and their average length, respectively, and $\mu$ denotes the fluid viscosity. Since $r_{ij}\in \left[\mathrm{4,10}\right]\hspace{0.17em}\mathrm{\mu }$m and L $\approx$ 2 $\mathrm{\mu }$m are of the same order for the ring canals, the Poiseuille conductance provides only an approximation, and we therefore explored a range of values around the Poiseuille prediction in our simulations (SI Appendix).

Despite its minimal phenomenological character, the flow-network model captures qualitatively essential features of the experimentally observed transport dynamics (SI Appendix, Fig. S4 A and B). Specifically, the best-fit model correctly reproduces both the hierarchical pattern of intercellular transport and time scale of NC dumping (Fig. 2F and SI Appendix). The model can be expanded to account for natural cell-to-cell variability in effective surface tension (36); such extensions successfully capture experimentally observed complex transport dynamics along the 16-cell tree. For example, our data show the L4 NC transiently increasing in size during NC dumping, which can occur if the L3 cell to which it is connected shrinks sufficiently such that it becomes smaller than the L4 cell. Such transient backflow away from the oocyte is a feature of NC dumping that has been observed and documented before (37) and is predicted by our model (SI Appendix, Fig. S4C and Movie S4). We also found that the gradient in NC and ring canal sizes, from smallest at the anterior to largest at the posterior end, is critical for the timely, directional, and hierarchical transport pattern observed experimentally; simulations in which these size gradients were ignored displayed aberrant intercellular transport patterns and dynamics (SI Appendix, Fig. S4D).

An insight provided by the model is the high sensitivity of intercellular transport to changes in ring canal size through the approximately quartic scaling of the hydraulic conductances. During oogenesis, ring canal diameters increase in size by $\sim$10-fold (12). However, ring canal diameter increases most rapidly in the stages of oogenesis prior to NC dumping (SI Appendix, Fig. S5A), through the differential recruitment of F-actin toward expansion of the cytoskeletal ring rather than increasing the thickness of the ring canal (38). Recent work has suggested a mechanosensory function for filamin in ring canal expansion, as rapid growth of the ring canal coincides with rapid growth of the egg chamber and increased tension on the cells’ plasma membrane (39). While onset of NC dumping is likely affected by factors such as interactions between the follicle cells and the germline, or by external cues, here we propose that the increase in ring canal size prior to NC dumping can also sharply accelerate cytoplasmic transport from NCs into the oocyte (SI Appendix, Fig. S5B).

Our model predicts that lowering of the effective NC surface tension will slow down the rate of intercellular transport, as the parameter $\gamma$ sets the overall time scale, but will not affect the hierarchical transport pattern. In a cell, surface tension is affected by the actomyosin cortex and can be reduced by inhibiting myosin (40). Therefore, to test how transport is affected by reducing surface tension, we quantified the spatiotemporal pattern of NC dumping in a mutant in the myosin RLC, encoded by sqh. In sqh${}^1$ mutant germline clones, sqh messenger RNA and protein levels are reduced by $\sim$90% (41, 42). We found that while Sqh-depleted germline cysts are “dumpless,” that is, do not complete NC dumping (Fig. 2G) (16), the hierarchical transport pattern observed in WT is largely maintained (Fig. 2 H and I and Movie S5). However, NC dumping in sqh${}^1$ mutants proceeded more slowly (Fig. 2I, Inset), which is consistent with myosin contributing to the baseline level of cortical tension required for Phase I but not to the onset, direction, or pattern of intercellular transport.

Phase II Requires Actomyosin Contractile Surface Waves.

Although transport of cytoplasm is initiated in sqh${}^1$ mutant egg chambers, NC dumping is not completed in these mutants, suggesting that actomyosin activity and its regulation are important. Indeed, live imaging of egg chambers with labeled myosin (sqh::mCh) and actin (F-tractin::TdTomato, and Utr::GFP) demonstrates that actomyosin is highly dynamic during Phase II of NC dumping. Myosin exhibits a diversity of spatiotemporally organized cortical waves, such as colliding myosin wave fronts, rotating cortical bands, and myosin rings traveling between the cell’s poles, which lead to local and dynamic NC shape deformations, as opposed to isotropic contractions of the entire cell (Fig. 3 A–E and Movie S6). We also found that actomyosin waves in the NCs travel at $\sim$0.3 $\mathrm{\mu }$m/s, a speed comparable to that of Rho-actin contraction waves observed in frog and starfish oocytes and embryos (18). Notably, the intercellular pattern of actomyosin wave onset mirrors that of cytoplasmic transport, starting in NCs closer to the oocyte, which shrink first, before appearing in NCs further away (Fig. 3F).

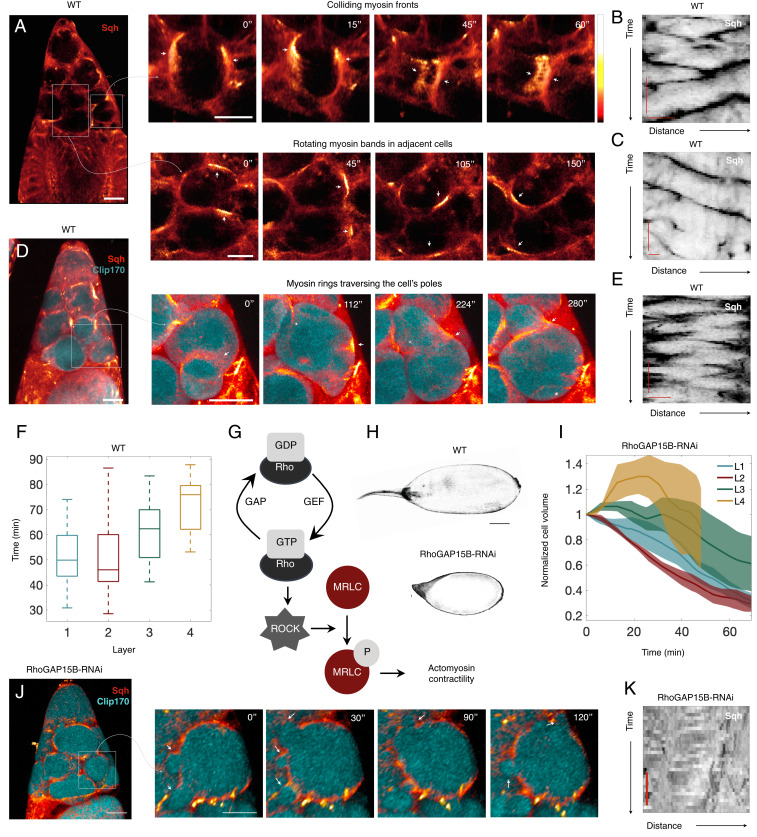
Fig. 3.

Complete NC dumping requires Rho-regulated wave-like actomyosin dynamics. (A) Heat map of an egg chamber expressing sqh::mCh; blowups show NCs with dynamic actomyosin cortical waves as colliding fronts (Top) and rotating bands (Bottom) in adjacent NCs, with respective kymographs of Sqh intensity around NCs’ perimeter (B and C). (D) Heat map of an egg chamber expressing sqh::mCh and Clip170::GFP (cyan); blowups show an NC with an actomyosin ring (arrowhead) traversing the cell’s opposing poles and deforming cell shape, with E showing a kymograph of Sqh intensity. (F) Box-and-whisker plot of time at which nonuniform and persistent cell deformations are first observed following onset of NC dumping in each layer (center line = median; edges = upper and lower quartiles; whiskers extend to extrema; n = 20, 22, 16, and cells for layers 1, 2, 3, and 4, respectively). (G) The RhoA/ROCK signaling pathway regulates phosphorylation of the myosin RLC (MRLC) and actomyosin contractility. (H) Comparison between WT (Top) and dumpless, RhoGAP15B-depleted (Bottom) egg chambers. (Scale bar: 50 $\mathrm{\mu }$m.) (I) Plot of normalized NC volumes during NC dumping for each layer from live imaging of RhoGAP15B knockdowns; $t=0$ is onset of NC dumping; solid line indicates average and envelopes show standard error (n = 7, 6, 3, and 2 cells for layers 1, 2, 3, and 4, respectively). The trajectory for the L4 cells stops at $t\sim 50$ min due to membrane breakdown. (J) RhoGAP15B-depleted germline expressing sqh::mCh and Clip170::GFP; blowup shows smaller short-lived cell protrusions as opposed to the cell-scale dynamic deformations observed in WT. (K) Kymograph of Sqh intensity along the perimeter of a cell in a RhoGAP15B knockdown at a time comparable to B, C, and E, illustrating disrupted wave dynamics; black indicates highest intensity. The time scale bar is 5 min, while the horizontal axis represents fractional distance along cell perimeter. (Scale bar in A, D, and J: 40 $\mathrm{\mu }$m; scale bar in blowups: 20 $\mathrm{\mu }$m; kymograph scale bars in B, C, and E: 5 min, 10 $\mathrm{\mu }$m.)

Dynamic actomyosin behaviors like those observed here are regulated through RhoA activation and inhibition (18, 43, 44). RhoA is a small GTPase activated by guanine nucleotide exchange factors and inhibited by GTPase-activating proteins (GAPs) (45, 46). Binding to downstream effectors, such as the Rho-associated and coiled-coil kinase (ROCK; Rok in Drosophila), results in increased contractility through myosin RLC phosphorylation (Fig. 3G) (47–49). Our data show that, similar to myosin, Rok, Utrophin, and F-Tractin exhibit wave-like behavior (SI Appendix, Fig. S6 and Movie S7), suggesting that dynamic RhoA regulation, rather than constitutive caspase cleavage-mediated activation of Rok (50), underlies myosin’s dynamics. Furthermore, through a genetic screen (43) we identified RhoGAP15B, the Drosophila homolog of ARAP1/3, as a critical regulator of wave dynamics; the RhoGAP domain of the human RhoGAP15B homolog exhibits highest specificity toward RhoA (51), consistent with RhoGAP15B’s regulating actomyosin contractility. We found that while RhoGAP15B depletion in the germline cyst led to a “dumpless” phenotype (Fig. 3H), onset of NC dumping and the time scale of Phase I transport were unaffected (Fig. 3I). The hierarchical pattern of Phase I transport was also largely unchanged, although there was greater variability between the timing of L1 and L2 in knockdown egg chambers (Fig. 3I). Instead, RhoGAP15B depletion disrupted myosin wave dynamics and concomitant cell-scale shape deformations otherwise observed during Phase II: cells displayed erratic myosin activity associated with smaller and more transient cell protrusions (Fig. 3 J and K and Movie S8). We confirmed that incomplete NC dumping in RhoGAP15B knockdowns is not attributable to obstructed or diminished ring canal sizes or disrupted actin cables that tether the NC nuclei (SI Appendix, Fig. S7) (15, 52). These data, therefore, suggest that incomplete cytoplasmic transport in RhoGAP15B knockdowns is due to disrupted actomyosin wave dynamics in Phase II of NC dumping.

Physical and Biochemical Mechanisms Are Required for Complete Transport.

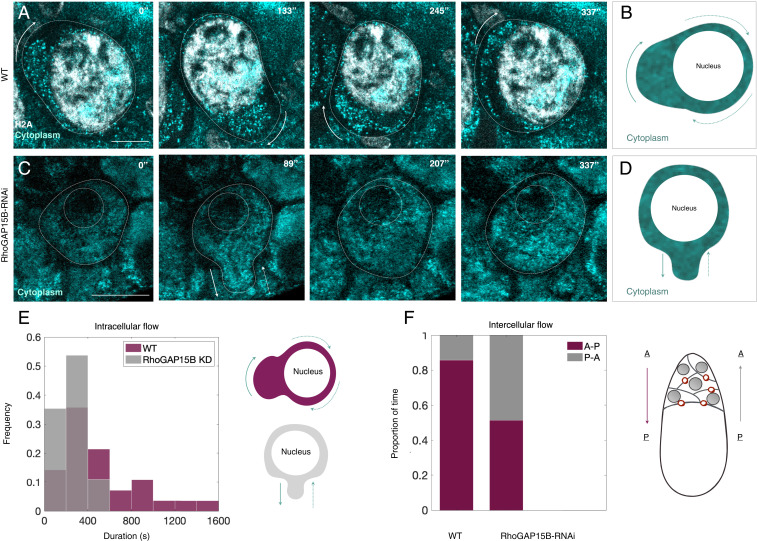
A clue to how actomyosin surface waves enable complete NC dumping came from directly visualizing inter- and intracellular cytoplasmic flow using reflection-mode microscopy. Following actomyosin wave onset and concomitant NC shape deformations, cytoplasm was observed flowing through spaces between NC nuclei and membranes and completing multiple revolutions around the large polyploid nuclei as intercellular anterior-to-posterior transport continued (Fig. 4 A and B and Movie S9). In contrast, intracellular flow in RhoGAP15B knockdowns appeared erratic and lacked the persistent radial motions around NC nuclei necessary for bringing cytoplasm in contact with a ring canal (Fig. 4 C and D). As a result, RhoGAP15B knockdowns exhibited interrupted anterior-to-posterior intercellular flow, repetitive and more frequent transport of cytoplasm away from the oocyte (Fig. 4 E and F and Movie S10), a greater degree of layer 4 expansion (Fig. 3I), and incomplete NC dumping. Given that actomyosin waves first appear in an NC once it has emptied most of its cytoplasmic contents (SI Appendix, Fig. S2E), we propose that wave-mediated NC deformations enable continued pressure-driven transport by creating spaces between plasma membranes and nuclei in shrunken NCs (SI Appendix, Fig. S8). Because the oocyte is the largest cell in the germline cluster, it will always have the lowest pressure and will therefore set the directionality of flow. As a result, wave-mediated cell deformations could create a path that allows cytoplasm to flow past nuclei from anterior to posterior ring canals and transport into the oocyte to run to completion.

Fig. 4.

Actomyosin contractions promote intracellular flow in shrunken NCs. (A) Time-lapse images from reflection-mode microscopy showing cytoplasm (cyan) flowing around an NC nucleus (H2A, white) as persistent actomyosin waves deform cell shape. (B) Illustration of cytoplasmic flow observed in A, where arrows point in the direction of flow. (C) Erratic and transient intracellular cytoplasmic flow in a germline RhoGAP15B knockdown, illustrated in D, highlighting the lack of persistent revolutionary motions observed in WT. (Scale bars in A and C: 20 $\mathrm{\mu }$m.) (E) Histogram of the duration of observed intracellular cytoplasmic flow events in WT and RhoGAP15B knockdowns (WT: n = 28 events; RhoGAP15B-RNAi: n = 82). (F) Bar plot of the proportion of time anterior-to-posterior (A-P) versus posterior-to-anterior (P-A) flows were observed through ring canals in WT and in RhoGAP15B-RNAi egg chambers (WT: six events of intercellular flow spanning 30 min total; RhoGAP15B knockdowns: 29 events spanning 54 min).

Discussion

Our joint experimental and theoretical results address a long-standing question concerning the origin and regulation of multicellular collective behavior during oocyte development: How do support sister cells in a germline cyst directionally transport the entirety of their cytoplasm into the future egg cell? Both experiments and theory show that baseline surface tension and differential cell size provide robust and highly tunable fluid-mechanical control over directional intercellular cytoplasmic flow, and that subsequent wave-like actomyosin contractions are essential to complete transport. These findings contrast with previous hypotheses for NC dumping, which suggested that cytoplasm is driven out of the NCs through a global increase in pressure mediated through upregulated cytoskeletal force generation, or squeezing (15, 28), requiring that actomyosin contractility increase at the onset of NC dumping (13). Such a model however does not mechanistically explain the directionality and hierarchical flow pattern that is observed during NC dumping, and our data show that changes in actomyosin localization and concomitant membrane blebbing do not occur until the NCs have emptied most of their cytoplasmic contents into the oocyte.

Model Limitations.

While the hydrodynamic model presented here faithfully reproduces the hierarchical dumping pattern, the interpretation of its parameters is limited by its partially phenomenological nature. The Young–Laplace term is biophysically motivated, with $\gamma$ playing the role of an effective surface tension reflecting the energetic cost of having an interface of a certain area. The second term of Eq. 1 is, however, a phenomenological correction to the Young–Laplace pressure. For a rubber balloon, $R_0$ is the radius at which the pressure difference across the balloon’s surface is zero; however, cells do not have a well-defined “empty” size. Indeed, a cell’s cortex always generates some baseline tension, such that even as the cell decreases in size the cortex is remodeled so that this baseline tension is maintained (53). Another important difference between the classical balloon experiment and the NC tree is the presence of the cell nuclei, which can hinder intra- and intercellular fluid transport once the cell volume has become comparable to the nucleus size. Therefore, for a cell, the $R_0$ parameter can be thought of as an effective limiting radius below which cortical tension alone no longer suffices to drive flux through the ring canals, defining the end of Phase I. Identifying the biochemical and biophysical mechanisms that trigger the transition from the hydraulic Phase I to the contractile wave-mediated Phase II, which may be cell-size-dependent or related to membrane–nucleus contact interactions, poses an interesting open question for future research.

Conclusions

The above analysis highlights the complementary importance of physical and biological mechanisms in achieving directed intercellular fluid transport during oogenesis and adds to the growing list of examples where hydrodynamics plays a critical role in development (1–4). This work has also revealed a diversity of myosin wave-like behaviors and a previously unknown function for excitable actomyosin dynamics. Indeed, by establishing surface cortical waves as one of the final facilitators of material transfer between sister germ cells, this work expands the repertoire of roles played by such waves in development (18–20, 54).

Materials and Methods

All experimental data are available in the main text or SI Appendix. Experimental protocols are described in SI Appendix. The strains and genetic crosses used in this study are in SI Appendix, Table S1. We used Fiji and Bitplane’s Imaris to analyze our images and movies and MATLAB for aligning data and generating plots. Measurements and sample sizes are recorded in SI Appendix, Table S2. The code used for numerical simulations is available on a public repository at https://github.com/NicoRomeo/balloon-dynamics. A summary of the initial conditions and adjustable parameters is given in SI Appendix, Table S3.

Immunofluorescence and Antibodies.

Flies were raised under standard conditions at $25^{\hspace{0.17em}○}$C and dissected using an established protocol (55). Ovaries from well-fed adult flies were dissected and fixed in 4% (wt/vol) paraformaldehyde at room temperature for 20 min and stained with primary antibodies: rat anti-E-cadherin (1:500; Developmental Studies Hybridoma Bank), rabbit anti-PTyr (1:500; Santa Cruz Biotechnology), and mouse anti-NPC (1:500; Abcam). We used goat anti-rat 647 nm, goat anti-rabbit 568 nm, and goat anti-mouse 488 nm as secondary antibodies diluted at 1:300. Phalloidin-Alexa-647 (Life Technologies), diluted 1:1,000, was used. Samples were mounted in a 50:50 mixture of Aqua-Poly/Mount (Polyscience) and RapiClear 1.47 (an optical clearing medium from SunJin Laboratory Co.).

Long-Term Live Imaging.

We used a modified version of the Prasad et al. (56) protocol for live imaging of dissected egg chambers. Ex vivo culturing of egg chambers took place. Ovaries from approximately two to five flies were dissected in Schneider’s Drosophila media (21720-001; Thermo Fisher) that was also used for ex vivo culturing; the separated egg chambers were then transferred to a MatTek dish (P35G-1.5-10-C) containing 200 $\mathrm{\mu }$L of media. Imaging took place on an inverted microscope while leaving the lid on the dish to prevent drying. For outlining membranes in the absence of a fluorescent membrane reporter, CellMask deep red plasma membrane stain (C10046; Invitrogen) was added to Schneider’s mix (1:1,000).

Microscopy.

Imaging was performed on a Zeiss LSM 710 point scanning confocal microscope with a 25× or 40×/1.2 Apochromat water objective lens, a 10× dry lens, an argon ion, 561-nm diode, 594-nm and 633-nm HeNe lasers, and the Zen software. Pinhole settings ranged from 1 to 2.5 Airy units. For two-color live imaging, band-pass filters were set at $\sim$490 to 565 nm for GFP (green fluorescent protein) and $\sim$590 to 690 nm for mCh (mCherry). For three-color imaging, band-pass filters were set at $\sim$480 to 560 nm for GFP, $\sim$580 to 635 nm for Alexa Fluor 568, and $\sim$660 to 750 nm for Alexa Fluor 647. Imaging using confocal reflection mode was performed by setting the detection to the excitation wavelength, that is, 488 or 561 nm, and using a mirror instead of a dichroic in the beam path. For live imaging of fluorescent reporters, stacks of 20 to 60 slices and a z-spacing of 2 to 3 $\mathrm{\mu }$m were acquired in succession without delay. For live imaging using reflection-mode microscopy, a single slice was imaged at a frame rate of $\sim$0.4 to 0.9 s per frame in succession. Both modes of imaging took place over the course of $\sim$0.5 to 3 h.

Genetic Screen for RhoGAP Dumping Mutants.

Standard Drosophila genetic techniques were utilized to genetically move together tagged proteins or to stimulate transcription of a reporter gene under UAS control through GAL4 expression. This screen was performed to identify maternal effect phenotypes for Rho GAPs, as previously described (43). Briefly, virgins for 22 Drosophila RhoGAP short hairpin RNA lines were crossed to mat67,15 drivers with fluorescent markers and egg phenotype (i.e., change in egg size) was scored using a dissecting microscope before imaging gastrulation by confocal. UAS hairpin RNAs were created by the Transgenic RNAi Project at Harvard Medical School (57). Only one of these lines (RhoGAP15B, HMJ02093) gave rise to smaller, “dumpless” eggs.

Data Availability

The code used for numerical simulations is available on a public repository at https://github.com/NicoRomeo/balloon-dynamics. All study data are included in the article and/or SI Appendix.