Selective constraints on global plankton dispersal

Significance

Microscopic plankton form the ecological and biogeochemical foundation of almost all marine ecosystems. In the fluid ocean environment, biodiversity and community structure are determined by the poorly constrained balance of local selection and global dispersal. While ocean currents have the capacity to rapidly connect distant locations, we use numerical simulations to show that extremely high rates of adaptation are required for populations to traverse large-scale gradients in environmental variables such as temperature. Changing the assumed balance of selection, adaptation, and dispersal in our simulations has pronounced effects on the simulated community structure, accounting for emergent patterns in the global ocean microbiome and emphasizing the importance of evolutionary history in global marine biodiversity and biogeography.

Abstract

Marine microbial communities are highly interconnected assemblages of organisms shaped by ecological drift, natural selection, and dispersal. The relative strength of these forces determines how ecosystems respond to environmental gradients, how much diversity is resident in a community or population at any given time, and how populations reorganize and evolve in response to environmental perturbations. In this study, we introduce a globally resolved population–genetic ocean model in order to examine the interplay of dispersal, selection, and adaptive evolution and their effects on community assembly and global biogeography. We find that environmental selection places strong constraints on global dispersal, even in the face of extremely high assumed rates of adaptation. Changing the relative strengths of dispersal, selection, and adaptation has pronounced effects on community assembly in the model and suggests that barriers to dispersal play a key role in the structuring of marine communities, enhancing global biodiversity and the importance of local historical contingencies.

Ocean microbial biogeography is determined by the balance of two opposing forces: dispersal by the ocean currents and selection by the local environment (1). In the limit where global dispersal is fast relative to population turnover, environmental conditions alone should be sufficient to predict the presence or absence of a particular species from any given location on Earth (2, 3). This is the view encapsulated in the hypothesis of Baas-Becking (4) that “everything is everywhere, but the environment selects.” On the other hand, if global dispersal is slow relative to population turnover, limited connectivity between ocean regions will tend to reinforce chance differences between isolated communities (5, 6), with geographically isolated but otherwise similar environments displaying significant differences in taxonomic composition.

Over evolutionary timescales, the balance of dispersal and selection will affect community assembly [through diversification and mass effects (7)], ecosystem function (through biogeochemical cycling), and ultimately, the resilience of marine ecosystems to environmental change (8). Therefore, understanding the mechanisms that lead to niche diversification and biogeographic structure in microbial communities is a fundamental pursuit of marine microbial research. A central question is to what degree are biogeographic patterns attributable to local selection based on contemporary environmental factors or to independent stochastic processes occurring in geographically isolated regions (SI Appendix, Fig. S1) (1).

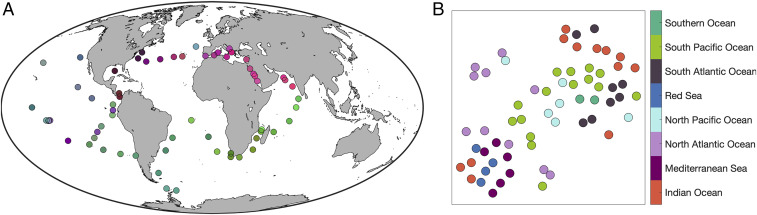
Recent analysis of metagenomic data (Fig. 1) (9) has shown that large-scale trends in community composition are correlated both with environmental variables and with geographic distance, with distinct clusters emerging along environmental gradients and among the most rapidly connected sites, suggesting that both history and environment play important roles. When sample sites are clustered based on metagenomic pairwise $\beta$-diversity (SI Appendix), there is discernible ecological similarity among sites within the same ocean basins (Fig. 1A), although we also see geographically proximate sites clustered far apart and sites from geographically remote locations clustered together (Fig. 1B and SI Appendix, Figs. S4 and S5). These broad patterns appear to reflect both geographic proximity and environmental selection (9). Nonetheless, it can be difficult to assign causal mechanisms, and the drivers of observed biogeography thus remain uncertain.

Fig. 1.

Taxonomic community similarity clusters in the 0.22- to 3-$\mathrm{\mu }$m size fraction across Tara Oceans sites (replotted using data from ref. 9). (A) Community similarity is shown with colors by projecting the Taxonomic Jaccard dissimilarity matrix into the “rgb” (red-green-blue) color space using the t-SNE (t-distributed stochastic neighbour embedding) dimension-reduction algorithm (10). (B) Links between community similarity clusters (dimensionless $x$ and $y$ coordinates) and spatial location (colors corresponding to ocean basins). SI Appendix, Fig. S1 has an interpretation of B.

The roles of selection and dispersal have both been examined using global-scale models but typically, with one in isolation from the other. On one hand, population dynamic models have focused on the role of selection from among a universal background of candidate species (11), in line with the Baas-Becking (4) hypothesis. On the other hand, a number of studies have addressed the question of global gene flow in oceanic microbial communities, using particle tracking models to assess connectivity through the surface waters (6, 12), but these have typically assumed ecological neutrality (5) and have thus ignored the role of selection. While some studies find that the ocean surface is very rapidly connected on timescales of decades or less (12), others suggest that current rates of passive dispersal are insufficient to overcome biogeographic differences created by chance mutations occurring in geographically isolated regions of the ocean (6).

In order to distinguish between the biogeographic effects of selection and dispersal, we need a framework that accounts for both processes together. In this paper, we develop a population genetic model representing taxonomic and phenotypic diversity within a single clonally reproducing plankton population, embedded within an empirically constrained representation of the ocean circulation (13). In contrast to previous studies, our model accounts for population size, stochastic demography, natural selection, adaptation, and transport through the ocean interior (we find that dispersal pathways restricted to the ocean surface are artificially sensitive to fluid convergence and divergence). With a more realistic transport term accounting for dispersal at all depths, we find that varying the degree of selection and adaptation leads to very different model outcomes in terms of community biogeography and global connectivity. We show that selection based on thermal niches acts as a major constraint on dispersal, with the clear effects on biogeographic organization at the global scale.

Simulations

To assess the rate of planktonic dispersal across the global ocean, we developed a model that tracks the relative abundances of adapting subpopulations in a globally distributed metapopulation, with spatially varying carrying capacity, $\mathbf{N}$ (SI Appendix, Fig. S2). At the beginning of each simulation, a resident subpopulation is assumed to have population frequency of one throughout the global ocean. However, at each of 94 “seed locations” distributed more or less evenly around the ocean (see dots in Fig. 3), the resident subpopulation is replaced with a taxonomically distinct (but ecologically identical) local subpopulation. From this initial condition, the model is integrated for 100 years in discrete time. Every 6 hours, plankton populations are dispersed by the ocean circulation. Every 24 hours, each population is replaced with a new generation of $\mathbf{N}$ cells, drawn stochastically from a probability distribution determined by the relative abundance of each subpopulation and where appropriate, a temperature-dependent selection coefficient, $s$ (14). In regions where a subpopulation is present in high abundance, the stochasticity of this process has no significant effect on the relative abundance, but it introduces a meaningful chance of local extinction wherever abundances are low (such as at edges of a subpopulation’s range). Repeating each simulation five times, we found no meaningful differences between iterations in terms of the presented results (Fig. 2).

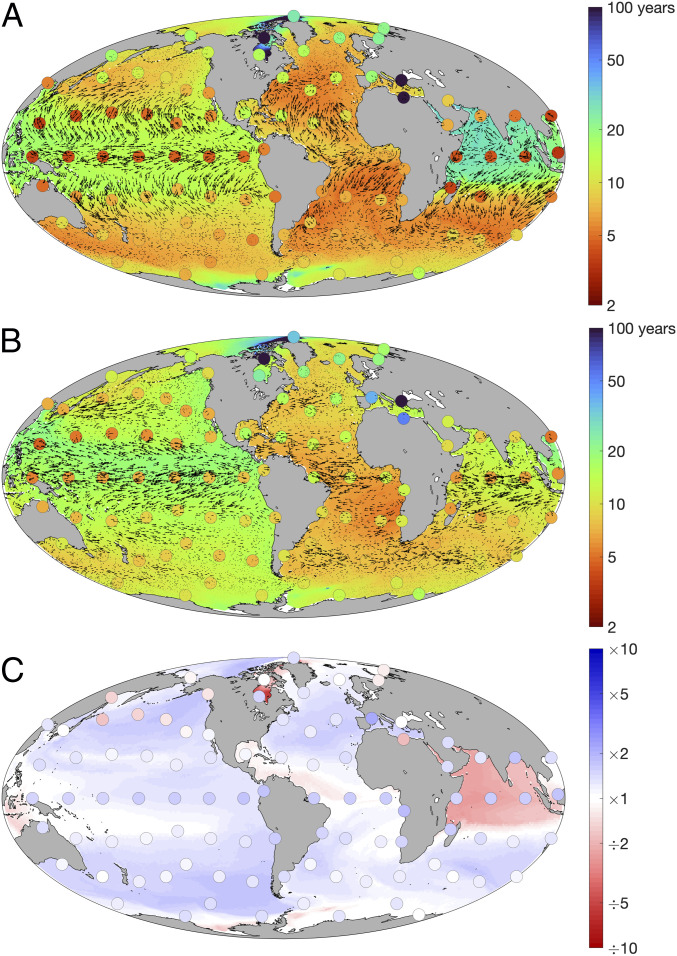
Fig. 3.

Immigration and emigration timescales (years) for ecologically neutral Prochlorococcus subpopulations, given (A) surface-only transport and (B) depth-integrated transport. Taxonomically distinct subpopulations were seeded in each of the 94 locations marked with dots. Emigration times, represented by the colored dots, are defined as the time taken for each seed subpopulation to disperse to 90% of all locations. Immigration times, represented by the background colors, are defined as the time taken for 90% of all seed subpopulations to arrive in each location. Planktonic transport velocities are shown as vectors. (C) Relative changes in global immigration and emigration times when switching from surface-only to depth-integrated transport (B $÷$ A).

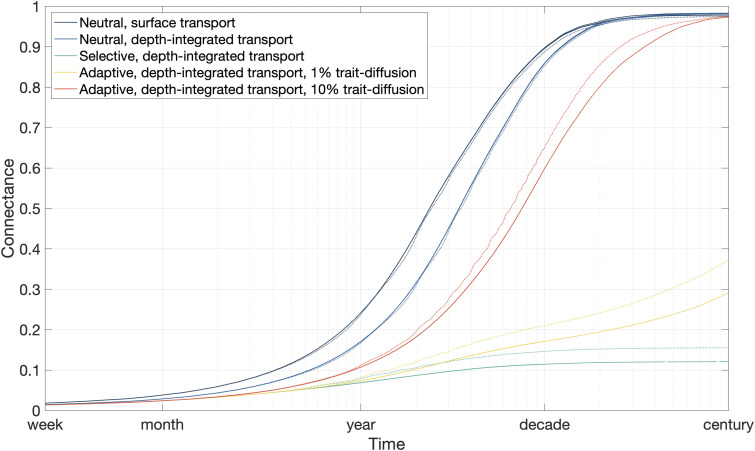
Fig. 2.

Fraction of connections between the 94 seed locations and the rest of the ocean through time. Solid lines show the results of simulations with time-invariant temperatures and carrying capacities. Dotted lines show the results of simulations with seasonally varying temperature and carrying capacity. Neutral simulations were repeated five times to 100 years. Selective and adaptive simulations were evaluated once to 100 years and four additional times to 10 years. (Please note that the replicate simulations are so alike that the lines are effectively plotted on top of each other.)

Our main set of simulations tracks the dispersal of a globally abundant Prochlorococcus population with a cellular diameter of approximately 0.6 μm, setting $\mathbf{N}$ to the depth-integrated cellular abundance within each grid box (SI Appendix, Fig. S2) (15). The results presented below are derived from simulations based on a single repeating year with time-invariant environmental temperatures and population carrying capacities. We also performed simulations where these variables followed a seasonal cycle, finding that the results were not overly sensitive to the change (Fig. 2).

Ecologically Neutral Dispersal by Surface Transport.

We initially considered a scenario where cells are transported exclusively within the surface layer, with all subpopulations equally well adapted at all temperatures [i.e., ecologically neutral (5)]. The dark blue lines in Fig. 2 show the timescales over which the 94 Prochlorococcus seed subpopulations reach the rest of the ocean. Largely in agreement with previous studies (12), almost 90% of the surface ocean is connected within a decade.

The global dispersal of the ecologically neutral subpopulations is broken down further in Fig. 3A. Here, immigration times (background colors in Fig. 3A) suggest that temperate latitudes are generally more easily invaded than the equatorial regions. Conversely, emigration times (colored dots in Fig. 3A) suggest that subpopulations initialized at lower latitudes are more rapidly dispersed throughout the ocean than those from higher latitudes.

These regional differences in immigration and emigration timescales are explained by the surface circulation patterns shown in Fig. 3A. The two-dimensional (2D) surface transport vectors are highly divergent in equatorial upwelling regions (SI Appendix, Fig. S3A), driving a consistent efflux of cells that must be topped up to the carrying capacity by reproduction of the local resident population. These regions thus export cells to the rest of the ocean while remaining resistant to immigration. The subtropical gyres, meanwhile, are characterized by convergent flow, with a consistent influx of cells diluting the local resident populations. These regions are thus easily invaded and are slower to export cells to the rest of the ocean.

Depth-Integrated Transport.

The assumption that horizontal dispersal of plankton occurs only in the surface layer ignores the potential role of subsurface connectivity. To test the sensitivity of our results to this pathway, we calculated the depth-integrated horizontal transport of cells across the entire water column, weighting transport fluxes at each depth by the local population abundance. After this adjustment to the transport component, we repeated our initial experiment in the same way. Accounting for subsurface transport generally decreases global ocean connectivity at timescales less than about 20 years, although there is a very slight increase in global connectivity from 20 years to the end of the simulation (pale blue line in Fig. 2).

The generally slower rate of global connectivity in the depth-integrated simulation occurs as the transport field incorporates slower fluxes through the ocean interior (compare the transport vectors in Fig. 3 A and B). Nonetheless, there are limited regions where the depth-integrated flow field markedly accelerates immigration, most notably the Indian Ocean and Hudson Bay. In these semienclosed regions, the large-scale circulation is characterized by inflow at depth and outflow at the surface, such that the influx of cells is markedly underestimated in the surface-only simulation.

Selection.

The previous experiments have assumed that all subpopulations are equally well adapted to conditions throughout the entire ocean, but we know that changing conditions select for different phenotypes along environmental gradients (16, 17) and that dispersing populations will be selected against as they stray beyond their optimal environments.

To test the influence of selection, we focused on a single exemplar trait, assigning thermal tolerance curves such that populations are preferentially selected when ambient temperatures align with their thermal optima (Eq. 4). Each seed population is assigned a thermal optimum matching the average temperature at its initial location. At the same time, the global resident population is divided into 77 subpopulations, each with thermal optima matching the average temperature at its initial location. This is consistent with the known prevalence of locally adapted resident populations (17) but ignores the ability of populations to themselves evolve over time (in the next section). The model was then evaluated with the depth-integrated circulation scheme.

The global dispersal of the 94 seed populations is severely restricted by temperature-based selection (green line in Fig. 2), with global connectivity not rising above 15% in the 100-year simulation.

Adaptation.

Temperature-related selection places a strong constraint on the dispersal of thermally adapted populations. If populations are to overcome this restriction, they must adapt dynamically to their environments by generating heritable phenotypic changes over time (17, 18). We included this capacity in the model by allowing all subpopulations to produce a small fraction of offspring with different thermal optima (Materials and Methods and SI Appendix). This “trait-diffusion” model is representative of a large range of molecular mechanisms, including heritable and plastic responses, standard mutations, sex, and horizontal gene transfer (19). We initialized the experiment as before, with each subpopulation optimally adapted to its local temperature, but allowed for a small diffusive flux between adjacent phenotypes (19, 20). In line with previous studies (19), we performed simulations with trait-diffusion rates of 1 and 10%.

Even with a very high trait-diffusion rate of 10%, global dispersal is markedly restricted by selection effects, with 90% connectivity only achieved after more than 30 years (orange line in Fig. 2). When the trait-diffusion rate is set to 1%, just under 30% of the ocean has been connected within 100 years (yellow line in Fig. 2).

Niche Breadth.

In the selective cases outlined above, the thermal tolerance curve is a Gaussian function of temperature with an interquartile range of $\sim \mathrm{10}°$C. To evaluate the sensitivity of dispersal to the breadth of the thermal niche, we repeated the selective and adaptive simulations increasing and decreasing the niche breadth parameter by a factor of two. SI Appendix, Fig. S8 shows that while a broader niche corresponds to more rapid global dispersal, this effect decreases as the rate of adaptation increases. Nonetheless, the requirement for relatively rapid rates of adaptation to overcome the selective restriction of dispersal appears robust to the evaluated breadths of the thermal niche.

Global Dispersal and Community Assembly.

The global distribution of a single seed population 100 years after it was initialized in the central North Atlantic ($\mathrm{35}°$N, $\mathrm{46}°$W) is shown in four illustrative cases in Fig. 4. In the neutral model, the highlighted population has complete global coverage, with highest concentrations in the Atlantic subtropical gyres (Fig. 4A). Without selection, all seed populations are globally dispersed after 100 years, with communities clustering strongly within and across ocean basins [here plotted as in Fig. 1 across the Tara Oceans sites (9)]. Sites within each ocean basin often cluster together, but there is little of the discrete separation between sites in adjacent basins (e.g., North and South Pacific; Indian Ocean and Red Sea) that we see in the Tara data (Fig. 1B).

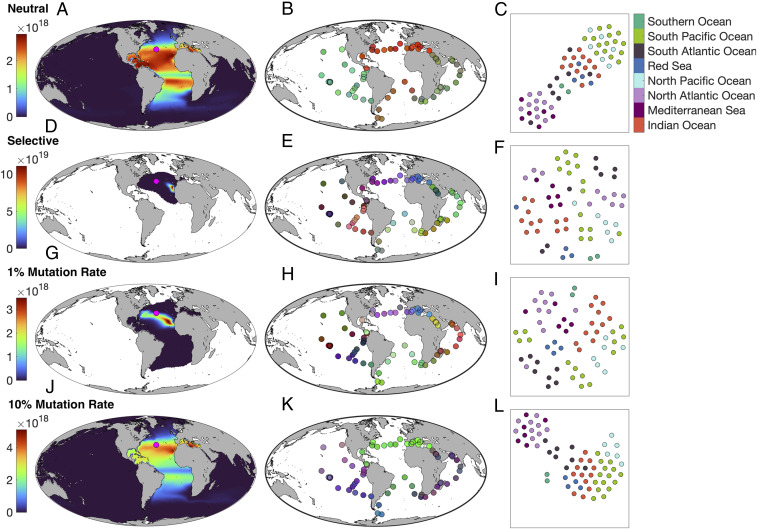
Fig. 4.

Global dispersal and taxonomic clustering of modeled subpopulations. Each row represents a different experiment. (A–C) Neutral case. (D–F) Selective case. (G–I) Adaptive case (1% mutation rate). (J–L) Adaptive case (10% mutation rate). A, D, G, and J map the global abundance distributions of individual seed populations, initialized at the site indicated by the pink dot (white areas indicate zero abundance). B, E, H, and K show community dissimilarity among the Tara Oceans sites, with similar sites assigned similar colors (cf. Fig. 1). C, F, I, and L show similar environmental clustering for the same Tara Oceans sites, with similar sites clustered together in the x and y coordinates. Colors indicate the ocean basin for each site. All panels show results after 100 years of dispersal.

With temperature-based selection enabled, but without adaptation, the distribution of the seed population is restricted to a relatively small area within the North Atlantic subtropical gyre (Fig. 4D), in waters between 5 °C and 28○C. The population is unable to disperse beyond its original North Atlantic habitat, excluded from thermally suitable environments in other ocean basins by the population’s inability to successfully traverse warmer or colder regions. In this case, we see multiple distinct clusters of sites within each ocean basin, indicative of the strong niche separation by temperature. Despite the presence of similar temperature niches in multiple ocean basins, we do not see any of the clustering across basins that is apparent in the Tara data (Fig. 1B). Indeed, only three clusters include sites drawn from different basins (Red Sea with Indian, North Pacific with South Pacific, and North Atlantic with Mediterranean).

The distribution of the same seed population when it is allowed to adapt with a mutation rate of 1% is shown in Fig. 4G. After 100 years, the lineage has dispersed much further into the South Atlantic, but the majority of its descendants remain trapped within the North Atlantic subtropical gyre. With trait diffusion enabled, we see fewer and slightly larger clusters, but there remains a relatively low degree of clustering among sites drawn from different regions.

Only when the trait-diffusion rate is increased to 10% does the seed population attain similar global dispersal to the neutral case after 100 years, and even then its distribution is centered more strongly on its original Atlantic habitat (Fig. 4J). With this extremely high rate of trait diffusion, we see the global metapopulation clustering strongly both within and across ocean basins.

Discussion

Plankton circulating within the global ocean are not dispersed as inert tracers. With their growth and relative fitness affected by the changing physical, chemical, and biotic environment, populations are continually under selection as a function of their environmental setting. In environments outside their optimal habitat, dispersing populations are likely to be outcompeted by better-adapted local populations, with an increasing risk of local extinction as their abundances decline (21). This selective process has the capacity to place very strong constraints on the global dispersal of individual populations and hence, on the flow of genetic information from one ocean region to another. In our experiments, global connectivity only seems to be assured—on timescales of decades to centuries—when subpopulations are able to rapidly adapt to changing conditions as they are dispersed.

While the model presented here is likely far too idealized to allow direct quantitative comparison with the Tara Oceans data in all their complexity, our simulations imply that even while the marine plankton are rapidly dispersed by the ocean circulation, significant barriers to viable dispersal exist—even for highly abundant and rapidly evolving microbial taxa. This has important implications for the study of plankton biogeography and community assembly and for the interpretation of a growing archive of bioinformatic information (22). In particular, to what extent might local community assembly in any one part of the ocean be constrained by its isolation from other ocean regions—either by limited dispersal or selective constraints? In other words, is “everything really everywhere” as Bass-Becking (4) suggests, or is a species’ global distribution fundamentally limited?

With physical rates of dispersal in the model well constrained (13), the balance between selection, dispersal, and adaptation as subpopulations are transported along environmental gradients appears to have a pronounced effect on the global biogeography of microscopic plankton (Fig. 4). In the neutral case, we find that abundant populations are rapidly distributed throughout the global ocean with gradual changes in community structure across distance. Enabling temperature-based selection places strong constraints on global dispersal (23), with distinct locally adapted communities emerging in environmentally dissimilar regions of the same ocean basins (Fig. 4 E and F). At the same time, very different communities can emerge in otherwise environmentally similar regions, especially within different ocean basins at lower latitudes, for which all connecting pathways must pass through the polar oceans where warm-adapted types are rapidly attenuated. The ability to sustain both within-basin and across-basin community differences is diminished with increasing rates of phenotypic adaptation, although the latter appears more robust over the $\le$100-year timescales examined here.

Faster rates of adaptation allow populations to adjust their traits as they are dispersed across environmental gradients, thus achieving global distributions much wider than their original habitat. Very little is known about rates of trait diffusion in natural populations, and empirical estimates of this are needed to constrain models of adaptation for microscopic plankton. However, given the rapidity with which phytoplankton adapt to environmental shift in laboratory experiments (24–26), very high rates of trait diffusion are not implausible.

Nonetheless, even with very rapid rates of adaptation, dispersing model populations remain extremely rare in regions that are far from their original seed locations. This is consistent with rank-abundance distributions characterized by a long tail of rare species in marine microbial communities (27), with community structure maintained as the homogenizing effects of ocean mixing are counterbalanced by local selection. Even when immigrant populations can adapt to local conditions, the necessity to compete with similarly adapted but much more abundant residents means that the incoming populations remain scarce.

We have shown that a number of factors influence connectivity, including subsurface circulation, selection, and rate of adaptation. We note that while we demonstrate temperature-based selection is likely to constrain dispersal, we have only considered one of many factors that are known to affect plankton fitness. Our model is highly simplified and includes just a single plankton group whose distribution is in reality set by a complex array of biotic and abiotic factors. For example, with the selection coefficient implemented as a simple function of temperature, we ignore the potential interaction of multiple complementary or contradictory selective pressures within the complex microbial community. Furthermore, we expect that the need to simultaneously adapt multiple traits along environmental gradients would likely decrease the likelihood of effective adaptation, further increasing selective constraints on dispersal. Global dispersal would likely also be more difficult among larger and more sparsely distributed plankton populations, for which regions of low abundance will act as population bottlenecks. On the other hand, we have also neglected a number of factors that may serve to increase connectivity, with the existence of dormant stages (with low growth and mortality) likely to play a key role for some major groups, such as diatoms.

Ultimately, the degree to which the dispersing populations are selected against in nonoptimal environments, and the degree to which they are able to adapt, will determine the ubiquity, or otherwise, of marine microbial species. We have shown that geographic proximity can be a strong correlate of microbial community structure even in an ecologically neutral model (6). However, the existence of distinct community clusters both within and across ocean basins (Fig. 1) is perhaps indicative of a system where everything is not everywhere because the environment selects. Correctly accounting for selection, speciation, and limited dispersal therefore appears critical to understanding community structure and biogeography in the ocean. Alongside global metagenomic surveys, our results suggest that when developing models of marine microbial biogeography and ecology, we need to go beyond the assumption that everything is everywhere and to consider the selective limitations to dispersal and the adaptive means by which these are overcome.

Materials and Methods

The Evolutionary Plankton Metacommunity Dynamics model considers the global distribution of an arbitrary number of planktonic subpopulations distributed across a 2D (latitude and longitude) ocean grid. The probability of survival for each subpopulation in each generation is a function of its relative abundance and (optionally) its thermal tolerance to the local environmental temperature (14). Plankton cells are circulated in physical space according to a realistic ocean circulation model (13, 28).

Passive Dispersal by the Ocean Circulation.

Plankton cells are transported between grid boxes using a $\left[J\times J\right]$ oceanic “transport matrix” $\mathbf{A}$ that describes the transport of $K$ populations of neutrally buoyant cells between $J$ points in the ocean grid (29). This transport can be written as

$${\mathbf{X}}_{t+1}=\mathbf{A}{\mathbf{X}}_t.$$ [1]

Here, ${\mathbf{X}}_t$ is the $\left[J\times K\right]$ matrix of population abundances in each grid box of the ocean model. Each element of the transport matrix $\mathbf{A}$ describes the transport of cells between source boxes (columns) and recipient boxes (rows). The transport matrix represents the annual mean transport during a single year of the “Estimating the Circulation and Climate of the Ocean” Version 4 ocean model (13, 28). It represents physical transport attributable to advection, diffusion, and parameterized subgrid-scale processes in the ocean model with 6-hour resolution. Results in the text use annual average circulation, temperature, and carrying capacities. We also performed simulations using monthly resolved temperatures and carrying capacities, finding that our results were not overly sensitive to the change (Fig. 2). We note that this may not be the case for plankton groups with more pronounced seasonal cycles, such as diatoms.

In the surface transport case, Eq. 1 does not conserve mass at the local scale because the surface flow field is divergent (SI Appendix, Fig. S3A). The associated imbalances are generally small ($\pm <5\%$) (SI Appendix, Fig. S3B) and are overcome as the local population is restored to the local carrying capacity by positive or negative net growth (as described in the next section). Transport in the depth-integrated cases is generally mass conservative (with the exception of very isolated regions of deep convection in the Irminger and Ross Seas).

Stochastic Demography.

We used a stochastic population model to estimate the global abundance of 94 ecologically neutral subpopulations ($i$) at the 60,646 surface grid points ($j$) defining the global ocean. Each subpopulation was initialized with population abundance, $X_{i,j}$, equal to the local carrying capacity, $N_j$, at 94 unique seed locations, distributed approximately evenly around the surface ocean. In addition to the seed populations, we included one additional tracer representing a globally resident species, with a local population abundance of $X_{i,j}=0$ at all seed locations and $X_{i,j}=N_j$ throughout the rest of the surface grid. The total number of individuals $X_{j,\mathrm{t}\mathrm{o}\mathrm{t}}$ of all subpopulations at any location, $j$, is equal to the carrying capacity, $N_j$.

Under the assumption that all species have equal fitness (and from now on ignoring subscripts), the number of individuals $X$ in each subpopulation surviving at each generation is drawn randomly from a probability distribution representative of the local population (after oceanic transport and mutation) with probability $p$ equal to the local population frequency ($x=X{N}^{-1}$). Under these assumptions, the expected population size in each generation is given by the multinomial distribution

$$X\sim \mathcal{M}\left(N,p\right).$$ [2]

For large values of $N$ considered here, Eq. 2 is well approximated by a normal distribution when $X\gtrsim 100$ (i.e., $p\gtrsim 1\times 10^{-20}$). We therefore adopt the (computationally efficient) normal distribution in all simulations:

$$X\approx \mathcal{N}\left(Np,\sqrt{Np\left(1-p\right)}\right).$$ [3]

This will not be the case as subpopulations approach extinction (or more generally, fixation), but we expect this error to be small in comparison with cell transport (Eq. 1). In cases where random draws from the normal distribution yield negative abundances, these are replaced with zeros.

Selection.

Selection can be further incorporated through the selection vector, $\mathbf{s}$, that defines the relative fitness of each population in $\mathbf{X}$. With a local water temperature of $T$, a plankton population with thermal optimum $T_{opt}$ and thermal niche breadth $w$ will have a selection coefficient of

$$s=\exp \left[-{\left(\frac{T_{env}-T_{opt}}{w}\right)}^2\right].$$ [4]

This is incorporated into the probability of selection such that the sum of all probabilities remains equal to one. The probability of selection for population $i$ at each location is thus

$$p_i=x_i{s}_i{\left[\sum _{k=1}^K{x}_k{s}_k\right]}^{-1},$$ [5]

where $K$ is the total number of populations.

In the nonadaptive simulations, each seed population is assigned a thermal optimum equivalent to the annual mean water temperature at its seed location. At the same time, the global resident population is divided into 77 subpopulations, each with thermal optima matching the average temperature at its initial location. All populations have a thermal niche breadth, $w$, of $\mathrm{6}°$C.

Adaptation.

Adaptive evolution is enabled by further dividing each subpopulation into 77 genotypes, each corresponding to a different thermal optimum. The genotypes are linearly spaced at 0.$\mathrm{5}°$C intervals from –2° C to $\mathrm{36}°$C, with only the locally optimum genotype initialized with nonzero biomass at the beginning of each simulation. At each time step, a small fraction of successfully reproducing individuals is diverted to adjacent genotypes in the same subpopulation with higher or lower thermal optima. In practice, this is achieved after each reproductive cycle by multiplying the population matrix ($\mathbf{X}$) by the $K\times K$ trait-diffusion matrix $\mathbf{M}$ (19, 20):

$${\mathbf{X}}_{t+1}=\mathbf{M}{\mathbf{X}}_t.$$ [6]

The trait-diffusion matrix itself is defined by the parameterized trait-diffusion rate (here, 1 or 10%). This is the fraction of daughter cells in each population that are diverted to the neighboring phenotypic class in each generation (19, 20).

Simulations.

In each case, the model was integrated for 100 years. The transport matrix was applied every 6 hours, with selection and adaptation applied every 24 hours.

Data Availability

Model code data have been deposited in GitHub (https://github.com/geebes/EPMD).