Anomalous nanoparticle surface diffusion in LCTEM is revealed by deep learning-assisted analysis

Significance

Liquid cell transmission electron microscopy (LCTEM) is an emerging technique, which enables nanoscale visualization and tracking of single nanoparticles near interfaces with unprecedented spatial resolution. Here, we studied the diffusion of nanoparticles in LCTEM experiments using techniques powered by deep neural networks and statistical tests. We observed two underlying regimes of diffusive behavior which are governed by the interaction of the electron beam, the nanoparticle, the nearby substrate, and the liquid environment. This understanding forms the foundation to use LCTEM for single-nanoparticle tracking for a broad range of nanoparticles, interfaces, and liquids.

Abstract

The motion of nanoparticles near surfaces is of fundamental importance in physics, biology, and chemistry. Liquid cell transmission electron microscopy (LCTEM) is a promising technique for studying motion of nanoparticles with high spatial resolution. Yet, the lack of understanding of how the electron beam of the microscope affects the particle motion has held back advancement in using LCTEM for in situ single nanoparticle and macromolecule tracking at interfaces. Here, we experimentally studied the motion of a model system of gold nanoparticles dispersed in water and moving adjacent to the silicon nitride membrane of a commercial LC in a broad range of electron beam dose rates. We find that the nanoparticles exhibit anomalous diffusive behavior modulated by the electron beam dose rate. We characterized the anomalous diffusion of nanoparticles in LCTEM using a convolutional deep neural-network model and canonical statistical tests. The results demonstrate that the nanoparticle motion is governed by fractional Brownian motion at low dose rates, resembling diffusion in a viscoelastic medium, and continuous-time random walk at high dose rates, resembling diffusion on an energy landscape with pinning sites. Both behaviors can be explained by the presence of silanol molecular species on the surface of the silicon nitride membrane and the ionic species in solution formed by radiolysis of water in presence of the electron beam.

Understanding the motion of nanoparticles in boundary layers is of fundamental importance in scientific fields such as biophysics and colloidal self-assembly, and of practical importance in technological applications such as drug delivery and additive manufacturing. The physics behind the motion of nanoparticles is particularly challenging to understand due to the multitude of effects including particle–-particle interactions, particle–surface interactions, and changes in the rheological properties in boundary layers close to a liquid–solid interface.

The common technique to study the motion of particles has been optical microscopy, which has limitations in terms of spatial resolution. The advent of in situ liquid cell transmission electron microscopy (LCTEM) has now made it possible to visualize the motion of nanoparticles near a surface with an unprecedented spatial resolution at the nanometer length scale (1–3). However, the electron beam of a transmission electron microscope (TEM), which is the key acquisition tool to enable nanoscale visualization, can significantly influence both interactions and dynamics of nanoparticles (4–6). Previous literature has reported that the motion of nanoparticles near the surface of an LC and in the presence of the electron beam is subdiffusive (i.e., non-Brownian, or “anomalous”) (7–16). Such subdiffusive motion suggests that the nanoparticle motion is significantly influenced by interactions with the nearby substrate or interface, but what precisely is the nature of these interactions and the forces that create them? Are they stable or fluctuating? Do they arise because of the electron beam or are they native to the system? How do the changes in rheology within a few nanometers of the interface figure into the picture? The nature of the observed anomalies are still very much under debate as the new technique of LCTEM continues to be developed (7–12, 14–16).

Two canonical processes that describe anomalous motion are continuous-time random walk (CTRW) and fractional Brownian motion (FBM) (17–20). In the context of particle diffusion, each of these types of subdiffusive motions implies a distinct physical picture of the environment. CTRW indicates a random energy landscape of potential wells, where the time a particle spends in any well diverges when averaged over all well depths. FBM, on the other hand, indicates a viscoelastic environment such as those found in crowded fluids (21–24). The goal of this work is to identify the type of anomalous motion of nanoparticles near the surface in LCTEM, elucidate the nanoscopic physical features in the system that give rise to this motion, and understand how the electron beam can influence them.

A key challenge in studying the motion of nanoparticles under the effect of the electron beam is that one needs to resort to a limited number of short trajectories from a single in situ LCTEM experiment. This is because achieving high spatial resolution requires a relatively small field of view, which limits the number of nanoparticles accessible (experiments are done in dilute solutions to avoid interactions between nanoparticles). Moreover, state-of-the-art cameras on TEMs are limited by lower bounds on time resolution (hundreds of frames per second) and upper bounds on measurement time (minutes-long trajectories) (25). This limitation creates a challenge for canonical methods used to characterize diffusive particle dynamics such as the mean-squared displacement (MSD) analysis. These methods often rely on features of the trajectory that converge upon averaging over very long single-particle trajectories (for systems obeying ergodicity) or hundreds of medium-length trajectories collected under the same experimental conditions (20, 26, 27). Here, we show that physics-informed artificial intelligence can be used as a complementary tool for LCTEM to extract hidden features that exist in short trajectories of single nanoparticles in LCTEM in order to elucidate the type of anomalous diffusion.

In this study, we collected a large dataset from a model system of gold nanoparticles dispersed in water and diffusing near a silicon nitride (SiN_x) membrane of a commercial LC irradiated by a broad range of electron beam dose rates. Inspired by the recent advances in using machine-learning tools to study the diffusion of single microparticles in biological media (26–29), we developed a convolutional deep neural-network model, dubbed MotionNet (MoNet), which solves an inverse problem of determining the underlying diffusion mechanism behind the anomalous motion of nanoparticles in LCTEM. The architecture of the neural network employed in MoNet is designed based on classical tests in statistics (30) and is trained on thousands of simulated short trajectories from three classes of diffusion, i.e., Brownian, FBM, and CTRW. Guided by MoNet, our analysis reveals that at low dose rates the anomalous diffusive motion of nanoparticles in LCTEM is governed by viscoelasticity-dominated FBM, while at high dose rates the motion is governed by a pinning-site-mediated CTRW process (24). The prediction results were benchmarked against the statistical $p$-variation test (30) to confirm the behavior in low and high dose-rate limits.

The dose-rate-dependent transition can be explained by the existence of silanol molecular groups on the surface of the SiN_x membrane, which act as pinning sites and exhibit a broad distribution of restoring forces (15, 31). At low dose rates, the binding strength of these pinning sites is high compared to the thermal energy and their effective restoring force acts similar to the effect of a viscoelastic environment. This results in nanoparticle motion confined to the local vicinity of a pinning site. Upon increasing the dose rate and thus passivating the charges on the pinning sites, the binding strength decreases, making nanoparticles more mobile, which allows them to diffuse over the SiN_x membrane only making intermittent stops on randomly distributed pinning sites. This understanding provides us with important insight into the mechanism of nanoparticle motion near a substrate in LCTEM and opens up the path to use in situ LCTEM as a technique for studying motions of nanoparticles in complex systems at the nanoscale. Furthermore, we show that neural networks can extract features to classify the underlying diffusive behavior of the system and determine the extent of anomaly, particularly when canonical statistical methods require extreme amounts of data and may not be able to classify the behavior of the system due to experimental limitations.

Results and Discussion

Anomalous Diffusion of Gold Nanorods.

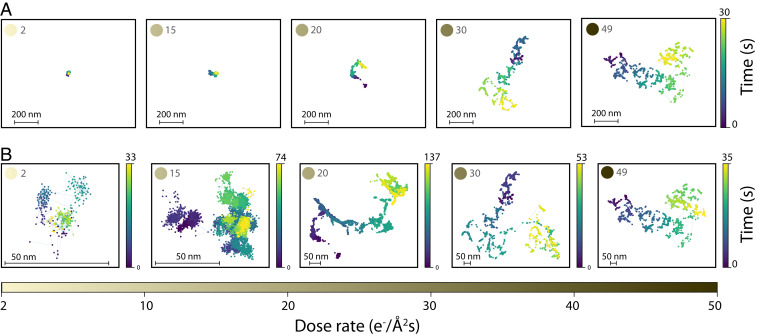
To study the effect of electron beam dose rate on the motion of nanoparticles near a surface, we chose a tunable model system of gold nanorods (AuNRs, 60 nm long) dispersed in water and probed their dynamics near the SiN_x membrane of a commercial TEM’s liquid cell (see Materials and Methods for details of synthesis). We collected a dataset comprising 459 subtrajectories that are 300 frames long, from 40 AuNRs for electron beam dose rates ranging from 2 to 49 e⁻/Ųs (see SI Appendix, Fig. S1 for all trajectories collected). Fig. 1A shows the first 30 s of five representative nanoparticles. Plotted at the same scale, these trajectories indicate that the effective diffusivity of AuNRs increases with increasing dose rate of the electron beam.

Fig. 1.

Representative trajectories of five gold nanorods as a function of dose rate varying between 2 and 49 e⁻/Ųs (A) in their first 30 s and scaled to the same size showing that the diffusivity increases upon increasing the dose rate; (B) diffusing for a longer time and magnified to show the change in the diffusive behavior upon increasing the dose rate.

Fig. 1B shows the same trajectories as Fig. 1A in their entirety, magnified to reveal details of the dynamics. In addition to the increase in effective diffusivity, a qualitative change in the dynamics is observed as the dose rate is increased from 2 to 49 e⁻/Ųs. At low dose rates, AuNR dynamics are dominated by motion confined to the vicinity of a local point. This motion is punctuated by infrequent, relatively long-distance jumps. At high dose rates, long-distance jumps between short periods of confinement become the dominant behavior at observation timescales.

To identify the underlying diffusive behavior and to understand how the electron beam changes the local environment and the local interactions, we first calculated the MSD. In the framework of anomalous diffusion, the MSD is described by the power law (20):

$$<\delta x^2\left(t\right)>\sim D_{\alpha }{t}^{\alpha }.$$ [1]

Here, brackets denote an ensemble average, and accordingly we refer to this as the ensemble-averaged or e-MSD. If $\alpha =1$ the process is characterized by Brownian motion, and if $\alpha <1$ or $\alpha >1$ the process is subdiffusive or superdiffusive, respectively. The MSD may also be computed by window averaging over a single trajectory, which we refer to as a time-averaged or t-MSD, and is defined by

$$\overline{\delta x^2\left(\mathrm{\Delta }\right)}=\frac{1}{T-\mathrm{\Delta }}{\displaystyle \underset{0}{\overset{T-\mathrm{\Delta }}{\int }}\text{d}t\hspace{1em}{\left(x\left(t\right)-x\left(t+\mathrm{\Delta }\right)\right)}^2}.$$ [2]

Here, $T$ is the total measurement time, $\mathrm{\Delta }$ is the time-delay window, and $\overline{(·)}$ indicates an average over time. For ergodic processes, the e-MSD and t-MSD are equal in the long time limit as $T\to \infty$. In case of nonergodic subdiffusive processes, the e-MSD contains more information about the underlying anomaly mechanism; however, it is not practically accessible in many experimental systems, including LCTEM as it is available today. The t-MSD measurements as a function of $\mathrm{\Delta }$ for all trajectories are presented in SI Appendix, Fig. S2. We also measured the related time-averaged diffusion constant $D_{\alpha }=\overline{\delta x^2\left(\mathrm{\Delta }\right)}/{\mathrm{\Delta }}^{\alpha }$, using Eq. 2, which varies between 10 and 10⁴ nm²/s for values of $\mathrm{\Delta }\le 0.25\hspace{0.17em}\mathrm{s}$ and for all dose rates studied across trajectories of 40 nanorods in 5 experiments; SI Appendix, Fig. S3. This shows that the motion of AuNRs near the surface is orders of magnitude slower than what is theoretically estimated for a Brownian nanoparticle in bulk water outside of TEM based on the Stokes–Einstein relation $D=k_{B}T/\left(6\pi \eta L\right)\approx 4\times {10}^6\hspace{0.17em}\mathrm{n}{\mathrm{m}}^2/\mathrm{s}$, with $\eta$ the viscosity of the medium and $L$ the characteristic size of the diffusing nanoparticle. The slow motion of AuNRs observed here is consistent with previous reports on the suppressed diffusive motion of nanoparticles in LCTEM experiments (8, 9, 11, 12, 14, 15, 32, 33). Furthermore, the time-averaged diffusion constant $D_{\alpha }$ increases as the dose rate is increased (SI Appendix, Figs. S2 and S3), consistent with the observations from Fig. 1A. However, it is not possible to identify the type of diffusion as well as whether it is anomalous or not based solely on the t-MSD curves. This can be explained by a closer look at two common anomalous diffusion models, subdiffusive CTRW and subdiffusive FBM, and their corresponding MSDs.

Models of Anomalous Diffusion.

Diffusion processes in which particles move with stop-and-go motion on an energy landscape with heterogeneous pinning sites are well described as a CTRW (20). In a CTRW process, a particle moves by making random jumps in space and time (see SI Appendix, section 1 for details). The particle remains immobile for a random “waiting time” $\tau$, drawn from distribution $\psi \left(\tau \right)$, before jumping in the distance and direction $\mathrm{\Delta }\mathit{x}$, drawn from the distribution $\lambda \left(\mathrm{\Delta }\mathit{x}\right)$ (23). If $\psi \left(\tau \right)$ is heavy-tailed, i.e., the asymptotic behavior at large $\tau$ decays as $\psi \left(\tau \right)\sim 1/{\tau }^{1+\alpha }$ with $0<\alpha <1$, the mean waiting time $\tau$ diverges $\left(\langle \tau \rangle \to \infty \right)$ and the resulting process is subdiffusive (22). The diverging $\langle \tau \rangle$ also indicates that ergodicity is broken; no matter how long the measurement time $T$ is, the t-MSD and the ensemble-averaged t-MSD (average of t-MSDs over an ensemble of particles, or et-MSD) will not be the same (22). It can be shown that the et-MSD for a CTRW process can be written as (see SI Appendix, section 1 for mathematical derivation) (34, 35)

$$⟨\overline{\delta x^2\left(\mathrm{\Delta }\right)}⟩\sim D_{\alpha }\frac{\mathrm{\Delta }}{T^{1-\alpha }}.$$ [3]

Eq. 3 shows that for a CTRW process, the et-MSD is a linear function of time delay, $\mathrm{\Delta }$. This property of the subdiffusive CTRW process makes it extremely difficult to identify and to estimate its inherent $\alpha$ value, when only a limited number of short trajectories from an experiment is accessible since no anomaly can be detected by measuring the t-MSD.

Another canonical model of subdiffusion is FBM (18). Subdiffusive FBM can be qualitatively described as a random process in which the direction of each step is anticorrelated with the previous step, resulting in the next step having a higher probability than random to be in the opposite direction (31). This correlation of positions at two different points in time $t_1$ and $t_2$ along the trajectory can be expressed as

$$\langle x\left(t_1\right)x\left(t_2\right)\rangle =D_{\alpha }\left({\left|t_1\right|}^{\alpha }+{\left|t_2\right|}^{\alpha }-{\left|t_1-t_2\right|}^{\alpha }\right),$$ [4]

where as before, $\alpha <1$ corresponds to subdiffusion. Unlike the CTRW model, an FBM process is ergodic, and thus t-MSD and its ensemble average, i.e., et-MSD, are the same and follow $⟨\overline{\delta x^2\left(\mathrm{\Delta }\right)}⟩=D_{\alpha }{\mathrm{\Delta }}^{\alpha }$ (see SI Appendix, section 1 for mathematical derivation of an FBM process).

Deep Learning Analysis.

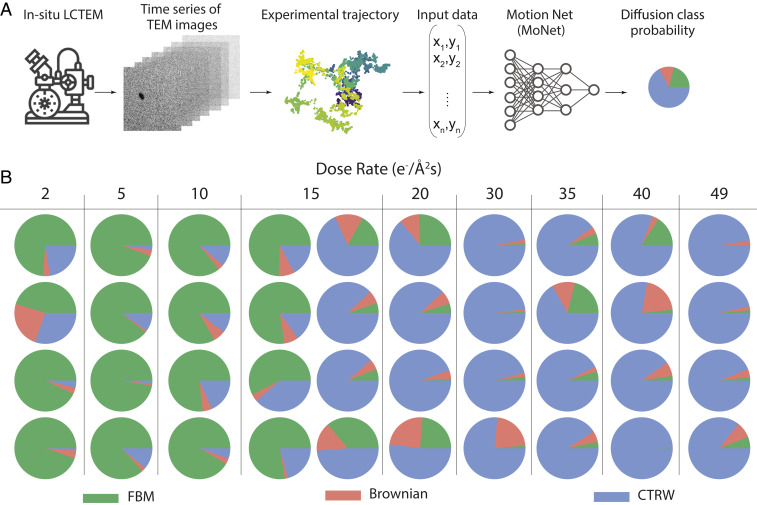
To identify the underlying anomalous diffusion process for a limited set of short trajectories in an LCTEM experiment, we developed a convolutional neural network model which we have named MoNet (shown in Fig. 2A). We trained MoNet on $\mathrm{10,000}$ simulated trajectories from three classes of diffusion: Brownian, subdiffusive FBM, and subdiffusive CTRW. Each simulated trajectory was $300$ frames in length: short enough to cover the shortest experimental trajectories collected and long enough to achieve more than 90% validation accuracy (SI Appendix, section 4 and Fig. S6). For consistency, the model was then applied to $300$-frame intervals of all nanoparticle trajectories. The final results are reported as the predicted probability for each diffusion class, averaged over the entire length of the trajectory (see SI Appendix, Fig. S6 for validation accuracy on an independent set of test data). As shown in Fig. 2A, MoNet receives input data in the form of a matrix comprising the $x$ and $y$ coordinate of the locations of the nanoparticle throughout the trajectory and outputs the probability of the predicted diffusion class, i.e., FBM, CTRW, and Brownian. The architecture of MoNet is inspired by previous literature for temporal sequence-type data such as particle trajectories (27, 36). See Materials and Methods and SI Appendix, section 4 for details of the architecture of MoNet.

Fig. 2.

(A) Deep neural-network pipeline for anomalous diffusion classification on in situ LCTEM data using MoNet. (B) Neural-network analysis results for all trajectories studied as a function of dose rate (increasing from left to right across the table). Pie charts show the diffusion class probability where at low dose rates, there is a higher probability associated with an FBM (green) and at high dose rates there is a higher probability associated with a CTRW (blue).

Fig. 2B presents the predicted probability of the diffusion class for all 40 nanoparticles estimated on 459 subtrajectories that are 300 frames long as a function of dose rate, increasing from left to right across the table; see SI Appendix, Fig. S7 for the probability values associated with each class. Interestingly, there is a cross-over from FBM to CTRW as the electron beam dose rate is increased, consistent with the qualitative picture of Fig. 1B. The cross-over occurs around the dose rate of 15 e⁻/Ųs, where eight trajectories have been collected. We performed a two-sided t test to reject the null hypothesis that the probability of FBM and CTRW classes are equal at low and high dose rates (SI Appendix, section 3 and Fig. S8). The result of our analysis show that for dose rates smaller than or equal to $10\hspace{0.17em}{\mathrm{e}}^{-}/{\mathrm{\AA }}^2\hspace{0.17em}\mathrm{s}$, the probability of FBM class is significantly higher than CTRW $\left(p<5\times {10}^{-7}\right)$, for dose rates larger than or equal to $20\hspace{0.17em}{\mathrm{e}}^{-}/{\mathrm{\AA }}^2\hspace{0.17em}\mathrm{s}$, the probability of CTRW class is significantly higher than FBM $\left(p<3\times {10}^{-21}\right)$, and for the dose rate of $15\hspace{0.17em}{\mathrm{e}}^{-}/{\mathrm{\AA }}^2\hspace{0.17em}\mathrm{s}$, we cannot reject the null hypothesis that the probability of FBM and CTRW are equal $\left(p=0.86\right)$. This clearly shows that the cross-over from a predominantly FBM behavior to a predominantly CTRW behavior happens at the dose rate of $15\hspace{0.17em}{\mathrm{e}}^{-}/{\mathrm{\AA }}^2\hspace{0.17em}\mathrm{s}$.

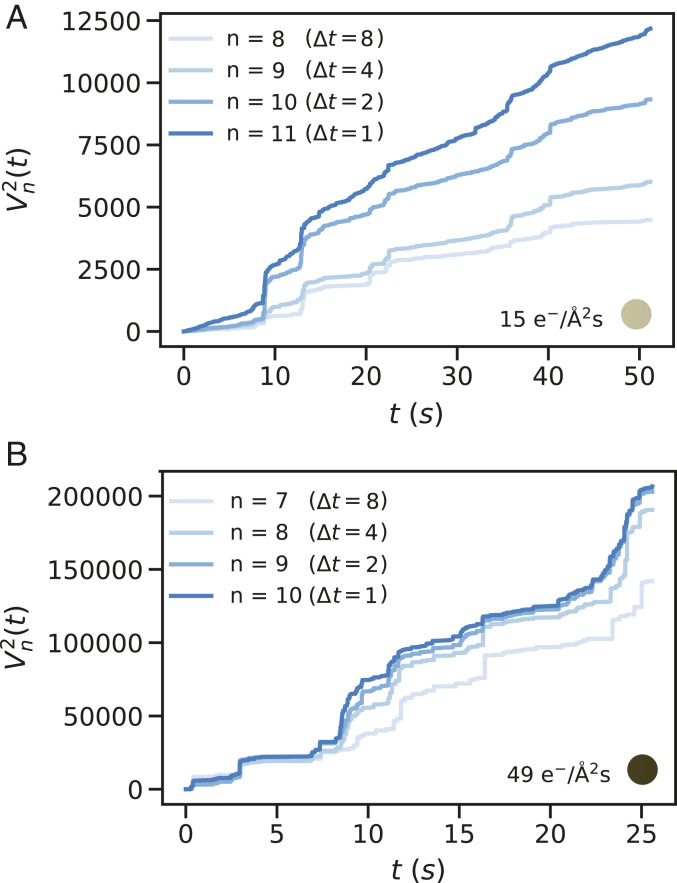
To verify the results we compared MoNet against a statistical method, known as the $p$-variation test, $V_n^p$ (see Materials and Methods for definition). $p$ variation has been successful in distinguishing FBM from CTRW for medium-length trajectories (30). Here, we have analyzed the quadratic variation (p variation for $p=2$), which measures the sum of squares of increments of a trajectory of length $T=2^{N_{\text{max}}}$, divided into $2^n$ segments. For an FBM process, the quadratic variation must diverge as $n\to \infty$ (i.e., the size of time increment $\mathrm{\Delta }t\to 1$ frame), while for a CTRW process, the quadratic variation must stabilize with increasing $n$ (30, 37). Comparison of our predictions with the quadratic variation results presented in SI Appendix, Fig. S9 confirms that there is indeed a cross-over from FBM to CTRW with increasing the dose rate. Fig. 3 shows the quadratic variation results for two example trajectories of Fig. 1B at dose rates 15 and 49 e⁻/Ųs. The unbounded increase in the slope of the quadratic variation vs. measurement time curve as $n\to N_{\text{max}}$(i.e., $\mathrm{\Delta }t\to 1$ frame) confirms that at dose rate 15 e⁻/Ųs, the trajectory is predominantly characterized by an FBM behavior. However, for a higher dose rate of 49 e⁻/Ųs, the quadratic variation curve does not show any specific dependence as $n\to N_{\text{max}}$, suggesting that the anomaly does not stem from an FBM process.

Fig. 3.

Quadratic-variation test results vs. measurement time, $t$, for trajectories collected at dose rates (A) 15 and (B) 49 e⁻/Ųs selected from Fig. 1B. (A) The slope of the quadratic-variation curve increases as $n$ increases (i.e., size of time increments $\mathrm{\Delta }t$ decreases to one frame) indicative of a FBM process; (B) the slope of the quadratic-variation curve converges as $n$ increases, indicative of a CTRW behavior at high dose rates.

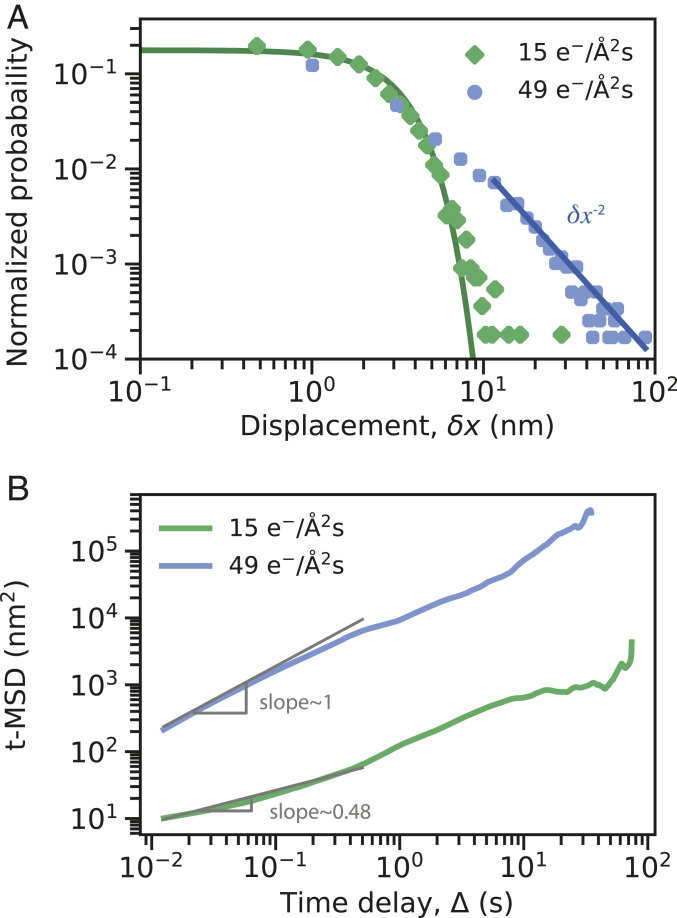
Another characteristic of FBM and CTRW processes in terms of displacement, $\delta x$, is their probability distribution of displacements $P\left(\delta x\right)$ (20, 31). Comparison of the distribution of displacements collected over time delays of 0.0125 s in Fig. 4A for two example trajectories at dose rates 15 and 49 e⁻/Ųs (same trajectories as Fig. 3) also confirms the presence of an FBM process at low dose rates with a Gaussian distribution and a CTRW process at high dose rates with a power-law tailed distribution. The power-law exponent of this tail is estimated to be about $-2.0$ (Fig. 4A). As shown in SI Appendix, Fig. S10, this power-law value of $-2.0$ is consistent for all high dose-rate trajectories studied here.

Fig. 4.

(A) Probability distribution of the absolute value of displacement for trajectories collected at the dose rates 15 and 49 e⁻/Ųs for time intervals of 0.0125 s, compared to a Gaussian fit (solid green line) and a power-law tail fit with power-law exponent of $-2$ (solid blue line). (B) Time-averaged MSD vs. time delay calculated for the same trajectories of A. Solid gray lines show the fit to the MSD curves at short time delays with the slope of 0.48 for the low dose rate and slope of 1 for the high dose rate.

The power-law decay of the probability distribution $P\left(\delta x\right)$ for large values of displacement, $\delta x$, at high dose rates does not necessarily mean that the underlying CTRW process is subdiffusive (38). However, it suggests that there is a broad distribution of binding sites on the surface of the SiN_x membrane. It is known that for harmonic energy potentials with equal binding stiffness $k$, the resulting probability distribution of displacements must follow a Gaussian form, $P\left(\delta x\right)=\text{exp}\left(-k{\left(\delta x\right)}^2/k_{B}T\right)$ (31, 39). Hence, the non-Gaussian and heavy-tailed probability distribution of displacements observed for all high dose-rate trajectories indicates that binding sites with various binding affinities exist over the surface of the SiN_x membrane, suggesting that an underlying CTRW process could be subdiffusive. To confirm that the CTRW process observed at high dose rates is subdiffusive, we used MoNet trained on 3,000 simulated CTRW trajectories with $\alpha$ values between 0.1 and 0.99, and predicted the $\alpha$ exponent for all trajectories collected (SI Appendix, Fig. S11). The results show that the underlying mechanism at high dose rates is subdiffusive with $\alpha$ exponents ranging from 0.7 to 0.8.

We also did a similar analysis using MoNet to predict $\alpha$ exponents of FBM processes [commonly known as the Hurst exponent $H=\alpha /2$ in the literature (40)]; SI Appendix, Fig. S11. The $\alpha$ exponent obtained from this analysis is very similar to the values of $\alpha$ extracted from t-MSD curves (SI Appendix, Fig. S11). Fig. 4B shows the t-MSD curves calculated for trajectories of dose rates 15 and 49 e⁻/Ųs with $\alpha$ exponents of 0.48 and 1, respectively. As shown in Eq. 3, the t-MSD curve of a CTRW process grows linearly in time delay $\mathrm{\Delta }$, consistent with our measurements shown in Fig. 4B. For subdiffusive FBM processes, the t-MSD curves grow sublinearly in time delay $\mathrm{\Delta }$. Therefore, the t-MSD curve can only provide us with a value of $\alpha$ at low dose rates, where the process is predominantly characterized by an FBM model and et-MSD measurements are further required to estimate the value of $\alpha$ for CTRW processes. Using MoNet predictions for the $\alpha$ exponent for both low and high dose-rate trajectories, we showed that at all dose rates studied the underlying diffusive process is subdiffusive.

Nanoscopic Interpretation.

The physical picture governing the different diffusive behavior at low and high electron beam dose rates may be explained by the molecular groups existing on the surface of the SiN_x membrane of the TEM liquid cell, which in turn are influenced by the electron beam. It has been previously reported that the surface of silicon nitride membrane hydrolyzes in water and forms negatively terminated silanol molecular species (41). There has been extensive studies on how changes in the local pH value can affect the charges of these molecular species and the electrostatic forces near the membrane (42–44). It has been shown that the SiN_x surface with these molecular groups remains net neutral at pH values of about 6, while it gets positively charged at lower and negatively charged at higher pH values. This problem has been revisited by more recent literature in the context of LCTEM studies which shows that the electron beam dose rate changes the local pH of the solution rather than charging the membrane itself (13, 15). These silanol groups formed on the surface of the membrane in contact with the aqueous solution are randomly distributed across the membrane and create pinning sites that can locally trap nanoparticles, which are positively charged with cetyltrimethylammonium chloride (CTAC) ligands. At low electron beam dose rates $\left(\le 15\hspace{0.17em}{\mathrm{e}}^{-}/{\mathrm{\AA }}^2\hspace{0.17em}\mathrm{s}\right)$, the thermal energy of AuNRs is smaller than the binding strength of these pinning sites resulting in particles being trapped for significant periods in the vicinity of a local pinning site, with membrane restoring forces and solvent interactions acting as a viscoelastic medium. This viscoelastic picture may be explained by the hydrogen bonding of the water molecules with the Si-O species on the surface of the SiN_x that may result in a gel-like viscoelastic water layer next to the membrane at low dose rates, leading to the FBM behavior at low dose rate. This is consistent with previous observations of formation of few nanometers thick viscoelastic interfacial water layer next to hydrophilic surfaces, where the hydrogen bonding of water molecules leads to 6–7 order of magnitude higher viscosity of the water next to silica surfaces (31, 45, 46). We note that a close inspection of the trajectories of Fig. 1B and SI Appendix, Fig. S1 shows that for some of our low dose-rate experiments, the immobility in pinning sites is punctuated by a few relatively long-distanced jumps. Yet, these jumps are smaller than 50 nm, which is smaller than the body length of the AuNRs studied $\left(\sim 60\hspace{0.17em}\hspace{0.17em}\mathrm{nm}\right)$ and could be explained as the head or tail of the same AuNR being trapped in the same pinning site.

Upon increasing the electron beam dose rate, the radiolysis in water occurs that lowers the local pH value of the solution near the membrane (47). Hence, the acid–base equilibrium shifts toward a more positively charged surface that partially passivates the Si-O groups on the surface of the membrane, reducing their binding strength. Therefore, at high dose rates, AuNRs can occasionally detrap and move with long-distance jumps until they get trapped in another pinning site associated with a waiting time $\tau$ drawn from a heavy tailed distribution function $\psi \left(\tau \right)$. This hypothesis is also consistent with previous observations on higher mobility of nanoparticles in acidic environments in LCTEM (13), as well as diffusion of polymeric chains over silica surfaces with protonated silanol groups in single-molecule fluorescence imaging (48).

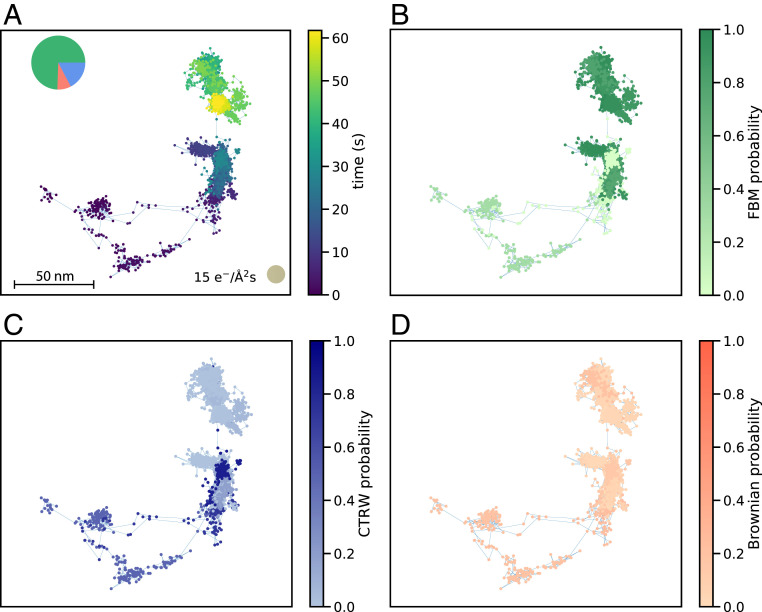
While this interpretation could explain this set of observations, we note that alternative scenarios may exist such as coexistence of both FBM and CTRW behavior. A close look at the predictions of Fig. 2B shows that for certain low dose rates (see 15 e⁻/Ųs) classified as FBM by MoNet, there is a nonnegligible probability associated with the CTRW class. By tracking the predicted probability of each diffusion class along the entire length of the trajectory for each segment ($300$-frame-long minitrajectories), we can see that segments that include long-distance jumps of $>50\hspace{0.17em}\mathrm{nm}$ are more likely to be classified as CTRW (Fig. 5 and SI Appendix, section 6 and Fig. S13).

Fig. 5.

(A) An example trajectory collected at the dose rate of 15 e⁻/Ųs that includes a long jump between trapping events. MoNet prediction for probability of (B) FBM, (C) CTRW, and (D) Brownian classes across the trajectory.

The presence of these jumps, even at low dose rates, also shows up in the t-MSD curves. The t-MSD curve for the dose rate of 15 e⁻/Ųs presented in Fig. 4B has an $\alpha$ exponent of 0.48 at short time delays, while at long time delays the exponent increases to 1. This is in contrast to high dose rates, where throughout the t-MSD curve, the $\alpha$ exponent remains constant at a value of 1. The change in the $\alpha$ exponent as well as the nonnegligible probability associated with the CTRW class at dose rates of 15 e⁻/Ųs suggests that both FBM and CTRW behavior could potentially coexist at this dose rate but at different timescales. Furthermore, the scatter in t-MSD curves for all dose rates in SI Appendix, Fig. S2 shows that that ergodicity might be broken even at low dose rates where the diffusion class is predominantly characterized by FBM, which is by definition an ergodic process. This is reminiscent of the subordinated diffusion processes reported in biological systems as well as single-molecule tracking experiments in water (31, 49–51). This type of subordinated diffusion is complex to capture through canonical methods and indeed requires data spanning multiple timescales both on short and long time delays. Therefore, while the current data are insufficient to support or nullify this hypothesis (especially at high dose rates), our analysis suggests the possibility of such a scenario. Regardless, the presence of predominantly FBM behavior at low dose rates and CTRW at high dose rates supports the interpretation that the diffusive motion at low dose rates is mostly influenced by the local viscoelasticity of the fluid next to the surface and at high dose rates the motion is governed by the heterogeneous pinning sites in the timescales studied $\left(\mathrm{\Delta }=0.01\hspace{0.17em}\hspace{0.17em}\mathrm{to}\hspace{0.17em}100\hspace{0.17em}\hspace{0.17em}\mathrm{s}\right)$. Therefore, the electron beam dose rate not only increases the diffusion coefficient, but also it fundamentally alters the fluid and the dominant diffusive behavior of nanoparticles near the membrane.

This understanding of how the electron beam can affect the local environment near the membrane, which in turn governs the diffusive motion of nanoparticles near the surface, can be used in applications of nanoparticles in LCTEM as nanoscale probes to study the local material properties of the fluid near the surface. The analysis presented here can also be applied to study the undamped motion of nanoparticles in bulk in LCTEM (52, 53), to investigate the effect of the electron beam on the material properties of the bulk fluid. Furthermore, the change in the local material properties of the fluid next to the surface in presence of the electron beam may play a role in other LCTEM studies such as in situ growth of nanocrystals (54–56). The knowledge base developed here can be also extended to study the motion of nanoparticles in LCTEM near surfaces with various combinations of nanoparticles, fluids, and surfaces with high spatial resolution. Additionally, this work is one of the early demonstrations of how physics-informed artificial intelligence and machine learning can help nanoimaging in LCTEM through data analysis (57).

Materials and Methods

Chemicals and Materials.

Hexadecyltrimethylammonium bromide (CTAB, $>98.0\hspace{0.17em}\%$), CTAC ($>95.0\hspace{0.17em}\%$) and sodium oleate (NaOL, $>97.0\hspace{0.17em}\%$) were purchased from TCI America. Acetone $\left(99.5\hspace{0.17em}\%\right)$ was purchased from Fisher Scientific. Hydrogen tetrachloroaurate trihydrate (HAuCl₄·3H₂O, $\ge 99.9\hspace{0.17em}\%$), l-ascorbic acid (BioXtra, $\ge 99.0\hspace{0.17em}\%$), silver nitrate (AgNO₃, $\ge 99.0\hspace{0.17em}\%$), sodium borohydride (NaBH₄, $99.99\hspace{0.17em}\%$), and hydrochloric acid (36.5–38.0% wt. %) were obtained from Sigma-Aldrich. NaBH₄ powder was stored in an argon glovebox. HAuCl₄·3H₂O, l-ascorbic acid, and AgNO₃ were stored in a vacuum desiccator at room temperature. Deionized water (DI water, Millipore) was used for all aqueous solutions. All the glassware was thoroughly cleaned using freshly prepared aqua regia ($3:1$ volume ratio of HCl and HNO₃, respectively) followed by fully rinsing with copious amounts of DI water. All chemicals were of reagent grade and used without further purification.

LC Preparation.

Commercially available silicon nitride liquid cell top (EPT-52W-10) and bottom (EPB-52DNS) microchips (Protochips Inc.) with electron transparent membranes and a 150-nm static spacer, were cleaned by being immersed in a clean Petri dish filled with acetone to remove the protective resist coating and immediately transferred to a second Petri dish filled with high-purity ethanol. The microchips were then dried by blotting them on a filter paper to remove the excess ethanol. The microchips were fully dried by gently blowing nitrogen gas parallel to their surface. Following that they were plasma-treated for $3$ min to remove any residual organic material and to improve their surface hydrophilicity. The microchips were then assembled in a Poseidon 200 holder according to the Protochips Inc. protocols with $0.75\hspace{0.17em}\hspace{0.17em}\mathrm{\mu L}$ of the AuNR solution containing an extra 5 mM of CTAC ligands.

TEM Imaging.

In situ experiments were performed on an FEI Tecnai T20 S-TWIN TEM operating at 200 KV with a LaB6 filament. Time series of images were collected using a Gatan Rio 16 IS camera in Digital Micrograph format at nominal magnifications of $25.3\hspace{0.17em}\mathrm{kx}$ and $38.1\hspace{0.17em}\mathrm{kx}$ with various exposures of $0.1$, $0.05$, $0.0125$, $0.01$, and $0.00625$ s corresponding to frame rates of $10$, $20$, $80$, $100$, and $160$ frames per second with $\mathrm{4,096}\times \mathrm{4,096}$, $\mathrm{2,048}\times \mathrm{2,048}$, and $\mathrm{1,024}\times \mathrm{1,024}$ pixels by pixels readout, resulting in $0.355208$, $0.710415$, and $1.42083\hspace{0.17em}\mathrm{nm}/\mathrm{pixel}$ resolutions, respectively. Prior to imaging, the electron beam dose rate was calibrated at each magnification using a custom digital micrograph script as described in the previous literature by converting counts to electrons with a conversion value of $124$ (58). The range of dose rates accessible after calibration at this magnification spans from $2$ to $49\hspace{0.17em}{\mathrm{e}}^{-}/{\mathrm{\AA }}^2\mathrm{s}$. Data were collected in three sets of experiments using the same dose rates to assure the consistency of the outcomes. Furthermore, dose rates were increased and decreased to verify the reversibility of the process. Time series of high-dimensional images were processed in MATLAB using custom scripts to obtain trajectories of nanoparticles presented in SI Appendix, Fig. S1 by tracking the centroid of AuNRs in each frame.

Synthesis of Gold Nanorods.

Homogeneous AuNRs were synthesized by a facile seed-mediated growth involving a binary surfactant mixture (59). The seed solution was prepared as follows: 10 mL of 0.1 M CTAB solution was mixed with $100\hspace{0.17em}\hspace{0.17em}\mathrm{\mu L}$ of 25 mM HAuCl₄ in a $20\hspace{0.17em}\hspace{0.17em}\mathrm{mL}$ scintillation vial under vigorous stirring. Then, $600\hspace{0.17em}\hspace{0.17em}\mathrm{\mu L}$ of ice-cooled $10\hspace{0.17em}\hspace{0.17em}\mathrm{mM}$ NaBH₄ was rapidly injected into the Au-CTAB solution and stirred for $2$ min. Upon the addition of NaBH₄, the color of the seed solution turned yellow-brownish. Afterward, the seed solution was left undisturbed at 28°C for 30 min prior to use in the following step.

The growth solution was obtained by first mixing $3.6\hspace{0.17em}\mathrm{g}$ of CTAB and 0.4936 g of NaOL in $196\hspace{0.17em}\hspace{0.17em}\mathrm{mL}$ of DI water in a 500-mL Erlenmeyer flask. The solution was heated with occasional agitation until all the CTAB was dissolved. The mixture was allowed to cool down to 30°C and 1.45 mL of 10 mM AgNO₃ was then added under stir at 700 rpm for 15 min. Afterward, 4 mL of 25 mM HAuCl₄ was added to the mixture and kept undisturbed at 28°C for 90 min. The yellowish color of growth solution turned colorless. Following that, $840\hspace{0.17em}\text{μ}\mathrm{L}$ of HCl was added to the solution and the mixture was stirred at 400 rpm for 15 min. Finally, $500\hspace{0.17em}\text{μ}\mathrm{L}$ of 0.064 M ascorbic acid was injected into the growth solution, and the mixture was vigorously stirred at 1,200 rpm for 30 s. $80\hspace{0.17em}\text{μ}\mathrm{L}$ of the seed solution was then injected, and the solution was stirred for 30 s before being left undisturbed at 28°C for 12 h to complete the growth process. 40 mL of the final products was isolated by centrifugation at 8,000 rpm for 15 min followed by careful removal of the supernatant. 50 mL of DI water was added to the pellet and the mixture was sonicated briefly to disperse the pellet for long-term storage. For the sample preparation of the LCTEM experiment, a second centrifugation step was performed at 5,500 rpm for 10 min followed by removal of the supernatant and adding 50 mL of DI water. 1 mL of the stock solution was centrifuged at 5,500 rpm for 8 min and the supernatant was carefully removed. 1 mL of 50 mM CTAC solution was added and sonicated for 10 min. The solution was centrifuged again at 5,500 rpm for 8 min followed by removal of the supernatant and adding 1 mL of the DI water.

Deep Learning.

MoNet architecture consists of six convolution layers (including five dilated convolution layers) followed by three dense layers. The dilated layers have 32 filters of sizes $k=2,\hspace{0.17em}\hspace{0.17em}3,\hspace{0.17em}\hspace{0.17em}4,\hspace{0.17em}\hspace{0.17em}10,\hspace{0.17em}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\hspace{0.17em}20$ with a combination of dilation factors of $2^n$ for $n=0,\hspace{0.17em}\hspace{0.17em}1,\hspace{0.17em}\hspace{0.17em}2,\hspace{0.17em}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\hspace{0.17em}3$ (inspired by p-variation method) to capture long-distance correlations existing in increment of $2^n$ along the trajectory. See SI Appendix, section 4 and Figs. S4 and S5 for the schematic of the neural net architecture. The validation accuracy of MoNet has been tested on simulated trajectories of different length (SI Appendix, Fig. S6). For a 300-frame-long trajectory the prediction accuracy of the diffusion class is about 90%. The mean-squared errors associated with the task of $\alpha$ prediction in CTRW and FBM models are 0.02 and 0.003, respectively. See SI Appendix, section 5 for more details.

$\mathit{p}$-Variation Test.

To distinguish between subdiffusive FBM and CTRW dynamics, Magdziarz et al. proposed the $p$-variation test (30, 37). This test generalizes the concept of the total variation $V$, in which the increments (i.e., particle displacements) are summed over the entire trajectory. The $p$-variation $V_n^p\left(t\right)$ generalizes the concept of total variation by exponentiating each increment by $p$ before summing (60):

$$V_n^p\left(t\right)={\displaystyle \sum _{j=1}^{\left(2^n\right)t}{\left|x\left(j/2^n\right)-x\left(\left(j-1\right)/2^n\right)\right|}^p}.$$

Given a trajectory with a length of $2^N$, in case of $p=2$ (quadratic variation) $V_n^2\left(t\right)$, we sum up the square of the increments which are spaced $2^{N-n}$ in time. See SI Appendix, section 3 and Fig. S4A for more details.

Data Availability

XLS data of nanoparticle trajectories have been deposited in Figshare, https://figshare.com/projects/Anomalous_Diffusion_LCTEM/87875. Deep learning analysis codes have been deposited in GitHub, https://github.com/AliviGitHub/MoNet.