Significance
How do social and infectious disease dynamics interact in group-living mammals? A significant cost to group living is increased transmission of pathogens. When a pathogen invades a group, members will be more vulnerable to mortality, Allee effects, and, ultimately, group extinction. The presence of a pathogen reduces the size of the population by reducing the number of social groups, allowing uninfected groups to grow larger from a reduction in intergroup aggression. Concomitantly, Allee effects are exacerbated in infected groups; this reduces the probability of pathogen persistence as infected groups die out more rapidly. Social structuring changes prevalence across scales and influences pathogen invasion and persistence. The models described here provide a framework for understanding the dynamics of these interactions.
Keywords: social groups, infectious disease, metapopulation, model, Yellowstone
Abstract
The population structure of social species has important consequences for both their demography and transmission of their pathogens. We develop a metapopulation model that tracks two key components of a species’ social system: average group size and number of groups within a population. While the model is general, we parameterize it to mimic the dynamics of the Yellowstone wolf population and two associated pathogens: sarcoptic mange and canine distemper. In the initial absence of disease, we show that group size is mainly determined by the birth and death rates and the rates at which groups fission to form new groups. The total number of groups is determined by rates of fission and fusion, as well as environmental resources and rates of intergroup aggression. Incorporating pathogens into the models reduces the size of the host population, predominantly by reducing the number of social groups. Average group size responds in more subtle ways: infected groups decrease in size, but uninfected groups may increase when disease reduces the number of groups and thereby reduces intraspecific aggression. Our modeling approach allows for easy calculation of prevalence at multiple scales (within group, across groups, and population level), illustrating that aggregate population-level prevalence can be misleading for group-living species. The model structure is general, can be applied to other social species, and allows for a dynamic assessment of how pathogens can affect social structure and vice versa.
Many vertebrate species live in social groups that shape behavioral interactions and demographic processes, particularly exposure to pathogens and their transmission. The social structure of groups varies considerably between species: at one end of this spectrum are diffuse, seasonal aggregations, as seen in migrating birds and many species of tropical fish; at the other end are social carnivores such as wolves (Canis lupus), wild dogs (Lycaon pictus), and lions (Panthera leo), in which groups hold territories for long time periods and both actively avoid and attack each other. The population dynamics of social species operate at the within-group and between-group scales, and the product of these interactions generates population-level dynamics. This modular population structure presents challenges to pathogen fitness in that behavior of group members minimizes contact and transmission rates between groups of hosts; thus, a pathogen must persist within each social group until an intergroup transmission event occurs (1–8).
There are several important analogies between this type of dynamic and those of metapopulations (9, 10)—in order for a pathogen to persist in the population, it must balance tradeoffs between virulence, infectious period, and transmission within and between groups (2, 6, 8, 11–13). The persistence of host groups depends on individual birth and death rates, group fission and fusion dynamics, and how often competing groups attack each other. These rates may be different in the presence of pathogens, and the pathogen could potentially modify within-group social dynamics. To quantify the effects of pathogens, we must first understand the drivers of host social system dynamics in the absence of pathogens—we develop a flexible and analytically tractable model framework for this. We then add different types of pathogens to the model and compare metapopulation dynamics in the presence of pathogens and between different pathogens.
Our central aim is to address the following question: “How do social and infectious disease dynamics interact in group-living mammals?” We answer this question by developing a hybrid form of metapopulation models that explicitly consider within-group dynamics of a hypothetical “average group” as well as the dynamics of the population of groups. We seek an understanding of the direct connections between a population’s vital rates, pathogen characteristics, group sizes, and number of groups in the population. Previously, socially structured disease models have assumed a static group structure and subsequently examined how networks of groups impact disease dynamics (6, 8, 14). This type of framework does not capture the impact of the pathogens on group structure and abundance (i.e., dynamics of the nodes themselves). For instance, mortality of some members within a social group can cause group dissolution and failed reproduction (e.g., ref. 15). Additionally, group size may influence contact among susceptible and infected individuals through dispersal and fission–fusion. The model framework we have developed allows us to explore this and compare the dynamics of the host population with and without pathogens.
While the initial temptation might be to develop a detailed simulation model that tracks the abundance of every individual in each group, such a model would quickly become specific to the system under study, and the effects and interactions between parameters would be harder to distinguish. We prefer to adopt an approach that simplifies model structure in a way that provides general insights that can be used to reconsider patterns in empirical data or to focus data collection on ways that might falsify these patterns. We explore these issues and use demographic data from two decades of Yellowstone wolf research to structure and parameterize a general model framework within which different host–pathogen systems could be examined (Table 1).
Table 1.
Host–pathogen systems that could be examined using our model framework
| Host(s) | Pathogen | Reference |
| Lions (Panthera leo) | Canine distemper virus | 14, 64 |
| Wild dogs (Lycaon pictus) | Rabies, canine distemper virus | 52, 65, 66 |
| White-tailed deer (Odocoileus virginianus), Reindeer (Rangifer tarandus) | Chronic wasting disease | 67, 68 |
| Bighorn sheep (Ovis canadensis) | Pneumonia (Mycoplasma ovipneumoniae) | 69, 70 |
| Bats (e.g., Desmodus rotundus) | Rabies | 71 |
| Red fox (Vulpes vulpes) | Sarcoptic mange | 72 |
| Seals (e.g., Pagophilus groenlandicus) | Phocine distemper virus | 73 |
| Small ruminants (i.e., sheep, goats) | Peste des petits ruminants virus | 74 |
| European badgers (Meles meles) | Bovine tuberculosis | 75 |
| Chimpanzees (Pan troglodytes verus) | Leprosy | 76 |
Wolf social structure is characterized by highly cohesive, matrilineal groups, similar to many canid and primate species. When interactions between these territorial social groups occur, they often involve high levels of aggression that may lead to fatalities (16–18). Most previous work on carnivore sociality has focused on the costs and benefits of living in a social group (19–22). Other than predator–prey models, there are relatively few studies that model the population dynamics of social carnivores, and these models have generally lacked the social structure of these populations (23, 24). Additionally, Allee effects have been observed in social carnivores such as wild dog and wolf populations (25, 26). Social groups may be subjected to Allee effects at small group size; this will lead to declines in recruitment and survival, which can have ramifications for group and population dynamics (27–32).
We initially present the underlying core model structure and then expand this framework to consider several key extensions: 1) Allee effects that cause the growth rate of small groups to slow, or even collapse, so the whole population will also decline when average group size becomes too small for individual groups to persist; 2) compartmental disease models that incorporate two types of pathogens that can be characterized by SIS (S = susceptible, I = infected); and 3) SIR (S = susceptible, I = infected, R = recovered) frameworks. The disease models are based on two monitored infectious diseases in the Yellowstone wolf population: mange and canine distemper virus (Canine morbillivirus, henceforth distemper) (33, 34). Mange is a skin disease caused by the mite Sarcoptes scabiei, and it is a relatively slow progressing infection that leads to hair loss, emaciation, and morbidity (35). Hosts can be reinfected with mange after clearance (36), and the dynamics act very much like a microparasite with rapid multiplication on the host and no specialized transmission stages; thus, we used an SIS framework for this disease. In contrast, canine distemper virus is a highly transmissible pathogen that causes an acute, highly immunizing infection with high juvenile mortality (33, 37); to characterize the dynamics of this second type of pathogen, we developed an SIR framework.
Methods
Social Groups Model.
The foundation for the social groups model is the dynamic interaction between mean group size, g, and number of groups, G. Traditionally, group or population size is regulated through a logistic growth framework that asymptotes at a carry capacity set a priori as K (e.g., ref. 38). Instead, we use a structure where the population equilibria emerge from the interaction between the model’s underlying birth and death rates and its density dependent terms (i.e., fission and resource limitation). This allows us to derive algebraic expressions in order to better appreciate how interactions at different scales determine group size and total number of groups, the product of which is total population.
There have been a number of previous approaches to model group size as an emergent property based on individual behavior or ecological factors (39–41). Other studies have followed groups through time (42) or have estimated group size for specific populations (43, 44). The principal aim of this study is to generalize group dynamics in the simplest way, allowing us to derive tractable analytical solutions for both average group size and number of groups.
Group size is primarily determined by the interaction between fission rate, f, and the per capita birth rate, b, and death rate, d. Initially, we assume all females in a group breed, as is the case for social ungulates. We subsequently modify the birth term and assume that only one or two females breed in any social group, as occurs in many carnivore species. In both cases we assume that hosts die at a constant rate, d, that is independent of group size. Fission is the process of individuals dispersing or emigrating out of a group and is a defining characteristic of many social carnivores such as African wild dogs, African lions, and spotted hyenas (Crocuta crocuta). However, for other social species, particularly ungulates, fission may occur on a faster timescale and may result in the group splitting (45, 46)—this can be accounted for by varying fission, f, and fusion rates (c, see below). We assume the fission rate of the group increases with group size as a density dependent function, fg2/(gf + g): fission increases as group size exceeds some critical number, gf, and mortality rates increase at a rate, e, as the number of groups, G, increases; this is in accordance with previous studies (47–50). The dynamics of the initial group in the population can initially be written as follows:
| [1] |
Fission creates a transient population of individuals, w, who meet at rate c, to create new groups. We use an equation that captures the dynamics of individuals that fission from an extant group, join a transient class, and then meet one of two fates: 1) censored from the population (die or emigrate) at normal death rate, d; or 2) form a new group at rate c. Here, dw/dt represents the dynamics of transient individuals that have fissioned from an increasing number of groups, G, and c is the rate that transients combine to form new groups:
| [2] |
Fission tends to operate on a much faster timescale than the other demographic rates included in the model—the time from fission to forming a new group is about 30 d for wolves in Yellowstone, while packs persist from 3 to over 20 y. Therefore, we assume the dynamics of this equation collapse down to give a transient population of individuals, w* = fg2G/(gf + g)(d + c). This equation for the transient population at equilibrium is substituted into the first half of the equation (Eq. 3), thereby replacing the simpler term in this equation for group formation (cw), and describes the changes in the number of groups, G. Thus, c/(c + d) is the proportion of dispersing, transient individuals that contribute to new groups. The dynamics of the total number of groups is determined by the rate at which groups are created by fission, cw, and the rate at which group mortality increases within an area, eG2. Thus, e is a density dependent rate describing the persistence time of groups and captures background mortality, group dissolution, resource limitation (e.g., food and den sites), and harvest.
| [3] |
This can readily be solved to give an expression for the carrying capacity of the environment as defined by the number of groups that inhabit it:
| [4] |
The individuals that form new groups change the size of the average group, so we need to expand the equation for the initial group (Eq. 1) by adding individuals back into average group size. To achieve this, the terms in fg2 are reorganized to give a modified equation for average size of all groups:
| [5] |
The dynamics produced by this framework are subtly different from those of a homogeneous population with density dependent dynamics (Fig. 1 A and B and SI Appendix, Fig. S1 A and B); the number of groups (rather than the number of individuals) increases and asymptotes in a logistic fashion. The total population size initially increases almost linearly as changes in the number of groups are offset by slow decreases in average group size as the population gets larger and competition for resources increases. The total population has a tendency to overshoot before equilibrating at a population size, K, which is the product of G* and g*: K = g*G* = N*.
Fig. 1.
Panel plots displaying population and group dynamics produced by the metapopulation models. (A) Basic model dynamics showing mean group size (dots), number of groups (dashes), and total population (lines) through time (Eqs. 6 and 7). (B) A plot of zero growth isoclines and the trajectory for the basic model; the arrows indicate rate of change of population at different points in gG space. (C) A plot comparing the model including aggression (black) and observed Yellowstone National Park wolf population data (blue), where Eq. 6 includes a set number of female breeders. The data reflect the northern portion of Yellowstone from 1995 to 2016. (D) The stable equilibrium for social groups without and with an Allee effect (A = 2); the zero-growth isoclines for group size and number of groups are illustrated by filled circles, and trajectories that include an Allee effect are open triangles. The arrows indicate the trajectory and annual rate of change in abundance without an Allee effect. See SI Appendix, Table S1 for parameter values used.
This basic groups model captures the observed dynamics of herbivore herds and fish shoals where intergroup aggression is minimal. This framework needs to be adapted for territorial predators, such as wolves and lions, in which a major source of mortality comes from groups attacking and killing individuals in different groups. The addition of an intergroup aggression term, a, allows us to characterize the rate at which groups attack each other. Intergroup aggression is a function of the number of groups, G, and we assume aggression increases linearly with the number of groups rather than exponentially (SI Appendix, Fig. S3B). The intraspecific mortality that occurs during aggressive interactions reduces both mean group size and the number of groups. Eqs. 5 and 3 now become the following:
| [6] |
| [7] |
The two equations can again be solved analytically at dg/dt = dG/dt = 0 to give expressions for the number of groups and average group size at equilibrium:
Inspection of these two equations tells us that group size is determined by the birth and death rates and the rate at which groups fission to form new groups (SI Appendix, Figs. S5 and S7). The total number of groups is dependent on these rates as well and declines with both rates of intergroup aggression and resource abundance. Overall, population dynamics are dependent upon birth, fission, and extinction rates, although these processes operate differently within and between groups. Unless stated otherwise, all social groups model simulations illustrated below utilized parameter values derived from the Yellowstone wolf population data in SI Appendix, Table S1.
The dynamics of the “social carnivore” model (Eqs. 6 and 7) are more restrained than those of the simpler “social ungulate model” (Eqs. 3 and 5) such that the presence of the aggression term reduces the tendency for the population to overshoot its final abundance, and the number of groups and average group size settle more rapidly to equilibrium. This pattern of population growth initial overshoot followed by decline to steady abundance was observed in the Yellowstone wolf population following their reintroduction in 1995 (Fig. 1C). For Yellowstone wolves, equilibria values settled to g > g0 and G > G0 (Fig. 1C). When initial conditions are above carrying capacity, the opposite dynamics occur in that g and G smoothly drop below equilibrium and then increase and stabilize. The nontrivial equilibrium for g* and G* is a stable focus (Fig. 1 B and D).
Allee Effect.
The interactions between Allee effects and pathogens have not been explored in population models as they have been considered to operate independently. We can account for the positive density dependence observed in small social groups by adding a term that captures an Allee effect that reduces recruitment when group size is small (SI Appendix, Fig. S4). The parameter A enters into the within-group dynamics equation as a term that modifies the underlying birth rate b(g/(g + A)). When g = A, this term reduces group birth rate by 50%; when g > A, the Allee term will approach unity and group growth rate will be minimally affected by Allee effects (SI Appendix, Fig. S4); when g < A, the net Allee term will approach zero, reducing group birth rate and creating an unstable equilibrium below which the group will collapse. The addition of a small to moderate Allee term slightly reduces equilibrium group size and number compared to the corresponding core groups model (Fig. 1D). Systems with the Allee term and high birth rates overshoot mean group size and number of groups and then settle at a lower equilibrium than their corresponding core groups models—this results in less-stable dynamics and a longer time to equilibrium. Significant Allee effects cause the population to crash as all groups have the same structure and dynamics and recruitment is not large enough to overcome death, fission, and mortality rates in the small group sizes. This is an artifact of assuming all groups are identical. In particular, the size of groups containing pathogens may decrease to levels in which Allee effects become more important for the dynamics of infected groups than for those without infection.
Adding Pathogens to the Model.
We used a compartmental framework to implement infectious diseases into the core social groups model. Specifically, the equations for the number of groups and mean group size were expanded to consider SIR individuals and groups. We track the number of groups in each class as well as the composition of the average group in terms of the numbers of SIR individuals it contains. For example, susceptible groups become infected groups when one individual in the group is infectious, but because all individuals within the group do not become infected immediately, both susceptible and infected individuals will coexist within the average infected group. Here, we make an additional modification to more closely correspond with social carnivores and only allow one (or two) females to breed in any social group (Bf), so the proportion of females breeding in the group is now 1/g (or 2/g).
S, I, and R groups move from one class to the next due to infection during intergroup encounters or by recovery as the infection dies out in the group, leaving only resistant and susceptible hosts (who either escaped infection or were recently born). Within groups, βW is the frequency dependent pathogen transmission rate between group members. Pathogen transmission between groups occurs at a frequency dependent, pathogen-specific rate, βB, where βB = βW*a, the product of the between-group contact rate and within-group transmission rate. Infected individuals can have a pathogen-induced mortality rate, α, and individuals recover from infection with rate σ. Infection is lost when an individual recovers or dies (σ + α). We have reduced the magnitude of e to allow a larger population size than the wolf population within Yellowstone as the park is too small to support continuous infection with these pathogens (51).
We will initially consider the SIS model used for nonimmunizing infections such as mange. G and I are the state variables for the number of groups that are susceptible or infected, g and s are the mean number of susceptible individuals in susceptible and infected groups, respectively, and i is the mean number of infected individuals in infected groups. We assume that infected individuals do not reproduce, but this can be easily modified. An Allee effect is also included for illustrative purposes in the SIS model but not in the SIR model.
| [8] |
| [9] |
| [10] |
| [11] |
| [12] |
We have a dummy variable τ that is set to a very low value (0.001); this stops the birth rate of infected groups going to infinity when no susceptible hosts, s, are present. It is sufficiently small to not reduce the fecundity of breeding females in these groups. We can calculate the pathogen’s basic reproductive number within each group, R0, or the number of secondary infections arising from a single infectious individual in a completely susceptible group: .
For pathogens such as canine distemper virus that result in immunological resistance to infection, we developed an SIR model, where R is a new state variable for the number of recovered groups. Additional new state variables include sR as the mean number of susceptible individuals in recovered groups and rR as the mean number of recovered individuals in recovered groups. sR only occurs when infected hosts recover from infection at a rate, σ, and immunity is then lost at a rate, φ, and they then return to the susceptible class. Since these infections tend to be acute, we assume that infected individuals do not reproduce or fission.
The SIR model in Fig. 2 can be described by Eqs. 13–21:
| [13] |
| [14] |
| [15] |
| [16] |
| [17] |
| [18] |
| [19] |
| [20] |
| [21] |
Fig. 2.
Flow diagram for the SIR groups model. Boxes represent the three group compartments, and ovals within the boxes represent the mean number of individuals in each compartment within their respective group. Group-level processes are denoted with open (unfilled/white) arrows; if the arrow outline is solid, the group transitions to a different compartment (e.g., S to I); if the arrow outline is dashed, the process occurs in groups in that compartment (e.g., I group fissions and creates more I groups). Filled arrows represent within-group processes (e.g., i individual recovers to r). Intergroup aggression is an underlying process that is primarily driven by the number of groups, and it effectively controls pathogen transmission rates because it is the only form of intergroup contact in these models (i.e., βB = βW*a). Infected and recovered individuals can also contribute to new susceptible individuals through birth, but these arrows are not included for simplicity.
For the SIR model, the basic reproductive number of the pathogen within a group of susceptibles is .
Transition rates between different group compartments have to be modified by group size as persistence time and speed of infection dynamics change as group size changes. Specifically, the rate at which recovery converts an I group to an R group slows down with an increase in the number of infected individuals (as does R to S)—these terms are expressed by scaling terms in the denominator (e.g., (1 + i), (sR + rR)). The term in ((sR + rR)/(sR + rR + τ)) in Eqs. 14 and 17 prevents the birth rate jumping to infinity before the resistant groups form from infected groups that have recovered. Similarly, the term (sR/(sR + rR)) in Eqs. 20 and 21 represents the reduced susceptibility to infection in R groups due to the presence of immunologically resistant individuals in these groups. This can be thought of as a subtle metapopulation form of within-group “herd immunity.” We assume that both within-group and between-group transmission is frequency dependent increasing to an asymptote (e.g., within groups: ).
Results
The model structure we have developed provides a number of important insights into the dynamics of hosts whose populations are divided into social groups. In general, the SIS model was able to maintain pathogens in the population while pathogens were more likely to fade out in the SIR model. For short-lived, immunogenic SIR-type pathogens, three mechanisms are important for persistence of the pathogen: 1) low contact rates between host groups such that between-group transmission events are rare (i.e., “social trapping”); 2) highly virulent infections kill too many hosts within one group before successful between-group transmission can occur; and 3) when pathogens are highly transmissible, the population quickly becomes dominated by individuals resistant to reinfection and the chain of transmission stutters and breaks.
The influence of pathogens on group dynamics is considerable. The presence of an SIS or an SIR pathogen reduces the number of groups in the population and the number of individuals in infected groups. Counterintuitively, it allows the uninfected groups in the population to grow slightly larger (Fig. 3). This occurs because the rate of intraspecific aggression between groups is reduced when the presence of the pathogen decreases the number of groups, which then allows healthy surviving groups to increase in size as they suffer lower rates of aggression. The total population typically settles to a smaller size with SIS pathogens because the chronic nature of these infections increases mortality for a substantial proportion of the population for an extended period of time (Fig. 4 and SI Appendix, Fig. S1 C and D). This effect is less pronounced in the case of the SIR pathogen, as the population size that persists in the presence of an SIR type pathogen is larger than for one infected by an SIS pathogen as infected individuals are able to clear their infections quickly (if they survive) and become immunologically resistant (for a period of time) (Fig. 4). Because the SIS pathogen system is dynamically simpler than the SIR pathogen system, it settles to equilibrium relatively quickly. The SIR pathogen is more unstable and tends to produce epidemic cycles that seem to fade out when the population is divided into social groups (SI Appendix, Fig. S1 E and F). We found that susceptible and recovered groups in a population with an SIR pathogen were able to grow larger when the pathogen was present because reductions in the numbers of groups reduced rates of intergroup aggression and group extinction (Fig. 3), but this effect was less pronounced than in the SIS model framework.
Fig. 3.
Cross-sectional diagrams of disease model outputs compared to models run without pathogens (“control,” green), producing relative differences in the number of groups (left column) and mean group size (right column). One parameter was increased incrementally—recovery rate (σ) in SIS models (top row) and within-group transmission (βW) in SIR models (bottom row). Groups and individuals were compartmentalized into susceptible (blue), infected (red), or recovered (purple). Individuals are also denoted by their group compartmentalization: susceptible groups (circle), infected groups (x), and recovered groups (triangle) (e.g., recovered individuals in an infected group are a purple x). Parameter values in A and B reflect a mange-like infection (βW = 8, βB = 1.5, α = 0.2, σ = 2, e = 0.001, f = 0.01, a = 0.01, and A = 0), while in C and D reflect a distemper-like infection (βW = 35, βB = 15, α = 1, σ = 12, φ = 0.25, e = 0.001, f = 0.01, and a = 0.01). The vertical dashed lines denote pathogen persistence (left = does not persist, right = persistence at year 50).
Fig. 4.
A panel plot displaying the dynamics of (A, C) SIS and (B, D) SIR pathogens. The top row zooms in on dynamics following initial pathogen introduction (years 1 through 5), and the bottom row displays long-term dynamics (years 1 through 50). Total population counts (black), mean number of groups (thick lines), and mean number of individuals within each group (thin lines) are shown through time, with different colors representing the three disease compartments: susceptible, infected, recovered. Parameters selected represent (A, C) mange-like (βW = 8, βB = 1.5, α = 0.2, σ = 2, e = 0.001, f = 0.05, a = 0.05, and A = 0) and (B, D) distemper-like pathogens (βW = 30, βB = 8, α = 2, σ = 12, φ = 0.25, e = 0.001, f = 0.05, and a = 0.05).
Both disease models capture the pathogen tradeoffs between virulence and between-group contact rate. For instance, distemper-like infections (highly transmissible, moderately lethal, and immunizing) die out quickly, and although there are many groups classified as infectious after an epidemic, they primarily consist of individuals who survived earlier infection with the pathogen (Figs. 3 and 4). A less-virulent pathogen may not infect the entire population, but a few infectious individuals remain in the population for much longer after the disease introduction. In contrast, a mange-like infection (low transmission, longer infectious period, and nonimmunizing) will persist for much longer in the population at higher levels within groups. Although it takes longer for the slower-moving infections to permeate the population, SIS infections were more likely than SIR infections to maintain a stable endemic equilibrium in our model runs. Importantly, the transmission threshold for invasion is higher for socially structured SIS and SIR models compared with similar homogeneous models (SI Appendix, Fig. S2). Homogeneous models always result in higher prevalence and seroprevalence than the structured metapopulation models across a wide range of viable transmission values.
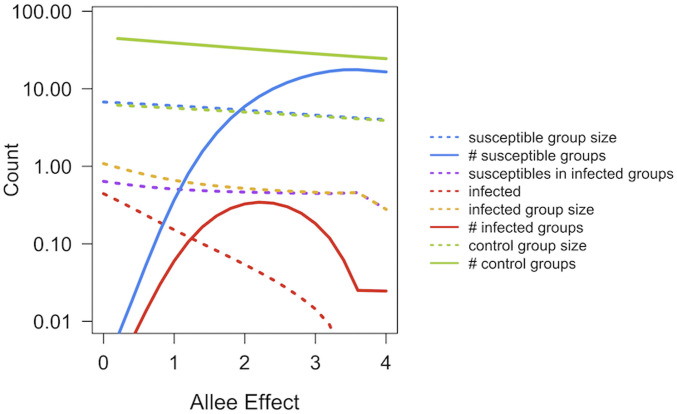
The Allee effect has an interesting interaction with the presence of pathogens: infected groups decrease in size because of pathogen-induced mortality, and these smaller groups exhibit a more pronounced Allee effect than larger uninfected groups (i.e., the probability of infected groups going extinct increases). Concomitantly, this slows the rate at which groups grow and recover from the presence of the infection. This is seen more clearly in the SIS case than for the SIR case, so we have only illustrated it for the SIS pathogen. In Fig. 5, we have compared the structure of healthy and diseased populations with Allee effects operating at different group sizes. These results suggest that the interaction between pathogens and Allee effects is subtle—they increase the chance that infected groups will go extinct and reduce population size (and number of groups), but this will also reduce the pathogen’s ability to persist in the population as groups containing the pathogen go extinct much more quickly than in the absence of Allee effects. If Allee effects only manifest themselves strongly during disease outbreaks, then field studies may tend to attribute the cause of group extinction or population decline to the pathogen, rather than its interaction with the Allee effect. This may be the case with recent studies of wild dogs (52).
Fig. 5.
Equilibrium mean group size (dashes) and number of groups (lines) for susceptible and infected groups using the SIS model for a moderately virulent pathogen, including Allee effects (susceptible groups = blue, infected groups = red, susceptibles in infected groups = purple, and infected group size = gold). These are compared to the model without a pathogen (“control,” green) at the same Allee values (βW = 30, βB = 9, α = 1, σ = 8, e = 0.001, f = 0.01, and a = 0.01).
Discussion
The organization of a host population into modular social groups alters the interactions between pathogens and their hosts. This is driven by the tensions between within- and between-group transmission: within a group, the pathogen spreads rapidly causing mortality and a decrease in group size, but it only transmits between groups when there is contact, such as during a boundary confrontation. This organization also constrains the vital dynamics of the pathogen that determine its transmission and virulence rates (6, 8, 53). The models presented here capture many of the important consequences of social organization within a framework that minimizes details while allowing for the investigation of key, dynamical features of the social system. In this system, the process of group fission regulates mean group size, while the number of groups in a population is regulated by intergroup aggression and density dependent group extinction rates. Group turnover, specifically the number of breeding females and their offspring production, is important in shaping group and population size. The inclusion of pathogens into this structure reduced population size mainly through a reduction in the number of groups. Our models provide a foundation for exploring relationships for many social species with varying levels of social complexity (Table 1). Their dynamics correspond well with empirical data collected for the Yellowstone wolf population (Fig. 1C).
From an epidemiological perspective, an important finding is that the three scales of interest—population, metapopulation, and within groups—had strikingly different prevalences: low prevalence at the population level can readily mask high levels of prevalence within infected groups and intermediate numbers of groups containing infected individuals (Fig. 6). This finding emphasizes the need for representative sampling in socially structured populations where reported prevalence levels do not often transcend scale (7, 54, 55). Wildlife researchers and managers should sample from many groups in a population in order to accurately depict disease prevalence. For social carnivores, this roughly equates to sampling across a larger area, and explicitly recognizing that population level prevalence tends to be lower than the number of groups infected, and the level of infection experienced by individuals in infected groups. This issue should be a central consideration when wildlife disease biologists are analyzing and interpreting prevalence and seroprevalence data (56–58).
Fig. 6.
Maximum infection prevalence with respect to within-group transmission rate (βW) at three scales: population (black), groups (red), and within groups (blue) using the SIS (A) and SIR (B) models (βB = βW/4, α = 1, σ = 6, φ = 0.5, e = 0.001, f = 0.08, and a = 0.1). If the initial prevalence was the maximum prevalence (i.e., pathogen died out very quickly), maximum prevalence was set to zero; therefore, prevalence > 0 shows pathogen invasion. We have used maximum prevalence rather than mean prevalence as the pathogen either drives the host population extinct or dies out at extreme transmission rates. In B, we included seroprevalence (dashes) as the sum of all infected and recovered groups or individuals to represent current or previous infections (i.e., we assume those who test seropositive include I and R individuals whose serostatus would be indistinguishable).
The central strength of this modeling approach is the ability to assess the relative impact of a pathogen on group size when we consider pathogens with different transmission coefficients, virulence, and infectious periods. Here, we note that the presence of pathogens always reduces the size of the host population—this is mainly driven by a reduction in the number of groups. A reduction in the average size of infected groups can also occur when infections are chronic and prolonged, but this effect is less pronounced for an SIR pathogen, such as distemper, than for an SIS pathogen, such as mange. As the number of groups increases, intergroup aggression and group extinction play an important role in determining the number of social groups and average group size. If disease reduces the number of social groups, there will be less intergroup aggression (the dominant form of density dependence in wolves and other social carnivores), thus groups without infected individuals may grow larger (Fig. 3). In contrast, infected groups are smaller in size in the presence of a pathogen, and in fact, Allee effects are at their strongest when partially masked by the presence of a pathogen.
The underlying size structure of the groups and the rates at which they interact constrains the characteristics of pathogens that can establish and persist in these populations (6, 8, 12). Our framework is partially constrained by the assumption that all groups are the same size and thus exhibit similar dynamics; this overlooks stochastic differences between groups that may have important consequences that could only be explored in a more detailed simulation framework. While differences among groups is likely more realistic, it would require the tracking of individual groups and, therefore, greater model complexity at the cost of loss of generality. The assumption that all groups become infected at the same rate can be modified by expanding the framework to consider groups of two different sizes or by adding spatial structure to the models so that each group can only infect its neighbors (such as in Eq. 2).
Obviously, many additional details could be included into the core model structure, particularly the presence of two sexes—males with a greater tendency to disperse and form transient subpopulations could readily be added. Similarly, age structure could be added to the within-group structure, and together these additions would capture specific and important details of social behavior that could be examined in the context of different social species. If we were considering the fission–fusion societies of primates or elephants, then e, a, and f could become sinusoidal functions that oscillate with the availability of seasonal resources. Similarly, we could consider the costs and benefits of group living within an adaptive model framework. The present model structure is well suited to these alterations and we will explore these extensions more fully in the future.
We illustrate one way to address increasing social complexity by adding an Allee effect, which often arises in social groups when birth rates decline as group size falls below a critical number of group members (59, 60). Allee effects have important consequences across many species and populations (27, 28, 30–32). In Yellowstone wolves, the number of pups born per breeding female declines in groups smaller than eight (26), which may be detrimental in small populations (25). Living in a large group may increase an individual’s likelihood of contracting a pathogen through high within-group contact rates, yet in some cases, as group size increases, the costs of infection decrease for infected individuals (4, 22). The latter “healthcare hypothesis” describes an increase in survival rates for infected individuals living in larger groups as the impact of the pathogen may be reduced when group members assist by obtaining resources, maintaining social status, removing ectoparasites, and providing comfort (61–63). These are potentially important aspects of social living to incorporate mechanistically in the future.
Host population social organization cannot be ignored when examining infectious disease dynamics. Our goal here was to provide a general model, applicable to any social species, that melds metapopulation and disease dynamics in a manner that provides broad, testable, and general insights into the interactions between social organization and disease. We think this model could be used to provide insights into the dynamics of a broad variety of host species, particularly as all parameters are measurable from field data. This type of research may help in the protection of endangered species by identifying the synergistic relationship between Allee effects and pathogens while also elucidating important and subtle interactions between host demographics, social structure, and pathogen characteristics.
Supplementary Material
Acknowledgments
We thank Yellowstone Wolf Project staff members for their assistance in data collection and Tim Coulson for his helpful insight. Earlier discussions between A.P.D., Janis Antonovics, and Peter Thrall sowed the seeds that are ultimately the genesis of the ideas developed in this paper. A.P.D. also thanks Mercedes Pascual and Steve Pacala for their insights on the models. Financial support includes the following: an endowment from Verne Willaman to E.E.B. and P.J.H.; US Geological Survey grant G17AC00427 to E.E.B. and P.C.C.; NSF Long Term Research in Environmental Biology (LTREB) grant DEB–1245373 to D.W.S.; and the many donors to Yellowstone Forever, especially Annie and Bob Graham and Valerie Gates. Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the US government.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2020023118/-/DCSupplemental.
Data Availability
The CSV files and R code scripts data have been deposited in Dryad (https://datadryad.org/stash/share/ccIfMEUnp8yz43xYcG2XJR9q8zlIUnU8YtRbOYnBjyQ). All other study data are included in the article and/or SI Appendix.
References
- 1.Hess G., Disease in metapopulation models: Implications for conservation. Ecology 77, 1617–1632 (1996). [Google Scholar]
- 2.Swinton J., Extinction times and phase transitions for spatially structured closed epidemics. Bull. Math. Biol. 60, 215–230 (1998). [DOI] [PubMed] [Google Scholar]
- 3.Gog J., Woodroffe R., Swinton J., Disease in endangered metapopulations: The importance of alternative hosts. Proc. Biol. Sci. 269, 671–676 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Altizer S., et al., Social organization and parasite risk in mammals: Integrating theory and empirical studies. Annu. Rev. Ecol. Evol. Syst. 34, 517–547 (2003). [Google Scholar]
- 5.Cross P. C., Lloyd-Smith J. O., Johnson P. L. F., Getz W. M., Duelling timescales of host movement and disease recovery determine invasion of disease in structured populations. Ecol. Lett. 8, 587–595 (2005). [Google Scholar]
- 6.Ryan S. J., Jones J. H., Dobson A. P., Interactions between social structure, demography, and transmission determine disease persistence in primates. PLoS One 8, e76863 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Manlove K. R., Cassirer E. F., Cross P. C., Plowright R. K., Hudson P. J., Costs and benefits of group living with disease: A case study of pneumonia in bighorn lambs (Ovis canadensis). Proc. Biol. Sci. 281, 20142331 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sah P., Leu S. T., Cross P. C., Hudson P. J., Bansal S., Unraveling the disease consequences and mechanisms of modular structure in animal social networks. Proc. Natl. Acad. Sci. U.S.A. 114, 4165–4170 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Levins R., Some demographic and genetic consequences of environmental heterogeneity for biological control. Am. Entomol. (Lanham Md.) 15, 237–240 (1969). [Google Scholar]
- 10.Hanski I., Single-species metapopulation dynamics: Concepts, models and observations. Biol. J. Linn. Soc. Lond. 42, 167–180 (1991). [Google Scholar]
- 11.Swinton J., Harwood J., Grenfell B. T., Gilligan C. A., Persistence thresholds for phocine distemper virus infection in harbour seal Phoca vitulina metapopulations. J. Anim. Ecol. 67, 54–68 (1998). [Google Scholar]
- 12.Cross P. C., Johnson P. L. F., Lloyd-Smith J. O., Getz W. M., Utility of R0 as a predictor of disease invasion in structured populations. J. R. Soc. Interface 4, 315–324 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Poletto C., Tizzoni M., Colizza V., Heterogeneous length of stay of hosts’ movements and spatial epidemic spread. Sci. Rep. 2, 476 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Craft M. E., Volz E., Packer C., Meyers L. A., Disease transmission in territorial populations: The small-world network of serengeti lions. J. R. Soc. Interface 8, 776–786 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Borg B. L., Brainerd S. M., Meier T. J., Prugh L. R., Impacts of breeder loss on social structure, reproduction and population growth in a social canid. J. Anim. Ecol. 84, 177–187 (2015). [DOI] [PubMed] [Google Scholar]
- 16.Mosser A., Packer C., Group territoriality and the benefits of sociality in the African lion, Panthera leo. Anim. Behav. 78, 359–370 (2009). [Google Scholar]
- 17.Cassidy K. A., MacNulty D. R., Stahler D. R., Smith D. W., Mech L. D., Group composition effects on aggressive interpack interactions of gray wolves in Yellowstone National Park. Behav. Ecol. 26, 1352–1360 (2015). [Google Scholar]
- 18.Smith D. W., et al., Infanticide in wolves: Seasonality of mortalities and attacks at dens support evolution of territoriality. J. Mammal. 96, 1174–1183 (2015). [Google Scholar]
- 19.Packer C., Pusey A. E., Adaptations of female lions to infanticide by incoming males. Am. Nat. 121, 716–728 (1982). [Google Scholar]
- 20.Grinnell J., Packer C., Pusey A. E., Cooperation in male lions: Kinship, reciprocity or mutualism? Anim. Behav. 49, 95–105 (1995). [Google Scholar]
- 21.Heinsohn R., Packer C., Complex cooperative strategies in group-territorial African lions. Science 269, 1260–1262 (1995). [DOI] [PubMed] [Google Scholar]
- 22.Almberg E. S., et al., Social living mitigates the costs of a chronic illness in a cooperative carnivore. Ecol. Lett. 18, 660–667 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Boyce M. S., Wolf Recovery for Yellowstone National Park: A Simulation Model (Springer, Dordrecht, 1992). [Google Scholar]
- 24.Varley N., Boyce M. S., Adaptive management for reintroductions: Updating a wolf recovery model for Yellowstone National Park. Ecol. Modell. 193, 315–339 (2006). [Google Scholar]
- 25.Courchamp F., Clutton-Brock T., Grenfell B., Multipack dynamics and the Allee effect in the African wild dog, Lycaon pictus. Anim. Conserv. 3, 277–285 (2000). [Google Scholar]
- 26.Stahler D. R., MacNulty D. R., Wayne R. K., vonHoldt B., Smith D. W., The adaptive value of morphological, behavioural and life-history traits in reproductive female wolves. J. Anim. Ecol. 82, 222–234 (2013). [DOI] [PubMed] [Google Scholar]
- 27.Amarasekare P., Allee effects in metapopulation dynamics. Am. Nat. 152, 298–302 (1998). [DOI] [PubMed] [Google Scholar]
- 28.Kramer A. M., Dennis B., Liebhold A. M., Drake J. M., The evidence for Allee effects. Popul. Ecol. 51, 341–354 (2009). [Google Scholar]
- 29.Brashares J. S., Werner J. R., Sinclair A. R. E., Social ‘meltdown’ in the demise of an island endemic: Allee effects and the Vancouver Island marmot. J. Anim. Ecol. 79, 965–973 (2010). [DOI] [PubMed] [Google Scholar]
- 30.Angulo E., Rasmussen G. S. A., Macdonald D. W., Courchamp F., Do social groups prevent Allee effect related extinctions?: The case of wild dogs. Front. Zool. 10, 11 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sanderson C. E., Jobbins S. E., Alexander K. A., With Allee effects, life for the social carnivore is complicated. Popul. Ecol. 56, 417–425 (2014). [Google Scholar]
- 32.Lerch B. A., Abbott K. C., Allee effects drive the coevolution of cooperation and group size in high reproductive skew groups. Behav. Ecol. 31, 661–671 (2020). [Google Scholar]
- 33.Almberg E. S., Mech L. D., Smith D. W., Sheldon J. W., Crabtree R. L., A serological survey of infectious disease in Yellowstone National Park’s canid community. PLoS One 4, e7042 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Almberg E. S., Cross P. C., Dobson A. P., Smith D. W., Hudson P. J., Parasite invasion following host reintroduction: A case study of Yellowstone’s wolves. Philos. Trans. R. Soc. Lond. B Biol. Sci. 367, 2840–2851 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pence D. B., Windberg L. A., Pence B. C., Sprowls R., The epizootiology and pathology of sarcoptic mange in coyotes, Canis latrans, from south Texas. Journ. Parasit. 69, 1100–1115 (1983). [PubMed] [Google Scholar]
- 36.Little S. E., et al., Responses of red foxes to first and second infection with Sarcoptes scabiei. J. Wildl. Dis. 34, 600–611 (1998). [DOI] [PubMed] [Google Scholar]
- 37.Greene C. E., Appel M. J., “Canine distemper” in Infectious Diseases of the Dog and Cat, Greene C. E., Ed. (Saunders/Elsevier, 2006), pp. 25–41. [Google Scholar]
- 38.Pearl R., Reed L. J., On the rate of growth of the population of the United States since 1790 and its mathematical representation. Proc. Natl. Acad. Sci. U.S.A. 6, 275–288 (1920). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gerard J. F., Bideau E., Maublanc M. L., Loisel P., Marchal C., Herd size in large herbivores: Encoded in the individual or emergent? Biol. Bull. 202, 275–282 (2002). [DOI] [PubMed] [Google Scholar]
- 40.Hoare D. J., Couzin I. D., Godin J. G. J., Krause J., Context-dependent group size choice in fish. Anim. Behav. 67, 155–164 (2004). [Google Scholar]
- 41.Estevez I., Andersen I. L., Nævdal E., Group size, density and social dynamics in farm animals. Appl. Anim. Behav. Sci. 103, 185–204 (2007). [Google Scholar]
- 42.Stephens P. A., Frey-roos F., Arnold W., Sutherland W. J., Model complexity and population predictions. The alpine marmot as a case study. J. Anim. Ecol. 71, 343–361 (2002). [Google Scholar]
- 43.Ridley J., Komdeur J., Sutherland W. J., Population regulation in group-living birds: Predictive models of the Seychelles warbler. J. Anim. Ecol. 72, 588–598 (2003). [DOI] [PubMed] [Google Scholar]
- 44.Hayakawa Y., Furuhashi S., Group-size distribution of skeins of wild geese. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 86, 031924 (2012). [DOI] [PubMed] [Google Scholar]
- 45.Clutton-Brock T., Mammal Societies (John Wiley & Sons, 2016). [Google Scholar]
- 46.Cross P. C., Lloyd-Smith J. O., Getz W. M., Disentangling association patterns in fission-fusion societies using African buffalo as an example. Anim. Behav. 69, 499–506 (2005). [Google Scholar]
- 47.Krause J., Ruxton G. D., Living in Groups (Oxford University Press, 2002). [Google Scholar]
- 48.Lehmann J., Boesch C., To fission or to fusion: Effect of community size on wild chimpanzee (Pan troglodytes versus) social organisation. Behav. Ecol. Sociobiol. 56, 207–216 (2004). [Google Scholar]
- 49.Stephens P. A., Russell A. F., Young A. J., Sutherland W. J., Clutton-Brock T. H., Dispersal, eviction, and conflict in meerkats (Suricata suricatta): An evolutionarily stable strategy model. Am. Nat. 165, 120–135 (2005). [DOI] [PubMed] [Google Scholar]
- 50.VanderWaal K. L., Mosser A., Packer C., Optimal group size, dispersal decisions and postdispersal relationships in female African lions. Anim. Behav. 77, 949–954 (2009). [Google Scholar]
- 51.Almberg E. S., Cross P. C., Smith D. W., Persistence of canine distemper virus in the Greater Yellowstone ecosystem’s carnivore community. Ecol. Appl. 20, 2058–2074 (2010). [DOI] [PubMed] [Google Scholar]
- 52.Woodroffe R., O’Neill H. M. K., Rabaiotti D., Within- and between-group dynamics in an obligate cooperative breeder. J. Anim. Ecol. 89, 530–540 (2020). [DOI] [PubMed] [Google Scholar]
- 53.Thrall P. H., Burdon J. J., The spatial scale of pathogen dispersal: Consequences for disease dynamics and persistence. Evol. Ecol. Res. 1, 681–701 (1999). [Google Scholar]
- 54.Farnsworth M. L., Hoeting J. A., Hobbs N. T., Miller M. W., Linking chronic wasting disease to mule deer movement scales: A hierarchical bayesian approach. Ecol. Appl. 16, 1026–1036 (2006). [DOI] [PubMed] [Google Scholar]
- 55.Cross P. C., et al., “Wildlife population structure and parasite transmission: Implications for disease management” in Management of Disease in Wild Mammals, Delahay R. J., Smith G. C., Hutchings M. R., Eds. (Springer, 2009), pp. 9–29. [Google Scholar]
- 56.Christensen J., Gardner I. A., Herd-level interpretation of test results for epidemiologic studies of animal diseases. Prev. Vet. Med. 45, 83–106 (2000). [DOI] [PubMed] [Google Scholar]
- 57.Branscum A. J., Gardner I. A., Johnson W. O., Bayesian modeling of animal- and herd-level prevalences. Prev. Vet. Med. 66, 101–112 (2004). [DOI] [PubMed] [Google Scholar]
- 58.Gilbert A. T., et al., Deciphering serology to understand the ecology of infectious diseases in wildlife. EcoHealth 10, 298–313 (2013). [DOI] [PubMed] [Google Scholar]
- 59.Allee W. C., Bowen E. S., Studies in animal aggregations: Mass protection against colloidal silver among goldfishes. J. Exp. Zool. 61, 185–207 (1932). [Google Scholar]
- 60.Stephens P. A., Sutherland W. J., Consequences of the Allee effect for behaviour, ecology and conservation. Trends Ecol. Evol. 14, 401–405 (1999). [DOI] [PubMed] [Google Scholar]
- 61.Goodall J., The Chimpanzees of Gombe: Patterns of Behavior (Belknap Press, Cambridge, MA, 1986). [Google Scholar]
- 62.Cremer S., Armitage S. A. O., Schmid-Hempel P., Social immunity. Curr. Biol. 17, R693–R702 (2007). [DOI] [PubMed] [Google Scholar]
- 63.Kappeler P. M., Cremer S., Nunn C. L., Sociality and health: Impacts of sociality on disease susceptibility and transmission in animal and human societies. Philos. Trans. R. Soc. Lond. B Biol. Sci. 370, 20140116 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Roelke-Parker M. E., et al., A canine distemper virus epidemic in Serengeti lions (Panthera leo). Nature 379, 441–445 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Kat P. W., Alexander K. A., Smith J. S., Munson L., Rabies and African wild dogs in Kenya. Proc. Biol. Sci. 262, 229–233 (1995). [DOI] [PubMed] [Google Scholar]
- 66.van de Bildt M. W. G., et al., Distemper outbreak and its effect on African wild dog conservation. Emerg. Infect. Dis. 8, 211–213 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Storm D. J., et al., Deer density and disease prevalence influence transmission of chronic wasting disease in white-tailed deer. Ecosphere 4, 1–14 (2013). [Google Scholar]
- 68.Benestad S. L., Mitchell G., Simmons M., Ytrehus B., Vikøren T., First case of chronic wasting disease in Europe in a Norwegian free-ranging reindeer. Vet. Res. (Faisalabad) 47, 88 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Cassirer E. F., et al., Spatio-temporal dynamics of pneumonia in bighorn sheep. J. Anim. Ecol. 82, 518–528 (2013). [DOI] [PubMed] [Google Scholar]
- 70.Manlove K., et al., “Mycoplasma ovipneumoniae in bighorn sheep: From exploration to action” in Wildlife Disease Ecology, Wilson K., Fenton A., Tompkins D., Eds. (Linking Theory to Data and Application, 2019), p. 368. [Google Scholar]
- 71.Blackwood J. C., Streicker D. G., Altizer S., Rohani P., Resolving the roles of immunity, pathogenesis, and immigration for rabies persistence in vampire bats. Proc. Natl. Acad. Sci. U.S.A. 110, 20837–20842 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Pisano S. R. R., et al., Spatiotemporal spread of sarcoptic mange in the red fox (Vulpes vulpes) in Switzerland over more than 60 years: Lessons learnt from comparative analysis of multiple surveillance tools. Parasit. Vectors 12, 521 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Daoust P. Y., et al., Detection and preliminary characterization of phocine distemper virus in a stranded harp seal (Pagophilus groenlandicus) from the gulf of St. Lawrence, Canada. J. Wildl. Dis. 56, 646–650 (2020). [DOI] [PubMed] [Google Scholar]
- 74.Herzog C. M., et al., Peste des petits ruminants virus transmission scaling and husbandry practices that contribute to increased transmission risk: An investigation among sheep, goats, and Cattle in Northern Tanzania. Viruses 12, 930 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.McDonald J. L., Delahay R. J., McDonald R. A., “Bovine tuberculosis in badgers: Sociality, infection and demography in a social mammal” in Wildlife Disease Ecology, Wilson K., Fenton A., Tompkins D., Eds. (Linking Theory to Data and Application, 2019), p. 342. [Google Scholar]
- 76.Hockings K. J., et al., Leprosy in wild chimpanzees. bioRxiv [Preprint] (2020). 10.1101/2020.11.10.374371. Accessed 5 December 2020. [DOI]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The CSV files and R code scripts data have been deposited in Dryad (https://datadryad.org/stash/share/ccIfMEUnp8yz43xYcG2XJR9q8zlIUnU8YtRbOYnBjyQ). All other study data are included in the article and/or SI Appendix.