Significance
Simple organisms manage to thrive in complex environments. Having memory about the environment is key in taking informed decisions. Physarum polycephalum excels as a giant unicellular eukaryote, being even able to solve optimization problems despite the lack of a nervous system. Here, we follow experimentally the organism’s response to a nutrient source and find that memory about nutrient location is encoded in the morphology of the network-shaped organism. Our theoretical predictions in line with our observations unveil the mechanism behind memory encoding and demonstrate the P. polycephalum’s ability to read out previously stored information.
Keywords: flow networks, adaptive networks, decision making, behavior
Abstract
The concept of memory is traditionally associated with organisms possessing a nervous system. However, even very simple organisms store information about past experiences to thrive in a complex environment—successfully exploiting nutrient sources, avoiding danger, and warding off predators. How can simple organisms encode information about their environment? We here follow how the giant unicellular slime mold Physarum polycephalum responds to a nutrient source. We find that the network-like body plan of the organism itself serves to encode the location of a nutrient source. The organism entirely consists of interlaced tubes of varying diameters. Now, we observe that these tubes grow and shrink in diameter in response to a nutrient source, thereby imprinting the nutrient’s location in the tube diameter hierarchy. Combining theoretical model and experimental data, we reveal how memory is encoded: a nutrient source locally releases a softening agent that gets transported by the cytoplasmic flows within the tubular network. Tubes receiving a lot of softening agent grow in diameter at the expense of other tubes shrinking. Thereby, the tubes’ capacities for flow-based transport get permanently upgraded toward the nutrient location, redirecting future decisions and migration. This demonstrates that nutrient location is stored in and retrieved from the networks’ tube diameter hierarchy. Our findings explain how network-forming organisms like slime molds and fungi thrive in complex environments. We here identify a flow networks’ version of associative memory—very likely of relevance for the plethora of living flow networks as well as for bioinspired design.
The ability to retain and access memories of past events when making decisions about future actions puts an individual into significant advantage over those lacking this ability (1). Consequently, the mechanisms of storing and recalling memories across species have evolved to be very complex (2). Even though the concept of memory has been traditionally associated with cognition (3), species devoid of nervous systems also possess abilities of memory encoding. Alternative strategies of nonneuronal organisms involve metabolic or gene expression pathways. As such, organisms cope in a multitude of ways, from epigenetic mechanisms and DNA inversion (4, 5) to tunable circadian clocks (6) and cell memory during chemotaxis (7). Yet, encoding memory by gene expression pathways takes at least half an hour in the simplest organisms (8) if not a full day (6), only allowing for slow decision processes.
The fast decision dynamics of 10 to 20 min of the often termed intelligent unicellular eukaryote Physarum polycephalum (9–11) suggest that so far unknown strategies to encode memory may exist. The network-shaped slime mold P. polycephalum is renowned for its capability to mount decisions that solve complex problems. P. polycephalum quickly reorganizes its tubular body plan to feed itself an optimal diet among multiple nutrient sources (10, 12), to find the shortest path between nutrients in a maze (13, 14), to connect nutrient sources with an optimized transport network (9), and to solve the two-armed bandit problem (15). Pure chemotaxis toward nutrient or avoidance of undesirable territory (16, 17) cannot account for the complexity of problems solved. P. polycephalum’s strategy to encode and read out memories about its environment remains unknown.
In the process of decision making, the network of P. polycephalum’s body constantly reorganizes its actomyosin-lined tubes. Actomyosin cortex drives rhythmic cross-sectional contractions of tubes (18). The contractions are spatially organized in a network-spanning peristaltic wave (19, 20). Contractions displace the cytoplasm in the tubes, thereby generating network-wide shuttle flows. Upon encountering a nutrient stimulus, tube contractions change to propagate the signal by fluid flow (21). However, the change in the contractions is transient (21, 22), indicating the existence of another mechanism that facilitates long-term memory encoding in the network of P. polycephalum.
The complex decisions of P. polycephalum emerge by migration or changes in its network morphology. Network morphology, in particular the hierarchy in tube diameters, is controlling flow-based transport within the network (23, 24). Migration is itself controlled by cytoplasmic flows (25–28) and is thus also governed by network morphology. This suggests that network morphology could be key to elucidating the memory-encoding abilities of the nonneural organism.
Here, we investigate how the location of a nutrient source is encoded in the network morphology of P. polycephalum. By analyzing the course of a network’s response to a nutrient stimulus in experiments, we find that the organism quickly imprints the stimulus by local tube dilation at the expense of other tubes shrinking, thereby setting up a new hierarchy of tube diameters. The signal to dilate tubes is propagated across the network by cytoplasmic flows generated by peristaltic contractions of the tubes, resulting in a permanent change in tube diameters. Based on our observations, we theoretically formulate a mechanism of encoding the location of a nutrient stimulus into the network hierarchy: the stimulus triggers the release of a chemical agent that causes the gel-like tube walls to soften, resulting in a significant dilation of tubes receiving sufficient soluble agent. The chemical agent propagates by contraction-driven cytoplasmic flows, initiating dilation downstream of the stimulus and thus, propagating the information about the stimulus location. Numerical solution of the theoretical model correctly predicts the experimentally observed flow-dependent tube diameter response to the stimulus—generating the new network hierarchy. Finally, we show that memories encoded in network hierarchy are read out as network morphology is shaping the direction of future migration. This strategy to encode information by strengthening existing transport connections close to the stimulus reminisces of associative memory formation and thus may be important for living flow networks in general.
Results
Changes in Tube Diameter Hierarchy Imprint Nutrient Stimulus Position.
To study the response of P. polycephalum to nutrient stimuli, we collected time series of bright-field images of the organism while foraging over approximately 5 h, during which a nutrient stimulus was applied as a single local source in close proximity to the network (Fig. 1). Within 45 min after stimulus application, the organism internally reorganized to create a new migration direction facing the stimulus. Subsequently (i.e., 90 and 310 min), the organism migrated toward the stimulus. At 310 min, the organism almost fully consumed the nutrient source and continued to forage. Strikingly, a ring of thick tubes around the consumed nutrient source imprinted the stimulus location in the network. This observation ignited the idea that tube diameters may encode the location of a nutrient source. Given that P. polycephalum is known to make decisions even within 10 to 20 min, we next focused on the immediate response after the stimulus was applied.
Fig. 1.
Memory of a nutrient stimulus’ position is encoded in network hierarchy. Bright-field images of a foraging P. polycephalum network subject to a localized nutrient stimulus (red arrow) applied at 0 min. The network previously migrating to the right reorganizes migration direction facing the nutrient within 45 min. Subsequently, nutrient is exhausted (90 min) until foraging is resumed (310 min). Nutrient location is imprinted in the network hierarchy by thick tubes formed around the nutrient source—persisting long after the nutrient is consumed.
To quantify network morphology and its dynamics in response to nutrient stimuli, we trimmed the specimen and analyzed networks with a stable morphology (i.e., before the onset of migration and without overt reaction to microscope light). We followed the initial reorganization during the 45 min after stimulus application (Fig. 2). We subsequently analyzed the time series of bright-field images to quantify the dynamics of tube diameters. A tube designates a segment between two network vertices. By diameter, we refer to the diameter trend of the rhythmically contracting tube in order to identify long-lasting changes in the network (Materials and Methods and SI Appendix). The network rapidly acquires a new spatial distribution of tube diameters within about 15 min after stimulus application—a pattern that persists until the end of the experiment (45 min), when the organism starts to migrate toward the stimulus.
Fig. 2.
Rapidly after nutrient stimulus application, hierarchy of tube diameters changes, establishing a new migration direction. (A) Bright-field images of a network before and after the application of a nutrient stimulus (red arrow). A new migration direction is being created at the top of the network. (B) Relative tube growth over the 45 min after stimulus (red dot) application. While overall mass is redistributed from the bottom to the top of the network, close to the stimulus site, initially larger tubes lose less mass, thus increasing network hierarchy. N(tubes) = 2,165.
Initially, application of the stimulus causes a large-scale increase in diameter of the tubes in immediate proximity to the stimulus location and a decrease in tube volume farther away from the stimulus location (Fig. 2A). Close inspection of the stimulus-induced relative changes in tube diameter across the network reveals spatial heterogeneity in the response: the diameters of the thick tubes directed toward the nutrient stimulus increase, while the diameters of thinner tubes in general decrease—the more the farther the distance from the stimulus or the farther from the thick tubes directed toward the stimulus location (Fig. 2B). Altogether, this heterogeneous response increases the hierarchy in network tube diameters (SI Appendix, Fig. S1).
The observation that thinner tubes that are close to thick tubes do not shrink compared with those farther away from thick tubes correlates with the dispersion pattern of chemicals in networks (24) and thus, suggests that fluid flows-based transport is at the basis of the observed network reorganization.
Fluid Flow Propagates Stimulus into the Network.
To investigate if transport by flow is underlying the change in tube diameters, we sort all network tubes by their Euclidean distance to the stimulus location and display their diameter dynamics (Fig. 3). We find that the dilation of tubes propagates in a wave-like manner from the stimulus site at the speed of , corresponding to the speed of particles advected through the network, orders of magnitude slower than change in pressure (21) yet outpacing the speed by diffusion (SI Appendix, Fig. S2). The heterogeneous spread of the dilation front further excludes diffusion as driver of transport (SI Appendix, Fig. S3). Direct observation of flow shear rate during changes in tube diameters also explicitly rules out shear forces as driver (SI Appendix, Fig. S4).
Fig. 3.
Tube dilation propagates by flow transport velocity from stimulus site. Here depicted is the evolution of relative tube diameters in the entire network. Individual tubes are sorted by their Euclidean distance to the stimulus site. Stimulus time is denoted by the white vertical line. The speed of the dilation front triggered by stimulus matches flow advection velocity of P. polycephalum networks. N(tubes) = 2,165.
A remarkable feature of the observed process is the persistence of tube dilation. The new distribution of tube diameters is established within about 15 min of stimulus application and persists to the end of the experiment (45 min). The stability of the new tube diameters indicates a lasting change of the mechanical properties of the tube material caused by the stimulus that would allow withstanding the rapid movement of mass by shuttle flows throughout the network. The rapid and significant, up to twofold, dilation of tubes near the stimulus site suggests that a chemical agent acts on the mechanical properties of the tubes. Direct softening of tube wall would also account for the network-wide transient increase in contraction amplitude (SI Appendix, Fig. S5). Agent-driven softening of tube walls is in line with observations of migration fronts being softer than the remaining tubular network, arising from the difference in actomyosin organization (29–32).
Mechanism of Encoding Memory in Differential Tube Diameter Dynamics.
Experiments suggest the following mechanism to encode memory of a stimulus location into network hierarchy. Upon stimulus application, a soluble chemical agent gets released within the cytoplasm at the stimulus location. The chemical agent softens tube wall material and thereby, triggers tube dilation. This effect spreads throughout the network as the agent gets advected by cytoplasmic flows.
To test whether this mechanism can explain experiments, we build a theoretical model with physiological parameters (Materials and Methods). More precisely, we compute tube diameter dynamics that arise from peristaltic contraction-driven transport of the chemical agent within the flow for different, experimentally determined contraction frequencies of the organism.
As the networks’ response is dominantly graded with distance to stimulus site (Fig. 3), we focus on the dynamics within a single tube of network size directed toward the stimulus site only. The cylindrical tube of radius extends along the longitudinal axis . The thin shell of the active, elastic tube represents the actomyosin cortex that is enclosing the incompressible, low-Reynolds number cytoplasmic fluid (Re ). The cortex exerts stress in radial direction, where is the contractile stress of the cortex activity and is the elastic restoring stress of the tube wall. As the tube is long and slender, , the flow velocity of the cytoplasm caused by tube contractions follows Stokes equation simplified with lubrication approximation (33):
| [1] |
where denotes cytoplasm viscosity. To describe the peristaltic contractions, the contractile stress is set to , being the amplitude of the contraction-inducing cortex tension and being the contraction frequency. The elastic stress is considered linear due to the small thickness of the tube wall compared with the radius of the tube: , where is the elastic modulus of the tube wall, is the tube wall height, and is its resting radius (34). We model the softening effect of the time-averaged concentration of the chemical agent on the elastic modulus as
| [2] |
where is the elastic modulus of the unperturbed tube wall and is the time average of the agent concentration released at the site of the stimulus along the tube.
To average out concentration gradients arising solely due to shuttle flow, we time average the concentration of the chemical agent over two contraction periods, , where is the characteristic stimulus–response timescale of the elastic modulus. The transport of the chemical agent by fluid flow is described by Taylor dispersion (35, 36), which we extend by a decay term accounting for the chemical being degraded:
| [3] |
where is the molecular diffusivity and is the decay rate of the chemical agent. Note that we here aim to model the very quick sensing response of the organism on the timescale of tens of minutes, which precedes the engulfment of the nutrient stimulus on the timescale of hours. Therefore, we account for a one-time release of the chemical agent due to sensing only. Finally, the total mass in the tube is conserved:
| [4] |
giving rise to self-organized tube radii. As before, we use the term diameter to refer to diameter trend of the contracting tube averaged over two contraction periods.
Memory-Encoding Mechanism Predicts Flow-Driven Tube Diameter Dynamics in Agreement with Experiments.
We test the memory-encoding mechanism by simulating a one-time, local release of the softening agent and tracking the diameter dynamics along the closed tube as the chemical gets advected by flow. We distinguish diameter dynamics at two segments along the tube at increasing distances from the stimulus site (Fig. 4A). Shortly after stimulus release close to tube end, the tube segment closest to the stimulus site dilates, while the other reference segment farther away decreases in diameter—due to conservation of fluid volume. Only as time progresses does the tube segment farther downstream receive softening agent by flow driving it to dilate subsequently (SI Appendix, Fig. S6). Yet, the tube segment downstream does not dilate as much as the segment close to the stimulus site, thereby creating a hierarchy of tube diameters in our beforehand uniform tube. The hierarchy arises as tube segments downstream receive less agent. These different softening agent concentrations are not caused by agent’s decay, which is very slow (here, also exemplified by the long-term persistence of the dilation). Rather, the flow velocity at stimulus site is much slower than in the middle of the tube due to the eminent closed boundary at the end of the tube. Thus, most of the soluble agent stays close to its release site, while only a part gets advected, causing the delayed and decreased response downstream.
Fig. 4.
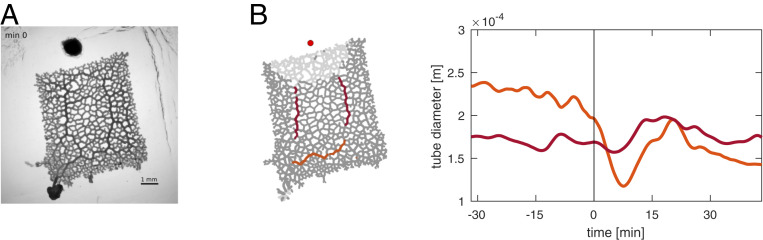
Theoretical model of elastic tube dilation triggered by flow-transported softening agent captures characteristic tube dynamics observed in the experiment. (A) Predictions of a theoretical model of a closed peristaltic tube (sketch) on the tube diameter dynamics at the marked segments. Releasing a soluble wall-softening agent (red symbol/vertical line) within the elastic tube predicts characteristic tube dilation and relaxation. Tube dilation response time (dotted line) is shifted in time due to the agent being transported by peristaltic flow. (B) A decrease in contraction frequency slowing down flows directly increases the tube segment’s response time until dilation. (C) Experimental tube diameter dynamics are fully classified into the two characteristic dynamics predicted by the model (sketch). The dynamics of the mean tube diameter averaged over each ensemble of tubes follow theoretically predicted tube dynamics. N(tubes) = 2,165. (D) Quantification of the response time until dilation in experimental datasets shows increase of response time with decreasing contraction frequency, in line with theory. Error bars show the full range of tube response times in every dataset. N(tubes) = 2,165, 486, 438, and 45 for 10, 8, 6, and 4 mHz, respectively.
We next aim to make a quantitative prediction from the model that exemplifies the crucial role of flow-based transport. To this end, we probe how the tube diameter response time is altered by changing flow velocities. Here, we use that contraction frequencies, which directly control flow velocities, vary naturally in P. polycephalum. We quantify as response time the time between stimulus application and minimal diameter in our tube segment farther along the tube (Fig. 4A) while decreasing contraction frequency (Fig. 4B). We find that the response time increases with decreasing contraction frequency, underlining the central role of flow-based transport in setting up the hierarchy in response to the stimulus.
Having in hand these two predictions on the tube diameters dynamics close and far to the stimulus and the response time, we return to our experimental data. We automatically sort all tubes in the network [N(tubes) = 2,165] by their response to the stimulus (described in SI Appendix), resulting in the two characteristic dynamics predicted by the model (Fig. 4C), with pure tube dilation close to the stimulus and tube shrinkage and subsequent dilation farther from the stimulus. This tube behavior is robust among all datasets (SI Appendix, Fig. S9–S13). Predicted dynamics along a single tube and experimentally observed dynamics within a network strongly resemble each other apart from two factors that arise due to the simplification of a single tube in the model. First, the magnitude of dilation and shrinkage is directly tied to the total volume of the tube (37) and as such, smaller in the single tube compared with the voluminous network. Second, in a network, the softening agent is diluted in the multitude of tubes: the farther it gets from the stimulus site, the less softening agent gets to an individual tube. This results in an on average smaller dilation and subsequent tube shrinkage. Taking these geometry-related considerations into account, the resemblance of predicted dynamics and observations is striking.
Finally, we categorize our experimental datasets by contraction frequency (SI Appendix, Fig. S7) and quantify the response time across the networks (Fig. 4D). As predicted, the observed response time increases as contraction frequency decreases—despite the very different morphologies and sizes of the networks. Taken together with the dynamics of tube diameters, this agreement of data and prediction confirms that the advection of a softening agent by fluid flows imprints nutrient location into a specific change in hierarchy of tube diameters.
Encoded Memory Is Read Out.
Taken together, our experiments and model show that a nutrient stimulus changes the hierarchy of tube diameters and thereby, imprints its location into the network. To state that the imprint in network hierarchy poses a memory for the organism, we need to test if the memory (i.e., network hierarchy) can be read out. Does the network respond differently to a new nutrient stimulus when previously having encountered one in the same direction or not?
Directly testing this is a futile approach as for P. polycephalum, there are never two identical networks to compare dynamics with and without memory. Furthermore, the innate tendency of the network to reorganize its topology and migrate becomes adverse to quantification beyond the time window used here. Fortunately, every network comes with a given hierarchy of tube diameters (Fig. 5A), with particularly thick tubes formed in response to nutrient stimuli (9, 13). We here use this fact to test if the memory of previous stimuli represented by thicker tubes affects the response to a new nutrient stimulus.
Fig. 5.
Network reads out memory encoded in network hierarchy by previous stimuli. (A) Bright-field image of the plasmodial network right after stimulus application as in Fig. 2. (B) Within the part of the network overall undergoing shrinkage (Fig. 4C), thick transport tubes positioned close (red) and far (orange) with respect to stimulus differ in dynamics. The average tube diameters of the tubes closer by flow-based travel time to stimulus undergo negligible shrinkage and recover their prestimulus diameter, whereas the tubes farther away shrink overall permanently.
At first sight, our analysis of Fig. 4C identifies two characteristic tube dynamics depending on Euclidean distance to food stimulus only. This suggests that initial tube diameter does not impact stimulus response. However, given the insight gained from our model, it is clear that particularly thick tubes matter for the stimulus response as thicker tubes have higher flow velocities (24) and thus, more effectively transport the softening agent. Indeed, analyzing only the dynamics of thick tubes highlighted in Fig. 5B reveals that thick tubes starting close to the stimulus hardly undergo a decrease in the diameter next to thin tubes drastically shrinking in an overall shrinking domain. Thus, at close inspection tube diameter hierarchy does impact stimulus response. Yet, memory retrieval is also not a mere self-reinforcement of thick tubes as observed in long-term network adaptation for P. polycephalum (9): Fig. 5 also highlights an even thicker tube far from the stimulus site that drastically shrinks (50% loss in diameter). The faraway tube is far in travel time by flow from the stimulus and therefore, hardly receives softening agent.
Hence, memories stored in the hierarchy of tube diameters and particularly in the location of thick tubes are subsequently layered on top of each other, with every new stimulus differentially reinforcing and weakening existing thick tubes in superposition of existing memories (SI Appendix, Fig. S8).
The key to why tube hierarchy represents memory and impacts organism behavior is the flow. Flows are the means to migrate toward a nutrient source. Ingeniously, these flows are used to enhance transport toward a nutrient source by growing specifically those tubes that are quickest to be reached from the stimulus site by flow-based transport. Having thick tubes as memories of previous stimuli positioned close to the stimulus allows the new stimuli to spread more quickly and reorganize mass transport more efficiently.
Discussion
Our observation of a nutrient stimulus leaving an imprint on network morphology leads to the discovery of memory formation in the living flow network P. polycephalum. We showed that the process of stimulus encoding starts with a local softening of tube walls, creating a stimulus-specific hierarchy in tube diameters. Both experiments and model show that softening is caused by a chemical agent transported by flows, propagating graded tube growth across the network. While the softening agent flows through the network, it reads out the existing hierarchy of tube diameters as it is encoding a new stimulus, thus using information stored by previous stimuli.
The quick process of memory formation by changing network hierarchy we observe has a long-lasting effect on the network as flow patterns are irretrievably changed, thus governing long-term network reorganization (9). An idle network decreases the established hierarchy of its tube diameters by pruning away the thin tubes first (23, 24), the tubes surviving longest being the tubes directly bearing the memory of the nutrient stimulus that led to their growth. Such persistence of the encoded memory, as well as the ability of the network to encode multiple consecutive stimuli, surpasses transient adaptation to nutrient source.
The identity of the chemical agent causing tube softening is still unknown. However, the phenomenon of actomyosin softening has been observed across living organisms [e.g., in fibroblasts (38) or blood vessel endothelial cells (39)]. The decreased density of the actomyosin cortex measured in the migration front of P. polycephalum (30) is in line with the softening hypothesis. Perhaps the most likely candidate for the chemical agent is adenosine triphosphate (ATP), whose concentration is found to be twice as high at the migration front compared with the back of the organism (40), the migration front formation here being a direct result of stimulus sensing.
Softening of tube walls to trigger their immediate growth is a mechanism that allows for very quick changes in tube diameter hierarchy. The timescale of less than 15 min observed by us explains P. polycephalum’s fast decisions within 10 to 20 min (9–11) that outcompete other basal organisms in speed (6, 8). Our observations show that these memories can be overwritten or reinforced as tubes close in flow-based travel times to stimuli keep being fueled. Finally, P. polycephalum’s ability to highlight the shortest path in a maze (13, 14) or solve the traveling salesman problem (41) seems the logical result of memories being formed. By identifying the mechanism the organism uses to initially encode the nutritive stimulus, we present the missing piece of the puzzle connecting nutrient encounter and long-term network reorganization that P. polycephalum is famous for (9).
The concept that tube diameter hierarchy serves as memory not only elucidates the remarkable problem-solving capabilities of P. polycephalum, but also demonstrates its ability to mimic phenomena known from higher organisms, in this case synaptic facilitation (42) or synaptic plasticity (43) and reinforcement learning (44). Demonstrating the ability of the network to exhibit a phenomenon reminiscent of associative memory (45) may very well be of relevance for the plethora of living flow networks and contribute to biologically inspired design for biomimetic materials and soft robots (46).
Materials and Methods
Culturing and Imaging of P. polycephalum.
Plasmodial networks were prepared from microplasmodia grown in a liquid culture using the medium by Daniel and Rusch (47) with hematin (5 mg/mL) instead of chicken embryo extract (48). The networks were imaged 24 to 36 h after plating on 1.5% agar and incubated under microscope light for 1 h after trimming to decrease the influence of light and cutting on the tube contraction (22). The plasmodia were imaged with a Zeiss Axio Zoom V.16 microscope equipped with a Hamamatsu ORCA-Flash 4.0 digital camera and a Zeiss PlanNeoFluar 1×/0.25 objective. The Zeiss Zen 2 (Blue Edition) software was used for imaging. An image was acquired every 3 s. Stimuli were applied by placing small pellets of heat-killed HB101 bacteria on the agar using an Eppendorf Microloader pipette tip. In two experiments presented in Movies S3 and S5, of a solution containing 0.5 M glucose and 0.1 M leucine was placed on the agar close to the network as a nutrient stimulus.
Image Analysis.
First, the network skeletons, pixel intensities, and tube radii dynamics were extracted using a custom-written MATLAB (The Mathworks) code (22). Subsequently, tube diameters are calculated from the time average of tube radii over 100 frames, thereby averaging out radii contractions.
Numerical Simulations.
The equations of the theoretical model were solved numerically in a custom-written MATLAB (The Mathworks) code using a theta-weighted Crank–Nicholson scheme with closed boundary conditions. Initially, the tube has a uniform radius . The softening agent is introduced at stimulus time, growing exponentially in time to a final concentration of 60.0 at 4 min. In space, the stimulus is represented as a narrow Gaussian concentration profile close to the left end of the tube. The parameters used in the simulations are as follows: resting tube radius , tube length = 0.5 cm, contraction frequency /120 s (32), wavelength of the traveling wave , dynamic viscosity of cytoplasm Ns/m2 (49), tube wall height , amplitude of contraction-inducing cortex tension (21), molecular diffusivity of small chemical species , and decay rate of the chemical agent . The parameters give rise to Reynolds number . The effective resting elastic modulus is from Young’s modulus of 100 Pa (20, 50), and for the feedback of chemical agent on cortex mechanics, and were chosen to result in at the minimum.
Supplementary Material
Acknowledgments
We thank Natalie Andrew for Movie S3. M.K. acknowledges the support of International Max Planck Research School for Physics of Biological and Complex Systems. This work was supported by the Max Planck Society.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
See online for related content such as Commentaries.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2007815118/-/DCSupplemental.
Data Availability
All study data are included in the article and/or Supporting Information.
References
- 1.Nairne J. S., VanArsdall J. E., Pandeirada J. N., Blunt J. R., Adaptive memory: Enhanced location memory after survival processing. J. Exp. Psychol. Learn. Mem. Cogn. 38, 495–501 (2012). [DOI] [PubMed] [Google Scholar]
- 2.Shohamy D., Daw N. D., Integrating memories to guide decisions. Curr Opin Behav Sci 5, 85–90 (2015). [Google Scholar]
- 3.Redish D. A., Mizumori S. J. Y., Memory and decision making. Neurobiol. Learn. Mem. 117, 1–3 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Casadesús J., D’Ari R., Memory in bacteria and phage. Bioessays 24, 512–518 (2002). [DOI] [PubMed] [Google Scholar]
- 5.Kinoshita T., Seki M., Epigenetic memory for stress response and adaptation in plants. Plant Cell Physiol. 55, 1859–1863 (2014). [DOI] [PubMed] [Google Scholar]
- 6.Pattanayak G. K., Phong C., Rust M. J., Rhythms in energy storage control the ability of the cyanobacterial circadian clock to reset. Curr. Biol. 24, 1934–1938 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Skoge M., et al. , Cellular memory in eukaryotic chemotaxis. Proc. Natl. Acad. Sci. U.S.A 111, 14448–14453 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Amir A., Kobiler O., Rokney A., Oppenheim A. B., Stavans J., Noise in timing and precision of gene activities in a genetic cascade. Mol. Syst. Biol. 3, 1–10 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tero A., et al. , Rules for biologically inspired adaptive network design. Science 327, 439–442 (2010). [DOI] [PubMed] [Google Scholar]
- 10.Latty T., Beekman M., Speed-accuracy trade-offs during foraging decisions in the acellular slime mould Physarum polycephalum. Proc. Biol. Sci. 278, 539–545 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Meyer B., Ansorge C., Nakagaki T., The role of noise in self-organized decision making by the true slime mold Physarum polycephalum. PloS One 12, e0172933 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dussutour A., Latty T., Beekman M., Simpson S. J., Amoeboid organism solves complex nutritional challenges. Proc. Natl. Acad. Sci. U.S.A 107, 4607–4611 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Nakagaki T., Yamada H., Tóth Á., Maze-solving by an amoeboid organism. Nature 407, 470 (2000). [DOI] [PubMed] [Google Scholar]
- 14.Bonifaci V., Mehlhorn K., Varma G., Physarum can compute shortest paths. J. Theor. Biol. 309, 121–133 (2012). [DOI] [PubMed] [Google Scholar]
- 15.Reid C. R., et al. , Decision-making without a brain: How an amoeboid organism solves the two-armed bandit. J. R. Soc. Interface 13, 20160030 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Smith-Ferguson J., Reid C. R., Latty T., Beekman M., Hänsel, Gretel and the slime mould—how an external spatial memory aids navigation in complex environments. J. Phys. D Appl. Phys. 50, 414003 (2017). [Google Scholar]
- 17.Reid C. R., Latty T., Dussutour A., Beekman M., Slime mold uses an externalized spatial “memory” to navigate in complex environments. Proc. Natl. Acad. Sci. U.S.A 109, 17490–17494 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kamiya N., Physical and chemical basis of cytoplasmic streaming. Annu. Rev. Plant Physiol. 32, 205–236 (1981). [Google Scholar]
- 19.Alim K., Amselem G., Peaudecerf F., Brenner M. P., Pringle A., Random network peristalsis in Physarum polycephalum organizes fluid flows across an individual. Proc. Natl. Acad. Sci. U.S.A. 110, 13306–13311 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Julien J. D., Alim K., Oscillatory fluid flow drives scaling of contraction wave with system size. Proc. Natl. Acad. Sci. U.S.A. 115, 10612–10617 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Alim K., Andrew N., Pringle A., Brenner M. P., Mechanism of signal propagation in Physarum polycephalum. Proc. Natl. Acad. Sci. U.S.A. 114, 5136–5141 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bäuerle F. K., Kramar M., Alim K., Spatial mapping reveals multi-step pattern of wound healing in Physarum polycephalum. J. Phys. D Appl. Phys. 50, 434005 (2017). [Google Scholar]
- 23.Baumgarten W., Hauser M. J. B., Functional organization of the vascular network of Physarum polycephalum. Phys. Biol. 10, 026003 (2013). [DOI] [PubMed] [Google Scholar]
- 24.Marbach S., Alim K., Andrew N., Pringle A., Brenner M. P., Pruning to increase Taylor dispersion in Physarum polycephalum networks. Phys. Rev. Lett. 117, 178103 (2016). [DOI] [PubMed] [Google Scholar]
- 25.Kuroda S., Takagi S., Nakagaki T., Ueda T., Allometry in Physarum plasmodium during free locomotion: Size versus shape, speed and rhythm. J. Exp. Biol. 218, 3729–3738 (2015). [DOI] [PubMed] [Google Scholar]
- 26.Zhang S., Guy R. D., Lasheras J. C., del Álamo J. C., Self-organized mechano-chemical dynamics in amoeboid locomotion of Physarum fragments. J. Phys. D Appl. Phys. 50, 204004 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rodiek B., Takagi S., Ueda T., Hauser M. J. B., Patterns of cell thickness oscillations during directional migration of Physarum polycephalum. Eur. Biophys. J. 44, 349–358 (2015). [DOI] [PubMed] [Google Scholar]
- 28.Lewis O. L., Zhang S., Guy R. D., del Alamo J. C., Coordination of contractility, adhesion and flow in migrating Physarum amoebae. J. R. Soc. Interface 12, 20141359 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Oettmeier C., Döbereiner H. G., A lumped parameter model of endoplasm flow in Physarum polycephalum explains migration and polarization-induced asymmetry during the onset of locomotion. PloS One 14, e0215622 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Oettmeier C., Lee J., Döbereiner H. G., Form follows function: Ultrastructure of different morphotypes of Physarum polycephalum. J. Phys. D Appl. Phys. 51, 134006 (2018). [Google Scholar]
- 31.Tero A., Kobayashi R., Nakagaki T., A coupled-oscillator model with a conservation law for the rhythmic amoeboid movements of plasmodial slime molds. Physica D 205, 125–135 (2005). [Google Scholar]
- 32.Rieu J. P., Delanoë-Ayari H., Takagi S., Tanaka Y., Nakagaki T., Periodic traction in migrating large amoeba of Physarum polycephalum. J. R. Soc. Interface 12, 20150099 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Takagi D., Balmforth N. J., Peristaltic pumping of viscous fluid in an elastic tube. J. Fluid Mech. 672, 196–218 (2011). [Google Scholar]
- 34.Vajravelu K., Sreenadh S., Devaki P., Prasad K. V., Peristaltic pumping of a Casson fluid in an elastic tube. J. Appl. Fluid Mech. 9, 1897–1905 (2016). [Google Scholar]
- 35.Taylor G. I., Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. A 219, 186–203 (1953). [Google Scholar]
- 36.Aris R., Taylor G. I., On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc. A 235, 67–77 (1956). [Google Scholar]
- 37.Sedzinski J., et al. , Polar actomyosin contractility destabilizes the position of the cytokinetic furrow. Nature 476, 462 (2011). [DOI] [PubMed] [Google Scholar]
- 38.Martens J. C., Radmacher M., Softening of the actin cytoskeleton by inhibition of myosin II. Pflügers Archiv 456, 95–100 (2008). [DOI] [PubMed] [Google Scholar]
- 39.Fels J., Jeggle P., Kusche-Vihrog K., Oberleithner H., Cortical actin nanodynamics determines nitric oxide release in vascular endothelium. PloS One 7, e41520 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ueda T., Matsumoto K., Akitaya T., Kobatake Y., Spatial and temporal organization of intracellular adenine nucleotides and cyclic nucleotides in relation to rhythmic motility in Physarum plasmodium. Exp. Cell Res. 162, 486–494 (1986). [DOI] [PubMed] [Google Scholar]
- 41.Zhu L., Aono M., Kim S. J., Hara M., Amoeba-based computing for traveling salesman problem: Long-term correlations between spatially separated individual cells of Physarum polycephalum. Biosystems 112, 1–10 (2013). [DOI] [PubMed] [Google Scholar]
- 42.Jackman S. L., Regehr W. G., The mechanisms and functions of synaptic facilitation. Neuron 94, 447–464 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lamprecht R., LeDoux J., Structural plasticity and memory. Nat. Rev. Neurosci. 5, 45–54 (2004). [DOI] [PubMed] [Google Scholar]
- 44.Neftci E. O., Averbeck B. B., Reinforcement learning in artificial and biological systems. Nat. Mach. Intell. 1, 133–143 (2019). [Google Scholar]
- 45.Takeuchi T., Duszkiewicz A. J., Morris R. G., The synaptic plasticity and memory hypothesis: Encoding, storage and persistence. Philos. Trans. R. Soc. B 369, 20130288 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Nakajima K., Li T., Hauser H., Pfeifer R., Exploiting short-term memory in soft body dynamics as a computational resource. J. R. Soc. Interface 11, 20140437 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Daniel J. W., Rusch H. P., The pure culture of Physarum polycephalum on a partially defined soluble medium. Microbiology 25, 47–59 (1961). [DOI] [PubMed] [Google Scholar]
- 48.Daniel J. W., Kelley J., Rusch H. P., Hematin–requiring plasmodial myxomycete. J. Bacteriol. 84, 1104–1110 (1962). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Swaminathan R., Hoang C. P., Verkman A. S., Photobleaching recovery and anisotropy decay of green fluorescent protein GFP-S65T in solution and cells: Cytoplasmic viscosity probed by green fluorescent protein translational and rotational diffusion. Biophys. J. 72, 1900–1907 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Alonso S., Radszuweit M., Engel H., Bär M., Mechanochemical pattern formation in simple models of active viscoelastic fluids and solids. J. Phys. D Appl. Phys. 50, 434004 (2017). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or Supporting Information.