The automatic construction of bootstrap confidence intervals

Abstract

The standard intervals, e.g., $\widehat{\theta }\pm 1.96\widehat{\sigma }$ for nominal 95% two-sided coverage, are familiar and easy to use, but can be of dubious accuracy in regular practice. Bootstrap confidence intervals offer an order of magnitude improvement–from first order to second order accuracy. This paper introduces a new set of algorithms that automate the construction of bootstrap intervals, substituting computer power for the need to individually program particular applications. The algorithms are described in terms of the underlying theory that motivates them, along with examples of their application. They are implemented in the R package bcaboot.

1. Introduction

Among the most useful, and most used, of statistical constructions are the standard intervals

$$\widehat{\theta }\pm z^{(\alpha )}\widehat{\sigma },$$ (1.1)

giving approximate confidence statements for a parameter θ of interest. Here $\widehat{\theta }$ is a point estimate, $\widehat{\sigma }$ an estimate of its standard error, and z^(α) the αth quantile of a standard normal distribution. If α = 0.975, for instance, interval (1.1) has approximate 95% coverage.

A prime virtue of the standard intervals is their ease of application. In principle, a single program can be written that automatically produces intervals (1.1), say with $\widehat{\theta }$ a maximum likelihood estimate (MLE) and $\widehat{\sigma }$ its bootstrap standard error. Accuracy, however, can be a concern: if X ~ Poisson(θ) is observed to be 16, then (1.1) gives 95% interval (8.16,23.84) for θ, compared to the exact interval (9.47,25.41) (obtained via the usual Neyman construction). Modern theory and computer power now provide an opportunity for the routine use of more accurate intervals, this being the theme of what follows.

Exact intervals for θ are almost never available in the presence of nuisance parameters, which is to say, in most applied settings. This accounts for the popularity of the standard intervals. Bootstrap confidence intervals (Efron, 1987; DiCiccio and Efron, 1996) were proposed as general-purpose improvements over (1.1). They are second - order accurate, having the error in their claimed coverage probabilities going to zero at rate O(1/n) in sample size compared to the first-order rate $O(1/\sqrt{n})$ for standard intervals. This is often a substantial improvement, yielding bootstrap limits (9.42,25.53) compared to the exact limits (9.47,25.41) in the Poisson problem.¹

Bootstrap standard error estimates have been used an enormous number of times, perhaps in the millions, but the story is less happy for bootstrap confidence intervals. Various limitations of previous bootstrap packages such as bootstrap have discouraged everyday use. The new suite of programs introduced here, bcaboot, has been designed to overcome four impediments to the routine “automatic” application of second-order accurate bootstrap confidence intervals:

1. For nonparametric intervals, in problems with n original observations, previous programs required n extra recomputations of the statistic of interest (for the assessment of the acceleration a) in addition to the B ~ 2000 replications needed to estimate the bootstrap histogram. This becomes a burden for contemporary sample sizes of say n = 10, 000. The new algorithm bcajack introduces a “folding” mechanism that groups the observations, say into 50 groups of size 200 each, now with n effectively only 50. This is done without requiring any extra intervention from the user. An alternate nonparametric confidence interval algorithm bcajack2 employs a novel theoretical approach to calulate the acceleration a without any need for the extra n recomputations

2. Parametric models, such as multivariate normal or logistic regression, are where bootstrap intervals show themselves to best advantage, but previous packages have required case-by-case special forms from the statistician. The new algorithm bcapar allows the user to calculate bootstrap replications using whatever function gave the original estimate, irregardless of its form. Again, this has to do with a novel characterization of the accel- eration a.

3. Both bcajack and bcapar allow the user to separately calculate the bootstrap replications. This is advantageous for large-scale applications where each replication takes substantial time, and where distributed computation may be necessary.

4. bcajack and bcapar provide estimates of the interval endpoints Monte Carlo errors, helping guide the choice of the number of bootstrap replications B necessary for reasonable accuracy. These are based on a novel use of jackknife theory, which requires almost no increase in computation.

Figure 1 concerns an application of bcajack. The diabetes data, Table 1 of Efron (2004), comprises n = 442 vectors in $\mathcal{R}$¹¹,

$$v_i=\left(x_i,y_i\right),i=1,2,\dots ,442;$$ (1.2)

x_i is a 10-vector of baseline predictors — age, sex, BMI, etc. — for patient i, while y_i is a real-valued measure of disease progression one year later. The data consists of

$$\mathit{X}\text{and}\mathit{y},$$ (1.3)

where X is the n×10 matrix with ith row x_i, and y the n-vector of y_i values. The full data set can be expressed as an n×11 matrix v, having v_i as the ith row.

Fig. 1.

Two-sided nonparametric confidence limits for adjusted R², diabetes data, plotted vertically versus nominal converage level. Bootstrap (solid curves); standard intervals (dotted curves). Small red vertical bars indicate Monte Carlo error in the bootstrap curves, from program bcajack (Section 3). Horizontal dashed line shows $\widehat{\theta }=0.507$, seen to lie closer to upper bootstrap limits than to lower ones.

Table 1.

Lower and upper confidence limits for θ having observed $\widehat{\theta }=1$ from the model $\widehat{\theta }\sim \theta ·{\text{Gamma}}_{10}/10$.

α	standard	pctile	bc	bca	exact
.025	.38	.48	.52	.585	.585
.16	.69	.69	.74	.764	.764
.84	1.31	1.31	1.39	1.448	1.448
.975	1.62	1.71	1.80	2.086	2.085

Suppose we are interested in the adjusted R² for ordinary linear regression of y on X, with point estimate $\widehat{\theta }=0.507$ for the diabetes data,

$${\widehat{R}}_{adj}^2={\widehat{R}}^2-(1-{\widehat{R}}^2)p/(n-p-1)$$ (1.4)

with n = 442 and p = 10 here. How accurate is this estimate?

The heavy curves in Figure 1 describe the lower and upper limits of nonparametric bootstrap confidence intervals for the true θ, with nominal two-sided coverages ranging from 68% at the left of the figure to 95% at the right. At 68%, the bootstrap limits are

$$(0.462,0.529),$$ (1.5)

compared to the standard limits (dotted curves)

$$(0.475,0.538),$$ (1.6)

from (1.1) with α = 0.84. The bootstrap standard error for $\widehat{\theta }$ was $\widehat{\sigma }=0.032$, so the bootstrap limits are shifted downward from the standard intervals by somewhat less than half a standard error. Figure 1 says that $\widehat{\theta }$ is substantially biased upward for the adjusted R², requiring downward corrections for second-order accuracy. (Bias corrections for $\widehat{\theta }$ are briefly discussed near the end of Section 3.)

The calculations for Figure 1 came from the nonparametric bootstrap confidence interval program bcajack discussed in Section 3. The call was

$$\mathrm{bcajack}(v,2000,\text{radj}),$$ (1.7)

with v the diabetes data matrix, B = 2000 the number of bootstrap replications, and radj a program for $\widehat{\theta }$: for any matrix v* having 11 columns radj(v*) linearly regresses the 11th column on the first 10 and returns the adjusted R².

There is nothing special about adjusted R². For any parameter of interest, say $\widehat{\varphi }=r(\mathit{v})$, the call bcajack(v,2000,r) produces the equivalent of Figure 1. All effort has been transferred from the statistician to the computer. It is in this sense that bcajack deserves to be called “automatic”.

Was the number of bootstrap replications, B = 2000, too many or perhaps too few? bcajack also provides a measure of internal error, an estimate of standard deviation of the Monte Carlo bootstrap confidence limits due to stopping at B replications. The vertical red bars in Figure 1 indicate ± one such internal standard deviation. In this example, B = 2000 was sufficient and not greatly wasteful. Stopping at B= 1000 would magnify the Monte Carlo error by about $\sqrt{2}$, perhaps becoming uncomfortably large at the lower bootstrap confidence limits.

Parametric bootstrap confidence intervals are inherently more challenging to automate. All nonparametric problems have the same basic structure, whereas parametric models differ from each other in their choice of sufficient statistics. Working within this limitation, the program bcapar (Section 4) minimizes the required input from the statistician: bootstrap replications of the statistic of interest along with their bootstrap sufficient statistics. This is particularly convenient for generalized linear models, where the sufficient vectors are immediately available.

One can ask whether second-order corrections are worthwhile in ordinary situations. The answer depends on the importance attached to the value of the parameter of interest θ. As a point of comparison, the usual student-t intervals $\overline{x}\pm t_n^{(\alpha )}\widehat{\sigma }$ make corrections of order only $O(\widehat{\sigma }/n)$ to (1.1), while the bootstrap corrections are $O(\widehat{\sigma }/\sqrt{n})$. An obvious comment, but a crucial one, is that modern computing power makes B = 2000 bootstrap replications routinely feasible in a great range of real applications. (The calculations for Figure 1 took three seconds.)

We proceed as follows: Section 2 gives a brief review of bootstrap confidence intervals. Section 3 discusses nonparametric intervals and their implementation in bcajack. Parametric bootstrap intervals, and their implementation by the program bcapar, are discussed in Section 4. Comments on the programs appear in the Appendix.

Barndorff-Nielsen (1983) initiated the study of advanced likelihood methods for the construction of second-order (and higher) accurate confidence intervals; see for instance Barndorff-Nielsen and Cox (1994). Skovgaard (1985) and several others carried on this line of work. The result has been an elegant asymptotic theory, but one that has proved difficult to apply in practice. More recently, Pierce and Bellio(2017) have developed a more practical version of likelihood confidence intervals, based on deviance residuals in exponential families, as is the work of DiCiccio and Young (2008). An example of the former is given in section Section 4.

The bca bootstrap approach, featured here, is less elegant than the likelihood theory, but easier to use. As the automatic in our title implies, the new bca algorithms have been developed with ease of application in mind. The basic bca theory is reviewed in what follows, without rigorous justification. DiCiccio and Efron (1996) give more of the background, while Hall (1992) is the standard theoretical reference.

2. Bootstrap confidence intervals

We present a brief review of the bca theory for bootstrap confidence intervals, which underlies algorithms bcajack and bcapar. More thorough expositions appear in DiCiccio and Efron (1996) and Chapter 11 of Efron and Hastie (2016).

The standard method level-α endpoint

$${\widehat{\theta }}_{\text{stan}}(\alpha )=\widehat{\theta }+z^{(\alpha )}\widehat{\sigma }$$ (2.1)

depends on two summary statistics, $\widehat{\theta }$ and $\widehat{\sigma }$. The bca level-α endpoints (Efron, 1987),

$${\widehat{\theta }}_{\text{bca}}(\alpha )=G^{-1}\mathrm{\Phi }\left({\widehat{z}}_0+\frac{{\widehat{z}}_0+z^{(\alpha )}}{1-\widehat{a}\left({\widehat{z}}_0+z^{(\alpha )}\right)}\right)$$ (2.2)

as plotted in Figure 1 (Φ the standard normal cdf), require three other quantities: G(·), the cdf of the bootstrap distribution of $\widehat{\theta }$, and two auxilliary constants discussed below: the bias corrector ${\widehat{z}}_0$ and the acceleration $\widehat{a}$. In almost all cases, G, ${\widehat{z}}_0$, and $\widehat{a}$ must be obtained from Monte Carlo simulations. Doing the bca calculations in fully automatic fashion is the goal of the programs presented in this paper.

The standard intervals (1.1) take literally the first-order approximation

$$\widehat{\theta }\stackrel{\cdot }{\sim }\mathcal{N}\left(\theta ,{\sigma }^2\right),$$ (2.3)

which can be quite inaccurate in practice. A classical tactic is to make a monotone transformation m(θ) to a more favorable scale,

$$\widehat{\varphi }=m(\widehat{\theta })\text{and}\varphi =m(\theta ),$$ (2.4)

compute the standard interval on the ϕ scale, and map the endpoints back to the θ scale by the inverse transformation m⁻¹(·). In the classical example, m(·) is Fisher’s z-transformation for the normal correlation coefficient. For the Poisson family $\widehat{\theta }\sim \mathrm{Poisson}(\theta )$, the square root transformation m(θ) = θ^1/2 is often suggested.

This argument assumes the existence of a transformation (2.4) to a normal translation family,

$$\widehat{\varphi }\sim \mathcal{N}(\varphi ,1).$$ (2.5)

(If the variance of $\widehat{\varphi }$ is any constant it can be reduced to 1 by rescaling.) The bca formula (2.2) is motivated by a less restrictive assumption: that there exists a monotone transformation (2.4) such that

$$\widehat{\varphi }\sim \mathcal{N}(\varphi -z_0{\sigma }_{\varphi },{\sigma }_{\varphi }^2),{\sigma }_{\varphi }=1+a\varphi .$$ (2.6)

Here the bias corrector z₀ allows for a bias in $\widehat{\varphi }$ as an estimate of ϕ, while the acceleration a allows for non-constant variance. Lemma 1 of Efron (1987) shows that (2.4)–(2.6) implies that the bca formula (2.2) gives correct confidence interval endpoints in a strong sense of correctness: the bca method is motivated by a (hidden) transformation to a simple translation model in which the exact interval endpoints are obvious, these transforming back to formula (2.2). Section 8 of DiCiccio and Efron (1992) gives a rigorous discussion.

Crucially, knowledge of the transformation (2.4) is not required; only its existence is assumed, serving as motivation for the bca intervals. Formula (2.2) is transformation invariant: for any monotone transformation (2.4), the bca endpoints transform correctly,

$${\widehat{\varphi }}_{\text{bca}}(\alpha )=m\left({\widehat{\theta }}_{\text{bca}}(\alpha )\right).$$ (2.7)

This isn’t true for the standard intervals, making them vulnerable to poor performance if applied on the “wrong” scale.

Under reasonably general conditions, Hall (1988) and others showed that formula (2.2) produces second-order accurate confidence intervals. See also the derivation in Section 8 of DiCiccio and Efron (1996).

Formula (2.2) makes three corrections to (2.1):

1. for non-normality of $\widehat{\theta }$ (through the bootstrap cdf G);

2. for bias of $\widehat{\theta }$ (through ${\widehat{z}}_0$);

3. for nonconstant standard error of $\widehat{\theta }$ (through $\widehat{a}$).

In various circumstances, all three can have substantial effects.

The parameters z₀ and a, and their estimates ${\widehat{z}}_0$ and $\widehat{a}$, are interesting in their own right. Standard intervals (1.1) depend on two estimated parameters, $\widehat{\theta }$ and $\widehat{\sigma }$; the approximate bca intervals called “abc” in Section 4 require just three more — ${\widehat{z}}_0$, $\widehat{a}$, and a measure of skewness of the bootstrap distribution $\mathcal{G}$ — to achieve second-order accuracy; see the discussion in Sections 3 and 4 of DiCiccio and Efron (1996). This simplifies the theory of second-order confidence intervals, and underlies the ease of application of bcajack and its parametric counterpart bcapar (Section 4).

As a particularly simple parametric example, where all the calculations can be done theoretically rather than by simulation, suppose we observe

$$\widehat{\theta }\sim \theta ·{\text{Gamma}}_{10}/10,$$ (2.8)

Gamma₁₀ a gamma variable with 10 degrees of freedom (density θ⁹ exp(−θ)/Г(10), θ > 0) so θ is the expectation of $\widehat{\theta }$.

Table 1 shows confidence limits at α = 0.025, 0.16, 0.84, and 0.975, having observed $\widehat{\theta }=1$. (Any other value of $\widehat{\theta }$ simply multiplies the limits.) Five different methods are evaluated: (1) the standard endpoint (2.1); (2) the percentile method ${\widehat{\theta }}_{\text{pct}}(\alpha )=G^{-1}(\alpha )$, i.e., taking z₀ and a = 0 in (2.2); (3) the bias-corrected method ${\widehat{\theta }}_{bc}(\alpha )$, setting a = 0 in (2.2); (4) the full bca endpoint (2.2); (5) the exact endpoint. Accuracy of the approximations increases at each step, culminating in near three-digit accuracy for the full bca method.

The three elements of the bca formula — G, z₀, and a — must usually be estimated by simulation. Figure 2 shows the histogram of 2000 nonparametric bootstrap replications of $\widehat{\theta }$, the adjusted R² statistic for the diabetes data example of Figure 1. Its cdf $\widehat{G}$ estimates G in (2.2).

Fig. 2.

2000 nonparametric bootstrap replications of the adjusted R² statistic for the diabetes example of Figure 1. Only 40.2% of the 2000 ${\widehat{\theta }}^{*}$ values were less than $\widehat{\theta }=0.507$, suggesting its strong upward bias.

We also get an immediate estimate for z₀,

$${\widehat{z}}_0={\mathrm{\Phi }}^{-1}\widehat{G}(\widehat{\theta }),$$ (2.9)

this following from $z_0=\underset{\varphi }{\mathrm{Pr}}\{\widehat{\varphi }\le \varphi \}$ in (2.6) (assuming the true value ϕ = 0). Only 40.2% of the 2000 ${\widehat{\theta }}^{*}$’s were less than the original value $\widehat{\theta }=0.507$, indicating a substantial upward bias in $\widehat{\theta }$. The estimated bias corrector

$${\widehat{z}}_0={\mathrm{\Phi }}^{-1}(0.402)=-0.327$$ (2.10)

accounts for most of the downward shift of the bca limits seen in Figure 1.

The acceleration a cannot in general be read from the bootstrap distribution $\widehat{G}$, this being an impediment to automatic bootstrap confidence intervals. The next two chapters include discussions of the computation of a in nonparametric and parametric situations, with further discussion in the Appendix.

3. Nonparametric bca intervals

Nonparametric inference begins with an observed data set

$$\mathit{x}=\left(x_1,x_2,\dots ,x_n\right),$$ (3.1)

where the x_i are independent and identically distributed (iid) observations from an unknown probability distribution F on a space $\mathcal{X}$,

$$x_i\stackrel{\mathrm{ind}}{\sim }F,i=1,2,\dots ,n.$$ (3.2)

The space $\mathcal{X}$ can be anything at all — one-dimensional, multidimensional, functional, discrete — with no parametric form assumed for F. The assumption that F is the same for all i makes (3.2) a one-sample problem, the only type we will consider here.

A real-valued statistic $\widehat{\theta }$ has been computed by applying some estimating algorithm t(·) to x,

$$\widehat{\theta }=t(\mathit{x});$$ (3.3)

we wish to assign a confidence interval to $\widehat{\theta }$. In the diabetes example of Section 1, x_i is v_i (1.2), n = 442, x is what was called v, and $\widehat{\theta }=t(\mathit{x})$ is the adjusted R² statistic (1.3)–(1.4).

A nonparametric bootstrap sample $x^{*}$,

$${\mathit{x}}^{*}=\left(x_1^{*},x_2^{*},\dots ,x_n^{*}\right),$$ (3.4)

is composed of n random draws, with replacement, from the set of original observations {x₁,x₂,..., x_n}. It produces a bootstrap replication

$${\widehat{\theta }}^{*}=t\left({\mathit{x}}^{*}\right)$$ (3.5)

of $\widehat{\theta }$. B such replications are independently drawn,

$${\widehat{\theta }}_i^{*}=t\left({\mathit{x}}_i^{*}\right),i=1,2,\dots ,B,$$ (3.6)

as shown in Figure 2 for the diabetes example, B = 2000. The bootstrap estimate of standard error is the empirical standard deviation of the ${\widehat{\theta }}_i^{*}$ values,

$${\widehat{\sigma }}_{\text{boot}}={\left[\sum _{i=1}^B{\left({\widehat{\theta }}_i^{*}-{\widehat{\theta }}^{*}\right)}^2/(B-1)\right]}^{1/2}$$ (3.7)

(where ${\widehat{\theta }}^{*}=\sum {\widehat{\theta }}_i^{*}/B$), which equals 0.032 in Figure 2.

The jackknife provides another estimate of standard error: let x_(i) be the data set of size n – 1 having x_i removed from x, and ${\widehat{\theta }}_{(i)}$ the corresponding estimate

$${\widehat{\theta }}_{(i)}=t\left({\mathit{x}}_{(i)}\right).$$ (3.8)

Then

$${\widehat{\sigma }}_{\text{jack}}={\left[\frac{n-1}{n}\sum _1^n{\left({\widehat{\theta }}_{(i)}-{\widehat{\theta }}_{(\cdot )}\right)}^2\right]}^{1/2},\left({\widehat{\theta }}_{(\cdot )}=\sum _1^n{\widehat{\theta }}_{(i)}/n\right),$$ (3.9)

which equals 0.033 in Figure 2; ${\widehat{\sigma }}_{\mathrm{jack}}$ isn’t used in the bca algorithm, but jackknife methodology plays an important role in the program bcajack.

The vector of bootstrap replications, say

$${\mathit{t}}^{*}=\left({\widehat{\theta }}_1^{*},{\widehat{\theta }}_2^{*},\dots ,{\widehat{\theta }}_B^{*}\right),$$ (3.10)

provides estimates $\widehat{G}$ (its cdf) and ${\widehat{z}}_0$ (2.9). For nonparametric problems, the jackknife differences

$$d_i={\widehat{\theta }}_{(i)}-{\widehat{\theta }}_{(\cdot )}$$ (3.11)

provide an estimate of the acceleration a,

$$\widehat{a}=\frac{1}{6}\sum _{i=1}^n{d}_i^3/{\left(\sum _{i=1}^n{d}_i^2\right)}^{3/2}.$$ (3.12)

The call bcajack(x, B, func) — where func represents t(x) (3.2) — computes $\widehat{G}$, ${\widehat{z}}_0$, and $\widehat{a}$, and the bca limits obtained from (2.2).

Our programs bcajack2 and bcapar use a different estimate of a based directly on bootstrap replications (see the Appendix). This allows an estimate “jsd” of variability for $\widehat{a}$; see Table 3 in Section 4. The likelihood-based confidence interval methods mentioned previously make corrections to standard intervals that involve quantities like there ${\widehat{z}}_0$ and $\widehat{a}$, so jsd-type calculations may be relevant, too.

Table 3.

Bcapar output for ratio of normal theory variance estimates of $\theta ={\sigma }_1^2/{\sigma }_2^2$ (4.20)–(4.21); bca limits are a close match to exact limits (4.24) given observed point estimate $\widehat{\theta }=1$. Including func=funcF (4.28) in the call added abc limits and statistics.

$lims
	bcalims	jacksd	pctiles	stand	abclims	exact.lims
.025	.420	.007	.074	−.062	.399	.422
.05	.483	.006	.112	.108	.466	.484
.1	.569	.006	.175	.305	.556	.570
.16	.650	.006	.243	.461	.639	.650
.5	1.063	.007	.591	1.000	1.050	1.053
.84	1.843	.018	.913	1.539	1.808	1.800
.9	2.150	.022	.958	1.695	2.151	2.128
.95	2.658	.067	.987	1.892	2.729	2.655
.975	3.287	.102	.997	2.062	3.428	3.247
$stats
	θ	${\widehat{\sigma }}_{\text{boot}}$	a	z0	sd.delta
est	1	.542	.099	.114	.513
jsd	0	.004	.004	.010	.004
ustats
	ustat	sdu	B
est	.948	.504	16000
jsd	.004	.005	0
$abcstats
a	z0
.1	.1

Contemporary sample sizes n can be large, or even very large, making the calculation of n jackknife values impractically slow. Instead, the observations can be collected into m groups each of size² g = n/m, with X_k the collection of x_i’s in group k. The statistic $\widehat{\theta }=t(\mathit{x})$ can just as well be thought of as a function of X = (X1, X2,..., Xm), say

$$\widehat{\theta }=T(\mathit{X}),$$ (3.13)

with X an iid sample taking values in the product space ${\mathcal{X}}^g$. Now only m, instead of n, recomputations are needed to evaluate $\widehat{a}$ from (3.8)–(3.12). (Note: bcajack does not require separate specification of T(·).) For the diabetes example, Figure 1 and Figure 2 were recomputed using m = 40, with only minor changes from m = 442.

There are two sources of error in the confidence limits ${\widehat{\theta }}_{\text{bca}}(\alpha )$: sampling error, due to the random selection of x = (x₁, x₂,...,x_n) from F, and internal error, due to the Monte Carlo selection of B bootstrap samples x*(1), x*(2),..., x*(B). The latter error determines how large B must be.

A different jackknife calculation provides estimates of internal error, based just on the original B bootstrap replications. The B-vector t* (3.10) is randomly partitioned into J groups of size B / J each, say J = 10. Each group is deleted in turn, and ${\widehat{\theta }}_{\text{bca}}(\alpha )$ recomputed. Finally, the jackknife estimate of standard error (3.9) is calculated from the J values of ${\widehat{\theta }}_{\text{bca}}(\alpha )$. The red vertical bars in Figure 1 indicate ± one such jackknife standard error.

Table 2 shows part of the bcajack output for the adjusted R² statistic, diabetes data, as in Figure 2. The internal standard error estimates for the bca limits ${\widehat{\theta }}_{\text{bca}}(\alpha )$ are labeled “jacksd”. The column “pct” gives the percentiles of the bootstrap histogram in Figure 2 corresponding to each ${\widehat{\theta }}_{\text{bca}}(\alpha )$; for example, ${\widehat{\theta }}_{\text{bca}}(0.975)$ corresponded to the 90.2 percentile of the 2000 ${\widehat{\theta }}^{*}$ values, i.e., the 1804th largest value. Having pct very near 0 or 1 for some α suggests instability in ${\widehat{\theta }}_{\text{bca}}(\alpha )$.

Table 2.

Partial output of nonparametric bootstrap confidence interval program bcajack for adjusted R² statistic, diabetes data, Figure 1 and Figure 2.

$lims
	bcalims	jacksd	standard	pct
.025	.437	.004	.444	.006
.05	.446	.003	.454	.013
.1	.457	.002	.466	.032
.16	.465	.003	.475	.060
.5	.498	.001	.507	.293
.84	.529	.002	.538	.672
.9	.540	.002	.547	.768
.95	.550	.002	.559	.862
.975	.560	.002	.569	.918
$stats
	$\widehat{\theta }$	${\widehat{\sigma }}_{\text{boot}}$	${\widehat{z}}_0$	$\widehat{a}$	${\widehat{\sigma }}_{\mathrm{jack}}$
est	.507	.032	−.327	−.007	.033
jsd	.000	.001	.028	.000	.000
$ustats
ustat	sdu
.496	.038

Also shown are the estimates $\widehat{\theta }$, ${\widehat{\sigma }}_{\mathrm{boot}}$, ${\widehat{z}}_0$, $\widehat{a}$, and ${\widehat{\sigma }}_{\text{jack}}$, as well as their internal standard error estimates “jsd”. ($\widehat{\theta }$, $\widehat{a}$, and ${\widehat{\sigma }}_{\text{jack}}$ do not involve bootstrap calculations, and so have jsd zero.) Acceleration $\widehat{a}$ is nearly zero, while the bias corrector ${\widehat{z}}_0$ is large, with a substantial jsd.

The argument B in bcajack can be replaced by t*, the vector of B bootstrap replications (3.10). Calculating the ${\widehat{\theta }}^{*}$ values separately is sometimes advantageous:

• In cases where one wishes to compare bcajack output in different settings, for instance, for different choices of the grouping parameter m.

• If there is interest in each of the components of a p-dimensional parameter Φ = T(x), a B × p matrix T* of bootstrap replications can be calculated from a single run of nonparametric samples, and bcajack executed separately for each column of T*.

• The “hybrid method,” discussed in Section 4, allows t* to be drawn from parametric probability models, and then analyzed with bcajack.

• For large data sets and complicated statistics $\widehat{\theta }$, distributed computation of the ${\widehat{\theta }}^{*}$ values may be necessary.

This last point brings up a limitation of bcajack. Even if the vector of bootstrap replications t* is provided to bcajack, the program still needs to execute t(·) for the jackknife calculations (3.8)–(3.12); an alternative algorithm bcajack2 entirely avoids step (3.8) (as discussed in the Appendix). It is able to provide nonparametric bca intervals from just the replication vector t*. (It also provides a slightly better estimate of internal error: bcajack cheats on the calculations of jacksd by keeping a fixed instead of recalculating it fold to fold, while bcajack2 is lets a vary.) Bcajack2 is designed for situations where the function $\widehat{\theta }=\mathrm{tfun}(\mathit{x})$ is awkward to implement within the bca algorithm.

Both bcajack and bcajack2 also return “ustat”, a bias-corrected version of $\widehat{\theta }$,

$$\text{ustat}=2\widehat{\theta }-\mathrm{mean}\left({\widehat{\theta }}^{*}\right),$$ (3.14)

so $\text{ustat}=\widehat{\theta }-(\mathrm{mean}({\widehat{\theta }}^{*})-\widehat{\theta })$. Also provided is “sdu”, an estimate of sampling error for ustat, based on the theory in Efron (2014). For the adjusted R² statistic of Table 2, ustat = 0.496 with standard error 0.038, compared to $\widehat{\theta }=0.507$ with standard error 0.038, a downward adjustment of about half a standard error.

4. Bootstrap confidence intervals for parametric problems

The bca method was originally designed for parametric estimation problems. We assume that the observed data y has come from a parametric density function

$$f_{\alpha }(\mathit{y}),$$ (4.1)

where α is the unknown parameter vector. We wish to set confidence intervals for a one-dimensional parameter of interest

$$\theta =s(\alpha ).$$ (4.2)

An estimate $\widehat{\alpha }=A(\mathit{y})$, perhaps its MLE, provides

$$\widehat{\theta }=s(\widehat{\alpha }),$$ (4.3)

a point estimate of θ. By sampling from $f_{\widehat{\alpha }}(\cdot )$ we obtain parametric bootstrap resamples y*,

$${\mathit{y}}^{*}\sim f_{\widehat{\alpha }}(\cdot ).$$ (4.4)

Each y* provides an ${\widehat{\alpha }}^{*}=A({\mathit{y}}^{*})$ and then a bootstrap replication of $\widehat{\theta }$,

$${\widehat{\theta }}^{*}=s\left({\widehat{\alpha }}^{*}\right).$$ (4.5)

Carrying out (4.4)–(4.5) some large number B of times yields a bootstrap data vector ${\mathit{t}}^{*}=({\widehat{\theta }}_1^{*},{\widehat{\theta }}_2^{*},\dots ,{\widehat{\theta }}_B^{*})$. Bca confidence limits (2.2) can be estimated beginning from t*, but we will see that there is one complication not present in nonparametric settings.

The parametric bootstrap confidence interval program bcapar assumes that f_α(y) (4.1) is a member of a p-parameter exponential family

$$f_{\alpha }(\mathit{y})=e^{{\alpha }^{\prime }\widehat{\beta }-\psi (\alpha )}{f}_0(\mathit{y}),$$ (4.6)

having α as the p-dimensional natural parameter and

$$\widehat{\beta }=\widehat{\beta }(\mathit{y})$$ (4.7)

as the p-dimensional sufficient statistic. Its expected value, the expectation parameter

$$\beta =E_{\alpha }\{\widehat{\beta }(\mathit{y})\}$$ (4.8)

is a one-to-one function of α; $\widehat{\beta }$ and its bootstrap replications ${\widehat{\beta }}^{*}$ play a central role in bcapar.

The parameter of interest θ = s(α) can also be expressed as a function of β, say θ = τ(β), and then $\widehat{\theta }$ written as a function of y,

$$\widehat{\theta }=\tau (\widehat{\beta }(\mathit{y}))\equiv t(\mathit{y}).$$ (4.9)

In familiar applications, either $s(\widehat{\alpha })$ or $\tau (\widehat{\beta })$ may have simple expressions, or sometimes neither. A key factor of bcapar is its ability to work directly with $\widehat{\theta }=t(\mathit{y})$ without requiring specification of s(·) or τ(·); see the Appendix.

As an important example of exponential family applications, consider the logistic regression model

$$\mathit{\eta }=\mathit{M}\alpha ,$$ (4.10)

where M is a specified n × p structure matrix, and η is an n-vector of logit parameters ${\eta }_i=\log {\pi }_i/\left(1-{\pi }_i\right)$. We observe

$$y_i=\{\begin{array}{ll}1\text{with}\text{probability}& {\pi }_i\\ 0& 1-{\pi }_i\end{array}$$ (4.11)

independently for $i=1,2,\dots ,n$. This is a p-parameter exponential family having natural parameter α, sufficient statistic

$$\widehat{\beta }={\mathit{M}}^{\prime }\mathit{y},$$ (4.12)

and expectation parameter β = M′π. In the neonate application below, θ = s(α) is the first coordinate of α.

The vector of bootstrap replicates ${\mathit{t}}^{*}=({\widehat{\theta }}_1^{*},{\widehat{\theta }}_2^{*},\dots ,{\widehat{\theta }}_B^{*})$ provides an estimated bootstrap cdf $\widehat{G}$ for substitution into (2.2), the formula for ${\widehat{\theta }}_{\text{bca}}(\alpha )$, and also the estimated bias-corrector ${\widehat{z}}_0={\mathrm{\Phi }}^{-1}\widehat{G}(\widehat{\theta })$ as at (2.9). This leaves the acceleration a. In parametric problems a depends on the choice of sufficient statistic $\widehat{\beta }=\widehat{\beta }(\mathit{y})$ (4.7); bcapar takes as input $t_0=t(\mathit{y})=\widehat{\theta }$, the B-vector t* of bootstrap replicates, and also b*, the B × p matrix of bootstrap sufficient vectors

$${\mathit{b}}^{*}={({\widehat{\beta }}_1^{*},{\widehat{\beta }}_2^{*},\dots ,{\widehat{\beta }}_B^{*})}^{\prime }.$$ (4.13)

In the logistic regression setting (4.10)–(4.12), the estimate $\widehat{\alpha }$ gives $\mathit{\eta }=\mathit{M}\widehat{\alpha }$ and the vector of estimated probabilities

$${\widehat{\pi }}_i=1/\left(1+e^{-{\widehat{\eta }}_i}\right),i=1,2,\dots ,n.$$ (4.14)

A parametric bootstrap sample ${\mathit{y}}^{*}=\left(y_1^{*},y_2^{*},\dots ,y_n^{*}\right)$ is generated from

$$y_i^{*}=\{\begin{array}{ll}1\text{with}\text{probability}& {\widehat{\pi }}_i\\ 0& 1-{\widehat{\pi }}_i\end{array}$$ (4.15)

independently for i=1,2,...,n. Each y* provides a ${\widehat{\theta }}^{*}=t\left({\mathit{y}}^{*}\right)$ and also

$${\widehat{\beta }}^{*}={\mathit{M}}^{\prime }{\mathit{y}}^{*},$$ (4.16)

the required inputs for bcapar.

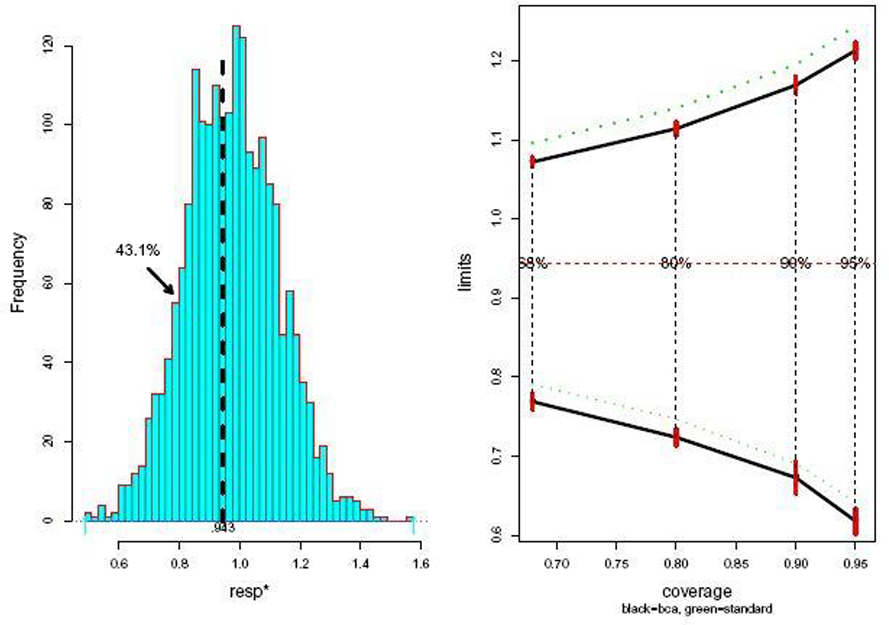
Figure 3 refers to a logistic regression application: 812 neonates at a large clinic in a developing country were judged to be at serious risk; 205 died within 10 days, while 607 recovered. It was desired to predict death versus survival on the basis of 11 baseline variables, of which “resp”, a measure of respiratory distress, was of particular concern; resp was the first coordinate of α so $\widehat{\theta }=s(\widehat{\alpha })={\widehat{\alpha }}_1$.

Fig. 3.

Neonate data. Left panel: 2000 parametric bootstrap replications resp*, MLE. Right panel: bca limits (solid) compared to standard limits (dotted), from bcapar. Estimates ${\widehat{z}}_0=-0.215$, $\widehat{a}=-0.019$.

A logistic regression analysis having M 812 × 11 (with the columns of M standardized), yielded MLE $t_0={\widehat{\alpha }}_1$ and bootstrap standard error for resp,

$$\text{resp}=0.943\pm \mathrm{0.155.}$$ (4.17)

Program bcapar, using B = 2000 bootstrap samples, provided the results pictured in Figure 3. The standard confidence limits for resp look reasonably accurate in this case, having only a small upward bias, about one-fifth of a standard error, compared to the bca limits, with almost all of the difference coming from the bias-corrector ${\widehat{z}}_0=-0.215$ (with internal standard error 0.024).

Bootstrap methods are particularly useful for nonstandard estimation procedures. The neonate data was reanalyzed employing model (4.10)–(4.11) as before, but now estimating α by the glmnet regression algorithm, a regularizing procedure that shrinks the components of $\widehat{\alpha }$, some of them all the way to zero. The algorithm fits an increasing sequence of α estimates, and selects a “best” one by cross-validation. Applied to the neonate data, it gave best $\widehat{\alpha }$ having

$$\text{resp}=0.862\pm \mathrm{0.127.}$$ (4.18)

Regularization reduced the standard error, compared with the MLE (4.15), but at the expense of a possible downward bias.

An application of bcapar made the downward bias evident. The left panel of Figure 4 shows that 66% of the B = 2000 parametric bootstrap replicates resp * were less than resp = 0.862, making the bias corrector large: ${\widehat{z}}_0=0.411$. The right panel plots the bca intervals, now shifted substantially upward from the standard intervals. Internal errors, the red bars, are considerable for the upper limits. (Increasing B to 4000 as a check gave almost the same limits.)

Fig. 4.

As in 3, but now using glmnet estimation for resp, rather than logistic regression MLE.

The two sets of bca confidence limits, logistic regression and glmnet, are compared in Figure 5. The centering of their two-sided intervals is about the same, glmnet’s large bias correction having compensated for its shrunken resp estimate (4.17), while its intervals are about 10% shorter.

Fig. 5.

Comparison of bca confidence limits for neonate coefficient resp, logistic regression MLE (solid) and glmnet (dashed).

As mentioned before, a convenient feature of bcapar that adds to the goal of automatic application is that both ${\widehat{\theta }}^{*}$ and ${\widehat{\beta }}^{*}$ can be directly evaluated as functions of y*, without requiring a specific function from ${\widehat{\beta }}^{*}$ to ${\widehat{\theta }}^{*}$ (which would be awkward in a logistic regression setting, for example). If, however, a specific function is available, say

$${\widehat{\theta }}^{*}=\tau \left({\widehat{\beta }}^{*}\right),$$ (4.19)

then bcapar provides supplementary confidence limits based on the abc method ( “approximate bootstrap confidence” intervals, as distinct from the more recent “ Approximate Bayesian Calculation” algorithm).

The abc method (DiCiccio and Efron, 1992) substitutes local Taylor series approximations for bootstrap simulations in the calculation of bca-like intervals. It is very fast and, if s(·) is smoothly defined, usually quite accurate. In a rough sense, it resembles taking B = ∞ bootstrap replications. It does, however, require function (4.19) as well as other exponential family specifications for each application, and is decidely not automatic.

Program abcpar, discussed in the Appendix, uses the bcapar inputs t* and b* (4.13) to automate abc calculations. If function τ(·) is supplied to bcapar, it also returns the abc confidence limits as well as abc estimates of z₀ and a. This is illustrated in the next example.

We suppose that two independent variance estimates have been observed in a normal theory setting,

$$\begin{gathered} {\widehat{\sigma }}_1^2\sim {\sigma }_1^2{\chi }_{n_1}^2/n_1, \\ {\widehat{\sigma }}_2^2\sim {\sigma }_2^2{\chi }_{n_2}^2/n_2, \end{gathered}$$ (4.20)

and that the parameter of interest is their ratio

$$\theta ={\sigma }_1^2/{\sigma }_2^2.$$ (4.21)

In this case the MLE $\widehat{\theta }={\widehat{\sigma }}_1^2/{\widehat{\sigma }}_2^2$ has a scaled F distribution,

$$\widehat{\theta }\sim \theta F_{n_1,n_2}.$$ (4.22)

Model (4.20) is a two-parameter exponential family having sufficient statistic

$$\widehat{\beta }=({\widehat{\sigma }}_1^2,{\widehat{\sigma }}_2^2).$$ (4.23)

Because (4.22) is a one-parameter scale family, we can compute exact level α confidence limits for θ,

$${\widehat{\theta }}_{\text{exact}}(\alpha )=\widehat{\theta }/F_{n_1,n_2}^{(1-\alpha )},$$ (4.24)

the notation indicating the 1−α quantile of a $F_{n_1,n_2}$ random variable.

Bcapar was applied to model (4.20)–(4.23), with

$$n_1=10\text{and}{n}_2=42.$$ (4.25)

That is, parametric resamples were obtained according to

$$\begin{gathered} {\widehat{\sigma }}_1^{2*}\sim {\widehat{\sigma }}_1^2{\chi }_{n_1}^2/n_1, \\ {\widehat{\sigma }}_2^{2*}\sim {\widehat{\sigma }}_2^2{\chi }_{n_2}^2/n_2, \end{gathered}$$ (4.26)

giving

$${\widehat{\theta }}^{*}={\widehat{\sigma }}_1^{2*}/{\widehat{\sigma }}_2^{2*}\text{and}{\widehat{\beta }}^{*}=({\widehat{\sigma }}_1^{2*},{\widehat{\sigma }}_2^{2*}).$$ (4.27)

The observed value $\widehat{\theta }$ simply scales the exact endpoints ${\widehat{\theta }}_{\text{exact}}(\alpha )$ and likewise ${\widehat{\theta }}_{\mathrm{bca}}(\alpha )$— correct behavior under transformations is a key property of the bca algorithm — so for comparison purposes the value of $\widehat{\theta }$ is irrelevant. It is taken to be $\widehat{\theta }=1$ in what follows. Table 3 shows the output of bcapar based on B = 16, 000 replications of (4.27). B was chosen much larger than necessary in order to pinpoint the performance of bcapar vis-à-vis ${\widehat{\theta }}_{\text{exact}}(\alpha )$. The match was excellent. Table 4 shows actual coverage levels for the endpoints of Table 3, bca almost exactly matching the nominal values.

Table 4.

Actual coverage levels of the bca, abc, and standard limits shown in Table 3.

nominal	bca	abc	standard
.025	.024	.021	.110
.05	.050	.046	.140
.1	.097	.097	.187
.16	.150	.158	.237
.5	.493	.503	.541
.84	.840	.849	.960
.9	.901	.909	.997
.95	.951	.958	1.000
.975	.976	.982	NA

Abc limits were also generated by including in the call, the function ratio(.)

$$\mathrm{ratio}\left({\widehat{\beta }}^{*}\right)={\widehat{\beta }}_1^{*}/{\widehat{\beta }}_2^{*},$$ (4.28)

this being $\tau ({\widehat{\beta }}^{*})$ in (4.19). The abc limits were less accurate for the more extreme values of α. On the other hand, there are theoretical reasons for preferring the abc estimates of a and z₀ in this case.

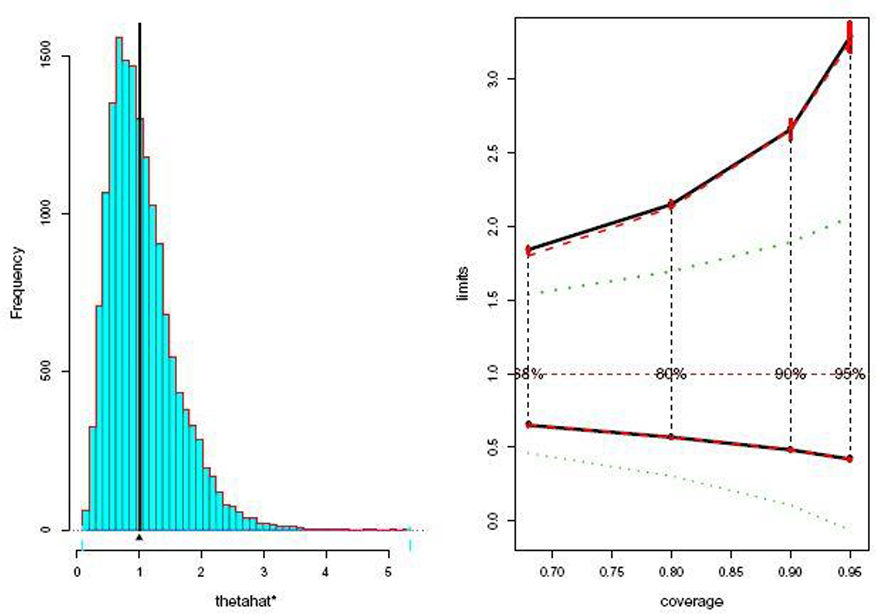
The standard, bca, and exact limits are graphed in the right panel of Figure 6. Two results stand out: bcapar has done an excellent job of matching the exact limits, and both methods suggest very large upward corrections to the standard limits. In this case the three bca corrections all point in the same direction: ${\widehat{z}}_0$ is positive, $\widehat{a}$ is positive, and $\widehat{G}$, the bootstrap cdf, is long-tailed to the right, as seen in the left panel of Figure 6. (This last point relates to a question raised in the early bootstrap literature, as in Hall (1988): if $\widehat{G}$ is long-tailed to the right shouldn’t the confidence limits be skewed to the left? The answer is no, at least in exponential family contexts.)

Fig. 6.

Left panel: B = 16000 bootstrap replications of ${\widehat{\theta }}^{*}$ (4.27). Right panel: confidence limits for θ having observed $\widehat{\theta }=1$; green standard, black bca, red dashed exact. The corrections to the standard limits are enormous in this case.

Even with B = 16, 000 replications there is still a moderate amount of internal error in ${\widehat{\theta }}_{\text{bca}}(0.975)$, as indicated by its red bar. The “pctiles” column of Table 3 suggests why: ${\widehat{\theta }}_{\text{bca}}(0.975)$ occurs at the 0.996 quantile of the B replications, i.e., at the 64th largest ${\widehat{\theta }}^{*}$, where there is a limited amount of data for estimating G(·). Bca endpoints are limited to the range of the observed ${\widehat{\theta }}^{*}$ values, and can’t be trusted when recipe (2.2) calls for extreme percentiles.

A necessary but “un-automatic” aspect of bcapar is the need to calculate the matrix of sufficient vectors b* (4.13). This can be avoided in one-sample situations by a hybrid application of bcapar–bcajack, at the risk of possible bias: the vector t* of B ${\widehat{\theta }}^{*}$ replications is drawn parametrically, as in the left panel of Figure 6. Then the call

$$\text{bcajack}\left({\text{t}}_0=\widehat{\theta },\text{B}={\mathit{t}}^{*},\text{r}\right)$$ (4.29)

uses t* to compute $\widehat{G}$ and ${\widehat{z}}_0$, as in bcapar. In the neonate example, r would take a 12-column matrix of predictors and responses, do a logistic regression or glmnet analysis of the last column on the first 11, and return the first coordinate of the estimated regression vector.

The bca analysis from (4.29) would differ only in the choice of acceleration a from a full use of bcapar. This made no difference in the neonate example, a being nearly 0 in both analyses.

If θ is a component of the natural parameter vector of a multiparameter exponential family then the theoretically ideal confidence linits for θ should be calculated conditionally on the other components of the MLE $\widehat{\alpha }$. Bca limits are calculates unconditionally. DiCiccio and Young (2008) in parametric bootstrap procedures, conclude that the unconditional intervals can perform well, even from a conditional point of view. Pierce and Bellio (2017) aim at a tougher goal than us, computing second-order accurate confidence intervals that allow for conditioning. Their algorithm accomplishes this but at the expense of requiring more from the user, among other things profile likelihood computations, that is, for each possible value of the parameter of interest, the constructed MLE for the vector ∂P nuisance parameter.

As an easy example, when there are no nuisance parameters, we return to the case when we observe x = 16 from a Poisson model with unknown mean θ. The 95% central confidence limits are shown in Table 5.

Table 5.

Exact and approximate central 95% confidence intervals for θ having observed x = 16 from X ∼ Poisson(θ).

	lower	upper
Exact	9.47	25.41
Pierce and Bellio	9.52	25.39
bcapar	9.82	25.53

5. Supplementary Materials

Title: bcaboot—Bias Corrected Bootstrap Confidence Intervals. Available on the Comprehensive R Archive Network (CRAN).

Script to reproduce figures: R scripts to reproduce figures in this paper (scripts.zip).

A. Appendix

What follows are some additional comments on the new bca programs and the underlying theory.

Bias correction and acceleration

The schematic diagram in Figure 7 relates to the estimates ${\widehat{z}}_0$ and $\widehat{a}$ in bcapar: $\widehat{\beta }$ is the MLE of the sufficient vector β in the exponential family (4.6); it gives the estimate $\widehat{\theta }=\tau (\widehat{\beta })$ (4.9) for the parameter of interest θ. $\mathcal{C}$ is the level surface of β vectors that give the same estimate of θ,

$$\mathcal{C}=\{\beta :\tau (\beta )=\widehat{\theta }\};$$ (A.1)

$\dot{\tau }$ is the gradient vector of $\tau (\beta )$ evaluated at $\widehat{\beta }$,

$$\dot{\tau }={\left(\partial \tau (\beta )/\partial {\beta }_j\right)}_{\widehat{\beta }},$$ (A.2)

and as such is orthogonal to $\mathcal{C}$ at $\widehat{\beta }$. The dots represent the bootstrap resamples ${\widehat{\beta }}_i^{*},i=1,2,\dots ,B$.

Fig. 7.

Schematic diagram concerning estimation of the acceleration a, and its relation to the bias-corrector z₀, as explained in the text.

Let ${\widehat{p}}_z$ be the proportion of the ${\widehat{\beta }}_i^{*}$ lying below $\mathcal{C}$ (i.e., in the direction opposite to $\dot{\tau }$). Then assuming certain monotonicity properties,

$${\widehat{z}}_0={\mathrm{\Phi }}^{-1}\left({\widehat{p}}_z\right),$$ (A.3)

as in (2.9).

Define

$$D_i^{*}={({\widehat{\beta }}_i^{*}-\widehat{\beta })}^t\dot{\tau },$$ (A.4)

and let ${\widehat{p}}_a$ be the proportion of ${\widehat{\beta }}_i^{*}$ vectors lying below $\mathcal{H}$. A standard two-term Edgeworth expansion (Hall, 1992, Chap. 2) gives the approximation

$${\mathrm{\Phi }}^{-1}\left({\widehat{p}}_a\right)\doteq \widehat{\gamma }/6,$$ (A.5)

where $\widehat{\gamma }$ is the empirical skewness of the B $D_i^{*}$ values. It can also be shown, following (6.7) in Efron (1987), that the acceleration a equals γ / 6, so that

$$\widehat{a}\doteq {\mathrm{\Phi }}^{-1}\left({\widehat{p}}_a\right)\doteq \widehat{\gamma }/6.$$ (A.6)

Both estimates of a are returned by bcapar, $\widehat{\gamma }/6$ labeled “a” and ${\mathrm{\Phi }}^{-1}\left({\widehat{p}}_a\right)$ labeled “az”. These were nearly the same in the examples of Section 4. Comparing (A.6) with (A.3), we can see that if $\mathcal{C}$ curves away from $\dot{\tau }$, as in Figure 7, we would have ${\widehat{z}}_0<\widehat{a}$. In a one-dimensional family, there is no curvature and ${\widehat{z}}_0=\widehat{a}$.

How is the least favorable direction $\dot{\tau }$ in Figure 7 calculated? This would be easy if the function $\widehat{\theta }=\tau (\widehat{\beta })$ were available. However, not requiring the user to provide $\tau (\widehat{\beta })$ is essential to making bcapar easy to apply in practice. Only the original form of the statistic as a function of the observed data, $\widehat{\theta }=t(\mathit{y})$, is required. Bcapar uses local linear regression to estimate $\dot{\tau }$:

• The B × p matrix b* (4.13) is standardized to, say, c*, having columns with mean 0 and variance 1.

• The rows $c_i^{*}$ of c* are ranked in terms of their length.

• The index set I* of the lowest “Pct” quantile of lengths is identified; Pct = 0.333 by default.

• Finally, $\dot{\tau }$ is set equal to the vector of ordinary linear regression coefficients of ${\widehat{\theta }}_i^{*}$ on $c_i^{*}$, within the set I*.

Theoretically, this estimate will approach $\dot{\tau }$ as Pct → 0. Empirically the calculation is not very sensitive to the choice of Pct.

Highly biased situations, indicated by very large values of the bias corrector ${\widehat{z}}_0$, destabilize the bca confidence limits. (Maximum likelihood estimation in high-dimensional models is susceptible to large biases.) The bias-corrected estimate ustat (3.14) can still be useful in such cases. Bcapar, like bcajack, returns ustat and its sampling error estimate “sdu”, and also estimates “jsd”, their internal errors. These errors are seen to be quite small in the example of Table 3.

Bcapar includes an option for also returning the bca confidence density, a form of posterior inference for θ given the data based on ideas of both Fisher and Neyman; see Section 11.6 of Efron and Hastie (2016) and, for a broader picture, Xie and Singh (2013).

bcajack and bcajack2

In the nonparametric setting, $\dot{\tau }$ can be closely approximated in terms of the jackknife differences $d_i={\widehat{\theta }}_{(i)}-{\widehat{\theta }}_{(\cdot )}$ (3.11) by taking the ith component to be

$${\dot{\tau }}_i=d_i\sqrt{n\cdot (n-1)}$$ (A.7)

(Efron and Hastie, 2016, formula (10.12)).

As discussed near the end of Section 3, using (A.7) in the calculation of the acceleration a makes bcajack require inputting the function for t(x) (3.8), even if the resamples ${\mathit{t}}^{*}=({\widehat{\theta }}_1^{*},{\widehat{\theta }}_2^{*},\dots ,{\widehat{\theta }}_B^{*})$ have been previously calculated. Bcajack2 instead uses a regression estimate for $\dot{\tau }$ and $\widehat{a}$, analogous to that in bcapar.

Nonparametric resamples ${\widehat{\theta }}^{*}=t\left({\mathit{x}}^{*}\right)$ (3.5) can also be expressed as

$${\widehat{\theta }}^{*}=T(Y),$$ (A.8)

Y the count vector Y = (Y₁, Y₂,...,Y_n), where, if x = (x₁, x₂,...,x_n),

$$Y_i=\#\{x_j^{*}=x_i\}.$$ (A.9)

The B × n matrix Y of count vectors for the B bootstrap samples plays the same role as b* (4.13) in parametric applications. Bcajack2 regresses the ${\widehat{\theta }}_i^{*}$ values on Y_i for a subset of the B cases having Y_i near (1,1,...,1), obtaining an estimate of $\dot{\tau }$ as in bcapar. A previously calculated list of the vector t* and the corresponding matrix Y can be entered into bcajack2, without requiring further specification of t(x)_.

abcpar

The original abc algorithm (DiCiccio and Efron, 1992) required, in addition to the function θ = τ(β) (4.19), a function mapping the expectation parameter β (4.8) back to the natural parameter α (4.6), say

$$\alpha =\mu (\beta ).$$ (A.10)

If $\tau (\cdot )$ is provided to bcapar, as at (4.28), it calculates an approximate formula $\alpha =\widehat{\mu }(\beta )$ using the “empirical exponential family” (Efron, 2014, Sect. 6) and then returns abc estimates, as in Table 3.

The abc method is local, in the sense of only using resamples ${\widehat{\beta }}^{*}$ nearby to $\widehat{\beta }$, which can be an advantage if $\widehat{\beta }$ falls into an unstable neighborhood of $\widehat{\theta }=\tau (\widehat{\beta })$. In any case, its results depend less on the resample size B, and provide a check on bcapar.