Integration and transfer learning of single-cell transcriptomes via cFIT

Significance

Overcorrection has been one of the main concerns in employing various data integration methods, which risk removing the biological distinction and are harmful for cell-type identification. Here, we present a simple yet surprisingly effective model named common factor integration and transfer learning for capturing various batch effects across experiments, technologies, subjects, and even species. The method generates robust results when batch effects are confounded with the variability of cell-type compositions and when the population exhibits continuous developing patterns. The successful integration and transfer uncover the transcriptional resemblance described by the proposed location-scale shift model across systems. In addition, the model enables transferring via low-rank matrix from more informative data to allow for precise identification in data of lower quality.

Abstract

Large, comprehensive collections of single-cell RNA sequencing (scRNA-seq) datasets have been generated that allow for the full transcriptional characterization of cell types across a wide variety of biological and clinical conditions. As new methods arise to measure distinct cellular modalities, a key analytical challenge is to integrate these datasets or transfer knowledge from one to the other to better understand cellular identity and functions. Here, we present a simple yet surprisingly effective method named common factor integration and transfer learning (cFIT) for capturing various batch effects across experiments, technologies, subjects, and even species. The proposed method models the shared information between various datasets by a common factor space while allowing for unique distortions and shifts in genewise expression in each batch. The model parameters are learned under an iterative nonnegative matrix factorization (NMF) framework and then used for synchronized integration from across-domain assays. In addition, the model enables transferring via low-rank matrix from more informative data to allow for precise identification in data of lower quality. Compared with existing approaches, our method imposes weaker assumptions on the cell composition of each individual dataset; however, it is shown to be more reliable in preserving biological variations. We apply cFIT to multiple scRNA-seq datasets of developing brain from human and mouse, varying by technologies and developmental stages. The successful integration and transfer uncover the transcriptional resemblance across systems. The study helps establish a comprehensive landscape of brain cell-type diversity and provides insights into brain development.

Individual single-cell RNA sequencing (scRNA-seq) experiments have been used to discover new cell states and reconstruct cellular differentiation trajectories. Recent studies have shown that cellular features can be preserved across experimental systems from related biological contexts (1). The information learned from different data sources can improve the analysis and interpretation of diverse biological systems. However, the advantages of integrated data can be compromised by differences due to experimental batch, sampling (sample acquisition and handling, sample composition, reagents or media, and sampling time), or technology (sequencing depth, sequencing lanes, read length, plates or flow cells, protocol) (2). The challenge is exacerbated when technical differences in data sources are confounded with biological heterogeneity. Many methods have been established to integrate scRNA-seq studies across multiple experiments. Some methods employ supervised cross-domain transfer learning (3–6) to remove domain effects with models learned from labeled datasets. These methods rely heavily on data labeling, thus failing to capture novel cell types and continuous trajectories. In contrast, unsupervised methods are less restrictive and therefore, more widely applied to integrate data from multiple resources (7–11). However, many of these methods tend to prioritize uniformity of mixing across different batches over preserving biological variation (2). Such a principle can lead to a loss in biological heterogeneity and interpretability, especially when integrating collections of datasets with considerable differences in cellular composition. Also, most existing methods work on the assumption that all datasets share most cell types or that the within-domain biological variance defining distinct cell types dominates the cross-domain effects (10, 12); such assumptions do not hold when integrating biologically heterogeneous datasets or data consisting of continuously transitioning cell types or refined subtypes.

Here, we present an effective unsupervised integration and transfer learning model, called cFIT (common factor integration and transfer learning). The model assumes a shared common factor space across datasets but with location-scale shifts on genewise expression unique by domain. Our model is motivated from the machine-learning subdomain of transfer learning (13–17), assuming that information is shared across different tasks, and common data representations can be learned and generalized to other unseen tasks. In this framework, the shared latent space represents the underlying biological processes across systems, such as common cell-type compositions and developmental trajectories across measurements, samples, or even species. After the robustness of a biological process is established, these learned latent spaces enable varied learning tasks across data platforms, modalities, and studies, through transfer learning.

The proposed model is capable of capturing various batch effects and integrating across various domains by employing a linear model that is more parsimonious than existing methods such as Linked Inference of Genomic Experimental Relationships (LIGER) (11). cFIT is powerful as it corrects for technical variation but does not remove biological heterogeneity, providing both flexibility and interpretability. For implementation, we derived an algorithm for inferring model parameters under an iterative nonnegative matrix factorization (NMF) framework. The algorithm is also applicable for synchronized integration of cross-domain assays. Finally, the learned biological signatures can apply transfer learning to allow for precise inference for data with lower quality or smaller sample size.

cFIT enables successfully integration of two independent datasets derived from the developing human cortex (18, 19). The integration disentangled the domain-specific technical effects with the biological processes unique to each dataset, where the latter is preserved and depicted in the recovered developing trajectories. The learned latent biological signatures were then transferred to several previously published datasets from fetal brain (20–23)—allowing for finer characterizations of cell identities and the biological process they are involved in, which would not be feasible otherwise. In addition, the resilience to overcorrection facilitates the detection of possible contaminations in the data source. By integration of data across species, we identified transcriptomic heterogeneity between mouse and human cells during the embryonic stage of interneuron (IN) development. The findings shed light on similarities and differences in IN fate between species. In aggregate, these analyses highlight the utility of the proposed method to borrow strength across multiple datasets and to transfer information between related datasets.

Results

Methods Overview.

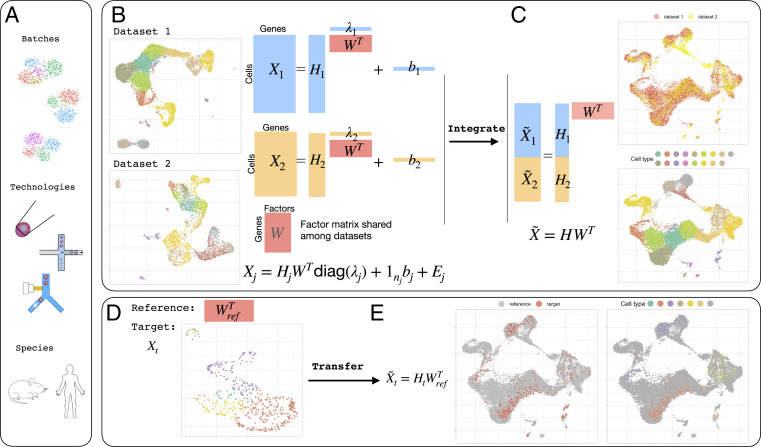
cFIT models the scRNA-seq expression of individual cells using its cellular identity and domain-specific factors. Here, domain refers to any standalone dataset profiled at a single laboratory using a single technology from one batch (Fig. 1). Specifically, we are given a total number of $N$ cells, and each cell $i$ is associated with a $p$-dimensional feature vector ${\mathit{x}}_i$ corresponding to its gene expression values (SI Appendix has data preprocessing steps). Each cell comes from a specific domain with a known domain identification. Given $M$ different domains, we use $m_i\in \left\{\mathrm{1,2},\dots ,M\right\}$ to denote the domain identification of cell $i$. We model the scRNA-seq data via a high-dimensional linear model with a latent low-dimensional structure. Let ${\mathit{x}}_i$ be the observation of cell $i$ that is generated from

$${\mathbf{x}}_i={\mathbf{\Lambda }}_{m_i}\mathit{W}{\mathit{h}}_i+{\mathit{b}}_{m_i}+{\mathit{ϵ}}_i,i=1,\dots ,N.$$ [1]

Here, we use the diagonal $\left(p\times p\right)$ matrix ${\mathbf{\Lambda }}_{m_i}=diag\left({\mathit{\lambda }}_{m_i}\right)$ to control the discrepancy of individual gene expression resulting from domain-specific technical effects. The matrix $\mathit{W}$ denotes a $\left(p\times r\right)$ nonnegative factor matrix shared across all samples and domains representing the gene expression profiles (signatures) associated with the cells; each vector ${\mathit{h}}_i$ is a cell-specific nonnegative vector of length $r$ representing the factor loading vector of cell $i$. The domain-specific vector ${\mathit{b}}_{m_i}$ is a nonnegative vector of length $p$ that captures the domain-associated shift. The noise terms ${\left\{{\mathit{ϵ}}_i\right\}}_{i=1}^N$ are modeled as independent, normally distributed random vectors with mean $\mathit{0}$ and variance ${\sigma }^2{\mathbf{I}}_p$ to account for measurement error from various sources.

Fig. 1.

cFIT integration and transfer approach overview. (A) cFIT performs integration or transfer among scRNA-seq datasets from different batches, technologies, and across species. (B) Data integration takes in two or more datasets from different domains, where some cell-level biological processes are shared. Each dataset is modeled by a low-dimensional latent space corresponding to gene-level features (gene expression signatures), $W$, shared across domains, domain-specific factor loading $H_j$ characterizing cell composition, and domain-unique scaling, ${\lambda }_j$, and shift, $b_j$, capturing the technical distinction. (C) The integration algorithm estimates the set of parameters through iterative NMF. The integrated data can be obtained by eliminating the technical distinctions and projected onto a common subspace, where downstream analysis can be performed, such as clustering and trajectory inference. (D) The transfer process takes a reference factor matrix representing the gene-level signature profiles and a target dataset sharing the signature space. (E) The transfer algorithm estimates the target-specific parameters to project the target data onto the same low-dimensional space as inferred from reference data. Cell labels can be assigned directly with unsupervised learning in low-dimensional space or querying reference data.

Let $n_j$ denote the number of cells from batch $j$ and $N={\sum }_{j=1}^M{n}_j$ the total number of cells. Concatenating the scRNA-seq expressions of all cells from each domain $j$ as an $\left(n_j\times p\right)$ matrix ${\mathit{X}}_j$, then model Eq. 1 in matrix form is

$${\mathit{X}}_j={\mathit{H}}_j{\mathit{W}}^{\top }{\mathbf{\Lambda }}_j+{\mathit{1}}_{n_j}{\mathit{b}}_j^{\top }+{\mathit{E}}_j,j=1,\dots ,M.$$ [2]

Here, ${\mathit{H}}_j$ is a nonnegative factor loading matrix, and ${\mathit{E}}_j$ is the noise matrix (Fig. 1B).

Note that ${\mathit{H}}_j$ captures the biological heterogeneity originating from disparate cell-type compositions, and $\left\{{\mathbf{\Lambda }}_j,{\mathit{b}}_j\right\}$ are domain-specific parameters that accommodate domain differences such as batch effects from samples and libraries, different sequencing technologies, and even species, whereas $\mathit{W}$ is the common factor space—the information shall be extracted and shared among datasets. The above model (Eq. 2) hinges upon the rationale that all of the samples belong to, after proper shift and rescaling, the same lower-dimensional linear subspace, which makes it possible to leverage information from diverse datasets.

The set of unknown parameters is estimated by minimizing the objective function provided in Methods. Then, one can use the integrated, low-dimensional representation of each dataset ${\mathit{H}}_i{\widehat{\mathit{W}}}^{\top }$ for downstream analysis, as well as leverage the common factor matrix $\widehat{\mathit{W}}$ for efficient transfer to a target dataset as detailed in Methods and SI Appendix.

Comparisons with other methods.

LIGER (11) is a popular linear method that employs a similar matrix factorization: it factorizes each batch expression matrix into a shared factor matrix $W$ and a batch-unique factor matrix with $p\times r$ parameters to describe the domain effects. By contrast, we consider a different modeling approach using only $2p$ parameters based on patterns of technical variations. By imposing a structural constraint on the dataset-specific effect in cFIT, we restrict the domain-specific effects to the deviation by location and scale but rely on the shared factor matrix to model the relative signature matrix. The remaining orthogonal effects are preserved as biological distinctions; thus, the corrected batch effects are less likely to confound with biological effects. Although our model is comparatively conservative, we shall show in our data analyses that the structured model is often sufficient to capture and remove the domain effects from various sources. Nonlinear methods, on the other hand, typically allow higher flexibility and have shown superior power and performance in blending multiple sources of data sharing similar compositions. These methods typically involve the identification of mappings between datasets and remove the differences accordingly. It can be achieved by finding the mutual nearest neighbors (MNNs), as used in MNNcorrect (12) and Seurat v3 (10), where the target data are mapped to the query data, guided by the pairwise points identified by MNN. Other types of nonlinear method leverage the alignment between clusters (distinct cell types) (8) to eliminate the batch effects within the clusters and/or between mapped clusters. The success of MNN relies heavily on the assumption that the batch effect is almost orthogonal to the biological subspace, and there is a substantial overlap of the cell compositions between the source and target data. As such, cluster-based methods require relatively well-separated clusters mapped across datasets. Apart from that, both types of approaches assume that the biological differences dominate the domain effects; however, this assumption is likely violated when cells are obtained along a continuous developmental trajectory with transitioning subtypes. These nonlinear methods eliminate the pairwise distinctions regardless of the source of distinctions. Therefore, they tend to overcorrect the biological variance. Alternatively, our method imposes less assumption on the distinctions of biological and domain effects by parsimoniously modeling the most likely generative source of domain effects. When our model assumptions are violated, it is likely that cFIT does not remove the batch effects that are unexplained by the model rather than falsely erasing signals. In this sense, cFIT is less prone to overcorrection.

Simulation Studies: Differential Expression Analysis and Robustness.

The performance of cFIT was first evaluated on differential expression gene (DEG) discovery, a key downstream analysis. The comparison assessed the integration methods’ ability to remove domain-specific factors while preserving biological signals. We compared with two widely used single-cell integration methods Seurat v3 (10) and MNNcorrect (12), which performed well in a benchmarking study (24). We do not compare with LIGER because this method does not produce a reconstructed scRNA expression matrix. We performed simulations with single-cell simulator under five settings with a combination of balanced/unbalanced batches, regular/high-dropout rates, and two/multiple biological groups. After obtaining the reconstructed expression matrices, we used the two-sided Wilcox rank-sum test for DEG detection and reported the false discovery rate (FDR) among top 50 and 100 discoveries. All three methods are effective in capturing the biological signals in some settings. Seurat v3 has advantages in the unbalanced batch/multiple group settings, while MNNcorrect shows better performances in the balanced batch scenarios. Overall, cFIT has the smallest FDR for most settings and is most robust across different parameter settings (SI Appendix, Fig. S1A).

We then evaluated the robustness of cFIT with respect to tuning parameters. In SI Appendix, we show that, with our proposed penalty term and parameter constraints, cFIT is identifiable and guaranteed to converge; furthermore, performance is enhanced using our initialization process. Hence, the only key tuning parameter remaining is $r$, the number of latent factors. Here, we demonstrate that our results are robust when $r$ is chosen from a reasonably wide range. By construction, the latent dimension $r$ corresponds to the number of biological groups. We considered two simulation designs such that the expression matrices follow model Eq. 2 with $r=5$, and 1) all five cell groups presented in both domains, 2) three cell groups presented in both domains, and each domain has a unique cell group. A Uniform Manifold Approximation and Projection (UMAP) visualization revealed the impact of severe batch effects (SI Appendix, Fig. S1 B and C). Provided $r\ge 5$, cFIT performed well, successfully integrating cells in each biological group into one cluster. Note that the second setting was challenging for most current integration methods, but cFIT was still able to recover the “unique cell groups.” In practice, when we do not have prior knowledge about the number of biological groups, taking into consideration the complexity of real datasets and computation cost, we recommend a choice of $r$ between 10 and 50.

Applications to Single-Cell Data.

Integration of scRNA-seq datasets from multiple technologies.

Next, we evaluated our approach on human pancreatic islet cell datasets produced across five technologies, CelSeq, CelSeq2, Fluidigm C1, SMART-Seq2, and InDrop. After applying the cFIT integration procedure, technical distinctions that originally grouped cells by batch were effectively removed, so that cells belonging to the same cell type, regardless of data sources, were well mixed (SI Appendix, Fig. S2). In addition to detecting all major cell classes (alpha, beta, delta, gamma, acinar, and stellar), we also identified some rare cell types (schawann and mast) with the integrated data that could not be reliably detected with a smaller number of cells through individual clustering analysis. We benchmarked the performance of cFIT against two popular methods: LIGER (11) and Seurat v3 (10). The integration results were compared using the alignment score, a measurement of how well different datasets mix (Methods and SI Appendix), and the accuracy for preserving the cell-type structure measured by the Adjusted Rand Index (ARI) on clustering. Methods that perform well in both metrics effectively matched populations across datasets without blending distinct populations. Results show that cFIT achieved comparable high alignment scores and clustering accuracy as Seurat, indicating the effectiveness of our method relying on a simpler linear model compared with the nonlinear multistep procedure employed by Seurat. LIGER produced lower clustering accuracy, due to overcorrection of the domain-specific effects that falsely removed the biological gene-level distinctions between cells from different cell types. LIGER promoted the use of a postquantile normalization step to further align the quantiles of the batches within obtained clusters. Similarly, we show that this step can also be coupled with cFIT and produces higher alignment scores, despite the increased risk of mixing distinct cell types.

Integration of datasets consisting of distinct cell types.

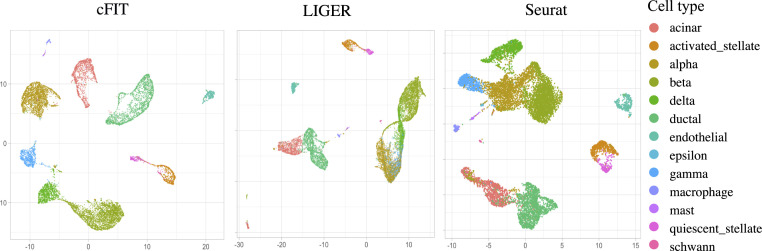
To examine the robustness of the proposed method on integrating populations with different cell-type compositions, we removed all cells of one prechosen type from each pancreas islet cells dataset. The cell type was randomly chosen as the largest or second-largest major cell type for each dataset (SI Appendix). The integration procedure was applied to these perturbed datasets to compare performance. cFIT successfully integrated the datasets without blending distinct cell types. As with the original data, cFIT achieved high clustering accuracy (ARI $\approx 0.9$) and alignment score (Fig. 2 and SI Appendix, Fig. S3). In contrast, LIGER and Seurat integration failed to preserve the cell-type structure, and cells from different cell types were mixed together. Specifically, in both LIGER and Seurat results, a fraction of ductal cells was clustered with acinar cells, and beta, delta, alpha, and gamma cells became entangled. The clustering accuracy (ARI) dropped to approximately 0.6 (SI Appendix, Fig. S3C). In summary, cFIT successfully characterized the domain-specific effects and was robust to the perturbation in relative cell-type compositions.

Fig. 2.

UMAP plots of integrated data from perturbed pancreas islet datasets, created by moving one major cell type from each dataset, comparing results from three methods: cFIT (Left), LIGER (Center), and Seurat (Right). Cells are colored by cell types.

To further ensure that cFIT was able to distinguish between the technical and biological effects when they were confounded, we jointly analyzed profiles of hippocampal oligodendrocytes and interneurons (INs) (25). The two cell classes share a common origin in mouse development, but they are born in distinct time frames and have very different functions in the mature brain. Therefore, we expected the two sets of mature cells to share few, if any, common cell populations. Compared with LIGER and Seurat, cFIT generated the minimum false alignment, which is apparent visually in the UMAP display of integrated data and by comparing the alignment scores (SI Appendix, Fig. S4).

Integration of human fetal cortical scRNA-seq data.

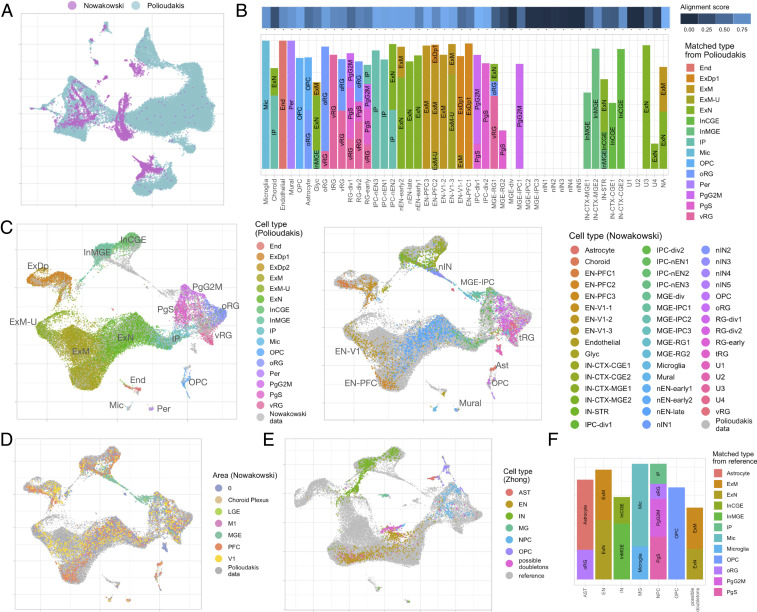
Several studies, all following a unified set of protocols, have dissected multiple regions of human fetal brain and sequenced single cells (18–23). These studies enable the study of cellular programs in early development, comparisons of regional differences in cell-type compositions and expression profiles, and mining associations between brain cell types and neurological disorders (19, 26). However, challenges remain to integrate these datasets, which have been produced using disparate technologies, providing different coverage of developmental stage and brain regions. As a first step, we integrated the two largest scRNA-seq datasets from fetal cortex: 1) the Polioudakis scRNA-seq data (19) (Drop-seq) of 33,976 cells from cortical anlage at gestation week 17 or 18 and 2) the Nowakowski data (18) (Fluidigm C1) of 4,261 cells from multiple brain areas and ranging in age from 5.85 to 37 postconception weeks (PCW). We aimed to borrow the advantages from both datasets via their integration, thus providing a more comprehensive characterization of human neocortical development. By applying our proposed algorithm on these datasets, we obtained integrated data with good overlap from initially divergent data sources, as indicated via UMAP visualization and alignment score (Fig. 3 A–C). Similar cell types matched perfectly, including oligodendrocyte progenitor cells (OPCs), radial glia, progenitor cells, and excitatory neurons (ENs), while others were unique to Nowakowski data, including IN progenitors (medial ganglionic eminences radial glia [MGE-RG], medial ganglionic eminences intermediate progenitor cell [MGE-IPC], newborn IN [nIN]) and unlabeled types (U1, U2). The IN progenitors were sampled from a brain region not included in the Polioudakis dataset; the unknown types could be other unrepresented cell types or artifacts. It was notable that cFIT did not force these cells to overlap with closely related cell types present in the larger Polioudakis dataset. Moreover, two maturation trajectories of ENs were revealed in the Nowakowski data. One ends at prefrontal cortex (PFC) maturing excitatory cells, and the other ends at primary visual cortex (V1) maturing excitatory cells; while the mature cells sampled from the two different brain regions were clearly differentiated, the immature cells were not. The Polioudakis data spanned this same space, but this study did not distinguish cells by region. Thus, by aligning the two datasets and noting the two trajectories apparent in the Nowakowski data, we can infer the regional origin of a portion of the Polioudakis cells (Fig. 3D). In addition, we were able to assign labels to previously unannotated cells and likely misidentified cells. For instance, a group of unlabeled cells (NA) in the Nowakowski data was identified via nearest neighbor matching as ENs due to their substantial overlap with migrating and maturing ENs in the Polioudakis data. A subset of 39 OPCs in Polioudakis data are likely astrocytes (ASTs) given they are matched to ASTs from the Nowakowski data and expressed ASTs markers GFAP, SOX9, and EGFR. Compared with the initial attempt to integrate the same datasets (19) using Seurat, cFIT results exhibited superior alignments, especially among ENs, while preserving the batch unique profiles in medial ganglionic eminences (MGE) lineage that were eliminated by Seurat integration.

Fig. 3.

(A–D) Integration of two scRNA-seq datasets from the fetal brain (Nowakowski and Polioudakis data). (A) UMAP plot of two datasets before integration. (B) Match of the identified clusters in Nowakowski data with major types identified from the Polioudakis data. The alignment score demonstrates how well each cluster in the Nowakowski data are aligned with cells from the Polioudakis data visualized in the color bar above. A higher score means the cells are well matched with cells from the other dataset. The bar plot shows the top matched cluster from the Polioudakis data for each cluster of the Nowakowski data. (C) UMAP of scaled factor loadings obtained from data integration. In Left, only cells from the Polioudakis data are colored into 16 major cell types. Similarly, in Right, only cells from Nowakowski data are colored according to the 48-cell-type label (see SI Appendix, Tabel S2 for detailed cell-type annotations from respective studies). (D) UMAP of integrated Polioudakis and Nowakowski data, colored by brain area annotated for the Nowakowski data, including prefrontal cortex (PFC), primary visual cortex (V1), medial ganglionic eminence (MGE), and lateral ganglionic eminence (LGE). (E and F) Transfer results on 2,309 cells from the Zhong data. (E) UMAP of 2,309 cells (colored by Zhong labels, SI Appendix, Table S2) overlaying on cells from the Polioudakis and Nowakowski (reference) datasets, among them a group of cells outside the range of reference cells and previously identified as possible doubletons (27). (F) The composition of cells based on matched cell types in reference datasets for each major group, with the alignment score computed for each major group measuring how well it matches with reference data.

Transfer the learned signature from a dataset with a larger number of human cortical cells to a dataset with a smaller number of human cortical cells.

The learned factor matrix from the integration of the Nowakowski and Polioudakis data can serve as a comprehensive reference that characterizes the cellular processes in the fetal brain, covering a wide range of developmental stages (6 to 37 PCW) and major and more specialized cell types. Thus, we applied our proposed transfer learning methods and used this comprehensive reference to enable cell-type identification for 2,309 PFC cells from the Zhong dataset (23), which contains 2,309 single cells from the human embryonic PFC from 8 to 26 PCW. Using the Seurat package, the authors identified six major clusters: neural progenitor cells (NPCs), ENs, INs, ASTs, OPCs, and microglia (MIC); these will be referred to as Zhong labels. Through the transfer procedure, we obtained the following results. First, the 2,309 cells, represented in low-dimensional space using estimated factor loadings, overlay substantially with cells from the Polioudakis and Nowakowski datasets. We were able to identify finer structure within each major group by matching group labels from the reference datasets. Among them, NPC consisted of cycling progenitors, intermediate progenitors, and radial glia. EN cells contain both migrating and maturing ENs. IN matched perfectly with MGE and caudal ganglionic eminence (CGE)-derived INs, OPC and MIC aligned perfectly with OPC and MIC from reference data, and AST aligned partially with ASTs and partially with outer radial glia (oRG). Most groups showed high alignment scores, except for the AST clusters, which while laying adjacent to each other, were not well mixed. This analysis showed that by transferring rich information, we were capable of delineating finer structures within each major type in another dataset. Second, we were able to identify cells from rare types that were likely misclustered in the Zhong analysis. For instance, previously labeled as INs, five cells were relabeled as endothelial, and another five cells were relabeled as pericytes. This finding was supported by the UMAP visualization, where these cells lie in clusters corresponding to endothelial and pericytes that were well separated from other types. Third, the migrating and maturing ENs align well with the PFC branch as identified from the Nowakowski data (the branch extends downward in the UMAP visualization), while the upper branch displays maturing ENs from the visual cortex. Fourth, we observed a fraction of EN cells that align poorly with the reference data (outside the gray range in the UMAP plot); among them, some were labeled as NPC. This was indicative of the underrepresentation of these cells in the reference. It was not clear whether these were unknown neuronal signatures characteristic of these cells or were mischaracterized cells. The latter is more likely because previous work (27) discovered a cluster of cells as possible doubletons (i.e., transcripts captured from two cells rather than one).

Transfer learning is particularly valuable when applied to much smaller datasets. We conducted similar transfer analysis on a variety of scRNA-seq datasets of human cortical cells (20–22), covering different technologies and populations. The Li data (22) contain 762 cells collected from nine brains ranging in age from 5 to 20 PCW. Applying cFIT, the cells were transferred to the reference data in the low-dimensional factor space and showed good alignment of most cell labels (SI Appendix, Fig. S5 A and C). The alignment was further validated by the incremental age along the trajectory observed (SI Appendix, Fig. S5B). By transferring onto well-characterized developmental trajectories, we were also able to identify some likely mislabeled cells, which likely arose due to having too few cells per type available originally: for instance, the rainbow points along the maturation trajectory of ENs and CGE/MGE INs. We next examined an even smaller scRNA-seq dataset from the fetal brain, with 220 cells sampled between 12 and 13 PCW (20). Guided by marker genes, these single cells were previously labeled into seven types in the original paper: two subtypes of apical progenitors (AP1, AP2), two subtypes of basal progenitors (BP1, BP2), and three subtypes of neurons (N1, N2, N3). By transferring these cells onto the reference data, we were able to validate the cell labels (SI Appendix, Fig. S5D). As a further step, we identified the finer structure within each cell group (different types of radial glia within apical progenitor cells and different progenitor cells within the basal progenitor group) (SI Appendix, Fig. S5E). We also revisited a widely studied dataset composed of both fetal and adult brain cells (21) (134 fetal cells and 334 adult cells from cortical tissues at 16 to 18 PCW). The transfer procedure evenly distributed the fetal cells along the reference trajectory, where labels were easily inferred (SI Appendix, Fig. S5F). By contrast, the transfer process projected all adult neurons outside of the fetal developing trajectory (SI Appendix, Fig. S5G).

Integrate cell expressions across species.

We further examined the performance of the proposed algorithm for integrating mouse and human brain cells. Although we expect differences between the two species, similarities have also been noted in some transcriptomic patterns (28), and once understood, shared features are likely to provide a deeper insight into the fundamental architecture underlying cellular development and physiology. Diverse subsets of cortical INs have vital roles in higher-order brain functions. Due to the limited number of profiled early inhibitory precursors from human, we leveraged several mouse scRNA-seq datasets collected along a developmental time course using multiple technologies (29, 30) and integrated them with human MGE progenitors and INs (18). We first examined the heterogeneity within the early development in MGE (mainly composed of mitotic progenitors within MGE before migrating to cortex). By integrating the 733 Nowakowski cells collected from MGE (age between 5 and 21 PCW) with 5,622 mouse cells from Drop-seq data (embryonic day 13.5), we identified a common mitotic developmental trajectory shared between the two species (SI Appendix, Fig. S6 A and B). In their prior work (29, 30), each mouse cell was assigned a maturation score (a continuous value quantifying the extent of cell development), allowing the cells to be divided into mitotic and postmitotic stages. We mapped this maturation score to human cells by averaging over the scores of neighboring mouse cells (among the 30 nearest neighbors). We observed a match between the maturation score and the reference labels of human cells, starting from the two subtypes of MGE-RG, followed by the dividing MGE progenitors, subtypes of MGE-IPC, and ending with newborn INs (SI Appendix, Fig. S6C). Seurat clustering analysis was performed, which identified eight major clusters, each composed of both mouse and human cells (SI Appendix, Fig. S6D). Clusters A to F are composed of mitotic cells concordant with the reference labels (SI Appendix, Fig. S6E). Meanwhile, the two clusters of postmitotic cells aligned with the reference branch labels. The newborn INs fell in branch 1 cluster, which was conjectured to give rise of cortical INs (29). The alignment score calculated per cluster demonstrates that the human cells were evenly distributed in each cluster, except for F (SI Appendix, Fig. S6E). Cluster F contained a fraction of newborn INs from a later developmental stage ($>$20 PCW), beyond the range covered by mouse cells.

Next, we investigated the full developmental process starting from mitotic progenitors in MGE, which differentiate and migrate to the cortex to become mouse mature INs, and examined whether the human MGE-derived INs developmental trajectory could be aligned. We integrated six datasets, a human dataset containing 733 cells from MGE and 271 MGE-derived cortical INs (18) (5 to 22 PCW) and five from mouse at different ages, and sequenced by different technologies (29, 30) (SI Appendix). We observed a continuous developmental trajectory from the integrated data (SI Appendix, Fig. S6F) starting from the mitotic cells, followed by those transitioning into the postmitotic stage where progenitors diverge and differentiated by distinct transcriptional states. The states aligned with the previously identified three branches (SI Appendix, Fig. S6H). Along branch 1, new subbranches emerged and ultimately arrived at distinct types of mature INs (Sst, Pvalb, Nos1, and Th) (SI Appendix, Fig. S6I). The human cell development largely resembled the mouse cells, where the human cells ranged from early mitotic to relatively mature INs along branch 1. In another trajectory endpoint, striatal INs (IN-STR) were blended with mouse cells from branch 2 (SI Appendix, Fig. S6J). This analysis identified 12 major groups, including three clusters of mitotic cells (1, 4, 11) and branch 1 clusters of four different subbranches: an Sst branch (cluster 3, 9); a Pvalb (cluster 2, 10); an Nos1 branch (cluster 7); and an unknown branch (cluster 8; expressing markers such as BmT7, Col2a1, Notch2, Cd9) (SI Appendix, Fig. S6 K and L). The human cells were grouped with mouse cells in corresponding clusters (SI Appendix, Fig. S7B). Particularly, a group of human cells in cluster 3 was identified as relatively mature precursors of Sst INs (SI Appendix, Fig. S7B). Our analyses revealed that transcriptional profiles underlying INal fate specification are largely conserved between mouse and human. It also highlighted the power of cFIT to capture and integrate the shared biological processes across different systems effectively. These are important steps toward the goal of harnessing information across species to understand mammalian neurodevelopment and its relevant physiology.

Discussion

We develop a method for integrating single-cell datasets and transferring knowledge to target settings that is robust and interpretable. cFIT assumes a shared common factor space across datasets, but it models distortions and shifts on genewise expression that are unique to each source. In doing so, it captures the advantages without the disadvantages of existing methods. Similar to LIGER, the nonnegativity constraint of NMF yields interpretable factors that can be biologically meaningful. While the shift in cFIT corresponds to the batch-specific factor in LIGER, their scaling is applied to all of the shared factors concurrently. Therefore, our model takes a different approach to characterize the impact of domain effects originated from different experimental tools and measurements employed. Nonlinear methods typically allow for higher flexibility and superior power to correct the varying sources of batch effects, while it comes with a much higher risk of false correction of biological effects. This can cause reduced power of downstream analysis such as identifying DEG. Seurat v3 intrinsically assumes batch effects being orthogonal to biological effects and a substantial overlap of cell-type compositions between target and source datasets and produces results dependent on the order of pairwise integration. By contrast, our method makes no assumptions on cell populations in individual data and can perform integration simultaneously across all data sources. Our method also does not depend on the degree of domain effects relative to biological differences (e.g., between cell types), as required to ensure the success of methods such as MNNcorrect (12). Notably, far fewer parameters are required by our model, and yet, it retains the power to capture domain effects. It maintains identifiability and robustness through the choice of tuning parameters. Like Seurat v3, our method also provides an estimate of a corrected expression matrix, which can be used as input for downstream analyses such as pseudotime or differential gene expression analysis. There are notable advantages to having access to corrected versions of both gene expression and lower-dimensional factor loadings, which can be used to reveal interesting biological features. We would also like to point out the possibility of using cFIT as a first step to eliminate major batch effects and then applying alternative methods to remove more subtle effects in a subsequent iteration.

Unlike many competing approaches, cFIT is less prone to removing biological heterogeneity, which facilitates combining datasets with strong biological heterogeneity and capturing the advantages of each source into a single dataset. We show this in simulations and several scRNA-seq datasets. Consequentially, in our analysis of fetal brain development, we were able to combine datasets sampled from widely divergent protocols, spanning different developmental epochs with both mouse and human cells. The resulting integrated analysis delineated closely related neuronal subtypes, drew inferences about developmental trajectories, and correctly classified rare cells from datasets with small numbers of cells sampled. These insights could not be obtained from any single dataset, nor with an integration approach that minimized biological differences between datasets.

Methods

To integrate multiple datasets, we start with selecting those informative genes and then normalize the expression of each cell by the library size and a log transformation (SI Appendix has more details). The set of unknown parameters $\left\{\mathit{W},{\left\{{\mathit{H}}_j,{\mathbf{\Lambda }}_j,{\mathit{b}}_j\right\}}_{j=1}^M\right\}$ is estimated by minimizing the following objective:

$$\begin{array}{ll}\hfill & \frac{1}{N}\sum _{j=1}^M{\Vert {\mathit{X}}_j-\left({\mathit{H}}_j{\mathit{W}}^{\top }{\mathbf{\Lambda }}_j+{\mathit{1}}_{n_j}{\mathit{b}}_j^{\top }\right)\Vert }^2\hfill \\ \hfill & +\gamma \sum _{l=1}^p{\left(\sum _{j=1}^M\frac{n_j}{N}{\mathbf{\Lambda }}_j\left(l,l\right)-1\right)}^2,\hfill \end{array}$$ [3]

subjecting to the nonnegative constraints for parameters $\mathit{W},{\mathit{H}}_j,{\mathbf{\Lambda }}_j,{\mathit{b}}_j$. Here, we use $\mathit{X}\left(i,j\right)$ to denote the $\left(i,j\right)$-th entry of matrix $\mathit{X}$. The positive parameter $\gamma$ determines how much penalization is imposed on the batch-specific parameter ${\mathbf{\Lambda }}_j$, which ensures the identifiability of the learned model.

To optimize the above nonconvex objective function, we adopt the widely used block coordinate descent approach (31, 32), with the details deferred to SI Appendix. Having eliminated the domain-related factors, the integrated scRNA-seq expression matrices are ready for downstreaming analysis, such as clustering and trajectory inference with the low-dimensional representation ${\mathit{H}}_j$ and inference of differentially expressed genes with the scaled cell by gene matrix ${\mathit{H}}_j{\mathit{W}}^{\top }$. With the estimated common factor matrix $\mathit{W}$, one can rapidly transfer the learned pattern to a target dataset through a transfer algorithm (detailed below). The dataset-specific factor loading ${\mathit{H}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$, scaling ${\mathbf{\Lambda }}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$, and shift ${\mathit{b}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$ are estimated with fixed reference factor matrix through a similarly block coordinate descent procedure. Ultimately, the proposed algorithm projects the target data onto the low-dimensional space estimated from the reference dataset. This procedure capitalizes on available information gleaned from prior analyses to optimize the value of small and low-quality datasets. Below, we briefly describe the steps for data integration and transfer tasks, with details deferred to SI Appendix.

Data Integration.

Given the solution $\left(\widehat{\mathit{W}},{\left\{{\widehat{\mathit{H}}}_j,{\widehat{\mathbf{\Lambda }}}_j,{\widehat{\mathit{b}}}_j\right\}}_{j=1}^M\right)$ to the aforementioned optimization problem, one can obtain the estimated data matrix in the shared lower-dimensional factor space as

$$\widehat{\mathit{X}}=\left[\begin{array}{c}\hfill {\widehat{\mathit{X}}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\widehat{\mathit{X}}}_M\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\widehat{\mathit{H}}}_1{\widehat{\mathit{W}}}^{\top }\hfill \\ \hfill ⋮\hfill \\ \hfill {\widehat{\mathit{H}}}_M{\widehat{\mathit{W}}}^{\top }\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\hat{\mathit{H}}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\hat{\mathit{H}}}_M\hfill \end{array}\right]{\hat{\mathit{W}}}^{\top }=\hat{\mathit{H}}{\hat{\mathit{W}}}^{\top },$$

and one can obtain the intrinsic low-dimensional representation as the estimated factor loadings $\hat{\mathit{H}}$. As is seen in our real data examples, these batch-adjusted observations are particularly useful for downstreaming analysis, such as cell-type identification.

Data Transfer.

We transfer the knowledge to a target dataset that is potentially of lower quality or contains smaller numbers of cells. Specifically, given the target expression matrix $X_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$ and the factor matrix ${\mathit{W}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ obtained from reference datasets, the goal is to recover parameters $\left({\mathit{H}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}},{\mathbf{\Lambda }}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}},{\mathit{b}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}\right)$ for the target dataset. Similarly, these parameters can be estimated through the following optimization problem:

$$\underset{\mathit{H},\mathbf{\Lambda },\mathit{b}}{min}G\left(\mathit{H},\mathbf{\Lambda },\mathit{b};{\mathit{W}}_{\mathrm{r}\mathrm{e}\mathrm{f}}\right)\hspace{0.17em}≔\hspace{0.17em}{\Vert {\mathit{X}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}-\left(\mathit{H}{\mathit{W}}_{\mathrm{r}\mathrm{e}\mathrm{f}}^{\top }\mathbf{\Lambda }+\mathit{1}{\mathit{b}}^{\top }\right)\Vert }_F^2,$$ [4]

subject to the nonnegative constraints $\mathit{H},\mathit{\lambda },\mathit{b}\ge 0$ and row stochastic constraint $\mathit{H}\mathit{1}=\mathit{1}$. The low-dimensional factor loadings ${\widehat{\mathit{H}}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$ can be directly used for further data analysis.

Scalability and Algorithm Speedup.

The computation complexity of cFIT scales linearly with the number of cells (SI Appendix, Fig. S8A). It can accommodate tens of thousands of cells within reasonable run time on a standard personal computer (depending on the number of genes $p$ and the number of factors $r$). To speed up the processing of millions of cells, we implemented a fast version of the algorithm employing the idea of random sketching (33) and stochastic proximal point (SPP) method (34). In each iteration, a random projection matrix ${\mathit{S}}_j\in {\mathbb{R}}^{{ñ}_j\times n_j}$ is generated for each batch independently. Then, the parameter sets are updated solving the sketched problem

$$J\left(\mathbf{\Theta };{\left\{{\mathit{S}}_j\right\}}_{j=1}^M\right)=\frac{1}{N}\sum _{j=1}^M{\Vert {\mathit{S}}_j{\mathit{X}}_j-{\mathit{S}}_j\left({\mathit{H}}_j{\mathit{W}}^{\top }{\mathbf{\Lambda }}_j+{\mathit{1}}_{n_j}{\mathit{b}}_j^{\top }\right)\Vert }^2$$ [5]

with the same constraints and penalty. For each coordinate descent subproblem, SPP is employed to ensure the solution stays close to the previous updates, thus encouraging consistency across different sketched problem. This is achieved by adding additional penalty in updating each block of parameters

$$\begin{array}{l}\hfill {\mathit{\theta }}^{\left(t+1\right)}=\underset{\mathit{\theta }\ge 0}{\arg min}\left[J\left(\mathit{\theta };{\mathit{S}}^{\left(t\right)},{\left(\mathbf{\Theta }\backslash \mathit{\theta }\right)}^{\left(t\right)}\right)+\frac{1}{2{\mu }_t}{‖\mathit{\theta }-{\mathit{\theta }}^{\left(t\right)}‖}^2\right],\\ \hfill \end{array}$$ [6]

where ${\mu }_t$ controls the diminishing step size. This procedure enables reduced run time roughly proportional to the fraction of subsample size (SI Appendix, Fig. S8B). More details can be found in SI Appendix.

Data Availability

There are no data underlying this work.