Covariance-based sample selection for heterogeneous data: Applications to gene expression and autism risk gene detection

Abstract

Risk for autism can be influenced by genetic mutations in hundreds of genes. Based on findings showing that genes with highly correlated gene expressions are functionally interrelated, “guilt by association” methods such as DAWN have been developed to identify these autism risk genes. Previous research analyze the BrainSpan dataset, which contains gene expression of brain tissues from varying regions and developmental periods. Since the spatiotemporal properties of brain tissue is known to affect the gene expression’s covariance, previous research have focused only on a specific subset of samples to avoid the issue of heterogeneity. This analysis leads to a potential loss of power when detecting risk genes. In this article, we develop a new method called COBS (COvariance-Based sample Selection) to find a larger and more homogeneous subset of samples that share the same population covariance matrix for the downstream DAWN analysis. To demonstrate COBS’s effectiveness, we use genetic risk scores from two sequential data freezes obtained in 2014 and 2020. We show COBS improves DAWN’s ability to predict risk genes detected in the newer data freeze when using the risk scores of the older data freeze as input.

1. Introduction

The genetic cause of autism spectrum disorder (ASD), a neurodevelopmental disorder that affects roughly 1–2% individuals in the United States, remains an open problem despite decades of research (Autism and Investigators, 2014). ASD is characterized primarily by impaired social functions and repetitive behavior (Kanner et al., 1943; Rutter, 1978). To better understand this disorder, scientists identify specific genes that are liable for increasing the chance of developing ASD when damaged or mutated (Sanders et al., 2015). These are genes are called risk genes. While breakthroughs in genomic technologies and the availability of large ASD cohorts have led to the discovery of dozens of risk genes, preliminary studies suggest there are hundreds of risk genes still unidentified (Buxbaum et al., 2012). In this work, we build upon the current statistical methodologies to further improve our ability to identify risk genes.

We focus on statistical methods that use gene co-expression networks to help identify risk genes. These networks are estimated from brain tissue’s gene expression data. Since these gene co-expression networks provide insight into genes that regulate normal biological mechanisms in fetal and early brain development, it was hypothesized that risk genes which alter these mechanisms should be clustered in these networks (Šestan et al., 2012). Early findings confirmed this hypothesis (Parikshak et al., 2013; Willsey et al., 2013). These results led to the development of the Detection Association With Networks (DAWN) algorithm which uses a “guilt by association” strategy – implicating new risk genes based on their connectivity to previously identified risk genes (Liu et al., 2014, 2015). However, the previous DAWN analyses suffer from statistical limitations that we will investigate and resolve in this article.

We challenge previous analyses’ assumptions regarding the homogeneity of the covariance matrix in gene expression data. Previous DAWN analyses assume that gene expression samples from the same brain tissue type share the same covariance matrix. This assumption was influenced by the findings in Kang et al. (2011) and Willsey et al. (2013), which showed that gene co-expression patterns differ among different brain regions and developmental periods on average. Statistically, this means that the covariance matrix among the gene expressions may differ with respect to the spatiotemporal properties of the brain tissue. Hence, previous DAWN analyses (Liu et al., 2014, 2015) use only samples from a particular brain tissue type chosen by the findings in Willsey et al. (2013). However, no further statistical analysis is performed to check for homogeneity of this specific subset of samples. In addition, since previous DAWN analyses limit themselves to a subset of gene expression samples, many other samples assumed to be heterogeneous are excluded. This leads to a potential loss of power when identifying risk genes.

To overcome these limitations, we develop a method called COBS (COvariance-Based sample Selection), a two-staged procedure designed to select a subset of gene expression samples in a data-driven way that yields a more homogeneous and larger sample than the fixed subset used previously. In the first stage, we take advantage of the recent developments in high-dimensional covariance testing (Cai et al., 2013; Chang et al., 2017) to determine whether if the gene expression from two different brain tissues share the same population covariance matrix. We combine this with a multiple-testing method called Stepdown that accounts for the dependencies among many hypothesis tests (Romano and Wolf, 2005; Chernozhukov et al., 2013). In the second stage, after determining which pairs of brain tissues have statistically indistinguishable covariance matrices, we develop a clique-based procedure to select which brain tissues to use in the downstream DAWN analysis. We show that COBS selects brain tissues within the BrainSpan dataset that align with current scientific knowledge and also leads to an improved gene network estimate for implicating risk genes. This article addresses the numerous algorithmic challenges needed to implement this idea.

In Section 2, we describe the data and statistical model for heterogeneity in the covariance matrix. In Section 3, we provide a visual diagnostic to investigate the homogeneity assumptions of previous DAWN analyses. In Section 4, we describe the different stages of COBS to find a subset of homogeneous samples within a dataset. In Section 5, we illustrate the properties of COBS on synthetic datasets. In Section 6, we apply our procedure on gene expression data to show that, when combined with DAWN, we have an improved gene network that can better implicate risk genes. Section 7 provides an overall summary and discussion.

2. Data and model background

Due to the challenge of obtaining and preserving brain tissue, datasets recording the gene expression patterns of brain tissue are rare. The BrainSpan project contributes one of the largest microarray expression datasets available (the “BrainSpan dataset” henceforth), sampling tissues from 57 postmortem brains with no signs of large-scale genomic abnormalities (Kang et al., 2011). Many studies have favored this dataset because its 1294 microarray samples capture the spatial and temporal changes in gene expression that occur in the brain during the entirety of development (De Rubeis et al., 2014; Dong et al., 2014; Cotney et al., 2015). While our paper focuses on this particular microarray expression dataset, our method would apply to other gene expression datasets such as RNA sequencing data.

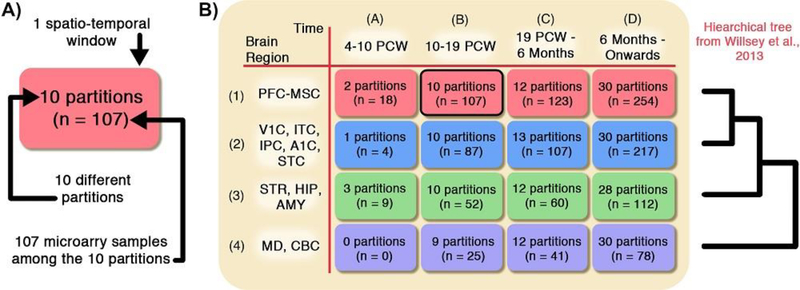
The heterogeneity of gene expression due to the spatiotemporal differences in brain tissues presents statistical challenges. As documented in Kang et al. (2011), the region and developmental period of the originating brain tissue contribute more to the heterogeneity than other variables such as sex and ethnicity. To understand this heterogeneity, we use the following schema to model the BrainSpan dataset. Each of the 1294 microarray samples is categorized into one of 16 spatiotemporal windows, or windows for short, depending on which brain region and developmental period the brain tissue is derived from. Within each window, all microarray samples originating from the same brain are further categorized into the same partition. There are 212 partitions in total. Figure 1 summarizes how many partitions and microarray samples belong in each window in the BrainSpan dataset. This schema allows us to model the microarray samples more realistically since the gene co-expression patterns vary greatly on average from window to window (Willsey et al., 2013). Additionally, Willsey et al. (2013) find that among all the windows, the known risk genes in Window 1B are most tightly co-expressed. Window 1B is highlighted in Figure 1 and contains the 107 microarray samples from the prefrontal cortex and primary motor-somatosensory cortex from 10 to 19 post-conceptual weeks. Due to this finding, previous DAWN analyses focus on all 107 samples from 10 partitions, assuming that these samples were homogeneous without further statistical investigation, and discard the remaining 1187 samples, (Liu et al., 2014, 2015). We seek to improve upon this heuristical sample selection procedure, first by formalizing a statistical model.

Fig. 1.

(A) 107 microarray samples grouped by the originating 10 brains. This forms 10 different partitions. Since all these partitions originate from the same brain region and developmental period, they are further grouped into the same window. (B) The 57 postmortem brains belong to 4 different developmental periods (columns). Here, PCW stands for post-conceptual weeks. Each brain is dissected and sampled at 4 different brain regions (rows). In total, over the 212 partitions, there are 1294 microarray samples, each measuring the expression of over 13,939 genes. Window 1B (outlined in black) is the window that previous work (Liu et al., 2015) focus on, and the hierarchical tree from Willsey et al. (2013) is shown to the right. Additional details about the abbreviations are given in Appendix B.

2.1. Statistical model

We use a mixture model that assumes that microarry samples from the same partition are homogeneous while samples among different partitions could be heterogeneous. For the pth partition, let ${\mathit{X}}_1^{(p)},\dots {\mathit{X}}_{n_p}^{(p)}\in {ℝ}^d$ denote n_p i.i.d. samples, and let w(p) denote the window that the partition p resides in. These n_p samples are drawn from either a distribution with covariance Σ, or another distribution with a different covariance matrix Σ_p. We emphasize that the distributions in consideration are not necessarily Gaussian, and Σ is the covariance matrix shared among all partitions while Σ_p may vary from partition to partition. A fixed but unknown parameter γ_w(p) ∈ [0,1] controls how frequently the partitions in window w are drawn from these two distributions, meaning it controls the amount of heterogeneity. For each partition p, this mixture model is succinctly described as,

$$\begin{gathered} I^{(p)}\sim \text{Bernoulli}\left({\gamma }_{w(p)}\right), \\ {\mathit{X}}_1^{(p)},\dots ,{\mathit{X}}_{n_p}^{(p)}\stackrel{i.i.d.}{\sim }\{\begin{array}{ll}D(\mathbf{\Sigma })& \text{if}{I}^{(p)}=1\\ D\left({\mathbf{\Sigma }}_p\right)& \text{otherwise},\end{array} \end{gathered}$$ (2.1)

where D(Σ) denotes an arbitrary fixed distribution parameterized by its covariance matrix Σ, and I^(p) is the latent variable that determines whether or not the samples in partition p have covariance Σ or Σ_p. With this model setup, our task is to determine the set of partitions that have the covariance matrix Σ, which we will call

$$\mathcal{P}=\left\{p:I^{(p)}=1\right\}.$$ (2.2)

The findings of Kang et al. (2011) and Willsey et al. (2013) inform us on how much heterogeneity to expect within a window via γ_w(p). While analyses such as Liu et al. (2015) assume that all the samples in Window aip1B are homogeneous, it is noted in Kang et al. (2011) that sampling variability in brain dissection and in the proportion of white and gray matter in different brain tissues can cause variability in the gene co-expression patterns. This means that scientifically, we do not expect all the partitions in Window 1B to be homogeneous (i.e., γ_w(p) = 1). Furthermore, Willsey et al. (2013) find a hierarchical clustering among the four brain regions. This is illustrated in Figure 1, where the gene co-expression patterns in the brain regions represented in the first row are most similar to those in the second row and least similar to those in the fourth row. The authors also find a smooth continuum of gene expression patterns across the different developmental periods, which are represented as the columns of the table in Figure 1. Hence, we expect γ_w(p) to decrease smoothly as the window w becomes more dissimilar to Window 1B, in both the spatial and temporal direction.

2.2. Connections to other work

Other work use models similar to (2.1) on microarray expression data to address different co-expression patterns among different tissues and subjects, but their methods differ from ours. One approach is to directly cluster the covariance matrices of each partition (Ieva et al., 2016). However, this approach does not account for the variability in the empirical covariance matrix, unlike our hypothesis-testing based method. Another approach is to explicitly model the population covariance matrix for each partition as the summation of a shared component and a partition-specific heterogeneous component. This is commonly used in batch-correction procedures where the analysis removes the heterogeneous component from each partition (Leek and Storey, 2007). However, we feel such an additive model is too restrictive for analyzing the BrainSpan dataset, as we do not believe there is a shared covariance matrix across all the windows of the brain. Instead, our approach will find specific set of partitions with statistically indistinguishable covariance matrices.

3. Elementary analysis

In this section, we develop a visual diagnostic to investigate if the 10 partitions in Window 1B used in previous work (Liu et al., 2014, 2015) are as homogeneous as these previous analyses assume. Using a hypothesis test for equal covariances, our diagnostic leverages the following idea: we divide the partitions into two groups and apply a hypothesis test to the samples between both groups. If all the partitions were truly drawn from distributions with equal covariances, then over many possible divisions, the empirical distribution of the resulting p-values should be roughly uniform. We can visualize this distribution by using a QQ-plot. The less uniform the p-values look, the less we are inclined to interpret our partitions to be all drawn from distributions with equal covariances. The following algorithm summarizes this diagnostic.

Algorithm 1:

Covariance homogeneity diagnostic

1. Loop over trials t =1,2, …, T:

(a) Randomly divide the selected partitions in the set $\mathcal{P}$ into two sets, ${\mathcal{P}}^{(1)}$ and ${\mathcal{P}}^{(2)}$, such that ${\mathcal{P}}^{(1)}\cup {\mathcal{P}}^{(2)}=\mathcal{P}$ and ${\mathcal{P}}^{(1)}\cap {\mathcal{P}}^{(2)}=Ø$.

(b) For each partition $p\in {\mathcal{P}}^{(1)}$, center the samples ${\mathit{X}}_1^{(p)},\dots ,{\mathit{X}}_{n_p}^{(p)}$. Then aggregate all samples in ${\mathcal{P}}^{(1)}$ to form the set of samples $$\mathcal{X}=\underset{p\in {\mathcal{P}}^{(1)}}{\cup }\left\{{\mathit{X}}_1^{(p)},\dots ,{\mathit{X}}_{n_p}^{(p)}\right\}.$$    Similarly, form the set of samples $\mathcal{Y}$ from the set of partitions ${\mathcal{P}}^{(2)}$.

(c) Compute the p-value for a hypothesis test that tests whether or not the samples in $\mathcal{X}$ and $\mathcal{Y}$ have the same covariance matrix.

2. Produce a QQ-plot of the resulting T p-values to see if empirical distribution of the p-values is close to a uniform distribution.

We remind the reader that the above procedure is a diagnostic. This is not necessarily a recipe for a goodness-of-fit test since the T p-values are highly dependent, which is difficult to analyze theoretically without a carefully designed global null test. However, as we will demonstrate in later sections of this article, this diagnostic is nonetheless able to display large-scale patterns in our dataset.

3.1. Specification of covariance hypothesis test

To complete the above diagnostic’s description, we describe a procedure to test for equality of covariance matrices developed by other authors. Following the model (2.1), let $\mathcal{X}=\left\{{\mathit{X}}_1,\dots ,{\mathit{X}}_{n_1}\right\}$ and $\mathcal{Y}=\left\{{\mathit{Y}}_1,\dots ,{\mathit{Y}}_{n_2}\right\}$ be n₁ and n₂ i.i.d. samples from d-dimensional distributions with covariance Σ_X and Σ_Y respectively, both with an empirical mean of 0. We define $\mathbb{X}\in {ℝ}^{n_1\times d}$ and $\mathbb{Y}\in {ℝ}^{n_2\times d}$ as the matrices formed by concatenating these samples row-wise. Define the empirical covariance matrices as ${\mathbf{\Sigma }}_X={\mathbb{X}}^{\top }\mathbb{X}/n_1$, and ${\mathbf{\Sigma }}_Y={\mathbb{Y}}^{\top }\mathbb{Y}/n_2$, denote the individual elements of these matrices as ${\mathbf{\Sigma }}_X={\left[{\widehat{\sigma }}_{X,ij}\right]}_{1\le i,j\le d}$ and likewise for Σ_Y.

We now discuss the hypothesis test for equal covariance, H₀ : Σ_X = Σ_Y, that we will consider in this article based on the test statistic defined in Chang et al. (2017) which extends Cai et al. (2013). In these works, the authors note that if Σ_X = Σ_Y, then the maximum element-wise difference between Σ_X and Σ_Y is 0. Hence, Chang et al. (2017) defines the test statistic $\widehat{T}$ as the maximum of squared element-wise differences between Σ_X and Σ_Y, normalized by its variance. Specifically,

$$\widehat{T}=\underset{ij}{\max }\left({\widehat{t}}_{ij}\right)\text{where}{\widehat{t}}_{ij}=\frac{{\left({\widehat{\sigma }}_{X,ij}-{\widehat{\sigma }}_{Y,ij}\right)}^2}{{\widehat{s}}_{X,ij}/n_1+{\widehat{s}}_{Y,ij}/n_2},i,j\in 1,\dots ,d,$$ (3.1)

where ${\widehat{s}}_{X,ij}=\sum _{m=1}^{n_1}{\left({\mathbb{X}}_{mi}{\mathbb{X}}_{mj}-{\widehat{\sigma }}_{X,ij}\right)}^2/n_1$ is the empirical variance of the variance-estimator ${\widehat{\sigma }}_{X,ij}$, and ${\widehat{s}}_{X,ij}$ is defined similarly.

Then, Chang et al. (2017) constructs an empirical null distribution of $\widehat{T}$ under H₀ : Σ_X = Σ_Y, using the multiplier bootstrap (Chernozhukov et al., 2013). On each of the b ∈{1, …, B} trials, the multiplier bootstrap computes a bootstrapped test statistic ${\widehat{T}}^{(b)}$ by weighting each of the n₁ + n₂ observations by a standard Gaussian random variable denoted collectively as $(g_1^{(b)},\dots ,g_{n_1}^{(b)},g_{n_1+1}^{(b)},\dots ,g_{n_1+n_2}^{(b)})$, drawn independently of all other variables. Specifically, we construct the bootstrap statistic for the bth trial as

$${\widehat{T}}^{(b)}=\underset{ij}{\max }\left({\widehat{f}}_{ij}^{(b)}\right)\text{where}{\widehat{t}}_{ij}^{(b)}=\frac{{\left({\widehat{\sigma }}_{X,ij}^{(b)}-{\widehat{\sigma }}_{Y,ij}^{(b)}\right)}^2}{{\widehat{s}}_{X,ij}/n_1+{\widehat{s}}_{Y,ij}/n_2},i,j\in 1,\dots ,d,$$ (3.2)

Where ${\widehat{\sigma }}_{X,ij}^{(b)}=\sum _{m=1}^{n_1}{g}_m^{(b)}\left({\mathbb{X}}_{mi}{\mathbb{X}}_{mj}-{\widehat{\sigma }}_{X,ij}\right)/n_1$ and ${\widehat{\sigma }}_{Y,tj}^{(b)}=\sum _{m=1}^{n_2}{g}_{n_1+m}^{(b)}\left({\mathbb{Y}}_{mi}{\mathbb{Y}}_{mj}-{\widehat{\sigma }}_{Y,ij}\right)/n_2$. We compute the p-value by counting the proportion of bootstrap statistics that are larger than the test statistic,

$$\text{p}-\text{value}=\frac{\left|\left\{b:\left|{\widehat{T}}^{(b)}\right|\ge \left|\widehat{T}\right|\right\}\right|}{B}.$$

Chang et al. (2017) prove that this test has asymptotically 1–α coverage under the null hypothesis as long as the all distributions in the distribution family D in (2.1) have sub-Gaussian and sub-exponential tails, even in the high-dimensional regime where d ≫ max(n₁,n₂)

3.2. Application to BrainSpan

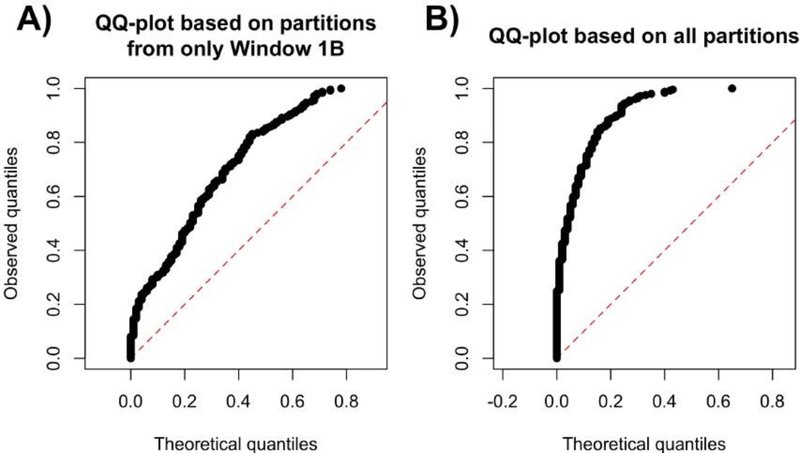
Equipped with a complete description of the diagnostic, we apply it to the BrainSpan dataset. Among the 10 partitions in Window 1B, we divide the partitions into two groups uniformly at random 250 times, and compute a p-value using Method 1 (with normalization) for each division using 200 bootstrap trials. The QQ-plot of the resulting p-values are shown in Figure 2A, where we see that the p-values are biased towards 0. This suggests that the 10 partitions in Window 1B are heterogeneous since they do not seem to all share the same covariance matrix. Furthermore, we apply this diagnostic to all partitions in the BrainSpan dataset with 5 or more samples. This results in using only 125 of the 212 partitions shown in Figure 1. The resulting p-values become more biased towards 0 (Figure 2B), suggesting that the dataset as a whole is more heterogeneous than the partitions in Window 1B. In the next section, we develop a method to resolve this issue by finding the largest subset of partitions possible among the 125 partitions in the BrainSpan dataset that share the same covariance matrix.

Fig. 2.

QQ-plots of the 250 p-values generated when applying our diagnostic to the BrainSpan dataset. (A) The diagnostic using only the partitions in Window 1B, showing a moderate amount of heterogeneity. (B) The diagnostic using all 125 partitions in the BrainSpan dataset, showing a larger amount of heterogeneity.

4. Methods: COBS (Covariance-based sample selection)

While we have discussed a method to test for equivalent covariance matrices between any two partitions in Section 3, we cannot directly apply this method to select a large number of homogeneous partitions in the BrainSpan dataset without suffering a potentially large loss of power due to multiple testing. Since there are r = 125 partitions with more than 5 samples, applying the hypothesis test to each pair of partitions results in $\left(\begin{array}{l}r\\ 2\end{array}\right)=7750$ dependent p-values. These p-values are dependent since each of the r partitions is involved in r – 1 hypothesis tests. Hence, standard techniques such as a Bonferroni correction are likely too conservative when accounting for these dependencies, leading to a loss of power.

To properly account for this dependency, we introduce our new method called COBS, which comprises of two parts. First, we use a Stepdown method in Subsection 4.1 that simultaneously tests all $\left(\begin{array}{l}r\\ 2\end{array}\right)$ hypothesis tests for equal covariance matrices, which builds upon the bootstrap test introduced previously in Section 3. After determining which of the $\left(\begin{array}{l}r\\ 2\end{array}\right)$ pairs of partitions do not have statistically significant differences in their covariance matrices, we develop a clique-based method in Subsection 4.2 to select a specific set of partitions $\mathcal{P}$.

4.1. Stepdown method: multiple testing with dependence

We use a Stepdown method developed in Chernozhukov et al. (2013) to control the family-wise error rate (FWER). We tailor the bootstrap-based test in Subsection 3.1 to our specific setting in the algorithm below. We denote ${\widehat{T}}_{(i,j)}$ as the test statistic formed using (3.1) to test if the covariance of samples between partition i and partition j are equal. Similarly, let ${\widehat{T}}_{(i,j)}^{(b)}$ denote the corresponding bootstrap statistics on the bth bootstrap trial. Here, quantile({x₁, …, x_n};1 – α) represents the empirical (1 – α)·100% quantile of the vector (x₁, …, x_n).

Algorithm 2:

Stepdown method

1. Initialize the list enumerating all $\left(\begin{array}{l}r\\ 2\end{array}\right)$ null hypotheses corresponding to the set of partition pairs, $\mathcal{L}=\{(1,2),\dots ,(r-1,r)\}$.

2. Calculate ${\widehat{T}}_{\ell }$ for each $\ell \in \mathcal{L}$, as stated in (3.1).

3. Loop over steps t = 1, 2, …:

(a) For each bootstrap trial b = 1, …, B:

i. Generate $N=\sum _p{n}_p$ i.i.d. standard Gaussian random variables, one for each sample in each partition, and compute ${\widehat{T}}_{\ell }^{(b)}$ for all $\ell \in \mathcal{L}$ as stated in (3.2).

ii. Compute $${\widehat{T}}^{(b)}=\max \left\{{\widehat{T}}_{\ell }^{(b)}:\ell \in \mathcal{L}\right\}.$$ (4.1)

(b) Remove any $\ell \in \mathcal{L}$ if $${\widehat{T}}_{\ell }\ge \text{quantile}\left(\left\{{\widehat{T}}^{(1)},\dots ,{\widehat{T}}^{(B)}\right\};1-\alpha \right).$$    If no elements are removed from $\mathcal{L}$, return the null hypotheses corresponding to $\mathcal{L}$. Otherwise, continue to step t + 1.

Using techniques in Romano and Wolf (2005) and Chernozhukov et al. (2013), it can be proven that this method has the following asymptotic FWER guarantee,

$$\mathbb{P}(\text{no}\text{true}\text{null}\text{hypothesis}\text{among}\mathcal{H}\text{null}\text{hypotheses}\text{are}\text{rejected})\ge 1-\alpha +o(1)$$ (4.2)

under the same assumptions posed in Chang et al. (2017). The reason Algorithm 2 is able to control the FWER without a Bonferroni correction is because the null distribution in the Stepdown method is properly calibrated to account for the joint dependence among the $\left(\begin{array}{l}r\\ 2\end{array}\right)$ tests. Specifically, when $\left(\begin{array}{l}r\\ 2\end{array}\right)$ tests are individually performed as in Subsection 3.1, the test statistics (3.1) are dependent, but the bootstrapped null distributions do not account for this dependence. Hence, accounting for the dependence via a Bonferroni correction after-the-fact can lead to a substantial loss in power. However, in the Stepdown procedure, the bootstrapped null distributions retain the dependencies jointly since they are generated from the same N Gaussian random variables in each trial. See Chernozhukov et al. (2013) (Comment 5.2) for a further discussion.

Robustness concerns

In practice, due to the maximum function in the test statistic ${\widehat{T}}_{\ell }$ displayed in (3.1), the Stepdown method could possibly erroneously reject a hypothesis due to the presence of outliers. One way to circumvent this problem to purposely shrink the value of the test statistic ${\widehat{T}}_{\ell }$ while leaving the bootstrapped statistics ${\widehat{T}}_{\ell }^{(b)}$ in (3.2) the same. Specifically, we can replace ${\max }_{ij}\left({\widehat{t}}_{ij}\right)$ in (3.1) with the $\left({\left\{{\widehat{t}}_{ij}\right\}}_{ij};1-ϵ\right)$, where ϵ is a positive number extremely close to 0. This has the desired effect of “discarding” the large values in ${\left\{{\widehat{t}}_{ij}\right\}}_{ij}$. Observe that this procedure would potentially lead to a slight loss in power, but the inferential guarantee in (4.2) still holds since there can only be strictly less rejections.

Computational concerns

While we use the test statistics (3.1) when describing the Stepdown method, we note that this method can apply to a broader family of test statistics based on statistical theory. In Appendix C, we discuss in detail one alternative to the test statistic in (3.1) that can dramatically reduce up the computation complexity of the Stepdown method. However, we defer this to the appendix because in our specific problem setting of testing equality of covariances, it does not seem to perform well empirically.

4.2. Largest quasi-clique: selecting partitions based on testing results

After applying the covariance testing with the Stepdown method described in the previous subsection, we have a subset of null hypotheses from $\mathcal{H}$ that we accepted. In this subsection, we develop a clique-based method to estimate $\mathcal{P}$, the subset of partitions that share the same covariance matrix defined in (2.2), from our accepted null hypotheses.

We conceptualize the task of selecting partitions as selecting vertices from a graph that form a dense subgraph. Let H_0,(i,j) denote the null hypothesis that the population covariance matrices for partition i and j are equal, and let G = (V, E) be the undirected graph with vertices V and edge set E such that

$$V=\{1,\dots ,r\},E=\left\{(i,j):H_{0,(i,j)}\text{is}\text{accepted}\text{by}\text{the}\text{Stepdown}\text{method}\right\}.$$ (4.3)

Since each of the $\left(\begin{array}{c}|\mathcal{P}|\\ 2\end{array}\right)$ pairwise tests among the partitions in $\mathcal{P}$ satisfies the null hypotheses, the vertices corresponding to $\mathcal{P}$ would ideally form the largest clique in graph G. However, this ideal situation is unlikely to happen. Instead, due to the probabilistic nature of our theoretical guarantee in (4.2), there are likely to be a few missing edges in G among the vertices corresponding to $\mathcal{P}$. Hence, a natural task is to instead find the largest quasi-clique, a task that has been well-studied by the computer science community (see Tsourakakis (2014) and references within). We say a set of k vertices form a γ-quasi-clique if there are at least $\gamma \left(\begin{array}{l}k\\ 2\end{array}\right)$ edges among these k vertices for some γ ∈ [0,1]. The largest γ-quasi-clique is the largest vertex set that forms a γ-quasi-clique. We justify the choice to search for this γ-quasi-clique since, by our model (2.1), the prevalent covariance matrix among the r partitions is the desired covariance matrix Σ we wish to estimate. Here, γ is an additional tuning parameter, but we set γ = 0.95 by default throughout this entire paper.

Unfortunately, many algorithms that could be used to find the largest γ-quasi-clique do not satisfy a certain monotone property in practice, which hinders their usability. Specifically, consider an algorithm $\mathcal{A}$ that takes in a graph G and outputs a vertex set, denoted by $\mathcal{A}(G)$ and for graphs G′ and G, let G′ ⊆ G denote that G′ is a subgraph of G. We say that algorithm $\mathcal{A}$ has the monotone property if

$$G^{\prime }\subseteq G\Rightarrow \left|\mathcal{A}\left(G^{\prime }\right)\right|\le \mathcal{A}(G)\mid ,\text{for}\text{any}\text{two}\text{graphs}G,G^{\prime }.$$ (4.4)

We are not aware of such a property being important in the quasi-clique literature, but it is a natural property to inherit from the multiple testing community. That is, a multiple testing procedure has the monotone property if increasing the signal-to-noise ratio (i.e., decreasing the p-values) yields more rejections (see (Hahn, 2018) and references within). Similarly in the quasi-clique setting, it is natural to expect that increasing the signal-to-noise ratio (i.e., removing edges in G) yields less partitions selected. The monotone property is crucial in practice since it can be shown that the chosen FWER level α and the graph G defined in (4.3) have the following relation,

$$\alpha \ge {\alpha }^{\prime }\Rightarrow G\subseteq G^{\prime },$$

where G and G′ are the graphs formed by FWER level α and α′ respectively. Hence, an algorithm that does not exhibit the property in (4.4) will be fragile – using a smaller α to accept more null hypotheses might counterintuitively result in less partitions being selected. As we will demonstrate in Section 5 through simulations, many existing algorithms to find the largest quasi-clique do not satisfy the monotone property empirically. Therefore, we develop the following new algorithm to remedy this.

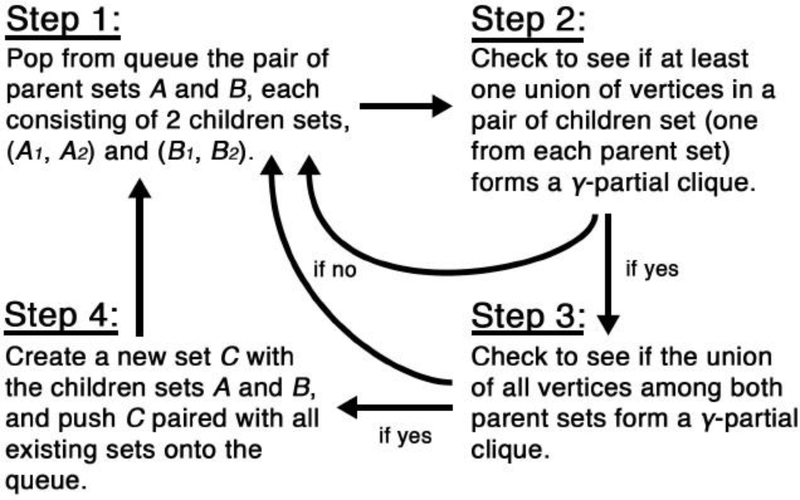
We describe the algorithm below. It starts by constructing a list containing all maximal cliques in the graph G described in (4.3). A maximal clique is a vertex set that forms a clique but is not a subset of a larger clique. The algorithm then proceeds by determining if the union of any two vertex sets forms a γ-quasi-clique. If so, this union of vertices is added to the list of vertex sets. The algorithm returns the largest vertex set in the list when all pairs of vertex sets are tried and no new γ-quasi-clique is found. We demonstrate in Section 5 that this algorithm exhibits the monotone property (4.4) empirically.

Algorithm 4:

Clique-based selection

1. Form graph G based on (4.3).

2. Form $\mathcal{Q}$, the set of all vertex sets that form a maximal clique in G. Each vertex set is initialized with a child set equal to itself.

3. While there exists a pair of vertex sets $A,B\in \mathcal{Q}$ that the algorithm has not tried yet:

(a) Determine if C = A ∪ B forms a γ-quasi-clique in G. If so, add C as a new vertex set into $\mathcal{Q}$, with A and B as its two children sets.

4. Return the largest vertex set in $\mathcal{Q}$.

A naive implementation of the above algorithm would require checking if an exponential number of vertex set unions C = A ∪ B forms a γ-quasi-clique, and each check requires O(r²) operations. However, we are able to dramatically reduce the number of checks required by using the following heuristic: we only check whether the union of A and B forms a γ-quasi-clique if the union of two children sets, one from each A and B, forms a γ-quasi-clique. This heuristic allows us to exploit previous calculations and reduce computational costs. We implement this idea by using one hash table to record which vertex sets are children of other vertex sets, and another hash table table to record if the union of two vertex sets forms a γ-quasi-clique. This idea is illustrated in Figure 4. Additional details on how to initialize and optionally post-process Algorithm 4 are given in Appendix D.

Fig. 4.

Schematic of Algorithm 4’s implementation. Step 2 is able to leverage hash tables which stores previous calculations to see if the union of vertices in a pair of children sets forms a γ-quasi-clique. This has a near-constant computational complexity. This can save tremendous computational time since Step 3, which checks if the union of vertices in both parent sets form a γ-quasi-clique, has a computational complexity of O(r²).

5. Simulation study

We perform empirical studies to show that COBS has more power and yields a better estimation of the desired covariance matrix Σ over conventional methods as the samples among different partitions are drawn from increasingly dissimilar distributions.

Setup

We generate synthetic data in r = 25 partitions, where the data in each partition has n = 15 samples and d = 1000 dimensions drawn from a non-Gaussian distribution. Among these r partitions, the first group of r₁ = 15 partitions, second group of r₂ = 5 partitions and third group of r₃ = 5 partitions are drawn from three different nonparanormal distributions respectively (Liu et al., 2009). The goal in this simulation suite is to detect these r₁ partitions with the same covariance structure. The nonparanormal distribution is a natural candidate to model genomic data with heavier tails and multiple modes (Liu et al. (2012) and Xue and Zou (2012)), and serves to demonstrate that our methods in Section 4 does not rely on the Gaussian assumption. Formally, a random vector $X=\left(X_1,\dots ,X_d\right)\in {ℝ}^d$ is drawn from a nonparanormal distribution if there exists d monotonic and differentiable functions f₁, …, f_d such that when applied marginally, Z = (f₁(X₁), …, f_d(X_d)) ~ N(μ, Σ), a Gaussian distribution with proxy mean vector μ and proxy covariance matrix¹ Σ. We provide the details of how we generate the three nonparanormal distributions in Appendix E, but we highlight the key features regarding Σ below.

We construct three different proxy covariance matrices Σ⁽¹⁾, Σ⁽²⁾, and Σ⁽³⁾ in such a way that for a given parameter β ∈ [0,1], we construct Σ⁽²⁾ and Σ⁽³⁾ to be more dissimilar from Σ⁽¹⁾ as β increases. We highlight the key features of our constructed proxy covariance matrices here. All three proxy covariance matrices are all based on a stochastic block model (SBM), a common model used to model gene networks (Liu et al., 2018; Funke and Becker, 2019). The first r₁ partitions are generated using the proxy covariance matrix Σ⁽¹⁾, which is an SBM with two equally-sized clusters where the within-cluster covariance is a = 0.9 and the between-cluster covariance is b = 0.1. The second r₂ partitions are generated using the proxy covariance matrix Σ⁽²⁾, which is similar to Σ⁽¹⁾ except a and b are shrunk towards 0.5 depending on the magnitude of β. The last r₂ partitions are generated using the proxy covariance matrix Σ⁽³⁾, which is similar to Σ⁽¹⁾ except an equal fraction of variables from both clusters break off to form a third cluster, depending on the magnitude of β. By generating Σ⁽¹⁾, Σ⁽²⁾, and Σ⁽³⁾ in this fashion, the parameter β can control the difficulty of the simulation setting – a larger β means COBS would ideally have more power in distinguishing among the first r₁ partitions from the other partitions. Figure 5 visualizes the resulting covariance matrices for the three nonparanormal distribution we generate in this fashion for β = 0.3 and β = 1.

Fig. 5.

(Top row) Heatmap visualizations of the empirical covariance matrix of the three partitions, each drawn from a different nonparanormal distribution when β = 0.3. The distributions using Σ⁽¹⁾, Σ⁽²⁾ and Σ⁽³⁾ are shown as the left, middle and right plots respectively. The darker shades of red denote a higher covariance. (Bottom row) Visualizations similar to the top row except for β = 1, so the dissimilarity comparing Σ⁽²⁾ or Σ⁽³⁾ to Σ⁽¹⁾ is increased.

Multiple testing

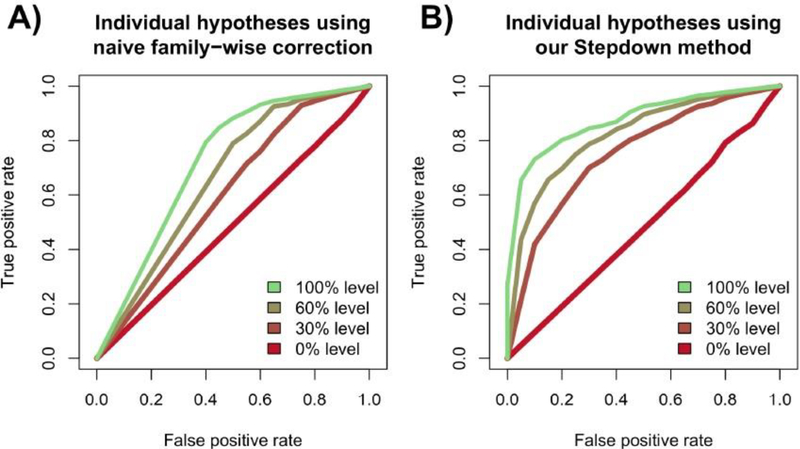
We use the Stepdown method described in Subsection 4.1 on our simulated data where β = {0,0.3,0.6,1} to see how the true positive rates and false positive rates vary with β. Let $\mathcal{L}=\left\{\left(i_1,j_1\right),\left(i_2,j_2\right),\dots \right\}$ denote the returned set of partition pairs that correspond to the accepted null hypotheses. Since our goal is to find the first r₁ partitions, we define the true positive rate and false positive rate for individual hypotheses to be

$$\text{True}\text{positive}\text{rate}(\text{TPR})\text{for}\text{hypotheses}=\frac{\mid \left\{(i,j)\in \mathcal{L}:i\le r_1\text{and}j\le r_1\right\}\mid }{\left(\begin{array}{l}{r}_1\\ 2\end{array}\right)},$$

$$\text{False}\text{positive}\text{rate}(\text{FDR})\text{for}\text{hypotheses}=\frac{\mid \left\{(i,j)\in \mathcal{L}:i>r_1\text{or}j>r_1\right\}\mid }{\left(\begin{array}{l}r\\ 2\end{array}\right)-\left(\begin{array}{l}{r}_1\\ 2\end{array}\right)}.$$

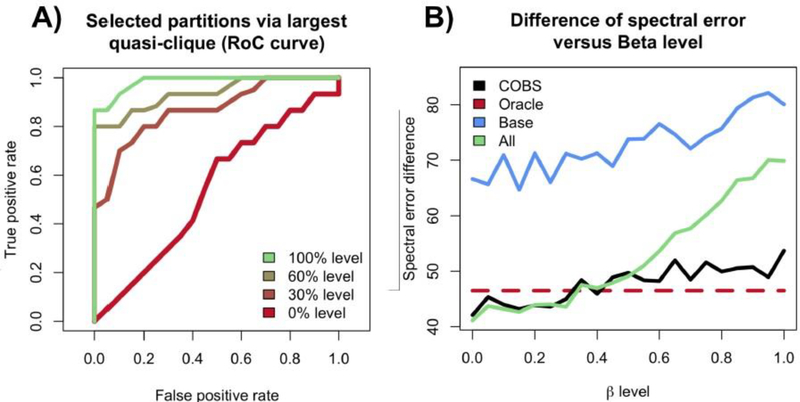
We plot the RoC curves visualizing the TPR and FPR in Figure 6. Each curve traces out the mean true and false positive rate over 25 simulations as α ranges from 0 (top-right of each plot) to 1 (bottom-left of each plot), where we use 200 bootstrap trials per simulation. Figure 6A shows the results of the naive analysis where we compute all $\left(\begin{array}{l}r\\ 2\end{array}\right)$ p-values, one for each hypothesis test comparing two partitions, and accept hypotheses for varying levels of α after using a Bonferroni correction. Figure 6B shows the results of the Stepdown method. In both plots, we see that as β increases, each method has more power. However, as we mentioned in Subsection 4.1, there is a considerable loss of power when comparing the Bonferroni correction to the Stepdown method. This is because the Bonferroni correction is too conservative when accounting for dependencies.

Fig. 6.

RoC curves for the accepted null hypotheses, for settings where β = (0,0.3,0.6,1), where each curve traces out the results as α varies from 0 to 1. (A) The curves resulting from using a Bonferroni correction to the $\left(\begin{array}{l}r\\ 2\end{array}\right)$ individual hypothesis tests. (B) The curves resulting from using our Stepdown method.

Partition selection

After using Stepdown, we proceed to select the partitions as in Subsection 4.2 to understand the monotone property and see how the true and false positive rates for partitions vary with β.

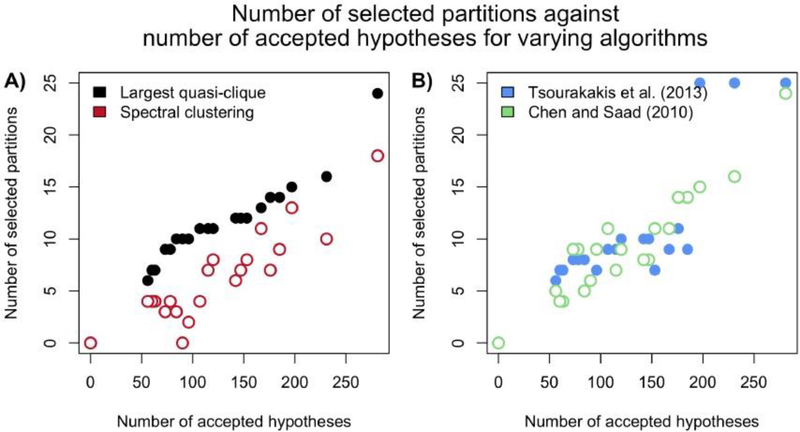
Figure 7 shows that three methods currently in the literature that can be used to find the largest quasi-clique violate the monotone property (4.4), whereas COBS retains this property. In Figure 7A, we compare our clique-based selection method, described in Subsection 4.2, against spectral clustering, a method used in network analyses designed to find highly connected vertices (Lei and Rinaldo, 2015), whereas in Figure 7B, two methods recently developed in the computer science community are compared (Chen and Saad (2010) and Tsourakakis et al. (2013)). These three methods are detailed in Appendix D, and all the methods receive the same set of accepted null hypotheses as the FWER level α varies. Recall that since the Stepdown method accepts more hypotheses as α decreases, the graph G formed by (4.3) becomes denser. However, as we see in Figure 7, the number of partitions selected by all but our method sometimes decreases as number of accepted null hypotheses increases, hence violating the desired monotone property.

Fig. 7.

Number of selected partitions for a particular simulated dataset as the number of accepted null hypotheses varies with the FWER level α. (A) Results using our clique-based selection method developed in Subsection 4.2 and spectral clustering. (B) Results using the methods developed in Tsourakakis et al. (2013) and Chen and Saad (2010). See Appendix D for more details of these methods.

Figure 8A shows the RoC curves on a partition-level for varying β as the FWER level α varies. This figure is closely related to Figure 6B. We use our clique-based selection method to find the largest γ-quasi-clique for γ = 0.95 $\mathcal{P}$ denote the selected set of partitions. Similar to before, we define the TPR and FPR in this setting as

$$\text{TPR}\text{for}\text{partitions}=\frac{\left|\left\{p\in \mathcal{P}:p\le r_1\right\}\right|}{r_1},$$

$$\text{FDR}\text{for}\text{partitions}=\frac{\left|\left\{p\in \mathcal{P}:p>r_1\right\}\right|}{r_2+r_3}.$$

Fig. 8.

A) Similar RoC curves to Figure 6, but for selected partitions selected by COBS. B) The mean spectral error of each method’s downstream estimated covariance matrix for varying β over 25 trials. The four methods to select partitions shown are COBS for α = 0.1 (black), the method that selects all partitions (green), the method that selects a fixed set of 5 partitions (blue), and the method that selects exactly the partitions that contain samples drawn from a nonparanormal distribution with proxy covariance Σ⁽¹⁾ (red).

We see that the power of the COBS increases as β increases, as expected.

Covariance estimation

Finally, we show that COBS is able to improve the downstream covariance estimation compared to other approaches. To do this, we use four different methods to select partitions and compute the empirical covariance matrix among the samples in those partitions. The first three methods resemble analyses that could be performed on the BrainSpan dataset in practice. The first method uses the COBS. The second method always selects all the partitions, which resembles using all the partitions in the BrainSpan dataset. The third method always selects the same 5 partitions – 3 partitions contain samples drawn from the nonparanormal distribution with proxy covariance Σ⁽¹⁾, while the other 2 partitions contain samples from each of the remaining two distributions. This resembles previous work (Liu et al., 2015) that consider only partitions in Window 1B. For comparison, the last method resembles an oracle that selects exactly the r₁ partitions containing samples drawn from the nonparanormal distribution with proxy covariance Σ⁽¹⁾.

Figure 8B shows that our partition selection procedure performs almost as well as the oracle method over varying β. Notice that for low β, COBS and the method using all partitions yield a smaller spectral error than the oracle method. This is because for low β, the covariance matrices Σ⁽¹⁾, Σ⁽²⁾, and Σ⁽³⁾ are almost indistinguishable. However, as β increases, the dissimilarities among Σ⁽¹⁾, Σ⁽²⁾ and Σ⁽³⁾ grow. This means methods that do not adaptively choose which partitions to select become increasingly worse. However, our procedure remains competitive, performing almost as if it knew which partitions contain samples drawn from the nonparanormal distribution with proxy covariance Σ⁽¹⁾. Additional simulations that go beyond the results in this section are deferred to Appendix F.

6. Application on BrainSpan study

We demonstrate the utility of COBS by applying it within the DAWN framework established in Liu et al. (2015). Specifically, in this section, we ask two questions. First, does COBS select reasonable partitions within the BrainSpan data, given our current scientific understanding outlined in Section 2? Second, does using COBS within the DAWN framework lead to a more meaningful gene co-expression network that can implicate genes using a “guilt-by-association” strategy?

Here, we discuss the different datasets relevant to the analysis in this section. DAWN relies on two types of data to identify risk genes: gene expression data to estimate a gene co-expression network and genetic risk scores to implicate genes associated with ASD. For the former, we use the BrainSpan microarray dataset (Kang et al., 2011), which has been the primary focus of this article so far. For the latter, we use the TADA scores published in De Rubeis et al. (2014) which are p-values, one for each gene, resulting from a test for marginal associations with ASD based on rare genetic variations and mutations.² For enrichment analysis, we use a third dataset consisting of TADA scores from Satterstrom et al. (2020). We use this third dataset only to assess the quality of our findings, and these TADA scores are derived as in De Rubeis et al. (2014), but include additional data assimilated since 2014. Relying on a later “data freeze,” this 2020 study has greater power to detect risk genes compared to the 2014 study: the two studies report 102 and 33 risk genes, respectively, with FDR cutoff of 10%. Additional details of our analysis in this section can be found in Appendix G.

6.1. Gene screening

We first preprocess the BrainSpan data by determining which genes to include in our analysis. This is necessary since there are over 13,939 genes in the BrainSpan dataset, most of which are probably not correlated with any likely risk genes. Including such genes increases the computationally cost and is not informative for our purposes. Hence, we adopt a similar screening procedure as in Liu et al. (2015), which involves first selecting genes with high TADA scores based on De Rubeis et al. (2014), and then selecting all genes with a high Pearson correlation in magnitude with any of the aforementioned genes within the BrainSpan dataset. We select a total of 3,500 genes to be used throughout the remainder of this analysis.

6.2. Partition selection

Motivated by the findings in Willsey et al. (2013), we analyze the BrainSpan dataset using COBS to find many partitions that are homogeneous with most partitions in Window 1B (Figure 1). We use the Stepdown method with 200 bootstrap trials and an FWER level of α = 0.1. This simultaneously finds which null hypotheses are accepted among the $\left(\begin{array}{c}125\\ 2\end{array}\right)$ hypotheses tested. Based on these results, we select the partitions that form the largest γ-quasi-clique for γ = 0.95.

We visualize the results of the Stepdown method in Figure 9, illustrating that COBS finds 24 partitions which have statistically indistinguishable covariance matrices, 7 of which are in Window 1B. We form the graph G based on the accepted null hypotheses, as described in (4.3). Figure 9A shows the full graph with all 125 nodes, while Figure 9B shows the connected component of G as an adjacency matrix. We can see that the 24 partitions we select, which contain 272 microarray samples, correspond to 24 nodes in G that form a dense quasi-clique.

Fig. 9.

(A) The graph G containing all 125 nodes. The red nodes correspond to the 24 selected partitions, while the pale nodes correspond to partitions not selected. (B) The adjacency matrix of a connected component of G, where each row and corresponding column represents a different node, similar to Figure 3. The dotted box denotes the 24 selected nodes that form a γ-quasi-clique.

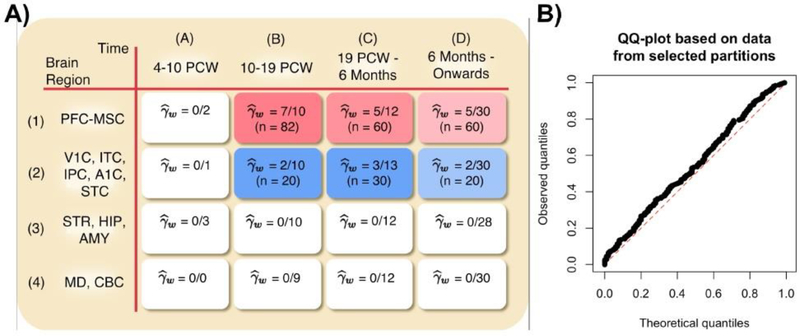
We visualize the proportion of selected partitions per window in the BrainSpan dataset in Figure 10A to demonstrate that our findings are consistent with the findings in Willsey et al. (2013). As mentioned in Section 2, Willsey et al. (2013) find that partitions in Window 1B are mostly homogeneous and are enriched for tightly clustered risk genes. The authors also found that, on average, gene expression varies smoothly across developmental periods, meaning there is greater correlation between gene expressions belonging to adjacent developmental windows. The authors also estimate a hierarchical clustering among the four brain regions. Indeed, our results match these finding. We select a large proportion of partitions in Window 1B, and the proportion of selected partitions smoothly decreases as the window representing older developmental periods as well as brain regions become more dissimilar to Window 1B.

Fig. 10.

(A) The number of partitions and samples (n) selected within each window. Partitions from 6 different windows are chosen, and the estimated γ_w is the empirical fraction of selected partitions within each window. The more vibrant colors display a higher value of ${\widehat{\gamma }}_w$. (B) A QQ-plot of the 250 p-values generated when applying our diagnostic to the 24 selected partitions, similar to Figure 2. While these p-values are slightly left-skewed, the plot suggests that the selected partitions are more homogeneous when compared to their counterparts shown in Figure 2.

Lastly, we apply the same diagnostic as in Section 3 to show in Figure 10B that the 272 samples within our 24 selected partitions are much more homogeneous than the 107 samples among the 10 partitions in Window 1B. The p-values we obtain after 250 divisions are much closer to uniform that those shown in Figure 2.

6.3. Overview of DAWN framework

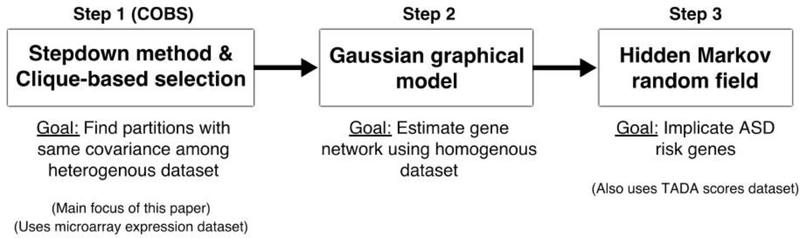
As alluded to in Section 1, DAWN estimates a gene co-expression network using the microarray partitions to boost the power of the TADA scores using a “guilt-by-association” strategy. Figure 11 illustrates this procedure as a flowchart. The first step uses COBS to select 24 partitions from the BrainSpan dataset, as stated in the previous subsection. In the second step, DAWN estimates a Gaussian graphical model via neighborhood selection (Meinshausen and Bühlmann, 2006) from the 272 samples in these partitions to represent the gene co-expression network. In the third step, DAWN implicates risk genes via a Hidden Markov random field (HMRF) model by combining the Gaussian graphical model with the TADA scores. The details are in Liu et al. (2015), but in short, this procedure assumes a mixture model of the TADA scores between risk genes and non-risk genes, and the probability that a gene is a risk gene depends on the graph structure. An EM algorithm is used to estimate the parameters of this HMRF model, after which a Bayesian FDR procedure (Muller et al., 2006) is used on the estimated posterior probabilities of being a risk gene to output the final set of estimated risk genes. The methodology in the second and third step are the same as those in Liu et al. (2015), as we wish to compare only different ways to perform the first step.

Fig. 11.

Flowchart of how COBS (Stepdown method and clique-based selection method) is used downstream to find risk genes within the DAWN framework. Step 2 and 3 are taken directly from Liu et al. (2015).

6.4. Investigation on gene network and risk genes

In this subsection, we show how COBS improves the estimated gene network by comparing the DAWN analysis using the 24 partitions selected by COBS (i.e., the “COBS analysis”) to the analysis using the 10 partitions in Window 1B originally used in Liu et al. (2015) (i.e., the “Window 1B analysis”).

Closeness of genes within the co-expression network

We demonstrate that the 102 genes detected by the newer TADA scores (Satterstrom et al., 2020) are roughly 10%−30% closer to the 33 genes detected by the older TADA scores (De Rubeis et al., 2014) in the gene network estimated in the COBS analysis than in the Window 1B analysis. This suggests that the COBS analysis estimates a more useful gene network, because when future TADA scores are published after Satterstrom et al. (2020), the next wave of detected risk genes are more likely to also be closer to the original risk genes detected in De Rubeis et al. (2014). We defer the details to Appendix G, but highlight here the procedure to derive this result. Effectively comparing the distances between genes in a network is a difficult problem since the estimated gene networks in the COBS and Window 1B analyses have a different number of edges. In addition, current research has suggested that natural candidates such as the shortest-path distance or the commute distance do not accurately capture the graph topology (Alamgir and Von Luxburg (2012) and Von Luxburg et al. (2014)). Hence, we use two different distance metrics to measure the closeness of two sets of genes that potentially overcome this problem. The first is using the path distance via the minimum spanning tree, and the second is using the Euclidean distance via the graph root embedding (Lei, 2018). Using either of these metrics lead to the same conclusion.

Enrichment analysis

We demonstrate that COBS improves DAWN’s ability to predict risk genes based on the newer TADA scores (Satterstrom et al., 2020) when utilizing the older TADA scores (De Rubeis et al., 2014) as input. Specifically, the COBS analysis and the Window 1B analysis implicate 209 and 249 risk genes respectively at an FDR cutoff of 10%. The risk genes implicated in the COBS analysis have a better enrichment for the 102 genes detected using the newer TADA scores (Satterstrom et al., 2020): 18.8% (COBS analysis) versus 14.6% (Window 1B analysis). We note that genes implicated by DAWN but not by the TADA scores are not considered false positives. In fact, He et al. (2013) suggests that there are upwards of 500 to 1000 genes that increase risk for ASD. Hence, we are unlikely to detect all of the true risk genes based on tests that rely on rare genetic variation alone.

Robustness to γ

We additionally verify the robustness of the above enrichment results to the parameter γ. Recall that γ controls the density of the edges in the quasi-clique, as introduced in Subsection 4.2, and we typically set γ = 0.95 by default. When we re-run the entire analysis with different values of γ varying from 0.85 to 0.97 at intervals of 0.01, we obtain 13 different sets of estimated risk genes. We stop at γ = 0.97 since larger values result in no partitions selected outside of Window 1B. When we intersect all 13 sets of risk genes together, we find that 144 risk genes are implicated regardless of the value of γ, of which 22.9% are in the list of 102 risk genes found using only the newer TADA scores (Satterstrom et al., 2020). This is a promising result, as it demonstrates that the implicated risk genes in the COBS analysis are more enriched than those in the Window 1B analysis for a wide range of γ.

7. Conclusion and discussions

In this article, we develop COBS to select many partitions with statistically indistinguishable covariance matrices in order to better estimate gene networks for ASD risk gene detection. Our procedure first applies a Stepdown method to simultaneously test all $\left(\begin{array}{l}r\\ 2\end{array}\right)$ hypotheses, each testing whether or not a pair of partitions share the same population covariance matrix. The Stepdown method is critical since it can account for the dependencies among all $\left(\begin{array}{l}r\\ 2\end{array}\right)$ hypotheses via bootstrapping the joint null distribution. Then, our procedure uses a clique-based selection method to select the partitions based on the accepted null hypotheses. The novelty in this latter method is its ability to preserve monotonicity, a property stating that less partitions should be selected as the number of accepted null hypotheses is smaller. We demonstrate empirically that the COBS achieves this property while common methods such as spectral clustering do not. When we apply COBS to the BrainSpan dataset, we select partitions that scientifically agree with the findings in Willsey et al. (2013). We also find that COBS aids in clustering the risk genes detected in Satterstrom et al. (2020) closer to the risk genes detected in De Rubeis et al. (2014) within the estimated gene co-expression network and in getting a better enrichment in implicated risk genes via the DAWN analysis.

The theoretical role of the FWER level α is not well understood mathematically. Specifically, while (4.2) provides a theoretical guarantee about the set of null hypothesis accepted, we would like to prove a theoretical guarantee about the set of selected partitions $\mathcal{P}$. Towards this end, we suspect that with some modification to COBS, closed testing offers a promising theoretical framework (see Dobriban (2018) and references within). This will be investigated in future work.

COBS is applied directly to help implicate risk genes for ASD, but this line of work has broader implications in genetics. Due to the improvement of high throughput technologies, it has become increasingly accessible to gather large amounts of gene expression data. This includes both microarray and RNA sequencing data. However, as we have seen in this article, gene expression patterns can vary wildly among different tissues. Hence, it is challenging to select samples that are relevant for specific scientific tasks. Beyond analyzing brain tissues, Greene et al. (2015) develop procedures to estimate gene co-expression networks for different tissue types by first selecting relevant samples amongst a corpus of microarray expression data. While Greene et al. (2015) does not motivate their method from a statistical model, our work provides a possible statistical direction for this research field to move towards.

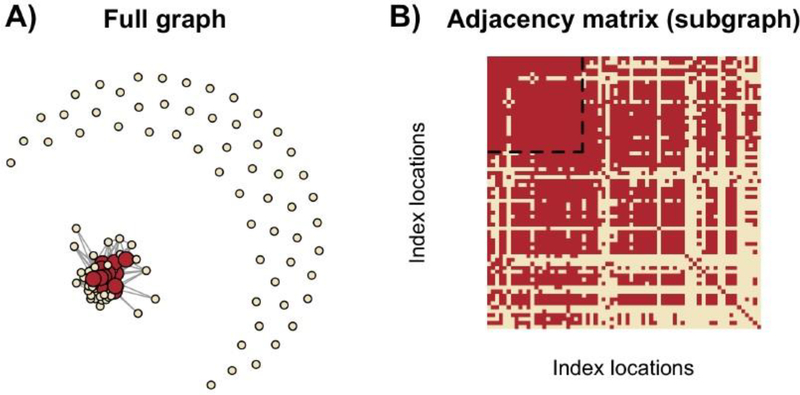
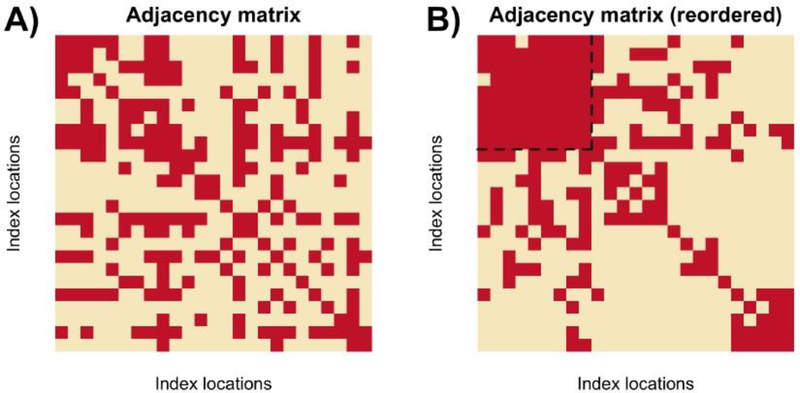
Fig. 3.

(A) Visualization of an (example) adjacency matrix that can be formed using (4.3), where the ith row from the top and column from the left denotes the ith vertex. A red square in position (i, j) denotes an edge between vertex i and j, and a pale square denotes the lack of an edge. (B) Illustration of the desired goal. The rows and columns are reordered from Figure A, and the dotted box denotes the vertices that were found to form a γ-quasi-clique.