Making Meaning, Doing Math: High School English Learners, Student-led Discussion, and Math Tracking

Abstract

Mathematics is not just memorized facts, but rather it is understanding how to approach and solve problems, and problem solving requires linguistic proficiency. Too often, English learners’ (ELs) relatively low math performance is dismissed due to their supposed “limited” English proficiency. Taking this perspective, a constructivist approach suggests that content-area discussions should improve EL students’ math performance. To test this hypothesis, we use nationally representative data from the Educational Longitudinal Study:2002 to examine the relationship between students’ reported participation in math discussions and their 10^th grade math performance (GPA), considering both course placement and linguistic status. While we find reported participation in student-led discussion to be positively associated with math performance for all students, we also find that EL students report higher participation in student-led discussions only in low-level math placement. This pattern suggests that for EL students, participation in student-led discussion may actually be necessary to counteract the limiting nature of low-track placement. We argue that although EL students appear to benefit from student-led discussions in these contexts, until school systems begin to address the overrepresentation of EL students in low-level coursework, instructional experiences alone will do little to improve their overall achievement.

Introduction

As we enter the 21^st century, the U.S. labor market turns increasingly toward careers in science, technology, engineering, and mathematics (STEM). Despite marketplace pressures, adolescent and young adult STEM participation is low overall (National Research Council, 2010) and particularly so among immigrant, bilingual youth, especially those identified by schools as bilingual English learner (ELⁱ) students (NASEM, 2018). In this context, it is notable that while bilingual EL students comprise one of the fastest growing youth populations (NCELA, 2011; Pew Hispanic Center, 2009), they also, unfortunately, demonstrate relatively low levels of STEM performance (NASEM, 2018; Lee et al., 2008), of concern to educators, researchers, and policy-makers alike. Although bilingual EL students’ STEM achievement lags behind that of their peers not in ESLⁱⁱ (Fry, 2008), the cause of, and solutions to these disparities remain a source of great scholarly debate (NASEM, 2018). To this end, educational researchers often identify two key factors that shape students’ STEM achievement in general: instructional experiences (Crosnoe, et al., 2010) and course placement, or tracking (Kotok, 2017). In the present study we explore how each factor relates to a student’s linguistic status to ultimately inform her math performance.

In an effort to broaden STEM participation overall, research has explored how instructional experiences in general, and linguistic engagement in particular, might improve EL students’ STEM achievement (de Oliveira, et al., 2019; O. Lee & Buxton, 2013), bringing more students into the field. Researchers have argued, and educators have largely concurred that bilingual EL students benefit from linguistically-rich content area experiences (August, et al., 2014; NASEM, 2018). In fact, in science, EL scholars have long advocated for inquiry-based, discussion-rich instructional experiences (Amaral, et al., 2002; O. Lee, 2005; Santau, Maerten-Rivera, & Huggins, 2011) to draw more EL students into the sciences. However, despite a long history of EL inquiry in math (Khisty, 1996; Moschkovich, 2015; Turner, Dominguez, Maldonado, & Empson, 2013) we found no research to date that quantifies the relationship between instructional experiences and math performance for EL youth relative to their peers not placed in ESL, either bilinguals or native English speakers.

To fully understand the nuances surrounding EL students’ math performance however, we must also consider its relationship with course placement. Research has found that pervasive instructional stratification in U.S. high schools limits students’ academic access and exposure (Muller, Riegle-Crumb, Schiller, Wilkinson, & Frank, 2010). In addition, secondary math classes are highly sequential, requiring advancement through a standardized set of prerequisites (Stevenson, Schiller, & Schneider, 1994) to successfully progress through the courses required for graduation and college entry. Complicating matters, not only do instructional experiences vary considerably by course placement (Estrada, 2014; Umansky, 2016a), but in the U.S., high school course placement has repeatedly been shown to be highly correlated with student race, gender, and social class (Lucas & Berends, 2007; Riegle-Crumb & Grodsky, 2010). We build on the prior research suggesting that it is also necessary to consider the relationship between linguistic status and course placement (Mosqueda, 2010) if we hope to improve bilingual EL students’ performance. Just as institutional mechanisms may produce and/or exacerbate disparities in achievement (Gutiérrez, 2008; Muller et al., 2010), instructional experiences have the potential to counter those processes and improve student achievement. In the present study, we examine how students’ linguistic status, instructional experiences in math (i.e., participation in student-led discussion), and math placement all inform their math performance.

Conceptual Framework

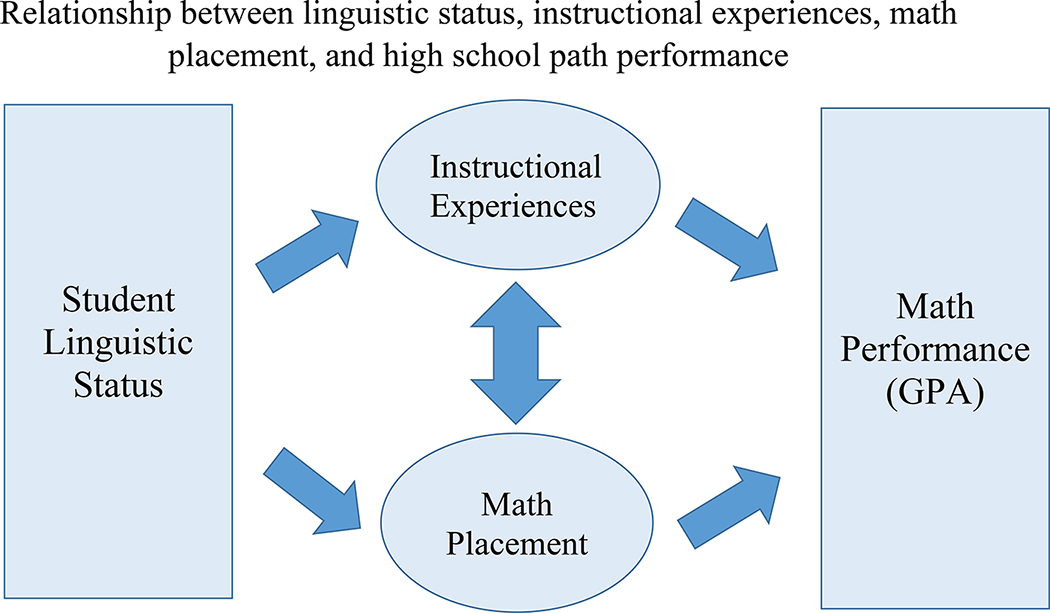
Prior research has identified multiple factors associated with bilingual EL students’ STEM achievement, and as such, we provide Figure 1 as a visual representation of our conceptual framework. We place the two key factors associated with math performance, course placement and instructional experiences, at the center of Figure 1. Here, we hypothesize not only the independent influence each factor has on math performance, but also how both are associated with one another, with a double arrow characterizing the relationship between the two. Next, we direct the reader’s attention to the left, to student linguistic status, which we hypothesize to inform a student’s instructional experiences, as well as her course placement. The left panel of our framework acknowledges both the research on linguistic tracking (Author 2010, 2016; Mosqueda & Maldonado, 2013) and linguistically engaging instructional experiences for bilingual EL students (de Oliveira, et al., 2019). What we know less about is whether and how these three factors function in tandem, in relation to one another, to inform bilingual EL students’ math performance. In the present inquiry, we focus on one linguistically engaging instructional experience in particular, students’ reported participation in math discussions, as it both embodies a sociocultural approach by actively engaging students in their own learning (Campbell, Adams, & Davis, 2007; Vygotsky, 1986) and has been found to occur in both high- and low-level content area coursework (Donaldson, LeChasseur, & Mayer, 2017).

Figure 1.

Relationship between linguistic status, instructional experiences, math placement, and high school path performance

REVIEW OF THE LITERATURE

Math Instructional Experiences, Achievement, and Linguistic Status

Beginning at the heart of our conceptual framework, we frame our inquiry in Vygotsky’s (1986) sociocultural theory which engages an interactive approach to learning processes, and focus first on instructional experiences in mathematics. The ability to negotiate meaning through discussion dates back to Socrates and is key to content area mastery and cognitive flexibility (Resnick, Michaels, & O’Connor, 2010). In content area classes, students often explain their thinking in order to not only demonstrate their competence, but also make connections and expand their learning (Crosnoe et al., 2010; Thadani et al., 2010). Designed to improve learning overall, content area discussions have the potential to improve EL achievement through simultaneous development of mathematical concepts and linguistic competence (Anstrom, et al., 2010), critical given the linguistic complexity of mathematics (Moschkovich, 2012, 2015). In addition, as an instructional experience, student-led discussion has the potential to develop the inference-based skills needed to facilitate math understanding and improve achievement.

The cognitive demands on students struggling to master both academic content and the English language can be overwhelming; scholars have recommended instructional experiences that engage the linguistic, cultural, and cognitive processes to ease the burden (Bunch, 2013; Stoddart, et al., 2010). For instance, Walqui (2006) has long suggested that the sociocultural foundations of interactive, linguistically rich instruction are particularly well-suited for bilingual EL students. Likewise, Knudson-Martin (2013) has argued that interactive instructional experiences more fully engage bilingual EL students in math in particular. To this end, Turner and colleagues (2013) found that experiences participating in math discussions facilitated bilingual EL students’ academic identity development. However, additional research linking these instructional experiences and math performance remains sparse at best.

Participation in concept building discussions is theorized to facilitate academic language development (Bunch, 2014) especially in science (Cervetti et al., 2012; Snow, 2010). However, the vast majority of studies we identified were limited in the generalizability of their findings, either due to their qualitative nature (Turner, et al., 2013) or relatively small samples, often lacking a non-EL reference group (See for example, O. Lee & Buxton, 2013). A few studies used inferential, quantitative analyses to understand this relationship and its variation across student groups (e.g., Valle, Waxman, Diaz, & Padrón, 2013), but again, these tend to be limited in the scope of the data. Although content area discussions may develop both bilingual EL students’ math knowledge and linguistic competence (Calderón, Slavin, & Sánchez, 2011; de Oliveira, et al., 2019), the literature to date suggests, but does not test, whether or how it might be associated with their achievement.

Math Placement, Achievement, Performance, and Linguistic Status

Historically, both math achievement and performance have been closely tied to students’ math placement in high school (Riegle-Crumb & Grodsky, 2010) with the secondary math sequence itself posing a specific form of academic stratification. In fact, research has found that enrollment in anything less than Algebra in 9^th grade limits a student’s ability to prepare for college (Schiller & Hunt, 2011; Stevenson, et al., 1994). Math placement shapes students’ access to various other high school opportunity structures; given evidence racial, gender, and other disparities in math placement (Battey, 2013; Riegle-Crumb, et al., 2011; Rogers-Chapman, 2014; Shifrer, 2016), we argue that research regarding additional types of stratification (i.e., linguistic) is needed.

Regarding the relationship between course placement and linguistic status, the qualitative literature richly details secondary bilingual EL students’ experiences in low-level, deficit-oriented coursework. Dabach’s work in particular has shed light on how placement into and interactions in EL-serving placements often force students to negotiate both stigmatizing and stigmatized contexts (2014) and limited content area access and exposure (2015). Similarly, Kanno’s research has documented not only the academic, but also social isolation experienced by secondary students placed in EL-serving programs (Kanno, 2018; Kanno & Kangas, 2014). Combined, their insights, along with others’ suggest a linguistically and academically anemic context for secondary EL students.

Bilingual EL Students’ Math Performance: Expanding the Empirical Lens

From the moment a bilingual EL student first enters the U.S. public school system, she must do double the work of a non-EL student to achieve academic success. Not only must she master math, science, and social studies content, but she must do so in English, while developing English proficiency (Valdés & Castellón, 2010). Traditionally, EL educational policies have privileged the learning of English as a marker of success, often to the detriment of students’ academic development (Gándara & Rumberger, 2009). However, the advent of No Child Left Behind (USDE, 2001) turned schools’ and districts’ attention towards bilingual EL students’ content area achievement, especially in mathematics and reading. The most recent reauthorization, the Every Student Succeeds Act: ESSA (2015) only further reified the central role of mathematics to school success. Understanding what shapes bilingual EL students’ math performance, and how, will only grow in importance in the coming decades.

Linguistic disparities in both instructional experiences and content area access and exposure (i.e., placement) not only reinforce negative stereotypes, but may also contribute to lower levels of achievement, limiting bilingual EL students’ academic and professional potential in young adulthood. On the whole, bilingual EL students demonstrate significantly lower levels of math performance and achievement than their non-EL peers (Estrada, 2014; Lewis, et al., 2012). Bilingual EL students’ relatively low achievement is fairly well documented (López, McEneaney, & Nieswandt, 2015; Rumberger & Tran, 2010), complicating the relationship between instructional experiences and English proficiency. We argue that math performance in particular reflects the multiple, related factors (Figure 1) that shape how students learn and how they experience schools and schooling, especially in adolescence. Building on prior research, we developed the present study to investigate how instructional experiences and math placement interact with linguistic status to shape bilingual El students’ math performance.

Problem Statement

In identifying our research question and designing our corresponding models, we remained mindful of the many covariates of student achievement. As illustrated in Figure 1, we hypothesize that students’ math performance and achievement may be a product not only of their instructional experiences in mathematics, but also their math placement. However, linguistic status tends to muddy the empirical waters, given both the literature regarding bilingual EL students’ instructional experiences (de Oliveira et al., 2019; NASEM 2018), and low level content area placement relative to non-EL students, regardless of prior performance (Mosqueda, 2010; Richardson-Bruna & Vann, 2007). Recognizing the complexity of these issues, as well as their interrelated nature, we felt it critical to consider all three simultaneously. To do so, we posed the overarching question, “Is students’ self-reported participation in math discussion differentially associated with their math grades based on linguistic status (i.e., bilingual EL student versus non EL student) and/or math placement?

In order to create a manageable set of questions, we broke our overarching question down into two distinct, yet related questions. First, we asked a basic descriptive research question (RQ1), who (linguistic status) reports participating in language-rich math instructional experiences (discussion) and in which contexts (placement)? To answer this first question, we explored the frequency of participation in student-led discussion by students’ linguistic status and course placement. We then posed a second, inferential, research question (RQ2), does the relationship between students’ linguistic status, self-reported participation in math discussion, and math performance vary by students’ math placement? We employed two sets of nested regression models to investigate this question: the first set explored these relationships for students in at- or above-grade level math placement, and the second set, for those placed in below grade level mathematics.

Methods, Data, and Sample

To answer these research questions, we used nationally representative data from the base year of the Educational Longitudinal Study (ELS: 2002), a nationally representative sample of approximately 15,000ⁱⁱⁱ high school sophomores nested in 750 schools during the 2001–2002 school year. We supplemented student surveys with information from parent, teacher, and school administrator questionnaires. High school transcripts were collected for the majority of students in the sample, providing detailed information on each student’s course taking and academic performance. The current study used data from the base-year survey and transcript study.

We limited our analytic sample to students who were in the base year survey of sophomores and had a valid transcript. A key control for understanding 10^th grade math grade point average (GPA) is previous math performance (i.e., 9^th grade math GPA); thus, our analyses included only students who were enrolled in a math course during both 9^th and 10^th grade. Finally, we dropped any students who are missing on our dependent variable (10^th grade math GPA). The inclusion of these filters resulted in a final analytic sample of 11,430 10^th graders in 705 schools, which remained representative of national trends in GPA, class placement, and reported participation in math discussion, our key variables of interest.

Dependent Variable

Math Performance

The dependent variable for our models, 10^th grade math GPA is a continuous variable with a range of 0–4 that represents the final grade a student earned in 10^th grade mathematics. Taken from transcript data, the variable is measured on a 13-point scale and then reverse-coded and converted to a standard 4-point scale using the National Center for Education Statistics documentation, ELS:2002, First Follow Up Transcript Component Data File Documentation^iv. This particular conversion to the standard 4-point scale carried out to the second decimal place used by most U.S. schools was made to facilitate readers’ comprehension and interpretation of the findings. Math GPA was close to normal distribution, with slightly lighter tails, not surprising given the nature of classroom grade assignment regarding both Fs and A+s.

In addition, we take a moment to discuss the choice of classroom-based math GPA over standardized math test scores. We argue that grades may be more sensitive to students’ classroom experiences and behaviors than test scores and is generally associated with academic engagement. Final models were designed to be as sensitive as possible to students’ instructional experiences in the 10^th grade math classroom, holding constant not only prior math performance (9^th grade math GPA), but also social class (parental education level, family income), gender, and race/ethnicity. While math GPA will, of course, also reflect teachers’ perceptions and students’ behaviors, we argue that grades are a closer approximation of students’ experiences than annual large-scale assessments that are arguably more heavily associated with student social class and school resources. Prior research indicates that variation in standardized test scores is driven largely by race, gender, social class, and other extant factors (Duncan & Magnuson, 2005; Reardon, 2003; Stull, 2013). In addition, collection of 10^th grade math test scores in ELS occurred in January of the 2001–2002 academic year, capturing, at most, half of the 10^th grade experience.

Independent Variables of Substantive Interest

Reported Participation in Student-led Math Discussion

The bulk of research exploring the association between classroom instruction and academic achievement draws from a constructivist perspective that stresses students’ ability to explain their thinking and shape their own learning (Campbell, et al., 2007). Building on this framework, we use students’ responses to a base year survey question (BYS29J) asking, “In your current or most recent math class, how often do/did you participate in student-led discussions?” in order to capture this particular aspect of a student’s instructional experiences in mathematics. In response, students could answer: (1) Never, (2) Rarely, (3) Less than once a week, (4) Once or twice a week, or (5) Every day or almost every day. A high value indicates that the student reported frequently participating in student-led math discussions; the mean value for this construct in the analytic sample is 2.34, with a standard deviation of 1.40.

Linguistic Status

Students’ linguistic status was determined through two dichotomous indicators: students’ native language (English: Yes/No), and placement in EL-serving^v coursework during high school (ESL: Yes/No). The first question, asked in the base-year survey, determines the student’s native language: “Is English your native language (the first language you learned to speak as a child)?” (Native English speaker=1). Non-native English speakers, or bilingual students, were then further sub-divided based on their placement in EL-serving programs during high school (ESL Placement=1). We determine placement in EL-serving programs using student transcript reports of high school course taking. Placement in EL-serving programs includes both language and content courses designed to serve EL students and meet their specific linguistic needs through discrete, language-based enrichment and modified academic content-area instruction (e.g., sheltered and bilingual math, science or social science content area coursework).

Together, these two indicators allowed us to identify the three mutually exclusive linguistic status groups at the core of our analyses:

1. Bilinguals placed in EL serving programs: Bilingual English learner (EL) students

2. Other Bilinguals (i.e., those not in EL-serving programs)

3. Native English speakers

Clearly, not all U.S. high school bilingual EL students are placed in ESL coursework, however arguably many, if not most, are and ESL placement often shapes their social, academic, and linguistic experiences in high school (Dabach, 2014, 2015; Author, 2009, 2010; Harklau, 2017; Kanno, 2018; Kanno & Kangas, 2014; Umansky, 2016b). For the purpose of the present study, we use the term “bilingual EL student” to refer to our focal group of interest: bilingual EL students, i.e., those placed in EL-serving programs.

Independent Variables: Sociodemographic Controls

Student and Family Background

Our models include additional base year student and family background characteristics. We consider each student’s gender, self-reported race/ ethnicity, age, and socioeconomic status (SES). Latino, black, Asian, and other race are in the regression models as dummy variables, with the reference category, white. Student age in 10^th grade is calculated by the birth date provided in the ELS restricted-use dataset. We measure SES using both parent education level and family income. Parent education is an ordinal variable indicating the highest level attained by either of the student’s parents, ranging from 1 (less than high school) to 5 (a professional degree). The family total income variable indicates an income category assigned by ELS, ranging from 1 (no income) to 13 (above $200,000).

Academic Controls

Prior math performance

In order to control for previous academic performance in mathematics, we include 9^th grade math GPA, also from the transcript survey, as well as 10^th grade standardized math test scores as measures of math achievement. The 10^th grade standardized math test scores come from assessments designed for ELS:2002 and used items from NELS:88, the National Assessment of Educational Progress (NAEP), and the Program for International Student Assessment (PISA).

Tenth grade math placement

Mathematical performance and instructional experiences may vary by math placement (V.E. Lee et al., 2012; Riegle-Crumb, 2006), thus our analyses account for students’ placement along the math pipeline. Using the nationally standardized Classification of Secondary School Course (CSSC) codes from the high school transcripts, we identified each student’s 10^th grade math placement. We then use these math course levels to divide students into two discrete groups. Those enrolled in Geometry, or a more advanced math course, are coded at-or-above grade level; those enrolled in Algebra I or a lower-level math course are coded below grade level. In making this modeling decision, we draw on the extant mathematics education research that documents the overwhelming adherence in U.S. high schools to the traditional Algebra 1, Geometry, Algebra II sequence (i.e., Muller, et al., 2010; Riegle-Crumb & Grodsky, 2010). In line with this literature, we considered Geometry placement in 10^th grade to be at grade level; however, we were also mindful that this is a conservative estimate, given the impressive growth of 8^th grade Algebra placement in the past two decades (Clotfelter, Ladd, & Vigdor, 2012; Domina, McEachin, Penner, & Penner, 2015; Spielhagen, 2010).

At this point, we take a moment to clarify for the reader that our coding for EL-serving programs included sheltered and SDAIE math coursework. While some research may conceptualize all sheltered or content area courses as below grade level, we made our delineations based on the math title and content of the course. Thus, a sheltered Geometry or Algebra II math course would be coded as at or above-grade level, while sheltered Algebra would be coded as below grade level.

Academic English competency

As we are motivated in part by the disparities in math performance by linguistic status, we include a measure of students’ self-reported academic English competency. We grounded the construction of this variable in the theory, history, and research examining academic English (Bailey, 2007; Bailey & Butler, 2003; Slama, 2012). The English competency construct draws from four items from the base year student survey in which all students, regardless of linguistic status, were asked to reflect on how well s/he can: understand difficult English texts, understand complex material in English class, do an excellent job on English tests, and master the skills taught in English class. Here, we are careful to note that this variable does not measure English proficiency, but rather a student’s self-reported academic skill set in English language arts. We found this measure intriguing as these very academic English skills are often correlated with students’ performance in the content areas (Cook, Boals, & Lundberg, 2011) and are thus likely to capture some of the variance in our models due to students’ overall academic competence. Thus, we are careful not to describe this measure as English proficiency, but rather as a way to measure students’ self-reported academic capacity. Ultimately, we include a composite measure of these four items to account for variation in students’ ability to manipulate the language for academic purposes. The resulting variable has a mean of 2.67 and a standard deviation of 0.80 (alpha=0.91).

Finally, we ran a correlation matrix of all independent variables to check for multicollinearity. Most correlations are very weak and only 2 correlations are above .4. Parental education and parental income have a correlation of 0.4320. Additionally, 9^th grade math GPA and 10^th grade math IRT score have a correlation of .4880, which would be expected as both measure students’ competency in math. (Table available upon request.)

School Level Indicators

Although not a central part of our story, we include controls for school characteristics in all models. School characteristics include region: (reference= northeast), south, west, Midwest; sector (public=1); as well as bilingual EL enrollment. As our research questions address the association between instruction and math performance for bilingual EL students, we include an indicator of student enrollment in a “high limited English proficiency (LEP)” school. While the NCES used the term LEP in the ELS:2002 dataset, for the purposes of our study, and to better situate the research in the growing field of asset-focused bilingual, EL research, we label this school-level variable “high bilingual/EL” as it measures a school’s percentage of EL-identified students in the school as reported in the ELS administrator survey. The vast majority of schools in the ELS dataset enroll less than 1% bilingual/EL students and the overall mean bilingual EL enrollment is 4.4%, suggesting a highly bifurcated distribution. For this reason, we dichotomized the measure, creating a dummy variable to indicate whether the student attended a school in the top quartile of the bilingual/EL enrollment distribution. Initial analyses included measures of percent racial/ethnic minority and percent low SES; however, both correlate highly with percent bilingual/EL, adding little to the model, and were thus eliminated.

Analytic Plan

We began our analyses comparing the means and proportions of our key independent variables by linguistic status: bilingual EL students, other bilinguals, and native English speakers. Then, to understand the relationship between student-led discussion, math placement, and linguistic status, we performed OLS regression for 10^th grade math GPA using a series of nested models.

To adjust for missing data in our sample, we used multiple imputation in Stata; we did not, however, impute values for either dependent variable (10^th grade math GPA) or the key independent variable, linguistic status. Rather, we dropped students missing on either of these two measures from the sample. All analyses were weighted using the transcript weight (F1TRSCWT^vi), which corresponds to students who had full or partially complete transcript data and base year survey responses. In addition, analyses accounted for clustering within schools by using the svy command in Stata. By using the transcript weight, the sample is representative of a population of approximately 2.59 million Spring term 2002 10^th grade students. To ensure that any variation in the relationship between instruction and math performance evidenced in our models was not due to differences between schools, we ran all models using Hierarchical Linear Modeling (HLM) software as well. HLM models (not shown, but available upon request) produce substantively and significantly similar results; for ease of interpretation and discussion, we present only OLS model results.

Findings

Descriptive Results: Participation in Student-led Discussions by Math Placement

In order to answer the first half of RQ1, who reports participating in language-rich math instructional experiences, we compared high school students’ characteristics by linguistic status in Table 1. Both the sample size used and the estimated population size (PE) are listed in the table. We present both means and proportions for each group, with bilingual EL students shown in the far left-hand column, other bilingual students (not in EL-serving programs) in the middle, and native English speakers in the column to the far right. Differences in background characteristics and academic experiences by linguistic status prove significant across the board. We began by examining two key analytic variables of interest, our dependent variable, math GPA, and our key analytic variable, math placement. Table 1 shows significant disparities in math performance (GPA), with native English speakers showing significantly higher math GPAs than both bilingual groups. In addition, math placement varied by linguistic status; a significantly higher proportion of bilingual EL students (52%) experienced below-grade level math placement relative to either native English speakers or other bilinguals (27% and 34% respectively). In addition, expected disparities in student and school characteristics surfaced by linguistic status as well. With respect to who participates in student-led discussions, how often, and where, we observed that bilingual EL students reported participating significantly more frequently than either native English speakers or other bilinguals, prompting us to examine trends by linguistic status within, and across math placement levels.

Table 1:

Weighted Means and Proportions for Analytic Sample by Linguistic Status

	Bilingual EL Students		Other Bilinguals		Native English Speakers
	n=390		n=1,540		n=9,500
	PE= 179,319		PE=278,525		PE= 2,232,810
10th grade math GPA	1.61	(1.16)	1.77	(1.15)	2.00	(1.10)	b, c
10th grade math placement
Below grade level	0.52		0.34		0.27		a, b, c
At or above level	0.48		0.66		0.73		a, b, c
Student-led math discussion	2.66	(1.42)	2.40	(1.43)	2.33	(1.40)	a, b
Background
Female	0.52		0.52		0.50
Race/Ethnicity
White (ref.)	0.08		0.13		0.69		a, b, c
Latino	0.74		0.57		0.09		a, b, c
Black	0.04		0.06		0.15		b, c
Asian	0.14		0.19		0.01		a, b, c
Other Race	0.01		0.05		0.06		a, b
Age	15.95	(0.88)	15.86	(0.72)	15.85	(0.60)
Parent Education Level
Less than high school	0.31		0.24		0.03		a, b, c
High school diploma/GED (ref.)	0.32		0.30		0.33
Some college	0.14		0.17		0.25		b, c
College degree or higher	0.23		0.29		0.39		b, c
Parent income	6.93	(2.43)	8.05	(2.41)	9.15	(2.28)	a, b, c
Academic Characteristics
9th grade math GPA	1.82	(1.17)	1.96	(1.08)	2.12	(1.07)	b, c
Math IRT score	27.53	(10.86)	34.13	(12.27)	38.45	(11.56)	a, b, c
English competency	2.35	(0.76)	2.61	(0.78)	2.69	(0.80)	a, b, c
School Characteristics
High percentage bilingual/EL	0.77		0.58		0.22		a, b, c
South	0.25		0.26		0.38		b, c
West	0.54		0.43		0.21		a, b, c
Midwest	0.12		0.18		0.28		a, b, c
Northeast	0.08		0.13		0.13		a, b
Private	0.01		0.03		0.03		a, b, c
Catholic	0.00		0.03		0.05
Public	0.99		0.94		0.92		a, b, c

NOTE. —

^a=difference between Bilingual EL Students and other bilinguals significant at p<0.05

^b=difference between Bilingual EL Students and native English speakers significant at least p<0.05

^c=difference between Bilingual Students not placed in EL-serving courses and native English speakers significant at p<0.05.

Standard Deviations displayed in parentheses.

In order to answer the second half of RQ1, who reports participating in language-rich math instructional experiences and in which contexts (placement), we include Table 2. Preliminary exploratory analyses (not shown, but available upon request) indicated that reported participation in math discussion was significantly higher among students enrolled in low math placement compared to their peers placed at-or-above grade level. The values in Table 2 show that within low math placement, bilingual EL students reported participating significantly more frequently in math discussions than either native English speakers or other bilinguals. No such significant differences exist by linguistic status within at-or-above grade level math placement. Our findings give credence to the prior research finding that placement in EL-focused mathematics (i.e., sheltered or SDAIE) classes (Bunch, Abram, Lotan, & Valdés, 2003) tends to be below grade level, where the teacher is expected to guide students through content-based discussions to develop their academic English competency. As the premise behind EL-serving coursework is to develop greater linguistic competency, it stands to reason that students would be more likely to report more frequent discussions in these courses. In the context of this prior research, our findings suggest the need to simultaneously consider course placement and linguistic status, thus our decision to run inferential models separately for high and low math placement.

Table 2:

Frequency of Reported Participation in Math Discussions by Math Course Placement, by Linguistic Status

	Bilingual EL Students	Other Bilinguals	Native English Speakers
Below Level Math Placement	2.81 a, b	2.52	2.40
At or Above Level Math Placement	2.52	2.34	2.30

NOTE—

^a= significantly higher than native English speakers in below grade level math placement

^b=significantly higher than other bilinguals, not in EL-serving courses and in below grade level math placement.

Inferential Results: Student-led Discussion and Math Grades

Our next analytic phase addressed RQ2, does the relationship between students’ linguistic status, self-reported participation in math discussion, and math performance vary by math placement? We first ran one set of regression models for students in at-or-above grade level math placement, then ran a second set for those in low math placement. Final models in both sets included an interaction term that allowed us to isolate the relationship between linguistic status and math discussion in that particular level of math placement. As noted earlier, we standardized the student-led discussion variable and chose to run two sets of models rather than including the math placement variable as a third interaction term, as we are most interested in whether and how the relationship between linguistic status and GPA varied by math placement itself. This was a critical analytic decision given the prevalence of EL students in low math placement. An interaction term would only tell us how much being at- or above-grade level in mathematics (if below-grade level is the reference) was associated with 10^th grade math GPA, not how the relationship might vary by either linguistic status or course level. Ultimately, the interaction terms isolated the relationship of content area discussion and performance for students in each of our three linguistic status groups.

At-or-above Grade Level Math Placement

Table 3 presents the results from our OLS models for final math grades for 10^th grade students placed in at-or-above grade level math, Geometry or higher. All models included a full set of school controls. Model 1 provided simple linguistic status baseline relationships, with the reference set to native English speakers; coefficients demonstrate an initial significant negative association between both bilingual groups and final math grades, regardless of placement in EL-serving programs, suggesting baseline achievement disparities by linguistic status. Model 2 accounted for background characteristics of gender, race/ethnicity, and social class. In doing so, the relationship between linguistic status and math performance was rendered insignificant, indicating that after controlling for background characteristics, no significant differences remained in 10^th grade math GPA by linguistic status. Next, Model 3 accounted for prior performance as well as participation in student-led discussions. Here, we note a significant positive relationship between math performance and prior math grades, math test scores, and participation in student-led discussions. Not surprisingly, given the high correlation of a student’s grades from one year to the next, a one-point increase in 9^th grade math GPA is associated with a .5-point increase in 10^th grade math GPA. Of interest to us, however, is that beyond this strong correlation, a one standard deviation increase in student-led discussions was also correlated with a .048 increase in 10^th grade math GPA.

Table 3.

OLS regression : 10^th grade math GPA for students placed in at or above grade level math

	Model 1	Model 2	Model 3	Model 4
Linguistic Status (ref: Native English Speakers)
Bilingual EL Students	−0.363** (0.117)	−0.123 (0.105)	0.074 (0.084)	0.134 (0.171)
Other Bilinguals	−0.129* (0.059)	0.040 (0.061)	0.051 (0.051)	−0.035 (0.072)
Background
Female		0.236*** (0.026)	0.178*** (0.022)	0.178*** (0.022)
Race (Ref. White)
Latino		−0.427*** (0.060)	−0.117* (0.047)	−0.117* (0.047)
Black		−0.653*** (0.053)	−0.142** (0.039)	−0.141** (0.039)
Asian		0.206** (0.069)	0.027 (0.054)	0.026 (0.054)
Other		−0.320*** (0.072)	−0.073 (0.058)	−0.072 (0.058)
Parent Education (Ref. High School)
Less than high school		−0.090 (0.068)	−0.023 (0.059)	−0.022 (0.059)
Some college		−0.005 (0.037)	−0.025 (0.029)	−0.025 (0.029)
College degree or more		0.282*** (0.036)	0.067* (0.029)	0.067* (0.029)
Parent income		0.043*** (0.007)	0.005 (0.005)	0.005 (0.005)
Age		−0.139*** (0.024)	−0.013 (0.019)	−0.014 (0.019)
Academics
9th grade math GPA			0.529*** (0.015)	0.529*** (0.015)
10th grade math test score			0.024*** (0.001)	0.024*** (0.001)
English competency			0.014 (0.018)	0.013 (0.018)
Reported participation in math discussion			0.048*** (0.012)	0.043** (0.012)
Interactions
Math discussion * Bilingual EL students				−0.023 (0.054)
Math discussion * Other bilinguals				0.37 (0.025)
Constant	2.072*** (0.069)	3.681*** (0.387)	−0.180 (0.318)	−0.166 (0.319)
R-Squared	.0290	.1510	.4903	.4906
Observations = 8,400; PE=1,843,906

^***p<0.001

^**p<0.01

^*p<0.05

^∼p<0.1

Note: Coefficients are unstandardized; All models control for school characteristics; Standard Errors displayed in parentheses

Finally, the inclusion of interaction terms in Model 4 allowed us to investigate whether participation in student-led discussion might work better for one group of students over another, i.e., whether bilingual EL students might in fact benefit more from participating in math discussions than their peers, the goal of most EL instructional modifications. In Model 4 both interaction terms emerged as nonsignificant, indicating that the practice correlates equally well with student grades for all students in at-or-above grade level math placement, regardless of linguistic status. Ultimately, net of all controls, as well as having tested for interactions, the main linguistic status coefficients demonstrated no significant differences in final math performance. However, it is worthwhile to note that our final model accounted for nearly half (49%) of the variance in math GPA (R²=0.4906) for 10^th grade students placed in at-or- above grade level math. Any language-based disparities are rendered insignificant when we take these other factors, most notably prior achievement and math discussion, into consideration.

Contextualizing the findings

Now, to more clearly disentangle the who and how much from the where in RQ2, we include Figure 2 to show the correlation between participation in student-led discussion and students’ grades. The solid, upper line shows estimated 10^th grade math GPA values for the average student taking at or above level math classes by reported participation in student-led discussion. For students who reported participating in student-led discussion at 2 standard deviations below the mean (tending toward never participating in class), their 10^th grade math GPA was about 2.1 or about a C^vii; however, for students who reported participating in student-led discussion at 2 standard deviations above the mean (tending to participate every day), their 10^th grade math GPA was about 2.4, which corresponds to about a C+ on the 4.0 grading scale.

Figure 2:

Predicted 10th Grade Mathematics GPA

Below Grade Level Math Placement

To address the second contextual aspect of RQ2, we present Table 4 to show results from our OLS models for final math grades for sophomores who experienced low math placement, i.e., Algebra 1 or below. Model 1 provided baseline coefficients for the two bilingual groups, with native English speakers serving as the reference group. Again, all models include a full set of school controls. Coefficients in Model 1 indicated a significant, negative association between other bilinguals’ linguistic status and final math grades; no such relationship is evident among bilingual EL students. Model 2’s inclusion of background characteristics, however, rendered the bilingual group coefficient insignificant; what initially appeared to be a language-based gap might actually better reflect social class.

Table 4.

OLS regression: 10^th grade math GPA for students placed in below grade level math

	Model 1	Model 2	Model 3	Model 4
Linguistic Status (ref: Native English Speakers)
Bilingual EL students	0.037 (0.118)	0.203 (0.128)	0.139 (0.096)	0.370* (0.169)
Other bilinguals	−0.178* (0.076)	−0.069 (0.079)	−0.054 (0.076)	−0.087 (0.124)
Background
Female		0.129** (0.048)	0.094* (0.044)	0.094* (0.044)
Race (Ref. White)
Latino		−0.268*** (0.080)	−0.079 (0.068)	−0.079 (0.067)
Black		−0.290*** (0.061)	−0.110∼ (0.060)	−0.111∼ (0.060)
Asian		0.069 (0.126)	0.098 (0.108)	0.093 (0.107)
Other		−0.092 (0.089)	−0.048 (0.085)	−0.048 (0.085)
Parent Education (Ref. High School)
Less than high school		0.008 (0.100)	−0.028 (0.083)	−0.030 (0.084)
Some college		0.009 (0.054)	−0.017 (0.050)	−0.018 (0.050)
College degree or more		0.193** (0.063)	0.087 (0.053)	0.085 (0.053)
Parent income		0.024* (0.010)	0.020* (0.009)	0.019* (0.009)
Age		−0.123*** (0.030)	−0.044 (0.027)	−0.044 (0.027)
Academics
9th grade math GPA			0.386*** (0.023)	0.387*** (0.023)
10th grade math test score			0.017*** (0.002)	0.017*** (0.002)
English competency			0.003 (0.036)	0.003 (0.036)
Reported participation in math discussion			0.040* (0.020)	0.045* (0.021)
Interactions
Math discussion *Bilingual EL students				−0.082 (0.051)
Math discussion * Other bilinguals				0.013 (0.048)
Constant	1.476*** (0.092)	3.180*** (0.489)	0.751 (0.472)	0.743 (0.471)
R-Squared	.0150	.0547	.2305	.2311
Observations = 3,030; PE = 746,750

^***p<0.001

^**p<0.01

^*p<0.05

^∼p<0.1

Note: Coefficients are unstandardized; All models control for school characteristics; Standard Errors displayed in parentheses

Model 3 proceeded to take prior academic indicators into account, including participation in student-led math discussions. Coefficients in Model 3 indicated a significant positive relationship between the outcome and academics, particularly prior math grades, math test scores, and participation in student-led math discussions. Once again, 9^th math GPA was highly correlated with 10^th grade math GPA; a one-point increase in 9^th grade was associated with a .386 increase in 10^th grade. Further, 10^th grade math test scores were significantly and positively related to 10^th grade math GPA. For our main independent variable, student-led discussion, a one standard deviation increase in participation correlated with an increase of .040 in students’ 10^th grade math GPA.

In Model 4, we included interaction terms by linguistic status which proved to be non-significant, indicating that self-reported participation in student-led math discussions does not influence the math GPA of one linguistic status group more or less than any other. Here, we take a moment to note that our final models now account for nearly a quarter (23%) of the variance in math GPA (R²=0.2311), with the inclusion of prior achievement and math discussion accounting for three-quarters of this share.

Contextualizing the findings

Here, we return our attention to Figure 2, with attention to the dashed line showing the estimated values of student-led discussion on students’ 10^th grade math GPA, for the average student taking below level math classes. We see that for students who participate in student-led discussion at 2 standard deviations below the mean (tending toward never participating in class), their 10^th grade math GPA is 1.7, about a C-; however, for students who participate in student-led discussion at 2 standard deviations above the mean (tending to participate every day), their 10^th grade math GPA is 1.9, which corresponds to about a C on the 4.0 grading scale. Here, higher levels of participation in student-led discussions put students at an advantage relative to those who never or very rarely participate.

Even net of rigorous academic and school-level controls, our models showed an equally beneficial, positive association between participation in student-led math discussions and math grades for all students, regardless of linguistic status and course level placement. This relationship supports a constructivist perspective that would advocate for the richest possible instruction for all students. This is not to suggest that incorporation of more, guided student-led math discussions would not benefit bilingual EL students in particular, but rather that educators and schools must be cognizant of the organizational forces that preclude these students’ placement into advanced level math classes to begin with.

Limitations

At this point, it is important to consider limitations to this study. First, and most salient to our discussion, while our findings indicate that bilingual EL students are overrepresented in lower level math placement, they cannot begin to address why this occurs. A rich body of qualitative and mixed-methods research has examined the what and the how of secondary bilingual EL students’ experiences in low-level course placement (Dabach, 2014; Gándara & Orfield, 2012; Olsen, 2010; Thompson, 2017; Yoon, 2010). While our quantitative findings reinforce many of the insights from this qualitative research corpus, additional questions remain. Future research is necessary to understand the why, the educational and social mechanisms that contribute to bilingual EL students’ overrepresentation in low math placement that we document.

Second, the variables available in the ELS dataset reporting instructional experiences do not clearly hang together to create factors that represent either constructivist, or more traditional instructional models. Ultimately, through various analytic iterations, reported participation in math discussion emerged as the one variable that was both substantively reflective of interactive instruction, and analytically solid. We explored creation of an index using other measures, but none contributed sufficiently, either substantively or statistically, to the constructs underlying the instructional experiences we hoped to capture. We explored adding other instructional variables as controls in our models, but doing so failed to alter the final models in any meaningful way.

Finally, our measure of student-led discussion gauges respondents’ self-reported participation, which precludes our ability to distinguish students’ self-reported frequencies from their real or perceived opportunities to participate. It could be that in high level math placements, bilingual EL students have ample opportunities to participate, however do not act on these opportunities due to social intimidation (Yoon, 2008, 2010). Alternatively, one might hypothesize that fewer opportunities avail themselves for students in low-level math placements relative to their peers placed in at or above grade level courses (Kelly & Carbonaro, 2012). We acknowledge that this particular variable does not readily capture nuanced differences in the quality, nature, and richness of these classroom discussions (Jackson, et al., 2013), especially in math, a linguistically complex content area (de Oliveira, et al., 2019; Schleppegrell, 2007). However, for the moment, it provides one of the few measures of instructional experiences captured in a nationally representative dataset. Further research is necessary to better understand EL students’ classroom participation patterns in and across secondary content areas.

Discussion

Our findings suggest a need to address the deeper, more substantive issues that contribute to disparities in math performance in general, and for bilingual EL students in particular. First, we note that bilingual EL students did in fact report participating more in math discussions, with the caveat being that this occurred only in low level math placement. This relatively high participation in low-level math contexts may be due to any number of factors, from teachers’ awareness of bilingual EL students’ needs for linguistic supports (Bunch, 2013) in low level classes, to their misguided attempts to protect them against challenges at school, academic or otherwise (Lewis, et al., 2012; Ream, 2003). Regardless, the most compelling take-home for us as EL researchers relates to the students’ perceptions of their own participation. We were initially optimistic that bilingual EL students were in fact participating more in student-led discussion, although later our optimism turned to concern when it appeared that this early finding was driven by those in lower level math placements. In short, as researchers working to improve bilingual EL students’ educational access and attainment, we must continue to search for and assess instructional modifications that may in fact matter more for these students, but more importantly, instructional experiences that will actively address existing inequities.

Second, regardless of linguistic status, participation in student-led discussions during mathematics appears to be positively associated with math performance for all students across all course levels. Simply put, participation did not function ‘better’ for bilingual EL students, an aspiration of many EL-oriented instructional approaches (Saunders & Goldenberg, 2010 ). Rather, given the disproportionate placement of bilingual EL students in lower level math, our findings suggest that while student-led discussion proves to be a powerful tool towards equity in achievement, it is not enough. Instead of providing the ‘extra boost’ bilingual EL students may require for equitable instruction, in low-level courses increased participation appears to temper the existing negative relationship between tracked placement and achievement.

Importantly, however, we take a moment to point to the final variance accounted for in each of our models. For students placed at or above grade level in mathematics, our models capture nearly half (49%) of the variance in their math GPA, in contrast to less than a quarter of the variance (23%) for those placed below grade level. Here we suggest that while our models addressed one set of questions about math placement, linguistic status, and math grades, other unmeasured factors appear to be at play, especially for students placed below grade level in mathematics. The list of factors not included in our models, much less any given study, are potentially infinite; however, prior research does suggest that grades are subjective, and our findings may hint at the need to more clearly measure this subjectivity across tracks, rather than at the aggregate grade level. It may be that grading is more subjective than even previously understood in below-grade level coursework, or other factors may be at play. Future research is needed to examine the wide range of factors causing and resulting from lower level course placement for students in general, but especially for bilingual EL youth.

Linguistic Status: Possible Math Misplacement?

Our analyses show that nationally, bilingual EL students are significantly more likely to be placed below grade level in mathematics than either native English speakers or other bilinguals. This may be because schools and districts limit offerings of EL-tailored content area coursework to the lower end of the math sequence (Estrada, 2014; Mosqueda, 2010), or because placement decisions are made that equate EL status with low academic ability (Dabach, 2015). That it is only in below grade level math classes that bilingual EL students report significantly higher participation in student-led discussions suggests a conflation of EL status and low math placement, one possible mechanism for this pattern of overrepresentation.

Alternatively, it may be that participating in class discussions is simply more taxing for bilingual EL students than it is for non-EL youth (Bunch, 2009; Yoon, 2010), making it a much more salient event for these students when the time comes to self-report participation. This, however, does not explain the linguistic disparity in participation in at-or-above grade level math. It is also possible that lower-level math teachers may be more likely to be EL-trained and/or certified, and thus more prepared to teach lower-level courses, making them more sensitive to bilingual EL students’ placement and needs (Turner & Celedón-Pattichis, 2011) and more likely to ensure participation. In addition, school engagement and student achievement research has found that placement below students’ ability level may prompt both social and academic disengagement (Bodovski & Farkas, 2007; Olsen, 2010). Such a response could be expected to result in even greater disparities in math performance. As it is clearly beyond the scope of the ELS data (2002) to address this level of nuanced inquiry, we propose misplacement as one possible mechanism that merits further investigation.

Instructional Experiences and Math Placement

Ultimately, the positive relationship between participation in student-led discussion and math grades exists for all students, regardless of linguistic status. Although one might conclude that beneficial strategies for bilingual EL students are simply good for all students, like de Jong and Harper (2005) we suggest that the association is more complex and discussion as a whole merits further investigation. We suggest that linguistically engaging instructional experiences, while critical and of course necessary, is only one necessary element of equitable STEM preparation (Jackson & Cobb, 2010). Prior research finds bilingual EL students’ status to be associated with not only low-level academic placement, but also limited content area exposure (Estrada, 2014; Thompson, 2017). While participation in student-led math discussions may benefit achievement for all, it appears that for bilingual EL students, this “boost” may do little more than counterbalance less than optimal experiences in low track math placement (Estrada, 2014). As long as bilingual EL students continue to be overrepresented in below grade level courses, their access to academically rigorous content will remain limited; any substantive change will require systemic responses to organizational constraints and barriers. It is our hope that once bilingual EL students begin to experience appropriate math placement, future research will be able to disentangle whether EL students do, in fact, experience a distinct relationship between student-led discussion and math performance, relative to their peers not placed in ESL. We suggest that, from a sociocultural perspective, student-led discussions have the potential to move the needle on EL achievement, but to do so, must occur alongside other, carefully implemented structural reforms (i.e., course placement protocols).

Implications for Research, Policy, and Practice

Our findings point to two key aspects of bilingual EL students’ academic experiences that carry implications for policy and practice: math placement and instructional experiences. We focus first on EL students’ disproportionate placement in below grade level math, and then turn to their significantly higher participation in student-led discussion in these low-level math courses. As educators and researchers, we must be sensitive to the classroom and school contexts in which learning and instruction occur; bilingual EL students are more likely to attend poorer schools, have fewer certified teachers, and enroll in lower level classes (Gándara & Rumberger, 2009; Gándara et al. 2003), all processes that limit their academic opportunities. In addition, our estimates of instructional experiences and access trend conservative by design. We consider students enrolled in Geometry in 10^th grade to be ‘at grade level’, however, the growing popularity of 8^th grade algebra (Rickles, Phillips, & Yamashiro, 2014; Spielhagen, 2006) suggests that our models may underestimate this trend, and that bilingual EL students may actually be two years behind their peers, rather than one^viii. In the ELS dataset, over half of bilingual EL students enrolled in below grade level mathematics in 10^th grade, compared to less than one-quarter of native English speakers, shedding some light on disparate math placement patterns. Track placement is so strongly correlated with both math performance and achievement (Thompson, 2017) that critical inquiry into course placement processes may be necessary before we can know whether or how any given instructional approach may or may not shape EL achievement.

Further, we draw attention to the salience of the relationship between participating in math discussions and math performance across all groups, regardless of linguistic status. While our variable, reported participation in student-led discussions, is a relatively imprecise measure of students’ broader instructional experiences, we take a moment here to consider several of the ways students might have interpreted the item. Deploying student-led discussions places heavy language demands on teachers and students alike. For effective mathematical discussion to occur, teachers must actively scaffold students’ experiences (Kersaint, Thompson, & Petkova, 2014; Makar, Bakker, & Ben-Zvi, 2015), frame them with probing questions (Hunter, Civil, Herbel-Eisenmann, Planas, & Wagner, 2018), carefully position them via discourse moves (Turner, et al., 2013), and mindfully pair and select students to share based on individual competencies (Bunch, 2009). Only with teachers’ intentional practice can students construct new mathematical understandings through spoken English.

Bilingual EL students’ academic development may depend not only on a learned set of skills, but also on the ability to be heard among other, more proficient and potentially more entitled voices (Bunch, 2009; Harklau, 2017; Yoon, 2010). While a sociocultural perspective capitalizes on adolescents’ inclination to discuss and debate, it also considers differences in power and status within the high school classroom. Bilingual EL students’ placement in classes with more or fewer EL-identified peers may be just as important as any given instructional experience (Turner et al., 2013; Hand, 2012), even one considered ‘good for all students’.

Ultimately, although bilingual EL students engaged in student-led discussions more frequently than their peers, they did so only when placed in low level math classes. We suggest that in this context, student-led math discussion may actually be necessary to counteract low placement, limiting its ability to ameliorate any existing linguistic-related disparities. Only when bilingual EL student placement corresponds less to their linguistic status and more to their aptitude, will researchers be able to disentangle the complex relationship between placement, instruction, and achievement to truly capture the STEM potential of this growing population.