Skip to main content
PMC home page
PLOS ONE logoLink to PLOS ONE
. 2021 Mar 15;16(3):e0248494. doi: 10.1371/journal.pone.0248494

Prediction of cycloplegic refraction for noninvasive screening of children for refractive error

Kazuyoshi Magome 1,2, Naoyuki Morishige 1,*, Akifumi Ueno 1, Taka-Aki Matsui 1, Eiichi Uchio 2
Editor: Ahmed Awadein3
PMCID: PMC7959391  PMID: 33720956

Abstract

Detection of refractive error in children is crucial to avoid amblyopia and its impact on quality of life. We here performed a retrospective study in order to develop prediction models for spherical and cylinder refraction in children. The enrolled 1221 eyes of 617 children were divided into three groups: the development group (710 eyes of 359 children), the validation group (385 eyes of 194 children), and the comparison group (126 eyes of 64 children). We determined noncycloplegic and cycloplegic refraction values by autorefractometry. In addition, several noncycloplegic parameters were assessed with the use of ocular biometry. On the basis of the information obtained from the development group, we developed prediction models for cycloplegic spherical and cylinder refraction in children with the use of stepwise multiple regression analysis. The prediction formulas were validated by their application to the validation group. The similarity of noncycloplegic and predicted refraction to cycloplegic refraction in individual eyes was evaluated in the comparison group. Application of the developed prediction models for spherical and cylinder refraction to the validation group revealed that predicted refraction was significantly correlated with measured values for cycloplegic spherical refraction (R = 0.961, P < 0.001) or cylinder refraction (R = 0.894, P < 0.001). Comparison of noncycloplegic, cycloplegic, and predicted refraction in the comparison group revealed that cycloplegic spherical refraction did not differ significantly from predicted refraction but was significantly different from noncycloplegic refraction, whereas cycloplegic cylinder refraction did not differ significantly from predicted or noncycloplegic values. Our prediction models based on ocular biometry provide estimates of refraction in children similar to measured cycloplegic spherical and cylinder refraction values without the application of cycloplegic eyedrops.

Introduction

Amblyopia is the most common but treatable pediatric ophthalmologic problem [1]. Early detection of amblyopia allows initiation of treatment at a younger age and consequent normal development of visual acuity in children [2–7]. Screening for refractive error underlying amblyopia in young patients requires the performance of autorefractometry under the cycloplegic condition as a result of the wide range of accommodation in children. However, in the clinical setting, it is often problematic to apply cycloplegic eyedrops to children because of their refusal or the refusal of their parents or of contraindications for the eyedrops [8–10]. Furthermore, the effects of such eyedrops can persist for several hours [11], resulting in disturbance of daily life during accommodation paralysis. Attempts to detect refractive errors in children without application of cycloplegic eyedrops have included the development of procedures for prediction of cycloplegic refraction. The refractive value in children can be estimated on the basis of the ratio of the keratometric value to ocular axial length [12–19]. However, such evaluations rely on spherical equivalent values, with the resultant findings therefore possibly including cylinder refraction, and they may fail to detect the precise refractive error underlying amblyopia. New approaches are therefore needed to determine cycloplegic spherical and cycloplegic cylinder refraction in a screening procedure for amblyopia without the use of cycloplegic eyedrops.

Optical biometry has been applied worldwide to calculate intraocular lens power [20, 21]. It relies on optical coherence to detect various ocular characteristics, and it allows the measurement of ocular axial length as well as corneal anterior curvature, anterior chamber depth (distance from the top of the cornea to the anterior capsule of the lens), lens thickness, and corneal thickness [22–25]. Furthermore, the latest optical biometric techniques based on Fourier domain interferometry minimize measurement times, thereby improving the reliability of the measurements [24, 26]. Such shorter examination times are especially important for measurements in children. Indeed, the application of optical biometry to children has been found to provide reliable measurements of ocular parameters [27, 28], and we therefore anticipated that it might be applicable to assessment of refraction in such young patients without the administration of cycloplegic eyedrops.

Under the noncycloplegic condition, the effect of accommodation in ocular examinations of children cannot be ignored. We therefore considered that a procedure for prediction of cycloplegic refraction in children would need to be based on several clinical parameters. In this study, we collected data for ocular parameters including corneal refraction, corneal astigmatism, ocular axial length, anterior chamber depth, and lens thickness by optical biometry, and we then developed and evaluated prediction models for ocular refraction in children. We found that these models are able to predict cycloplegic spherical and cycloplegic cylinder refraction on the basis of the noncycloplegic measurements made by ocular biometry. Furthermore, the predicted spherical refraction was closer to cycloplegic spherical refraction than was noncycloplegic spherical refraction. Our models may therefore provide a comfortable refractive screening procedure for children without the use of undesirable cycloplegic eyedrops, and they may thus contribute to the early detection and treatment of amblyopia.

Subjects and methods

Subjects

The study design was retrospective. Children aged 2 to 9 years who visited Ohshima Eye Hospital from April 2016 through July 2019 were candidates for this clinical study. Out of these 3321 children, those who met the following criteria were eligible for enrollment in the study: (1) their parents provided consent for the examinations; (2) clinical information was available for before and after cyclopentolate application; (3) the standard deviation of the axial length values obtained by ocular biometry was <0.5%; and (4) the range of the values for ocular refraction measured by autorefractometry was <0.75 D. Candidates with diseases of the cornea, lens, or retina, with infectious diseases, with eyelid or orbit abnormalities, or with a history of ocular surgery were excluded from the study. A total of 1221 eyes of 617 children (266 boys and 351 girls; mean age ± SD of 6.47 ± 2.00 years, with a range of 2 to 9 years) was eventually enrolled (Fig 1). The subjects were then divided into three groups on the basis of the time period during which they underwent examinations. To develop the prediction models, we selected subjects who were examined from April 2016 through December 2017 as the development group (710 eyes of 359 children; 160 boys and 199 girls, with a mean age ± SD of 6.46 ± 2.05 years and age range of 2 to 9 years). We selected subjects who were examined from January 2018 through March 2019 as a validation group to validate the prediction models (385 eyes of 194 children; 81 boys and 113 girls, with a mean age ± SD of 6.49 ± 1.89 years and age range of 2 to 9 years). Finally, the predicted refraction was compared with measured cycloplegic refraction and noncycloplegic refraction in a comparison group consisting of subjects who were examined from April 2019 through July 2019 (126 eyes of 64 children; 25 boys and 39 girls with a mean age ± SD of 6.81 ± 1.84 years and age range of 2 to 9 years). This retrospective observational study was approved by the Institutional Review Board of Ohshima Eye Hospital (approval no. OEH-2019-03) and adhered to the tenets of the Declaration of Helsinki. Informed consent was obtained from the parents of all subjects.

Fig 1. Flow chart of subject and group selection.

Fig 1

Open in a new tab

B, boy; G, girl.

Collection of clinical information

All subjects underwent three examinations under noncycloplegic conditions by ocular biometry (IOLMaster 700; Carl Zeiss Meditec AG, Jena, Germany) and by autorefractometry (TONOREFII; NIDEK, Gamagoori, Japan). The examinations were performed by examiners who were unaware of this study. After the noncycloplegic examinations, the subjects received two drops of 1% cyclopentolate (Santen, Osaka, Japan) in each eye with an interval of 5 min between drops. One hour after application of cyclopentolate, loss of direct light reaction and mydriasis was confirmed and the eyes were examined three times by autorefractometry to obtain cycloplegic spherical and cylinder refraction. The median of all observed values was recorded and used for analysis. The clinical parameters collected by ocular biometry for development of the prediction models were ocular axial length (mm), anterior chamber depth (mm), lens thickness (mm), mean corneal refractive power (D), and corneal astigmatic value (D).

Development of the prediction models

On the basis of the collected biometric and autorefractometric data, we developed prediction models for spherical refraction and cylinder refraction by applying multiple regression analysis. We first designated axial length [12], anterior chamber depth [29], lens thickness [29], corneal refractive power [12], corneal astigmatism [30], sex [31], and age [32–34] as independent variables, given that they had previously been identified or implicated as factors related to ocular refraction. Cycloplegic spherical refraction and cycloplegic cylinder refraction were considered as dependent (objective) variables. We then applied stepwise multiple regression analysis to identify independent variables that significantly affect prediction of the dependent variables.

Statistical analysis

We applied stepwise multiple regression analysis to identify statistically significant independent variables for prediction of cycloplegic spherical and cylinder refraction, as described above. The multicollinearity between the selected independent variables had a variance inflation factor of <10. The accuracy of each prediction formula was evaluated by Pearson’s correlation coefficient. The Kruskal-Wallis test was applied for multiple comparisons of noncycloplegic refraction, cycloplegic refraction, and predicted refraction in the comparison group. The Dunn-Bonferroni test was applied for comparisons between two groups. A P value of <0.05 was considered statistically significant. All statistical analysis was performed with IBM SPSS Statistics software version 24 (IBM, Armonk, NY).

Results

Development of the prediction models

With the clinical parameter values obtained from the development group, we developed formulas to predict cycloplegic spherical refraction and cycloplegic cylinder refraction. The statistical method of stepwise multiple regression analysis provides the best combination of suggested independent variables for indication of dependent variables. Such analysis revealed that axial length, anterior chamber depth, lens thickness, corneal refractive power, corneal astigmatism, sex, and age constituted the best combination of independent variables for prediction of spherical refraction (Table 1). Similarly, axial length, corneal refractive power, corneal astigmatism, sex, and age were selected as the best combination of independent variables for prediction of cylinder refraction (Table 2).

Table 1. Stepwise multiple regression analysis for predicted spherical refraction based on clinical information in the development group (710 eyes of 359 subjects).

Parameter Regression coefficient Standard error t ratio P value Variance inflation factor
Intercept 96.803 1.756 55.116 <0.001
Age 0.285 0.021 13.533 <0.001 1.719
Sex (boy = 1, girl = 0) 0.453 0.071 6.381 <0.001 1.141
Corneal refractive power –0.985 0.026 –38.528 <0.001 1.263
Corneal astigmatism 0.377 0.037 10.169 <0.001 1.088
Axial length –2.588 0.034 –76.006 <0.001 1.975
Anterior chamber depth 1.501 0.183 8.220 <0.001 3.458
Lens thickness –0.479 0.200 –2.395 0.017 2.742
Open in a new tab

Table 2. Stepwise multiple regression analysis for predicted cylinder refraction based on clinical information in the development group (710 eyes of 359 subjects).

Parameter Regression coefficient Standard error t ratio P value Variance inflation factor
Intercept –2.877 0.788 –3.649 <0.001
Age –0.028 0.011 –2.486 0.013 1.377
Sex (boy = 1, girl = 0) 0.077 0.042 1.839 0.066 1.068
Corneal refractive power 0.031 0.014 2.134 0.033 1.095
Corneal astigmatism 0.911 0.022 40.553 <0.001 1.083
Axial length 0.055 0.018 3.052 0.002 1.495
Open in a new tab

On the basis of the stepwise multiple regression analysis, we developed the following multiple regression equation for prediction of cycloplegic spherical refraction:

Predictedsphericalrefraction=96.803+(–2.588×axiallength[mm])+(–0.985×cornealrefractivepower[D])+(0.285×age[years])+(1.501×anteriorchamberdepth[mm])+(0.377×cornealastigmatism[D])+(0.453×sex[boy=1,girl=0])+(–0.479×lensthickness[mm])

The correlation coefficient of this multiple regression equation was 0.960 (R2 = 0.922). The error average of the equation was –0.001, and the root mean squared residual (RMSR) was 0.874. Statistical analysis revealed that the P value of this equation was <0.001.

We similarly developed the following multiple regression equation for prediction of cycloplegic cylinder refraction:

Predicted cylinder refraction = –2.877 + (0.911 × corneal astigmatism [D]) + (0.077 × sex [boy = 1, girl = 0]) + (0.055 × axial length [mm]) + (–0.028 × age [years]) + (0.031 × corneal refractive power [D])

The correlation coefficient of the multiple regression equation was 0.844 (R2 = 0.712). The error average of this equation was 0.01, and the RMSR was 0.532. Statistical analysis again revealed that the P value of the multiple regression equation was <0.001.

Validation of the prediction models

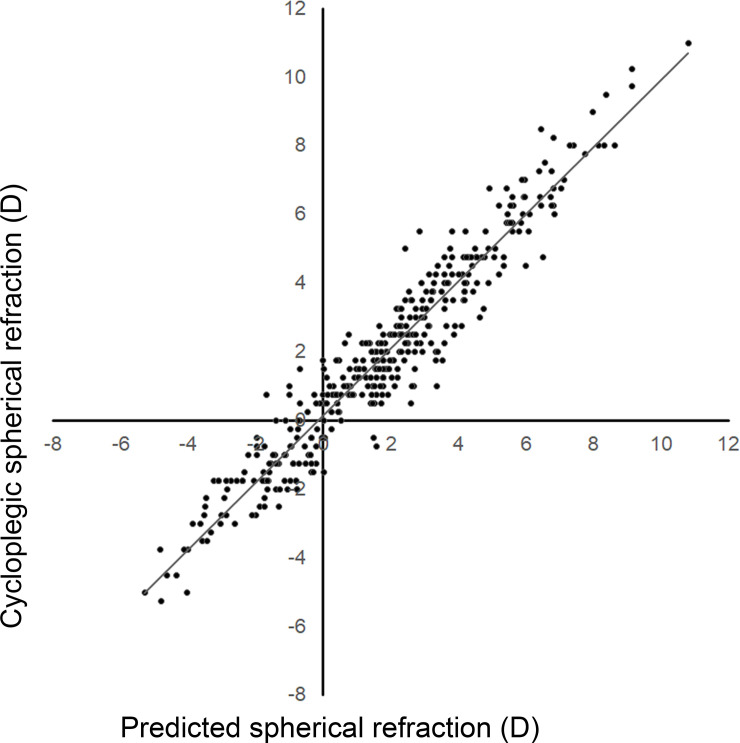
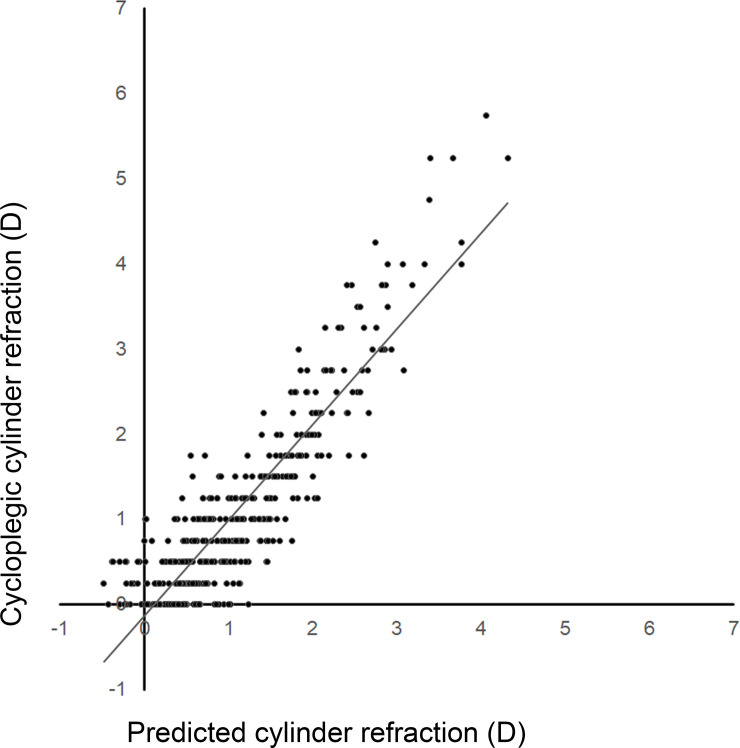
To validate the prediction equations for cycloplegic spherical and cylinder refraction, we applied the clinical information for the validation group to the prediction models and then compared the predicted spherical and cylinder refraction values with the actual cycloplegic spherical and cylinder refraction values for each eye. Fig 2 shows the distribution of cycloplegic spherical refraction and predicted spherical refraction values for the eyes in the validation group. The correlation coefficient of the correlation curve for cycloplegic spherical refraction versus predicted spherical refraction was 0.961 (R2 = 0.924). The error average of the correlation curve was –0.11, and the RMSR was 0.816 (Table 3). Statistical analysis revealed that the P value for the multiple regression equation for cycloplegic spherical refraction and predicted spherical refraction was <0.001. Similarly, the correlation coefficient of the correlation curve for cycloplegic cylinder refraction versus predicted cylinder refraction was 0.894 (R2 = 0.799). The error average of the correlation curve was –0.006, and the RMSR was 0.498 (Fig 3, Table 4). Statistical analysis revealed that the P value for the multiple regression equation for cycloplegic cylinder refraction and predicted cylinder refraction was <0.001.

Fig 2. Distribution of cycloplegic spherical refraction and predicted spherical refraction in the validation group.

Fig 2

Open in a new tab

Spherical refraction estimated by the prediction formula was highly correlated with cycloplegic spherical refraction (R2 = 0.924).

Table 3. Validation of model performance for prediction of spherical refraction compared with measured cycloplegic spherical refraction in the validation group (385 eyes of 194 subjects).

Mean SD Minimum Median Maximum
Cycloplegic spherical refraction 1.81 2.94 –5.25 1.75 11.00
Predicted spherical refraction 1.71 2.90 –5.30 1.73 10.82
Residual error of spherical refraction –0.11 0.81 –2.66 0.14 2.36
Open in a new tab

The root mean squared residual was 0.816.

Fig 3. Distribution of cycloplegic cylinder refraction and predicted cylinder refraction in the validation group.

Fig 3

Open in a new tab

Cylinder refraction estimated by the prediction formula was correlated with cycloplegic cylinder refraction (R2 = 0.799).

Table 4. Validation of model performance for prediction of cylinder refraction compared with measured cycloplegic cylinder refraction in the validation group (385 eyes of 194 subjects).

Mean SD Minimum Median Maximum
Cycloplegic cylinder refraction 1.13 1.09 0.00 0.75 5.75
Predicted cylinder refraction 1.12 0.86 –0.47 0.95 4.32
Residual error of cylinder refraction –0.006 0.50 –1.85 0.03 1.24
Open in a new tab

The root mean squared residual was 0.498.

Comparisons among noncycloplegic refraction, cycloplegic refraction, and predicted refraction values

The major and primary procedure used for measurement of spherical and cylinder refraction in the clinic is autorefractometry. We therefore compared cycloplegic measurements obtained by autorefractometry with noncycloplegic measurements obtained by autorefractometry and with the predicted refraction values obtained by application of clinical parameters measured by ocular biometry for eyes in the comparison group. The correlation coefficient for comparison between cycloplegic spherical refraction and noncycloplegic spherical refraction was 0.929 (R2 = 0.863). The error average of the correlation curve was –0.95, and the RMSR was 1.438 (Table 5). The correlation coefficient for comparison between cycloplegic spherical refraction and predicted spherical refraction was 0.967 (R2 = 0.935). The error average of the correlation curve was –0.12, and the RMSR was 0.727 (Table 5). Similarly, comparison between cycloplegic cylinder refraction and noncycloplegic cylinder refraction yielded a correlation coefficient of 0.980 (R2 = 0.960). The error average of the correlation curve was 0.008, and the RMSR was 0.218 (Table 6). The comparison between cycloplegic cylinder refraction and predicted cylinder refraction revealed a correlation coefficient of 0.910 (R2 = 0.828). The error average of the correlation curve was –0.05, and the RMSR was 0.429 (Table 6). We then compared the distributions of the measured and predicted values of spherical or cylinder refraction. In the case of spherical refraction, the distribution of noncycloplegic measurement values differed significantly from that of cycloplegic measurement values (P = 0.019) as well as from that of predicted values (P = 0.017), whereas the distributions of cycloplegic measurement values and predicted values were not significantly different (Fig 4). In the case of cylinder refraction, the distributions of cycloplegic measurement values, noncycloplegic measurement values, and predicted values did not differ significantly (Fig 5).

Table 5. Comparison of cycloplegic spherical refraction with noncycloplegic and predicted spherical refraction in the comparison group (126 eyes of 64 subjects).

Mean SD Minimum Median Maximum
Noncycloplegic refractive value 0.25 2.32 –6.00 0.00 8.75
Cycloplegic refractive value 1.20 2.82 –5.75 1.25 9.75
Predicted refractive value 1.08 2.65 –5.87 1.05 9.15
Noncycloplegic vs. cycloplegic
    Refractive residual error –0.95 1.08 –5.50 –0.50 0.25
Predicted vs. cycloplegic
    Refractive residual error –0.12 0.72 –1.95 –0.15 1.51
Open in a new tab

The root mean squared residuals for comparison of noncycloplegic or predicted refraction with cycloplegic refraction were 1.438 and 0.727, respectively.

Table 6. Comparison of cycloplegic cylinder refraction with noncycloplegic and predicted cylinder refraction in the comparison group (126 eyes of 64 subjects).

Mean SD Minimum Median Maximum
Noncycloplegic cylinder value 1.07 1.08 0.00 0.75 5.50
Cycloplegic cylinder value 1.05 1.02 0.00 0.75 5.25
Predicted cylinder value 1.01 0.86 –0.30 0.75 4.21
Noncycloplegic vs. cycloplegic
    Cylinder residual error 0.008 0.22 –0.50 0.00 0.50
Predicted vs. cycloplegic
    Cylinder residual error –0.05 0.43 –1.36 0.04 1.24
Open in a new tab

The root mean squared residuals for comparison of noncycloplegic or predicted refraction with cycloplegic refraction were 0.218 and 0.429, respectively.

Fig 4. Box-and-whisker plots showing the distribution of spherical refraction values obtained by noncycloplegic measurement, cycloplegic measurement, and the prediction model.

Fig 4

Open in a new tab

The top and bottom of each box represent the third and first quartiles, respectively, with the center line representing the median value; whiskers indicate maximum and minimum values; and open circles and crosses denote outliers and the mean, respectively. *P < 0.05; N.S., not significant. The distribution of noncycloplegic measured values was significantly different from that of cycloplegic measured values (P = 0.019) and from that of the predicted values (P = 0.017). The distribution of cycloplegic measured values was not significantly different from that of the predicted values.

Fig 5. Box-and-whisker plots showing the distribution of cylinder refraction values obtained by noncycloplegic measurement, cycloplegic measurement, and the prediction model.

Fig 5

Open in a new tab

N.S., not significant. The distributions of the three groups did not differ significantly from each other.

Discussion

In this study, we developed prediction models for cycloplegic spherical and cylinder refraction in children based on clinical parameters measured by ocular biometry. The prediction equations were found to be precise enough to predict cycloplegic spherical refraction and astigmatism in children. Furthermore, the predicted spherical refraction obtained with our formula was more similar to the measured cycloplegic value than was the noncycloplegic value measured by autorefractometry. Our prediction models are therefore potentially applicable to screening of children for amblyopia and identification of the need for follow-up assessments. They would save time in the clinical evaluation of such children as well as avoid the adverse effects of cyclopentolate eyedrops.

The correlation coefficients for comparisons of predicted spherical refraction with cycloplegic spherical refraction and of predicted cylinder refraction with cycloplegic cylinder refraction in the validation group were 0.961 and 0.894, respectively, suggesting that our prediction models yielded acceptable refractive information in children. It is worthy to note that our formulas estimate cycloplegic refraction values on the basis of ocular biometry data obtained under the noncycloplegic condition. Previous studies have proposed formulas for prediction of refraction values, but the correlation coefficients for comparison of the predicted and measured cycloplegic values ranged from 0.53 to 0.89 [12–19]. The correlation coefficients for comparisons of predicted and cycloplegic values were 0.53 to 0.81 [12–16] and 0.78 to 0.89 [17–19] in clinical studies of children (3 to 13 years of age) and adults (18 to 39 years of age), respectively. These studies applied clinical information for axial length and corneal curvature. The relatively low precision of prediction in young children was speculated to be due to the ongoing development of ocular structure. In comparison with previous studies, our prediction models showed high correlation coefficients between the predicted and cycloplegic values. The application of multiple regression for development of the prediction models, the use of several clinical parameters, and the separate analyses of spherical refraction and astigmatism may all have contributed to the precise prediction of spherical and cylinder refraction in children.

We found that the difference between cycloplegic spherical refraction and either the value predicted by our model or the noncycloplegic value was –0.12 and –0.95, respectively. Younger children show wider accommodation than do adults [35–38]. Furthermore, noncycloplegic autorefraction tends to show a minus overcorrection error in comparison with cycloplegic autorefraction [39–44]. It has thus been difficult to obtain precise measurements of refraction under the noncycloplegic condition in younger individuals as a result of the wider accommodation and myopic shift errors. The predicted spherical refraction provided by our formula was less minus-shifted, and so may be less affected by accommodation in younger children.

On the other hand, our analysis revealed that the difference between cycloplegic cylinder refraction and either cylinder refraction predicted by our formula or noncycloplegic cylinder refraction was –0.05 and 0.008, respectively. Moreover, the correlation coefficients between cycloplegic cylinder refraction and predicted cylinder refraction or noncycloplegic cylinder refraction in the comparison group were 0.910 and 0.980, respectively. Our data thus suggest that measurement of cylinder refraction under the noncycloplegic condition may provide an estimation of cycloplegic cylinder refraction that is as good as or better than that provided by our prediction model, indicating that measurement of astigmatism is less affected by accommodation than is that of spherical refraction.

The collection of refraction data without any effect of accommodation in children requires the application of cyclopentolate eyedrops. The use of cyclopentolate for such cycloplegic evaluation, however, has several disadvantages. Development of the cycloplegic effect requires at least 45 min, and the associated photophobia persists for several hours. Children receiving these eyedrops may also experience ocular irritation, which may result in a lack of patient cooperation. Furthermore, cyclopentolate is associated with a risk for the development of mental disorders or toxicity to the central nervous system [45, 46] or cardiovascular system [47]. These disadvantages sometimes preclude the use of cycloplegic evaluation by application of cyclopentolate eyedrops as a screening procedure to detect refractive errors in children. In the present study, we performed ocular biometry to obtain precise values for axial length, anterior chamber depth, lens thickness, corneal refractive power, and corneal astigmatism within 10 seconds for each eye. Our formulas were developed on the basis of these parameters obtained under the noncycloplegic condition, and they provided predicted refraction values highly similar to the measured cycloplegic refraction values. Thus, with the application of our formulas, ocular biometric evaluation can provide precise estimates of ocular refraction in children without the adverse effects of cyclopentolate eyedrops and shows potential for screening of children for refractive errors.

However, there are some limitations related to the use of our prediction models. First, there are some challenges to performing ocular biometery in children. The examination requires fixation of the face on the equipment and visual fixation for 5 seconds, which may be difficult to achieve with uncooperative children, especially infants. Second, the astigmatism prediction sometimes yields values less than zero, which may have to be ignored.

In conclusion, we have proposed prediction models based on ocular biometry data for the detection of spherical refractive and astigmatic errors in children. These models provide estimates of spherical and cylinder refraction equivalent to those measured by autorefractometry under the cycloplegic condition while avoiding the risks associated with the use of cyclopentolate eyedrops. Our methodology may also avoid failure to identify anisometropia. We expect that the introduction of our models would allow more accurate noninvasive screening of children for amblyopia and thereby contribute to the prompt management of affected individuals.

Data Availability

The data underlying the results presented in the study are available from (https://doi.org/10.6084/m9.figshare.13650038.v1).

Funding Statement

The authors received no specific funding for this work.

References

  • 1.Pediatric Eye Disease Investigator G. A randomized trial of atropine vs. patching for treatment of moderate amblyopia in children. Arch Ophthalmol. 2002;120(3):268–78. Epub 2002/03/15. 10.1001/archopht.120.3.268 . [DOI] [PubMed] [Google Scholar]
  • 2.Holmes JM, Kraker RT, Beck RW, Birch EE, Cotter SA, Everett DF, et al. A randomized trial of prescribed patching regimens for treatment of severe amblyopia in children. Ophthalmology. 2003;110(11):2075–87. Epub 2003/11/05. 10.1016/j.ophtha.2003.08.001 . [DOI] [PubMed] [Google Scholar]
  • 3.Repka MX, Kraker RT, Beck RW, Birch E, Cotter SA, Holmes JM, et al. Treatment of severe amblyopia with weekend atropine: results from 2 randomized clinical trials. J AAPOS. 2009;13(3):258–63. Epub 2009/06/23. 10.1016/j.jaapos.2009.03.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Fulton AB, Mayer DL. Esotropic children with amblyopia: effects of patching on acuity. Graefes Arch Clin Exp Ophthalmol. 1988;226(4):309–12. Epub 1988/01/01. 10.1007/BF02172956 . [DOI] [PubMed] [Google Scholar]
  • 5.Holmes JM, Lazar EL, Melia BM, Astle WF, Dagi LR, Donahue SP, et al. Effect of age on response to amblyopia treatment in children. Arch Ophthalmol. 2011;129(11):1451–7. Epub 2011/07/13. 10.1001/archophthalmol.2011.179 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Stewart CE, Stephens DA, Fielder AR, Moseley MJ, Cooperative M. Modeling dose-response in amblyopia: toward a child-specific treatment plan. Invest Ophthalmol Vis Sci. 2007;48(6):2589–94. Epub 2007/05/26. 10.1167/iovs.05-1243 . [DOI] [PubMed] [Google Scholar]
  • 7.Friedburg D, Kloppel KP. [Early correction of hyperopia and astigmatism in children leads to better development of visual acuity]. Klin Monbl Augenheilkd. 1996;209(1):21–4. Epub 1996/07/01. 10.1055/s-2008-1035271 . [DOI] [PubMed] [Google Scholar]
  • 8.Stone RA, Quinn GE, Francis EL, Ying GS, Flitcroft DI, Parekh P, et al. Diurnal axial length fluctuations in human eyes. Invest Ophthalmol Vis Sci. 2004;45(1):63–70. Epub 2003/12/24. 10.1167/iovs.03-0294 . [DOI] [PubMed] [Google Scholar]
  • 9.Robinson BE. Factors associated with the prevalence of myopia in 6-year-olds. Optom Vis Sci. 1999;76(5):266–71. Epub 1999/06/22. 10.1097/00006324-199905000-00011 . [DOI] [PubMed] [Google Scholar]
  • 10.Manh V, Chen AM, Tarczy-Hornoch K, Cotter SA, Candy TR. Accommodative performance of children with unilateral amblyopia. Invest Ophthalmol Vis Sci. 2015;56(2):1193–207. Epub 2015/01/30. 10.1167/iovs.14-14948 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Bartlett JD. Administration of and adverse reactions to cycloplegic agents. Am J Optom Physiol Opt. 1978;55(4):227–33. Epub 1978/04/01. 10.1097/00006324-197804000-00003 . [DOI] [PubMed] [Google Scholar]
  • 12.Foo VH, Verkicharla PK, Ikram MK, Chua SY, Cai S, Tan CS, et al. Axial Length/Corneal Radius of Curvature Ratio and Myopia in 3-Year-Old Children. Transl Vis Sci Technol. 2016;5(1):5. Epub 2016/03/02. 10.1167/tvst.5.1.5 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Ojaimi E, Rose KA, Morgan IG, Smith W, Martin FJ, Kifley A, et al. Distribution of ocular biometric parameters and refraction in a population-based study of Australian children. Invest Ophthalmol Vis Sci. 2005;46(8):2748–54. Epub 2005/07/27. 10.1167/iovs.04-1324 . [DOI] [PubMed] [Google Scholar]
  • 14.Ip JM, Huynh SC, Kifley A, Rose KA, Morgan IG, Varma R, et al. Variation of the contribution from axial length and other oculometric parameters to refraction by age and ethnicity. Invest Ophthalmol Vis Sci. 2007;48(10):4846–53. Epub 2007/09/28. 10.1167/iovs.07-0101 . [DOI] [PubMed] [Google Scholar]
  • 15.Kimura S, Hasebe S, Miyata M, Hamasaki I, Ohtsuki H. Axial length measurement using partial coherence interferometry in myopic children: repeatability of the measurement and comparison with refractive components. Jpn J Ophthalmol. 2007;51(2):105–10. Epub 2007/04/03. 10.1007/s10384-006-0410-5 . [DOI] [PubMed] [Google Scholar]
  • 16.He X, Zou H, Lu L, Zhao R, Zhao H, Li Q, et al. Axial length/corneal radius ratio: association with refractive state and role on myopia detection combined with visual acuity in Chinese schoolchildren. PLoS One. 2015;10(2):e0111766. Epub 2015/02/19. 10.1371/journal.pone.0111766 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Gonzalez Blanco F, Sanz Fernandez JC, Munoz Sanz MA. Axial length, corneal radius, and age of myopia onset. Optom Vis Sci. 2008;85(2):89–96. Epub 2008/02/26. 10.1097/OPX.0b013e3181622602 . [DOI] [PubMed] [Google Scholar]
  • 18.Iyamu E, Iyamu J, Obiakor CI. The role of axial length-corneal radius of curvature ratio in refractive state categorization in a nigerian population. ISRN Ophthalmol. 2011;2011:138941. Epub 2011/01/01. 10.5402/2011/138941 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Grosvenor T, Scott R. Role of the axial length/corneal radius ratio in determining the refractive state of the eye. Optom Vis Sci. 1994;71(9):573–9. Epub 1994/09/01. 10.1097/00006324-199409000-00005 . [DOI] [PubMed] [Google Scholar]
  • 20.Chen YA, Hirnschall N, Findl O. Evaluation of 2 new optical biometry devices and comparison with the current gold standard biometer. J Cataract Refract Surg. 2011;37(3):513–7. Epub 2011/01/20. 10.1016/j.jcrs.2010.10.041 . [DOI] [PubMed] [Google Scholar]
  • 21.Kaswin G, Rousseau A, Mgarrech M, Barreau E, Labetoulle M. Biometry and intraocular lens power calculation results with a new optical biometry device: comparison with the gold standard. J Cataract Refract Surg. 2014;40(4):593–600. Epub 2014/04/01. 10.1016/j.jcrs.2013.09.015 . [DOI] [PubMed] [Google Scholar]
  • 22.Arriola-Villalobos P, Almendral-Gomez J, Garzon N, Ruiz-Medrano J, Fernandez-Perez C, Martinez-de-la-Casa JM, et al. Agreement and clinical comparison between a new swept-source optical coherence tomography-based optical biometer and an optical low-coherence reflectometry biometer. Eye (Lond). 2017;31(3):437–42. Epub 2016/11/12. 10.1038/eye.2016.241 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Omoto MK, Torii H, Masui S, Ayaki M, Tsubota K, Negishi K. Ocular biometry and refractive outcomes using two swept-source optical coherence tomography-based biometers with segmental or equivalent refractive indices. Sci Rep. 2019;9(1):6557. Epub 2019/04/27. 10.1038/s41598-019-42968-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Srivannaboon S, Chirapapaisan C, Chonpimai P, Loket S. Clinical comparison of a new swept-source optical coherence tomography-based optical biometer and a time-domain optical coherence tomography-based optical biometer. J Cataract Refract Surg. 2015;41(10):2224–32. Epub 2015/12/26. 10.1016/j.jcrs.2015.03.019 . [DOI] [PubMed] [Google Scholar]
  • 25.Yang CM, Lim DH, Kim HJ, Chung TY. Comparison of two swept-source optical coherence tomography biometers and a partial coherence interferometer. PLoS One. 2019;14(10):e0223114. Epub 2019/10/12. 10.1371/journal.pone.0223114 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Akman A, Asena L, Gungor SG. Evaluation and comparison of the new swept source OCT-based IOLMaster 700 with the IOLMaster 500. Br J Ophthalmol. 2016;100(9):1201–5. Epub 2015/12/18. 10.1136/bjophthalmol-2015-307779 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Carkeet A, Saw SM, Gazzard G, Tang W, Tan DT. Repeatability of IOLMaster biometry in children. Optom Vis Sci. 2004;81(11):829–34. Epub 2004/11/17. 10.1097/01.opx.0000145020.33250.c0 . [DOI] [PubMed] [Google Scholar]
  • 28.Hussin HM, Spry PG, Majid MA, Gouws P. Reliability and validity of the partial coherence interferometry for measurement of ocular axial length in children. Eye (Lond). 2006;20(9):1021–4. Epub 2005/08/13. 10.1038/sj.eye.6702069 . [DOI] [PubMed] [Google Scholar]
  • 29.Yuan Y, Zhang Z, Zhu J, He X, Du E, Jiang K, et al. Responses of the Ocular Anterior Segment and Refraction to 0.5% Tropicamide in Chinese School-Aged Children of Myopia, Emmetropia, and Hyperopia. J Ophthalmol. 2015;2015:612728. Epub 2015/10/13. 10.1155/2015/612728 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Mohammadpour M, Heidari Z, Khabazkhoob M, Amouzegar A, Hashemi H. Correlation of major components of ocular astigmatism in myopic patients. Cont Lens Anterior Eye. 2016;39(1):20–5. Epub 2015/07/19. 10.1016/j.clae.2015.06.005 . [DOI] [PubMed] [Google Scholar]
  • 31.Czepita D, Mojsa A, Ustianowska M, Czepita M, Lachowicz E. Role of gender in the occurrence of refractive errors. Ann Acad Med Stetin. 2007;53(2):5–7. Epub 2008/06/19. . [PubMed] [Google Scholar]
  • 32.Gwiazda J, Grice K, Held R, McLellan J, Thorn F. Astigmatism and the development of myopia in children. Vision Res. 2000;40(8):1019–26. Epub 2000/03/18. 10.1016/s0042-6989(99)00237-0 . [DOI] [PubMed] [Google Scholar]
  • 33.Wu JF, Bi HS, Wang SM, Hu YY, Wu H, Sun W, et al. Refractive error, visual acuity and causes of vision loss in children in Shandong, China. The Shandong Children Eye Study. PLoS One. 2013;8(12):e82763. Epub 2014/01/01. 10.1371/journal.pone.0082763 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.O’Donoghue L, Breslin KM, Saunders KJ. The Changing Profile of Astigmatism in Childhood: The NICER Study. Invest Ophthalmol Vis Sci. 2015;56(5):2917–25. Epub 2015/05/30. 10.1167/iovs.14-16151 . [DOI] [PubMed] [Google Scholar]
  • 35.Duane A. Studies in Monocular and Binocular Accommodation, with Their Clinical Application. Trans Am Ophthalmol Soc. 1922;20:132–57. Epub 1922/01/01. [PMC free article] [PubMed] [Google Scholar]
  • 36.Kragha IK. Amplitude of accommodation: population and methodological differences. Ophthalmic Physiol Opt. 1986;6(1):75–80. Epub 1986/01/01. . [PubMed] [Google Scholar]
  • 37.Leon A, Estrada JM, Rosenfield M. Age and the amplitude of accommodation measured using dynamic retinoscopy. Ophthalmic Physiol Opt. 2016;36(1):5–12. Epub 2015/09/12. 10.1111/opo.12244 . [DOI] [PubMed] [Google Scholar]
  • 38.Anderson HA, Stuebing KK. Subjective versus objective accommodative amplitude: preschool to presbyopia. Optom Vis Sci. 2014;91(11):1290–301. Epub 2015/01/21. 10.1097/OPX.0000000000000402 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Zhao J, Mao J, Luo R, Li F, Pokharel GP, Ellwein LB. Accuracy of noncycloplegic autorefraction in school-age children in China. Optom Vis Sci. 2004;81(1):49–55. Epub 2004/01/30. 10.1097/00006324-200401000-00010 . [DOI] [PubMed] [Google Scholar]
  • 40.Choong YF, Chen AH, Goh PP. A comparison of autorefraction and subjective refraction with and without cycloplegia in primary school children. Am J Ophthalmol. 2006;142(1):68–74. Epub 2006/07/04. 10.1016/j.ajo.2006.01.084 . [DOI] [PubMed] [Google Scholar]
  • 41.Fotedar R, Rochtchina E, Morgan I, Wang JJ, Mitchell P, Rose KA. Necessity of cycloplegia for assessing refractive error in 12-year-old children: a population-based study. Am J Ophthalmol. 2007;144(2):307–9. Epub 2007/07/31. 10.1016/j.ajo.2007.03.041 . [DOI] [PubMed] [Google Scholar]
  • 42.Rotsos T, Grigoriou D, Kokkolaki A, Manios N. A comparison of manifest refractions, cycloplegic refractions and retinoscopy on the RMA-3000 autorefractometer in children aged 3 to 15 years. Clin Ophthalmol. 2009;3:429–31. Epub 2009/08/18. 10.2147/opth.s5145 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Funarunart P, Tengtrisorn S, Sangsupawanich P, Siangyai P. Accuracy of noncycloplegic refraction in primary school children in southern Thailand. J Med Assoc Thai. 2009;92(6):806–11. Epub 2009/06/18. . [PubMed] [Google Scholar]
  • 44.Fotouhi A, Morgan IG, Iribarren R, Khabazkhoob M, Hashemi H. Validity of noncycloplegic refraction in the assessment of refractive errors: the Tehran Eye Study. Acta Ophthalmol. 2012;90(4):380–6. Epub 2010/10/28. 10.1111/j.1755-3768.2010.01983.x . [DOI] [PubMed] [Google Scholar]
  • 45.Carpenter WT Jr. Precipitous mental deterioration following cycloplegia with 0.2 percent cyclopentolate HCl. Arch Ophthalmol. 1967;78(4):445–7. Epub 1967/10/01. 10.1001/archopht.1967.00980030447006 . [DOI] [PubMed] [Google Scholar]
  • 46.Kennerdell JS, Wucher FP. Cyclopentolate associated with two cases of grand mal seizure. Arch Ophthalmol. 1972;87(6):634–5. Epub 1972/06/01. 10.1001/archopht.1972.01000020636004 . [DOI] [PubMed] [Google Scholar]
  • 47.Shiuey Y, Eisenberg MJ. Cardiovascular effects of commonly used ophthalmic medications. Clin Cardiol. 1996;19(1):5–8. Epub 1996/01/01. 10.1002/clc.4960190104 . [DOI] [PubMed] [Google Scholar]

Decision Letter 0

Ahmed Awadein

25 Nov 2020

PONE-D-20-33313

Prediction of Cycloplegic Refraction for Noninvasive Screening of Children for Refractive Error

PLOS ONE

Dear Dr. Morishige,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

==============================

ACADEMIC EDITOR:

The manuscript needs grammatical revision. In addition, the study design is not very clear. More details of the study design and the study methods is needed.

==============================q

Please submit your revised manuscript by Jan 09 2021 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

  • A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.

  • A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.

  • An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.

If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols

We look forward to receiving your revised manuscript.

Kind regards,

Ahmed Awadein, MD, Ph.D, FRCS

Academic Editor

PLOS ONE

Journal Requirements:

When submitting your revision, we need you to address these additional requirements.

1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at

https://journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and

https://journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.

2.  We note that you have indicated that data from this study are available upon request. PLOS only allows data to be available upon request if there are legal or ethical restrictions on sharing data publicly. For information on unacceptable data access restrictions, please see http://journals.plos.org/plosone/s/data-availability#loc-unacceptable-data-access-restrictions.

In your revised cover letter, please address the following prompts:

a) If there are ethical or legal restrictions on sharing a de-identified data set, please explain them in detail (e.g., data contain potentially identifying or sensitive patient information) and who has imposed them (e.g., an ethics committee). Please also provide contact information for a data access committee, ethics committee, or other institutional body to which data requests may be sent.

b) If there are no restrictions, please upload the minimal anonymized data set necessary to replicate your study findings as either Supporting Information files or to a stable, public repository and provide us with the relevant URLs, DOIs, or accession numbers. Please see http://www.bmj.com/content/340/bmj.c181.long for guidelines on how to de-identify and prepare clinical data for publication. For a list of acceptable repositories, please see http://journals.plos.org/plosone/s/data-availability#loc-recommended-repositories.

We will update your Data Availability statement on your behalf to reflect the information you provide.

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Yes

Reviewer #2: Yes

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: Yes

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: No

Reviewer #2: Yes

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: Comments:

A welll performed study.

Do you think your prediction models would vary in different ethnic groups considering the high prevalence of myopia in Asia and hyperopia elsewhere?

Can these formulas be incorporated or programmed in ocular biometry machines ?

Line Numbering would have helped greatly with the review.

Grammatical errors:

Abstract:

line 7: "as well as.." replace by" in addition several noncycloplegic parameters were assessed using ocular biometry."

line 12: " were eye" instead of "was"

line 16: "and" instead of 'or"

Introduction:

page 5 line 13: rephrase "precise measurement"

page 6 line 6: "than was measured" replace by " than noncycloplegic..."

Collection of clinical information:

page 8 line 12: remove "the" correct to "under noncycloplegic condition..."

Discussion

page 16: line 15: "of note" replace by " it is worthy to note that "

page 17: line 1: "In particular" needs rephrasing

line 11: remove " by our models"

page 18: line 11: "than is that" change to " than that"

line 15: remove word "thus"

line 16 &17: waht do you mean by "ocular stimulation"?

Page 19: line 14: " however" should be placed at beginning of sentence.

Line 14: Rephrasing needed maybe like " there are some challenges while performing biometery in children"

page 20: line 1: remove word "here".

line 3: provide instead of " provided"

line 4: rephrasing needed maybe to " under cycloplegic condition while avoiding..."

line 5: "or with the failure to ....." start new sentence and rephrase.

Reviewer #2: This study tried to introduce a prediction formula for cycloplegic refraction in children, based on non-cycloplegic ocular biometry parameters. This can avoid the difficulties and the potential hazards encountered with performing cycloplegic refraction, allowing for easier screening and management of amblyopia. The following comments are proposed to improve the work.

Major comments:

1. Abstract: Please mention the study design in the “abstract”.

2. Methods:

• it would be more informative for the reader if you begin the “Methods” section by describing the study design.

• The study design is not clear: Was it totally retrospective? was all participants’ data retrieved by chart review? So, for what purpose did children undergoing refractive error evaluation have routine ocular biometry?

• Page 13: regarding these 2 sentences “Statistical analysis revealed that the P value for the multiple regression equation for cycloplegic spherical refraction and predicted spherical refraction was <0.001.” and “Statistical analysis revealed that the P value for the multiple regression equation for cycloplegic cylinder refraction and predicted cylinder refraction was <0.001”…….What statistical test or parameter did you use for comparison between predicted and measured refraction?

• Regarding comparison group: This group has the same inclusion and exclusion criteria of the validation group. What did this third group add? Why could not such comparison be performed on the validation group?

3. Results: regarding figures: please add a brief description of the figure to figure legends; to allow readers to understand the key message of the figure without referring to the text.

Minor comments:

1. Page 18: “Children receiving these eyedrops may also experience ocular stimulation, which may result in a lack of patient cooperation.” What does “ocular stimulation” refer to?

2. Page 19: “In the present study, we performed ocular biometry to obtain precise values for axial length, anterior chamber depth, lens thickness, corneal refractive power, and corneal astigmatism within 10 s for each eye.” …. “seconds” is better to be written in full.

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at figures@plos.org. Please note that Supporting Information files do not need this step.

Decision Letter 1

Ahmed Awadein

1 Mar 2021

Prediction of Cycloplegic Refraction for Noninvasive Screening of Children for Refractive Error

PONE-D-20-33313R1

Dear Dr. Morishige,

We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it meets all outstanding technical requirements.

Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.

An invoice for payment will follow shortly after the formal acceptance. To ensure an efficient process, please log into Editorial Manager at http://www.editorialmanager.com/pone/, click the 'Update My Information' link at the top of the page, and double check that your user information is up-to-date. If you have any billing related questions, please contact our Author Billing department directly at authorbilling@plos.org.

If your institution or institutions have a press office, please notify them about your upcoming paper to help maximize its impact. If they’ll be preparing press materials, please inform our press team as soon as possible -- no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact onepress@plos.org.

Kind regards,

Ahmed Awadein, MD, Ph.D, FRCS

Academic Editor

PLOS ONE

Additional Editor Comments (optional):

Reviewers' comments:

Acceptance letter

Ahmed Awadein

5 Mar 2021

PONE-D-20-33313R1

Prediction of cycloplegic refraction for noninvasive screening of children for refractive error

Dear Dr. Morishige:

I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

If we can help with anything else, please email us at plosone@plos.org.

Thank you for submitting your work to PLOS ONE and supporting open access.

Kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Dr. Ahmed Awadein

Academic Editor

PLOS ONE

Associated Data

    This section collects any data citations, data availability statements, or supplementary materials included in this article.

    Supplementary Materials

    Attachment

    Submitted filename: Response to Reviewers.docx

    Click here for additional data file. (24.4KB, docx)

    Data Availability Statement

    The data underlying the results presented in the study are available from (https://doi.org/10.6084/m9.figshare.13650038.v1).

    Articles from PLoS ONE are provided here courtesy of PLOS

    RESOURCES