Phase separation at the nanoscale quantified by dcFCCS

Significance

Liquid–liquid phase separation causes formation of membraneless condensates containing concentrated biomolecules, which play essential roles in diverse cellular processes. Currently, micrometer-scale phase-separated condensates are examined routinely to elucidate their functions and mechanisms in details. However, limited by current commonly used methods, the transition process from miscible individual molecules to micrometer-scale condensates is mostly unknown. Herein, we captured formation of nanoscale condensates, whose size, growth rate, molecular stoichiometry, and binding affinity to recruit client molecules were all quantified. To achieve this, we developed a dual-color fluorescence cross-correlation spectroscopy (dcFCCS) method, and we expect that dcFCCS can be widely applied to investigate phase separation of other biomolecules at the nanoscale.

Abstract

Liquid–liquid phase separation, driven by multivalent macromolecular interactions, causes formation of membraneless compartments, which are biomolecular condensates containing concentrated macromolecules. These condensates are essential in diverse cellular processes. Formation and dynamics of micrometer-scale phase-separated condensates are examined routinely. However, limited by commonly used methods which cannot capture small-sized free-diffusing condensates, the transition process from miscible individual molecules to micrometer-scale condensates is mostly unknown. Herein, with a dual-color fluorescence cross-correlation spectroscopy (dcFCCS) method, we captured formation of nanoscale condensates beyond the detection limit of conventional fluorescence microscopy. In addition, dcFCCS is able to quantify size and growth rate of condensates as well as molecular stoichiometry and binding affinity of client molecules within condensates. The critical concentration to form nanoscale condensates, identified by our experimental measurements and Monte Carlo simulations, is at least several fold lower than the detection limit of conventional fluorescence microscopy. Our results emphasize that, in addition to micrometer-scale condensates, nanoscale condensates are likely to play important roles in various cellular processes and dcFCCS is a simple and powerful quantitative tool to examine them in detail.

Live cells contain many canonical membrane-bound organelles, such as the endoplasmic reticulum and Golgi apparatus, to separate complex biochemical reactions into distinct compartments. In addition, membraneless organelles, including nucleoli, Cajal bodies, and promyelocytic leukemia protein nuclear bodies in the nucleus as well as stress granules, P-bodies, and germ granules in the cytoplasm, serve as an alternative approach to concentrate biomolecules and to provide unique microenvironments different from their surroundings (1–4). Besides these well-known membraneless organelles, many other biomolecular condensates exhibiting liquidlike properties were discovered (4–8). These condensates are formed through liquid–liquid phase separation driven by multivalent interactions between macromolecules (9–11) and play important roles in many processes involving RNA metabolism, ribosome biogenesis, DNA damage response, and cell signaling (4).

To characterize the morphology, dynamics, and functions of micrometer-scale condensates, optical microscopy, especially confocal fluorescence microscopy, is the most commonly used method to visualize liquid–liquid phase separation in vitro and in live cells. The spatial resolution of commonly used fluorescence microscopy is restricted by the optical diffraction limit (∼200 nm). Therefore, various superresolution microscopy has been applied to reveal the formation, movement, and organization of biomolecular condensates beyond the optical diffraction limit (12–21). Still, small free-diffusing condensates are less well studied, let alone to quantify their molecular stoichiometry, growth rate, and their ability to recruit client molecules.

Fluorescence correlation spectroscopy (FCS) is a powerful method based on measuring the fluctuation of fluorescence intensity of illuminant particles within small excitation volumes (22–24). FCS analysis provides precise measurements of the concentration of fluorescent molecules in the observation volume and their diffusion coefficients, from which hydrodynamic radii of fluorescent molecules can be quantified (25). FCS technique has been extensively employed for study thermodynamics and kinetics of inter- and intramolecular interactions, including formation of biomolecular complexes and soluble aggregates beyond the optical diffraction limit (26–28) and nanoscopic phase separations in lipid membranes (29). FCS has also been applied to quantify concentration and diffusion dynamics of proteins within biomolecular condensates (12, 29–31). Here, we demonstrate that dual-color fluorescence cross-correlation spectroscopy (dcFCCS), an extension of FCS method to simultaneously quantify the concentration and diffusion characteristics of two different fluorescent species as well as their reaction product in solution (32), is able to capture condensates formed at the nanoscale.

As far as the phase-separation system is concerned, we decided to engineer a homogeneous, high-valent system for better understanding the kinetics of multivalence-driven phase separation at low concentrations. It has been reported that the Saccharomyces cerevisiae SmF (referred to as ySmF hereafter) protein is a homogeneous, superstable tetradecameric (double-heptameric rings) complex (Fig. 1A) upon expression alone in bacteria (33). We have recently shown that interactions between interacting partners fused to ySmF readily induce robust liquid–liquid phase separation (34). In this study, we mainly used a ySmF-derived phase-separation system as a model. dcFCCS enables us to quantify the radius, growth rate, molecular composition, and binding affinity of nanoscale condensates formed over a broad concentration range of the model system. A simple Monte Carlo simulation was established to mimic growth of condensates, whose results agreed well with our experimental measurements. Overall, our experiments and simulations both suggest that the critical concentration to form rapid-growing nanoscale condensates is ∼50 nM, which is an order of magnitude lower than the detection limit of the commonly used confocal microscopy. Together, our studies not only revealed existence of phase separation at the nanoscale but also provide a quantitative tool to examine composition and dynamics of nanoscale condensates in detail to elucidate their contributions in various cellular processes.

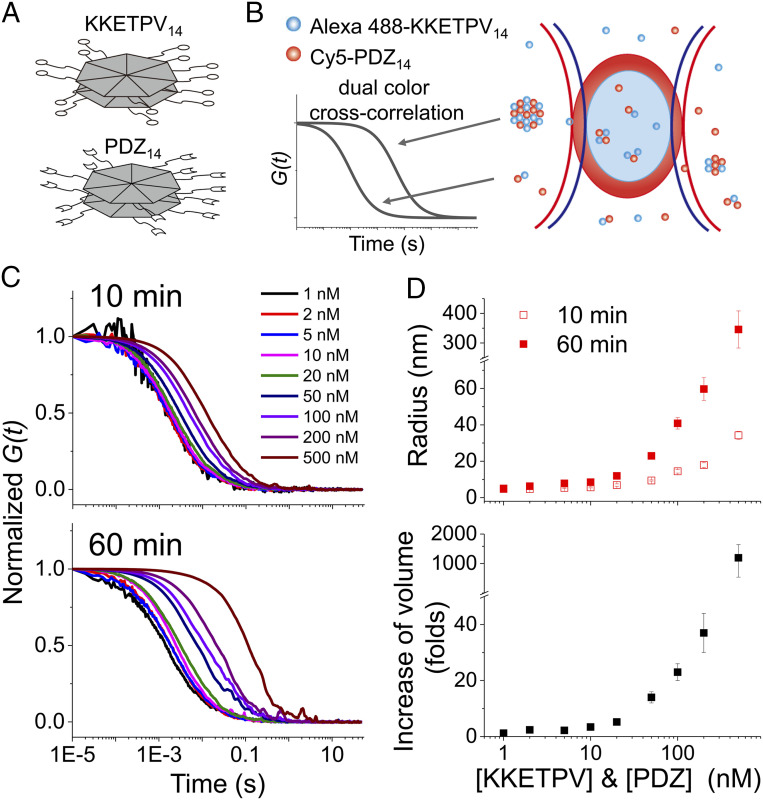
Fig. 1.

dcFCCS assay to capture heterocomplexes formed from Alexa 488-KKETPV₁₄ and Cy5-PDZ₁₄. (A) Schematic diagram of KKETPV₁₄ and PDZ₁₄, which have homoheptameric ring structure formed from 14 identical molecules. (B) Scheme of dcFCCS assay. Alexa 488-KKETPV₁₄ (blue dots) and Cy5-PDZ₁₄ (red dots) molecules freely diffuse through the confocal detection volume of 488 nm (blue oval) and 640 nm (red oval) lasers. Only heterocomplexes containing both Alexa 488 and Cy5 fluorophores contribute to dcFCCS curves, whose relaxation times correlate with the size of complexes. (C) Normalized dcFCCS curves of mixtures of Alexa 488-KKETPV₁₄ and Cy5-PDZ₁₄ taken right after mixing (Top) and after 1-h incubation (Bottom). Concentrations of ySmF monomers were listed. (D) Hydrodynamic radius of KKETPV₁₄-PDZ₁₄ heterocomplexes right after mixing (hollow dots) and after 1 h incubation (solid dots) calculated from relaxation times of dcFCCS curves (Top). Increasing of hydrodynamic volume after 1-h incubation (Bottom). Error bars denote the SEM of three or more independent experiments.

Results

dcFCCS Assay to Capture and to Quantify Biomolecular Heterocomplexes Formation.

To apply dcFCCS to capture biomolecular condensates, we generated two yeast SmF (ySmF) variants to serve as a model system to form liquid–liquid phase separation in vitro. ySmF spontaneously forms a homoheptameric ring containing 14 identical molecules (33). Thus, engineered ySmF variants containing a short peptide KKETPV or a PDZ domain at their C-termini form 14-mers with 14 copies of KKETPV or PDZ, which were named as KKETPV₁₄ or PDZ₁₄, respectively (Fig. 1A) (34). Examined by a fluorescence microscope, we showed that liquid–liquid phase separation occurred at ∼500 nM or higher concentrations with mixtures of Alexa 488 labeled KKETPV₁₄ (Alexa 488-KKETPV₁₄) and Cy5 labeled PDZ₁₄ (Cy5-PDZ₁₄), which was further confirmed by fluorescence recovery after photobleaching assay (SI Appendix, Fig. S1). Concentrations of ySmF monomers were used here and afterward. PEG-passivated slides were used to prevent unspecific binding (details in SI Appendix) (35, 36).

Next, dcFCCS measurements were performed by mixing Alexa 488-KKETPV₁₄ and Cy5-PDZ₁₄, whose concentrations varied from 1 to 500 nM. Only heterocomplexes containing both Alexa 488-KKETPV₁₄ and Cy5-PDZ₁₄ contributed to cross-correlation curves of dcFCCS measurements (Fig. 1B), whose relaxation times correlated with residence times of heterocomplexes within the detection volume (37). Therefore, large complexes have longer relaxation times than small ones (Fig. 1B). Even with 1 nM of Alexa 488-KKETPV₁₄ and Cy5-PDZ₁₄, significant cross-correlation between Alexa 488 and Cy5 signals was captured (Fig. 1C), indicating formation of heterocomplexes under such low concentration. Relaxation times of dcFCCS curves increased at high concentrations and with long incubation times, indicating that heterocomplexes grew under these conditions (Fig. 1C and SI Appendix, Fig. S2). Eighty-one different combinations of concentrations of Alexa 488-KKETPV₁₄ and Cy5-PDZ₁₄ were captured (SI Appendix, Table S1); for clarity, only dcFCCS curves captured using the same concentrations of Alexa 488-KKETPV₁₄ and Cy5-PDZ₁₄, are shown in figures. In summary, dcFCCS assay is able to capture formation of KKETPV₁₄-PDZ₁₄ heterocomplexes over a broad concentration range.

A single-component diffusion model (Eq. 2 in Materials and Methods) is sufficient to well describe most dcFCCS curves, from which relaxation times (${\tau }_D$) were extracted and listed in SI Appendix, Table S1. To quantify sizes of KKETPV₁₄-PDZ₁₄ heterocomplexes, we used the fluorophore Alexa 488, whose radius R₀ is 0.58 nm, as a standard. In our instrument, the relaxation time (${\tau }_0$) of autocorrelation curve of Alexa 488 under 488-nm laser excitation is 0.12 ms and the correlation factor of relaxation time between dcFCCS and autocorrelation curves (Cr_488x) is 0.65. Approximating hydrated heterocomplexes as spheres, their hydrodynamic radii were described via $R_{\text{H}}=\frac{{\tau }_D}{{\tau }_0}C{r}_{488x}{R}_0$ and plotted in Fig. 1D.

When concentrations of Alexa 488-KKETPV₁₄ and Cy5-PDZ₁₄ were 10 nM or lower, ${\tau }_D$ and $R_{\text{H}}$ of heterocomplexes remained constant around 1.5 ms and 5 nm (Fig. 1D and SI Appendix, Table S1), respectively, suggesting that the majority of heterocomplexes were formed as the smallest composition containing one Alexa 488-KKETPV₁₄ and one Cy5-PDZ₁₄ under these conditions. On the other hand, when concentrations were 50 nM or higher, sizes of heterocomplexes and their growth rates increased dramatically. The hydrodynamic radii of heterocomplexes formed from 50, 200, and 500 nM of ySmF variants after 1-h incubation were 23 ± 2 nm, 60 ± 7 nm, and 350 ± 60 nm, respectively, which agreed well with the values measured by negative-stain transmission electron microscopy (36 ± 9 nm, 73 ± 14 nm, and 390 ± 90 nm, respectively, SI Appendix, Fig. S3 A–C). Therefore, these heterocomplexes formed at high concentrations should be considered as condensates of the nanoscale. In addition, using their size distributions measured from electron microscopy (SI Appendix, Fig. S3 A–C), we calculated polydispersity index (PDI), an indicator of broadness of molecular weight distribution. Their PDI values were 1.4–1.6, agreeing with typical values of chain-growth polymerization (38). Furthermore, dcFCCS curves simulated using these size distributions can be well fitted by the single-component diffusion model, whose fitting results were consistent with the mean radii of the data used to generate simulated curves (SI Appendix, Fig. S3D). Together, dcFCCS is a quantitative method to examine formation of nanoscale condensates beyond the detection limit of the commonly used fluorescence microscopy.

Under our experimental conditions, both unbound 14-mers (Alexa 488-KKETPV₁₄ and Cy5-PDZ₁₄) and free-diffusing heterocomplexes and condensates contribute to autocorrelation curves, in which contributions of different species are proportional to the square of their particle brightness. At low concentrations, sizes of heterocomplexes and 14-mers are close to each other, which is less likely to cause autocorrelation curves to significantly deviate from the single-component diffusion model (see examples in SI Appendix, Fig. S3). On the other hand, condensates are significantly larger and brighter than 14-mers at high concentration, causing the domination of autocorrelation curves by large condensates. We did find that several autocorrelation curves around 50 nM moderately deviated from the single-component model, indicating the presence of both condensates and unbound 14-mers.

Stoichiometry of KKETPV₁₄ and PDZ₁₄ within Condensates.

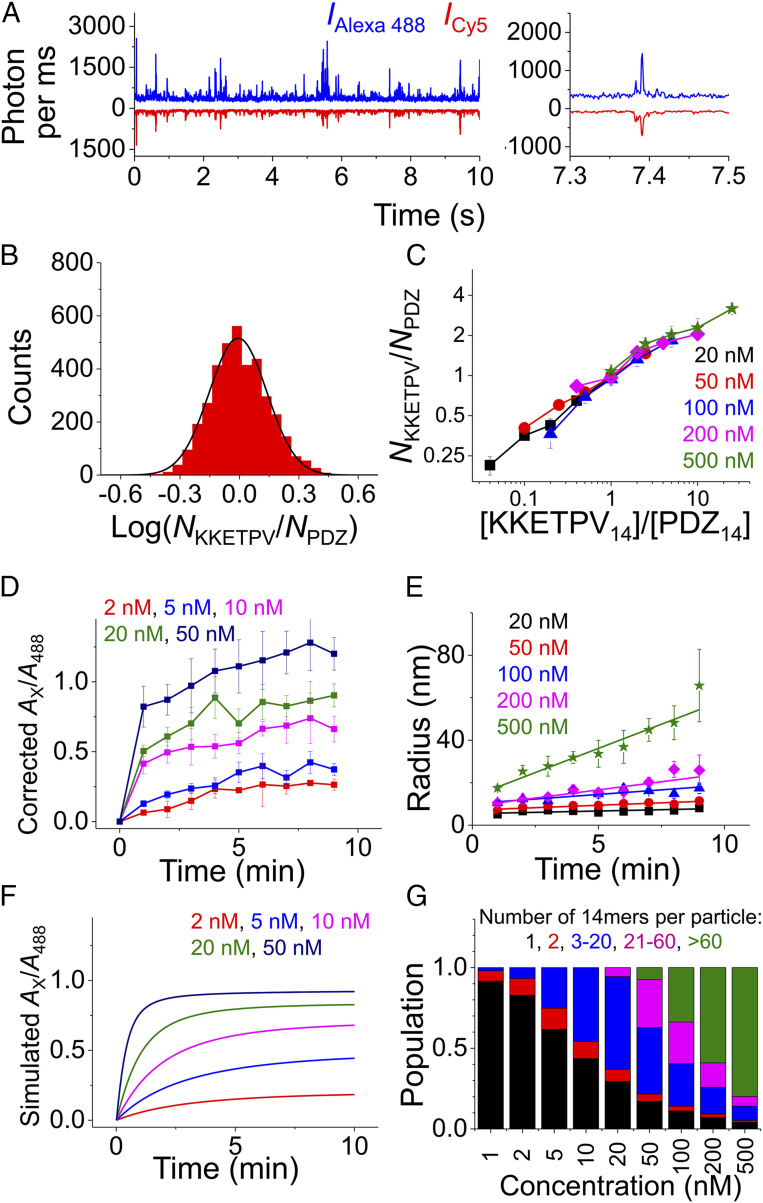
When a nanoscale condensate diffused through the confocal volume, it generated sudden fluorescence signal bursts in both Alexa 488 and Cy5 fluorescence detection channels (Fig. 2A). The ratio of Alexa 488:Cy5 intensities in these sparsely distributed fluorescence bursts enabled us to quantify the stoichiometry of KKETPV₁₄:PDZ₁₄ within condensates (Fig. 2B). Due to the low laser power (∼2.5 μW after the objective), individual 14-mer molecules and most small-sized heterocomplexes formed at concentration of 10 nM or lower would not cause significant fluorescence bursts under our experimental conditions (SI Appendix, Fig. S4). Therefore, we quantified the stoichiometry of KKETPV₁₄:PDZ₁₄ within condensates formed at concentrations of 20 nM and higher, after correcting for relative intensity and background (Fig. 2 B and C). When concentrations of KKETPV₁₄ and PDZ₁₄ were the same, the stoichiometry of KKETPV₁₄:PDZ₁₄ within condensates was 0.99 ± 0.05, suggesting both 14-mers have similar abilities to participate in condensates. In addition, we quantified that 10-fold change in the concentration ratio of KKETPV₁₄:PDZ₁₄ only led to 2.6 ± 0.2-fold change in the molecular stoichiometry of KKETPV₁₄:PDZ₁₄ within condensates (Fig. 2C), indicating molecular composition of condensates is less sensitive to change of concentration in the dilute phase.

Fig. 2.

Stoichiometry and growth rate of KKETPV₁₄-PDZ₁₄ heterocomplexes and condensates. (A) One-ms binned fluorescence trajectory of a mixture of 500 nM Alexa 488-KKETPV₁₄ and Cy5-PDZ₁₄. A zoom-in trajectory is shown on the right. (B) Distributions of KKETPV₁₄: PDZ₁₄ stoichiometry of individual condensate particles extracted from the trajectory shown in A). (C) Relation between KKETPV₁₄: PDZ₁₄ stoichiometry in condensates and the concentration ratio of KKETPV₁₄:PDZ₁₄ in solution when concentrations are 20 nM and higher. Color code is based on [KKETPV₁₄]. (D) Increase of corrected A_x/A₄₈₈ in the first 9 min after mixing when concentrations are 50 nM and lower. (E) Growth of condensate radius in the first 9 min after mixing when concentrations are 20 nM and higher. (F) Increase of A_x/A₄₈₈ in the first 10 min estimated by our Monte Carlo simulation. (G) Proportions of KKETPV₁₄, PDZ₁₄, and heterocomplexes of different sizes after 1-h incubation estimated by simulation. For clarity, heterocomplexes were divided into four groups containing 2, 3–20, 21–60, and >60 14-mers, respectively. KKETPV₁₄ and PDZ₁₄ were combined into one group containing only one 14-mer.

Growth Rate of Heterocomplexes and Condensates.

To examine dynamics of heterocomplex formation, all 9-min-length raw fluorescence data collected right after mixing Alexa 488-KKETPV₁₄ and Cy5-PDZ₁₄ to generate dcFCCS curves in Fig. 1C were divided into nine 1-min-length data. Amplitudes (A_x) and relaxation times (${\tau }_{\text{D}}$) of dcFCCS curves calculated from these 1-min-length data enabled us to quantify dynamics of growth. When the concentration was 10 nM or lower, ${\tau }_{\text{D}}$ remained almost constant over time. However, the ratio of A_x to amplitude of autocorrelation curve of Alexa 488 channel (A₄₈₈) after correction of laser overlap volume, which defined the proportion of PDZ₁₄ participating in heterocomplexes, increased significantly over time (Fig. 2D). The ratio of A_x to amplitude of autocorrelation curve of Cy5 channel (A_Cy5) after correction displayed the same trend (SI Appendix, Fig. S5A). On the other hand, when the concentration was 50 nM or higher, corrected A_x/A₄₈₈ and A_x/A_Cy5 both had a sudden increase in the first 1 min, followed by a gradual minor increase. These phenomena indicated that the majority of KKETPV₁₄ and PDZ₁₄ participated in condensates within 1 min after mixing them together. In addition, over the first 9-min period, their ${\tau }_{\text{D}}$ increased gradually indicating the growth of condensates, which was quantified as growth rates of their radii over time (Fig. 2E and SI Appendix, Table S2).

Next, we established a simple Monte Carlo simulation to mimic growth of heterocomplexes and condensates, which was built on three basic assumptions. 1) According to our measurements (Fig. 2B), the molecular ratio of KKETPV₁₄:PDZ₁₄ within any particle is set between 1/3 and 3. This boundary condition is enforced throughout the simulation. 2) The second-order binding rate between any two molecules or particles is set constant as k_on, because diffusion-driven collision rate is insensitive to the size of particles (39). 3) The dissociation rate of a KKETPV₁₄ molecule from a particle is defined as N_sPV·k_off, in which N_sPV is the number of surface exposed KKETPV₁₄ molecules. The dissociation rate of a PDZ₁₄ molecule from a particle is defined in the same way. Further details of the Monte Carlo simulation are described in Materials and Methods. Then, we estimated the concentrations of different heterocomplex species over time using different initial concentrations of KKETPV₁₄ and PDZ₁₄ (SI Appendix, Fig. S6), with which A_x/A₄₈₈ was calculated (Fig. 2F). Using k_on = 0.034 min^−1⋅nM⁻¹ and k_off = 0.22 min⁻¹, our simulated A_x/A₄₈₈ curves were quite similar to measured curves (Fig. 2 D and F and SI Appendix, Fig. S5), which validated our simulation model.

Our simulation suggests that when initial KKETPV₁₄ and PDZ₁₄ concentrations are 10 nM or lower, only small-sized heterocomplexes are formed and more than half of KKETPV₁₄ and PDZ₁₄ remain in unbound state after 1 h (Fig. 2 F and G). On the other hand, when initial concentrations are 50 nM or higher, large-sized condensates are formed and only a small portion of KKETPV₁₄ and PDZ₁₄ remains unbound (Fig. 2 F and G). Together, both our experiments and simulation indicated that at 50 nM or higher, most KKETPV₁₄ and PDZ₁₄ are formed into large-sized condensates, which rapidly grow (Figs. 1 C and D and 2 E and G).

Quantification of Binding Affinity with and without Condensate Formation.

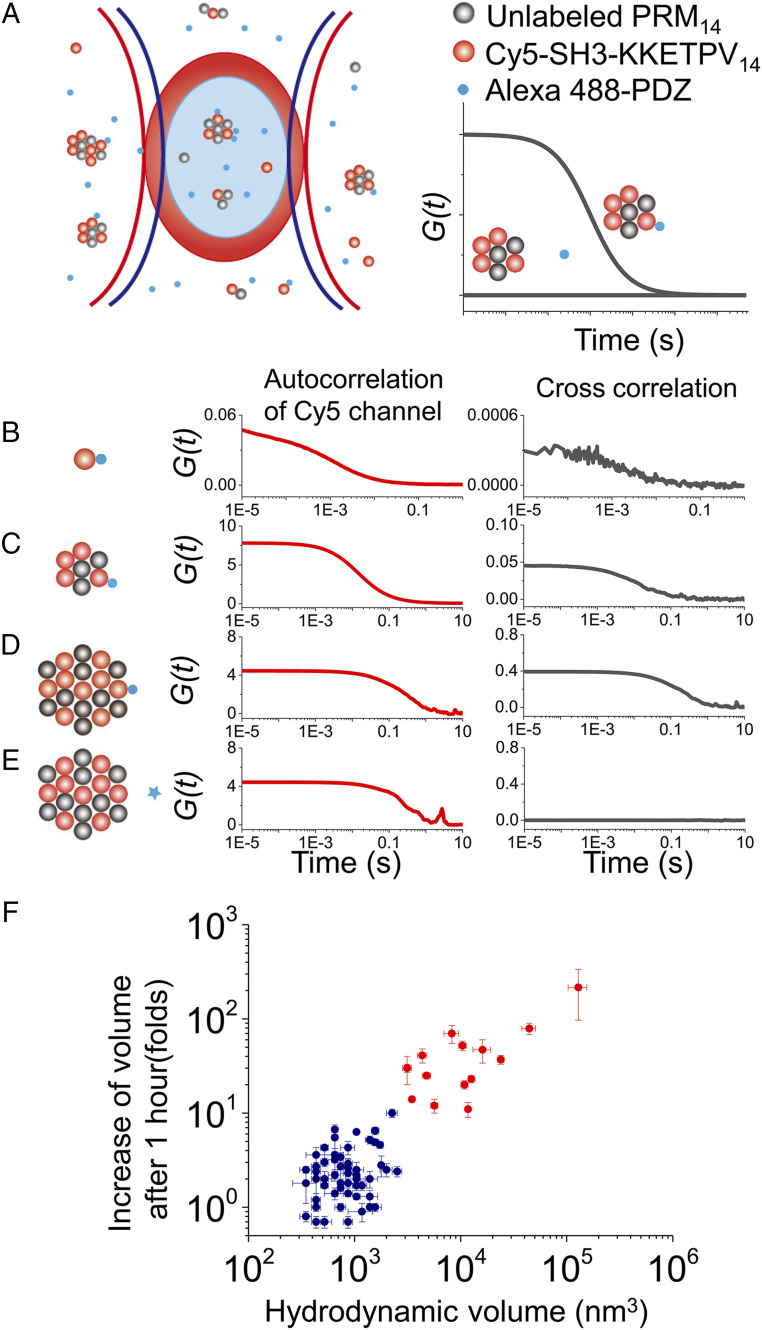
We generated two additional yeast ySmF variants, forming PRM₁₄ and SH3₁₄, respectively, to serve as another phase-separation model system (SI Appendix, Fig. S7). The short peptide KKETPV was introduced to the C terminus of SH3, which allowed phase-separated PRM₁₄-(SH3-KKETPV)₁₄ condensates to recruit PDZ monomer. With dcFCCS assay, we quantified the amount of Alexa 488 labeled PDZ monomer (Alexa 488-PDZ) bound with Cy5 labeled (SH3-KKETPV)₁₄, which was defined as the ratio of amplitudes A_x/A_Cy5 (Fig. 3A) (details in Materials and Methods). Firstly, the fraction of 200 nM Alexa 488-PDZ bound with 200 nM Cy5-(SH3-KKETPV)₁₄ was quantified as 0.7% ± 0.1% (Fig. 3B), from which we estimated the dissociation constant (K_d) between KKETPV and PDZ is 29 ± 4 μM in the absence of condensate. When 400 nM PRM₁₄ was included with 200 nM Cy5-(SH3-KKETPV)₁₄ to form nanoscale condensate (radius 52 ± 10 nm), 0.8 ± 0.2% of 200 nM Alexa 488-PDZ was bound with condensate (Fig. 3C). In addition, 7 ± 1% of 200 nM Alexa 488-PDZ was bound with large-sized condensate (radius 700 ± 200 nm) formed from 4 μM PRM₁₄ and 2 μM Cy5-(SH3-KKETPV)₁₄ (Fig. 3D). As a negative control, no cross-correlation (A_x = 0), indicating no significant interaction, was detected between 200 nM elongation factor G and condensate under the same experimental condition (Fig. 3E). Using results shown in Fig. 3 C and D, we estimated that K_d between KKETPV and PDZ are 25 ± 4 μM and 29 ± 4 μM in the presence of condensates of different sizes. Therefore, we concluded that binding affinity between KKETPV and PDZ is almost unaffected by the highly crowded environment of condensates and their sizes. In addition, the K_d between Alexa 488-KKETPV₁₄ and Cy5-PDZ₁₄ is ∼10 nM (Fig. 2D), which agrees with previous reports that multivalent interactions significantly strengthen binding affinity between macromolecules (40).

Fig. 3.

Quantification of client molecule recruitment and clustering analysis. (A) Scheme of dcFCCS assay. The presence of complexes containing both Alexa 488-PDZ (blue dots) and Cy5-(SH3-KKETPV)₁₄ (red dots) contributes to positive correlation in dcFCCS curves, whereas no interaction between Alexa 488 labeled and Cy5 labeled molecules leads to a flat dcFCCS curve showing no correlation. (B–E) Autocorrelation curves of Cy5 intensity (red) and dcFCCS curves between Alexa 488 and Cy5 intensities (black) under different conditions, which were 200 nM Cy5-(SH3-KKETPV)₁₄ without PRM₁₄ (B), 200 nM Cy5-(SH3-KKETPV)₁₄ with 400 nM PRM₁₄ (C), and 2 μM Cy5-(SH3-KKETPV)₁₄ with 4 μM PRM₁₄ (D and E). Two hundred nM Alexa 488-PDZ (B–D) or 200 nM Alexa 488 labeled elongation factor G (E, negative control) was used. (F) Clustering analysis using hydrodynamic volumes of heterocomplexes right after mixing and increasing of volumes after 1-h incubation.

One major function of phase-separated condensates is to enrich certain species and to accelerate their related chemical reaction rates (4). Using fluorescence signals of Alexa 488-PDZ within and outside of condensates, we quantified that PDZ monomer is enhanced by 34 ± 6-fold within condensates formed from 4 μM PRM₁₄ and 2 μM Cy5-(SH3-KKETPV)₁₄ (SI Appendix, Fig. S8). Under chemical equilibrium, enrichment of PDZ within condensates is determined by the binding affinity between KKETPV and PDZ (K_d) and the concentration of KKETPV within condensate. Our measurements showed that K_d is independent of phase separation and the size of condensate. In addition, as an important signature of the separated phase, the concentration of KKETPV within condensate is independent of the size of condensate. Together, our results indicate that PDZ is highly concentrated within condensates in a size-independent manner.

Discussion

Here, with the dcFCCS method, we are able to examine formation of free-diffusing phase-separated condensates from engineered ySmF variants over a broad range of concentration (1–500 nM). At 10 nM or lower concentrations, the majority of KKETPV₁₄ and PDZ₁₄ remained in the unbound state and only small heterocomplexes containing several 14-mer molecules were formed. On the other hand, close-to-micrometer-scale condensates were formed and visualized by confocal fluorescence microscopy at 500 nM or higher concentrations. Through our quantitative analysis, 50 nM is likely to be the critical concentration to form phase separation at the nanoscale, because 50 nM or higher concentrations are needed to generate rapid-growing nanoscale condensates (Figs. 1 C and D and 2 E and G). Our assignment of the critical concentration was further supported by a two-dimensional clustering analysis, which takes both the size and growth rate into account (details in SI Appendix). Using relaxation times of dcFCCS curves before and after 1-h incubation (SI Appendix, Table S1), hydrodynamic volumes of heterocomplexes right after mixing and increasing of their volumes after 1 h were calculated. Results obtained from 81 different combinations of concentrations were clustered into two groups (Fig. 3F). One group contained conditions when at least one of [KKETPV₁₄] and [PDZ₁₄] was below 50 nM, whereas the other group contained conditions when both [KKETPV₁₄] and [PDZ₁₄] were 50 nM or higher. Together, the critical concentration (∼50 nM) defined by our dcFCCS measurements is an order of magnitude lower than the detection limit of the commonly used confocal microscopy (SI Appendix, Fig. S1). As another proof-of-concept example, the critical concentration defined by dcFCCS to form phase-separated condensates from RNA containing GC-rich repeats is 3–4-fold lower than the detection limit of confocal microscopy (SI Appendix, Fig. S9).

Main biological functions of condensates include recruiting or sequestering molecules, regulating reaction specificity, and buffering molecular concentrations (4). Recruitment of client molecules is controlled in a switchlike fashion by the molecular composition of condensates, whose stoichiometry is highly sensitive to concentrations of scaffold molecules (40). Here, we demonstrated dcFCCS as a powerful tool to quantify the stoichiometry of scaffold molecules within each individual condensate particles, which indicates that change of stoichiometry in condensates is less sensitive to change of concentration in the dilute phase. In addition, dcFCCS enables us to quantify that binding affinity between PDZ domain and KKETPV peptide is not affected by the presence and size of condensates, which indicated that client molecule PDZ is highly concentrated in both nanoscale and close-to-micrometer-scale condensates in a size-independent manner.

We are aware that in highly dynamic cellular environments, the size of condensates should be an important aspect to regulate their functions, even when thermodynamic binding constants remain the same. For instant, we estimated that the number of PDZ molecules recruited into the PRM₁₄-(SH3-KKETPV)₁₄ condensates of 52- and 700-nm radii were about 2.4 and 5.9 × 10³ per condensate particle, respectively (Fig. 3 C and D). Clearly, large condensates serve as better buffering zones for both recruited client molecules and surrounding soluble molecules than small ones. On the other hand, it is easier for the small-sized condensates to assemble and disassemble and to exchange their own components with surrounding solution, which makes them more suitable for dynamic regulation to provide rapid response. Consistent with our speculation, transient small (∼100-nm) clusters of Mediator and Pol II in cells have been captured by superresolution microscopy with an average lifetime of ∼10 s, whereas large clusters of Mediator and Pol II are much more stable (>100 s) (13). Live cell imaging also revealed that the growth or shrinkage of Synphilin1 clusters directly correlates with their sizes (14). In addition, subdiffraction-sized clusters formed from transcription factors are discovered to active transcription through highly dynamic, rapid, and reversible interactions between transcription factors and Pol II (12), which underlines the importance to capture nanoscale condensates and clusters and to elucidate their physiological functions in detail.

In summary, our results demonstrated that phase-separated condensates are able to form at both nanoscale and microscale. Although our dcFCCS measurements were performed using a phase-separation model system constructed from purified proteins, FCS and dcFCCS methods are routinely used to examine individual living cells and their optimal concentrations are nanomolar to micromolar (41–43), which generally match the endogenous protein levels (44). Dynamic information of individual molecules, oligomers, and chromatin structures have all been captured by FCS and dcFCCS methods, which proves that dcFCCS is suitable for molecules and complexes of different sizes (41–43) in cells. Therefore, dcFCCS serves as a simple and useful tool to quantify size, growth rate, molecular composition, and recruitment ability of condensates both in solution and in living cells, which has great potential to reveal how condensates of different sizes play important roles in various cellular functions through their unique strategies.

Materials and Methods

Phase Separation Examined by dcFCCS.

dcFCCS measurements were performed on a home-built confocal microscope, based on a Zeiss AXIO Observer D1 fluorescence microscope with an oil-immersion objective (Zeiss, 100×, numerical aperture = 1.4), and solid-state 488-, 532-, and 640-nm excitation lasers (Coherent Inc. OBIS Smart Lasers). Powers of all lasers at the samples were ∼2.5 μW. The laser focus was 10 μm above the coverslip interface. The reproducibility and time-dependent stability of our instrument were confirmed (SI Appendix, Fig. S10). Fluorescence signals from the sample passed through a pinhole (diameter 50 μm) and were separated by a 50/50 beamsplitter (Thorlabs). Two identical dichroic mirrors (T635lpxr, Chroma) were placed on both paths to separate signals onto four avalanche photodiode (APD) detectors (Excelitas, SPCM-AQRH-14). Signals were further filtered by bandpass filters ET525/50m (for Alexa 488, Chroma) or ET585/65m (for Cy3, Chroma) and ET700/75m (for Cy5, Chroma) before detected by APDs. Raw data of photon arriving time was recorded for 9 min right after mixing samples and for another 9 min after 50-min incubation, with which anticorrelation and cross-correlation of fluorescence signals were calculated by a home-made MATLAB script. In our instrument, signals of each fluorescence detection channel (Alexa 488, Cy3 or Cy5) were separated by the 50/50 beamsplitter into two APDs, with which autocorrelation curves were calculated to avoid after-pulses. To calculate cross-correlation curves, signals of the same fluorescence channel divided into two APDs were added together. For each experimental conditions, three repeats were performed.

For ySmF variants, dcFCCS experiments were performed with 488- and 640-nm lasers at 25 °C in 50 mM Tris⋅HCl pH 7.5, 150 mM NaCl, and 1 mM TCEP. For RNAs, dcFCCS experiments were performed with 532- and 640-nm excitation lasers at 25 °C in 10 mM Tris⋅HCl pH 7.0, 10 mM MgCl₂, 25 mM NaCl, or 50 mM NaCl. Coverslips were passivated with polyethylene glycol as previously described (35, 36).

dcFCCS Data Analysis.

Autocorrelation traces of Alexa 488 and Cy5 detection channels were fitted using the following equation that modeled both diffusion and triplet processes of the fluorophores and labeled proteins:

$$\begin{array}{c}G\left(\tau \right)=A\left[1+\frac{T}{1-T}\exp \left(-\frac{\tau }{{\tau }_T}\right)\right]{\left(1+\frac{\tau }{{\tau }_D}\right)}^{-1}{\left(1+\frac{\tau }{S^2{\tau }_D}\right)}^{-1/2}\end{array},$$ [1]

in which $A$ is the amplitude of the autocorrelation function, T is the triplet-state fraction, ${\tau }_T$ is the triplet relaxation time of the dye, ${\tau }_D$ is the diffusion time of the labeled proteins, and S = ω_z/ω_xy is the ratio of the polar and equatorial radii in the confocal volume. A₄₈₈ and A₆₄₀ were defined as amplitude of the autocorrelation function of Alexa 488 channel under 488-nm laser excitation and Cy5 channel under 640-nm laser excitation, respectively. Alexa 488, whose hydrodynamic radiuses is 0.58 nm (45), was used as the standard sample to calibrate confocal detection volume following previous procedure (46).

The cross-correlation curves were fitted using

$$\begin{array}{c}{G}_x\left(\tau \right)=A_x{\left(1+\frac{\tau }{{\tau }_D}\right)}^{-1}{\left(1+\frac{\tau }{S^2{\tau }_D}\right)}^{-1/2}\end{array}.$$ [2]

In theory, the amplitude of the cross-correlation function A_x is given by

$$\begin{array}{c}{A}_{\text{x}}=\frac{N_{\text{X}}}{N_{488}{N}_{640}}\end{array},$$ [3]

in which N_x, N₄₈₈, and N₆₄₀ are the average number of doubly labeled molecules, Alexa 488 labeled molecules, and Cy5 labeled molecules within the confocal volume, respectively. Because A₄₈₈ = 1/N₄₈₈, A₆₄₀ = 1/N₆₄₀ and correlation factors need to be included to adjust the difference of detection volumes between 488-nm laser, 640-nm laser, and overlap between them. Therefore, the fraction of Cy5 labeled molecules that formed doubly labeled heterocomplexes was calculated by

$$N_x/N_{640}=A_x/\left(A_{488}·C{r}_{488}\right),$$ [4]

and the fraction of Alexa 488 labeled molecules that formed doubly labeled heterocomplexes was calculated by

$$N_x/N_{488}=A_x/\left(A_{640}·C{r}_{640}\right).$$ [5]

According to published procedure (37), correlation factors Cr₄₈₈ and Cr₆₄₀ were determined to be 0.58 ± 0.05 and 0.76 ± 0.02, respectively, using a doubly labeled dsDNA containing both Alexa 488 and Cy5.

Burst Analysis and Estimation of Stoichiometry.

Raw photon arrival-time data were binned into 1-ms bins to generate fluorescence trajectories. Only bursts exceeding the threshold, defined as three SDs above the mean, were selected to calculate intensity ratio between Alexa 488 and Cy5 detection channel (I_{Alexa 488}/I_Cy5). Varying the threshold from 2 SDs above the mean to 4 SDs above the mean had only minor effects on the intensity ratio I_{Alexa 488}/I_Cy5. The molecular brightness of Alexa 488-KKETPV₁₄ (16.8 ± 0.4 counts per ms) and Cy5-PDZ₁₄ (9.2 ± 0.6 counts per ms), estimated from autocorrelation traces of Alexa 488-KKETPV₁₄ and Cy5-PDZ₁₄, respectively, was used to calculate stoichiometry of Alexa 488-KKETPV₁₄ and Cy5-PDZ₁₄ from I_{Alexa 488}/I_Cy5.

See SI Appendix for further details of sample preparation, conventional fluorescence microscopy, negative-stain electron microscopy, Monte Carlo simulation, and clustering analysis.

Data and Materials Availability.

All study data are included in the article and SI Appendix.