Automated Cross-Sectional Measurement Method of Intracranial Dural Venous Sinuses

Abstract

BACKGROUND AND PURPOSE:

MRV is an important blood vessel imaging and diagnostic tool for the evaluation of stenosis, occlusions, or aneurysms. However, an accurate image-processing tool for vessel comparison is unavailable. The purpose of this study was to develop and test an automated technique for vessel cross-sectional analysis.

MATERIALS AND METHODS:

An algorithm for vessel cross-sectional analysis was developed that included 7 main steps: 1) image registration, 2) masking, 3) segmentation, 4) skeletonization, 5) cross-sectional planes, 6) clustering, and 7) cross-sectional analysis. Phantom models were used to validate the technique. The method was also tested on a control subject and a patient with idiopathic intracranial hypertension (4 large sinuses tested: right and left transverse sinuses, superior sagittal sinus, and straight sinus). The cross-sectional area and shape measurements were evaluated before and after lumbar puncture in patients with idiopathic intracranial hypertension.

RESULTS:

The vessel-analysis algorithm had a high degree of stability with <3% of cross-sections manually corrected. All investigated principal cranial blood sinuses had a significant cross-sectional area increase after lumbar puncture (P ≤ .05). The average triangularity of the transverse sinuses was increased, and the mean circularity of the sinuses was decreased by 6% ± 12% after lumbar puncture. Comparison of phantom and real data showed that all computed errors were <1 voxel unit, which confirmed that the method provided a very accurate solution.

CONCLUSIONS:

In this article, we present a novel automated imaging method for cross-sectional vessels analysis. The method can provide an efficient quantitative detection of abnormalities in the dural sinuses.

Idiopathic intracranial hypertension (IIH) (also known as “pseudotumor cerebri”) is a disorder of increased intracranial pressure without clinical, laboratory, or radiologic evidence of an intracranial space-occupying lesion or cerebral sinus vein thrombosis, predominantly affecting women of childbearing age with obesity. The annual incidence of IIH in the general population is estimated between 1 and 2 per 100,000. However, the incidence has risen to 3.5–12 per 100,000 in women 20–44 years of age, and among women with obesity in this age group, it has climbed to 7.9–21 per 100,000.^25,30

To rule out occlusion or stenosis in patients with IIH, performing CTV and cerebral MRV is now accepted. However, drawbacks to CTV include concerns about radiation exposure, potential for iodine contrast material allergy, and issues related to the use of contrast in the setting of poor renal function. In some settings, MRV is preferable to CTV because of these concerns.²⁷ Doppler sonography is not considered a standard for the current study.²⁶

Cross-sectional changes in the cerebral venous system in patients with IIH have received increased attention in recent years. In >90% patients with IIH, there is stenosis in the transverse dural sinuses,^1–5 and after medical treatment and normalization of the intracranial pressure in patients with IIH, there is no change in venous diameter.⁶ However, another study presented cases of IIH in which an increase in venous diameter occurred after lumbar puncture (LP); in 1 patient, there was a decrease in venous diameter after stopping a CSF leak with a blood patch.⁷ In agreement with a previous study, another study showed narrowing of the transverse sinuses on MRV in all patients with IIH and an increased diameter of the cerebral sinuses after LP.^1,8 This change was different for all patients and was more prominent at the right than left transverse sinus. All venous sinuses had an increased diameter in response to LP, and this change was not confined to the transverse sinuses.⁸ In some patients with IIH, all dural sinuses appeared narrowed over long distances; this appearance gave the impression that these sinuses were compressed.^9–11 After we normalized against intracranial hypertension, the sinus volumes increased to normal values. However, there is controversy about the observation of the dynamic behavior of the sinus diameter.^12–15

A novel “venous distension sign” for the diagnosis of intracranial hypotension³⁰ has recently been introduced. The cross-sectional contour of the transverse sinus normally has a triangular inferior border. In cases of intracranial hypotension, the inferior border acquires a distended appearance with a convex bulging. However, the estimation of the venous distension sign was performed on the basis of whether the latter was present or absent for each image set. In the present study, we propose using circularity and triangular-shape characteristics to quantify contour changes of the dural sinuses.

MRV is an important tool for blood vessel imaging and for the evaluation of stenosis (abnormal narrowing), occlusion, or aneurysms. Yet no accurate image-processing tool for quantitative measurement of the size and shape of the sinuses has so far been developed, to our knowledge. In previous reports, the sinuses were only estimated by using a descriptive, subjective method (ie, according to the impression of the radiologist). The main purpose of this study was to develop a technique for the accurate point-to-point assessment of cross-sectional alterations in cerebral sinuses before and after LP in patients with IIH. The method was validated by using computer models. A single control CT and MRV data were used for validating the technique. The method was implemented in 4 patients with IIH who were internally controlled against themselves (before and after LP).

Materials and Methods

Subjects

Images of 4 female patients with IIH were retrospectively included in the study. The mean age of the examinees was 33.7 ± 10 years; mean body mass index, 27.9 ± 7.6. Patients with IIH were diagnosed according to modified Dandy criteria.^7,28 Each participant underwent 2 MR imaging examinations: One was performed before the LP and another after. The timeframe for obtaining the second MR imaging was not to exceed 48 hours post-LP. Opening pressure on LP was >250 mm H₂O in all patients. The LP was performed by a neurologist with the patient under local anesthesia with lidocaine 1%, with the patient lying in the lateral decubitus position. Opening pressure was measured, and 10 mL of CSF was withdrawn. This study was conducted according to a protocol approved by the local ethics committee at Soroka University Medical Center, Diagnostic Imaging Department (Beer-Sheva, Israel).

Image Acquisition

A patient with IIH, a control subject, and 2 phantoms each had MR imaging performed with a 1.5T scanner (Intera; Philips Healthcare, Best, the Netherlands) by using a 6-channel head coil for sensitivity encoding. A contrast-enhanced 3D spoiled gradient-echo sequence (T1WI) was used for imaging. The sequence parameters were the following: TR, 5.7 ms; TE, 1.75 ms; section width, 2 mm (reconstructed to 1 mm); in-plane resolution, 0.74 × 1.05 mm; flip angle, 40°; sensitivity encoding reduction factor, 2.5; and scan time, 40.8 seconds. In addition, a single control subject and phantoms were used for validating the technique. The former had both an MR imaging and a contrast-enhanced head CT scan (in-plane resolution, 0.556 mm; section thickness, 1 mm; iopromide, Ultravist [Bayer HealthCare, Berlin, Germany], 300 mg/mL with a dose of 2 mL per kg; scan delay, 40 seconds after injector application).

The algorithm for vessel cross-sectional analysis included 7 main steps: 1) image registration, 2) masking, 3) segmentation, 4) skeletonization, 5) cross-sectional planes, 6) clustering, and 7) cross-section analysis.

The implementation of the algorithm used Matlab (MathWorks, Natick, Massachusetts).

Image Processing

Image Registration (Step 1).

The MRV images before and after LP from patients with IIH were used. The images were mapped to a standard brain²⁹ to avoid artifacts due to head movements and to allow accurate pixel-based comparison among scans and even among patients for group study analysis. The registration method applied mutual information (that measured the amount of information that one variable contained about the other) to measure statistical dependence between image intensities of corresponding voxels in both images (SPM12; http://www.fil.ion.ucl.ac.uk/spm/software/spm12; Matlab). Mutual information was assumed maximal when the images were geometrically aligned. Image transformation was restricted to rigid-body transformation only.

Masking (Step 2).

A masking procedure was used to extract sinuses from the brain volume and separate them from other tissues of similar intensity. The brain mask was created by using a segmentation routine (SPM12). Three objects were created because of this procedure: gray matter, white matter, and CSF. These objects were combined. Morphologic closing, simply defined as dilation followed by erosion with the same structuring element for both operations, was applied to create a solid brain mask by removing all remaining gaps and inner spaces of the combined object.

Segmentation (Step 3).

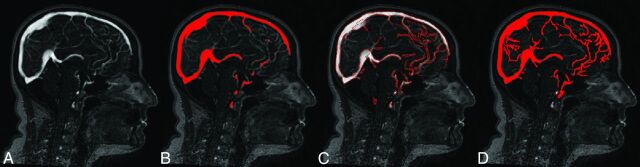
This step included segmentation of sinuses in the brain mask volume of interest. The integrated segmentation procedure developed in this study combined global and local image information (Fig 1).

Fig 1.

Integrated segmentation procedure. A, Gray-scale image. B, Global threshold region (red). Only thick sinuses could be detected by using this method. C, Edge detection. D, Region-growing segmentation. The method allowed the detection of most of the thin, low-intensity sinuses.

Before applying the segmentation method, noise was reduced by filtering the data with a 3D Gaussian smoothing function with support and σ that approximated the size of background texture (support = 1 voxel; σ = 2 voxels).

The set of edges, detected with the Canny method¹⁷ combined with the globally segmented region,¹⁶ was used as an initial seed object. Starting with the seed object, the final vessel region was iteratively grown by appending to each seed the neighboring voxels that had intensities similar to the seed. To this end, the original gray-scale intensities of the seed object were dilated in 3D with a sphere-shaped structuring element that had a small radius (2 voxels). The gray-scale dilation was used to compute the local maximum-intensity values in every structuring element for the 26-neighborhood. The Gaussian-weighted values of dilated intensities served as local thresholds. Voxels connected to the seed object with gray values higher than the local threshold values were appended to the seed object. The described procedure was run iteratively until no more voxels could be added. This region-growing part of the algorithm was adapted, in part, from a method previously described.^18,19

The edge inclusion criteria were developed to reduce the risk of thickening the sinuses. Only strong edges were considered true edges and included in the final vessel object (Fig 2).

Fig 2.

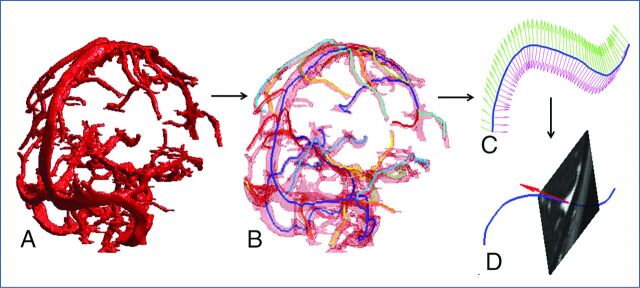
Segmentation and skeletonization. A, Segmented sinus object. B, Superimposition of skeleton branches (shown in different colors) with the segmented vessel object (transparent red). C, Typical definition of the cross-sectional planes for a single skeleton branch (blue line). D, Typical extraction of a cross-sectional plane from image volume.

Skeletonization (Step 4).

The 3D MultiStencils Fast Marching Method was applied to extract a central path of the segmented vessel object (Fig 2).^20–22 The method was used to calculate the shortest distance from a list of points to all other voxels in the image by solving the Eikonal equation. This method gave more accurate distances by using second-order derivatives and cross-neighbors. The skeletonization procedure was implemented in custom-built code (Matlab) and C code. The number of skeleton branches was determined automatically from the maximum diameter of the vessel object. The termination condition for the new branched search occurred when the length of the new branch was smaller than the diameter of the largest vessel.

Cross-Sectional Planes (Step 5).

Each skeleton branch was smoothed by using a cubic smoothing spline to provide continuous derivatives at every point. The moving reference frame of the orthonormal vectors of Serret²³ and Frenet^23,24 was used to describe a branch curve γ(t):

• T(t) = γ′(t)/‖γ′(t)‖,

where T(t) was the unit tangent vector at every point t.

The unit normal vector to the cross-sectional plane took the form

• N(t) = T(t).

The cross-sectional plane at every skeleton point t (x_t, y_t, z_t) was determined by the point itself and N(t) at that point (Fig 2). To minimize computational time, we extracted cross-sections from small portions of the segmented vessel object by application of a disc-shaped mask at each point t. To define the size of the disc-shaped mask, we calculated the Euclidean distance transform map of the vessel object. To this end, each skeleton voxel was assigned a number that was the distance between the voxel itself and the nearest background (zero) voxel. The diameter of the disc-shaped mask was estimated as 4×the distance transform value at point t.

Clustering (Step 6).

Some vessel cross-sections may have included an intersection with other sinuses; therefore, to separate a single-vessel cross-section from the other sinuses, we developed a special clustering procedure. Component labeling was applied to select the connected vessel object with the centroid at point t. This operation allowed detection of an initial vessel shape by removing all disconnected elements. The attached components were separated from the initial vessel object (Fig 3).

Fig 3.

Clustering procedure for removal of intersecting or touching sinuses (yellow arrow points to adjacent components). A, A single cross-sectional plane extracted from the image volume. The vessel object had an attached component. B, An overlay of the initial segmented vessel object onto a gray-scaled image at the extracted cross-sectional plane. C, The Euclidean distance transform map. D, The watershed transform. E, The final result of the separation procedure (red line) overlaid onto the original data.

This procedure included several substeps. The Euclidean distance transform map of the vessel object was calculated (Fig 3). To create catchment basins for the further watershed transform, we calculated differences between the maximal distance transform value and the distance transform map. All nonobject pixels were set to zero. The watershed transform was performed (Fig 3), and the watershed region containing the central point t was identified. An overlay of the outer boundary of the vessel object onto a gray-scaled plane was used for visual inspection of separation.

Cross-Section Analysis (Step 7).

The boundary points of vessel cross-sections detected in the previous step were used to derive geometric measurements, including circumference, area, circularity, and triangularity. The circumference (L_t) and area (A_t) were directly calculated as polygon length and area. Circularity, which was a parameter of shape compactness, was defined as

• Circularity = 4 πA_t / L_t².

Triangularity of the vessel cross-section was estimated as

• Triangularity = A_{t_fit} / A_t,

where A_{t_fit} was the area of the largest triangle inscribed in the polygon.

Validation of the Method

Validation experiments were performed to evaluate the performance of the presented algorithm. The method was validated with 2 phantom silicon catheters filled with the contract agent Gd-DTPA and 1 digitally created phantom. The silicon catheters had inner diameters of 1.5 and 3 mm and were scanned at an isometric resolution of 0.5 mm.

The diameters of all phantoms were digitally expanded by 5 mm each. The expansion of the catheters was done by morphologic dilation by using a spheric structural element (radius = 2.5 mm). The automatic procedure described (steps 3–7) was applied to reconstruct phantom cross-sections with altered diameters.

To test the accuracy, potential bias, and reproducibility of the calculation routine, we compared the actual phantom diameters with the computed ones.

Method Application

The sinus analysis algorithm was initially tested on 4 patients. Only 4 large sinuses were chosen for the analysis (right and left transverse sinuses, superior sagittal sinus, and straight sinus). The images before and after LP were aligned with standard brain, and the skeletonization procedure was applied only to the segmented vessel object after LP. To minimize computational time, we performed the cross-sectional calculations at every other skeleton point of the sinuses selected for analysis (step distance, 2 mm between skeleton points).

Statistical Methods

The comparison of the cross-sectional area, triangularity, and circularity between before and after LP was performed with a t test. P < .05 was considered significant.

Results

The sinus analysis algorithm showed a high degree of stability with <3% of cross-sections manually corrected. The automated algorithm was completed in <10 minutes, including all steps of the cross-sectional analysis in which 350 cross-sections were analyzed for each patient.

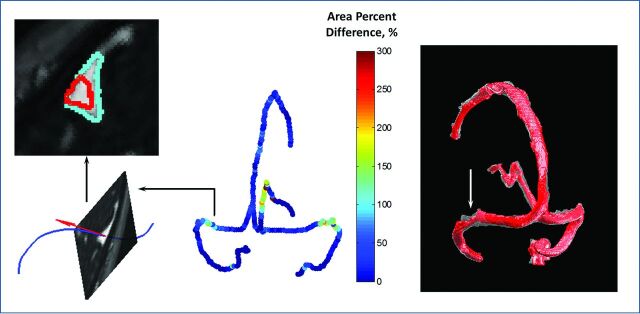
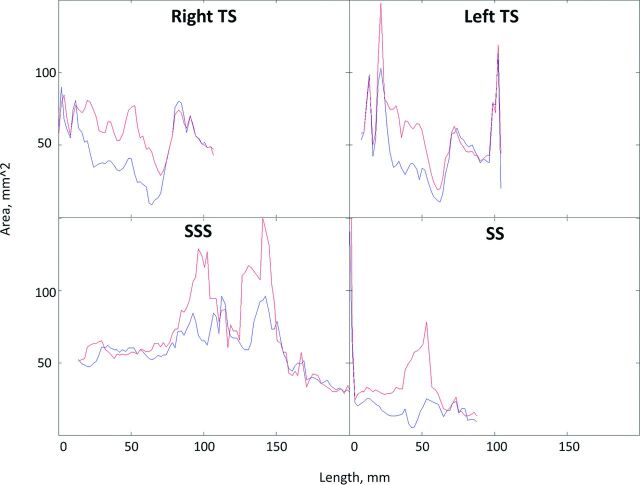
Distribution of the percentage difference before and after LP (Fig 4) showed that the patient with IIH had bilateral narrowing of the lateral part of the transverse sinus, with a more prominent right-than-left transverse sinus. All investigated principal cranial blood sinuses had a significant cross-sectional area increase after LP (P ≤ .05) (Table 1). Typical behavior of the cross-sectional area measured along blood sinuses showed narrowing regions in all 4 investigated sinuses before LP, which were expanded after LP (Fig 5).

Fig 4.

Changes in cross-sectional areas between images before and after LP in IIH. Left: Typical shape-changed areas for a single cross-section (red line, before LP; cyan line, after LP). Middle: Each skeleton point was assigned with a value of percentage difference of cross-sectional areas before and after LP. Right: Superimposition of before (red, nontransparent) and after (transparent) LP vessel objects reconstructed for the 4 main sinuses (right and left transverse sinuses, superior sagittal sinus, and straight sinus). No cross-sectional data analysis was performed at vessel intersections (shown as gaps).

Table 1:

Cross-sectional area measurements in the principal cerebral sinuses^a

Sinus	Cross-Sectional Area (mm2)
	Before LP		After LP
Right transverse	40 ± 21b	(4–76)	52 ± 22	(6–79)
Left transverse	45 ± 20b	(7.5–78)	52 ± 23	(8–78)
Superior sagittal	52 ± 21b	(17–88)	54 ± 21	(17–88)
Straight	23 ± 13b	(2–45)	30 ± 16	(4–48)

^aN = 4 patients. Data are reported as mean (range).

^bSignificant difference (P ≤ .05) between measurements before and after LP.

Fig 5.

Typical cross-sectional area plot along 4 principal cranial blood sinuses before (blue) and after (red) LP.

As an application of the method, statistical distribution of the sinus cross-sectional circularity and triangularity was tested; the shape of the sinuses became slightly more triangular after LP. The mean triangularity of the transverse sinuses was increased, and the mean circularity of the sinuses was decreased by 6% ± 12% after LP (Table 2).

Table 2:

Cross-sectional shape-change measurements in the principal cerebral sinuses^a

Sinus	Cross-Sectional Shape Measurement (mm2)
	Before LP		After LP
	Circularity	Triangularity	Circularity	Triangularity
Right transverse	72 ± 11	61 ± 9	66 ± 13	64 ± 11
Left transverse	75 ± 11b	59 ± 8	71 ± 12	62 ± 10
Superior sagittal	77 ± 10	60 ± 8	77 ± 12	59 ± 8
Straight	84 ± 16b	60 ± 6	78 ± 17	62 ± 9

^aN = 4 patients. Data are reported as means.

^bSignificant differences (P ≤ .05) between measurements before and after LP.

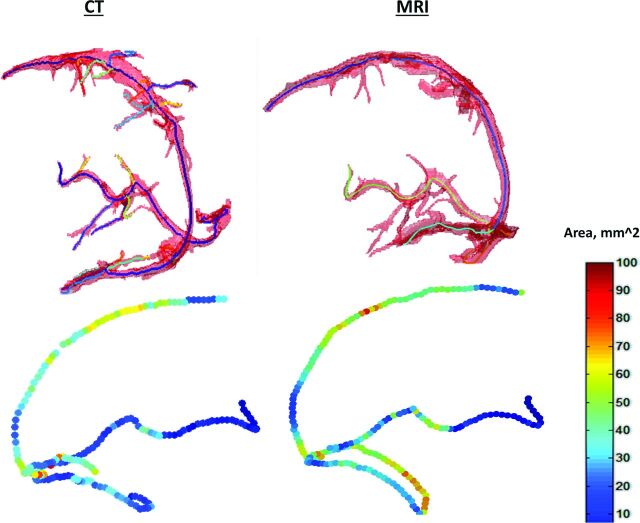
In addition, cross-sectional vessel analysis was performed for CT and MR imaging data of a control patient (Fig 6). The mean percentage difference of the calculated areas along 4 large sinuses was 12% ± 14%.

Fig 6.

Cross-sectional vessel analysis for both CT and MR imaging data of a control patient. Top: Segmented sinus object with an overlaid central line. Bottom: Calculated cross-sectional areas along central lines of the sinuses. Right: MR imaging data. Left: CT data.

To evaluate the accuracy of the algorithm, we compared the diameters calculated from the phantom images and real ones. There were >100 cross-sections calculated along each phantom skeleton curve. All computed errors were <1 voxel unit, which showed that this method provided a very accurate solution (Table 3). In addition, the behavior of the algorithm was tested by altering the size of the phantoms. For this purpose, the phantoms were digitally expanded by morphologic dilation with a spheric structural element. The relative diameter changes were calculated at each cross-section across the phantom skeletons. To various degrees, all errors in measurement were dependent on the phantom diameter. Phantoms with wider diameters were associated with smaller measurement errors. This was reasonable because the segmentation and calculation errors depended on image resolution and object size.

Table 3:

Average error, SD, and maximum error for phantom data used to validate the methods^a

Phantom Catheter	ID (mm)	Diameter Measurement		Relative Diameter Change after Digital Expansion		Image Resolution (mm)
		Mean (mm)	Maximum Error (mm)	Mean (mm)	Maximum Error (mm)
1.5-mm catheter	1.5	0.2 ± 0.3	0.46	0.1 ± 0.2	0.31	0.5
3.0-mm catheter	3	0.06 ± 0.2	0.23	0.04 ± 0.08	0.16	0.5

Note:—ID indicates inner diameter of catheter.

^aData are reported as mean or value.

Discussion

The principal aim of this study was to develop an automated method for the point-to-point cross-sectional analysis and comparison of blood sinuses. The accuracy of the sinus segmentation was determined by visual assessment. For this purpose, an overlay of a segmented image onto the gray-scale image was examined for each section. The advantage of the proposed hybrid segmentation method is that it combined global and local image statistical information. The global segmentation method made use of global optimality criteria and might produce significant results but typically might have poor localization of the regional boundaries. This outcome occurred because the criteria used were based on statistics obtained from all pixels in the entire image region and did not reflect local characteristics. In contrast, the local region-growing method offered accurate boundary localization but usually did not have sufficient global information.

The goal of the proposed integrated segmentation method was to combine global and regional edge information to enable the use of both image-wide statistics and local edge responses. The results of this method were segmented regions with accurate boundary localizations at places where the edge-detection operators produced reasonably strong responses.

This proposed segmentation technique helped create connected and homogeneous segmented sinus objects.

Precise detection of the centerline of the vessel object (skeleton) is important for the accurate detection of cross-sectional planes across the vessel objects. The skeletonization method used in this study computed subvoxel precise skeletons by using a fast-marching method. The very robust, fully automatic technique did not depend on the complexity of the skeleton structure (number and curvature of branches) and was not limited to tubular structures with roughly circular cross-sections.

The present automated algorithm may run without user intervention. Therefore, a special 2-step clustering technique was developed for rendering the vessel cross-sectional circumference. The technique was tested across all analyzed cross-sections by visual inspection of the automatically detected clusters overlaid onto vessel cross-sectional planes. Qualitatively, visual inspection showed a high capability for accurate identification of vessel circumference. Furthermore, the method was automatic and did not require fine-tuning of the initially determined input parameters such as filters, global thresholds, and morphologic distances for each sample or patient in the study. These input parameters may vary with different scan protocols and may be affected by scan resolution. Thus, preliminary adjustment of the input parameters may be necessary before applying the procedure to a study.

As an additional input option during the skeletonization step, the user is asked to select a specific sinus (skeleton branches) for further analysis. There are several methods of vessel selection, including automatic (vessel length, maximal diameter, or the entire skeleton) and manual selection. In addition, the user can define the calculation step or distance value between the 2 next skeleton points where the cross-sectional data will be calculated.

All 4 sinuses increased their diameter in response to LP, not only the transverse sinuses. In agreement with a previous report,⁸ this finding suggests that intracranial pressure and volume changes influence all sinuses.

The recently discovered venous distension sign phenomenon was not yet given for quantification.²⁷ The recognition of the venous distension sign was somewhat subjective on the basis of reader interpretation and was categorized as absent or present. The proposed shape quantification circularity and triangularity parameters can provide a quantitative measure of the phenomena. In addition, the venous distension sign can also be measured by estimation of whether the shape is more concave or convex. In agreement with a previous review,³⁰ the shape of the sinuses tends to become slightly more triangular (or less circular) after LP. Potentially, the technique can be applied for evaluation of normal cross-sectional contour variation of the normal dural sinuses.

Cross-sectional area plots before and after LP demonstrate changes along the vessels. They can be helpful in revealing the most prominent cross-sectional change regions following LP. The presented method can be applied to characterize the sinuses of a healthy population with normal MR imaging findings and create normograms of them. Therefore, comparison of the IIH sinus characteristics with the norm can be critical in establishing pathologic conditions with changes in the intracranial pressure.

We have developed the special clustering procedure for separation of a single-vessel cross-section from the other sinuses. However, there still could be some complicit intersections defined. This definition may result in some sharp peaks on cross-sectional area plots, but one can remove the peaks by smoothing them out.

The limitation of the presented method is related to the small number of patients enrolled in the study. Therefore, a larger scale study is warranted to validate our findings.

Conclusions

A quantitative method to evaluate the size of the dural sinuses of the brain has not been described yet, and estimation of change in the size of the sinuses—whether the sinus is narrow or wide—is decided subjectively according to the impression of the reader in a descriptive method. The method presented and tested here is fast and accurate and can be used in cross-sectional vessel analysis in different vascular systems. Implementation of the technique can provide new insight on the mechanisms underlying the development of IIH.

ABBREVIATIONS:

IIH

idiopathic intracranial hypertension

LP

lumbar puncture