A new statistical approach to model the counts of novel coronavirus cases

Abstract

This study proposes new statistical tools to analyze the counts of the daily coronavirus cases and deaths. Since the daily new deaths exhibit highly over-dispersion, we introduce a new two-parameter discrete distribution, called discrete generalized Lindley, which enables us to model all kinds of dispersion such as under-, equi-, and over-dispersion. Additionally, we introduce a new count regression model based on the proposed distribution to investigate the effects of the important risk factors on the counts of deaths for OECD countries. Three data sets are analyzed with proposed models and competitive models. Empirical findings show that air pollution, the proportion of obesity, and smokers in a population do not affect the counts of deaths for OECD countries. The interesting empirical result is that the countries with having higher alcohol consumption have lower counts of deaths.

Introduction

The first case of the COVID-19 (coronavirus disease 2019) was reported in Wuhan, China, in December 2019. The World Health Organization (WHO) has declared that the COVID-19 is a pandemic on the date of March 11, 2020. After this date, all countries have increased their measures to decrease the spread rate of the COVID-19 by closing schools, shopping centers, airlines, and also their borders. As of date May 17, 2020, the counts of COVID-19 cases are over 4.72 million and the counts of deaths are 313, 221. This number may be of little importance to anyone, but almost half the population of Luxembourg.

The researchers and academicians have spent their time finding medical solutions such as drugs and vaccines to return our normal life. Besides these medical researchers, the researchers have also focused on the mathematical and statistical modeling of the COVID-19 outbreak. For instance, [1] predicted the needed hospital beds and personnel for Italy under the exponential trend. [2] used autoregressive time-series models based on the two-piece scale mixture normal distributions to forecast the recovered and confirmed COVID-19 cases. [3] predicted the daily new COVID-19 cases in China by using the mathematical model, called SIR. As in [3, 4] also used the SIR model to predict COVID-19 cases. Caccavo [5] introduced the SIRD compartmental model to predict COVID-19 cases in China and Italy. Ayyoubzadeh et al. [6] predicted COVID-19 cases in Iran by using long short-term memory (LSTM) which is a deep-learning method.

This study aims to model the daily new cases and deaths of the COVID-19 employing a new statistical tool. To achieve this aim, we introduce a new flexible two-parameter discrete model, called as discrete analogous of the generalized Lindley, shortly DsGLi, distribution. The generalized Lindley distribution was introduced by Nedjar [7] and modified by Messaadia [8]. We introduce the DsGLi distribution by applying the survival discretization method of [9]. The question may come to mind of anyone: Why do we need this distribution? In primary data analysis, we have realized that most of the existing probability distributions do not provide acceptable results for modeling the COVID-19 cases. The reason is that the counts of deaths or daily new cases exhibit excessive over-dispersion (see Sect. 2 for the definition of the over-dispersion). At this point, we see the advantage of DsGLi distribution over other distributions, because the proposed distribution, DsGLi, provides a new opportunity to model all kinds of dispersed count data sets. Some important properties of the DsGLi distribution can be summarized as follows: (1) It has closed-form expressions for its statistical properties, (2) it has increasing hazard rate function (hrf), and (3) it can be used to model both skewed and leptokurtic count data sets. Additionally, a new count regression model is defined based on the DsGLi distribution to analyze the effects of explanatory variables such as smoking, obesity, air pollution on the daily cases, and deaths of the COVID-19 outbreak.

The remaining parts of the presented study are organized as follows: Sect. 2 deals with the statistical properties of the DsGLi distribution. In Sect. 3, we discuss the parameter estimation process of the DsGLi distributions with maximum likelihood estimation method, and the performance of the estimation method is investigated by a simulation study for its finite sample size behavior. In Sect. 4, we introduce the DsGLi regression model and clarify its parameter estimation process and residual analysis. Section 5 contains three applications to COVID-19 data sets. The empirical results obtained in Sect. 5 are discussed in Sect. 6 in detail. Sect. 7 contains some important remarks about the presented study.

Discrete analogue of GLi distribution

[9] introduced a new method to generate a new discrete distribution based on the survival function of any continuous probability distribution. This method is called a survival discretization method. Let the continuous random variable X has the survival function (sf) $S(x;\xi )=Pr(X>x)$, then the probability mass function (pmf), corresponding to $S(x;\xi )=Pr(X>x)$, is

$$\begin{array}{c}\hfill Pr(X=x)=S(x;\xi )-S(x+1;\xi );x=0,1,2,3,\dots \end{array}$$ 1

This approach has been received considerable attention over the recent years, for instance, [10–21] and references cited therein. Note that there are some different discretization methods in order to construct new discrete distribution for modeling count data. Some of them are presented in [22] and [23].

Nedjar [7] proposed a new probability distribution for modeling data, in the so-called gamma Lindley (GLi) distribution. It is a mixture of a gamma($2,\theta$) and Lindley($\alpha$) distribution. The pdf of GLi distribution can be expressed as

$$\begin{array}{cc}& f(x;\alpha ,\theta )=\frac{{\theta }^2}{\alpha (1+\theta )}\left(\left[\theta ,\alpha ,+,\alpha ,-,\theta \right],x,+,1\right)e^{-\theta x};\hfill \\ \hfill & x>0,\alpha >0,\theta >0.\hfill \end{array}$$ 2

Unfortunately, Eq. (2) is not a proper PDF, because it can be negative for some values of the parameters $\alpha >0$ and $\theta >0$. [8] modified the parameter space to be $\alpha \ge \frac{\theta }{1+\theta }$ and $\theta >0$, and consequently, the proper pdf of GLi model can be written as

$$\begin{array}{cc}& f(x;\alpha ,\theta )=\frac{{\theta }^2}{\alpha (1+\theta )}\hfill \\ \hfill & \left(\left[\theta ,\alpha ,+,\alpha ,-,\theta \right],x,+,1\right)e^{-\theta x};\hfill \\ \hfill & x>0,\alpha \ge \frac{\theta }{1+\theta },\theta >0.\hfill \end{array}$$ 3

The sf corresponding to Eq. (3) is

$$\begin{array}{cc}\hfill R(x;\alpha ,\theta )=& \frac{(\theta x+1)(\theta \alpha +\alpha -\theta )+\theta }{\alpha (1+\theta )}\hfill \\ \hfill & e^{-\theta x};x>0,\hfill \end{array}$$ 4

where $\alpha \ge \frac{\theta }{1+\theta }$ and $\theta >0$. Using the survival discretization method and sf of GLi distribution, we define the rf of the DsGLi given as follows:

$$\begin{array}{cc}\hfill S(x;\alpha ,\eta )=& \frac{(1-ln{\eta }^{x+1})(\alpha -\alpha ln\eta +ln\eta )-ln\eta }{\alpha (1-ln\eta )}\hfill \\ \hfill & {\eta }^{x+1};x\in {\mathbb{N}}_0,\hfill \end{array}$$ 5

where $\alpha \ge \frac{-ln\eta }{1-ln\eta }$, $0<\eta <1$, and ${\mathbb{N}}_0=\left\{0,,,1,,,2,,,3,,,\dots ,,,k\right\}$ for $0<k<\infty$. The pmf and cumulative distribution function (cdf) of the DsGLi distribution are given, respectively, by

$$\begin{array}{cc}& P_x(x;\alpha ,\eta )=\frac{{\eta }^x}{1-ln\eta }\hfill \\ \hfill & \left\{1,-,\eta ,-,ln,\eta ,\left[1,+,x,-,\eta ,(,x,+,2,)\right],+,(1-\frac{1}{\alpha }),{(ln\eta )}^2,\left[x,-,\eta ,(,x,+,1,)\right]\right\},\hfill \end{array}$$ 6

$$\begin{array}{cc}& F(x;\alpha ,\eta )=1\hfill \\ \hfill & -\frac{(1-ln{\eta }^{x+1})(\alpha -\alpha ln\eta +ln\eta )-ln\eta }{\alpha (1-ln\eta )}{\eta }^{x+1},\hfill \end{array}$$ 7

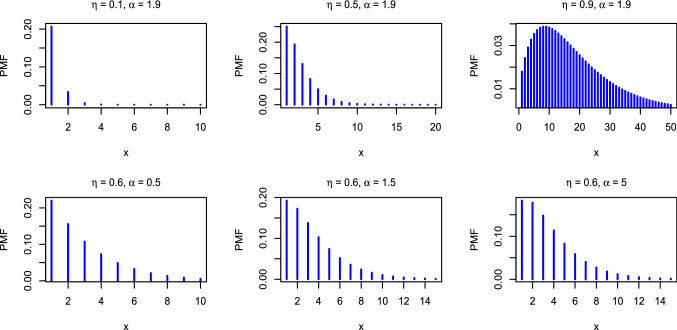
where $x\in {\mathbb{N}}_0$. The pmf in (6) is log-concave, where $\frac{P_x(x+1;\alpha ,\eta )}{P_x(x;\alpha ,\eta )}$ is a decreasing function in x for all values of the model parameters. Figure 1 shows the pmf plots for different values of the model parameters. From Fig. 1, the pmf of the DsGLi distribution is unimodal and right-skewed.

Fig. 1.

The pmf plots of the DsGLi distribution

The hrf of the DsGLi is expressed as

$$\begin{array}{cc}\hfill h(x;\alpha ,\eta )=& 1\hfill \\ \hfill & -\frac{\left[(1-ln{\eta }^{x+1}),(\alpha -\alpha ln\eta +ln\eta ),-,ln,\eta \right]\eta }{(1-ln{\eta }^x)(\alpha -\alpha ln\eta +ln\eta )-ln\eta };\hfill \\ \hfill & x\in {\mathbb{N}}_0,\hfill \end{array}$$ 8

where $h(x;\alpha ,\eta )=\frac{P_x(x;\alpha ,\eta )}{S(x-1;\alpha ,\eta )}$. Figure 2 shows the hrf plots of the DsGLi distribution. It is noted that the shape of the hrf is increasing. Further, the value of failure rate decreases with $\eta ⟶1$ for fixed value of $\alpha$.

Fig. 2.

The hrf plots of the DsGLi distribution

Properties

The statistical properties of the DsGLi distribution are obtained and reported in this section. Let X be random variable having a pmf in (6). The probability generating function (pgf) of X is

$$\begin{array}{cc}& G_X\left(z\right)=\sum _{x=0}^{\infty }{z}^x{G}_x(x;\alpha ,\eta )\hfill \\ \hfill & =\frac{-2\eta (\alpha -1)(z-1)ln\eta +\alpha \left({\eta }^2,z,-,2,\eta ,+,1\right)ln\eta -\alpha (\eta -1)(\eta z-1)}{\alpha (ln\eta -1){(\eta z-1)}^2}.\hfill \end{array}$$ 9

By replacing z by $e^z$ in (9), one can obtain the moment generating function (mgf) of X which is given by

$$\begin{array}{c}\hfill M_X\left(z\right)=\frac{-2\eta \left(\alpha -1\right)\left(e^z-1\right)ln\left(\eta \right)+\alpha \left({\eta }^2{e}^z-2\eta +1\right)ln\eta -\alpha \left(\eta -1\right)\left(\eta e^z-1\right)}{\alpha \left(ln\eta -1\right){\left(\eta e^z-1\right)}^2}.\end{array}$$ 10

The similar relation is also valid between the mgf and characteristic function (cf). The cf function of X is obtained by replacing $e^z$ by $e^{\mathit{iz}}$. Then, we have

$$\begin{array}{c}\hfill {\phi }_X\left(z\right)=\frac{-2\eta \left(\alpha -1\right)\left(e^{\mathit{iz}}-1\right)ln\left(\eta \right)+\alpha \left({\eta }^2{e}^{\mathit{iz}}-2\eta +1\right)ln\eta -\alpha \left(\eta -1\right)\left(\eta e^{\mathit{iz}}-1\right)}{\alpha \left(ln\eta -1\right){\left(\eta e^{\mathit{iz}}-1\right)}^2}.\end{array}$$ 11

The partial derivatives of (10) according to z at $z=0$ give raw moments of X. Using this property, the first two moments of the DsGLi model are given, respectively, by

$$\begin{array}{cc}\hfill \text{E}(X)=& -\eta \frac{\left(\alpha ,-,1\right)ln{\eta }^2+\alpha (\eta -2)ln\eta -\alpha (\eta -1)}{\alpha (ln\eta -1){(\eta -1)}^2},\hfill \end{array}$$ 12

$$\begin{array}{cc}\hfill \text{E}(X^2)=& \eta \frac{\left(3,\alpha ,\eta ,+,\alpha ,-,3,\eta ,-,1\right)ln{\eta }^2+\alpha ({\eta }^2-3\eta -2)ln\eta -\alpha {\eta }^2+\alpha }{\alpha (ln\eta -1){(\eta -1)}^3}.\hfill \end{array}$$ 13

The variance of the DsGLi distribution can be calculated by using $\text{Var}\left(X\right)=\text{E}\left(X^2\right)-\text{E}{\left(X\right)}^2$. The skewness and kurtosis measures of the DsGLi can be also easily calculated by using well-known relations. The other important measure of any discrete distribution is dispersion index (DI) which is defined as $\text{DI}=\text{Var}\left(X\right)/\text{E}\left(X\right)$. The flexibility of the DI measure is important to model different types of data sets such as over-dispersed ($\text{DI}>1$), equi-dispersed ($\text{DI}=1$), and under-dispersed ($\text{DI}<1$). The statistical measures of the DsGLi distribution are computed and reported in Tables 1 and 2. To interpret the individual effects of the parameters $\alpha$ and $\eta$, the results are calculated for fixed $\alpha =0.9$ and $\eta =0.01$. As seen from Table 1, the mean, variance, and DI are the increasing function of the parameter $\eta$ for fixed $\alpha =0.90$, whereas the skewness and kurtosis decrease when the parameter $\eta$ increases. As given in Table 2, the mean and variance are the increasing function of $\alpha$. The DI, skewness, and kurtosis decrease when the parameter $\alpha$ increases. As seen from these results, the DsGLi distribution has flexible DI which can be over or under one. So, the DsGLi distribution can be an appropriate choice in modeling all types of count data.

Table 1.

The numeric values of the statistical measures of the DsGLi distribution for $\alpha =0.9$

	$\eta$
Measure	0.01	0.05	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
Mean	0.0141	0.0803	0.1751	0.4082	0.7182	1.1438	1.7557	2.6959	4.2971	7.5582	17.478
Variance	0.0143	0.0852	0.1976	0.5248	1.0663	1.9968	3.6960	7.1035	15.049	39.363	179.20
DI	1.0118	1.0612	1.1283	1.2855	1.4845	1.7457	2.1051	2.6348	3.5022	5.2079	10.253
Skewness	8.5415	3.8420	2.8210	2.1538	1.8816	1.7274	1.6251	1.5508	1.4947	1.4528	1.4249
Kurtosis	77.619	19.256	12.369	8.9408	7.7616	7.1397	6.7437	6.4663	6.2648	6.1217	6.0321

Table 2.

The numeric values of the statistical measures of the DsGLi distribution for $\eta =0.01$

	$\alpha$
Measure	1.5	3.0	4.5	6.0	7.5	9.0	10.5	12.5	15.0	17.5	20.0
Mean	0.0313	0.0442	0.0485	0.0506	0.0519	0.0527	0.0534	0.0539	0.0545	0.0548	0.0551
Variance	0.0314	0.0438	0.0479	0.0499	0.0511	0.0519	0.0525	0.5301	0.5355	0.0538	0.0541
DI	1.0025	0.9915	0.9876	0.9857	0.9845	0.9837	0.9831	0.9826	0.9821	0.9818	0.9815
Skewness	5.6703	4.6978	4.4593	4.351	4.289	4.2489	4.2208	4.1943	4.1714	4.1552	4.1432
Kurtosis	35.341	24.741	22.438	21.431	20.866	20.504	20.253	20.017	19.815	19.6729	19.567

Estimation

The unknown parameters of the DsGLi distribution are obtained by the maximum likelihood estimation (MLE) method. This method is based on the maximization of the log-likelihood function for a given data set. Let us assume that we have a sample that comes from the DsGLi distribution, denoted as $X_1,X_2,\dots ,X_n$. Then, we have the following log-likelihood function for the DsGLi distribution

$$\begin{array}{cc}\hfill \ell (x;\alpha ,\eta )=& ln\eta \sum _{i=1}^n{x}_i-nln\left(1,-,ln,\eta \right)\hfill \\ \hfill +& \sum _{i=1}^{n}ln\left(1,-,\eta ,-,ln,\eta ,\left[1,+,x_i,-,\eta ,(x_i+2)\right],+,(1-\frac{1}{\alpha }),{(ln\eta )}^2,\left[x_i,-,\eta ,(x_i+1)\right]\right).\hfill \end{array}$$ 14

We have two choices to obtain the MLEs of the parameters $\alpha$ and $\eta$. The first way, we can use (14) to direct maximization of the log-likelihood to get the MLEs of the parameters, say $\widehat{\alpha }$, and $\widehat{\eta }$. The second way, the score vectors, given below, can be simultaneously solved for zero.

$$\begin{array}{c}\hfill \frac{\partial \ell }{\partial \alpha }=\sum _{i=1}^n\frac{{\left(\frac{ln\eta }{\alpha }\right)}^2\left[x_i,-,\eta ,(x_i+1)\right]}{1-\eta -ln\eta \left[1,+,x_i,-,\eta ,(x_i+2)\right]+(1-\frac{1}{\alpha }){(ln\eta )}^2\left[x_i,-,\eta ,(x_i+1)\right]},\end{array}$$ 15

$$\begin{array}{cc}\hfill \frac{\partial \ell }{\partial \eta }=& \frac{1}{\eta }\sum _{i=1}^n{x}_i+\frac{n}{\eta \left(1,-,ln,\eta \right)}\hfill \\ \hfill +& \sum _{i=1}^n\frac{\left(x_i,+,2\right)\left(ln,\eta ,+,1\right)-\frac{1+x_i}{\eta }-1+ln\eta \left(1,-,\frac{1}{\alpha }\right)\left(\frac{2x_i-2\eta (x_i+1)}{\eta },-,(x_i+1),ln,\eta \right)}{1-\eta -ln\eta \left[1,+,x_i,-,\eta ,(x_i+2)\right]+(1-\frac{1}{\alpha }){(ln\eta )}^2\left[x_i,-,\eta ,(x_i+1)\right]}.\hfill \end{array}$$ 16

In this study, we prefer the first choice, direct maximization of (14) by means of constrOptim function of R. To obtain the asymptotic standard errors and confidence intervals, the observed information matrix is used evaluated at $\widehat{\alpha }$ and $\widehat{\eta }$. The observed information matrix can be numerically calculated by hessian function of R software.

Simulation

We assess the finite sample performance of the MLE method in estimating the unknown parameters of the DsGLi distribution. Therefore, we conduct a simulation study. The simulation replication number, N, is taken as 1, 000. The true parameter values are used as $\alpha =0.5$ and $\eta =0.5$. There is no specific reason to use these parameter values. Different parameter settings can be used. We generate random samples from the DsGLi distribution with $n=50,55,60,\dots ,300$ sample sizes. The simulation results are interpreted based on the estimated biases, mean square errors (MSEs), and mean relative errors (MREs). The required mathematical formulations of these metrics can be found in the works of [24, 25]. We expect to see that biases and MSEs are near the zero and MREs are near the one for sufficiently large sample sizes. The simulation results are graphically summarized and displayed in Fig. 3. These results confirm our expectation that the estimated biases and MSEs are near the zero for nearly all samples of sizes. Also, the estimated MREs are near the one, as expected. These results also show that the MLEs of the parameters of the DsGLi distribution are asymptotically unbiased and consistent. The similar results are obtained for different parameter settings, but not reported here for the sake of simplicity.

Fig. 3.

The simulation results of the DsGLi distribution

DsGLi regression model

When modeling the discrete response variable with associated covariates, the Poisson regression model is the first thing come to mind. However, it is well known that the Poisson regression produces inaccurate results when the response variable is over-dispersed or under-dispersed, except equi-dispersion. In this study, we propose an alternative model to provide new opportunities in predicting the over-dispersed counts. Let Y be a random variable following a DsGLi density. Using the below re-parametrization

$$\begin{array}{c}\hfill \alpha =\frac{\eta ln{\left(\eta \right)}^2}{\left(ln\left(\eta \right)-1\right)\left(\left(\eta -1\right)\left(\eta +\mu \left(\eta -1\right)\right)+\eta ln\left(\eta \right)\right)},\end{array}$$ 17

we have

$$\begin{array}{c}\hfill \mathrm{P}\left(y_i;\eta ,\mu \right)=\frac{{\eta }^{y_i}}{1-ln\left(\eta \right)}\left\{\begin{array}{c}1-\eta -ln\left(\eta \right)\left[1+y-\eta \left(y+2\right)\right]\hfill \\ +\left(\frac{\gamma \left(\eta ,\mu \right)-1}{\gamma \left(\eta ,\mu \right)}\right)ln{\left(\eta \right)}^2\left[y_i-\eta \left(y_i+1\right)\right]\hfill \end{array}\right\},\end{array}$$ 18

where

$$\begin{array}{c}\hfill \gamma \left(\eta ,{\mu }_i\right)=\frac{\eta ln{\left(\eta \right)}^2}{\left(ln\left(\eta \right)-1\right)\left(\left(\eta -1\right)\left(\eta +{\mu }_i\left(\eta -1\right)\right)+\eta ln\left(\eta \right)\right)}.\end{array}$$ 19

The density in (18) is denoted as $Y\sim \text{DsGLi}\left(\alpha ,,,\mu \right)$. After this re-parametrization, the mean of the random variable is $\text{E}\left(Y\right)=\mu$ and its variance is

$$\begin{array}{c}\hfill \mathrm{Var}\left(Y\right)=\frac{\mu \left(3\eta +1\right)}{1-\eta }-\frac{2{\eta }^2}{{\left(1-\eta \right)}^2}-{\mu }^2.\end{array}$$ 20

The parameter $\eta$ is a dispersion parameter of the re-parametrized DsGLi distribution. Now, using the density in (18), we propose a new count regression model. Let the response variable Y follow the density in (18) and consider the regression structure given as follows:

$$\begin{array}{c}\hfill g\left({\mu }_i\right)={\mathbf{x}}_i^T\mathit{\beta },\end{array}$$ 21

where ${\mathbf{x}}_i^T=\left(x_{i1},,,x_{i2},,,\dots ,,,x_{\mathit{ik}}\right)$ is the explanatory variable vector and $\mathit{\beta }=\left({\beta }_0,,,{\beta }_1,,,\dots ,,,{\beta }_k\right)$ is the vector of regression parameters. The function in (21) is known as link function. The link functions play an important role in generalized linear models to construct a bridge between predictors and the mean of the response variable. The suitable choice of the link function depends on the domain the response variable. Since the response variable is defined on ${\mathbb{Z}}_{+}$, the log-link function is used.

Estimation process

The log-link is defined as ${\mu }_i=exp\left({\mathbf{x}}_i^T,\mathit{\beta }\right)$. Using the log-link function, the log-likelihood function of the DsGLi regression model is given by

$$\begin{array}{c}\hfill \begin{array}{c}\ell \left(\eta ,\mathit{\beta }\right)=ln\left(\eta \right)\overline{y}-nln\left(1-ln\left(\eta \right)\right)\hfill \\ +\sum _{i=1}^{n}ln\left\{\begin{array}{c}1-\eta -ln\left(\eta \right)\left[1+y-\eta \left(y+2\right)\right]\hfill \\ +\left(1-\frac{\left(ln\left(\eta \right)-1\right)\left(\left(\eta -1\right)\left(\eta +exp\left({\mathbf{x}}_i^T,\mathit{\beta }\right)\left(\eta -1\right)\right)+\eta ln\left(\eta \right)\right)}{\eta ln{\left(\eta \right)}^2}\right)\hfill \\ \times ln{\left(\eta \right)}^2\left[y_i-\eta \left(y_i+1\right)\right]\hfill \end{array}\right\}\hfill \end{array},\end{array}$$ 22

where n is the sample size, $\eta$ is the unknown dispersion parameter, and $\mathit{\beta }$ is the unknown regression parameters. Let $\mathit{\gamma }=\left(\eta ,,,\mathit{\beta }\right)$ be an unknown parameter vector. Under the regularity conditions of the MLE, the asymptotic distribution of the $\mathit{\gamma }-\widehat{\mathit{\gamma }}$ is the $\left(k,+,2\right)$-variate normal distribution with zero mean and variance–covariance matrix, ${\mathrm{\Sigma }}_{(k+2)\times (k+2)}$ which is obtained by the inverse of observed information matrix, $I_{(k+2)\times (k+2)}$ calculated at the MLE of the $\mathit{\beta }$, $\widehat{\mathit{\beta }}$. To estimate the unknown parameter vector, $\mathit{\gamma }$, the below estimation process is implemented.

1. First, the underlying data set is fitted by Poisson regression model to get the initial parameter vector of the $\mathit{\beta }$ for DsGLi regression model.

2. Next, using the estimated regression parameters of the Poisson regression model as an initial parameter vector for the $\mathit{\beta }$ and setting the initial value of $\eta =0.5$, the minus log-likelihood function, $-\ell \left(\eta ,\mathit{\beta }\right)$ in (22), is minimized by constrOptim function in R since the parameter $\eta \in \left(0,,,1\right)$.

3. Then, using the hessian function in R, we obtain the observed information matrix, $I_{(k+2)\times (k+2)}$, calculated at $\widehat{\mathit{\gamma }}$.

Residual analysis

Residual analysis is carried out to be sure about the accuracy of the DsGLi regression model for the used data set. The randomized quantile residual (rqr) is used for this purpose. Let the random variable Y have a cdf $F\left(y,;,\eta ,,,\mu \right)$ which is the cdf of the re-parametrized DsGLi distribution. Then, the rqr is defined as

$$\begin{array}{c}\hfill r_{q,i}={\mathrm{\Phi }}^{-1}\left(u_i\right),\end{array}$$ 23

where $u_i=F\left(y_i;{\widehat{\alpha },\mu }_i\right)$. Note that the rqr is distributed as $N\left(0,,,1\right)$ when the model is acceptable for the used data.

Data analysis

The empirical importance of the proposed models is proved by three applications to COVID-19 data sets. The proposed models are compared with some competitive models to see its competitive power. The competitive models are listed in the following.

In the first two empirical studies, we compare the fit of the DsGLi distribution with competitive models listed in Table 3. The goodness-of-fit test and Kolmogorov–Smirnov ($K-S$) are implemented to select a best-fitted model for COVID-19 data sets. The models having p value higher than 0.05 are evaluated as possible accurate models, and the information criteria, listed below, are used to decide best-fitted model in final stage. The data source is https://www.worldometers.info/coronavirus/. In the third application, we assess the performance of the DsGLi regression model by applying the model to the COVID-19 data set of the OECD countries.

$\bullet$

Akaike information criterion (AIC).

$\bullet$

Hannan–Quinn information criterion (HQIC).

$\bullet$

Bayesian information criterion (BIC).

$\bullet$

Corrected Akaike information criterion (CAIC).

Table 3.

The competitive models

Model	Abbreviation	References
Poisson	Poi	–
Discrete Lindley	DsLi	Gómez-Déniz and Calderín-Ojeda [10]
Discrete Burr-XII	DsB-XII	Krishna and Pundir [26]
Discrete Pareto	DsPs	Krishna and Pundir [26]
Discrete Burr–Hatke	DsBH	El-Morshedy et al. [16]
Discrete log-logistic	DsLogL	Para and Jan [27]
Discrete inverse Weibull	DsIW	Jazi et al. [28]
Discrete inverse Rayleigh	DsIR	Hussain and Ahmed [29]

South Korea

In the first application, we consider the daily new deaths in South Korea. The data are available at https://www.worldometers.info/coronavirus/country/south-korea/ and contain the daily new deaths between February 15 and December 14, 2020.

This data set is modeled with DsGLi and other competitive models. Table 4 contains the estimated parameters and their corresponding standard errors (SEs) as well as confidence intervals (CIs) for all fitted models. The results of the information criteria and goodness-of-fit test are given in Table 5. The best-fitted model should have the lowest values of these statistics. From Table 5, we conclude that the DsGLi model is the best-performed model among others since it has the lowest values of AIC, BIC, CAIC, HQIC, and K–S test statistic. The higher value of the p value of the KS test shows the better-fitted model. If the p value is less than 0.05, it means that the model cannot be used to predict the counts of COVID-19 cases. According to the modeled data set, DsGLi and DsLi distributions have p values higher than 0.05. However, the p value of DsGLi distribution is higher than those of DsLi distribution. Therefore, the proposed model is the best choice for modeling the data used.

Table 4.

The estimated parameters of the fitted models for South Korea data set

Model	$\alpha$			$\eta$
	MLE	SE	CI	MLE	SE	CI
DsGLi	0.804	0.239	[0.335, 1.272]	0.530	0.029	[0.472, 0.589]
DsLi	0.513	0.015	[0.484, 0.542]	$-$	−	−
DsIR	0.227	0.023	[0.182, 0.273]	$-$	−	−
DsLogL	1.727	0.096	[1.540, 1.915]	1.875	0.106	[1.667, 2.084]
DsIW	0.269	0.025	[0.219, 0.318]	1.407	0.083	[1.245, 1.569]
DsB-XII	0.593	0.031	[0.532, 0.654]	2.469	0.248	[1.983, 2.956]
DsPa	0.379	0.021	[0.337, 0.420]	$-$	−	−
DsBH	0.905	0.020	[0.866, 0.945]	$-$	−	−
Poi	1.918	0.079	[1.763, 2.073]	$-$	−	−

Table 5.

The goodness-of-fit test for South Korea data set

X	OF	Expected frequency (EF)
		DsGLi	DsLi	DIR	DsLogL	DsIW	DsB-XII	DsPa	DsBH	Poi
0	89	90.464	86.208	69.501	80.799	82.217	92.948	149.889	167.504	44.938
1	79	72.982	74.824	141.745	93.092	104.218	98.301	50.804	54.918	86.205
2	50	51.969	54.078	48.289	51.910	44.822	43.023	25.664	26.837	82.683
3	29	34.597	35.790	19.391	27.702	22.598	21.399	15.514	15.651	52.870
4	19	22.079	22.488	9.459	15.798	13.108	12.322	10.404	10.094	25.355
5	17	13.689	13.653	5.272	9.689	8.373	7.859	7.468	6.947	9.728
6	9	8.309	8.089	3.225	6.322	5.728	5.388	5.625	5.00	3.110
7	7	4.964	4.707	2.112	4.338	4.123	3.893	4.391	3.722	0.852
8	6	2.928	2.700	1.457	3.099	3.085	2.927	3.524	2.840	0.204
9	1	4.019	3.463	5.549	13.251	17.728	19.940	32.717	12.487	0.055
Total	306	306	306	306	306	306	306	306	306	306
$-L$		570.712	573.966	613.699	583.049	593.090	593.984	640.256	627.311	628.313
AIC		1145.424	1148.932	1229.399	1170.099	1190.180	1191.968	1282.512	1256.622	1258.625
CAIC		1145.463	1148.945	1229.412	1170.138	1190.220	1192.008	1282.525	1256.635	1258.638
BIC		1152.871	1153.656	1233.122	1177.546	1197.627	1199.415	1286.236	1260.346	1262.349
HQIC		1148.402	1150.421	1230.888	1173.077	1193.159	1194.946	1284.001	1258.111	1260.114
${\chi }^2$		3.154	4.286	111.544	25.884	42.918	29.137	130.491	121.219	158.077
df		5	6	6	6	5	5	7	7	5
p value		0.676	0.638	$\le 0.001$	0.0002	$\le 0.001$	$\le 0.001$	$\le 0.001$	$\le 0.001$	$\le 0.001$

Figure 4 displays the estimated pmfs and probability–probability (PP) plots of the fitted models. These figures prove the suitability of the DsGLi distribution for modeling the counts of COVID-19 deaths South Korea.

Fig. 4.

The estimated pmf (top) and PP plots (bottom) for South Korea data set

Table 6 lists the theoretical values of the mean, variance, and DI measures of the DsGLi distribution obtained under the estimated parameters. The empirical mean, variance, and DI of the used data set are 1.918, 4.180, and 2.179, respectively. The theoretical mean, variance, and DI are closed to empirical ones.

Table 6.

The numerical values for the statistical properties of the DsGLi distribution for South Korea data set

Mean	Variance	DI
1.915	4.342	2.267

Armenia

In the second application, we consider the daily new deaths in Armenia. The data are available at https://www.worldometers.info/coronavirus/country/armenia/ and contain the daily new cases between February 15 and October 4, 2020.

The above data set is modeled with DsGLi and other competitive models, and the estimated parameters and goodness-of-fit results are reported in Tables 7 and 8, respectively. According to the results in Table 8, we conclude that the DsGLi distribution is the best choice among other competitive models since it has the lowest values of the goodness-of-fit statistics. Additionally, the only distribution having the p value higher than 0.05 is DsGLi. Therefore, the proposed model is the best choice for modeling the data used.

Table 7.

The estimated parameters of the fitted models for Armenia data set

Model	$\alpha$			$\eta$
	MLE	SE	C. I	MLE	SE	C. I
DsGLi	0.228	0.089	[0.053, 0.404]	0.784	0.037	[0.712, 0.855]
DsLi	0.692	0.012	[0.668, 0.716]	$-$	−	−
DsIR	0.112	0.019	[0.075, 0.149]	$-$	−	−
DsLogL	2.871	0.2426	[2.395, 3.346]	1.388	0.086	[1.219, 1.557]
DsIW	0.201	0.026	[0.149, 0.252]	0.958	0.060	[0.839, 1.076]
DsB-XII	0.643	0.034	[0.576, 0.711]	1.811	0.210	[1.399, 2.223]
DsPa	0.493	0.0229	[0.448, 0.538]	−	−	−
DsBH	0.976	0.01136	[0.953, 0.998]	−	−	−
Poi	4.207	0.135	[3.943, 4.471]	$-$	−	−

Table 8.

The goodness-of-fit test for Armenia data set

X	OF	EF
		DsGLi	DsLi	DsIR	DsLogL	DsIW	DsB-XII	DsPa	DsBH	Poi
0	56	43.852	28.244	25.963	43.595	46.600	61.116	89.881	118.830	3.455
1	31	35.735	32.849	108.220	43.908	54.931	51.488	35.422	39.565	14.535
2	22	29.078	31.939	47.702	32.046	30.935	28.237	19.636	19.748	30.573
3	25	23.629	28.475	20.435	22.694	19.142	17.094	12.704	11.823	42.874
4	11	19.176	24.116	10.220	16.344	12.936	11.396	8.997	7.860	45.089
5	14	15.545	19.741	5.765	12.076	9.313	8.146	6.747	5.598	37.937
6	14	12.587	15.774	3.552	9.152	7.023	6.123	5.280	4.181	26.601
7	10	10.182	12.378	2.336	7.115	5.487	4.777	4.262	3.241	15.986
8	11	8.229	9.578	1.615	5.647	4.406	3.842	3.524	2.5801	8.407
9	3	6.643	7.328	1.165	4.549	3.619	3.159	2.967	2.101	3.929
10	10	5.359	5.556	0.863	3.738	3.022	2.649	2.540	1.741	1.653
11	7	4.320	4.180	0.661	3.127	2.566	2.255	2.202	1.465	0.632
12	4	3.480	3.125	0.513	2.615	2.204	1.944	1.933	1.248	0.222
13	5	2.801	2.323	0.411	2.232	1.914	1.696	1.709	1.075	0.072
14	2	2.252	1.719	0.329	1.916	1.679	1.494	1.524	0.934	0.022
15	2	1.811	1.267	0.271	1.679	1.485	1.327	1.371	0.819	0.006
$\ge 16$	6	7.321	3.408	1.979	19.566	24.738	25.257	31.300	9.191	0.008
Total	232	232	323	232	232	232	232	232	232	232
$-L$		590.8589	604.567	719.922	609.5819	625.479	629.887	644.982	657.924	836.109
AIC		1185.718	1211.134	1441.844	1223.164	1254.958	1263.773	1291.963	1317.848	1674.220
CAIC		1185.770	1211.151	1441.862	1223.216	1255.011	1263.825	1291.981	1317.865	1674.237
BIC		1192.611	1214.58	1445.291	1230.057	1261.852	1270.666	1295.410	1321.295	1677.666
HQIC		1188.498	1212.524	1443.234	1225.944	1257.738	1266.553	1293.353	1319.238	1675.610
${\chi }^2$		19.025	53.708	397.614	39.965	75.526	82.634	113.538	185.041	486.741
d.f		11	11	6	10	9	8	9	8	7
p value		0.061	$\le 0.001$	$\le 0.001$	$\le 0.001$	$\le 0.001$	$\le 0.001$	$\le 0.001$	$\le 0.001$	$\le 0.001$

Figure 5 displays the estimated pmfs and PP plots of the fitted models. From these figures, it is concluded that the DsGLi model provides acceptable modeling performance for the used data.

Fig. 5.

The estimated pmf (top) and PP plots (bottom) for Armenia data set

Additionally, the theoretical values of the mean, variance, and DI measures of the DsGLi distribution are reported in Table 9 for Armenia data set. The empirical mean, variance, and DI of the used data set are 4.207, 19.783, and 4.703, respectively. The theoretical mean and skewness are closed to empirical ones.

Table 9.

The numerical values for the statistical properties of the DsGLi distribution for Armenia data set

Mean	Variance	DI
4.208	21.250	5.049

OECD

In the third application, the counts of deaths due to the COVID-19 are modeled for the OECD countries by the DsGLi regression model. The predictive performance of the DsGLi regression model is compared with Poisson regression. The response variable is the counts of deaths up to the date May 16, 2020. According to the Health at a Glance report (see OECD [30]), the important risk factors on health are the use of smoking and alcohol, overweight (obese), and air pollution. These variables are available in [30] and measured in the year 2019. We try to explain the variability in the counts of deaths ($y_i$) due to the coronavirus with covariates, smoking ($x_{i1}$, % population aged $15+$), alcohol ($x_{i2}$, % population aged $15+$), and overweight ($x_{i3}$, % population with BMI $\ge 25$ for population aged $15+$). We also consider the population size for each country as an explanatory variable. The population size is transformed in three-level categorical variable and two dummy variables are created: the population size between 7 and 35 million ($x_{i5}$, 1 = yes, 0 = no) and the population size over 35 million $x_{i6}$, 1 = yes, 0 = no). The population size lower than 7 million is considered as a baseline category. To avoid the extreme outlier observations, we exclude the countries having less than 1 million population and over 100 million population sizes. The regression model in (24) is fitted by DsGLi and Poisson regression models.

$$\begin{array}{c}\hfill {\mu }_i=exp\left({\beta }_0+{\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+{\beta }_3{x}_{i3}+{\beta }_4{x}_{i4}+{\beta }_5{x}_{i5}+{\beta }_6{x}_{i6}\right).\end{array}$$ 24

The estimated regression parameters and their corresponding standard errors (SEs), as well as p values, are listed in Table 10. The mean and variance of the response variable are 5391.4 and 104275974, which shows that it is highly over-dispersed. Because of the over-dispersed response variable, the Poisson regression model produces inaccurate results with higher AIC and BIC values than the DsGLi regression model. There are dramatic differences between the AIC and BIC values of two regression models. The DsGLi regression model enables to model over-dispersed response variable on the contrary to the Poisson regression model.

Table 10.

The results of Poisson and DsGLi regression models

Parameters	Poisson			DsGLi
	Estimates	SEs	p values	Estimates	SEs	p values
${\beta }_0$	5.0493	0.0295	$<0.0001$	7.0174	0.0033	$<0.0001$
${\beta }_1$	0.1108	0.0007	$<0.0001$	0.1075	0.0734	0.14303
${\beta }_2$	-0.0899	0.0017	$<0.0001$	-0.2265	0.0763	0.0029
${\beta }_3$	0.0070	0.0003	$<0.0001$	-0.0097	0.0099	0.3265
${\beta }_4$	-0.0206	0.0002	$<0.0001$	-0.0472	0.0296	0.1108
${\beta }_5$	3.6286	0.0190	$<0.0001$	4.2760	0.0119	$<0.0001$
${\beta }_6$	1.5763	0.0202	$<0.0001$	2.0978	0.0114	$<0.0001$
$\eta$	-	-	-	0.9998	$<0.0001$	-
$-\ell$	72891.2000			273.6595
AIC	145796.4000			563.3190
BIC	145806.2000			574.5286

Figure 6 displays the results of the residual analysis of the DsGLi regression model. As seen from these figures, there is no observation to be evaluated as an outlier observation since all plotted points are in the envelopes.

Fig. 6.

The residual results of DsGLi regression model

Discussion of empirical results

In this section, the empirical results are interpreted in detail. The first two applications are based on the modeling of the counts of daily deaths of South Korea and Armenia, respectively. Using the estimated model parameters, some probabilities can be calculated. For instance, a researcher wants to know what is the probability that 3 or more deaths will occur in South Korea and Armenia in one day. To answer these research question, the estimated parameters of the DsGLi distribution and its cdf can be used. The probabilities related to this research question are calculated for different values of the count of deaths and reported in Table 11.

Table 11.

The calculated probabilities of the daily deaths for South Korea and Armenia

Counts of deaths in South Korea	Probability for South Korea	Counts of deaths in Armenia	Probability for Armenia
Over 3	0.0722	Over 3	0.3776
Over 5	0.0214	Over 5	0.2322
Over 7	0.0061	Over 7	0.1427

The counts of deaths in OECD countries are modeled with some covariates by using the DsGLi and Poisson regression models in the third application. According to the estimated regression parameters, we conclude the following results.

$\bullet$

The proportion of smokers in the population does not affect the counts of deaths.

$\bullet$

In a kind of funny way, the countries having more alcohol consumption have lower counts of deaths.

$\bullet$

The proportion of obese individuals in the population does not affect the counts of deaths.

$\bullet$

The air pollution does not affect the counts of deaths.

$\bullet$

The countries with a population of over 35 million have $exp(4.2760)=71.9521$ times more counts of deaths than countries with a population below 7 million.

$\bullet$

The countries with a population of 7–35 million have $exp(2.0978)=8.1482$ times more counts of deaths than countries with a population below 7 million.

Conclusion remarks

COVID-19 is still an unclear infectious disease. Each country’s social and policy responsibility is affected by the COVID-19 outbreak. In this paper, our aim is to try to serve humanity in this difficult situation by modeling this outbreak by utilizing a new probability distribution, and therefore, we have proposed a new two-parameter discrete gamma Lindley distribution for modeling such these count data. Some important statistical properties have been derived in closed forms which makes this model more flexible in practical fields. The model parameters have been estimated by using the maximum likelihood approach which gives a unique estimator. The flexibility of the proposed model has been explained by utilizing three COVID-19 data sets in different countries.

Statistical modeling is very important to combat such epidemics. With the help of the models proposed in this study, the expected number of new cases and deaths during the epidemic can be predicted. Thus, controlling the epidemic can be achieved more quickly. The modeling phase can also be divided into cities or smaller settlements instead of the whole country. We hope that the results obtained here will be useful for researchers, politicians, and healthcare organizations.