Abstract
The sudden outbreak of coronavirus disease 2019 (COVID-19) revealed the need for fast and reliable automatic tools to help health teams. This paper aims to present understandable solutions based on Machine Learning (ML) techniques to deal with COVID-19 screening in routine blood tests. We tested different ML classifiers in a public dataset from the Hospital Albert Einstein, São Paulo, Brazil. After cleaning and pre-processing the data has 608 patients, of which 84 are positive for COVID-19 confirmed by RT-PCR. To understand the model decisions, we introduce (i) a local Decision Tree Explainer (DTX) for local explanation and (ii) a Criteria Graph to aggregate these explanations and portrait a global picture of the results. Random Forest (RF) classifier achieved the best results (accuracy 0.88, F1–score 0.76, sensitivity 0.66, specificity 0.91, and AUROC 0.86). By using DTX and Criteria Graph for cases confirmed by the RF, it was possible to find some patterns among the individuals able to aid the clinicians to understand the interconnection among the blood parameters either globally or on a case-by-case basis. The results are in accordance with the literature and the proposed methodology may be embedded in an electronic health record system.
Keywords: COVID–19, Criteria graph, Decision tree, Explainable artificial intelligence, Machine learning
1. Introduction
COVID-19, the disease associated with the SARS-CoV-2 virus, was declared a pandemic by the World Health Organization (WHO) on March 11th, 2020 [1]. This pandemic has impacted all aspects of life, politics, education, economy, social, environment and climate and set off a warning about how governments, civil society and health systems can deal with an unknown disease. Although many scientific advances have been made and an intense vaccination program is being carried out in several countries, the severe situation is not effectively controlled yet.
An accurate and reliable diagnosis is crucial in providing timely medical aid to suspected or infected individuals and helps the government agencies to prevent its spread and save people's lives. The standard test for COVID-19 is the Reverse Transcriptase Polymerase Chain Reaction, known as RT-PCR, reviewed in Ref. [2]. However, it has limitations in terms of resources and specimen collection [3], it is time-consuming [[3], [4], [5], [6]], it has high specificity and low sensitivity1 [3,7,8], high misclassification in the early symptomatic phase [6] and, also, it is unavailable in many countries and societies making the real extent of the spread still unknown [8,9].
In addition to the RT-PCR, AI-based approaches may be used to assist in the screening of patients suspected of being contaminated by SARS-CoV-2, supporting the medical decision. In the field of Machine Learning (ML), a branch of Artificial Intelligence (AI) that studies methods that allow computers to learn tasks by examples, many researches studied the diagnosis of COVID-19 either through the analysis of medical images or routine blood tests, as in Refs. [6,[8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19]].
Routine blood tests play an important role in the diagnosis of COVID-19 and other respiratory diseases. Parameters such as white blood cells (WBC), C-reactive protein (CRP), neutrophils (NEU), lymphocytes (LYM), monocytes (MONO), eosinophils (EOS), basophils (BAY), aspartate and alanine aminotransferase (AST and ALT, respectively), lactate dehydrogenase (LDH) and others have shown high correlations in patients diagnosed with COVID-19 [6,[8], [9], [10],14,[18], [19], [20], [21], [22], [23]].
These hematological features have been used for identifying patterns through ML approaches to verify whether the patient is infected or not. Meng et al. [4] used different indicators of whole blood count, coagulation test, and biochemical examination to build a Multivariate Logistic Regression (MLR) that was embedded in a COVID-19 diagnosis aid system. Kukar et al. [11] provided a model called “Smart Blood Analytics (SBA)” based on routine blood tests for patients with various bacterial and viral infections and COVID-19 patients. Wu et al. [13] extracted 11 blood indices through Random Forest (RF) algorithm to build an online assistant discrimination tool. Batista et al. [9] used Artificial Neural Networks (ANN), RF, Gradient Boosting Tree (GBT), Logistic Regression (LR) and Support Vector Machines (SVM) to predict the risk of positive COVID-19 using as predictors only results from emergency care admission exams. Brinati et al. [8] developed two classification models using hematological values from Italian patients. RF and Three-Way RF (TWRF) models showed the best results. A Decision Tree was used for explanation. Barbosa et al. [14,15] proposed the Heg. IA as a support system for the diagnosis of COVID-19. RF is used as the classifier.
Although these models bring promising results in COVID-19 diagnosis, their transparency and trust can be questionable. A model can be defined as explainable if a human can understand its decisions [24]. Any fully automated method without the possibility for human verification would be potentially dangerous in a practical setting, in particular, in the medical field. Explainable ML, or Explainable AI (xAI), typically refers to post hoc analysis and techniques used to understand a pre-trained model or its predictions. The ability of a system to explain its decisions is a central paradigm in symbolic or logic-based machine learning [25]. A model-agnostic explainer [25] can interpret a black-box model prediction without assumptions on the underlying black-box model. They are usually employed after the training step (post-hoc explainability), see for instance LIME [26] and SHAP [27], providing an understandable output by showing graphically the results and highlighting the features that most contributed to the black-box model decision.
In this work, we search for an accurate ML model for COVID-19 screening based on hematological data and propose the use of a decision tree explainer to improve the interpretability of the best model. We argue that a decision tree more closely resembles the decision-making process of a human healthcare worker and because of that it may be more useful in a real-world environment. We also introduce a criteria graph to aggregate explanations allowing for a generalization of the decision process and a deeper understanding of the interaction of factors leading to a diagnosis.
The main contributions and findings are listed below:
-
•
A literature review of ML methods applied to COVID-19 screening in routine blood tests;
-
•
Reasonable results from different ML techniques (including an ensemble) to support the diagnosis of COVID-19 using usual blood exams;
-
•
A decision tree-based methodology for the explanation of the model which can be given to the health teams;
-
•
Individual explanations in a graph that shows the relative importance of each attribute and their interactions;
-
•
Further evidence that simple blood tests might help identifying false positive/negative RT-PCR tests.
The remainder of the paper is organized as follows: Section 2 reviews the application of AI for diagnosing COVID-19. Section 3 discusses the Decision-Tree based Explainer (DTX) used for local interpretation. Section 4 presents the proposed Criteria Graph that can be used for global model interpretation. Section 5 explains the ML process, such as models and dataset used, evaluation process and explainability. Section 6 presents the results and discussion. Section 7 provides future directions and conclusions.
2. AI-based approaches in the COVID-19 pandemic
Since the announcement of the pandemic, the scientific community has been working hard to investigate SARS-CoV-2 dynamics. As a result, the volume of papers about COVID-19 has increased exponentially [5]. Reviews were carried out to organize, summarize, and merge the amount of information available in such a short time. For instance, Mohamadou, Halidou and Kapen [28] revised 61 studies dealing with mathematical modelling, AI and datasets related to COVID-19. They reported that most models are either based on Susceptible-Exposed-Infected-Removed (SEIR) as in Ref. [29] or SIR model. Toledo et al. [17] provided a historic review of the virus, its epidemiology and pathophysiology, emphasizing the laboratory diagnosis, particularly in hematological changes found during the disease. Wynants et al. [30] provided a systematic review and critic appraisal of current models for COVID-19 for the prognosis of patients and for identifying people at increased risk of becoming infected or being admitted to hospital with the disease. Kermali et al. [10] revised 34 papers discussing biomarkers and their clinical implications. Zheng et al. [31] provided a meta-analysis of the risk factors of critical/mortal cases and non-critical COVID-19 patients, with 13 studies including 3027 patients, in which critical patient conditions and parameters were highlighted.
Regarding AI and ML-based works, Yan et al. [21] applied an Extreme Gradient Boosting Machine (XGBoost) algorithm to predict risk mortality, in which a single-tree was used to build an explanation for the model. Tian et al. [32] investigated the predictors of mortality in hospitalized patients in a total of 14 studies documenting the outcome of 4659 patients. Comorbidities such as hypertension, coronary heart disease, and diabetes were associated with a significantly higher risk of death amongst infected patients. Clinical manifestation laboratory examinations that could imply the progression of COVID-19 were presented. Shi et al. [33] analyzed AI techniques in imaging data acquisition, segmentation, and diagnosis. These images, either X-ray or CT images, can improve the work efficiency of the specialists by an accurate delineation of infections. Also in the AI context, Bullock et al. [5] revised datasets, tools, resources to confront many aspects of the COVID-19 crisis at different scales including molecular, clinical, and societal applications. In the clinical aspect, medical images, outcomes prediction and noninvasive measurements were discussed. Although these works have made valuable contributions to dealing with the pandemic, the decision made by the automatic learning model on the samples is still unclear.
In the revised literature, important hematological features were highlighted such as CRP [21], LDH [8,21,23,34], AST, ALT, NEU [8], LYM and WBC [8,9,11,34], EOS [8,9] and others, see also [4,6,13,14,16,20]. These features are detailed in Table 2 with a short description of each hematological parameter, the reference value for males and female and the percentage of missing rates presented in the dataset used. In the literature, they were commonly estimated either through statistics as in Refs. [6,16,20] or a ML model or metric, such as RF in Ref. [8], Least Absolute Shrinkage and Selection Operator (LASSO) in Ref. [4], Multi-tree XGBoost in Ref. [21] or an evolutionary strategy as in Ref. [14].
Table 2.
Papers that applied ML models for prediction of COVID-19, datasets and models used (the best model reported is the bold one), features analyzed, interpretability (Inter.), metric results in each paper. The methods are BN: Bayesian Networks, CRT: Classification and Regression Tree, DNN: Deep Neural Networks, DT: Decision Trees, ET: Extremely Randomized Trees, GBT: Gradient Boosting Trees, KNN: k-Nearest Neighbors, LR: Logistic Regression, MLP: Multilayer Perceptron, MLR: Multivariate Logistic Regression, NB: Naive Bayes, NN: Neural Networks, RF: Randon Forest, SVM: Support Vector Machine, TWRF: Three-Way RF, XGBoost: Extreme Gradient Boosting Machine.
| Ref | Description | Dataset | Methods | Features | Inter. | Metric results |
|---|---|---|---|---|---|---|
| [9] | Predict the risk of positive cases using as predictors only results from emergency care admission exams | 235 patients from Hospital Israelita Albert Einstein in São Paulo, Brazil. | NN, RF, GBTrees, LR, SVM | 15 blood parameters | No | AUC 0.85, SE 0.68, SP 0.85, PPV 0.74, NPV 0.77 |
| [4] | ML-based diagnosis model and a COVID-19 diagnosis aid application | 620 patients from West China Hospital | MLR | Age, gender and more 35 indicators | No | AUC 0.87, PPV 0.86, NPV 0.85 |
| [8] | ML models using hematochemical values from routine blood exams | 279 patients from San Rafaele Hospital in Milan, Italy | DT, ET, KNN, LR, NB, RF, SVM, TWRF | Several | DT | For RF: ACC 0.82, AUC 0.84, SE 0.92, SP 0.65, PPV 0.83. For TWRF: ACC 0.86, SE 0.95, SP 0.75, PPV 0.86 |
| [11] | Smart Blood Analytics (SBA) predictive model on patients with various bacterial and viral infections, and COVID-19 patients | 5333 patients from Department of Infectious Diseases, University Medical Center Ljubljana, Slovenia. | RF, DNN, XGBoost | 35 blood parameters | No | AUC 0.97, SE 0.82, SP 0.98 |
| [13] | RF model and an online assistant tool. | 253 samples from 169 suspected patients collected from multiple sources. | RF | 49 clinical available blood test data. | No | ACC 0.96, AUC 0.96, SE 0.95, SP 0.97, MCC 0.96, Related AUC 1.00 |
| [14] | Heg.IA: An intelligent system to support the diagnosis of Covid-19 based on blood tests | 5644 patients provided by Hospital Israelita Albert Einstein (São Paulo, Brazil). 559 had positive diagnosis. | MLP, SVM, RT, RF, BN and NB | 24 blood tests | No | ACC 0.95, PR 0.94, SE 0.97, SP 0.94, Kappa index 0.90 |
| [21] | Predict the mortality risk and explain the model. | 2779 validated or suspected COVID-19 patients from Tongji Hospital in Wuhan, China. | XGBoost | Several | Single Tree XGB | F1 0.93, PR 0.95, SE 0.92 |
| [16] | Detect the COVID-19 severely ill patients from those with only mild symptoms. | 137 clinically confirmed cases from the Tongji Hospital Affiliated to Huazhong University of Science and Technology. | LR, SVM, RF, KNN, AdaBoost | 100 features (8 clinical, 76 blood, and 16 urine) | No | ACC 0.79, SE 0.76, SP 0.70 |
| [22] | Predict mortality risk | 70 survivors from SMS Medical College, Jaipur (Rajasthan, India). | LR | Several | No | ACC 0.70, AUC 0.95, SE 0.90, SP 0.89 |
| [34] | Identify patients at risk for deterioration during their hospital stay | 6995 patients were evaluated at Sheba Medical Center, China | RF, NN, CRT | Several | No | ACC 0.79, AUC 0.79, SE 0.68, SP 0.81. All of them with Apache II |
| [18,19] | Prediction of the diagnosis based on blood count results and age | 1157 patients made available by the repository COVID-19 Data Sharing/BR | XGBoost | Several | No | ACC 0.80, F1 0.70, AUC 0.81, SE 0.76, PPV 0.65, NPV 0.88 |
The state-of-the-art algorithms have been the most used, such as the Support Vector Machine (SVM) in Refs. [9,16], XGBoost in Refs. [11,21] and RF in Refs. [8,13]. For the sake of simplicity, in Table 2 we summarize the works that used ML techniques to classify patients suspected of being infected with SARS-CoV-2 using hematological parameters. There is a short description of the papers, methods used (the best one is in bold), features analyzed, and the results for each performance metric.
A series of recently published papers have reported the epidemiological and clinical characteristics of patients with COVID-19 disease, however there is no standard for data collection. Many public datasets available have different features and a large number of missing values, making it difficult to aggregate this data into a single ML model.
Although many papers have presented ML-based support approaches to deal with COVID-19 screening in routine blood tests, only Brinati et al. [8] and Yan et al. [21] have raised the necessity of some sort of transparency in the model's decisions. The former presents a Decision Tree as an interpretable model but in doing so accuracy is getting sacrificed. In the latter, the authors used the XGBoost algorithm to obtain the relative importance of the features and built a Single-Tree XGBoost on the three most important (LDH, LYM and high-sensitivity CRP). Again, this is an approach that trades accuracy by interpretability.
In this paper, we evaluate different ML methods, including ensembles, for COVID-19 diagnosis from routine blood tests. Besides, our methods include cleaning and pre-processing steps, imbalance class treatment, the creation of ensemble models, and an interpretability module. The proposed methodology can be generalized to other contexts as a pipeline for the ML workflow. Local interpretability is provided by using a Decision Tree-based explainer (DTX) (Section 3) and global interpretability is obtained with the criteria graph (Section 4) proposed herein. The DTX presents an explanation for the high-accuracy black-box model. Therefore, the quality of the predictions does not have to be sacrificed. On the other hand, this means that the explanations are individual. Thus, to get an insight into the models global behaviour, the Criteria Graph compresses the information of all the explanations and presents it in a single image.
3. Decision–tree based explainer
The post hoc explanation approaches aim to explain the predictions of a particular pre-trained ML model. These explanations can be of two types:
-
•
Instance explanation: aims to explain predictions of the black-box model for individual instances. It provides local scope for interpretability.
-
•
Model explanation: it is usually the result of aggregating instance explanations over many training or testing instances. This approach provides global level interpretability, generalizing local explanations. The aggregation of many instances enables the identification of the impact of features in the classification and knowledge extraction from the ML model.
The interpreter applied in this work is known as Decision Tree-based Explainer (DTX). DTX can be defined as a model-agnostic, post hoc, perturbation-based, feature selector explainer. This approach generates a readable tree structure that provides classification rules, which reflect the local behaviour of the complex ML model around the instance to be explained. The explainer can understand the black-box model according to:
| (1) |
where is the DT prediction, is the black-box model prediction, η is a noise set created around the instance to be explained, is the number of samples around the instance to be explained, measures the distance between the black-box prediction and DTX prediction, for instance, in classification problems we can use accuracy.
The set η is created with artificial samples generated around the instance that we want to explain. This set is used to fit the explainer and to measure the accuracy of the explainer concerning the black-box model. Equation (1) implies local fidelity of the explainer to the predictions provided by the black-box model. The correctness of the prediction is orthogonal to the correctness of the explanation, but enforcing local fidelity to better models (in terms of higher accuracy) might enable better explanations.
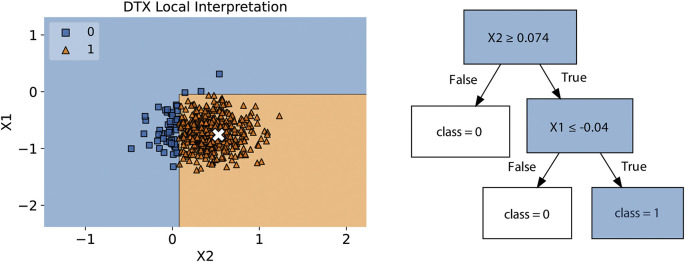
Fig. 1 illustrates how the DTX presents an understandable visual output. The left side shows the noise set η around the sample (x) that is going to be explained. It also shows the decision boundaries defined by the explainer. The right side shows the tree structure generated by DTX for a local explanation. Also, DTX works as a feature selector, since the features presented in the tree are the most important for the method around the neighbourhood of .
Fig. 1.
In the left side, there is a noise set η generated by DTX around the instance to be explained, x. The decision boundary is based on the DTX output. In the right side there is a tree structure representing the rules responsible for explaining the black-box prediction.
In the example in Fig. 1, the explanation provided for why sample is classified as class 1 (positive class), is given by the path in the tree that lead to this outcome: and .
4. Criteria graph for pattern identification in explanations
From the previous section, one can see that the decision tree explainer returns a rule of the type:
| (2) |
where a criterion is defined as and is one of , , or operators.
This kind of rule is easy to understand and provides valuable information to the health worker. Nevertheless, each patient will have its own local explanation and it might be useful to understand relationships between criteria over the whole population.
To provide this information, in this work, we also propose a global interpretability method named Criteria Graph, which works as follows:
Given a set of rules, , where each rule, , is the explanation for the patient's diagnosis, and m is the number of patients. First, for each attribute, we discretize the values of each criterion. Being the mean value of that attribute, μ, and the standard deviation, σ, if a is in the interval it gets the label . If it gets the label and if it gets the value .
After discretization, each criterion becomes a node in the graph. The size of the node is proportional to the number of patients for which that criterion was used in the diagnosis. If two criteria appear in the same rule, a link is created between them and the width of the link is proportional to the number of patients for which the two criteria are used in the diagnosis.
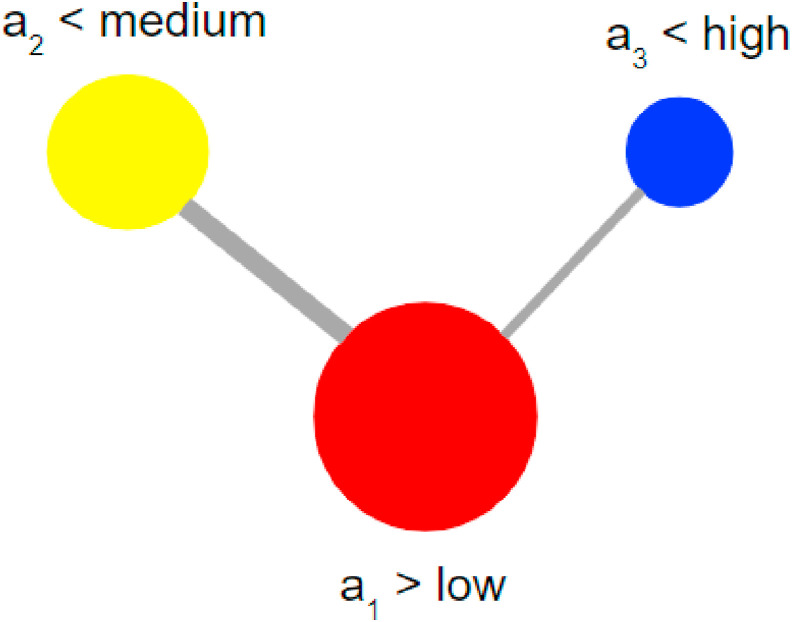
Fig. 2 shows the result of this procedure applied to the set below. Notice that the color of each node provides an extra visual cue related to the value of the criterion. Red for , Blue for and Yellow for .
Fig. 2.
Criteria graph.
The Criteria Graph is a model explanation obtained by aggregating instance explanations, as provided by DTX, over many instances, to identify patterns in explanations.
5. Methods
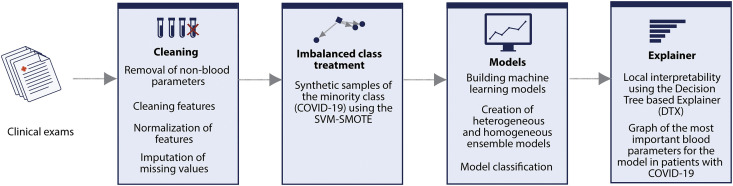
In this paper, we focus on COVID-19 binary classification using a public dataset detailed in subsection 5.1. The ML procedures for generating classifiers with evolving explanations consist, basically, of two main steps: (i) evaluation of different artificial learning models, and (ii) comparison among SHAP, LIME and DTX for local interpretation of the output and criteria graph for global interpretation. Fig. 3 provides an overview of the entire process.
Fig. 3.
Diagram of the proposed method of generating ensemble classifiers with local explainability.
5.1. Dataset
The dataset contains anonymous data from patients seen at the Hospital Israelita Albert Einstein, São Paulo, Brazil, and who had samples collected to perform the SARS-CoV-2 by RT-PCR and additional laboratory tests during the visit. The dataset is publicly available in Ref. [43] for collaborative research and it is often updated. The raw version we used contained 5644 samples and 111 features, standard normalized (z-score), related to the medical tests, such as blood, urine and others.
5.2. Pre-processing
To select the most representative parameters in the dataset we first define a threshold of 95% for removing features with several missing values greater than it. Non-blood features were also discarded, such as urine tests and other contagious infectious diseases. These diseases include respiratory infections, such as influenza A and B; parainfluenza 1, 2, 3 and 4; enterovirus infections and others. We remove these features since the dependence of the diagnosis on a variety of other infectious diseases for COVID-19 prediction is not a practical situation in the emergency context. Furthermore, a false negative result of one of these diseases would generate a spread of the error.
However, the diagnostic results for the others infectious diseases could be used to train a multiple output classifier, which may assist the health professional in the process of diagnosing simultaneous diseases. But this is not the focus of this work.
The set of final features were detailed in Table 1. After the cleaning process, we found a total of 608 observations, being 84 positive and 524 negative COVID-19 confirmed cases through RT-PCR being, thus, an imbalanced data problem. The distribution for each class is approximately 1:6 ratio. Since many null values remained, it was necessary an imputation technique to deal with. The “Iterative Imputer” technique from Scikit-learn package [44] showed the best performance in experimental tests compared with mean or median.
Table 1.
Description of the features used, abbreviation (Abb.) often used/adopted, reference values for male and female, missing rates (Miss. %) and some related references that reported the feature's relationship with COVID-19.
| Abb. | Feature | Description | Reference Value |
Miss. % | Ref | |
|---|---|---|---|---|---|---|
| Female | Male | |||||
| HCT | Hematocrit | The amount of whole blood that is made up of red blood cells | 36–46% | 41–53% | 0.82 | [11,35] |
| HGB | Hemoglobin | It is the oxygen-carrying component of red blood cells | 12–16 g/dL | 13.5–17.5 g/dL | 0.82 | [11,35] |
| PLT | Platelets | A tiny, disc-shaped piece of cell that helps form blood clots to slow or stop bleeding and to help wounds heal | 150–400 | 150–400 | 0.98 | [6,10,35] |
| RBC | Red blood Cells | The blood cell that carries oxygen | 3.5–5.5 | 4.3–5.9 | 0.98 | [35] |
| LYM | Lymphocytes | A type of white blood cells | 0.5–4.0 | 0.5–4.0 | 0.98 | [10,21,36] |
| MCH | Mean corpuscular hemoglobin | It corresponds to the average hemoglobin weight in a population of erythrocytes | 25.4–34.6 pg/cell | 25.4–34.6 pg/cell | 0.98 | [11,35] |
| MCHC | MCH concentration | Mean of the internal hemoglobin concentration in a population of erythrocytes | 31–36% Hb/cell | 31–36% Hb/cell | 0.98 | [11,35] |
| WBC | Leukocytes | White Blood Cells that help the body fight infections and other diseases. | 4500–11000 | 4500–11000 | 0.98 | [11,12,34,35] |
| BAY | Basophils | Type of white blood cell (leukocyte) with coarse, bluish-black granules of uniform size within the cytoplasm | 0.0–0.1 | 0.0–0.1 | 0.98 | [13,36] |
| EOS | Eosinophils | Normal type of white blood cell that has coarse granules within its cytoplasm | 0.1–0.5 | 0.1–0.5 | 0.98 | [11,36,37] |
| LDH | Lactate dehydrogenase | Enzyme of the anaerobic metabolic pathway, that catalyzes the conversion of lactate to pyruvate, important in energy production | 140–280 U/L | 140–280 U/L | 0.98 | [23,38] |
| MCV | Mean corpuscular volume | Average volume of an erythrocyte population | 80–100 | 80–100 | 0.98 | [35] |
| RWD | Red blood cell distribution width | A measurement of the range in the volume and size of red blood cells | <15% | <15% | 0.98 | [39] |
| MONO | Monocytes | A type of immune cell that has a single nucleus and fights off bacteria, viruses and fungi | 0.3–0.8 | 0.3–0.8 | 1.15 | [39] |
| MPV | Mean platelet volume | Average size of platelets | 7.2–11.7 fL | 7.2–11.7 fL | 1.48 | [40] |
| NEU | Neutrophils | A type of immune cell that is one of the first cell types to travel to the site of an infection and help by ingesting microorganisms and releasing enzymes that kill them | 1.8–7.7 | 1.8–7.7 | 15.62 | [10,16,20,34,39] |
| CRP | C-reactive protein | Plasma protein produced by the liver and induced by various inflammatory mediators such as interleukin-6 | <10 mg/L | <10 mg/L | 16.77 | [6,8,10,20,21,34] |
| CREAT | Creatinine | A chemical waste molecule generated from muscle metabolism. | 44–97 μmol/L | 53–106 μmol/L | 30.26 | [11,13,13,41] |
| UREA | Urea | A nitrogen-containing substance normally cleared from the blood by the kidney into the urine. | 2.5–7.1 mmol/L | 2.5–7.1 mmol/L | 34.70 | [11,20] |
| K+ | Potassium | A metallic element that is important in body functions such as regulation of blood pressure | 3.5–5.5 mEq/L | 3.5–5.5 mEq/L | 38.98 | [42] |
| Na | Sodium | A mineral needed by the body to keep body fluids in balance | 135–145 mmol/L | 135–145 mmol/L | 39.14 | [34] |
| AST | Aspartate transaminase | An enzyme found in the liver, heart, and other tissues. A high level of AST released into the blood may be a sign of liver or heart damage, cancer, or other diseases | 0–35 U/L | 0–35 U/L | 62.82 | [6,20,34] |
| ALT | Alanine transaminase | An enzyme that is normally present in liver and heart cells and it is released into blood when the liver or heart is damaged | <41.0 U/L | <31.0 U/L | 62.99 | [6,20] |
5.3. Evaluation of predictive models
In this paper, we use as a baseline the state-of-the-art of Logistic Regression [45], XGBoost [46] and Random Forest [47], since these algorithms have shown good results in problems with imbalanced data, as in Refs. [8,11,13,21]. We also tested the SVM and MLP methods.
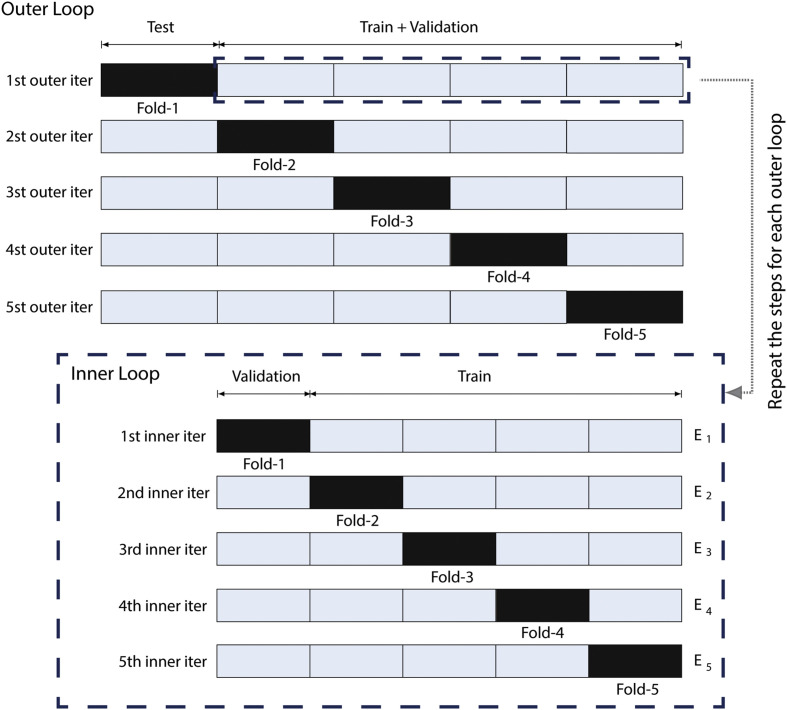
We train and evaluate these models through a nested cross-validation procedure [48]. As illustrated in Fig. 4 , first, in each iteration, the dataset is stratified between two subsets: training + validation and test set. In the inner loop, training + validation are divided into k folds and the model being trained in partitions. The other fold, which does not participate in the training, is used for model validation and for selecting the best set of hyperparameters through the Grid Search algorithm. At the end of an iteration, the model is evaluated in the test set. In the outer loop, this process is repeated in other different training + validation and test set folds, mutually exclusive. The nested cross-validation method, in this way, allows a more reliable evaluation of the model generalization.
Fig. 4.
The nested cross validation method.
For the evaluation of the models, we chose the known f1–score [49] to measure the best set of hyperparameters. Since 524 patient observations had no detection of the SARS-CoV-2 (86% of the dataset), the evaluation of accuracy does not provide a representative measure. F1–score, in its turn, provides a measure of the discrimination capacity of the models.
For the RF algorithm, we vary the number of estimators in the set of trees, while we change the maximum depth of the tree in the set of . For the XGBoost, the same set of hyperparameters was applied, adding a learning rate of . For the SVM, we vary the cost hyperparameter in the set of and linear and rbf kernels. In the MLP algorithm, we test hidden layers of size and , with constant or adaptive learning rate. We define the hyperparameter alpha in the set of .
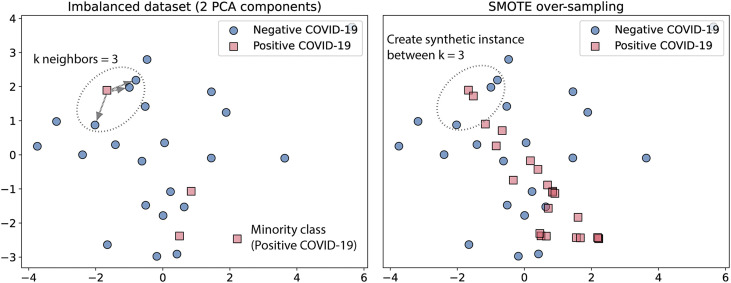
We train each algorithm using the SVM–Synthetic Minority Over-sampling Technique (SVM–SMOTE) [50]. Through this technique, minority class data are synthetically over-sampled, presenting for the training subset the same proportion of instances for the positive and the negative class. Resampling by this technique is performed by creating a synthetic sample between the k neighbors closest to the instance, as shown in Fig. 5 . For this task, we select a number of neighbors.
Fig. 5.
Example of synthetic sample generated by SMOTE.
Through the nested cross-validation method, we generate five final models for each algorithm, which correspond to the number of external partitions. Thus, we choose the best of the five models generated for each method and retrain it in 10 iterations using the selected hyperparameters to measure their ability to generalize. For each iteration, we split the data in 80% for training and the rest for the test set. Considering the imbalanced data, we applied the SMOTE again, but only for the training data, for each of the interactions, synthetically super-sampling the minority class data.
5.4. Ensemble
To compose the ensemble, we combine the best nested cross-validation models of RF, LR, XGBoost, SVM, and MLP. The label was predicted based on the majority voting decision. For weighting the votes, the model that obtained the best performance received a weight equal 2 and the worst one a weight equal 0.
After generating the ensemble, we evaluated the combined models in each test subset of the 10 iterations, using the following evaluation metrics: accuracy, f1–score, sensitivity and specificity. In the end, the average and standard deviation values are calculated for each of the metrics, obtaining the result that represents the model's generalization.
5.5. Explainability
We propose a methodology to provide a local explanation of the black box model using a single decision tree. In this step, we performed the following experiments:
-
1
Select a test instance for local explainability;
-
2
Generate new samples around the instance (noise set η);
-
3
Using the RF, classify the noise set and also the test instance;
-
4
The classification results are assigned as labels for these new samples;
-
5
With these labels and data, a DT is trained;
-
6
Then, the DT is used to provide a local explanation of the black-box model by taking the path in the tree that leads to the classification.
For global explanation, the local explanations obtained with DTX are aggregated over many instances to build the Criteria Graph (see section 4).
6. Results and discussion
Table 3 shows the results for the classification of COVID-19 using the metrics accuracy, f1–score, sensitivity, specificity and area under the ROC curve (AUROC). We also summarize the classification results in the normalized confusion matrix per class (positive or negative) for each algorithm in Table 4 .
Table 3.
Results of the classification of COVID-19.
| Model/Score | Accuracy | F1–score | Sensitivity | Specificity | AUROC |
|---|---|---|---|---|---|
| LR | 0.820.03 | 0.710.05 | 0.730.13 | 0.840.02 | 0.850.05 |
| RF | 0.880.02 | 0.760.03 | 0.660.10 | 0.910.02 | 0.860.05 |
| XGBoost | 0.870.02 | 0.730.03 | 0.600.10 | 0.910.02 | 0.850.04 |
| SVM | 0.840.02 | 0.700.05 | 0.560.14 | 0.890.02 | 0.850.05 |
| MLP | 0.850.02 | 0.680.06 | 0.420.13 | 0.920.02 | 0.810.04 |
| Ensemble | 0.880.02 | 0.760.03 | 0.670.10 | 0.910.02 | 0.870.05 |
Table 4.
Normalized confusion matrices for the ML methods tested. For each actual class, the sum of the corresponding row is 1.00
| (a) LR | |||
| Predicted | |||
| Negative |
Positive |
||
| Actual | Negative | 0.84 | 0.16 |
| Positive |
0.26 |
0.74 |
|
| (b) RF | |||
| Predicted | |||
| Negative |
Positive |
||
| Actual | Negative | 0.91 | 0.09 |
| Positive |
0.34 |
0.66 |
|
| (c) XGBoost | |||
| Predicted | |||
| Negative |
Positive |
||
| Actual | Negative | 0.91 | 0.09 |
| Positive |
0.40 |
0.60 |
|
| (d) SVM | |||
| Predicted | |||
| Negative |
Positive |
||
| Actual | Negative | 0.89 | 0.11 |
| Positive |
0.44 |
0.56 |
|
| (e) MLP | |||
| Predicted | |||
| Negative |
Positive |
||
| Actual | Negative | 0.92 | 0.08 |
| Positive |
0.58 |
0.42 |
|
| (f) Ensemble | |||
| Predicted | |||
| Negative |
Positive |
||
| Actual | Negative | 0.90 | 0.10 |
| Positive | 0.35 | 0.65 | |
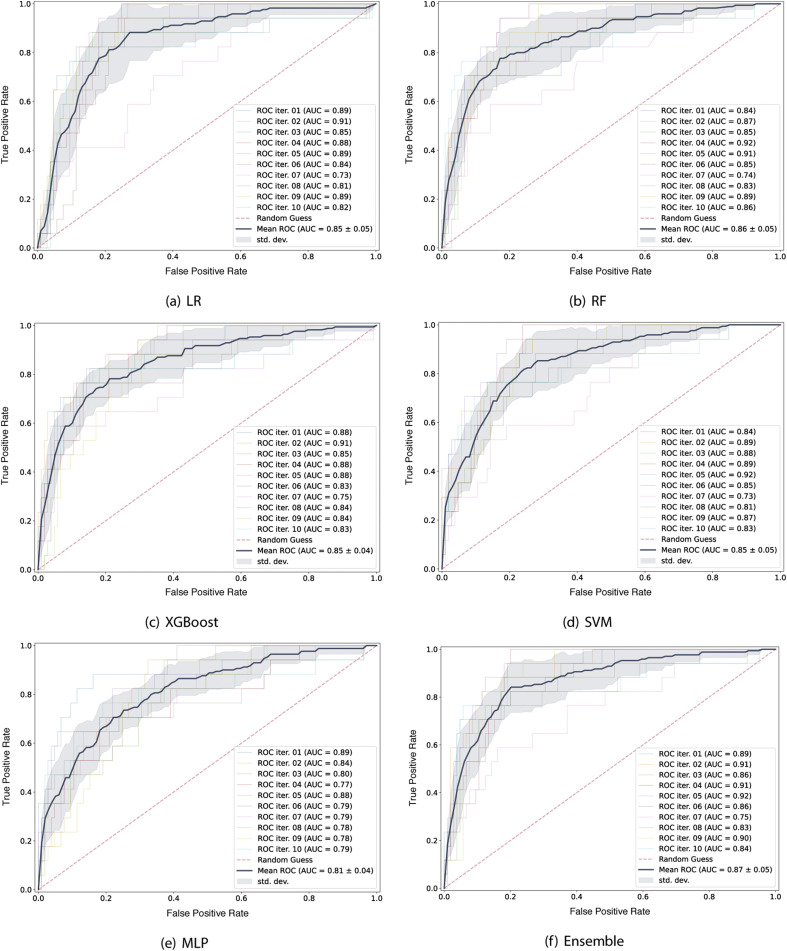
Fig. 6 shows the average of the ROC curve obtained for each one of the algorithms evaluated. This curve is computed by varying the decision threshold, obtaining true positive and false positive rates for each of them. The closer the area is to 1, the greater the discrimination capacity of the model in the diagnostic test.
Fig. 6.
AUROC for each algorithm.
Using the f1–score for comparison, the best models obtained were the RF, with maximum tree depth equal to 8 and 45 estimators, and the heterogeneous ensemble. In both models we obtain an f1–score of 76%. Thus, prioritizing simplicity, we chose the RF model to apply our proposed Criteria Graph for the global explanations and the DTX for the local explanations. For the RF model, in 9 of the 10 iterations, the area under the curve ROC was and the final average was equal to 0.86.
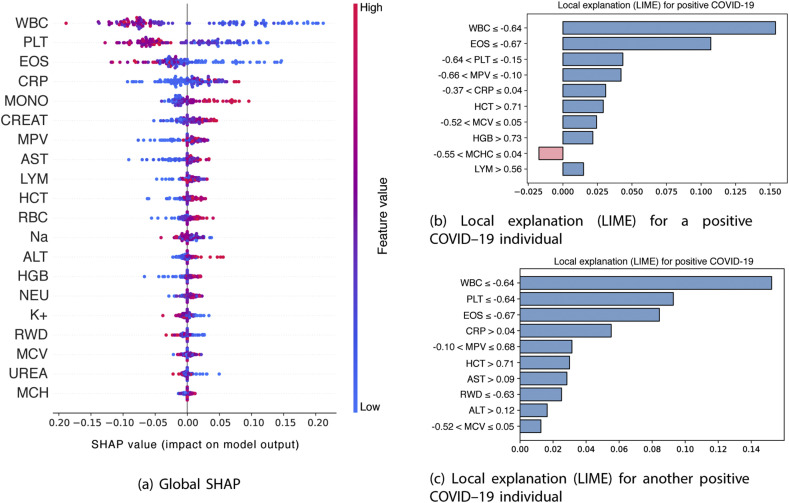
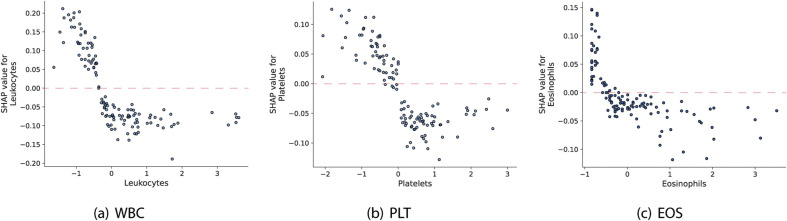
Fig. 7a shows the importance of the blood features for the model decision using the global SHAP values, which reflects the positive or negative contributions of each feature to the model output. A positive SHAP value represents a positive contribution to the target variable, while a negative SHAP value represents a negative contribution. These importances are classified in a descending way, suggesting that the main features that contributed to the target variable are the WBC, PLT and the EOS.
Fig. 7.
Explanations provided by SHAP and LIME
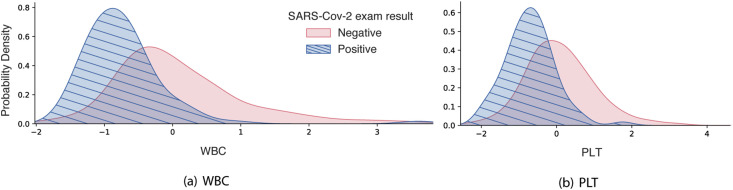
In addition to this information, the coloring of the points on the chart is related to the normalized values of the blood parameters of the patient, such as the number of WBC. The closer to blue, the lower the value of the characteristic and the closer to pink, the higher its value. Thus, a low value of the number of WBC, as well as the number of PLT, seen in blue, tends to positively impact the positive COVID–19 output. To corroborate this result, Fig. 8 shows the kernel density estimate for each of these two variables, for visualizing the distribution of observations of SARS–CoV–2 exam result across the dataset. For WBC and PLT values there is a central tendency around normalized values lowest of these characteristics. This is consistent with the literature, that suggest that the platelet count may reflect the pathological changes of patients with COVID–19 [51]. This tendency is also observed for EOS and the eosinopenia, characterized low EOS levels, appear to be related to disease severity [52]. In the case of CRP, higher values of this marker tend to positively impact the positive COVID–19 output.
Fig. 8.
Kernel density estimation of WBC and PLT.
Fig. 7b and c shows examples of local explanations for two different patients with COVID-19, using the Local Interpretable Model–agnostic Explanations (LIME). This algorithm works by generating new samples around the instance to be explained and obtaining the prediction of the local noise using the original model. Then, based on the proximity to the given instance, the sample is weighted and a linear regression is constructed using these new samples and the considered instance. Through this method, the learned linear model is valid on a local scale.
The bars pointing to the right in Fig. 7b and c displays the features that have a positive correlation with the output, while the bars on the left show the features that have a negative correlation. Thus, for the two patients, low WBC values (with WBC -0.64) and low EOS values (with EOS -0.67) have a positive correlation with the positive COVID–19, according to LIME explanations.
We also show the values of the first three most important blood parameters presented in Fig. 7a as a function of the corresponding SHAP value (Fig. 9 ), which represents the marginal effect that these features have on the predicted result of the model. Values of the normalized number of WBC, PLT and EOS above the highlighted lines, tend to contribute to increasing the probability of the positive class.
Fig. 9.
Marginal effect of blood features on the target variable.
6.1. Decision–tree based explainer and criteria graph
Table 5 shows the rules for the decision tree-based explainer for 12 positive COVID–19 patients which reflect the models behaviour. Since the explanations are local and built with high fidelity to the high accuracy model, differently from Refs. [8,21] one does not have to compromise accuracy. Also, the decisions trees allow us to represent non-linear behaviour which is an advantage against LIME.
Table 5.
Explanations for the COVID-19 inference of the 12 COVID-19 positive patients in the test set.
| ID | Decision Tree Explanation |
|---|---|
| 1 | EOS -0.51 and PLT 0.16 and CRP -1.74 and EOS -0.61 and MPV -0.82 and NEU -0.42 and MCHC 1.90 |
| 2 | CRP -0.43 and EOS 0.63 and AST -0.41 and UREA -0.91 and MCV 0.12 and CREAT -0.88 and K+ -0.52 |
| 3 | EOS 0.54 and WBC -0.97 and MCV -0.13 and ALT 2.13 and CRP -0.51 and PLT -2.98 and HGB 0.96 and Sodium 0.12 |
| 4 | AST -0.43 and CRP -0.46 and PLT 0.26 and WBC -0.44 and LYM -1.29 and EOS 0.76 and CREAT -0.75 and PLT 0.06 and AST -0.37 and PLT -3.57 |
| 5 | EOS -0.59 and CRP -0.53 and PLT -0.33 and CREAT -0.30 and AST -0.34 and EOS 0.39 and MONO -0.49 and WBC -0.58 and LYM 1.11 and HCT -0.50 |
| 6 | CRP -0.50 and MPV -0.99 and EOS 0.82 and PLT 0.21 and LYM -1.17 and CREAT -0.64 and EOS 0.37 and WBC -0.40 and HGB 0.44 and PLT -4.22 |
| 7 | CRP -0.52 and PLT 0.08 and EOS -0.07 and HGB -0.83 and CREAT -0.87 and EOS -0.67 and RBC -1.02 and MONO -0.16 |
| 8 | HGB -0.83 and LYM -1.13 and CRP -0.47 and CREAT -0.48 and HCT -1.09 and EOS 0.77 and AST 0.23 and MCV -6.31 and WBC -0.88 and PLT -0.05 |
| 9 | EOS -0.59 and PLT -0.08 and MPV -1.00 and HCT 0.48 and UREA 2.35 and WBC -1.04 and MPV -0.97 and MCHC -1.08 |
| 10 | EOS -0.55 and PLT 0.13 and MPV -1.02 and WBC 0.09 and PLT -0.11 and ALT -1.13 and WBC -0.29 and MONO -0.28 |
| 11 | EOS -0.62 and AST -0.46 and EOS 0.52 and WBC -0.47 and CREAT -0.46 and CRP -0.68 and PLT -0.04 and MONO -0.03 and MCH -1.77 and AST 1.04 |
| 12 | PLT 0.10 and MPV -1.04 and EOS -0.54 and MPV -1.01 and WBC -0.58 and LYM -1.48 and MCH -1.48 and HGB 1.07 and ALT -0.54 and MCHC -0.22 |
It can be seen that the model uses different criteria to “diagnose” each patient. This indicates that the COVID-19 affects a number of parameters in the blood and that the variation of these parameters is individual dependent.
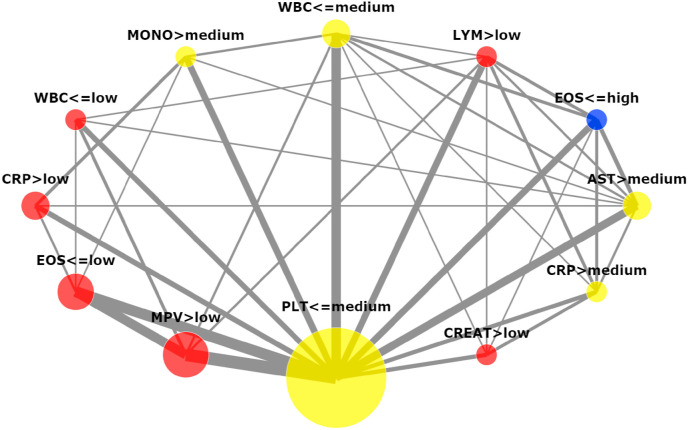
Looking at the set of rules it is hard to identify patterns that can be important in the search for a more universal and robust diagnosis methodology. For these reasons, the criteria graph (Section 4) was built for the explanations described in Table 5 and can be visualized in Fig. 10 . Different from LIME [26] and SHAP [27], the Criteria Graph not only shows the importance of the features (the area of the nodes which they represent) but also how the features are inter-connected.
Fig. 10.
Criteria Graph for the decision tree explanations. Only factors and interactions that appeared in more than one third of the patients are depicted.
The five largest nodes in the criteria graph correspond to PLT, MPV, EOS, CRP, and AST. Meanwhile, the 5 most important attributes according to their SHAP values (see Fig. 7a) were WBC, PLT, EOS, CRP and MONO. Notice that there is a lot of overlap between the two rankings. Although WBC does not figure in the top five attributes, it has two nodes in the graph. That means that the WBC was important for the inference but its threshold value was not very clear. Thus, it seems to make sense that as a whole the attribute loses strength. The graph also shows a strong relationship between the criteria , and pointing to a route towards a more reliable diagnosis procedure.
Increasing the number of patients used to produce the graph may increase the strength of the identified patterns. Nevertheless, the Criteria Graph provides information that other explanation methods lack and that this information may be extremely useful for the application expert. For instance, neither SHAP [27] nor LIME [26] present information about features interactions.
In Fig. 7b and c it can be seen that LIME presents information about the thresholds used in the classification. However, as it happens with the DTX, the information is only local (individual dependent). The criteria graph addresses this drawback by aggregating the results of all the explanations.
SHAP can inform the user about possible feature thresholds with the marginal effects plot as shown in Fig. 9. Such approach can be cumbersome if the number of features is high. In this context, the criteria graph is able to more clearly show the robustness of the thresholds by compressing the information about each feature in few nodes which are all displayed in a single plot. Thus, the amount artefacts presented to the user is reduced which tends to reduce the analysis time.
6.2. Practical application
As aforementioned stated, the RF and heterogeneous ensemble models achieved the best results. Looking for the simplest model (often called parsimony), we follow with the RF as the preferred one plus the Criteria Graph for global explanations and DTX for local ones. Utilizing a web application, the healthcare professional may be able to input the patient's blood test results (similar, for instance, with that available in Ref. [13]). The system may be able, for instance, (i) to provide for the decision-maker both the results (infected or not), (ii) shows the rules to facilitate her/his valuable interpretation regarding local and global explanations, (iii) to be pre-configured to streamline the medical work and provide faster and more reliable diagnostics and (iv) offer intelligent prescription, which can be filled automatically in the correct standards of the medical prescription. The implementation must be focused on reusing the code, since once new strains of the virus are appearing, adaptations in the code/system may be required to make it useful in the future.
There are many advantages of using electronic medical records, such as security and availability of patient information, standardization/integration of data, and automation of procedures, to name a few. We know that SARS-CoV-2 is highly transmissible and rapid tests are already in place to diagnose the disease. Therefore, we emphasize that the proposed solution has the objective of supporting the decision making of clinicians, providing more information for helping them. Moreover, a considerable differential of the proposed methodology is the presentation of explanations of the model, making such information comprehensible to the health professional, being able to assist her/him in the final result of the diagnosis.
7. Conclusion
Recent research suggests that some parameters assessed in routine blood tests are indicative of COVID-19. It is well known that machine learning techniques excel in finding correlations in all sorts of data. Thus, it seems natural to try these techniques for the problem of COVID-19 screening through routine blood test data. However, there is significant barrier to the application of such methods in the real world due to their lack of transparency, meaning that human specialists may find it difficult to trust the ML decisions.
In this context, in this work, we search for an accurate machine learning model for COVID-19 screening based on hematological data and propose two methods to improve the interpretability of the ML decisions, a Decision Tree Explainer and a Criteria Graph. The decision Tree Explainer is used to provide an individual explanation for each classified sample in terms of If … then rules. The Criteria Graph is used to aggregate the set of rules produced by the decision tree to provide a global picture of the criteria that guided the model decisions and show the interactions among these criteria.
From the tested ML techniques, the best results were obtained with a RF which is an opaque model. It presented an accuracy of 0.88 0.02, F1–score of 0.76 0.03, Sensitivity of 0.66 0.10, and Specificity 0.91 0.02. The Decision Tree was then used to produce explanations for the classification of twelve confirmed COVID-19 cases and finally, the Criteria Graph was used to aggregate the explanations and portrait a global picture of the model results. The obtained Criteria Graph was in accordance with the well know techniques for interpretability SHAP and LIME indicating its adequacy and the adequacy of the Decision Tree Explainers. In addition, it could be seen that the Criteria Graph presents valuable information, such as the interaction among different criteria and the robustness of a criteria with respect to its threshold value, which is not provided by other techniques.
Given the urgency of the pandemic and the need to generate immediate results, much of the research has been published in repositories such as arXiv or medRxiv. Some methodologies discussed in the literature review are not clear enough to be reproducible or the model decision is not comprehensible. Lastly, we made comparisons between our proposed work and others from the literature that have not been peer-reviewed and published yet in the scientific literature. However, their data confirm our finding that ML models using routine blood parameters are useful in the diagnosis of COVID-19.
7.1. Future work
We employed hematological data from the Hospital Israelita Albert Einstein in São Paulo, Brazil, which is available as public data. However, this data is arguably not large and it is normalized (using z-normalization). Since we do not have access to the values used to normalize the data, the original values of the features are not accessible. Applying the proposed methods with larger data is an important step in our future work.
Still, the solution we offer brings good results, it is reproducible and the model explainable. Additionally, we intend to integrate it with other fronts, such as chest X-rays and CT scans. In this way, ML models may serve as a way to support the diagnosis of the disease, regardless of the stage of contagion, and can help in the validation of RT-PCR.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
M.A. Alves, G.Z. de Castro and B.A.S. Oliveira declare that this work has been supported by the Brazilian agency CAPES (Coordination of Improvement of Higher Education Personnel).
J.A. Ramírez, R. Silva and F.G. Guimarães declare that this work has been supported by the Brazilian agencies CAPES, CNPq (National Council for Scientific and Technological Development).
Footnotes
In medical diagnosis, specificity refers to the potential of a test to correctly identify those without the disease (true negative rate), whereas sensitivity refers to the potential of a test to correctly detect those with the disease (true positive rate).
References
- 1.World Health Organization . 2020. Coronavirus Disease (Covid-19) Pandemic.https://www.who.int/emergencies/diseases/novel-coronavirus-2019 URL. [Google Scholar]
- 2.Zimmermann K., Mannhalter J.W. Technical aspects of quantitative competitive pcr. Biotechniques. 1996;21:268–279. doi: 10.2144/96212rv01. [DOI] [PubMed] [Google Scholar]
- 3.Ai T., Yang Z., Hou H., Zhan C., Chen C., Lv W., Tao Q., Sun Z., Xia L. 2020. Correlation of Chest Ct and Rt-Pcr Testing in Coronavirus Disease 2019 (Covid-19) in china: a Report of 1014 Cases; p. 200642. Radiology. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Meng Z., Wang M., Song H., Guo S., Zhou Y., Li W., Zhou Y., Li M., Song X., Zhou Y., et al. medRxiv; 2020. Development and Utilization of an Intelligent Application for Aiding Covid-19 Diagnosis. [Google Scholar]
- 5.Bullock J., Pham K.H., Lam C.S.N., Luengo-Oroz M., et al. 2020. Mapping the Landscape of Artificial Intelligence Applications against Covid-19; p. 11336. arXiv preprint arXiv:2003. [Google Scholar]
- 6.Ferrari D., Motta A., Strollo M., Banfi G., Locatelli M. Routine blood tests as a potential diagnostic tool for covid-19. Clin. Chem. Lab. Med. 2020;1 doi: 10.1515/cclm-2020-0398. [DOI] [PubMed] [Google Scholar]
- 7.Kanne J.P., Little B.P., Chung J.H., Elicker B.M., Ketai L.H. 2020. Essentials for Radiologists on Covid-19: an Update—Radiology Scientific Expert Panel. Radiology. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Brinati D., Campagner A., Ferrari D., Locatelli M., Banfi G., Cabitza F. Detection of covid-19 infection from routine blood exams with machine learning: a feasibility study. J. Med. Syst. 2020;44:1–12. doi: 10.1007/s10916-020-01597-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Batista A.F.d.M., Miraglia J.L., Donato T.H.R., Chiavegatto Filho A.D.P. 2020. Covid-19 Diagnosis Prediction in Emergency Care Patients: a Machine Learning Approach. medRxiv. [Google Scholar]
- 10.Kermali M., Khalsa R.K., Pillai K., Ismail Z., Harky A. Life Sciences; 2020. The Role of Biomarkers in Diagnosis of Covid-19–A Systematic Review; p. 117788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kukar M., Gunčar G., Vovko T., Podnar S., Černelč P., Brvar M., Zalaznik M., Notar M., Moškon S., Notar M. 2020. Covid-19 Diagnosis by Routine Blood Tests Using Machine Learning. arXiv preprint arXiv:2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zheng H.-Y., Zhang M., Yang C.-X., Zhang N., Wang X.-C., Yang X.-P., Dong X.-Q., Zheng Y.-T. Elevated exhaustion levels and reduced functional diversity of t cells in peripheral blood may predict severe progression in covid-19 patients. Cell. Mol. Immunol. 2020;17:541–543. doi: 10.1038/s41423-020-0401-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wu J., Zhang P., Zhang L., Meng W., Li J., Tong C., Li Y., Cai J., Yang Z., Zhu J., et al. 2020. Rapid and Accurate Identification of Covid-19 Infection through Machine Learning Based on Clinical Available Blood Test Results. medRxiv. [DOI] [Google Scholar]
- 14.Barbosa V.A.d.F., Gomes J.C., Santana M.A., Almeida Albuquerque J.E., Souza R.G., Souza R.E., Santos W.P., ia Heg. 2020. An Intelligent System to Support Diagnosis of Covid-19 Based on Blood Tests. medRxiv. [Google Scholar]
- 15.Barbosa V.A.d.F., Gomes J.C., Santana M.A., Lima C.L., et al. 2020. Covid-19 Rapid Test by Combining a Random Forest Based Web System and Blood Tests. medRxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhang N., Zhang R., Yao H., Xu H., Duan M., Xie T., Pan J., Huang J., Zhang Y., Xu X., et al. SSRN; 2020. Severity Detection for the Coronavirus Disease 2019 (Covid-19) Patients Using a Machine Learning Model Based on the Blood and Urine Tests.https://ssrn.com/abstract=3564426 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Toledo S.L.d.O., Nogueira L.S., Carvalho M.d.G., Rios D.R.A., Pinheiro M.d.B. Covid-19: review and hematologic impact. Clin. Chim. Acta. 2020;510:170–176. doi: 10.1016/j.cca.2020.07.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Silveira E.C. Prediction of covid-19 from hemogram results and age using machine learning. Frontiers in Health Informatics. 2020;9:39. doi: 10.30699/fhi.v9i1.234. [DOI] [Google Scholar]
- 19.Silveira E.C. Prediction of covid-19 from hemogram results and age using machine learning. Iranian Journal of Medical Informatics. 2020;9 [Google Scholar]
- 20.Mardani R., Vasmehjani A.A., Zali F., Gholami A., Nasab S.D.M., Kaghazian H., Kaviani M., Ahmadi N. Laboratory parameters in detection of covid-19 patients with positive rt-pcr: a diagnostic accuracy study. Archives of Academic Emergency Medicine. 2020;8 [PMC free article] [PubMed] [Google Scholar]
- 21.Yan L., Zhang H.-T., Xiao Y., Wang M., Sun C., Liang J., et al. 2020. Prediction of Criticality in Patients with Severe Covid-19 Infection Using Three Clinical Features: a Machine Learning-Based Prognostic Model with Clinical Data in Wuhan. MedRxiv. [DOI] [Google Scholar]
- 22.Bhandari S., Shaktawat A.S., Tak A., Patel B., Shukla J., Singhal S., Gupta K., Gupta J., Kakkar S., Dube A., et al. Logistic regression analysis to predict mortality risk in covid-19 patients from routine hematologic parameters. Ibnosina J. Med. Biomed. Sci. 2020;12:123. [Google Scholar]
- 23.Henry B.M., Aggarwal G., Wong J., Benoit S., Vikse J., Plebani M., Lippi G. Lactate dehydrogenase levels predict coronavirus disease 2019 (covid-19) severity and mortality: a pooled analysis. Am. J. Emerg. Med. 2020 doi: 10.1016/j.ajem.2020.05.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ferreira L.A., Guimarães F.G., Silva R. 2020 IEEE Congress on Evolutionary Computation (IEEE CEC 2020) IEEE; 2020. Applying genetic programming to improve interpretability in machine learning models. [DOI] [Google Scholar]
- 25.Molnar C. 2019. Interpretable Machine Learning.https://christophm.github.io/interpretable-ml-book/ URL. [Google Scholar]
- 26.Ribeiro M.T., Singh S., Guestrin C. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ‘16. Association for Computing Machinery; New York, NY, USA: 2016. “Why should I trust you?”: explaining the predictions of any classifier; pp. 1135–1144. [DOI] [Google Scholar]
- 27.Lundberg S.M., Lee S.-I. In: Advances in Neural Information Processing Systems 30. Guyon I., Luxburg U.V., Bengio S., Wallach H., Fergus R., Vishwanathan S., Garnett R., editors. Curran Associates, Inc.; 2017. A unified approach to interpreting model predictions; pp. 4765–4774. [Google Scholar]
- 28.Mohamadou Y., Halidou A., Kapen P.T. A review of mathematical modeling, artificial intelligence and datasets used in the study, prediction and management of covid-19. Appl. Intell. 2020;50:3913–3925. doi: 10.1007/s10489-020-01770-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Silva P.C., Batista P.V., Lima H.S., Alves M.A., Guimarães F.G., Silva R.C. Covid-abs: an agent-based model of covid-19 epidemic to simulate health and economic effects of social distancing interventions, Chaos. Solitons & Fractals. 2020;139:110088. doi: 10.1016/j.chaos.2020.110088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wynants L., Van Calster B., Bonten M.M., Collins G.S., Debray T.P., De Vos M., Haller M.C., Heinze G., Moons K.G., Riley R.D., et al. Prediction models for diagnosis and prognosis of covid-19 infection: systematic review and critical appraisal. BMJ. 2020;369 doi: 10.1136/bmj.m1328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zheng Z., Peng F., Xu B., Zhao J., Liu H., Peng J., Li Q., Jiang C., Zhou Y., Liu S., et al. Risk factors of critical & mortal covid-19 cases: a systematic literature review and meta-analysis. J. Infect. 2020 doi: 10.1016/j.jinf.2020.04.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tian W., Jiang W., Yao J., Nicholson C.J., Li R.H., Sigurslid H.H., Wooster L., Rotter J.I., Guo X., Malhotra R. Predictors of mortality in hospitalized covid-19 patients: a systematic review and meta-analysis. J. Med. Virol. 2020;92:1875–1883. doi: 10.1002/jmv.26050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shi F., Wang J., Shi J., Wu Z., Wang Q., Tang Z., He K., Shi Y., Shen D. Review of artificial intelligence techniques in imaging data acquisition, segmentation and diagnosis for covid-19. IEEE Reviews in Biomedical Engineering. 2020 doi: 10.1109/RBME.2020.2987975. [DOI] [PubMed] [Google Scholar]
- 34.Assaf D., Gutman Y., Neuman Y., Segal G., Amit S., Gefen-Halevi S., Shilo N., Epstein A., Mor-Cohen R., Biber A., et al. 2020. Utilization of Machine-Learning Models to Accurately Predict the Risk for Critical Covid-19, Internal and Emergency Medicine; pp. 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dean L., Dean L. vol. 2. NCBI; Bethesda, Md, USA: 2005. (Blood Groups and Red Cell Antigens). [Google Scholar]
- 36.NHSFoundation . 2020. Full Blood Count (Fbc) Reference Ranges.https://www.yorkhospitals.nhs.uk/seecmsfile/?id=2396 URL. [Google Scholar]
- 37.Xiuli Ding M., Geqing Xia M., Zhi Geng M., Wang Z., Wang L. medRxiv; 2020. A Simple Laboratory Parameter Facilitates Early Identification of Covid-19 Patients. [DOI] [Google Scholar]
- 38.Farhana A., Lappin S.L. StatPearls. StatPearls Publishing; 2020. Biochemistry, lactate dehydrogenase (ldh) [Internet] [PubMed] [Google Scholar]
- 39.Lichtman M.A., Kaushansky K., Prchal J.T., Levi M.M., Burns L.J., Armitage J. McGraw Hill Professional; 2017. Williams Manual of Hematology. [Google Scholar]
- 40.Demirin H., Ozhan H., Ucgun T., Celer A., Bulur S., Cil H., Gunes C., Yildirim H.A. Normal range of mean platelet volume in healthy subjects: insight from a large epidemiologic study. Thromb. Res. 2011;128:358–360. doi: 10.1016/j.thromres.2011.05.007. [DOI] [PubMed] [Google Scholar]
- 41.Pagana K.D., Pagana T.J. Elsevier Health Sciences; 2012. Mosby's Diagnostic and Laboratory Test Reference-E-Book. [Google Scholar]
- 42.Rastegar A. Clinical Methods: the History, Physical, and Laboratory Examinations. third ed. 1990. Serum potassium. Butterworths. [Google Scholar]
- 43.Hospital Israelita Albert Einstein Diagnosis of Covid-19 and its Clinical Spectrum - Ai and Data Science Supporting Clinical Decisions (From 28th Mar to 3st Apr) https://www.kaggle.com/einsteindata4u/covid19,2020.Online
- 44.Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V., et al. Scikit-learn: machine learning in python. J. Mach. Learn. Res. 2011;12:2825–2830. [Google Scholar]
- 45.Hosmer D.W., Jr., Lemeshow S., Sturdivant R.X. vol. 398. John Wiley & Sons; 2013. (Applied Logistic Regression). [Google Scholar]
- 46.Chen T., Guestrin C. Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining. ACM; 2016. Xgboost: a scalable tree boosting system; pp. 785–794. [DOI] [Google Scholar]
- 47.Ho T.K. vol. 1. IEEE; 1995. Random decision forests; pp. 278–282. (Proceedings of 3rd International Conference on Document Analysis and Recognition). [DOI] [Google Scholar]
- 48.Cawley G.C., Talbot N.L. On over-fitting in model selection and subsequent selection bias in performance evaluation. J. Mach. Learn. Res. 2010;11:2079–2107. [Google Scholar]
- 49.Jeni L.A., Cohn J.F., De La Torre F. 2013 Humaine Association Conference on Affective Computing and Intelligent Interaction. IEEE; 2013. Facing imbalanced data–recommendations for the use of performance metrics; pp. 245–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Chawla N.V., Bowyer K.W., Hall L.O., Kegelmeyer W.P. Smote: synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002;16:321–357. doi: 10.1613/jair.953. [DOI] [Google Scholar]
- 51.Zhao X., Wang K., Zuo P., Liu Y., Zhang M., Xie S., Zhang H., Chen X., Liu C. Early decrease in blood platelet count is associated with poor prognosis in covid-19 patients—indications for predictive, preventive, and personalized medical approach. EPMA J. 2020:1. doi: 10.1007/s13167-020-00208-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Sun Y., Dong Y., Wang L., Xie H., Li B., Chang C., Wang F.-s. Characteristics and prognostic factors of disease severity in patients with covid-19: the beijing experience. J. Autoimmun. 2020;112:102473. doi: 10.1016/j.jaut.2020.102473. [DOI] [PMC free article] [PubMed] [Google Scholar]