BhGLM: Bayesian hierarchical GLMs and survival models, with applications to genomics and epidemiology

Abstract

Summary

BhGLM is a freely available R package that implements Bayesian hierarchical modeling for high-dimensional clinical and genomic data. It consists of functions for setting up various Bayesian hierarchical models, including generalized linear models (GLMs) and Cox survival models, with four types of prior distributions for coefficients, i.e. double-exponential, Student-t, mixture double-exponential and mixture Student-t. These functions adapt fast and stable algorithms to estimate parameters. BhGLM also provides functions for summarizing results numerically and graphically and for evaluating predictive values. The package is particularly useful for analyzing large-scale molecular data, i.e. detecting disease-associated variables and predicting disease outcomes. We here describe the models, algorithms and associated features implemented in BhGLM.

Availability and implementation

The package is freely available from the public GitHub repository, https://github.com/nyiuab/BhGLM.

1 Introduction

Large-scale molecular data generated by high-throughput technologies have provided extraordinary opportunities for detecting disease-associated factors and improving outcome prediction (Collins and Varmus, 2015). However, there are considerable challenges in analyzing high-dimensional molecular and clinical data (Barillot et al., 2012), including (i) how to select disease-associated and predictive factors among numerous candidates, (ii) how to build a high-dimensional predictive model with accurate estimations of the parameters and (iii) how to integrate biological information. To address these challenges, efficient methods and computer software are crucially required.

Hierarchical modeling is the commonly used and efficient method for analyzing large-scale and structured data (Gelman et al., 2014). We have developed a series of Bayesian hierarchical models for analyzing large-scale molecular and clinical data (Tang et al., 2017a,b, 2018; Yi and Banerjee, 2009; Yi and Ma, 2012; Zhang et al., 2017, 2018), and released a freely available R package BhGLM that implements our methods. The package BhGLM provides functions for setting up and fitting various Bayesian hierarchical models, including generalized linear models (GLMs) for various continuous and discrete outcomes, ordinal models for ordinal outcomes and Cox survival models for censored survival outcomes. These functions are based upon the commonly used R functions, glm in stats, polr in MASS, and coxph in survival, for fitting conventional models (Venables and Ripley, 2002), and glmnet for analyzing high-dimensional data (Friedman et al., 2010; Simon et al., 2011). Thus, they incorporate the well-developed and powerful features of these standard tools. The algorithms implemented in BhGLM are fast and stable, particularly suitable for fitting large-scale models. BhGLM also supplies functions for summarizing fitted models numerically or graphically and for evaluating the predictive performance using cross-validation or sample-split methods. Thus, BhGLM provides a comprehensive framework for Bayesian hierarchical modeling with the focus on analyzing high-dimensional molecular and clinical data.

2 Models and algorithms

Bayesian analysis is based on the posterior distribution that is proportional to the product of the likelihood function and the prior distribution of parameters (Gelman et al., 2014):

$$p(\beta ,\varphi \left|y,X)=C p(y\right|\beta ,\varphi ,X)p(\beta ,\varphi )$$ (1)

where y and X represent observed values of outcome and predictors, respectively, β is a vector of coefficients (effects) of predictors, ϕ includes additional parameters (e.g. dispersion or other parameters) if existing, and C is a constant that can be ignored. The likelihood function p(y | β, ϕ, X) is set up as in the conventional framework, which is the generalized linear likelihood for GLMs including linear, Poisson, logistic regressions, etc., the ordinal regression likelihood for ordinal outcomes, and the Cox partial likelihood for survival models. The conventional analysis is to estimate the parameters only based on the likelihood function, which has been implemented in standard R functions, glm, polr and coxph. However, the conventional models cannot be directly applied to large-scale data.

The package BhGLM employs uniform prior on ϕ, and four types of informative priors on β. The first two priors are double-exponential and Student-t:

$${\beta }_j\sim \text{de}(0,\varphi s_j), \text{and} {\beta }_j\sim t_{\nu }(0,\varphi s_j)$$ (2)

where smaller scale s_j induces stronger shrinkage on β_j. The Student-t distribution includes normal (e.g. ν = +∞) and Cauchy (e.g. ν  =  1) distributions as special cases. Different scale values s_j can be specified for different predictors. If lacking prior information about the importance of the predictors, BhGLM takes a common scale s for all predictors and allows user to choose an optimal scale. The last two types of priors are spike-and-slab mixture double-exponential and Student-t distributions:

$${\beta }_j\sim \text{de}(0, \left(1-{\gamma }_j\right)s_0+{\gamma }_j{s}_1), \text{and} {\beta }_j\sim t_{\nu }(0, \left(1-{\gamma }_j\right)s_0+{\gamma }_j{s}_1)$$ (3)

where γ_j is the indicator variable and assumed to follow a binomial prior Bin(1, θ) with uniform prior on the probability parameter θ, s₀ and s₁ are chosen to be small and large, for modeling irrelevant and relevant coefficients, respectively. The spike-and-slab priors include the additional parameters γ_j and θ, which will be estimated along with the coefficients.

With appropriate scales, these four types of priors have long-tails and a peak at zero, thus performing less (strong) shrinkage for relevant (irrelevant) predictors and leading to robust inferences on large-scale data. The spike-and-slab priors not only induce different shrinkages on different coefficients, but also can incorporate biological pathway information by imposing group-specific priors on the indicator variables: γ_j ∼ Bin(1, θ_g) for the predictors in pathway g.

The BhGLM package estimates the parameters by maximizing the log joint posterior density log[p(β, ϕ | y, X)]. The functions, bglm, bpolr and bcoxph, fit Bayesian hierarchical GLMs, ordinal models and Cox survival models with the EM-IWLS, quasi-Newton (BFGS) and EM-Newton algorithms, respectively. These algorithms are fast and stable, while providing not only point estimates but also P-values for testing hypotheses β_j= 0. The function bmlasso fits GLMs and Cox survival models with the spike-and-slab priors using the EM coordinate decent algorithm, which estimates the coefficients to either zero or nonzero. Thus, it automatically performs variable selection.

3 Features

The package BhGLM constructs a comprehensive Bayesian hierarchical modeling toolset for analyzing various types of large-scale data. The functions, bglm, bpolr and bcoxph, are Bayesian counterparts of the functions, glm, polr and coxph, respectively, which accept the same basic syntax in these well-established functions and have additional arguments for hierarchical modeling. Thus, the data inputs and the likelihood specifications are the same as in these functions, which grant users to incorporate all the features of the well-established functions into the hierarchical framework. The function bmlasso works by repeated calls to the commonly used function glmnet, and thus incorporates the extremely fast coordinate decent algorithm into the EM procedure.

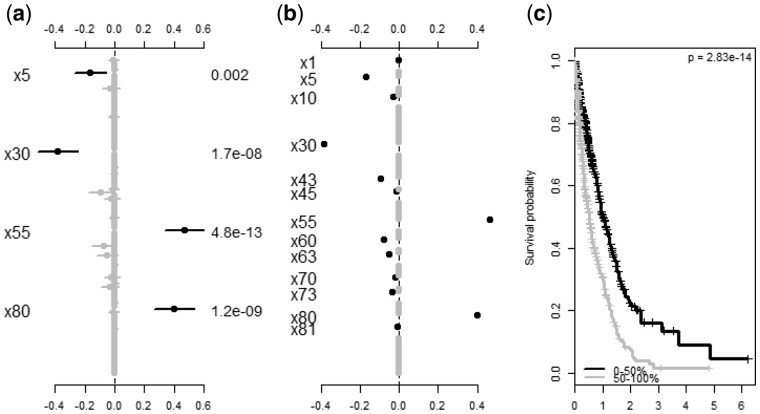
BhGLM streamlines the data analysis procedure with its ancillary functions that facilitate data preparation and result presentation. The covariates function allows users to transform the predictors to a roughly common scale and fill in missing data, which is a vital step in hierarchical modeling (Gelman et al., 2014). The function summary.bh numerically summarizes the output from the modeling functions, displaying the coefficient estimates, their standard errors and their P-values. The function plot.bh plots the outputs from bglm, bpolr, bcoxph and bmlasso, which uses different colors to distinguish between significant and insignificant predictors and assists users to visualize the effects of many predictors. Examples of plot.bh output are shown inFigure 1a and b.

Fig. 1.

Summary plots from analyzing simulated data: a censored survival outcome associated with four predictors (×5, ×30, ×55, ×80); (a) bcoxph: points, lines and values represent the coefficient estimates, 95% confidence intervals and P values, and only predictors with P values smaller than 0.01 are labeled; (b) bmlasso: points represent the coefficient estimates, and only predictors with non-zero estimates are labeled; (c) cv.bh and surv.curves: cross-validated survival curves for two groups of individuals

Lastly, the BhGLM package provides functions to evaluate a fitted model and its predictive performance. The function predict.bh calculates various measures for assessing the fitted model and also the predictive values for new data. The cv.bh function performs K-fold cross-validation to assess the predictive performance. BhGLM also includes functions, e.g. surv.curves, to visualize the predictive values (see Fig. 1c).

4 Discussion

We have developed a freely available R package BhGLM that provides a comprehensive framework for Bayesian hierarchical modeling with the focus on analyzing large-scale molecular and clinical data. The BhGLM package provides functions for setting up and fitting various Bayesian hierarchical models. It also can numerically and graphically summarize the results, and evaluate the predictive performance. BhGLM inherits the modeling interface from the standard R functions, granting simplicity and flexibility to users. Meanwhile, BhGLM adapts stable and fast algorithms, improving the computation efficiency when analyzing high-dimensional data. Overall, the package and the methods are versatile, which can be used to analyze both general data and large-scale data.

Funding

National Institute of Health (R01GM069430, R01CA216108) and the National Natural Science Foundation of China (81773541, 81573253).

Conflict of Interest: none declared.