EpistasisRank and EpistasisKatz: interaction network centrality methods that integrate prior knowledge networks

Abstract

Motivation

An important challenge in gene expression analysis is to improve hub gene selection to enrich for biological relevance or improve classification accuracy for a given phenotype. In order to incorporate phenotypic context into co-expression, we recently developed an epistasis-expression network centrality method that blends the importance of gene–gene interactions (epistasis) and main effects of genes. Further blending of prior knowledge from functional interactions has the potential to enrich for relevant genes and stabilize classification.

Results

We develop two new expression-epistasis centrality methods that incorporate interaction prior knowledge. The first extends our SNPrank (EpistasisRank) method by incorporating a gene-wise prior knowledge vector. This prior knowledge vector informs the centrality algorithm of the inclination of a gene to be involved in interactions by incorporating functional interaction information from the Integrative Multi-species Prediction database. The second method extends Katz centrality to expression-epistasis networks (EpistasisKatz), extends the Katz bias to be a gene-wise vector of main effects and extends the Katz attenuation constant prefactor to be a prior-knowledge vector for interactions. Using independent microarray studies of major depressive disorder, we find that including prior knowledge in network centrality feature selection stabilizes the training classification and reduces over-fitting.

Availability and implementation

Methods and examples provided at https://github.com/insilico/Rinbix and https://github.com/insilico/PriorKnowledgeEpistasisRank.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Hubs in gene co-expression networks likely play an important role in understanding the regulation of biological processes and phenotypes. Recent studies have investigated the potential for co-expression network hubs to be used to prioritize genes for statistical inference. GeneRank (Morrison et al., 2005) used the PageRank (PR) algorithm (Page et al., 1999) to prioritize genes by combining gene co-expression with external information, such as Gene Ontology and protein–protein interactions. The constant damping constant in PR was extended to a damping vector in Fu et al., 2006, and the usage of this damping vector to incorporate prior knowledge in GeneRank was discussed in Demidenko, 2015.

Co-expression network hubs do not explicitly use outcome or phenotype information. This controls the risk of over-fitting in classification but also loses important contextual information about connectivity influenced by the phenotype. We developed a gene expression centrality [EpistasisRank (ER)] that includes phenotype context by computing statistical interactions (e.g. epistasis) between transcripts (Lareau et al., 2015) in an epistasis-expression or differential co-expression network (McKinney et al., 2013). Prior to this generalization to expression data, we had developed a SNPrank centrality for epistasis networks in GWAS (Hu et al., 2013; McKinney et al., 2009). In the current study, we extend the generalized ER method to use a gene-wise interaction prior probability vector, and we develop a new epistasis network centrality based on Katz centrality (Katz, 1953) that combines main and interaction effects as well as prior knowledge when ranking the importance of predictors.

2 Materials and methods

2.1 ER and EpistasisKatz centrality with gene-wise prior probability

ER centrality operates on a regression-based Genetic Association Interaction (reGAIN) network (Pandey et al., 2012), which is a weighted NxN matrix, B, where N is the number of genes. The diagonal, B_ii, represents the main effect regression coefficient of the gene on the phenotype and the off-diagonal B_ij, is the interaction effect coefficient between genes on the phenotype. The formula for ER is a system of equations that can be solved through least squares:

$${\mathrm{E}\mathrm{R}}_i=\frac{B_{ii}}{N·\text{Tr}\left(B\right)}+d_i\sum _{j\ne i}\frac{B_{ij}{·\mathrm{E}\mathrm{R}}_j}{k_j}+\frac{1-d_i}{N}.\mathrm{ }$$ (1)

In the first term, each gene i gets a contribution to network importance from the gene’s main effect (B_ii), where the trace of B, Tr(B), is a normalization. In the second term, each gene i gets a contribution from its interaction partners (B_ij) proportional to the importance of the partners, ER_j, normalized by the degree of gene j, k_j (non-zero), from the B matrix. This total interaction contribution is weighted by the prior probability d_i for gene i to be involved in interactions. The prior probability vector d_i is the normalized degree of the Integrative Multi-species Prediction (IMP) network. The last term gives all genes a uniform importance proportional to the complement of its inclination for interaction, (1–d_i).

Katz centrality is a two-parameter extension of eigenvector centrality (Supplementary Material). We extend Katz to EpistasisKatz (EK) with prior knowledge as follows

$${\mathrm{E}\mathrm{K}}_i=d_i\sum _{j\ne i}{B}_{ij}{\mathrm{E}\mathrm{K}}_j+\mathrm{ }{B}_{ii}.\mathrm{ }$$ (2)

In the first term, each gene i is given network importance based on the EK weights, EK_j, of its interaction partners and their B_ij reGAIN regression weights. The interaction term is weighted by IMP prior knowledge vector d_i. In standard Katz, this prefactor is a constant that attenuates the centrality contribution of more distant connections. Thus, we extend the attenuation constant in Katz to allow for gene-specific attenuation (d_i), which is the IMP-based prior probability for interactions. In the second term, sometimes referred to as the bias vector, each gene is assigned importance based on its main effect, B_ii. In standard Katz, this second term is a vector of repeated constants. This extends Katz to allow a vector of gene-wise constants.

2.2 Data processing

We identified two gene expression datasets from GEO for major depressive disorder that we refer to as Cambridge (Leday et al., 2017) and Japan (Miyata et al., 2016). We Z-transformed each dataset based on their respective controls to make the datasets more comparable to each other (Wang et al., 2016). We were also concerned about the imbalanced case/control ratio in the Cambridge (training) data with its 128 cases and 64 controls. Thus, we under-sampled (Lina, 2015) the case samples in the Cambridge dataset to obtain a balance of 64 cases and 64 controls. In the Japan (testing) dataset, there are 20 cases and 12 controls. In addition, we filtered the top 5000 genes using coefficient of variation across the 2 datasets. For prior knowledge, we used the 5000 genes to query IMP to construct a network based on predicted functional interactions, and then we computed the normalized degree of each gene i of the IMP network as the prior knowledge vector d_i.

3 Results

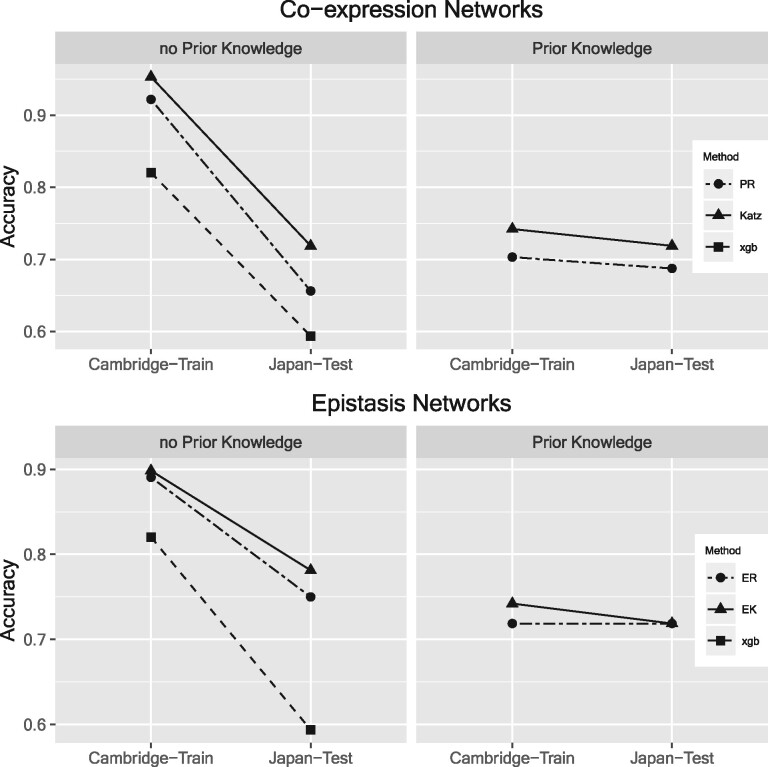
We compared training accuracy and validation accuracy using each centrality method (PR, Katz, EK and ER) for feature selection with and without prior knowledge (Fig. 1). To avoid over-fitting, we used nested cross-validation (CV) to prevent feature selection from causing over-fitting (Le et al., 2017; Varma and Simon, 2006). We used xgboost binary classification on boosted decision trees (Chen and Guestrin, 2016) for the outer CV loop and centrality feature selection methods in the inner CV loop.

Fig. 1.

Training accuracy (Cambridge data) and independent validation accuracy (Japan data) with centrality feature selection without prior knowledge (left panels) and with prior knowledge (right panels). Top: Co-expression network centrality feature selection methods, PR and Katz. Bottom row: Expression-epistasis network centrality methods, ER and EK. Accuracies computed by xgboosted trees with nested CV. Xgboost accuracies without feature selection also shown (squares)

All centrality feature selection methods improve validation accuracy over xgboost classification without feature selection (Fig. 1). Katz-based centralities have the highest accuracies. Without prior knowledge (left panels of Fig. 1), all feature selection methods show a large drop in validation accuracy relative to the training accuracy (over-fitting) despite use of nested CV. Use of prior knowledge to inform centrality (right panels of Fig. 1) yields more stable accuracy across training and validation sets. The training accuracies are lower than without prior knowledge; however, they are more consistent with and a more realistic estimate of the independent validation accuracy.

4 Discussion

In a previous study, we used the Integrative Multi-species Prediction (IMP) database (Wong et al., 2012) to predict functional networks from epistasis network seed genes from SNPrank in GWAS data (McKinney et al., 2016). In the current study, we compute the degree centrality (d_i) of each gene i from an IMP network and use this as a prior probability vector for the interaction term in the new ER and EK epistasis-expression centralities for a network from an independent dataset. We hypothesize that incorporating functional-connectivity prior knowledge into epistasis-expression network centrality will improve the generalization of classification accuracy.

We extended the ER centrality to include a gene-wise vector to integrate prior knowledge. We generalized Katz centrality in EK to include a gene-specific vector, which we use to incorporate the prior probability for interaction effects. We extended the constant bias vector term in Katz to incorporate main effect contributions from the reGAIN matrix. We found prior knowledge led to more stable training accuracy and improved testing validation accuracy in gene expression analysis of major depressive disorder.

Prior knowledge also led to an increase in the number of significantly enriched relevant pathways (Supplementary Material). For example, including prior knowledge led to statistically significant enrichment of Serotonin Receptor and G coupled protein receptor pathways, which are related to mood disorders (Imbrici et al., 2013). The ER and EK methods apply to epistasis networks in GWAS as well as gene expression, and the prior probability vector can blend information between heterogeneous data-driven networks as well as prior knowledge from IMP or other prior networks.

The network construction and centrality methods, including EpistasisRank and EpistasisKatz, are included in our Rinbix R package at https://github.com/insilico/Rinbix. The specific feature selection and classification analysis in the current study is reproduced in https://github.com/insilico/PriorKnowledgeEpistasisRank.

Funding

This work was supported in part by the National Institute of Health GM121312 and GM103456 (B.A.M.) and the William K. Warren Jr. Foundation.

Conflict of Interest: none declared.