Abstract
Conformational disorder is emerging as an important feature of biopolymers, regulating a vast array of cellular functions, including signaling, phase separation, and enzyme catalysis. Here we combine NMR, crystallography, computer simulations, protein engineering, and functional assays to investigate the role played by conformational heterogeneity in determining the activity of the C-terminal domain of bacterial Enzyme I (EIC). In particular, we design chimeric proteins by hybridizing EIC from thermophilic and mesophilic organisms, and we characterize the resulting constructs for structure, dynamics, and biological function. We show that EIC exists as a mixture of active and inactive conformations and that functional regulation is achieved by tuning the thermodynamic balance between active and inactive states. Interestingly, we also present a hybrid thermophilic/mesophilic enzyme that is thermostable and more active than the wild-type thermophilic enzyme, suggesting that hybridizing thermophilic and mesophilic proteins is a valid strategy to engineer thermostable enzymes with significant low-temperature activity.
Keywords: enzyme regulation, bacterial PTS, metadynamics, NMR relaxation, protein dynamics
Enzyme I (EI) is the first protein in the phosphoenolpyruvate (PEP)-dependent sugar phosphotransferase system (PTS), a signal transduction pathway that controls sugar uptake in bacteria and regulates several other cellular functions, including catabolic gene expression, coupling between central nitrogen and carbon metabolism, chemotaxis, and biofilm formation, via phosphorylation dependent protein–protein interactions [1–5]. The phosphorylation state of the PTS components is controlled by the intracellular level of PEP, which initiates the PTS by acting as phosphoryl donor for EI [2,6]. As such, inhibition of the EI autophosphorylation reaction was shown to impair PTS-mediated regulatory mechanisms and to result in reduced bacterial growth and virulence [3,7–12].
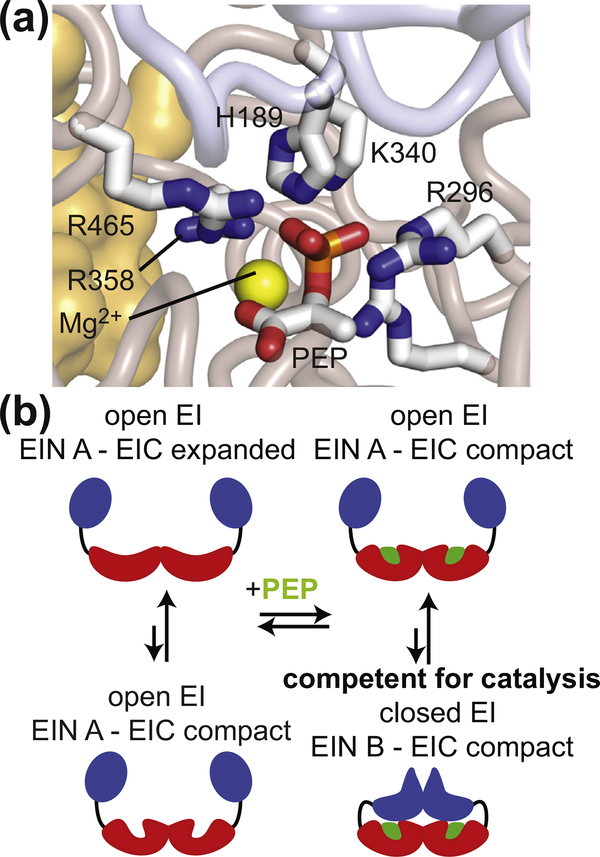
EI is a 128-kDa homodimer composed of two structurally and functionally distinct domains separated by an 11-residue helical linker [13]. The phosphoryl-transfer N-terminal domain (EIN; residues 1–249) contains the phosphorylation site (His-189) and the binding site for HPr (the second PTS protein). The C-terminal domain (EIC; residues 261–575) contains the binding site for PEP, is responsible for EI dimerization [13], and activates PEP for catalysis [14]. In particular, EIC locks the substrate into a high-energy conformation in which the phosphate group lays outside of the plane formed by the three conjugated sp2 carbons, and forms salt-bridges with the small molecule that provide stabilization to the transition state of the phosphoryl-transfer reaction (Figure 1(a)). Functional regulation of EI is achieved through synergistic coupling of multiple intra- and interdomain conformational equilibria that are modulated by substrate and cofactor binding (Figure 1(b)). Specifically, EI was shown to undergo (i) a monomer–dimer equilibrium [18,19], (ii) a compact-to-expanded equilibrium within the EIC domain [14,17], (iii) a g+-to-g− equilibrium within the rotameric state of the His189 side-chain [20], (iv) a state A-to-state B equilibrium within the EIN domain [16,21], and (v) an open-to-close equilibrium describing a reorientation of EIN relative to EIC [16,17,21,22]. Binding of PEP to EIC promotes transition to the dimer/compact/g−/state B/closed form and activates the enzyme for catalysis [17,18]. Therefore, in addition to being a promising pharmaceutical target, EI is also an important model system to study the interplay between ligand binding, post-translational modifications, and conformational dynamics that determines the activity of complex multidomain enzymes.
Figure 1.
EI conformational rearrangements during catalysis. (a) Structural model of PEP bound in the active site of closed EI. Modeling was performed based on the crystal structure of the tEIC–PEP complex [15] and on the X-ray structure of a phosphorylated eEI intermediate captured immediately after the autophosphorylation reaction [16]. Details on the modeling are provided elsewhere [17]. The positioning of PEP and of the His189 side-chain allows in-line phosphoryl transfer from PEP bound to the EIC domain to the EIN domain. PEP, the side-chain of His189, and side-chains of residues from the EIC domain that interact with the phosphate group of PEP are shown as solid sticks. The magnesium ion is displayed as a yellow sphere. The backbone of the EIN and EIC domains are shown as transparent blue and salmon tubes, respectively. The second subunit is shown as a transparent orange surface. (b) Schematic view of EI conformational equilibria. The EIN and EIC domains are colored blue and red, respectively. The PEP molecule is colored green.
In this contribution, we investigate the role played by EIC intradomain conformational dynamics in activation of PEP. In particular, we engineer hybrid thermophilic/mesophilic EIC constructs with modulated thermal stability and active-site flexibility, and we test their ability to catalyze hydrolysis of PEP. Although non-physiological, the latter enzymatic reaction has the advantage of being independent from the EIN domain [14], therefore allowing us to assess the contribution of EIC to PEP activation without interference from the open-to-close equilibrium of the full-length enzyme. Our data demonstrate that, in the presence of substrate, EIC does not adopt a single, catalytically active conformation but exists as a collection of active and inactive states. The thermodynamic balance between active and inactive states is finely controlled by the amino acid sequence of EIC, with the mesophilic enzyme favoring active conformations and the thermophilic enzyme favoring inactive states. Rescaling the turnover number by the fractional population of active EIC is sufficient to recapitulate the difference in activity observed among all EIC variants analyzed here. Our results provide evidence for a regulatory role of conformational disorder in activation of PEP by EIC, which supports an increasing body of literature suggesting that conformational disorder and structural heterogeneity control the activity of several native enzymes [23–29].
Results and Discussion
In this work, we investigate the structure/dynamics/function relationship of EIC from two organisms: a mesophilic bacterium (Escherichia coli) and a thermophilic organism (Thermoanaerobacter tengcongensis). The two proteins will be referred to as eEIC and tEIC, respectively, throughout the manuscript. Similar notation will be used for the full-length enzymes (eEI and tEI, respectively). eEI and tEI share a similar sequence (overall identity 54%; EIC identity 60%; active-site identity 100%, Supplementary Figure S1) and 3D structure [15,16,30,31]. While the temperature dependence of eEI and tEI activities has not been investigated yet, the E. coli and T. tengcongensis PTSs were shown to be optimally active at 37 °C and 65 °C, respectively [15].
Temperature-dependence of the expanded-to-compact equilibrium
EIC displays a (β/⍺)8-barrel fold with active-site residues localized at the C-terminal ends of the β-barrel domain, and within the β2⍺2 (residues 296–309), β3⍺3 (residues 332–360), and β6⍺6 (residues 454–477) loops (Figure 2(a) and Supplementary Figure S1). The active-site loops of eEIC were shown to undergo conformational dynamics in the apo form between a lowly populated state that closely resembles the PEP-bound conformation, and a major state in which the active site is likely more expanded [14,17]. Binding of PEP was observed to shift this expanded-to-compact conformational equilibrium toward the compact form [14,17]. In the full-length eEI, quenching of the C-terminal domain dynamics induced by PEP-binding triggers the open-to-close interdomain rearrangement and activates the enzyme for the autophosphorylation reaction (Figure 1(b)) [17]. Here, the temperature dependence of the expanded-to-compact equilibrium in eEIC and tEICwas investigated by means of 15Nand 13Cmethyl relaxation dispersion (RD) NMR [32]. Experiments were acquired on U-[2H,15N]/Ile(d1)-13CH3/Val, Leu-(13CH3/12C2H3)-labeled EIC at two static fields (600 and 800 MHz) and four different temperatures (25, 30, 35, and 40 °Cfor eEIC, and 40, 50, 60, and 70 °C for tEIC). Simultaneous investigation of RD data measured at multiple temperatures returns a deep characterization of the kinetics and thermodynamics of conformational exchange processes between species with distinct chemical shifts occurring on a timescale ranging from ~100 μs to ~10 ms, by providing enthalpy (ΔH), entropy (ΔS), activation enthalpy (Δ‡H), and activation entropy (Δ‡S) for the conformational equilibrium [33].
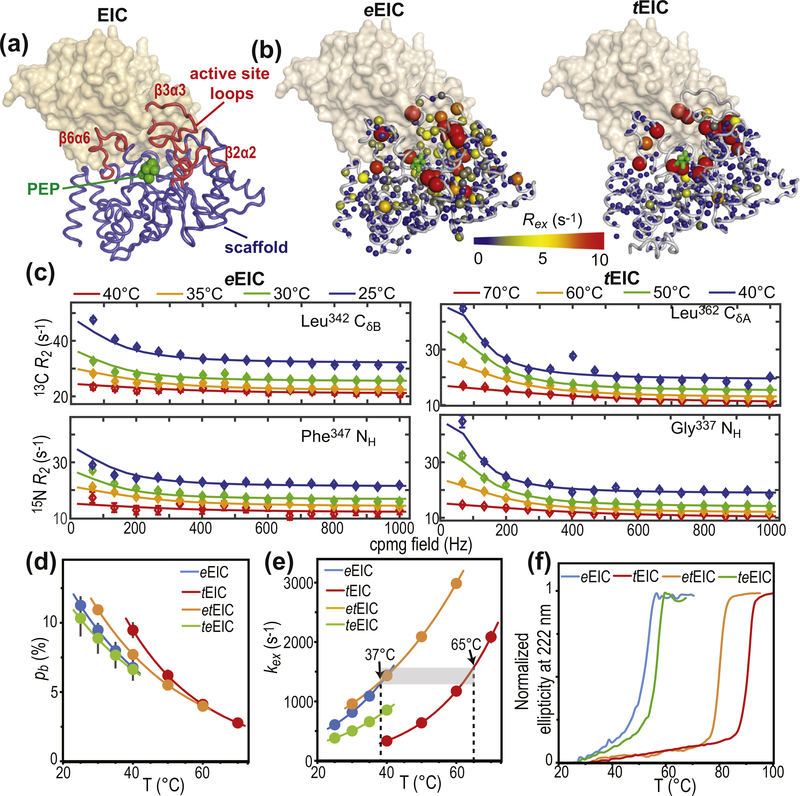
Figure 2.
Design of thermophilic/mesophilic EIC hybrids. (a) Crystal structure of tEIC–PEP complex. Active-site loops are shown as red tubes. Protein scaffold is shown as blue tubes. PEP is displayed as green spheres. The second subunit is shown as a transparent orange surface. (b) 800-MHz exchange contribution to the transverse relaxation rates (Rex) measured for eIEC and tEIC and 25 and 40 °C, respectively, are plotted on the EIC structure as spheres with the relationship between size and color of each sphere and Rex value depicted by the color bar. Rex values are displayed on one subunit of the EIC dimer. The second subunit is shown as a transparent surface. (c) Examples of typical 800-MHz RD data measured for eEIC (left panel) and tEIC (right panel) at four different temperatures. Data are shown for the Leu342-δ methyl group (top) and Phe347 amide group (bottom) of eEIC, and for the Leu362-δ methyl group (top) and Gly337 amide group (bottom) of tEIC. Experimental data are represented by filled-in circles. Best-fit curves are shown as solid lines. Different colors correspond to different temperatures (blue, green, orange, and red correspond to 25, 30, 35, and 40 °C, respectively, for eEIC, and to 40, 50, 60, and 70 °C, respectively, for tEIC). Similar plots for all the analyzed NMR signals are shown in Supplementary Figures S3–S6. Fitted pb (d) and kex (e) for the expanded-to-compact equilibrium in apo eEIC (blue), tEIC (red), etEIC (orange), and teEIC (green) are plotted versus the experimental temperature. Experimental data are represented by filled-in circles. Modeling of the experimental data using the van’t Hoff (for pb) and Eyring (for kex) equations is shown as solid lines. Vertical dashed lines are at the optimal PTS temperatures for eEIC (37 °C) and tEIC (65 °C). Fits performed without enforcing Eyring and van’t Hoff temperature dependence for kex and pb, respectively, are shown in Supplementary Figure S2. (f) Temperature-induced unfolding of eEIC (blue), tEIC (red), etEIC (orange), and teEIC (green).
As expected, several residues within and surrounding the active-site loops of eEIC and tEIC display exchange contribution to the transverse relaxation rate (Rex) significantly larger than zero (Figure 2(b)), which is indicative of conformational dynamics in the μs–ms timescale. Of note, while for tEIC residues with positive Rex are confined within the area of the active-site loops, μs–ms timescale dynamics in eEIC propagate to the β-barrel region of the enzyme (Figure 2(b) and Supplementary Figure S3). All RD curves with Rex > 5 s−1 at 25 and 40 °C for eEIC and tEIC, respectively, were selected for further analysis and used to obtain a quantitative description of the detected conformational equilibria. Interestingly, for both the mesophilic and thermophilic constructs, all the analyzed 15N and 13Cmethyl RD curves measured at multiple temperatures and static magnetic fields could be fit simultaneously to a model describing the interconversion of two conformational states (Figure 2 (c) and Supplementary Figures S3 and S4), confirming that the active site in apo EIC undergoes concerted motion between two conformations. In this global fitting procedure, the activation (Δ‡G) and standard (ΔG) free energy of the conformational equilibrium were optimized as global parameters, whereas the 15N and 13C chemical shift differences between the two conformational states (ΔωN and ΔωC, respectively) were treated as peak-specific and temperature independent parameters. The exchange rate (kex) and the fractional population of the minor conformational state (pb) were calculated at each temperature from the fitted values of Δ‡G and ΔG using the general form of the Eyring and reaction isotherm equations, respectively (see Methods). This fitting procedure effectively reduces the number of optimized parameters and is justified if the heat capacity of activation remains constant over the experimental temperature range [34] (25–40 °C and 40–70 °C for eEIC and tEIC, respectively). An example of the fit is provided in Figure 2(c). The full set of experimental RD curves used in the fitting procedure is shown in Supplementary Figures S3 and S4 for eEIC and tEIC, respectively. The good agreement between experimental and back-calculated data indicates that no additional variable parameter is required to fulfill the experimental RD curves. Values for the forward and backward rate constants (kab and kba, respectively) at the different experimental temperatures were calculated from corresponding values of kex (= kab + kba) and pb. The temperature dependence of pb, kab, and kba was modeled using the van’t Hoff (for pb) and Eyring (for kab and kba) equations to obtain ΔH, ΔS, Δ‡H, and Δ‡S of the expanded-to-compact conformational equilibrium. Thermodynamic, kinetic, and chemical shift parameters obtained for the two enzymes are summarized in Figures 2(d) and (e) and 3(b), and Supplementary Table S1. From these data, it is apparent that the expanded-to-compact equilibrium occurs with negative ΔH and ΔS (Supplementary Table 1), which explains the decrease in pb (i.e. the population of compact state) with increasing temperature (Figure 1(d)), and is consistent with the hypothesis that the compact state is more ordered and structurally stabilized by a higher number of interatomic contacts than the expanded conformation [14,17].
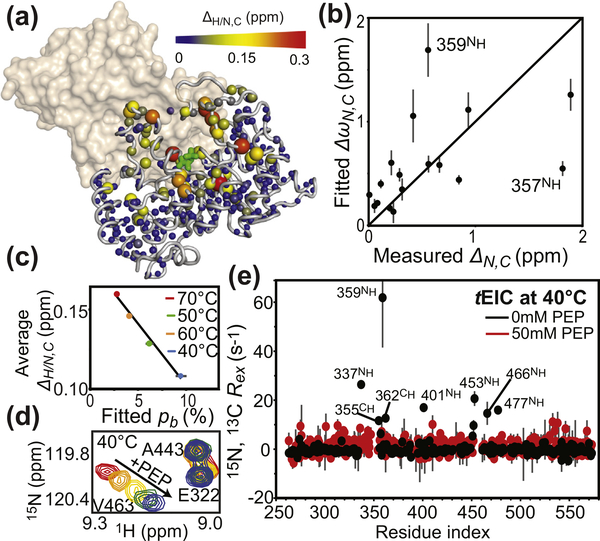
Figure 3.
NMR analysis of holo tEIC. (a) Weighted combined chemical shift perturbations (ΔH/N,C) induced by 10 mM PEP on the 1H–15N and 1H–13Cmethyl TROSY correlation spectra of tEIC displayed on the structure of the tEIC–PEP complex as spheres with the relationship between size and color of each sphere and chemical shift perturbation depicted by the color bar. ΔH/N,C values are displayed on one subunit of the EIC dimer. The second subunit is shown as a transparent surface. (b) The ΔωN,C parameters obtained from the fits of the RD data on apo tEIC are plotted versus the 15N and 13C chemical shift perturbations (δN,C) induced by addition of 10 mM PEP to tEIC at 70 °C. Tyr357 and Ala359 show a poor agreement between ΔωN and ΔN. These residues are adjacent to Arg358 that establishes salt-bridges with the phosphate group of PEP. Therefore, the presence of PEP is likely to induce additional perturbations to the 15N chemical shift of Tyr357 and Ala359 that are not reflected in the corresponding ΔωN (which is fitted from RD data on the apo protein). (c) ΔH/N,C measured at different temperatures for tEIC are averaged over all the NMR peaks and plotted versus the population of compact state obtained by fitting the RD data on the apo protein. Data measured at 40, 50, 60, and 70 °C are shown as blue, green, orange, and red circles, respectively. Linear regression of the data is shown as a solid black line. (d) Close-up view of the 1H–15N TROSY spectrum of tEIC showing the effect of increasing concentrations of PEP on selected cross-peaks at 40 °C. The color code is as follows: red, 0 mM PEP; orange, 0.2 mM PEP; yellow, 0.5 mM PEP; green, 1.0 mM PEP; blue, 2.0 mM PEP. The fact that peak position follows a linear path upon increasing PEP concentration indicates that the free and bound forms of tEIC are in fast exchange [35]. (e) Exchange contribution to the transverse relaxation rates (Rex) at 800 MHz and 40 °C measured for samples of tEIC in the absence (black) and in the presence (red) of 50 mM PEP. As PEP is slowly degraded by the enzyme, RD data for holo tEIC were measured in the presence of a large excess of substrate and using a low protein concentration (300 μM) and a low number of scans (16) for NMR signal averaging. Therefore, we ascribe the small fluctuations in Rex observed for holo tEIC to experimental error.
Addition of substrate to tEIC causes line-broadening beyond detection level for the NMR peaks of the residues directly facing PEP. However, large 1H/15N (ΔH/N) and 1H/13Cmethyl (ΔH/C) chemical shift perturbations can still be observed within the active site of tEIC upon substrate binding (Figure 3(a)), suggesting that structural rearrangements are occurring within this region of the enzyme. As previously reported for eEIC [14,17], the perturbations on the 15N (ΔN) and 13Cmethyl (ΔC) chemical shifts of tEIC observed upon PEP binding are in good agreement with the ΔωN and ΔωC values obtained from the RD measurements on apo tEIC (Figure 3(b)), supporting the hypothesis that binding of PEP shifts the expanded-to-compact equilibrium detected in apo EIC toward the compact state [14,17]. In this respect, it is also interesting to note that the measured ΔH/N and ΔH/C values increase with increasing temperature and are inversely proportional to the population of compact state in apo tEIC (Figure 3 (c)). As chemical shifts in fast-exchanging systems are population-weighted quantities (note that free and PEP-bound EIC are in fast exchange on the chemical shift timescale, Figure 3(d)), these observations further confirm that PEP-binding shifts the pre-existing equilibrium between the expanded and compact EIC conformations. Consistent with this conformational-shift model, analysis of the structural models of holo EIC [14–17] shows that salt bridges between the phosphate group of PEP and the side-chains of Arg296, Arg332, Lys340, Arg358, and Arg465 provide structural stabilization to the active-site loops in the compact form (Figure 4(a)). Interestingly, these electrostatic interactions also result in near complete suppression of the Rex’s measured for tEIC (Figure 3(e)). While these results indicate unambiguously that PEP binding has a dramatic effect on the expanded-to-compact equilibrium, it is not possible to ascertain if the Rex suppression observed in the RD data upon substrate binding is the result of (i) a complete quench of the expanded-to-compact equilibrium, (ii) a shift of the kinetics for the expanded-to-compact equilibrium outside the μs–ms timescale regime detectable by RD experiments, or (iii) a drastic reduction of ΔωN and ΔωC between the expanded and compact conformations in holo EIC compared to the apo enzyme.
Figure 4.
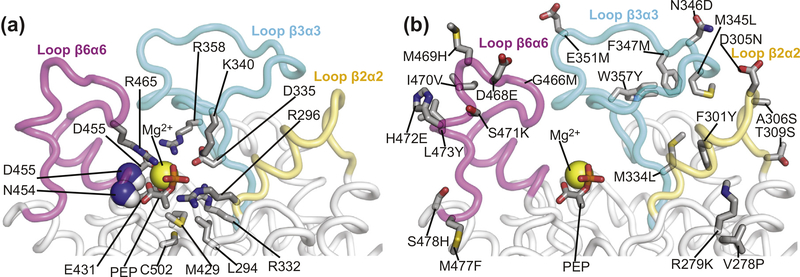
Active-site loops of EIC. Close-up view of the active-site loops of eEIC highlighting the position of (a) residues involved in binding of the substrate and metal cofactor and (b) the 21 single-point mutations performed to engineer the thermophilic/mesophilic EIC hybrids. PEP and relevant side-chains are shown as solid sticks. Backbone amides in contact with PEP are shown as spheres. The magnesium ion is displayed as a yellow sphere. The β2⍺2, β3⍺3, and β6⍺6 loops are colored yellow, light blue, and purple, respectively. The second subunit is not shown. Note that residues 278 and 279 do not belong to the active-site loops of EIC but were mutated in the hybrids because they face the β2⍺2 loop in the three-dimensional structure of the enzyme.
Engineering of hybrid eEIC/tEIC constructs
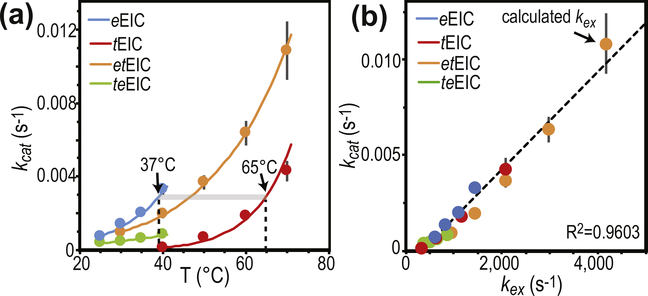
The analysis of the temperature dependence of the expanded-to-compact equilibrium has revealed similar thermodynamic parameters for the conformational change in apo eEIC and tEIC (ΔH and ΔS in Supplementary Table S1), which is reflected in the similar temperature dependence of pb obtained for the two EIC constructs (Figure 2(d)). On the other hand, the RD NMR data indicate the existence of significant differences in the kinetics of the conformational equilibrium in the mesophilic and thermophilic enzyme, with the expanded-to-compact transition occurring with a ~4-fold higher kex in eEIC than in tEIC at 40 °C (Figure 2(e)). Interestingly, plotting kex versus temperature reveals that the two enzymes display similar exchange rate constant at their optimal PTS temperature (37 and 65 °C for eEIC and tEIC, respectively) (Figure 2(e)), which suggests a possible role for the expanded-to-compact equilibrium in functional regulation of EIC.
To investigate the relationship between activity and active-site conformational dynamics in EIC, we have engineered hybrid thermophilic/mesophilic constructs by merging the scaffold of one enzyme with the active-site loops of the other enzyme (Figure 2(c)). In particular, the hybrid formed by the active-site loops of the mesophilic protein and the scaffold of the thermophilic enzyme is referred to as etEIC, while the hybrid comprised of the active-site loops of the thermophilic protein and the scaffold of the mesophilic enzyme is referred to as teEIC. This protein engineering effort required 21 single-point mutations per hybrid construct. A list of the performed mutations and their localization within the EIC structure is provided in Supplementary Figure S1. The 21 mutations point away from the catalytic site (Figure 4(b)) and do not perturb the fold and oligomeric state of the enzyme, as revealed by X-ray crystallography and analytical ultracentrifugation (Figure 5). On the other hand, RD NMR data indicate that the mutations have a profound effect on the μs–ms timescale conformational dynamics of eEIC and tEIC. Indeed, incorporating the mesophilic active-site loops into the scaffold of the thermophilic enzyme is sufficient to increase the rate of the active site dynamics at the same level observed for the mesophilic enzyme (note that eEIC and etEIC have very similar temperature dependence of kex, Figure 2(e)). In contrast, implanting the active-site loops of tEIC onto the scaffold of eEIC increases the activation energy for the expanded-to-compact conformational change and results in slower kex compared to the mesophilic enzyme (Figure 2(e)). However, it should be noted that the exchange kinetics of teEIC do not follow the same temperature trend observed for tEIC (Figure 2(e)). This finding is likely due to the fact that the conformational dynamics in eEIC are not localized exclusively in the active-site loops but extend to the β-barrel region of the enzyme (note, for example, the large Rex values measured for residues Ile426 and Gly427 in eEIC and teEIC, Supplementary Figures S3 and S6). Coupling the β-barrel fromeEIC and the loops from tEIC results in intermediate kinetics for the expanded-to-compact equilibrium in teEIC. In this regard, it is also important to notice that these results are not an artifact of the global fitting procedure, as repeating the fit using only the RD data from loop residues (Met302, Leu334, Ile336, Leu345, Ala462, and Asp464) returns identical thermodynamic and kinetic parameters for the conformational equilibrium (Supplementary Table S1).
Figure 5.
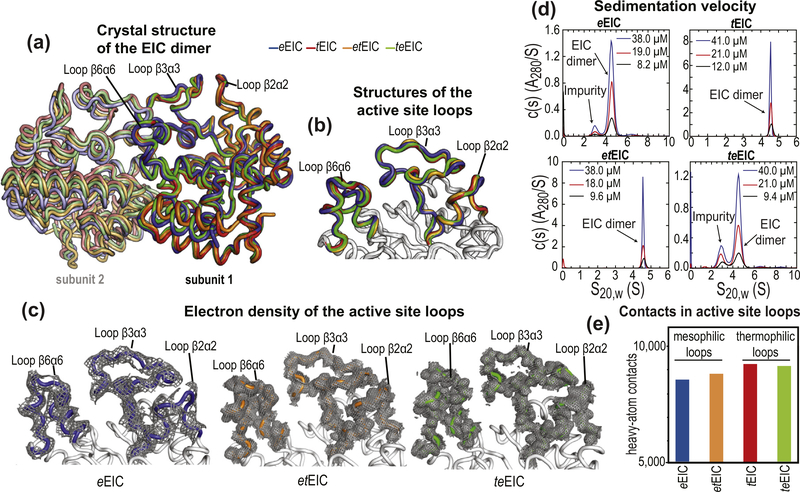
Crystal structures of EIC. (a) Overlay of the crystal structure of eEIC (blue), tEIC (red), etEIC (orange), and teEIC (green). Subunits 1 and 2 are indicated with bright and pale colors, respectively. (b) Close-up view of the active-site loops in eEIC (blue), tEIC (red), etEIC (orange), and teEIC (green). Statistics for crystal structure of eEIC, etEIC, and teEIC (obtained in this work) are shown in Supplementary Table S3. (c) Electron density maps (2fo − fc) of the active-site loops in eEIC (left), etEIC (center), and teEIC (right) are shown as a gray mesh contoured at 0.5σ. (d) c(s) distributions for eEIC (top-left), tEIC (top-right), etEIC (bottom-left), and teEIC (bottom-right) obtained at different loading concentrations (ranging from ~50 to 10 μM) based on sedimentation velocity absorbance data collected at 50 kilo-revolutions per minute and 20 °C (see Methods). The sedimentation experiments indicate that EIC is dimeric for all tested constructs within the tested concentration range. Peaks at S20,W < 4 S that do not show concentration dependent c(s) absorbance profiles (i.e. they do not report on the monomer–dimer equilibrium) are attributed to small amounts of contaminants in the analytical ultracentrifugation sample. (e) Number of interatomic contacts among heavy atoms in the active-site loops of eEIC (blue), tEIC (red), etEIC (orange), and teEIC (green). Contacts for atom i were calculated as the number of heavy atoms within a distance of 5 Å from atom i. Data displayed in bar graph are the sum of intrasubunit and intersubunit contacts. NMR spectra for all EIC constructs and chemical shift perturbations introduced by the 21 single-point mutations are shown in Supplementary Figures S8 and S9.
The temperature-induced unfolding of all EIC constructs was monitored by circular dichroism (CD), and the transition temperatures (Tm) were determined from the first derivatives of the unfolding curves [36]. Tm values of 54, 57, 80, and 91 °C were obtained for eEIC, teEIC, etEIC, and tEIC, respectively (Figure 2(f)), indicating that the 21 single-point mutations have a small but opposite effects on the temperature stability of eEIC and tEIC. In particular, introducing the active-site loops from the thermophilic construct into mesophilic EIC results in a 3 °C increase in Tm (compare Tm values measured for eEIC and teEIC), while incorporating the mesophilic active-site loops into thermophilic EIC results in a 11 °C decrease in Tm (compare Tm values measured for tEIC and etEIC). As the analysis of the crystal structures of eEIC, teEIC, etEIC, and tEIC indicates that thermophilic active-site loops are better packed and establish a larger number of interatomic contacts than the mesophilic ones (Figure 5(e)), we ascribe the small changes in melting temperature to small variations in the ΔH of folding among the investigated EIC constructs.
Temperature-dependence of PEP hydrolysis catalyzed by EIC
EI catalyzes an autophosphorylation reaction in which a phosphoryl group is transferred from PEP, bound to C-terminal domain, to the His189 residue, located on the N-terminal domain of the enzyme (Figure 1(a)) [13]. In this catalytic process, EIC does not act as mere scaffold for PEP binding, but plays a role in the enzymatic reaction by activating PEP for catalysis. Indeed, isolated EIC was shown to catalyze hydrolysis of PEP in the absence of the EIN domain [14]. This reaction is 6 orders of magnitude slower than the direct phosphoryl transfer to EIN catalyzed by the full-length enzyme, but it occurs via a similar mechanism (Supplementary Figure S7a) [14]. As His189 is the only residue from the EIN domain that is in direct contact with PEP in activated, closed EI (Figure 1(a)), investigating the PEP hydrolysis reaction is a valuable strategy to study the role of EIC in PEP activation without interferences due to the presence of the EIN domain.
Here, we have established a method using real-time NMR to detected degradation of PEP and assay the activity of isolated EIC over a wide temperature range (5–70 °C; these limits are determined by the temperature range accessible to our NMR probe) (Supplementary Figure S7). Results of our enzymatic assay reveal that the hydrolysis of PEP by eEIC, tEIC, etEIC, and teEIC follows Michaelis–Menten kinetics (Supplementary Figure S7e). Fitted values for the Michaelis constant (KM) and turnover number (kcat) at different temperatures (25, 30, 35, and 40 °C for eEIC; 40, 50, 60, and 70 °C for tEIC; 30, 40, 50, 60, and 70 °C for etEIC; and 25, 30, 35, and 40 °C for teEIC) are reported in Figure 6 and Supplementary Table S2 for all investigated EIC constructs.
Figure 6.
Temperature dependence of PEP hydrolysis. (a) Turnover number (kcat) versus temperature for the PEP hydrolysis reaction catalyzed by eEIC (blue), tEIC (red), etEIC (orange), and teEIC (green). Experimental data are shown as filled-in circles. Modeling of the experimental data using the Eyring equation is shown as solid lines. Vertical dashed lines are at the optimal PTS temperatures for eEIC (37 °C) and tEIC (65 °C). (b) kcat values are plotted versus the corresponding kex values (i.e. kcat measured for eEIC at 40 °C is plotted versus kex measured for eEIC at 40 °C). Blue, red, orange, and green circles are for eEIC, tEIC, etEIC, and teEIC, respectively. The value of kex at 70 °C for etEIC was calculated using the Eyring equation and the Δ‡H and Δ‡S values reported in Supplementary Table S1.
KM values measured for eEIC and tEIC range between 300 and 500 μM (Supplementary Table S2), which agrees well with previously reported KM values for the EI-PEP interaction (~350 μM) [14]. On the other hand, KM’s obtained for the PEP complexes with etEIC and teEIC (in the 400–1300 μM range; Supplementary Table S2) are larger by a factor of ~2 compared to the ones obtained for the wild-type enzymes. This increase in KM indicates that swapping the mesophilic with the thermophilic active-site loops or, vice versa, the thermophilic with the mesophilic active-site loops in EIC produces a similar effect on the EIC–PEP interaction, with both hybrid constructs binding PEP less tightly than the wild-type proteins.
Analysis of the temperature-dependence of kcat indicates that eEIC is more active toward PEP hydrolysis than tEIC at low temperature (Figure 6 (a)), suggesting that eEIC is more suited than tEIC at activating PEP for the phosphoryl-transfer reaction. Interestingly, etEIC (i.e. the hybrid construct incorporating the active-site loops of eEIC and the scaffold of tEIC) has increased low-temperature turnover compared to tEIC, while teEIC (i.e. the hybrid construct incorporating the active-site loops of tEIC and the scaffold of eEIC) has overall lower kcat compared to eEIC (Figure 6(a)). These results provide evidence of a direct involvement of the active-site loops in functional regulation of EIC, specifically that the amino acid sequence of the active-site loops of mesophilic EIC is better suited for activation of PEP, resulting in faster turnover for PEP hydrolysis.
Conformational disorder in functional regulation of EIC
The catalytic core of EIC consists of 12 residues (Leu294, Arg296, Arg332, Asp335, Lys340, Arg358, Met429, Glu431, Asn454, Asp455, Arg465, and Cys502) that are in direct contact with PEP and the Mg2+ ion in the holo enzyme (Figure 4(a) and Supplementary Figure S1) and are highly conserved across species. As these residues are fully conserved in the four EIC constructs investigated in this work (Supplementary Figure S1), the observation that eEIC, tEIC, etEIC, and teEIC catalyze PEP hydrolysis with different turnover numbers (Figure 6(a)) implies a regulatory role for residues that are not in direct contact with the substrate or metal cofactor. Interestingly, the NMR analysis of the expanded-to-compact equilibrium and the investigation of the enzyme kinetics reported above revealed that kex and kcat are linearly correlated (Figure 6(b)), suggesting that functional regulation of EIC might be achieved via modulation of conformational dynamics within the active site. Indeed, similar linear correlations between kcat and kex were previously reported for enzymatic reactions in which enzyme’s conformational dynamics are rate limiting for catalysis [37–42]. Such catalytic systems undergo conformational transitions that are essential for catalysis (either in the enzyme activation or product release process) on a time scale that is slow compared to the chemical step, causing kcat to be similar to the exchange rate constant, kex. Therefore, the fact that for the PEP hydrolysis reaction investigated here kcat is 6 orders of magnitude smaller than kex (Figure 6(b)) excludes the hypothesis that the expanded-to-compact conformational change regulates EIC by being the slow step in catalysis. Consistent with this observation, addition of imidazole to the reaction mixture speeds up degradation of PEP by EIC (Figure 7(a)). Imidazole is an analog of the His189 side-chain and better acceptor of the phosphoryl group than water. Therefore, we expect formation of phospho-imidazole (confirmed by 31P NMR, Supplementary Figure S7c) to occur with a lower activation energy than PEP hydrolysis. The fact that the turnover rate for enzymatic degradation of PEP (i.e. the combination of the PEP hydrolysis and imidazole phosphorylation reactions measured by our 1H NMR assay, Supplementary Figure S7b) increases linearly with the concentration of imidazole (Figure 7(a)) indicates that kcat is independent on the kex of the expanded-to-compact equilibrium and is determined by the chemical step.
Figure 7.
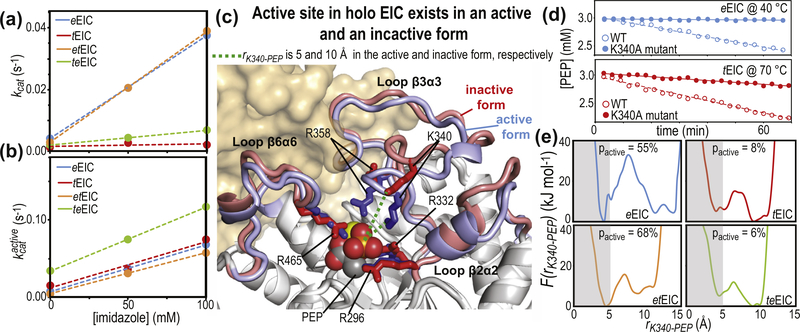
Conformational heterogeneity regulates EIC activity. (a) Turnover number (kcat) versus imidazole concentration for PEP degradation (i.e. the sum of PEP hydrolysis and imidazole phosphorylation, see Supplementary Figure S7c) catalyzed by eEIC (blue), tEIC (red), etEIC (orange), and teEIC (green). Experimental data are shown as filled-in circles. Linear regressions are shown as dashed lines. (b) kcat values reported in (a) are rescaled according to , were pactive is the fractional population of activated EIC and is the turnover number associated with EIC in the active conformation. (c) The coordinates of eEIC from the crystal structure of phosphorylated, closed eEI (that was used to generate the atomic-resolution model of the eEIC–PEP complex, see caption to Figure 1(a)) are superimposed onto the crystal structure of the tEIC–PEP complex. The active-site loops are colored blue and red for eEIC and tEIC, respectively. Positively charged side-chains coordinating PEP are shown as solid sticks. PEP is shown as spheres. The magnesium ion is shown as a yellow sphere. The second subunit is shown as transparent surface. The distance between the phosphate group of PEP and the ε-ammonium group of Lys340 (rK340-PEP) is shown as a dashed green line. (d) PEP concentration versus time measured on samples containing 3 mM PEP and 50 μM enzyme. Data in the top panel are for the wild-type eEIC (filled-in blue circles) and the eEIC Lys340Ala mutant (open blue circles) at 40 °C. Data on the bottom panel are for the wild-type tEIC (filled-in red circles) and the tEIC Lys340Ala mutant (open red circles) at 70 °C. Linear regressions of the data are shown as solid or dashed lines for the wild-type and mutant enzymes, respectively. (e) Potential of mean force versus rK340-PEP obtained from 1-μs MTD simulations run on the complexes formed by PEP with eEIC (blue), tEIC (red), etEIC (orange), and teEIC (green). Values of pactive were obtained by integrating F(rK340-PEP) over rK340-PEP < 5 Å (gray box).
Next, we have evaluated the possibility that EIC is functionally regulated by conformational disorder in the active site. Indeed, it is now widely accepted that proteins need to be considered as conformational ensembles of a range of interconverting microstates [43,44]. As different microstates may exhibit different catalytic ability [45,46], the observed , where pi and are the fractional population and turnover number of microstate i, respectively [26–29,47]. Inspection of the available structural models for holo EIC [14–17] suggests that the EIC–PEP complex exists in two major conformations, in which the β3⍺3 loop adopts an open or closed conformation, respectively (Figure 7(c)). The side-chains of Lys340 and Arg358 coordinate the phosphate group of PEP and stabilize the transition state in the closed form of the enzyme, but do not contact the substrate in the open conformation. Therefore, we hypothesize that only microstates associated with closed EIC can efficiently catalyze PEP degradation. Consistent with this hypothesis, a single-point mutation (Lys340Ala) that breaks the interaction between PEP and Lys340 abolishes the enzymatic activity of EIC (Figure 7(d)), indicating that PEP-Lys340 contacts are crucial for catalysis and that modulating the thermodynamics of the open-to-close equilibrium within the β3⍺3 loop can provide functional regulation to the enzyme. It is important to notice that this conformational equilibrium differs from both (i) the open-to-close equilibrium depicted in Figure 1(b) for the full-length enzyme, which involves reorientation of EIN relative to EIC, and (ii) the expanded-to-compact equilibrium observed in the apo enzyme, which involves concerted dynamics of all active-site loops. Also, no conformational dynamics are detected by RD experiments on holo EIC (Figure 3(e)), indicating that the kinetics of the open-to-close transition of the β3⍺3 loop fall outside of the μs–ms timescale detectable by RD NMR and/or that the difference in chemical shift between the open and closed conformations is too small to produce detectable Rex values.
As the thermodynamics of the open-to-close equilibrium of the β3⍺3 loop cannot be characterized by RD NMR, free-energy profiles for the conformational equilibrium in the PEP complexes with eEIC, tEIC, etEIC, and teEIC were estimated at 40 °C by well-tempered metadynamics (WT-MTD), a method for enhancing the sampling of collective variables of interest in constant temperature molecular dynamics simulations [48]. As a result of a WT-MTD run, we obtain a free-energy surface as a function of selected collective variables [49]. In particular, 1-μs-long MTDs were performed on the four EIC–PEP complexes by using the distance between the phosphate group of PEP and the ε-ammonium group of Lys340 (rK340-PEP) as the collective variable. In addition, as in the available structural models for the EIC–PEP complex rK340-PEP ranges between 5 and 10 Å, a wall potential was applied to restrain sampling of the collective variable within the 2–15 Å range. Additional details on the construction of the starting structures, equilibration steps, and setup and analysis of the MTD runs are provided in Methods.
Inspection of the energy profiles constructed for the open-to-close conformational change by WT-MTD reveals the presence of two major energy wells corresponding to the closed (rK340-PEP < 7 Å) and open (rK340-PEP > 7 Å) states of the β3⍺3 loop (Figure 7(e)). While the boundaries of the closed conformation are well defined by our simulations, the energy well corresponding to the open state shows more variability and spreads over different rK340-PEP values in the four EIC–PEP complexes (Figure 7(e)), reflecting the higher disorder associated with the open conformation (in which the side-chain of Lys340 is not structurally stabilized by the salt-bridge with PEP). It is also interesting to note that for the eEIC–PEP and etEIC–PEP complexes, the energy minimum corresponding to the closed state has a lower energy than the minima associated with the open conformation, while the opposite is true for the PEP complexes with tEIC and teEIC (Figure 7(e)). This finding indicates that the mesophilic β3⍺3 loop (present in eEIC and etEIC) has a higher propensity than the thermophilic one (present in tEIC and teEIC) to sample the catalytically active, closed conformation.
The contribution of the thermodynamics of the open-to-close equilibrium to regulation of EIC was estimated by assuming that only closed conformations with rK340-PEP < 5 Å are competent for catalysis and that the observed , where pactive and are the fractional population and turnover number of activated EIC. A threshold of rK340-PEP < 5 Å was chosen to discriminate between active and inactive enzyme as (i) it corresponds to the rK340-PEP distance measured in the crystallographic model of closed, holo EIC (Figure 7(c)), (ii) it contains the energy minima associated with closed EIC in all our WT-MTD simulations (Figure 7(e)), and (iii) previous studies reported that complete loop closure is absolutely critical for efficient catalysis by TIM-barrel enzymes [29]. The populations of active and inactive enzyme were calculated by integrating the potential of mean force over rK340-PEP < 5 Å and rK340-PEP > 5 Å, respectively. pactive values of 55%, 8%, 68%, and 6% were obtained for eEIC, tEIC, etEIC, and teEIC, respectively (Figure 7(e)). The values of for the four EIC constructs at 40 °C and different imidazole concentrations were calculated from the corresponding values of kcat using the formula: . Interestingly, the four enzymes show very similar dependence of over the concentration of imidazole (Figure 7(b)). These results indicate that, once in the active conformation, eEIC, tEIC, etEIC, and teEIC catalyze PEP degradation with similar turnover, and that functional regulation among these EIC constructs is achieved by modulating the thermodynamics of the open-to-closed equilibrium of holo EIC.
Another important question to address is if, among the 21 single-point mutations introduced to hybridize EIC, specific amino acids can be pinpointed that are responsible for thermodynamic regulation of the open-to-closed equilibrium. However, as the active-site loops of EIC are involved in the dimer interface and establish several mutual interactions, addressing this question with confidence would require several additional studies that are currently in progress.
Conclusion
Structural biology studies reported over the past 70 years have shown that proteins can display different degrees of structural heterogeneity, going from proteins that fold into a unique rigid structure to intrinsically disordered proteins, with a continuum of possibilities in between. The degree of conformational heterogeneity can be finely tuned by external factors such as pH, ionic strength, and/or the presence of binding partners [50]. Therefore, it is no surprise that conformational disorder has been found to be implicated in regulation of important biological processes, such as signaling cascades, enzyme catalysis, and liquid–liquid phase transitions [50]. In particular, in the context of enzyme catalysis, conformational plasticity at the active site is known to control substrate specificity, with more flexible enzymes being in general more promiscuous and capable to process substrates with diverse chemical structures [51,52]. In addition, structural heterogeneity was proposed to control turnover in several enzymatic systems [26–29]. For example, computational studies on the enzymes triosephosphate isomerase [29] and ketol-acid reductoisomerase [26] have been reported indicating that only a subset of the conformational space sampled by the enzyme–substrate complex is competent for catalysis. Based on these results, reengineering enzymes to preferentially populate regions of the conformational space that promote reactivity was suggested as a promising strategy to increase turnover of industrially relevant reactions [26].
In this contribution, we have provided evidence that conformational heterogeneity at the active site determines kcat of the PEP degradation reaction catalyzed by EIC. Specifically, we have studied the structure/dynamics/function relationship in a mesophilic and a thermophilic variant of EIC (referred to as eEIC and tEIC, respectively) and in two additional EIC constructs (referred to as etEIC and teEIC) engineered to have hybrid thermal stability and active-site flexibility (Figure 2). By combining NMR, crystallography, computer simulations, and functional assays, we have demonstrated that holo EIC exists as a mixture of states with different catalytic abilities and that the observed turnover number is determined by the thermodynamic balance between active and inactive conformations (Figure 7). Interestingly, our data indicate that dilution of the catalytically competent states in a sea of inactive conformations is chiefly responsible for the low activity of the thermophilic enzyme at low temperature, suggesting that modulation of conformational disorder plays a role in thermal adaption of EIC. Studies are currently ongoing to investigate how temperature affects the conformational space sampled by the mesophilic and thermophilic variants of EIC, and to understand if conformational disorder is responsible for the observation that eEIC and tEIC catalyze PEP hydrolysis with similar turnover at their optimal PTS temperature (Figure 6(a)). Our data also indicate that conformational dynamics at the active site of holo EIC are important for activating PEP for catalysis, and that altering the conformational space sampled by the C-terminal domain is a possible avenue to achieve inhibition of the full-length EI.
EIC displays a (β/⍺)8-barrel fold (also known as TIM barrel fold) that, due to its ability to carry very efficient and versatile active sites, has been selected by nature to catalyze a large number of reactions [53]. All known (β/⍺)8-barrel enzymes have the active-site residues localized at the C-terminal ends of the β-strands and within the β⍺-loops (which connect the C-terminal end of β-strand n to the N-terminal end of ⍺-helix n), while residues located within the core, at the N-terminal ends of the β-strands, and within the ⍺β-loops (which connect the C-terminal end of ⍺-helix n − 1 to the N-terminal end of β-strand n) are responsible to maintain protein stability. The presence of a catalytic face and a stability face makes the (β/⍺)8-barrel fold highly evolvable and the most common enzyme fold in nature [53]. As a consequence, (β/⍺)8-barrel enzymes were the subject of several protein engineering efforts aimed at designing new or improved functionalities by reshuffling of individual (β⍺)-units or de novo design [53]. Here, we have engineered thermophilic/mesophilic constructs of EIC by merging the stability face of one enzyme with the catalytic face of the other enzyme (Figure 2). The newly designed proteins have hybrid structural properties, with the construct incorporating the scaffold of tEIC and the active loops of eEIC (etEIC) being highly flexible and thermostable, and the opposite hybrid (teEIC) displaying high rigidity and low thermal stability (Figure 2). Interestingly, functional characterization of our hybrid constructs revealed that etEIC catalyze PEP hydrolysis with ~20 and ~3 times higher kcat than tEIC at 40 and 70 °C, respectively (Figure 6), suggesting that engineering hybrid mesophilic/thermophilic constructs might be a strategy to obtain highly stable (β/⍺)8-barrel enzymes with significant low-temperature activity. In this respect, it should be noted that production of chimera proteins by hybridizing the active site of two enzymes it is not a trivial task as the hybrid constructs might sample unproductive regions of the conformational space [54]. This might be particularly true for (β/⍺)8-barrel enzymes that display complex regulatory mechanisms linked to oligomerization equilibria [18] or to the eventual presence of binding sites for allosteric inhibitors and/or activators [18,55]. As the kinetic and thermodynamic parameters of these equilibria might be affected by swapping active-site loops between thermophilic and mesophilic enzymes, the generality of the mesophilic/thermophilic hybridization strategy proposed here remains to be tested.
Methods
Protein expression and purification
eEIC and teEIC were cloned into a pET21a vector and were expressed and purified using protocols described previously for eEIC [14]. tEIC and etEIC were cloned into a vector incorporating a His-tagged EIN solubility tag at the N terminus [56]. Expression and purification of tEIC and etEIC was performed as previously described for tEIC [57]. U-[2H,15N]/Ile (d1)-13CH3/Val, Leu-(13CH3/12C2H3)-labeled (for RD experiments) and U-[2H,15N,13C]/Ile(d1)-13CH3/Val, Leu-(13CH3/12C2H3)-labeled (for NMR resonance assignment experiments) EIC were prepared following standard protocols for specific isotopic labeling of the methyl groups in Ile, Leu, and Val side-chains [58].
Thermal unfolding and CD
The progress of temperature-induced unfolding was monitored at 222 nm in a 0.1-cm cuvette using a Jasco J-710 spectropolarimeter. The midpoint of the thermal unfolding transition (Tm) was calculated as the maximal value of the first derivative of the CD signal at 222 nm with respect to temperature. Protein concentration was ~0.4 mg/ml.
Analytical ultracentrifugation
Sedimentation velocity experiments were conducted at 50,000 rpm and 20 °C on a Beckman Coulter ProteomeLab XLI analytical ultracentrifuge following standard protocols [59]. Samples of the EIC were studied at concentrations ranging from ~10 to 40 μM in 100 mM NaCl, 20 mM Tris (pH 7.4), 2 mM DTT, and 4 mM MgCl2. Samples were loaded in standard 12-mm, two-channel centerpiece cells, and data were collected using both the absorbance (280 nm) and Rayleigh interference (655 nm) optical detection systems. Time-corrected [60] sedimentation data were analyzed in SEDFIT 16.01c [61] in terms of a continuous c(s) distribution of sedimenting species with a resolution of 0.05 S and a maximum entropy regularization confidence level of 0.68. The solution density, solution viscosity, and protein partial specific volume were calculated in SEDNTERP [62], and sedimentation coefficients s were corrected to standard conditions s20,w.
X-ray crystallography
Crystals of etEIC grew in well C12 of the Morpheus crystallization screen (Molecular Dimensions) using a 96-well hanging-drop vapor diffusion plate setup with 100 μl reservoirs, 210 nl drop volumes, 1:1 ratio of protein to reservoir solutions and incubated at 25 °C. The Morpheus C12 well solution consisted of 0.09 M NPS salts (sodium nitrate, sodium phosphate dibasic, ammonium sulfate), 0.1 M Buffer System 3 (Tris, Bicine (pH 8.5)), and 50% of Precipitant Mix 4 (25% MPD, 25% PEG 1000, 25% PEG 3350). etEIC crystals did not require cryoprotection prior to flash-freezing. Crystals of teEIC grew in well C10 of the PACT premier Eco screen (Molecular Dimensions) using the same hanging drop plate setup as described above. The PACTC10 well solution consisted of 0.2M magnesium chloride hexahydrate, 0.1 M Hepes (pH 7.0), and 20%w/v PEG6000. Prior to flash-freezing in liquid nitrogen, teEIC crystals were cryoprotected using mother liquor plus 15% glycerol. Crystals of eEIC grew in well G8 of the XP Screen (MiTeGen, LLC) using a 96-well sitting-drop vapor diffusion plate setup with 50 μl reservoirs and 210 nl drop volume with a 1:1 ratio of protein to reservoir solutions, and incubated at 18 °C. Well G8 of the XP Screen consisted of 1.0 M lithium sulfate, 0.5 M ammonium sulfate, 0.1 M tri-sodium citrate (pH 5.6), and 1.0 mM TEW. Prior to flash-freezing in liquid nitrogen, teEIC crystals were cryoprotected using mother liquor plus 15% glycerol.
X-ray diffraction data for etEIC and teEIC crystals were collected at the Advanced Light Source (Beamline 4.2.2), processed with XDS [63] and scaled with AIMLESS within the CCP4 software suite [64]. X-ray diffraction data for eEIC crystals were collected at the Advanced Photon Source (Beamline 23ID-D), processed with iMOSFLM [65], and scaled with AIMLESS within the CCP4 software suite. The crystal structures of etEIC, teEIC, and eEIC were solved by molecular replacement with the tEIC model (PBD ID code 2XZ7) [15] using the program Phaser [66]. Model building and refinement were carried out using PHENIX autobuild [67] and phenix.refine [68]. Coot [69] was used for graphical map inspection and manual refinement of coordinates. MolProbity was used for structural validation [70]. The atomic coordinates and structure factors have been deposited in the RCSB Protein Data Bank, with the following PDB IDs, 6VBJ (etEIC), 6V9K (teEIC), and 6VU0 (eEIC). Statistics on the data collection and the final models are given in Supplementary Table S3.
Molecular dynamics simulations
Molecular dynamics simulations were performed using Gromacs 2018.3 [71] patched with PLUMED2.5 [72]. We used Charmm36 force field for the four enzyme variants. The CGENFF was used for generating the Charmm36 compatible field for the PEP ligands. The crystal structure of the tEIC–PEP complex [15] and the structural model of the tEIC–PEP complex [17] (see caption to Figure 1 for more details on the modeling) were used as the starting structure for the thermophilic and mesophilic enzyme, respectively. Starting coordinates for the PEP complexes with etEIC and teEIC were obtained by mutating the coordinate files of the tEIC–PEP and eEIC–PEP complexes, respectively, in CHARMM-GUI. All PEP bound enzyme structures were solvated with TIP3P water molecules in a rhombic dodecahedral box resulting in ~90,000 number of molecules. Appropriate number of Na+ and Cl− were added to neutralize the system and set the bulk salt concentration at 130 mM.
The long-range electrostatic interactions were evaluated by using the particle mesh Ewald method. All the systems were first minimized for 10,000 steps via a steepest descent method. The system was then gradually heated up to 313 K in 200 ps subject to positional restraints. The restraint force constants were gradually decreased from 103 to 0 kJ nm−2 mol−1. For the production simulations, we have kept harmonic restraints on PEP with force constant 40 kJnm−2 mol−1 to restraint the ligand in fixed orientation enabling cleaner comparisons between free energy profiles of enzymes with modified sequences.
The rest of the degrees of freedom were fully unrestrained to evolve at 313 K with Nose–Hoover thermostat and a relaxation time of 0.5 ps. The pressure was maintained at 1 bar using the Parrinello–Rahman coupling scheme. The LINCS algorithm was employed to constrain the H-atoms bonds. The time step of the production simulations was 2.0 fs. The cutoff of the non-bonded interactions was set to 10 Å.
After 50-ns equilibration in NPT ensemble, WT-MTD simulations of 1-μs duration were run with the distance between the center of mass of the phosphate group of PEP and the center of mass of the ε-ammonium group of Lys340 as the collective variable (rK340-PEP). The parameters of 0.8 for hill height and 8 for the visa factor were used for carrying out WT-MTD runs. Plumed2.5 plugin was employed for monitoring and processing the results. To limit the comparison between near native states, we have further imposed wall potentials at 1.5-nm distance with harmonic potentials and a force constant of 1500 kJ nm−2 mol−1.
Free energy difference between the active and inactive EIC conformations was computed by integrating potential of mean force over basins rK340-PEP = 2–5 Å and rK340-PEP =5–15 Å, respectively. The differences are robust with respect to the choice of basins as long as they include all global and local minima. We note here that due to disordered and high entropy nature of the open state, the free energy difference is a fluctuating quantity the convergence of which has been assessed by obtaining stable mean of the free energy difference between open and closed forms which has been collected over the last 100 ns of the simulation. The Potential of Mean profiles report the averaged free energy profiles over last 100 ns showing the stable mean free energy differences between open and closed forms. See Supplementary Figure S10 for more details on simulated structures of enzymes and convergence assessment.
NMR spectroscopy
NMR samples were prepared in 20 mM Tris buffer (pH 7.4), 100 mM NaCl, 4 mM MgCl2, 1 mM ethylenediamine tetraacetic acid (EDTA), 2 mM dithiothreitol (DTT), and 90% H2O/10% D2O. The protein concentration (in subunits) was ~1.0 mM for all protein detected experiments (unless stated otherwise).
NMR spectra were recorded on Bruker 800, 700, and 600 MHz spectrometers equipped with a z-shielded gradient triple resonance cryoprobes. Spectra were processed using NMRPipe [73] and analyzed using the program SPARKY. 1H–15N TROSY (transverse relaxation optimized) [74] and methyl-TROSY [75] experiments have been acquired using previously described pulse schemes. Resonance assignments of the 1H–15N TROSY and methy-TROSY spectra of eEIC and tEIC were achieved by transferring the assignments obtained previously [14,57,76,77]. Sequential 1H/15N/13C backbone assignment of the etEIC and teEIC was carried out using TROSY versions [74,78] of conventional 3D triple resonance correlation experiments (HNCO, HNCA, HNCACB, HN(CO)CA, and HN(CO)CACB) [79]. Assignment of the 1H–13Cmethyl correlations of etEIC and teEIC was performed using out-and-back experiments [76]. Only non-stereospecific assignments are obtained for the methyl groups of the Leu and Val residues of the EIC constructs analyzed here. Therefore, methyl-TROSY correlations for such resonances were arbitrarily assigned as δA and δB (for Leu), and γA and γB (for Val). Chemical shifts assigned for etEIC and teEIC have been deposited in the BioMagRes-Bank (accession nos. 28080 and 28079, respectively).
Weighted combined 1H/15N (ΔH/N) and 1H/13C (ΔH/C) chemical shift perturbations resulting from the addition of PEP were calculated using the following equation: ΔH/N,C = ((ΔδH WH)2 + (ΔδN,C WN,C)2)1/2 [80], where WH, WN, and WC are weighing factors for the 1H, 15N, and 13C shifts, respectively (WH = |γH/γH| = 1, WN = |γN/γH| = 0.101, WC = |γC/γH| = 0.251); ΔδH, ΔδN, and ΔδC are the 1H, 15N, and 13C chemical shift differences in ppm, respectively, between free and bound states; and γH, γN, and γC are the 1H, 15N, and 13C gyromagnetic ratios, respectively.
15N and 13Cmethyl RD experiments were conducted at multiple temperatures (see Results and Discussion) using a pulse sequence that measures the exchange contribution for the TROSY component of the 15N magnetization [81] or a pulse scheme for 13C singe quantum Carr–Purcell–Meinboom–Gill (CPMG) RD described by Kay and co-workers [82]. Off-resonance effects and pulse imperfections were minimized using a four-pulse phase scheme [83]. Experiments were performed at 600 and 800 MHz with a fixed relaxation delay but a changing number of refocusing pulses to achieve different effective CPMG fields [84]. The transverse relaxation periods were set to 60 and 30 ms for the 15N and 13Cmethyl experiments, respectively. Experimental errors on the R2 values were propagated from the errors on the signal intensity estimated using the program SPAKY. The resulting RD curves were fit to a two-state exchange model using the Carver–Richards equation [85]:
| (1) |
with
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
Here, R2,eff is the measured 15N or 13C transverse relaxation rate; R2,int is the 15N or 13C transverse relaxation rate in the absence of conformational exchange; n is the number of 180° refocusing pulses in the CPMG train; 2δ is the spacing between the centers of successive 180° pulses; kex is the exchange rate constant; pa and pb are the fractional populations of the major and minor species, respectively; and ΔωN,C is the nitrogen or carbon chemical shift differences between the two conformational states in rad s−1.
The optimization was run using pb and kex as global parameters. pa was calculated using the formula pa = 1 – pb. R2,int and ΔωN,C were fit as a peak-specific parameters (i.e. each RD curve will have its own R2,int and ΔωN,C).
In order to reduce the number of adjustable parameters in the fit, the RD curves measured for each EIC construct at four different temperatures were fit simultaneously. In this global fitting procedure, the residue-specific ΔωN,C’s were treated as temperature independent parameters, while kex and pb at each temperature were calculated from the activation (Δ‡G) and standard (ΔG) free energy of the conformational equilibrium using the formulas:
| (11) |
and
| (12) |
with
| (13) |
where T is the temperature in Kelvin, R is universal gas constant, and Keq is the equilibrium constant for the conformational change.
Enzymatic assays
Enzymatic activity of eEIC, tEIC, etEIC, and teEIC for degradation of PEP to inorganic phosphate, phospho-imidazole, and pyruvate was assayed by real-time 1H NMR by monitoring the disappearance of the alkene proton signals (Supplementary Figure S7). The reaction mixtures were prepared in 20 mM Tris buffer (pH 7.4), 100 mM NaCl, 4 mM MgCl2, 1 mM EDTA, 2 mM DTT, 1 mM trimethylsilylpropanoic acid (TSP), and 99.99% D2O. Enzyme concentrations were 50 μM for eEIC, tEIC and etEIC, and 80 μM for teEIC. Enzymatic assays were run in duplicate, and the integrals of the signals measured for the alkene protons were converted to mM units by reference to the internal standard TSP. Integration of the NMR signals was performed using the software MNova (https://mestrelab.com/download/mnova/). Initial velocities were determined from the linear portion of the progress curves and were fit using the Michaelis–Menten equation (Supplementary Figure S7). As at temperatures approaching Tm, the enzyme may unfold and aggregate, and the concentration of EIC was estimated before and after each enzymatic reaction by gel electrophoresis.
Accession numbers
Coordinates and structure factors have been deposited in the Protein Data Bank with accession numbers 6VU0, 6VBJ, and 6V9K
Supplementary Material
Acknowledgments
We thank Dr. Julien Roche for critical reading of the manuscript. This work was supported by funds from NIGMS R35GM133488 (to V.V.), from the Roy J. Carver Charitable Trust (to V.V.), and from the Intramural Research Program of the National Institutes of Health, the National Institute of Diabetes and Digestive and Kidney Disease) (to R.G.). Beamline 4.2.2 of the Advanced Light Source, a DOE Office of Science User Facility under Contract No. DE-AC02-05CH11231, is supported in part by the ALS-ENABLE program funded by the National Institutes of Health, National Institute of General Medical Sciences, grant P30 GM124169-01. We specifically thank Jay Nix (ALS) for assistance with instrumentation, data collection, and processing. Additionally, this research used resources of the Advanced Photon Source (Beamline 23ID-D), a US Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. D.A.P. acknowledges the financial support as a Carlyle G. Caldwell Endowed Chair of the Department of Chemistry, Iowa State University.
Abbreviations used
- EI
Enzyme
- PEP
phosphoenolpyruvate
- PTS
phosphotransferase system
- RD
relaxation dispersion
- CD
circular dichroism
- Tm
transition temperature
- WT-MTD
well-tempered metadynamics
- CPMG
Carr–Purcell–Meinboom–Gill
Footnotes
Declarations of Competing Interests
The authors declare no conflict of interest.
Data Availability
All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
Appendix A. Supplementary data
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jmb.2020.05.024.
References
- [1].Clore GM, Venditti V, (2013). Structure, dynamics and biophysics of the cytoplasmic protein–protein complexes of the bacterial phosphoenolpyruvate: sugar phosphotransferase system. Trends Biochem. Sci, 38, 515–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Deutscher J, Ake FM, Derkaoui M, Zebre AC, Cao TN, Bouraoui H, et al. , (2014). The bacterial phosphoenolpyruvate: carbohydrate phosphotransferase system: regulation by protein phosphorylation and phosphorylation-dependent protein–protein interactions. Microbiol. Mol. Biol. Rev, 78, 231–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Postma PW, Lengeler JW, Jacobson GR, (1996). Phosphoenolpyruvate: carbohydrate phosphotransferase systems. in: Neidhardt FC, Lin EC, Curtiss R (Eds.), Escherichia Coli and Salmonella: Cellular and Molecular Biology 1996, pp. 1149–1174. [Google Scholar]
- [4].Doucette CD, Schwab DJ, Wingreen NS, Rabinowitz JD, (2011). alpha-Ketoglutarate coordinates carbon and nitrogen utilization via enzyme I inhibition. Nat. Chem. Biol, 7, 894–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Venditti V, Ghirlando R, Clore GM, (2013). Structural basis for enzyme I inhibition by alpha-ketoglutarate. ACS Chem. Biol, 8, 1232–1240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Hogema BM, Arents JC, Bader R, Eijkemans K, Yoshida H, Takahashi H, et al. , (1998). Inducer exclusion in Escherichia coli by non-PTS substrates: the role of the PEP to pyruvate ratio in determining the phosphorylation state of enzyme IIAGlc. Mol. Microbiol, 30, 487–498. [DOI] [PubMed] [Google Scholar]
- [7].Huang KJ, Lin SH, Lin MR, Ku H, Szkaradek N, Marona H, et al. , (2013). Xanthone derivatives could be potential antibiotics: virtual screening for the inhibitors of enzyme I of bacterial phosphoenolpyruvate-dependent phosphotransferase system. J Antibiot, 66, 453–458. [DOI] [PubMed] [Google Scholar]
- [8].Kok M, Bron G, Erni B, Mukhija S, (2003). Effect of enzyme I of the bacterial phosphoenolpyruvate: sugar phosphotransferase system (PTS) on virulence in a murine model. Microbiology, 149, 2645–2652. [DOI] [PubMed] [Google Scholar]
- [9].Edelstein PH, Edelstein MA, Higa F, Falkow S, (1999). Discovery of virulence genes of Legionella pneumophila by using signature tagged mutagenesis in a guinea pig pneumonia model. Proc. Natl. Acad. Sci. U. S. A, 96, 8190–8195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Hava DL, Camilli A, (2002). Large-scale identification of serotype 4 Streptococcus pneumoniae virulence factors. Mol. Microbiol, 45, 1389–1406. [PMC free article] [PubMed] [Google Scholar]
- [11].Jones AL, Knoll KM, Rubens CE, (2000). Identification of Streptococcus agalactiae virulence genes in the neonatal rat sepsis model using signature-tagged mutagenesis. Mol. Microbiol, 37, 1444–1455. [DOI] [PubMed] [Google Scholar]
- [12].Lau GW, Haataja S, Lonetto M, Kensit SE, Marra A, Bryant AP, et al. , (2001). A functional genomic analysis of type 3 Streptococcus pneumoniae virulence. Mol. Microbiol, 40, 555–571. [DOI] [PubMed] [Google Scholar]
- [13].Chauvin F, Brand L, Roseman S, (1996). Enzyme I: the first protein and potential regulator of the bacterial phosphoenolpyruvate: glycose phosphotransferase system. Res. Microbiol, 147, 471–479. [DOI] [PubMed] [Google Scholar]
- [14].Venditti V, Clore GM, (2012). Conformational selection and substrate binding regulate the monomer/dimer equilibrium of the C-terminal domain of Escherichia coli enzyme I. J. Biol. Chem, 287, 26989–26998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Navdaeva V, Zurbriggen A, Waltersperger S, Schneider P, Oberholzer AE, Bahler P, et al. , (2011). Phosphoenolpyruvate: sugar phosphotransferase system from the hyperthermophilic Thermoanaerobacter tengcongensis. Biochemistry, 50, 1184–1193. [DOI] [PubMed] [Google Scholar]
- [16].Teplyakov A, Lim K, Zhu PP, Kapadia G, Chen CC, Schwartz J, et al. , (2006). Structure of phosphorylated enzyme I, the phosphoenolpyruvate:sugar phosphotransferase system sugar translocation signal protein. Proc. Natl. Acad. Sci. U. S. A, 103, 16218–16223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Venditti V, Tugarinov V, Schwieters CD, Grishaev A, Clore GM, (2015). Large interdomain rearrangement triggered by suppression of micro- to millisecond dynamics in bacterial Enzyme I. Nat. Commun, 6, 5960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Nguyen TT, Ghirlando R, Venditti V, (2018). The oligomerization state of bacterial enzyme I (EI) determines EI’s allosteric stimulation or competitive inhibition by alpha-ketoglutarate. J. Biol. Chem, 293, 2631–2639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Patel HV, Vyas KA, Savtchenko R, Roseman S, (2006). Themonomer/dimer transition of enzyme I of the Escherichia coli phosphotransferase system. J. Biol. Chem, 281, 17570–17578. [DOI] [PubMed] [Google Scholar]
- [20].Suh JY, Cai M, Clore GM, (2008). Impact of phosphorylation on structure and thermodynamics of the interaction between the N-terminal domain of enzyme I and the histidine phosphocarrier protein of the bacterial phosphotransferase system. J. Biol. Chem, 283, 18980–18989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Schwieters CD, Suh JY, Grishaev A, Ghirlando R, Takayama Y, Clore GM, (2010). Solution structure of the 128 kDa enzyme I dimer from Escherichia coli and its 146 kDa complex with HPr using residual dipolar couplings and small- and wide-angle X-ray scattering. J. Am. Chem. Soc, 132, 13026–13045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Venditti V, Schwieters CD, Grishaev A, Clore GM, (2015). Dynamic equilibrium between closed and partially closed states of the bacterial Enzyme I unveiled by solution NMR and X-ray scattering. Proc. Natl. Acad. Sci. U. S. A, 112, 11565–11570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Palombo M, Bonucci A, Etienne E, Ciurli S, Uversky VN, Guigliarelli B, et al. , (2017). The relationship between folding and activity in UreG, an intrinsically disordered enzyme. Sci. Rep, 7, 5977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Larion M, Miller B, Bruschweiler R, (2015). Conformational heterogeneity and intrinsic disorder in enzyme regulation: glucokinase as a case study. Intrinsically Disord Proteins, 3, e1011008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].DeForte S, Uversky VN, (2017). Not an exception to the rule: the functional significance of intrinsically disordered protein regions in enzymes. Mol. BioSyst, 13, 463–469. [DOI] [PubMed] [Google Scholar]
- [26].Bonk BM, Weis JW, Tidor B, (2019). Machine learning identifies chemical characteristics that promote enzyme catalysis. J. Am. Chem. Soc, 141, 4108–4118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Ghose R, (2019). Nature of the pre-chemistry ensemble in mitogen-activated protein kinases. J. Mol. Biol, 431, 145–157. [DOI] [PubMed] [Google Scholar]
- [28].Glowacki DR, Harvey JN, Mulholland AJ, (2012). Taking Ockham’s razor to enzyme dynamics and catalysis. Nat. Chem, 4, 169–176. [DOI] [PubMed] [Google Scholar]
- [29].Liao Q, Kulkarni Y, Sengupta U, Petrovic D, Mulholland AJ, van der Kamp MW, et al. , (2018). Loop motion in triosephosphate isomerase is not a simple open and shut case. J. Am. Chem. Soc, 140, 15889–15903. [DOI] [PubMed] [Google Scholar]
- [30].Evangelidis T, Nerli S, Novacek J, Brereton AE, Karplus PA, Dotas RR, et al. , (2018). Automated NMR resonance assignments and structure determination using a minimal set of 4D spectra. Nat. Commun, 9, 384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Oberholzer AE, Bumann M, Schneider P, Bachler C, Siebold C, Baumann U, et al. , (2005). Crystal structure of the phosphoenolpyruvate-binding enzyme Idomain from the Thermoanaerobacter tengcongensis PEP: sugar phosphotransferase system (PTS). J. Mol. Biol, 346, 521–532. [DOI] [PubMed] [Google Scholar]
- [32].Mittermaier A, Kay LE, (2006). New tools provide new insights in NMR studies of protein dynamics. Science, 312, 224–228. [DOI] [PubMed] [Google Scholar]
- [33].Purslow JA, Nguyen TT, Egner TK, Dotas RR, Khatiwada B, Venditti V, (2018). Active site breathing of human Alkbh5 revealed by solution NMR and accelerated molecular dynamics. Biophys. J, 115, 1895–1905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Nguyen V, Wilson C, Hoemberger M, Stiller JB, Agafonov RV, Kutter S, et al. , (2017). Evolutionary drivers of thermoadaptation in enzyme catalysis. Science, 355, 289–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Purslow JA, Khatiwada B, Bayro MJ, Venditti V, (2020). NMR methods for structural characterization of protein–protein complexes. Front. Mol. Biosci, 7, 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Greenfield NJ, (2006). Using circular dichroism spectra to estimate protein secondary structure. Nat. Protoc, 1, 2876–2890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Eisenmesser EZ, Millet O, Labeikovsky W, Korzhnev DM, Wolf-Watz M, Bosco DA, et al. , (2005). Intrinsic dynamics of an enzyme underlies catalysis. Nature, 438, 117–121. [DOI] [PubMed] [Google Scholar]
- [38].Fraser JS, Clarkson MW, Degnan SC, Erion R, Kern D, Alber T, (2009). Hidden alternative structures of proline isomerase essential for catalysis. Nature, 462, 669–673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Henzler-Wildman KA, Lei M, Thai V, Kerns SJ, Karplus M, Kern D, (2007). A hierarchy of timescales in protein dynamics is linked to enzyme catalysis. Nature, 450, 913–916. [DOI] [PubMed] [Google Scholar]
- [40].Henzler-Wildman KA, Thai V, Lei M, Ott M, Wolf-Watz M, Fenn T, et al. , (2007). Intrinsic motions along an enzymatic reaction trajectory. Nature, 450, 838–844. [DOI] [PubMed] [Google Scholar]
- [41].Rozovsky S, McDermott AE, (2001). The time scale of the catalytic loop motion in triosephosphate isomerase. J. Mol. Biol, 310, 259–270. [DOI] [PubMed] [Google Scholar]
- [42].Whittier SK, Hengge AC, Loria JP, (2013). Conformational motions regulate phosphoryl transfer in related protein tyrosine phosphatases. Science, 341, 899–903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Frauenfelder H, Sligar SG, Wolynes PG, (1991). The energy landscapes and motions of proteins. Science, 254, 1598–1603. [DOI] [PubMed] [Google Scholar]
- [44].Tokuriki N, Tawfik DS, (2009). Protein dynamism and evolvability. Science, 324, 203–207. [DOI] [PubMed] [Google Scholar]
- [45].Lu HP, Xun L, Xie XS, (1998). Single-molecule enzymatic dynamics. Science, 282, 1877–1882. [DOI] [PubMed] [Google Scholar]
- [46].Smiley RD, Hammes GG, (2006). Single molecule studies of enzyme mechanisms. Chem. Rev, 106, 3080–3094. [DOI] [PubMed] [Google Scholar]
- [47].Elias M, Wieczorek G, Rosenne S, Tawfik DS, (2014). The universality of enzymatic rate-temperature dependency. Trends Biochem. Sci, 39, 1–7. [DOI] [PubMed] [Google Scholar]
- [48].Barducci A, Bussi G, Parrinello M, (2008). Well-tempered metadynamics: a smoothly converging and tunable free-energy method. Phys. Rev. Lett, 100, 020603. [DOI] [PubMed] [Google Scholar]
- [49].Laio A, Parrinello M, (2002). Escaping free-energy minima. Proc. Natl. Acad. Sci. U. S. A, 99, 12562–12566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Uversky VN, (2019). Protein intrinsic disorder and structure–function continuum. Prog. Mol. Biol. Transl. Sci, 166, 1–17. [DOI] [PubMed] [Google Scholar]
- [51].Campbell E, Kaltenbach M, Correy GJ, Carr PD, Porebski BT, Livingstone EK, et al. , (2016). The role of protein dynamics in the evolution of new enzyme function. Nat. Chem. Biol, 12, 944–950. [DOI] [PubMed] [Google Scholar]
- [52].Jacquet P, Hiblot J, Daude D, Bergonzi C, Gotthard G, Armstrong N, et al. , (2017). Rational engineering of a native hyperthermostable lactonase into a broad spectrum phosphotriesterase. Sci. Rep, 7, 16745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Sterner R, Hocker B, (2005). Catalytic versatility, stability, and evolution of the (betaalpha)8-barrel enzyme fold. Chem. Rev, 105, 4038–4055. [DOI] [PubMed] [Google Scholar]
- [54].Moise G, Morales Y, Beaumont V, Caradonna T, Loria JP, Johnson SJ, et al. , (2018). A YopH PTP1B chimera shows the importance of the WPD-loop sequence to the activity, structure, and dynamics of protein tyrosine phosphatases. Biochemistry, 57, 5315–5326. [DOI] [PubMed] [Google Scholar]
- [55].Lisi GP, Currier AA, Loria JP, (2018). Glutamine hydrolysis by imidazole glycerol phosphate synthase displays temperature dependent allosteric activation. Front. Mol. Biosci, 5, 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Khatiwada B, Purslow JA, Underbakke ES, Venditti V, (2020). N-terminal fusion of the N-terminal domain of bacterial enzyme I facilitates recombinant expression and purification of the human RNA demethylases FTO and Alkbh5. Protein Expr. Purif, 167, 105540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Dotas RR, Venditti V, (2017). (1)H, (15)N, (13)C backbone resonance assignment of the C-terminal domain of enzyme I from Thermoanaerobacter tengcongensis. Biomol NMR Assign, 12, 103–106. [DOI] [PubMed] [Google Scholar]
- [58].Tugarinov V, Kanelis V, Kay LE, (2006). Isotope labeling strategies for the study of high-molecular-weight proteins by solution NMR spectroscopy. Nat. Protoc, 1, 749–754. [DOI] [PubMed] [Google Scholar]
- [59].Zhao H, Brautigam CA, Ghirlando R, Schuck P, (2013). Overview of current methods in sedimentation velocity and sedimentation equilibrium analytical ultracentrifugation. Curr Protoc Protein Sci, 12 Chapter 20:Unit20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Ghirlando R, Balbo A, Piszczek G, Brown PH, Lewis MS, Brautigam CA, et al. , (2013). Improving the thermal, radial, and temporal accuracy of the analytical ultracentrifuge through external references. Anal. Biochem, 440, 81–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Schuck P, (2000). Size-distribution analysis of macromolecules by sedimentation velocity ultracentrifugation and lamm equation modeling. Biophys. J, 78, 1606–1619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Cole JL, Lary JW, T PM, Laue TM, (2008). Analytical ultracentrifugation: sedimentation velocity and sedimentation equilibrium. Methods Cell Biol, 84, 143–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Kabsch W, (2010). Xds. Acta Crystallogr D Biol Crystallogr., 66, 125–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Evans PR, (2011). An introduction to data reduction: space-group determination, scaling and intensity statistics. Acta Crystallogr D Biol Crystallogr., 67, 282–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Battye TG, Kontogiannis L, Johnson O, Powell HR, Leslie AG, (2011). iMOSFLM: a new graphical interface for diffraction-image processing with MOSFLM. Acta Crystallogr D Biol Crystallogr., 67, 271–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].McCoy AJ, Grosse-Kunstleve RW, Adams PD, Winn MD, Storoni LC, Read RJ, (2007). Phaser crystallographic software. J. Appl. Crystallogr, 40, 658–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Terwilliger TC, Grosse-Kunstleve RW, Afonine PV, Moriarty NW, Zwart PH, Hung LW, et al. , (2008). Iterative model building, structure refinement and density modification with the PHENIX AutoBuild wizard. Acta Crystallogr D Biol Crystallogr., 64, 61–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Liebschner D, Afonine PV, Baker ML, Bunkoczi G, Chen VB, Croll TI, et al. , (2019). Macromolecular structure determination using X-rays, neutrons and electrons: recent developments in Phenix. Acta Crystallogr D Struct Biol., 75, 861–877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Emsley P, Cowtan K, (2004). Coot: model-building tools for molecular graphics. Acta Crystallogr D Biol Crystallogr., 60, 2126–2132. [DOI] [PubMed] [Google Scholar]
- [70].Chen VB, Arendall WB 3rd 3rd, Headd JJ, Keedy DA, Immormino RM, Kapral GJ, et al. , (2010). MolProbity: allatom structure validation for macromolecular crystallography. Acta Crystallogr D Biol Crystallogr., 66, 12–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Abraham MJ, Murtola T, Schulz R, Páll S, Smith JC, Hess B, et al. , (2015). GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX, 1, 19–25. [Google Scholar]
- [72].Tribello GA, Bonomi M, Branduardi D, Camilloni C, Bussi G, (2014). PLUMED 2: new feathers for an old bird. Comput. Phys. Commun, 185, 604–613. [Google Scholar]
- [73].Delaglio F, Grzesiek S, Vuister GW, Zhu G, Pfeifer J, Bax A, (1995). NMRPipe: a multidimensional spectral processing system based on UNIX pipes. J. Biomol. NMR, 6, 277–293. [DOI] [PubMed] [Google Scholar]
- [74].Pervushin K, Riek R, Wider G, Wuthrich K, (1997). Attenuated T2 relaxation by mutual cancellation of dipoledipole coupling and chemical shift anisotropy indicates an avenue to NMR structures of very large biological macromolecules in solution. Proc. Natl. Acad. Sci. U. S. A, 94, 12366–12371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Tugarinov V, Hwang PM, Ollerenshaw JE, Kay LE, (2003). Cross-correlated relaxation enhanced 1H[bond]13C NMR spectroscopy of methyl groups in very high molecular weight proteins and protein complexes. J. Am. Chem. Soc, 125, 10420–10428. [DOI] [PubMed] [Google Scholar]
- [76].Tugarinov V, Venditti V, Marius Clore G, (2014). A NMR experiment for simultaneous correlations of valine and leucine/isoleucine methyls with carbonyl chemical shifts in proteins. J. Biomol. NMR, 58, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Dotas RR, Venditti V, (2019). Resonance assignment of the 128 kDa enzyme I dimer from Thermoanaerobacter tengcongensis. Biomol NMR Assign, 13, 287–293. [DOI] [PubMed] [Google Scholar]
- [78].Tugarinov V, Muhandiram R, Ayed A, Kay LE, (2002). Four-dimensional NMR spectroscopy of a 723-residue protein: chemical shift assignments and secondary structure of malate synthase g. J. Am. Chem. Soc, 124, 10025–10035. [DOI] [PubMed] [Google Scholar]
- [79].Clore GM, Gronenborn AM, (1998). Determining the structures of large proteins and protein complexes by NMR. Trends Biotechnol, 16, 22–34. [DOI] [PubMed] [Google Scholar]
- [80].Mulder FA, Schipper D, Bott R, Boelens R, (1999). Altered flexibility in the substrate-binding site of related native and engineered high-alkaline Bacillus subtilisins. J. Mol. Biol, 292, 111–123. [DOI] [PubMed] [Google Scholar]
- [81].Loria JP, Rance M, Palmer AG 3rd 3rd, (1999). A TROSY CPMG sequence for characterizing chemical exchange in large proteins. J. Biomol. NMR, 15, 151–155. [DOI] [PubMed] [Google Scholar]
- [82].Lundstrom P, Vallurupalli P, Religa TL, Dahlquist FW, Kay LE, (2007). A single-quantum methyl 13C-relaxation dispersion experiment with improved sensitivity. J. Biomol. NMR, 38, 79–88. [DOI] [PubMed] [Google Scholar]
- [83].Yip GN, Zuiderweg ER, (2004). A phase cycle scheme that significantly suppresses offset-dependent artifacts in the R2-CPMG 15N relaxation experiment. J. Magn. Reson, 171, 25–36. [DOI] [PubMed] [Google Scholar]
- [84].Mulder FA, Skrynnikov NR, Hon B, Dahlquist FW, Kay LE, (2001). Measurement of slow (micros-ms) time scale dynamics in protein side chains by (15)N relaxation dispersion NMR spectroscopy: application to Asn and Gln residues in a cavity mutant of T4 lysozyme. J. Am. Chem. Soc, 123, 967–975. [DOI] [PubMed] [Google Scholar]
- [85].Carver JP, Richards RE, (1972). A general two-site solution for the chemical exchange produced dependence of T2 upon the Carr–Purcell pulse separation. J. Magn. Reson, 6, 89–105. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.