Detection of Volume-Changing Metastatic Brain Tumors on Longitudinal MRI Using a Semiautomated Algorithm Based on the Jacobian Operator Field

Abstract

BACKGROUND AND PURPOSE:

Accurate follow-up of metastatic brain tumors has important implications for patient prognosis and management. The aim of this study was to develop and evaluate the accuracy of a semiautomated algorithm in detecting growing or shrinking metastatic brain tumors on longitudinal brain MRIs.

MATERIALS AND METHODS:

We used 50 pairs of successive MR imaging datasets, 30 on 1.5T and 20 on 3T, containing contrast-enhanced 3D T1-weighted sequences. These yielded 150 growing or shrinking metastatic brain tumors. To detect them, we completed 2 major steps: 1) spatial normalization and calculation of the Jacobian operator field to quantify changes between scans, and 2) metastatic brain tumor candidate segmentation and detection of volume-changing metastatic brain tumors with the Jacobian operator field. Receiver operating characteristic analysis was used to assess the detection accuracy of the algorithm, and it was verified with jackknife resampling. The reference standard was based on detections by a neuroradiologist.

RESULTS:

The areas under the receiver operating characteristic curves were 0.925 for 1.5T and 0.965 for 3T. Furthermore, at its optimal performance, the algorithm achieved a sensitivity of 85.1% and 92.1% and specificity of 86.7% and 91.3% for 1.5T and 3T, respectively. Vessels were responsible for most false-positives. Newly developed or resolved metastatic brain tumors were a major source of false-negatives.

CONCLUSIONS:

The proposed algorithm could detect volume-changing metastatic brain tumors on longitudinal brain MRIs with statistically high accuracy, demonstrating its potential as a computer-aided change-detection tool for complementing the performance of radiologists, decreasing inter- and intraobserver variability, and improving efficacy.

Metastatic brain tumors (MBTs) occur in 24%–45% of patients diagnosed with primary cancers outside the brain.¹ Accurate assessment of MBTs on follow-up imaging is critical for better prognosis and selecting the most appropriate treatment such as chemotherapy, surgery, and radiation therapy or a combination of the aforementioned.^2–4 This is becoming more important with increasing use of stereotactic radiosurgery.⁵

Contrast-enhanced 3D T1-weighted (3D-T1-Gad) MR imaging is commonly used for detection and follow-up of MBTs and is the sequence of choice for stereotactic radiosurgery planning of MBTs.^5,6 During follow-up of MBTs, longitudinal volumetric imaging is performed every 2–3 months.⁵ This results in a large amount of data to process and a demanding workload for radiologists.⁷ Moreover, the inherent limitations of viewing scans section by section, changes in head position from one scan to another, and user subjectivity result in the potential for increased inter- and intraobserver variability in both detection and volume assessment, especially with small MBTs or subtle volume changes.⁸

Although several studies have investigated the efficiency of computer-aided detection techniques in MBTs on a single MR scan,^9–14 the literature is limited in studies evaluating the efficacy of computer algorithms in the follow-up of MBTs¹⁵ and detection of volume-changing MBTs (ΔMBTs) as an indicator of treatment response. Tracking volumetric changes is of high clinical value, and implementing computer-aided techniques in the follow-up of MBTs can improve diagnostic accuracy and efficiency^16–19 and complement current single-scan detection algorithms.

While computer-aided detection tools are limited for MBTs, automated change-detection techniques in MS are an active area of research and development.²⁰ Like MBTs, in MS, quantitative analyses are important for assessing disease progression,²¹ activity,²² and treatment evaluation.²³ The literature on automatic change detection of MS lesions broadly divides existing approaches into deformation-based (analysis of deformation fields resulting from nonrigid registration of scans) and intensity-based (voxel-to-voxel comparison between scans) methods and suggests a potentially strong role for deformation field-based and combined techniques.^20,23 Furthermore, techniques based on the deformation field have been proposed as promising in detecting structural changes on longitudinal brain MR imaging^24–27 and encompass techniques based on vector displacement fields such as those centered around divergence²⁸ and Jacobian operator fields (JOFs).²⁹

To detect ΔMBTs on longitudinal brain MRIs, a semiautomated algorithm based on the JOF is proposed here. The JOF has certain advantages compared with other methods because it can be used independently to detect local volume changes²⁸ compared with divergence techniques³⁰ and is computationally less expensive than other deformation field morphometry approaches.²⁰

In conjunction with other image-processing methods, the JOF is used in this study to identify MBT candidates that have changed in size, independent of changes in intensity or contrast compared with surrounding structures. We hypothesized that our algorithm can detect ΔMBTs with statistically high accuracy compared with a reference standard, defined here as detection by a board-certified neuroradiologist with 5 years of experience.

Materials and Methods

Dataset Extraction

This retrospective study was approved by the Research Ethics Board of our institution (Sunnybrook Health Sciences Centre, Toronto, Ontario, Canada) with a waiver of informed consent. Patient datasets from June 2014 to June 2015 were extracted from the PACS of our institution. All patients included in this study were adults (older than 18 years of age) with MBTs, who had undergone 2 consecutive 3D-T1-Gad scans at our institution. Patients with other brain pathologies—such as primary brain neoplasms, MS lesions, or stroke—or those who had undergone a brain operation for any reason were excluded. Datasets were divided into 2 groups based on magnetic field strength (1.5T versus 3T) to assess the performance of the algorithm in 2 different scenarios. The 1.5T group had MR images obtained on 2 identical 1.5T TwinSpeed Excite scanners (GE Healthcare, Milwaukee, Wisconsin) with a standard 8-channel head coil. The parameters for 3D-T1-Gad included the following: TR/TE/flip angle, 8.6 ms/4.2 ms/20°; FOV, 220 × 220 mm; and voxel size, 0.58 × 0.58 × 1.5 mm. The 3T group had MR images obtained on a 3T Achieva TX scanner (Philips Healthcare, Best, the Netherlands) with a standard 8-channel head coil. The parameters for 3D-T1-Gad included the following: TR/TE/flip angle, 9.5 ms/2.3 ms/8°; FOV, 312 × 206 mm; and voxel size, 0.67 × 0.67 × 1.5 mm. The parameters are part of the routine contrast-enhanced brain MR imaging protocol at our institution.

Image Analysis

Overview and Definitions.

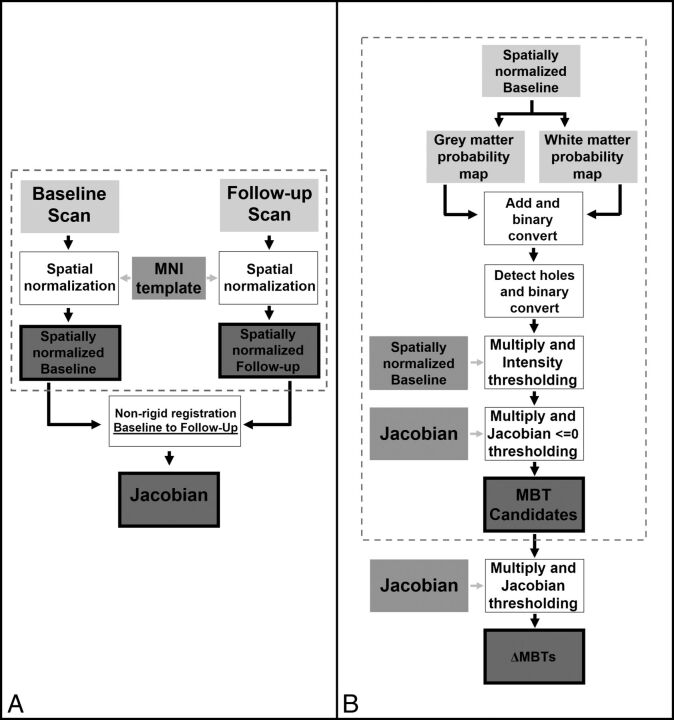
In this section, the image-processing pipeline used to detect ΔMBTs is described (Fig 1).

Fig 1.

Steps summarizing the preprocessing of patient datasets (dotted box) and calculation of the Jacobian operator field in the forward direction (A) and for segmentation of metastatic brain tumor candidates (dotted box) and detection of shrinking MBTs in the forward direction (B).

ΔMBTs were classified by the authors as either ΔMBT_ts, which represent ΔMBTs present on both baseline and follow-up scans, or ΔMBT_os, which only appear on 1 scan (ie, newly developed or resolved MBTs). The volume change ratio (VCR) of an object across 2 scans was defined as the ratio of its volume change across time over its initial volume. This metric was defined because it is accepted that the values of JOFs are directly associated with the VCR of the brain, and higher JOF values suggest higher VCR and vice-versa.²⁰

Concerning volume changes, “growing” MBTs refer to all MBTs that have grown in volume from baseline to follow-up scans, including newly developed MBTs. “Shrinking” MBTs refer to MBTs that shrank in size from baseline to follow-up, including resolved MBTs. Note that to detect growing MBTs in the forward direction (ie, from baseline to follow-up), our algorithm detected shrinking MBTs in the reverse direction (ie, from follow-up to baseline) because the JOF provides richer information in the shrinking field.³⁰ In addition, this approach allowed detection of newly developed MBTs that do not have a corresponding MBT on baseline, though the processes going in the forward and reverse directions are identical. While our algorithm identified growing MBTs by detecting shrinking MBTs in the reverse direction, for clarity, here we will describe the process going in the forward direction only. SPM12 (http://www.fil.ion.ucl.ac.uk/spm/software/spm12) and Matlab (MathWorks, Natick, Massachusetts) software packages were used for data processing. All average values are presented as mean ± SD.

Spatial Normalization.

To ensure that longitudinal baseline and follow-up scans were comparable and could be registered to one another for analyzing changes, we spatially normalized both scans to the Montreal Neurological Institute template³¹ with the methods described by Ashburner et al³² (Fig 1A) on SPM12 software (Fig 2).³³

Fig 2.

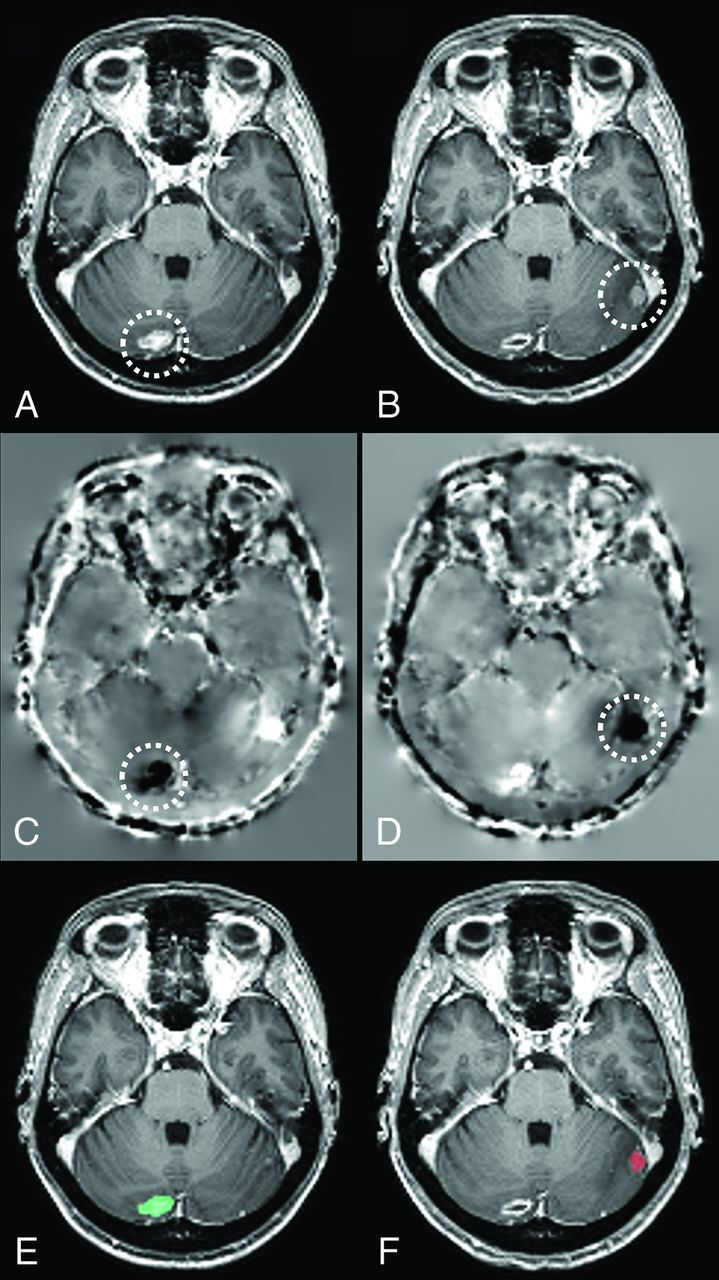
Axial sections of a patient's baseline (A) and follow-up (B) scans. The Jacobian operator field, calculated from the deformation field in the forward (C) and reverse (D) directions. The final output of our algorithm produced for baseline (E) and follow-up (F) scans, highlighting volume-changing metastatic brain tumors on each scan. Note that darker voxels on C and D correspond to negative JOF values and brighter voxels correspond to positive JOF values. The location of a metastatic brain tumor that has shrunk in size across the scans has been circled on A–D. The green on E indicates shrinkage, and the red on F indicates growth. Note that while this image is demonstrated in 2D, various operations as described here were performed in 3D.

Deformation Field.

Next, a nonrigid registration technique, based on joint diffeomorphic and rigid-body registration and proposed for intrasubject registration,³⁴ was used to align the images using SPM12.³³ This generated a 3D displacement field, which determined structural changes between the 2 scans (Fig 1A).

Calculation of the JOF.

To determine whether a tumor shrank between time points, the JOF—which quantifies local volume changes—was computed from the displacement field (Fig 2C, -D), using SPM12.³³

Segmentation of MBT Candidates.

To segment MBT candidates, we used a modified version of the approach proposed by Seghier et al³⁵ for lesion segmentation. First, a probabilistic segmentation of GM and WM was computed with the methods described by Ashburner and Friston.³² These 2 tissue maps were then added together to create a brain mask, which was then converted to binary in which voxels of nonzero value were retained. Because MBTs generally appear on MR images as bright objects fully or partially confined within the brain matter, they are not detected during this step and are therefore excluded from the binary mask, leaving “holes” within the brain mask. To detect MBT candidates, we created a binary mask of the holes, and this mask was multiplied to the original intensity image to identify MBT candidates in the intensity domain. Automatic postprocessing, with no user interaction, was completed to remove irrelevant objects that had an intensity lower than the average intensity of GM and WM.

False-Positive Reduction and Detection of ΔMBTs.

To limit MBT candidates to islands that shrank, we converted the MBT candidates to binary, multiplied to the JOF, and discarded 2D islands in the axial dimension with a positive median value, permitting false-positive reduction. To detect ΔMBTs, we then thresholded these MBT candidates using various JOF values. For each threshold value, 3D islands present on at least 1 section in the axial dimension with a median value of the threshold value or less were retained (Figs 1B and 2E, -F).

Statistical Analysis

The presence and location of ΔMBTs were confirmed and extracted by a board-certified neuroradiologist with 5 years of experience, blinded to the technical details of our detection algorithm using Medical Image Processing, Analysis & Visualization (MIPAV; National Institutes of Health, Bethesda, Maryland); this defined our reference standard. To validate the algorithm, we considered its accuracy in detecting ΔMBTs in the 1.5T and 3T groups separately. For statistical analysis of the accuracy of our algorithm and to find the optimal threshold value of the JOF, we used receiver-operating characteristic (ROC) analysis.³⁶ At each threshold value, a detection was marked as a true-positive if it overlapped an ΔMBT identified by the neuroradiologist; the rest were marked as false-positives. The area under the curve (AUC) of the ROC curve was used to evaluate accuracy, for which an AUC > 0.9 corresponds to a technique with statistically high accuracy.³⁷ For verification of our results, in addition to assessing the algorithm using 2 independent datasets, we used the jackknife approach,³⁸ with evaluation of the AUC, sensitivity, specificity, and false-positive rate (FPR) at the optimal threshold value of each iteration. To assess the potential role of our algorithm in complementing the performance of radiologists and reducing interobserver variability, we compared the true-positives detected by our algorithm against those detected by a different board-certified neuroradiologist with 3 years of experience, blinded to the technical details of our algorithm. The Mann-Whitney U test was used to compare the following: 1) the accuracy, sensitivity, specificity, and FPR of our algorithm at 1.5T and 3T; 2) the VCR of missed-versus-detected ΔMBTs; and 3) the VCR of ΔMBT_os versus the VCR of ΔMBT_ts. A P < .05 defined statistical significance.

Results

Patient MR Imaging Datasets

The 1.5T group, comprising 30 patients, had 74 MBTs. The 3T group, comprising 20 patients, had 76 MBTs. Table 1 summarizes information about patient demographics, scan timeline, and MBT details.

Table 1:

Summary of information on patients, scans, and MBTs

Variable	1.5T	3T
Sex
Male (total %)	15 (50%)	11 (55%)
Female (total %)	15 (50%)	9 (45%)
Age (yr)
Averagea	60.3 ± 13.1	58.7 ± 15.7
Range	23.4–91.0	27.3–84.5
Time between baseline and follow-up (days)
Averagea (per patient)	147 ± 155	132 ± 129
Range	26–676	17–532
Number of ΔMBTs
Total	74	76
ΔMBTts	58	67
ΔMBTos	16	9
Averagea (per patient)	4.4 ± 3.1	3.8 ± 3.9
ΔMBT volume (mL)
Averagea	2.4 ± 4.0	2.2 ± 3.8
Range	4.0 × 10−3–1.9 × 101	2.0 × 10−2–3.0 × 101
ΔMBT volume change (mL)
Averagea	1.5 ± 2.2	2.2 ± 3.5
Range	3.4 × 10−3–3.5 × 101	9.1 × 10−2–2.0 × 101
ΔMBT VCR (%)
Averagea	7.0 × 101 ± 29.5	7.6 × 101 ± 1.7 × 101
Range	7.8 × 10−1–1.0 × 102	4.2–1.0 × 102

^aAverage ± SD.

Algorithm Performance

Detecting ΔMBTs.

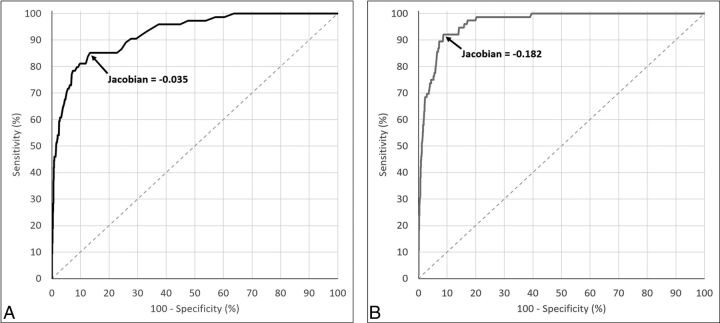
For the 1.5T group, an ROC curve with 233 points (0 to −0.232, separated by −0.001) and, for the 3T group, an ROC curve with 656 points (0 to −0.655, separated by −0.001) were constructed by thresholding MBT candidates using various values of the JOF (Fig 3 and Table 2). Both ROC curves showed statistically high accuracy with an AUC of 0.925 and 0.965 for the 1.5T and 3T groups, respectively. There was no significant difference in the VCR between the detected and missed ΔMBTs for either group (P > .05).

Fig 3.

A, Illustration of the receiver operating characteristic curve of our algorithm for detecting volume-changing metastatic brain tumors at 1.5T, constructed from 233 different thresholding values of the Jacobian operator field (from 0 to −0.232, separated by −0.001). The arrow shows the optimal point of balance. B, Illustration of the ROC curve of our algorithm for detecting ΔMBTs at 3T, constructed from 656 different thresholding values of the Jacobian operator field (from 0 to −0.655, separated by −0.001). The arrow shows the optimal point of balance between sensitivity and specificity, which happens at the Jacobian value of −0.182.

Table 2:

Summary of ROC analysis, for detecting all 1.5T and 3T ΔMBTs and 1.5T ΔMBT_ts only, and the VCR of detected and missed ΔMBTs

Variable	1.5T	3T
ROC curve
AUC	0.925	0.965
Optimal Jacobian threshold	−0.035	−0.182
Sensitivitya (%)	85.1	92.1
Specificitya (%)	86.7	91.3
FPRa (per section)	0.208	0.227
FPRa (per scan)	25.1	27.5
Detecteda ΔMBT VCR (%)
Averageb	7.1 × 101 ± 2.8 × 101	7.7 × 101 ± 1.7 × 101
Median	7.9 × 101	7.5 × 101
Range	7.8 × 10−1–1.0 × 102	4.2–1.0 × 102
Misseda ΔMBT VCR (%)
Averageb	6.2 × 101 ± 3.8 × 101	7.3 × 101 ± 1.9 × 101
Median	7.5 × 101	8.2 × 102
Range	3.9–1.0 × 102	4.3 × 101–8.6 × 101

^aAt the optimal Jacobian threshold.

^bAverage ± SD.

False-Positives

False-positives detected by the algorithm were divided into 5 categories (Table 3): 1) arteries: branches of anterior and middle cerebral arteries and vertebrobasilar system; 2) veins: superficial cortical veins, deep veins including internal cerebral veins, and basal veins of Rosenthal; 3) dural venous sinuses; 4) dura, tentorium, and falx cerebelli; and 5) choroid plexus. Vessels, including arteries, veins, and dural venous sinuses, were responsible for 79.0% ± 24.0% and 77.8% ± 18.5% of false-positives in the 1.5T and 3T groups, respectively. Visual inspection of the datasets suggested that at times, subtle structural differences such as pulsation of vessels between scans resulted in high JOF values and, consequently, detection as false-positives. However, these can easily be dismissed on visual inspection by a radiologist.

Table 3:

Categories and distribution of false-positives at the optimal Jacobian threshold

False-Positive Categories	1.5T	3T
Arteriesa (%)	49.8 ± 25.3	44.9 ± 22.9
Veinsa (%)	16.0 ± 8.7	17.3 ± 12.8
Dural venous sinusesa (%)	13.2 ± 15.9	15.5 ± 14.4
Duraa (%)	16.6 ± 23.5	12.0 ± 12.3
Choroid plexusa (%)	4.4 ± 5.4	10.2 ± 12.5

^aAverage ± SD.

False-Negatives

At its optimal threshold value, the algorithm did not detect 11 ΔMBTs in the 1.5T group and 6 ΔMBTs in the 3T group. ΔMBT_ts false-negatives could subsequently be divided into the following (Table 4): 1) those that had a size of ≤2 voxels on one of the scans, or 2) those segmented poorly during the candidate segmentation portion of the algorithm, which consequently negatively affected the evaluation of their JOF values.

Table 4:

Categories and distribution of false-negatives at the optimal Jacobian threshold

False-Negative Categories	1.5T	3T
ΔMBTos (percentage of total)	4 (36.3%)	0 (0%)
ΔMBTts (percentage of total)	7 (63.7%)	6 (100%)
≤2 voxels	3 (27.3%)	1 (16.7%)
Poorly segmented	4 (36.4%)	5 (83.3%)

In the 1.5T group, the sensitivity of the algorithm in detecting ΔMBT_os showed inferior values compared with its sensitivity in detecting ΔMBT_ts (75% versus 87.9%, respectively). This is even though ΔMBT_ts had a significantly lower VCR than ΔMBT_os (P < .0001). These results suggested that ΔMBT_os may be a major source of false-negatives for our algorithm. To assess this, we evaluated the performance of the algorithm with ΔMBT_os omitted. This analysis was only performed in the 1.5T group because all instances of ΔMBT_os were detected in the 3T group. Like ΔMBT detection, an ROC curve with 302 points (0 to −0.301, separated by −0.001) was generated with an AUC of 0.929. At its optimal performance (achieved at a threshold value of −0.035), the algorithm had a sensitivity of 87.9%, specificity of 86.6%, and FPR of 0.210 per section, equivalent to 25.4 per scan. Note that detected the ΔMBT_os was included in the calculation of specificity and FPR.

Verification

In addition to performing all analyses on 2 independent patient datasets, as demonstrated above, we conducted jackknifing for further verification of findings. Results from jackknifing were like the findings before the procedure, verifying initial results (Table 5). Furthermore, statistical analysis of the mean AUC of the algorithm and the sensitivity of the algorithm when applied to jackknifed 1.5T ΔMBT_ts-only data versus jackknifed 1.5T ΔMBT data showed significant improvement (P < .0001 for both AUC and sensitivity).

Table 5:

Summary of ROC analysis after jackknifing datasets, for detecting all 1.5T and 3T ΔMBTs and 1.5T ΔMBT_ts only

Variable	1.5T	1.5T: ΔMBTts Only	3T
AUC of ROC curve
Averagea	0.925 ± 0.003	0.929 ± 0.003	0.965 ± 0.002
Median	0.924	0.928	0.965
Sensitivityb (%)
Averagea	85.1 ± 0.8	87.9 ± 0.8	92.2 ± 0.5
Median	84.9	87.7	92.0
Specificityb (%)
Averagea	86.7 ± 0.3	86.6 ± 0.3	91.3 ± 0.6
Median	86.7	86.6	91.1
FPR (per section)
Averagea	0.208 ± 0.005	0.210 ± 0.005	0.227 ± 0.02
Median	0.209	0.211	0.232

^aAverage ± SD.

^bAt the optimal Jacobian threshold.

Effect on Performance

Of the 150 ΔMBTs in our datasets, a second neuroradiologist could detect 144 ΔMBTs, equivalent to 96% sensitivity. Of the 6 ΔMBTs missed by the neuroradiologist, 2 ΔMBTs, consisting of 1 ΔMBT_os and 1 ΔMBT_ts, were missed by both the algorithm and neuroradiologist. However, 1 ΔMBT_os and 3 instances of ΔMBT_ts were missed by the neuroradiologist but detected by the algorithm. Inspection of those 4 ΔMBTs revealed subtle volume changes, ranging from 9.1 × 10⁻² to 2.5 × 10⁻¹ mL. The addition of these detections would improve the neuroradiologist's sensitivity to 98.7%.

Discussion

In this article, we have presented our semiautomated algorithm for detecting ΔMBTs in longitudinal brain MRIs with statistically high accuracy at 1.5T and 3T (AUC > 0.9). Our approach uses the JOF—a vector displacement field operator—which quantifies longitudinal structural changes of the brain on the basis of the deformation field. At its optimal performance, our algorithm had a sensitivity of 85.1% and 92.1% and a specificity of 86.7% and 91.3% for the 1.5T and 3T groups, respectively. Although performances at the optimal thresholds were similar, the difference in optimal JOF threshold values for the 2 groups indicated the effect of scan parameters on optimal threshold values and the need to identify a unique optimal threshold value for each set of scan parameters. Moreover, missed and detected ΔMBTs had a statistically similar VCR, suggesting that the detection ability of our algorithm is not dependent on VCR values. Compared with manual reading, this can be considered an advantage of our algorithm because manual reading of longitudinal brain MR images is biased against subtle changes.¹⁶ Thus, the findings in this study supported the potential of our algorithm to aid performance by identifying lesions with subtle volume change that could otherwise be missed by the user. Although it is accepted that the values of the Jacobian operator field are directly associated with the VCR of the brain,²⁰ we speculate that this association may not be the case for VCR values of individual brain regions because the missed and detected ΔMBTs of our algorithm had statistically similar VCRs despite differences in JOF values. Although this difference may limit the information provided by the JOF about the amount of volume change, our results demonstrate the adequacy of the JOF in detecting ΔMBTs, even for relatively small VCR values, and support its potential to serve as a diagnostic aid.

At present, the literature is limited in studies concerning the follow-up and volume-change detection of MBTs. Chitphakdithai et al¹⁵ proposed a method for tracking MBTs, relying on a 4-level label map to denote the intensity-correspondence relation between baseline and follow-up images. Although authors reported a sensitivity of 92% in detecting ΔMBTs, this was verified on only a limited dataset comprising 3 patients. In addition, the authors did not report specificity or FPR; this omission prevented accurate comparison with our algorithm.

With our algorithm, nonlinear registration of baseline and follow-up scans was used to detect structural changes. One of its main limitations is the infinite number of displacement fields for a given pair of scans, depending on the registration technique used.¹⁶ More important, these techniques rely on the assumption that a lesion or tissue region exists on both scans with similar intensity.¹⁶ This assumption limits the detection of ΔMBT_ts of negligible size on one of the scans and ΔMBT_os. Reviewing the detections of the algorithm showed that most false-negatives were of the aforementioned 2 categories. Moreover, although our algorithm could detect 75% of ΔMBT_os at 1.5T, this was inferior to the general sensitivity of our algorithm; however, this problem was not isolated to our algorithm.

A similar problem exists in MS, in which computer-aided detection tools are more developed and prevalent in the clinical environment. Although MS computer-aided detection tools focus more on the amount of volume change as opposed to mere detection of change, both techniques use automated quantitative analysis techniques that can be compared. A recent study by Cabezas et al³⁹ combined subtraction and deformation field analyses to detect new MS lesions on T2-weighted images. Using this approach on 36 patient datasets, Cabezas et al reported a 70.8% sensitivity.³⁹ Comparatively, our 1.5T datasets consisted of 30 patients with 16 instances of ΔMBT_os. When these were omitted, the AUC and sensitivity of our algorithm improved; this change suggests that ΔMBT_os has a negative effect on its performance. However, because detecting ΔMBT_os is equivalent to detecting MBTs on a single scan, this limitation can be addressed by combining our algorithm with previously described MBT computer-aided detection tools.^9–14

Further enhancement of the clinical utility of our algorithm rests on improving its FPR. Like other studies concerned with automatic MBT detection on 3D-T1-Gad,^9–13 bright vessels were a major source of false-positives. Differentiating vessels and MBTs could be achieved by incorporating 3D template matching–based algorithms for MBT segmentation^9–13 in place of our current method. This may also improve the sensitivity of our algorithm because some of the false-negatives of our technique were a direct result of poor MBT segmentation. Further false-positive reduction may be achieved with vessel filters^40,41 or cerebrovascular atlases.⁴² The use of black-blood MR imaging can also address this problem¹⁴ because this technique has been shown to be superior in capturing smaller MBTs compared with other MR images.^43,44 More recently, Pérez-Ramírez et al¹³ proposed the use of a degree of anisotropy to distinguish blood vessels and MBTs.

Conclusions

The proposed semiautomated algorithm presented in this article could detect volume-changing MBTs on longitudinal brain MR imaging with high accuracy. With the growing quantity and quality of automated techniques for MBT detection, implementation of some of these elements may further improve the sensitivity, specificity, and FPR of our algorithm. The clinical role of our technique lies in its potential to improve the high workload⁷ and ambiguity¹⁶ associated with manual reading, which is crucial for appropriate treatment.⁵ Through demonstrating the potential of deformation-based techniques and our algorithm, this study serves as an initial step in developing a computer-aided change-detection tool to complement the performance of radiologists.

ABBREVIATIONS:

AUC

area under the curve

3D-T1-Gad

contrast-enhanced 3D T1-weighted

ΔMBT

volume-changing MBT

ΔMBT_os

newly developed or resolved MBT

ΔMBT_ts

changing MBT present on both baseline and follow-up scans

FPR

false-positive rate

JOF

Jacobian operator field

MBT

metastatic brain tumor

ROC

receiver operating characteristic

VCR

volume change ratio