A Simplified Model for Intravoxel Incoherent Motion Perfusion Imaging of the Brain

Abstract

BACKGROUND AND PURPOSE:

Despite a recent resurgence, intravoxel incoherent motion MRI faces practical challenges, including limited SNR and demanding acquisition and postprocessing requirements. A simplified approach using linear fitting of a subset of higher b-values has seen success in other organ systems. We sought to validate this method for evaluation of brain pathology by comparing perfusion measurements using simplified linear fitting to conventional biexponential fitting.

MATERIALS AND METHODS:

Forty-nine patients with gliomas and 17 with acute strokes underwent 3T MRI, including DWI with 16 b-values (range, 0–900 s/mm²). Conventional intravoxel incoherent motion was performed using nonlinear fitting of the standard biexponential equation. Simplified intravoxel incoherent motion was performed using linear fitting of the log-normalized signal curves for subsets of b-values >200 s/mm². Comparisons between ROIs (tumors, strokes, contralateral brain) and between models (biexponential and simplified linear) were performed by using 2-way ANOVA. The root mean square error and coefficient of determination (R²) were computed for the simplified model, with biexponential fitting as the reference standard.

RESULTS:

Perfusion maps using simplified linear fitting were qualitatively similar to conventional biexponential fitting. The perfusion fraction was elevated in high-grade (n = 33) compared to low-grade (n = 16) gliomas and was reduced in strokes compared to the contralateral brain (P < .001 for both main effects). Decreasing the number of b-values used for linear fitting resulted in reduced accuracy (higher root mean square error and lower R²) compared with full biexponential fitting.

CONCLUSIONS:

Intravoxel incoherent motion perfusion imaging of common brain pathology can be performed by using simplified linear fitting, with preservation of clinically relevant perfusion information.

Initially proposed by Le Bihan et al in the 1980s,^1,2 the intravoxel incoherent motion (IVIM) model enables simultaneous evaluation of diffusion and perfusion through a multi-b-value diffusion-weighted MRI acquisition. This approach offers theoretical advantages over other perfusion imaging strategies; namely, it is inherently quantitative, provides intrinsic coregistration between perfusion and diffusion parameters, and does not rely on intravenous contrast injection or estimation of an arterial input function. While early investigations were hampered by various technical limitations,³ advances in field strength, gradient hardware, and echo-planar and parallel imaging technology have led to a resurgent interest in IVIM for a wide range of clinical applications.^4–18

Brain imaging with IVIM is particularly challenging due to the low blood volume fractions of cerebral tissues^19–21 and CSF partial volume contamination.²² Nonetheless, IVIM has now been validated for quantitative evaluation of brain perfusion using clinically available hardware and pulse sequences.²³ Recent work in neuro-oncology has shown the potential for IVIM in differentiating tumor recurrence from posttreatment effects,^9,10 in the preoperative evaluation of tumor grade,^6,18 and in differentiating primary CNS lymphoma from glioblastoma.¹⁶ IVIM has also been applied in the setting of acute stroke,^7,24,25 where perfusion imaging without gadolinium is of particular interest given the association between cerebrovascular disease and renal insufficiency.²⁶

Despite these promising advancements, practical issues such as low SNR and demanding acquisition and postprocessing requirements may impede more widespread adoption of IVIM in clinical and research settings. Conventional IVIM requires acquisition of a large number of b-values (from 10 to 36),²⁷ including low b-values sensitive to microcirculatory blood flow (ie, pseudodiffusion) and high b-values in the regime where true molecular diffusion dominates. A biexponential fit is then performed over the full range of b-values using a nonlinear fitting procedure.^11,23

In contrast, an alternate solution to the IVIM equation can be obtained by performing a linear fit of the log-transformed data, using only a subset of higher b-values. This simplified procedure, also referred to as asymptotic fitting,^19,27 offers potential advantages over biexponential fitting, including shorter acquisition protocols, computational simplicity, and reduced uncertainty in the setting of low SNR.¹⁹ In principle, this method allows estimation of IVIM parameters using as few as 2 nonzero b-values. Linear fitting has been applied for imaging of the liver,¹³ kidneys,¹⁵ pancreas,⁵ prostate,¹² and breast,⁴ and in the evaluation of head and neck malignancies.^14,17 To our knowledge, there has been no systematic comparison of simplified linear fitting with standard biexponential fitting for the evaluation of brain pathology.

Therefore, the purpose of this study was: 1) to compare the perfusion fraction (f) estimates obtained using simplified linear fitting with those of conventional biexponential fitting, and 2) to examine the effect of reducing the number of b-values on the quality of the resulting perfusion maps. We performed this analysis in 2 common clinical scenarios, namely, evaluation of brain gliomas and acute strokes.

Materials and Methods

Subjects

Subjects were participants in a study of IVIM for the evaluation of brain gliomas at the University of Lausanne from May 2011 to July 2014 and a bicentric study of IVIM for evaluation of acute stroke at the University of Lausanne and the University of Virginia from February 2011 to August 2013. Institutional ethics review board approval at both institutions was obtained, and patient consent was waived. This retrospective analysis includes subject overlap with 2 previously published studies, which applied conventional IVIM methodology for the evaluation of gliomas⁶ and strokes,⁷ respectively. Inclusion criteria for patients with gliomas were: 1) preoperative imaging, including 16 b-value IVIM acquisition, without corruption by motion artifacts; 2) no relevant treatment history at the time of imaging, including chemotherapy, radiation therapy, or antiangiogenic therapy; and 3) histopathologic tumor diagnosis and grading according to the World Health Organization criteria. Due to the relatively low number of patients with histopathologically confirmed low-grade gliomas (n = 10), 6 additional patients with diagnosis of low-grade glioma on radiologic criteria alone were included in the analysis.⁶ Inclusion criteria for patients with stroke were: 1) MRI within 5 days of symptom onset, including successful 16-b-value IVIM acquisition, without corruption by motion artifacts; 2) supratentorial diffusion-restricting infarct of >0.5 cm in minimal diameter; and 3) no hemorrhagic transformation at the time of imaging.

MRI Acquisition

All imaging was performed on 3T MRI systems (Magnetom Skyra, Verio, or Trio; Siemens, Erlangen, Germany) using 32-channel phased array receiver coils. The IVIM acquisition consisted of a Stejskal-Tanner diffusion-weighted EPI spin-echo pulse sequence,²⁸ with diffusion-weighting obtained along 3 orthogonal directions using 16 different b-values (b = 0, 10, 20, 40, 80, 110, 140, 170, 200, 300, 400, 500, 600, 700, 800, 900 s/mm²). Images were acquired in the axial plane, with nominal in-plane resolution = 1.2 × 1.2 mm², section thickness = 4 mm, NEX = 1, acceleration factor = 2, bandwidth = 1086–1106 Hz/pixel, TR = 4000 ms, TE = lowest achievable for each scanner (89–102 ms). For patients with tumors, DSC perfusion MRI was performed using a T2*-weighted gradient-echo EPI pulse sequence (nominal in-plane resolution = 1.8 × 1.8 mm², section thickness = 6 mm, TR = 1950 ms, TE = 43 ms) sequentially acquired after IV injection of gadoterate meglumine (Dotarem; Guerbet, Aulnay-sous-Bois, France) with a dose of 0.2 mL/kg and a rate of 3 mL/s. Additional conventional images were obtained according to the institutional brain tumor and stroke imaging protocols.

Conventional IVIM Model

The standard 2-compartment model of diffusion proposed by Le Bihan et al² was assumed, described by the biexponential equation:

where the first term represents intravascular signal loss due to blood flow in the microvasculature, characterized by the pseudo-diffusion coefficient D*, and the second term represents extravascular signal loss due to molecular diffusion of water, characterized by the diffusion coefficient D. The perfusion fraction f represents the proportion of MR–visible water contained within the microcirculation (ie, the intravascular or “fast” diffusion compartment).

For the conventional IVIM calculation, a voxelwise fitting of Equation 1 was performed using a 2-step procedure as previously described.^6,23 Briefly, the S(b) / S₀ curve was fitted for b > 200 s/mm² to solve for the parameter D, under the assumption that D* ≫ D so that pseudodiffusion effects can be ignored for higher b-values.²⁹ A nonlinear fit of Equation 1 was then performed over all 16 b-values to solve for f and D* while holding D constant, using the Levenberg-Marquardt algorithm³⁰ (Matlab, Optimization Toolbox; MathWorks, Natick, Massachusetts). This 2-step procedure has been shown to provide robust parameter estimates under biologic conditions.²³ The perfusion fraction calculated using this method was defined as f_{biexponential}.

Simplified IVIM Model

Under the assumptions that D* ≫ D,²⁹ the first term of Equation 1 (corresponding to the intravascular compartment) has a negligible contribution to the signal S(b) for higher b-values. Taking the natural logarithm of Equation 1, this allows for the following simplification²:

Equation 2 provides a linear relationship with slope − D and intercept ln(1 − f), which can be solved for f and D using as few as 2 nonzero b-values, provided they are selected from the regime in which pseudodiffusion effects are negligible. Voxelwise linear least squares regression was applied to solve Equation 2 using different combinations of b-values of >200 s/mm² (Table 1). The perfusion fraction calculated using this simplified linear fitting method was defined as f_linear. Note that this approach does not allow estimation of the pseudo-diffusion coefficient, D*.

Table 1:

Combinations of b-values used for linear fitting

No. of Nonzero b-Values	b-Values (sec × mm−2)
7	300, 400, 500, 600, 700, 800, 900
4	300, 500, 700, 900
3	300, 600, 900
2	300, 900

DSC Reconstruction

Leakage-corrected CBV maps were reconstructed from T2*-weighted gradient-echo images using a Boxerman-Weiskoff correction for contrast agent extravasation,³¹ implemented using the Dynamic Susceptibility Contrast MR Analysis plug-in for ImageJ (DSCoMAN, Version 1.0, https://sites.duke.edu/dblab/dscoman). Successful DSC perfusion imaging was obtained in 40 of the 49 patients with brain tumors included in this study.

ROI Analysis

Voxels with D > 2.5 × 10⁻³ (approximately 1 SD below the mean diffusion coefficient for CSF)³² were presumed to contain predominantly CSF and were excluded from the analysis. Voxels with f < 0 or f > 0.3 were considered nonphysiologic (likely contaminated by image noise or volume averaging with flowing CSF)²³ and were also excluded. For patients with gliomas, ROIs were manually placed within the tumor encompassing the region of maximum perfusion fraction by the consensus of 2 neuroradiologists. Regions of intratumoral hemorrhage and necrosis were excluded through close reference to conventional imaging sequences. To evaluate interobserver reliability, an additional radiologist independently retraced all tumor ROIs using an identical procedure, without reference to the initial ROIs or clinical data. To evaluate intraobserver reliability, one radiologist retraced these ROIs during a separate review session, without reference to the initial ROI results. Intraclass correlation coefficients were calculated for interobserver and intraobserver reliability. For patients with DSC perfusion imaging, ROIs were manually copied onto the CBV maps with close reference to anatomic landmarks, and an ROI was placed in the contralateral deep WM to permit normalization and calculation of relative CBV (rCBV). For patients with stroke, a semiautomated procedure was used to define an ROI encompassing the infarct core, by applying a threshold to the diffusion coefficient map under supervision of a single neuroradiologist. A homologous ROI was manually traced within the contralateral hemisphere.

The mean perfusion fraction estimated using the biexponential model (f_{biexponential}) and the simplified linear model (f_linear) was calculated for each ROI. A linear least squares regression of f_linear on f_{biexponential} was then performed for tumors (n = 49) and infarcts (n = 17). The coefficient of determination (R²) and root mean square error for f_linear compared with f_{biexponential} were calculated for each ROI. This procedure was repeated for estimates of f_linear using each of the b-value combinations listed in Table 1.

All calculations were performed on a Dell PC (Intel Core i5–2300 CPU at 2.8 GHz, 6 GB of RAM; www.dell.com).

Statistical Analysis

Statistical analysis was performed using SPSS, Version 16.0 (IBM, Armonk, New York). For tumors, a 2-way mixed ANOVA was performed with perfusion fraction as the dependent variable, tumor grade (low or high) as a between-subjects factor, and IVIM model (f_{biexponential} using 16 b-values or f_linear using 2, 3, 4, or 7 nonzero b-values) as a within-subjects factor. For strokes, a 2-way repeated-measures ANOVA was performed with perfusion fraction as the dependent variable and tissue type (stroke or contralateral brain) and IVIM model as within-subjects factors. For each ANOVA, the threshold for statistical significance was set as .05/3 = .017—that is, Bonferroni correction for 3 comparisons (2 possible main effects and 1 possible interaction). The Mauchly test was used to evaluate the assumption of sphericity, and dfs were corrected according to the Greenhouse-Geisser (for ε < 0.75) or Huynh-Feldt (for ε > 0.75) method as appropriate. If either ANOVA demonstrated a significant main effect for the IVIM model in the absence of a significant interaction term, post hoc pair-wise comparisons were performed between f_{biexponential} and each of the 4 linear IVIM models (4 comparisons) using the Bonferroni correction.

Results

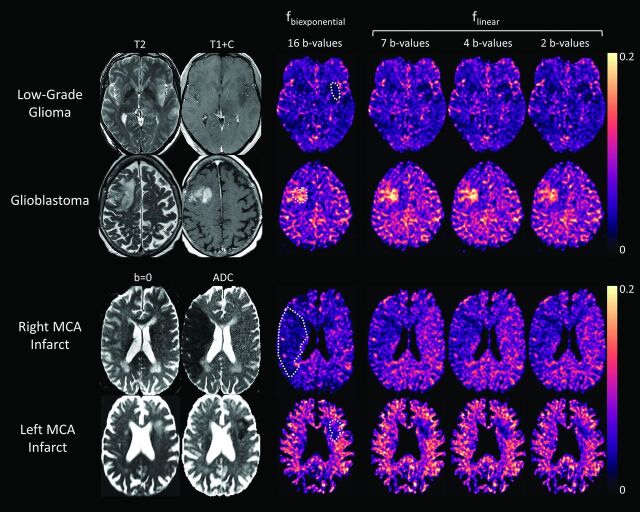
Perfusion fraction maps created using the simplified linear model (f_linear) were qualitatively similar to those obtained using the conventional biexponential model (f_{biexponential}) for low- and high-grade gliomas and for acute infarcts, even when as few as 2 nonzero b-values were used in the fitting procedure (Fig 1). Interobserver reliability for ROI measurements was “substantial” (intraclass correlation coefficient = 0.78) and intraobserver reliability was “almost perfect” (intraclass correlation coefficient = 0.89) according to the standard interpretation of Landis and Koch.³³ Quantitative comparisons of the perfusion fraction for each pathology and IVIM model are provided in Figs 2 and 3.

Fig 1.

Anatomic images and IVIM perfusion maps for 4 clinical cases. f_{biexponential} is the perfusion fraction estimate of the conventional biexponential fit (16 b-values) and f_linear is the perfusion fraction estimate of the simplified linear fit using 2–7 nonzero b-values. Upper row: T2-weighted image, postgadolinium T1-weighted image, and perfusion maps for a patient with a histopathologically confirmed low-grade glial tumor (World Health Organization grade II). A subtle T2-hyperintense, hypoenhancing lesion in the left insular cortex corresponds to a focal region of low perfusion fraction on all perfusion maps. Second row: T2-weighted image, postgadolinium T1-weighted image, and perfusion maps for a patient with histopathologically confirmed glioblastoma (World Health Organization grade IV). A solid enhancing right frontal mass corresponds to a region of increased perfusion fraction on all perfusion maps. Third row: b=0 (ie, T2-weighted) image, ADC map, and perfusion maps for a patient with a large acute right MCA territory infarct, demonstrating a wedge-shaped area of decreased perfusion fraction corresponding to the area of restricted diffusion (infarct core). Lower row: Similar findings in a different patient with a smaller left MCA territory infarct. ROIs for tumors and strokes are shown overlaid on the conventional f_{biexponential} perfusion maps (dotted white lines).

Fig 2.

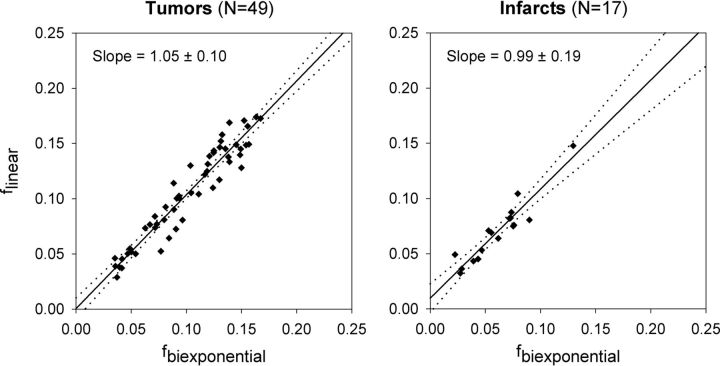
Plots comparing the perfusion fraction estimated using the conventional 16 b-value biexponential fit (f_{biexponential}) with those using simplified linear fitting of 7 nonzero b-values (f_linear) for tumors (left) and infarcts (right). Solid line indicates the least squares optimal linear regression; dotted lines indicate the 95% confidence interval for the line of best fit. The slope and its 95% confidence interval are also provided for each regression line.

Fig 3.

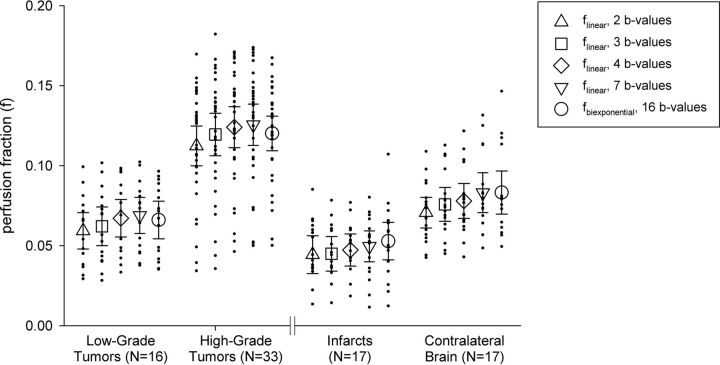
Comparison of the perfusion fraction between low- and high-grade tumors (left) and between acute infarcts and contralateral brain tissue (right). Triangle, square, diamond, and inverted triangle markers indicate the mean perfusion fraction calculated by the simplified linear method using 2, 3, 4, and 7 nonzero b-values, respectively (Table 1). Circle markers indicate the mean perfusion fraction calculated using the conventional 16 b-value biexponential method. Error bars indicate 95% confidence intervals.

For tumors, ANOVA demonstrated significant main effects for tumor grade (elevated perfusion fraction in high-grade tumors) and IVIM model (both P < .001). The interaction term was not statistically significant, indicating that the observed differences in perfusion fraction between low- and high-grade gliomas did not depend on the choice of IVIM model. In paired post hoc comparisons between IVIM models, f_linear calculated using 2 nonzero b-values was significantly lower than f_{biexponential} (P < .001). There were no significant differences between f_{biexponential} and f_linear calculated using 3, 4, or 7 nonzero b-values.

For strokes, ANOVA demonstrated significant main effects for tissue type (decreased perfusion fraction in acute infarcts) and IVIM model (both P < .001). The interaction term was not statistically significant, indicating that the observed differences in perfusion fraction between infarcts and contralateral brain did not depend on the choice of the IVIM model. In paired post hoc comparisons between IVIM models, f_linear calculated using 2 nonzero b-values was significantly lower than f_{biexponential} (P < .005). There were no significant differences between f_{biexponential} and f_linear calculated using 3, 4, or 7 nonzero b-values.

The effect of the decreasing number of b-values on the accuracy of f_linear is shown in Table 2, which provides the R² and root mean square error for f_linear calculated using each of the b-value combinations listed in Table 1. Decreasing the number of b-values was associated with reduced accuracy, reflected by decreasing R² and increasing root mean square error.

Table 2:

Measurements of fit and error for f_linear compared with f_{biexponential}

No. of Nonzero b-Valuesa	ROI
	Tumors (n = 49)		Infarcts (n = 17)
	R2	RMSE	R2	RMSE
7	0.913	0.0131	0.887	0.0128
4	0.890	0.0140	0.871	0.0113
3	0.870	0.0152	0.749	0.0139
2	0.853	0.0164	0.719	0.0144

Note:—R² indicates coefficient of determination for linear regression of f_linear on f_{biexponential}; RMSE, root mean square error.

^aIndicates the total number of nonzero b-values used in the estimation of f_linear (specific b-values are provided in Table 1).

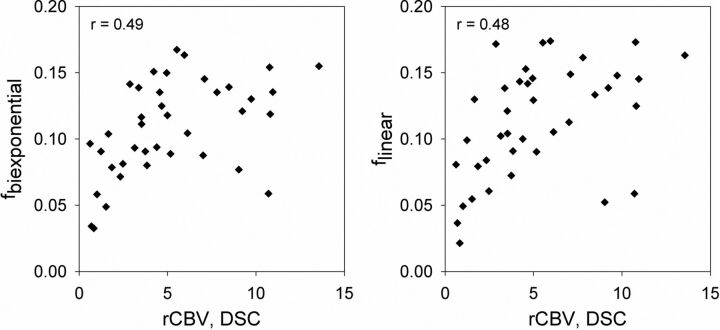
For patients with gliomas, the relationship between the IVIM perfusion fraction and DSC-derived rCBV is shown in Fig 4. A moderate correlation was observed between rCBV and each of the IVIM models considered in this study, with correlation coefficients r = 0.49 for f_{biexponential} and r = 0.48, 0.50, 0.50, and 0.48 for f_linear with 7, 4, 3, and 2 nonzero b-values, respectively.

Fig 4.

Correlation between IVIM perfusion fraction (f) and DSC-derived relative CBV for patients with brain gliomas. The relationship between f and rCBV is shown for conventional biexponential fitting (left panel) and for simplified linear fitting of 7 nonzero b-values (right panel). Plotted values indicate the mean perfusion fraction and rCBV over the tumor ROI for n = 40 patients. The correlation coefficient (r) for each relationship is also provided.

Time to reconstruct a complete perfusion fraction dataset for a single patient was approximately 2 minutes for f_linear compared with 36 minutes for f_{biexponential}.

Discussion

Our results demonstrate that clinically relevant perfusion information can be obtained using a simplified IVIM methodology based on linear (asymptotic) fitting of as few as 2 nonzero b-values. We validated this method for 2 commonly encountered clinical scenarios: evaluation of brain gliomas and acute strokes. Perfusion maps constructed using the simplified fitting procedure were qualitatively similar to those obtained with conventional biexponential fitting.

As expected, reducing the number of b-values in the estimation of f_linear came at a cost of reduced accuracy in the resulting perfusion maps compared with full biexponential fitting. However, clinically meaningful differences in the perfusion fraction (between high- and low-grade tumors and between ischemic and healthy brain tissue) were observed independent of the choice of model and number of b-values used in the fit. For both gliomas and strokes, f_linear underestimated f_{biexponential} when only 2 nonzero b-values were used. Given the assumptions of the simplified model, this underestimation may be due to high values of f (as seen in high-grade tumors) and/or low values of the product bD*, resulting in pseudodiffusion effects that are not negligible for b > 200 s/mm². In addition, reducing the number of b-values resulted in increased variability (lower R²) in the estimated perfusion fraction. This variability may be more problematic in the evaluation of strokes than in tumors because the large perfusion fraction observed in high-grade gliomas would be easier to detect than the small differences in the perfusion fraction between ischemic and normal brain tissue. On the basis of these results and the data presented in Table 2, we propose a recommended minimum of 4 nonzero b-values for clinical application of the simplified IVIM procedure. Although admittedly arbitrary, this threshold provides acceptable root mean square error (<0.015) and R² (>0.85) across all the ROIs considered.

The simplified linear fitting procedure has been applied in other organ systems.^4,5,12,13,15 However, only 2 very limited studies have applied this method to brain imaging.^25,27 In the first, f_linear was compared with f_{biexponential} for normal brain tissue but not for clinical pathology.²⁷ Interestingly, the authors found that f_linear correlated more closely than f_{biexponential} to CBV measured by DSC perfusion imaging, possibly due to greater uncertainty associated with biexponential fitting in the setting of low SNR.¹⁹ In the second study, f_linear was evaluated in a small number of patients with acute stroke; however, no comparison with f_{biexponential} could be performed due to the limited range of b-values obtained.²⁵ The present study is the first to systematically compare f_linear with f_{biexponential} for the evaluation of brain pathology.

With respect to gliomas, results using simplified linear fitting are in agreement with prior studies using conventional IVIM methods,^6,18 suggesting that the perfusion fraction obtained by either fitting procedure is valuable in the preoperative evaluation of tumor grade. Interestingly, a recent study did not show a significant association between IVIM and conventional DSC perfusion parameters,³⁴ while the present study and another study with partial subject overlap⁶ showed only a moderate correlation. The data in Fig 4 suggest that this relationship may depend on the value of rCBV, with stronger correlation for lower rCBV and an apparent plateau for higher rCBV values. Our results are consistent with the hypothesis that IVIM parameters may contain slightly different information than classically defined perfusion measurements, as has been previously postulated on theoretical grounds.^6,35

One explanation for the difference between IVIM and DSC perfusion may be the inherent sensitivity of IVIM to flow in the microcirculation, with a lower contribution from larger arteries and veins which contain faster blood flow. The weighting of the IVIM perfusion fraction toward the capillary network is supported by immunohistochemical measurements of microvessel density in animal models.^36,37 IVIM parameters could therefore provide complementary information to conventional perfusion measurements, and the ability to obtain this information rapidly using an easily implemented protocol may be of great interest to the broader neuro-oncology community. For example, a recent study found that the IVIM perfusion fraction was prognostic for 2-year survival in a small cohort of patients with gliomas.³⁸

IVIM in acute stroke has been less well-studied.^24,25 In our study, f_linear and f_bexponential were both capable of differentiating between ischemic and contralateral healthy brain tissues. The ability to rapidly obtain simultaneous diffusion and perfusion information using a simplified linear fitting procedure may prove useful in the setting of acute stroke. Beyond obvious advantages such as lack of dependence on gadolinium administration or estimation of an arterial input function, the local nature of IVIM perfusion measurements may make them more sensitive to flow from leptomeningeal collaterals, which is a known challenge for other MR perfusion methods.³⁹ Further, the intrinsic coregistration between perfusion and diffusion maps provided by IVIM may enable more precise assessment of diffusion-perfusion mismatch.⁴⁰ These areas require further investigation.

Our study has several limitations. First, the simplified fitting methodology does not allow estimation of the pseudo-diffusion coefficient D*. However, the interpretation of D* itself is challenging, and experimental evidence suggests that signal decay in the low b-value regime is likely multicompartmental, with distinct arterial and venous contributions.⁴¹ Further, there is good theoretical evidence that D and f can be more reliably measured than D*,¹⁹ and a recent investigation using Monte Carlo simulations demonstrated significant limitations on the uncertainty in D* that could reasonably be achieved in a clinical examination.⁴² In contrast, the interpretation of f is more straightforward, and recent studies suggest that f may be the most clinically important of the IVIM parameters.^6,16,18 Other limitations include the retrospective nature of our analysis and the inclusion of data from only 2 centers using a single hardware platform. Further evaluation at multiple institutions using a variety of hardware configurations is required to demonstrate the broader applicability of the simplified IVIM methodology for brain imaging. Finally, while it appears that IVIM provides clinically valuable information regarding the cerebral microcirculation, the underlying physiologic interpretation of IVIM perfusion parameters requires further study.³⁴

Conclusions

IVIM perfusion information for common brain pathology can be obtained using simplified linear fitting of as few as 2 nonzero b-values. Decreasing the number of b-values comes at a cost of reduced accuracy in the resulting perfusion maps, and we have proposed a recommended minimum of 4 nonzero b-values when applying linear fitting for quantitative evaluation of clinical pathology. The reduced acquisition times and simple postprocessing requirements of this technique may facilitate more widespread adoption of IVIM for brain imaging in clinical and research settings.

ABBREVIATIONS:

D

diffusion coefficient

D*

pseudo-diffusion coefficient

f

perfusion fraction

IVIM

intravoxel incoherent motion

rCBV

relative cerebral blood volume