Characterization of Cyclic CSF Flow in the Foramen Magnum and Upper Cervical Spinal Canal with MR Flow Imaging and Computational Fluid Dynamics

SUMMARY:

CSF flow has been shown to exhibit complex patterns in MR images in both healthy subjects and in patients with Chiari I. Abnormal CSF flow oscillations, according to prevailing opinion, cause syringomyelia and other clinical manifestations that affect some patients with the Chiari I malformation. For this article, we reviewed the literature on PC MR of CSF flow, collected the published CFD studies relevant to CSF flow, and performed flow simulations. PC MR creates cine and still images of CSF flow and measurements of flow velocities. CFD, a technique used to compute flow and pressure in liquid systems, simulates the CSF flow patterns that occur in a specific geometry or anatomy of the SAS and a specific volume of flow. Published PC MR studies show greater peak CSF velocities and more complex flow patterns in patients with Chiari I than in healthy subjects, with synchronous bidirectional flow one of the characteristic markers of pathologic flow. In mathematic models of the SAS created from high-resolution MR images, CFD displays complex CSF flow patterns similar to those shown in PC MR in patients. CFD shows that the pressure and flow patterns vary from level to level in the upper spinal canal and differ between patients with Chiari and healthy volunteers. In models in which elasticity and motion are incorporated, CFD displays CSF pressure waves in the SAS. PC MR and CFD studies to date demonstrate significant alterations of CSF flow and pressure patterns in patients with Chiari I. CSF flow has nonlaminar complex spatial and temporal variations and associated pressure waves and pressure gradients. Additional simulations of CSF flow supplemented by PC MR will lead to better measures for distinguishing pathologic flow abnormalities that cause syringomyelia, headaches, and other clinical manifestations in Chiari I malformations.

The Chiari I malformation, defined by the aberrant position of the cerebellar tonsils in the upper cervical spinal canal, occurs in 0.8% of individuals. Most malformations (referred to here as “symptomatic Chiari I malformation”) have signs or symptoms attributable to them, but some (“asymptomatic Chiari I malformation”) do not.¹ Signs and symptoms include spinal cord cysts (syringomyelia), headache, motor dysfunction, sensory dysfunction, abnormal eye movements, and other neurologic findings. Syringomyelia and other signs and symptoms typically resolve after surgery in patients selected for cranio-occipital decompression. Simple reliable clinical tests to distinguish patients who will respond to surgical treatment from those who will not still are the subject of research.

According to prevailing opinion, hyperkinetic CSF flow in the Chiari malformation results in the associated signs and symptoms. CSF oscillates in an out of the cranial vault secondary to the expansion of the brain and intracranial blood vessels with each cardiac systole (Monro-Kellie doctrine). PC MR displays CSF flow patterns, shows spinal cord and tonsil motion, and measures changes in CSF flow velocities during the cardiac cycle. PC MR flow studies show large flow jets and synchronous bidirectional CSF flow.^2–11 PC MR studies also show CSF flowing in a symmetric sinusoidal pattern in some cases¹¹ and in less symmetric patterns in others.⁷ PC MR distinguishes different flow patterns in symptomatic compared with asymptomatic Chiari I malformations, but with imperfect sensitivity and specificity.¹² PC MR typically includes flow data in only 1 plane and, therefore, incompletely demonstrates the effect of tonsil position on CSF flow. Furthermore, PC MR does not measure CSF pressures or shear stresses on the spinal cord, parameters that may relate more directly to the formation of syrinx and the production of neurologic symptoms in patients with Chiari I.

CFD, an engineering tool used to calculate fluid flow, provides a means to analyze CSF flow patterns. For a 3D model of the domain to be studied and for specified rates of flow, CFD software calculates flow with greater spatial and temporal resolution than that achieved with PC MR and also displays pressures, flow structures, stresses, and pressure waves. It has the power to refine our measurements of CSF flow and to improve our understanding of how anatomic variations alter flow, pressure, and stresses; how CSF flow produces clinical signs and symptoms; and how it may cause a syrinx often distant from the location of CSF obstruction.

The purpose of this work was to collate published data from PC MR and from CFD with the goal of depicting CSF flow throughout the cardiac cycle and the SAS. CFD studies are reviewed and compared with PC MR results to test the validity of the CFD models and to improve the characterization of CSF flow. How CSF flow patterns vary with physiologic parameters, such as the shape of the SAS, the elasticity of its walls, the temporal variation in the flow, is illustrated.

Modeling the SAS to Simulate CSF Flow

The simplest flow models are 1-dimensional. One-dimensional pressure–volume models are used to study how pressure and volume are related and how pressure waves travel and transform in a system. The Monro-Kellie doctrine of oscillatory CSF flow exemplifies a 1-dimensional model of flow and volume. Analysis of pressure-volume relationships in a 1-dimensional model shows that decreasing compliance in the cranial vault increases the pressures in the central spinal canal.^13,14 The response of intracranial compliance to craniovertebral decompression may be a significant indicator for the effect of surgery. One-dimensional models have been used to show reduced compliance in the SAS in arachnoiditis and in syringomyelia.^14,15 Problems in correlating 1-dimensional models with 3D data limit the suitability of these models for studying human CSF flow patterns.

To simulate fluid flow in a space, we created 3D models of that space from geometric shapes or from images or measurements that define the actual boundaries of that space. The physical space is converted to a mathematic model—that is, a series of interconnected points or nodes that define the space. The number of nodes determines the resolution of the model and the length of time needed for computation. The mathematic model, if displayed graphically, appears as a mesh (Fig 1). The boundaries can be assumed to be rigid or nonrigid with properties of elasticity, movement, and compressibility. The physical characteristics of the fluid and its flow volume per unit time (boundary conditions) are specified. The flow may be specified as constant or as varying with time.

Fig 1.

An illustration of the computational model of the SAS used in the fluid dynamics simulations. The SAS is displayed as a series of connected points outside the spinal cord and inside the external boundary of the SAS. Flow and pressure are calculated for each point for a fluid with specific properties and flow rates. The number of points and their distance from each other determine the resolution of the computations and the length of time required for computation.

Effect on CSF Flow of Varying Anatomy and Boundary Conditions in Rigid Models of the SAS

Patients with Chiari I have different SAS dimensions and a different tonsil position than healthy individuals. The posterior fossa is reported to have smaller dimensions in patients with Chiari I than it does in controls.^16–19 The cerebellar tonsils extend up to 3 cm into the spinal canal in patients with the Chiari I malformation. The anatomic differences between patients with Chiari I and controls cause differences in CSF flow patterns and velocities.

The effect of anatomic variation on CSF flow can be studied in idealized geometric models of the SAS (Fig 2). The models can be created with a combination of geometric shapes, such as funnels and tubes. With CFD, the shapes and dimension can be varied systematically to determine their effect on CSF flow, without the problem of individual variation experienced in clinical studies. In the idealized model, the flow and velocity can be calculated for different boundary conditions, such as different patterns of temporal changes in flow volume during the cardiac cycle (Fig 3).

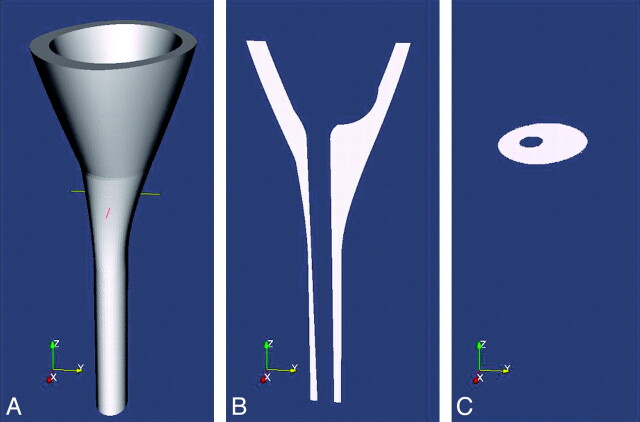
Fig 2.

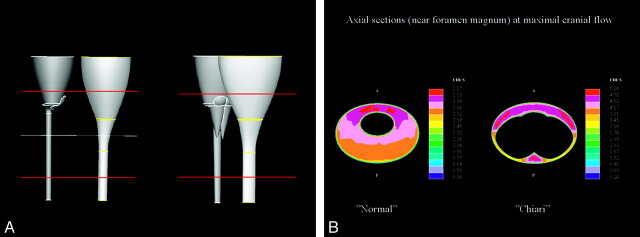
Sketches illustrating an idealized model of the SAS for CFD. A, A 3D hollow funnel-shaped structure is used to represent the surfaces of the SAS in the lower cranial vault and in the cervical spine. The internal surface of the SAS is created by the idealized model of the brain and spinal cord inserted into a nearly funnel-shaped structure. The transverse line in A represents the location of the craniovertebral junction in the model. B, A sagittal section of the structure shows the SAS as white and tissues external and internal to it as gray. C, An oblique axial section at the craniovertebral junction shows the SAS as white. Reprinted with permission from Linge et al.²²

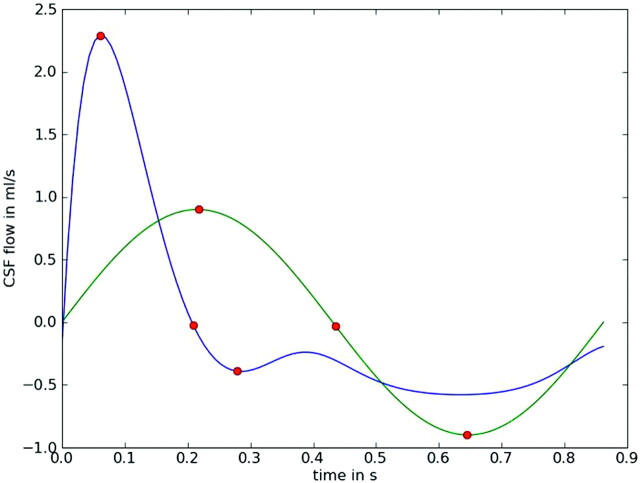
Fig 3.

Line graphs demonstrating different time courses for CSF flow that can be used as input functions in CFD simulations. The y-axis shows the magnitude of flow in positive and negative directions; the x-axis shows time as a decimal fraction of the cardiac cycle. One time course (green line) illustrates CSF flowing in a sinusoidal manner, similar to that observed in some PC MR studies.¹¹ The other (blue line) illustrates CSF flowing in a less symmetric manner as observed in other PC MR studies.⁷ The 3 red points illustrate first the maximal velocity in a positive direction (systolic flow) and then the change in direction from a positive to a negative flow and then maximal negative (diastolic) flow. Systolic flow lasts a shorter time and has a greater magnitude than diastolic flow in the second plot. Net flow during the cardiac cycle is zero in both plots.

The shape and dimensions of the SAS affect CSF flow patterns. By means of CFD, the effect of changing the shape or size of the spinal cord on CSF flow patterns can be demonstrated (Fig 4). Fluid flow in idealized models has an inhomogeneous pattern with flow jets in a portion of the SAS, similar to the flow pattern seen with PC MR in human subjects and patients. With simulations, the effect of changing geometry of flow can be shown (Fig 4).

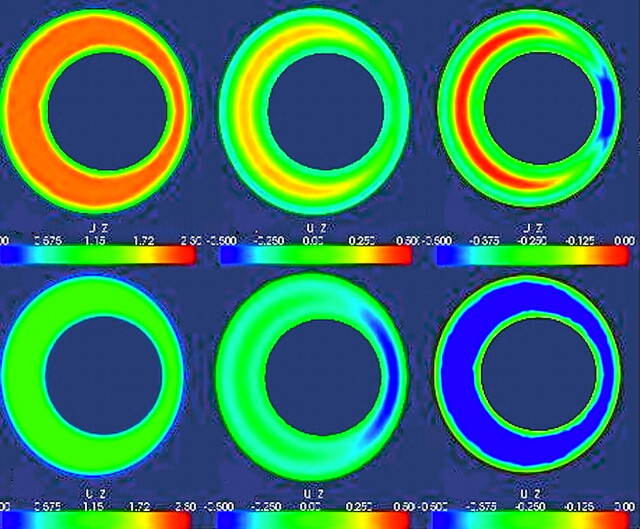
Fig 4.

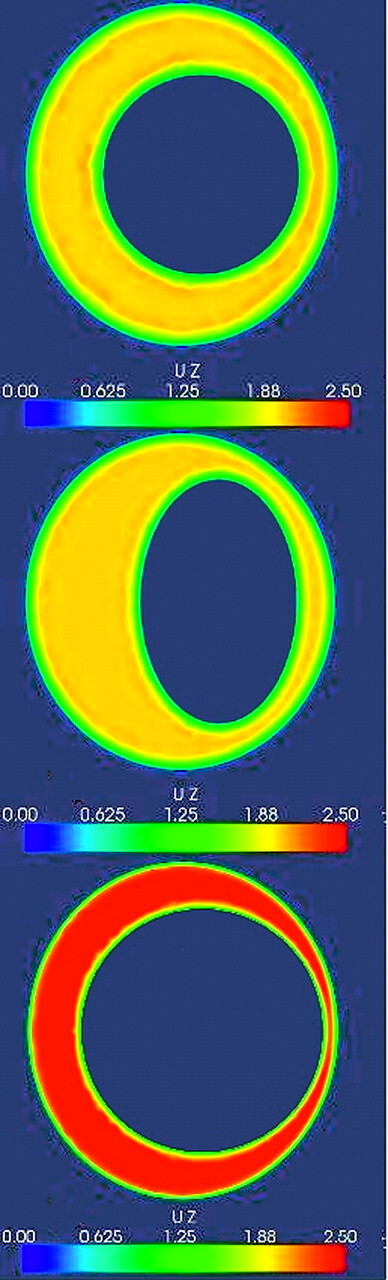
Examples of CSF velocity simulations for maximal systolic flow for a single axial section in an idealized model of the SAS with different cord shapes or sizes. The asymmetric CSF flow pattern from Fig 3 is assumed for this simulation. The upper image shows velocities for a SAS containing a cord assumed to have a cylindric shape. The next image shows systolic flow when the cord is modeled with an elliptic rather than a circular cross-section. The boundary conditions are otherwise the same as those for the upper image. Note that changing the shape of the spinal cord changes the flow pattern during systole. The bottom image illustrates velocities in a model with a larger cylindric spinal cord and a smaller SAS. Note the marked increase in velocities due to a smaller SAS.

Different temporal flow patterns—that is different boundary conditions—produce different CSF flow patterns and velocities. In clinical studies, CSF flow may have a regular pattern approximating a sinusoid or an irregular pattern.^{2,7,11,13,20,21} Flow cycling with an irregular pattern results in greater velocities and greater flow inhomogeneity than a symmetric sinusoidal flow pattern (Fig 5). CFD is well suited to demonstrating the effects of boundary conditions on flow velocities and flow patterns.

Fig 5.

Effect of different temporal patterns of CSF flow on the homogeneity and magnitude of CSF velocities. In the first model used in Fig 4, CSF velocities at peak systolic flow (left column), at the transition to diastolic flow (middle column), and at peak diastolic flow (right column) are shown for an asymmetric temporal flow pattern (top row) and a symmetric sinusoidal flow pattern (lower row). For the asymmetric flow pattern, systolic velocities are greater than those for the symmetric flow pattern. Simultaneous cephalad (negative) and caudad flow (positive) at the transition is more obvious for the asymmetric flow pattern. During peak diastolic flow (right column), both positive and negative flow velocities are noted for the asymmetric flow patterns.

Simulations of CSF flow in patient-specific models of the SAS have been made, with the simplifying assumption that the boundaries are rigid.^20,22,23 CSF velocities computed for the SAS of a healthy adult volunteer and of a patient with a Chiari I malformation show greater CSF velocities and pressures in the patient with the Chiari malformation than in the healthy subject for both maximal systolic flow and maximal diastolic flow (Fig 6).²³ CSF flow patterns in both the patient-specific and the volunteer-specific models duplicate the patterns observed in PC MR images of CSF flow.¹¹ The effect of tissue webs in the SAS and the effect of CSF generation in the fourth ventricle can be added to the patient-specific models.²¹

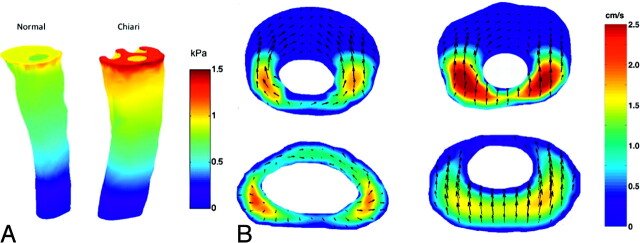
Fig 6.

CSF flow velocities and pressures simulated in patient-specific models of the SAS for a healthy subject (left) and a patients with Chiari I (right). A, Pressure distribution at the inlet and along the outer spinal canal surface for the normal (left) and Chiari I (right) models during peak systole. B, Axial sections at the foramen magnum (upper images) and 4 cm lower in the spinal canal (lower images) are shown. The magnitude of flow through the axial section is indicated in centimeters per second by a color scale (reader's far right). The magnitude and direction of secondary (in section) flow are indicated by arrows. Flow is more inhomogeneous and faster in the patient with Chiari than in the healthy subject. Velocities are greater in both subjects at the foramen magnum than at the selected lower section. Courtesy of Alejandro Roldan.

With idealized or patient-specific models of the cranial and spinal SAS, simulations show temporal and spatial variations in CSF flow velocities and pressures throughout the SAS and throughout the cardiac cycle, with high spatial and temporal resolution.²² The flow pattern in a cross-section below the foramen magnum resembles the typical flow patterns described in human subjects and patients. In the idealized models and patient-specific models, CSF pressures vary with the position of the tonsils and with the cervical spinal cord level. In a plane 4 cm below the craniovertebral junction in the idealized model, pressure fluctuations have greater magnitude and a different temporal course than at the foramen magnum. Pressures and velocities are increased when the tonsils descend into the spinal canal (Fig 7). Flow simulations and derived 3D animations²² convey a comprehensive view of CSF flow.

Fig 7.

Idealized models (above) of the brain, spinal cord, and SAS for simulating CSF flow in a healthy subject (left) and in a patient with Chiari (right). The red lines indicate the volume for which flow was calculated, and the yellow lines, the location of the axial section (below). In the axial sections, the flow patterns are heterogeneous in both the healthy subject (left in A and B) and the patient with Chiari (right in A and B). Peak velocities reach 2.27 cm/s in the healthy volunteer and 5.24 cm/s in the patient with Chiari (color scales to the right of the images).

The CFD studies in patient-specific and idealized models show important points about CSF flow: It has significantly greater velocities below the foramen magnum than at the foramen magnum, it has inhomogeneous patterns in both healthy individuals and patients with Chiari I, it has greater velocities lateral to the midline than in the midline, and it has greater flow inhomogeneity and peak CSF velocities in the presence of tonsilar herniation. The study in idealized models shows an additional finding: CSF flows simultaneously in both craniad and cephalad directions (synchronous bidirectional flow) at the end of systole and the end of diastole in both the healthy model and the Chiari model, but to a greater degree in the patient. That study suggests that synchronous bidirectional flow occurs normally, and in patients with Chiari I, it occurs to a such a degree that it can be detected on PC MR.

The idealized models are suited to evaluating the effect on CSF flow of variations in the temporal patterns of CSF flow and variations in the elastic properties of the models. The temporal course of flow during the cardiac cycle can be assumed or can be measured with PC MR in patients and in controls. CFD facilitates the investigation of how different temporal flow patterns affect velocities and pressures.

Effect of Tissue Elasticity, Motion, and Compressibility on CSF Flow in Nonrigid Models of the SAS

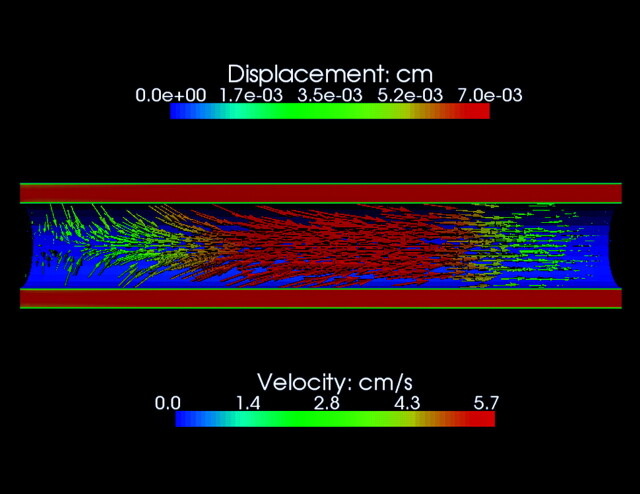
Adding tissue elasticity, compressibility. and motion to models of the SAS introduces flow characteristics such as pressure waves not seen in rigid models. Anatomic simplification of the nonrigid models is required to avoid excessive computation times. For CFD, the SAS may be modeled with coaxial fluid-filled tubular structures, 1 or both of which have elastic properties.^20,24–28 In such models with elastic properties, pressure waves are evident traveling at approximately 4–20 m/s.^5,25 Wave speeds in the model depend on the ratio of cross–sectional areas of the inner and outer tubes.^24,26 If a stenosis is incorporated into the model, pressure waves are reflected, and localized pressure fluctuations are magnified.^25,26 The steepness of the pressure peak varies with the amount and distribution of flow in the space. Typically, the spinal cord and the dura deform under pressure to a degree that is determined by the elastic properties of the materials. Because the spinal cord is more elastic than the dura, it deforms more. In addition, the dura is constrained with respect to outward movement by fat and bone, while the cord is not constrained by other tissues.^29,30 The elasticity of the cord and the dura vary with the direction of measurement, such that the spinal cord deforms more in the radial direction than in the longitudinal direction. Figure 8 illustrates deformation of the spinal cord at the time of peak pressure in the CSF, assuming isotropic elasticity in the cord and a rigid dural surface. The spinal cord deforms before the moment of peak pressure and deforms more as the elasticity increases.

Fig 8.

Deformation of the spinal cord secondary to CSF flow calculated by a CFD program that includes equations for the effect of elasticity. For the simulation, isotropic linear elasticity in the spinal cord is assumed. The diagram shows a sagittal view through the SAS and the spinal cord at the time of maximal systolic pressure. The CSF velocity, indicated by the color scale below the model, reaches 4–7 cm/s in the SAS while approaching zero near the dura and spinal cord. The velocity also changes from left (cephalad) to right (caudad), due to the effect of deformation on the cross-sectional area of the spinal cord. When the pressure wave passes along the cord, it initiates a caudad movement of the cord that results in narrowing the cord cephalad to the pulse. Where the cord is narrowed, the CSF velocity is diminished due to the increased volume of the SAS. The spinal cord deformation is indicated in this diagram by arrows that show the direction and colors that show the magnitude according to the scale above. Note that most of the deformation is longitudinal in a caudad direction, but radial deformation of lesser magnitude occurs cephalad to the pressure wave (left). CSF velocity and spinal cord deformation vary with the phase of the cardiac cycle. Integrated for the entire cycle, the spinal cord deformation and the CSF flow are zero at each spinal level. Although not illustrated here, the magnitude of deformation increases as the elasticity in the model is increased.

The spinal cord, dura, epidural space, and tonsils not only deform but they also move, contributing to CSF velocity and pressure changes. The cerebellar tonsils appear to move approximately a millimeter in patients and heathy subjects during the cardiac cycle,³¹ and when the spinal canal is opened during decompressive surgery, they appear to have much larger movements.⁹ The spinal cord moves in synchrony with the tonsils.³² The cord moves caudally at the start of systolic CSF flow and moves more slowly in a cephalad direction during diastole. The motion of the spinal cord may be greater and earlier in patients with Chiari I with syringomyelia than in those without.⁷ Transient anteroposterior and right-left movement of the spinal cord is also observed.^33,34 The effects of these motions on CSF velocities and pressures require further study. Finally, the different duration of systole in patients with Chiari I may be related to movement of the spinal cord or changes in the shape of the SAS during the cardiac cycle.

Conclusions

Oscillatory CSF flow has been characterized with PC MR and CFD. PC MR provides measurements of the temporal pattern of CSF flow, the dimensions and shape of the SAS, and the velocities of CSF through the cardiac cycle at specific locations. CFD, by simulating CSF flow in patient-specific and in idealized models of the SAS, provides flow descriptions with greater temporal and spatial resolution than those obtained with PC MR and provides other parameters of flow, such as pressures, pressure gradients, pressure waves, and stresses. Future studies with CFD and PC MR will expand our knowledge of oscillatory CSF flow, depending on the models and hypotheses used in simulations. In this article, we have focused on PC MR data that help to characterize CSF flow and on CFD studies that have the best illustrated CSF flow patterns, pressure patterns, waves, and deformations. The anatomy or geometry of the SAS and the temporal flow pattern determine CSF flow and pressures throughout the SAS. Parameters of CSF flow, such as pressure waves, vary dramatically with the elastic properties of the SAS. The magnitude and speed of these waves may help to explain how and where syringes develop in the spinal cord in patients with the Chiari I malformation or in idiopathic syringomyelia. This review suggests some directions for future studies with CFD and PC MR. It suggests that in the evaluation of patients, CSF flow imaging at several levels may be more useful than single sections to detect the abnormal patterns and velocities and to select patients for craniovertebral decompression.

Abbreviations

CFD

computational fluid dynamics

PC MR

phase-contrast cardiac-gated MR studies

SAS

subarachnoid space