Rest versus Exercise Hemodynamics for Middle Cerebral Artery Aneurysms: A Computational Study

Abstract

BACKGROUND AND PURPOSE:

Exercise is an accepted method of improving cardiovascular health; however, the impact of increases in blood flow and heart rate on a cerebral aneurysms is unknown. This study was performed to simulate the changes in hemodynamic conditions within an intracranial aneurysm when a patient exercises.

MATERIALS AND METHODS:

Rotational 3D digital subtraction angiograms were used to reconstruct patient-specific geometries of 3 aneurysms located at the bifurcation of the middle cerebral artery. CFD was used to solve for transient flow fields during simulated rest and exercise conditions. Inlet conditions were set by using published transcranial Doppler sonography data for the middle cerebral artery. Velocity fields were analyzed and postprocessed to provide physiologically relevant metrics.

RESULTS:

Overall flow patterns were not significantly altered during exercise. Across subjects, during the exercise simulation, time-averaged WSS increased by a mean of 20% (range, 4%–34%), the RRT of a particle in the near-wall flow decreased by a mean of 28% (range, 13%–40%), and time-averaged pressure on the aneurysm wall did not change significantly. In 2 of the aneurysms, there was a 3-fold order-of-magnitude spatial difference in RRT between the aneurysm and surrounding vasculature.

CONCLUSIONS:

WSS did not increase significantly during simulated moderate aerobic exercise. While the reduction in RRT during exercise was small in comparison with spatial differences, there may be potential benefits associated with decreased RRT (ie, improved replenishment of nutrients to cells within the aneurysmal tissue).

Increasing availability and improving sensitivity of noninvasive imaging techniques have led to increased detection of unruptured cerebral aneurysms in the general population.¹ This group of people with asymptomatic aneurysms is enlarged by screening of family members of patients with aneurysms and of populations with inherited disorders, such as autosomal dominant polycystic kidney disease. The risk-reward balance for intervention in unruptured aneurysms remains finely balanced because of the uncertainty over the natural history of asymptomatic aneurysms and the risk of their growth and rupture. In such situations, a noninvasive therapy that promotes aneurysm stabilization through remodelling, coupled with regular monitoring, would be of benefit to patient welfare.

Exercise is known to reduce mortality rates from arterial disease and is considered to be a very low-risk therapy.² The exact mechanism by which exercise improves arterial health is not fully understood. Taylor et al³ noted that regions of low-oscillatory WSS are considered to be prone to the development of endothelial dysfunction with associated atherosclerosis, and they observed that in the abdominal aorta, these areas of disturbed flow were removed or reduced with the onset of exercise.

The formation of an aneurysm is a complex physiologic process that is not yet clearly understood. However, the physiologic mechanisms that give rise to an aneurysm involve the interplay between the local mechanical forces acting on the arterial wall and the biologic processes at the cellular level. During the growth phase of aneurysm development, the wall will adapt in response to the imposed mechanical loading consisting of cyclic stretching, systemic blood pressure, and local hemodynamic effects on the endothelium (ie, WSS, oscillatory flow). The structure of the arterial wall is maintained by the cells that degrade and deposit the constituent structural proteins. The functionality of the cells is regulated by mechanical signals; deviations of the local mechanical environment of the cells from homeostatic levels may signal the cells to remodel the wall through increased production of structural proteins (procollagen messenger ribonucleic acid) and degradative enzymes (MMP-2, MMP-9) until a new homeostasis is achieved. Fibroblasts play a key role in this process; by sensing changes in the mechanical strains, the fibroblasts may respond by adjusting their expression and synthesis of extracellular matrix molecules.⁴ The rupture of an aneurysm is ultimately due to a mechanical failure of the tissue—that is, the applied loading results in stresses that exceed the strength of the tissue at that instant in time. Under normal conditions, loading will be dominated by the transmural load, developed due to the intraluminal pressure and thus the systemic blood pressure.

This study uses computational simulations of flow in cerebral aneurysms to investigate intra-aneurysmal changes in dynamic pressure, WSS, and other derived quantities that occur due to variations in pulsatile blood flow during rest and exercise. The differences observed between the 2 states are quantified, and their physiologic relevance is explored.

Materials and Methods

Imaging data for 3 saccular aneurysms located in close proximity to the middle cerebral artery bifurcation were selected from a data bank. A 54-year-old man presented with ruptured aneurysm 1, which was small with a narrow neck; it measured 9 mm from neck to dome and the AR (aneurysm depth / width at neck) was 4.8. Aneurysm 2 was an unruptured aneurysm from a 54-year-old woman; it was wide-neck (10 mm) with an AR of 1.4. Aneurysm 3 was an unruptured aneurysm from a 65-year-old man; it was long (23 mm) and multilobular with an AR of 9.2.

To simulate the hemodynamic conditions in patient-derived geometries, one must take a series of steps in a consistent manner. First, the geometry is acquired from angiographic data. Next, a computational mesh is generated on which the pertinent equations of blood flow are set up and then solved. Boundary conditions are based on velocity data obtained from a published transcranial Doppler sonography study.⁵ Postprocessing and visualization of the computational solution are performed to yield quantities of interest.

Geometry Acquisition

Rotational angiographic data were acquired for the 3 aneurysms on a clinical C-arm x-ray system (Axiom Artis dBA; Siemens, Erlangen, Germany) during standardized pump injections of radiographic contrast in the ipsilateral internal carotid arteries. Following reconstruction of a 256 × 256 × 256 image dataset, voxel size of 0.43 × 0.43 × 0.43 mm, the image stack was imported into a commercial segmentation suite (Amira; Visage Imaging, Carlsbad, California), where a threshold-based segmentation algorithm was applied. In all aneurysms, the distance between the aneurysm neck and the inlet boundary plane was maximized while excluding any upstream bifurcations. To avoid biasing the downstream flow rates, we stipulated comparable pressure drops by ensuring that there was a similar distance between each outlet boundary and the aneurysm neck under the assumption of similar vessel caliber and comparable tortuosity. No geometric changes were applied to account for exercise because Moraine et al⁶ noted that at least up to the anaerobic threshold, dynamic exercise does not change middle cerebral artery diameter.

Flow Computation

The Navier-Stokes equations along with conservation of mass are the basic partial differential equations that describe the flow of a viscous fluid. Blood was modeled as an incompressible fluid with a fixed attenuation, ρ of 1060 kg m⁻³.⁷ In line with previous studies^8,9 that have shown that intra-aneurysmal flow patterns are insensitive to the model of viscosity used, Newtonian behavior was assumed with dynamic viscosity (μ) of 0.00357 kg m⁻¹ s⁻¹ and 0.00392 kg m⁻¹ s⁻¹ on the basis of previously reported values for rest and exercise respectively.¹⁰ The change in viscosity during exercise was attributed to plasma volume losses, which result in increases to hematocrit and the concentration of hemoglobin and plasma proteins. Solution of the governing equations was performed in a computational suite (CFD-ACE+; ESI Software, Paris, France) by using an implicit finite volume approach with a co-located variable arrangement. For this study, a commercial mesh generator (Gambit; Fluent, Lebanon, New Hampshire) was used to produce an unstructured mesh. All simulations were conducted with second-order spatial discretization and second-order Crank-Nicholson temporal discretization. Pressure-velocity coupling was achieved by using the SIMPLEC approach.¹¹ No-slip conditions were applied on the wall; pressure on the outlet boundaries was set to zero.

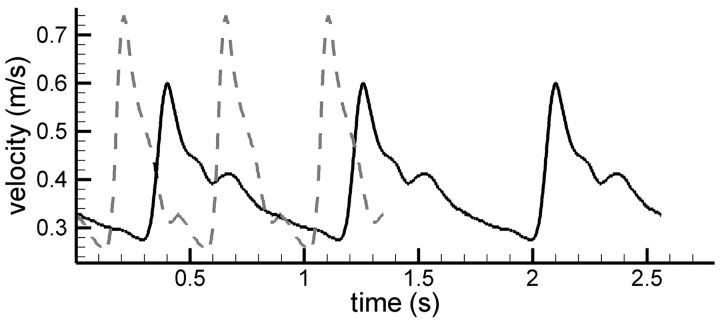
Inlet velocity waveforms for rest and exercise were taken from a transcranial Doppler sonography study conducted by Poulin et al,⁵ who measured blood-flow velocities in the middle cerebral artery of subjects at rest and during cycling. A comparable intensity of exercise was maintained across subjects by stipulating that oxygen consumption must be maintained at 40% of each subject's maximum. This intensity of exercise was chosen because a previous study¹² showed that it elicited the greatest change in cerebral blood perfusion. This is an intensity of exercise that can be achieved by the general population and, therefore, is a condition relevant to individuals with an intracranial aneurysm. The intensity-weighted mean velocity waveforms were digitized and then decomposed into a Fourier series (n_coeff = 10), which was applied as a plug flow inlet condition (Fig 1). At rest, the average heart rate was 69.6 bpm (T = 0.86207 seconds); the inlet flow rate was 2.43 × 10⁻⁶m³s⁻¹. During exercise, the average heart rate was 120.7 bpm (T = 0.49710 s), and the average inlet flow rate was 2.62 × 10⁻⁶m³s⁻¹ (8% increase). During rest, most of the cardiac cycle is spent in diastole, while during exercise, the reverse is true. The Re is a dimensionless quantity relating the balance between inertial forces (high Re) and viscous forces:

where U is fluid velocity and D is vessel diameter. During rest, the Re based on average flow rate was 317, and this was slightly reduced to 312 during exercise. The PI, originally proposed by Gosling et al,¹³ provides a measure of the temporal fluctuations in the velocity profile:

During exercise, PI increased from 0.87 to 1.20. This indicates that during exercise, the inlet velocity exhibits greater variability in magnitude on top of the aforementioned increase in average flow rate. The Womersley number, a, is another dimensionless parameter used to classify flows:

where ω is angular frequency. At low (<1) Womersley numbers, the flow is quasisteady and the velocity profile across the vessel would be parabolic. As the Womersley number increases, this assumption is no longer valid because there are significant deviations from the parabolic profile; for example, flow reversal may occur near the wall. The Womersley numbers during rest and exercise were 2.08 and 2.79, respectively; as such, flow reversal would not be expected in a straight vessel.

Fig 1.

Inlet velocity profiles. Solid line indicates a rest condition; dashed line, an exercise condition. Data taken from Poulin et al.⁵

Postprocessing

The WSS vector, here denoted as τ, defines the direction and magnitude of the frictional force due to the blood flow that acts on the endothelial layer of the arterial wall. The OSI is a measure used to locally highlight temporal deviations in the direction of the WSS vector with respect to its time-averaged direction. Equation 4 gives the definition of OSI as proposed by Ku et al¹⁴:

where t denotes time and T is the duration of the cardiac cycle. A WSS vector with constant direction would have an OSI = 0; a WSS vector with temporally variant direction will have a nonzero OSI, with a theoretic maximum value of OSI = 0.5. A WSS vector with OSI = 0.5 would spend half the cycle facing in 1 direction before instantaneously rotating 180° for the remainder of the cycle. OSI is insensitive to the magnitude of WSS.

Himburg et al¹⁵ proposed an additional measure based on an approximation to the RRT of a particle within the flow that is dependent on both the OSI and the time average WSS:

where the time averaged WSS magnitude, τ̄ is given by

Note that RRT increases with decreasing WSS and increasing OSI. The parameter is of interest because it identifies regions of stagnation in the flow. The local amplitude of WSS variations is captured by τ_amplitude:

Finally, the measure λ_WSS:

is included to quantify the fraction of a heartbeat under exercise conditions whereby the local WSS exceeds the bounds observed during the rest condition.

Flow rate in a pipe is determined by the pressure difference across the section of pipe studied. This is, of course, connected with the fact that in the governing equations of fluid motion (ie, the Navier-Stokes equations) appear spatial pressure gradients only, and not the absolute values of pressure itself, for incompressible flows. Thus, it is the variation of pressure from location to location in a field that is driving the flow. In this study, the flow solver computes the pressure difference required to achieve the stipulated inlet boundary flow velocity. The pressure computed will equate to the pressure difference across the region of interest—that is, the computed pressure difference will be the same as the difference in systemic pressure between the inlet and outlet. However, the magnitude of the computed pressure field is not directly related to the magnitude of systemic pressure.

Results

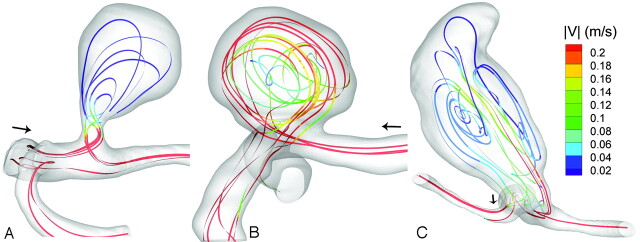
All 3 aneurysms exhibited complex recirculating flow patterns within the aneurysmal sac (Fig 2). In aneurysm 1, the primary direction of flow at the aneurysm neck correlated with the direction of the longest axis of the sac. The velocity magnitude within the aneurysm was significantly below that of the parent vessels (Fig 2). Aneurysm 3 presented a particularly interesting flow pattern (Fig 3); a low velocity jet entered the aneurysm, traversed the wall, peaked, and then receded. The flow velocity in the wide-neck aneurysm (aneurysm 2) was of a magnitude similar to that in the parent vessel (Fig 2). The predominant flow pattern was a jet, which followed the aneurysm wall, leaving low-velocity recirculating flow in the central region.

Fig 2.

Lines tangent to the instantaneous velocity vectors at systole, colored by velocity magnitude during the exercise simulation. A, Aneurysm 1. B, Aneurysm 2. C, Aneurysm 3.

Fig 3.

An overview of the aneurysm hemodynamics for aneurysm 3, illustrated with an isosurface of velocity magnitude (v = 0.15 m/s at selected points of the cycle). A, Mid-diastole (T = 50 ms). B, Early systole (T = 200 ms). C, Peak systole (T = 270 ms). D, Early diastole (T = 350 ms); E, Dichotic notch (T= 470 ms).

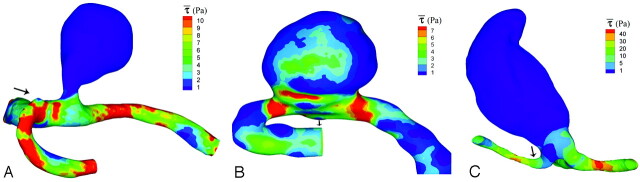
With respect to the zero-pressure outlet boundary (neglecting systemic pressure), the time-averaged pressure loading on the sac in aneurysms 1 and 3 was spatially homogeneous (<0.2% variation in magnitude), but the exercise simulation for aneurysm 1 showed an increase of 22% from basal (rest) conditions. Aneurysm 3 exhibited a 20% rise. Aneurysm 2 was not spatially homogeneous (range, 76% of average) and exhibited a 25% rise at the neck of the aneurysm. Patterns of time-averaged WSS were qualitatively similar during the rest (Fig 4, note that scales differ between aneurysms) and exercise (data not shown) simulations; for aneurysms 1 and 3, the magnitude of WSS on the wall was below that of the surrounding vasculature. The time-averaged WSS was spatially homogeneous in both of these aneurysms; increases of 34% and 3% were observed for aneurysms 1 and 3, respectively. The WSS pattern on aneurysm 2 was not significantly below that of the daughter vessels and was highest around the neck (26% increase from rest to exercise). Patterns of maximum pressure and WSS were similar to the time-averaged patterns (data not shown). The average increase in τ_amplitude from rest to exercise was 67%; for aneurysm 1, the increase in τ_amplitude was greater on the aneurysm sac (+16%) than on the surrounding vasculature and was lower for aneurysms 2 (−8%) and 3 (−16%). The τ_WSS was 41% for aneurysm 1 (21% upon the sac), 29% for aneurysm 2 (26% on the sac), and 36% for aneurysm 3 (13% on the sac).

Fig 4.

Time-averaged WSS (τ, see equation 6) on the aneurysm wall during the rest simulation. A, Aneurysm 1. B, Aneurysm 2. C, Aneurysm 3. Note that the scales differ between aneurysms.

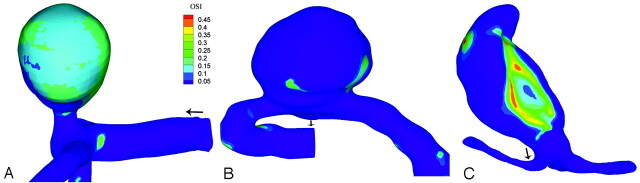
OSI is insensitive to the magnitude of WSS because the pattern of WSS did not significantly differ between rest and exercise nor did OSI. Figure 5 shows the OSI as calculated for the exercise simulation. Aneurysm 3 presented a small area of elevated OSI, which correlated with the inflow jet that pulsed along the aneurysm wall (Fig 3). Similarly, the large area of elevated OSI in aneurysm 1 was due to the pulsating inflow that occurred around peak systole. Aneurysm 2 did not exhibit elevated OSI. Unlike aneurysms 1 and 3, the jet that flows along the perimeter of the aneurysm was present for the duration of the cycle; hence, there was no flow reversal. In all 3 aneurysms, there were only small areas of elevated OSI on the parent and daughter vessels.

Fig 5.

OSI (see equation 4) during simulated exercise. A, Aneurysm 1. B, Aneurysm 2. C, Aneurysm 3.

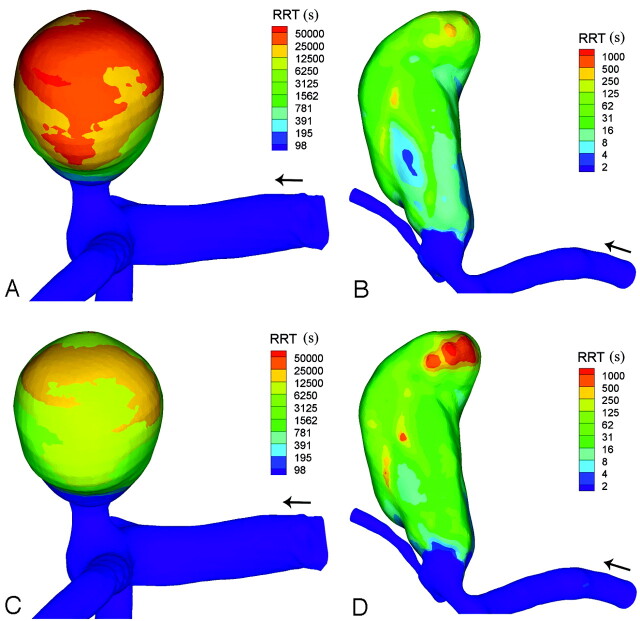
The average RRT on the aneurysm wall decreased from rest to exercise by 40% for aneurysm 1, 13% for aneurysm 2%, and 31% for aneurysm 3. One striking point of the images depicting RRT (Fig 6) is the 3-fold order-of-magnitude difference between the parent or daughter vessels and the tip of the aneurysm fundus. As noted by Himburg et al,¹⁵ this new measure will only differ significantly from the pattern of OSI when the OSI is high. This was true in aneurysm 2, where there was little difference between the 2 measures (data not shown).

Fig 6.

RRT (see equation 5) as calculated for the rest simulation in aneurysm 1 (A) and aneurysm 3 (B) and for the exercise simulation in aneurysm 1 (C) and aneurysm 3 (D). Note the exponential scale.

Discussion

CFD continues to provide a unique means for evaluating hemodynamics in intracranial aneurysms. 3D PC-MRA is emerging as an alternative; however, with voxel sizes of approximately 1 mm³ and temporal resolution around 50 ms (20 frames per heartbeat), this technique cannot currently compete with CFD, for which spatial and temporal resolution are only limited by the computational power available or the time the user is willing to wait for a solution. While 3D PC-MRA correlates well with laser Doppler velocimetry in straight arteries, intra-aneurysmal flows are frequently slow and highly disturbed; in such regions, obtaining a high signal intensity–to-noise ratio is difficult.¹⁶ Ford et al¹⁷ found that pulsatile intra-aneurysmal hemodynamics obtained from CFD captured the gross and finer flow details compared with particle-image velocimetry.

This study performed simulations based on published velocity waveforms for the middle cerebral artery; and as such, the simulations are not specific to the aneurysms studied. As the heart rate rises above 120.7 bpm, the flow velocity in the middle cerebral artery will decrease. By not examining simulations with higher heart rates, we are assuming that the changes occur primarily due to flow velocity as opposed to the time period of the cycle or changes in the shape of the waveform (ie, the ratio of systole to diastole). Analysis of the Fourier inlet velocity profile (on-line material) illustrated that the results obtained are relatively independent of possible cycle-to-cycle variations of the inlet velocity entering the aneurysm. Proof of solution grid independence was performed and is available in the on-line material. The prescribed changes in viscosity due to plasma-volume losses mean that the conditions prescribed most closely mimic steady-state moderate-intensity exercise.

Ujiie et al¹⁸ reported that almost 80% of ruptured aneurysms showed an AR >1.6. In this small-scale study, we observed that the 2 aneurysms with high AR exhibited reduced flow velocity within the sac; WSS on the aneurysm was below that of the surrounding vasculature and was spatially uniform. The reduced diameter at the neck compared with the parent and daughter vessels chokes the flow within the sac, and potentially, it is this fact that is being highlighted by the AR measure. Szikora et al¹⁹ noted that the aneurysm-to-parent-vessel angle was the most significant determinant of flow patterns in the sac. Aneurysms in line with the axis of flow in the parent artery exhibit intrasaccular jet flow; and perpendicular aneurysms, vortex flow. Vortex flow is characterized by inflow at the distal edge, outflow at the proximal edge, and vortex flow within the center of the aneurysm lumen. Szikora et al considered an aneurysm to be perpendicular if the angle between the parent vessel and a line drawn from the neck to the dome of the aneurysm was greater than 45°. This finding was mirrored in our study; aneurysms 1 and 2, classified as perpendicular to the parent vessel, exhibited vortex flow, while aneurysm 3 had a dominant inflow jet that had developed parallel to the vessel. The bleb at the tip of aneurysm 3 developed away from the inflow jet in a region of low WSS. This is in contrast to the results of Tateshima et al,²⁰ who found that the aneurysmal dome blebs were exposed to higher fluid-induced shear stress than any other measured points on the aneurysmal wall. Cebral et al²¹ observed that in 1 of 7 aneurysms studied, bleb formation occurred in a region of low WSS associated with the outflow zone. The perianeurysmal environment will influence aneurysm morphology: Satoh et al²² observed that marked and minor deformations of the wall at the aneurysmal dome were influenced by contact with perianeurysmal structures.

Two of the aneurysms had spatially homogeneous pressure fields, while aneurysm 2 displayed a spatially heterogeneous pressure field. However, note that the magnitude of the spatial variations (∼100 Pa, 0.75 mm Hg) was 2 orders of magnitude below the mean systolic pressure (120 mm Hg). Hence for structural analyses, the assumption of a spatially uniform pressure field is appropriate. In Shojima et al,²³ it is suggested that loading applied by the pulsatile inflow jet is insignificant in comparison with the loading imparted by the transmural pressure. Although this may be the case regarding purely mechanical (structural) loading, we must note that there is growing evidence that such small pressure differences (due to impingement for example) may have significant implications in terms of biologic processes, remodelling, growth, and rupture.²¹

During the exercise simulation, all aneurysms studied exhibited a rise in pressure. During acquisition of the velocity profile applied as an inlet condition in this study, a 15% increase in systemic pressure was observed.⁵ On average, one would expect to see a 15% increase in the pressure drop across every segment of the vasculature; the 20% increase computed in this study is in line with this value—the presence of the aneurysm does not appear to significantly alter the local vascular resistance. Circadian pressure variations are approximately 34% of the mean²⁴; near-maximal exercise can elicit a 64% change.¹² Weight training can lead to a 400% increase in arterial pressure, and there have been reports of aneurysm rupture subsequent to weight training.²⁵ Matsuda et al²⁶ observed the precipitating events associated with subarachnoid hemorrhage and found that exercising had one of the lowest incidence rates (2.7%). Normalized against duration, the activity with highest incidence rate was defecation/micturition. Micturition can lead to increases in average systolic pressures that are ≤ 97% of the value during rest.²⁷ It is clear that the intensity and type of exercise are important determinants of the rise in systolic pressure and, therefore, potentially the immediate risk of rupture. However, exercise at moderate intensities results in relatively modest pressure changes compared with those during micturition and repetitive weight training.

Kataoka et al²⁸ reported that in contrast to ruptured aneurysms, most unruptured aneurysms exhibit an inner surface that is completely covered with normally shaped arterial ECs. Hence, the ECs may, up to a point, influence the growth and remodelling of the aneurysm.²⁹ The WSS is sensed by various mechanosensors on/within the EC and is transduced into chemical signals that activate signaling pathways within the EC, which control its functionality³⁰ and the functionality of the artery. The molecular mechanism of action for WSS with regard to the growth and rupture of cerebral aneurysms is still unknown,³¹ and as such, there are competing hypotheses: High WSS is related to the initiation of cerebral aneurysm formation²⁰ and low WSS, to the continual enlargement, and possibly rupture, of cerebral aneurysms by causing degenerative changes in the wall.³²

A combination of high WSS and a high WSS gradient may represent a dangerous hemodynamic condition that predisposes to aneurysm formation.³³ In all aneurysms, there was an increase in the amplitude (τ_amplitude) of WSS conditions; in aneurysm 1, the increase in amplitude was greater on the aneurysm wall than on the surrounding vasculature. On average, the local WSS conditions during exercise exceed the bounds observed during the rest simulation for 35% of the heartbeat. However, for all aneurysms, this value was lower on the aneurysm wall than on the surrounding vasculature. It seems probable that in the aneurysms examined in this study, the endothelial cells were still operating within their normal conditions and were unlikely to produce abnormal signaling or be damaged due to excessive loading.

In all 3 aneurysms, there were small areas of elevated OSI within the parent and daughter vessels. This is in agreement with the Womersley number prescribed at the inlet, which indicates that flow reversal would not occur in a straight pipe. In this study, we observed heterogeneous patterns across subjects, with aneurysms 1 and 3 exhibiting large areas of elevated OSI. Elevated OSI is a marker of disturbed flow lacking a definitive direction; Chien³⁴ noted that in areas of disturbed flow, the ECs lack a clear orientation and the cytoskeleton and intercellular junction proteins are not organized. Ku et al¹⁴ were interested in the development of atherosclerotic plaques and correlated OSI with increased intimal thickness. More recently, Himburg et al¹⁵ noted that endothelial permeability increases slightly with OSI. It is unclear how such findings relate to the diseased aneurysmal wall where, in principle, increased intimal thickness would provide a beneficial effect through a reduction in the distending hoop stress within the wall.

OSI is also related to the RRT of a cell or protein near the wall. The 3-fold order-of-magnitude difference in RRT between the aneurysm sac and the surrounding vasculature is in overall agreement with previous steady-state residence time simulations based on direct-particle tracking.³⁵ A high residence time may mean that a protein or cell has more time to migrate across the wall. However, in a transport-limited environment, areas of elevated residence time could become depleted of macromolecules and proteins and consequentially may receive insufficient nutrients. Given that the developed aneurysm consists of a network of collagen fibers maintained by fibroblasts, the functionality of the fibroblasts must play a critical role in determining whether the aneurysm stabilizes in size or continues to enlarge. If the fibroblasts are starved of sufficient nutrients, this may give rise to deleterious remodelling of the tissue. In aneurysm 3, RRT was at a maximum at the tip of a bleb located at the dome of the parent aneurysm. This potentially implicates a lack of nutrition or blood-derived biochemical signaling within this focus of presumed new growth. However, it is also possible that this observation is an effect rather than a driver of the bleb formation.

Conclusions

In a rest-exercise study of the abdominal aorta, Taylor et al³ observed that exercise eliminated regions of low WSS and high OSI. In this small-scale study, we observed that OSI did not significantly change during exercise but WSS markedly increased in the aneurysm with the widest neck width (aneurysm 2). In the other 2 aneurysms, while WSS on the aneurysm increased, it still remained at a magnitude that was significantly below that of the surrounding vasculature. In all 3 aneurysms, the change in pressure observed during exercise was insignificant compared with the magnitude and reported changes in systemic pressure. In 2 of the aneurysms, there was a significant difference in RRT between the aneurysm sac and the surrounding vasculature. Further research is required to characterize the relationship between the short-term changes to hemodynamics elicited by the onset of exercise and the long-term cellular responses that determine growth and remodelling.

Abbreviations

AR

aspect ratio

bpm

beats per minute

CFD

computational fluid dynamics

EC

endothelial cell

max

maximum

min

minimum

MMP

matrix metalloproteinase

OSI

oscillatory shear index

PC-MRA

phase-contrast MR angiography

PI

pulsatility index

Re

Reynolds number

RRT

relative residence time

SIMPLEC

semi-implicit method for pressure-linked equations consistent

T

time period

V

velocity

WSS

wall shear stress