Softness of Endovascular Coils

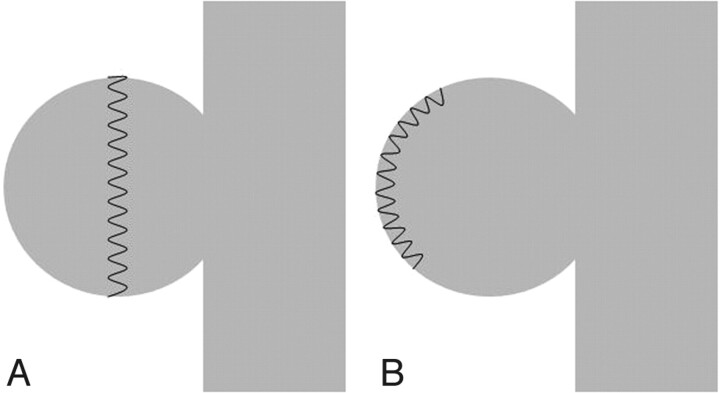
The softness of endovascular coils enables the packing of an intracranial aneurysm at a higher density so complete embolization is possible. While softness is an important concept, it is rarely discussed in a quantitative fashion. This information is often regarded as proprietary by manufacturers and is not available to the public. Thus, we do not know what makes a coil soft and what makes a coil stiff. White et al reviewed the physics of coils in an article in the American Journal of Neuroradiology,¹ but we think that there is a need to clarify the definition of coil stiffness (or softness) further. In their article, stiffness of a coil is defined as the spring constant of the secondary structure. This might be the easiest way to analyze a coil because coil structure is very similar to a spring in appearance. However, the coil is not compressed to fill the aneurysm during an endovascular procedure (as in Fig 1A). Instead, a coil is often bent to fit the available space as in Fig 1B. It is much easier to bend a coil than to compress it, and for this reason, one can hardly compress a spring (say, taken from a retractable pen) without buckling it first. On the other hand, the pitch of the secondary structure is usually very small, so a coil has little capacity for compression.

Fig 1.

Filling an aneurysm by compressing (A) and bending (B) a coil.

Bending of a coil actually twists the wire of a coil (the primary coil structure). Bending stiffness of a coil is defined as

where G is the shear modulus, ν the Poisson ratio, p the pitch, γ the pitch angle, and D₁ and D₂ are the diameters of the primary and secondary structures, respectively.² The pitch angle is related to the pitch in the following way: tan(γ) = p/πD₂. The equation itself may appear to be complicated, but bending stiffness is proportional to GD₁⁴ sin(γ) after simplification. The basic principle has been explored in Marks et al,³ when they described how the coil responded to bending; the stiffness is the slope in Fig 3 of their article.

Both equation 1 and the formula in White et al¹ show that the stiffness is proportional to the fourth power of the primary structure diameter (D₁). The major difference between bending and compression is that bending stiffness is not inversely proportional to D₂³. Therefore, the diameter of the secondary structure is less important in determining the stiffness; the pitch angle, on the contrary, is quite critical in the stiffness of a coil. Last, the pitch affects the bending stiffness, not the spring constant. Fine-tuning the compression stiffness of a coil by changing the pitch simply cannot be achieved by the way described in White et al¹ because the pitch did not appear in their definition of softness.

Coils used for endovascular therapy have multiple structures at various scales, and the mechanics of coils are actually quite complex. The first and last few coils used in a procedure may require completely different considerations. It is critical to fully examine all possible deformations before we can determine the softness of a coil.