Abstract
BACKGROUND AND PURPOSE:
Although the number of enhancing lesions is the typical outcome measure of choice in clinical trials in MS, a potentially more sensitive and statistically more powerful outcome measure is the volume of enhancing lesions. In this study, we assessed the distribution and statistical power of the volume of enhancing brain lesions as an outcome measure by means of their required sample size, and we compared the results with the number of enhancing lesions.
MATERIAL AND METHODS:
First, a literature search was performed to compare the effects of treatment on the number and volume of enhancing lesions. Then, a statistical model was proposed to describe the distribution of the volume of enhancing lesions in 2 datasets of patients with RRMS, and sample sizes for enhancing-lesion volume as primary outcome measure were calculated.
RESULTS:
A mixture of the binomial and Weibull distribution was determined to model enhancing-lesion volumes in patients. Sample size calculations for enhancing-lesion volumes showed that approximately 94 patients per arm would be required to detect a combination of 20% decrease in lesion volume and 20% increase in patients without enhancing lesions, whereas calculations for enhancing-lesion counts showed that approximately 129 patients would be required to detect a 50% decrease.
CONCLUSIONS:
The mixture of the binomial and Weibull distribution is a suitable approach in modeling new enhancing-lesion volumes in MS and yielded feasible sample size estimates for clinical trials, showing lesion volumes to be an advantageous outcome measure compared with lesion counts in terms of statistical power.
M R imaging is a sensitive tool for visualizing the characteristic inflammatory activity in patients with MS. On Gd-enhanced T1-weighted images, focal breaches of the blood-brain barrier appear as contrast-enhancing lesions and serve as an objective marker to monitor the extent of inflammation.1 In MS clinical trials, the reduction in the number of enhancing lesions is often used as the outcome measure of choice, while the reduction in the volume of enhancing lesions is of secondary importance. Immunomodulatory compounds, however, not only reduce the number of enhancing lesions but also diminish the inflammatory activity and size of the lesions that still originate. Di Rezze et al2 showed that treatment with interferon beta-1b not only led to a decrease in the cumulative number of enhancing lesions but also to a reduction of the size of the enhancing lesions originating during treatment. In a study by Gupta et al,3 a comparable result was shown for re-enhancing lesions, in which enhancing lesions appearing during treatment with interferon beta were significantly smaller than enhancing lesions arising during treatment with a placebo. These studies show that total enhancing-lesion volume accounts for 2 efficacy components (number and size) and, thus, is a potentially more sensitive outcome measure to detect anti-inflammatory treatment effects compared with enhancing-lesion counts alone. Moreover, the use of enhancing-lesion volume is statistically advantageous, being a continuous variable and likely yielding higher statistical power.
With the widespread use of approved therapies altering the practice of clinical trials in MS, use of more sensitive and powerful outcome measures to maximize the ability of detecting treatment effects is becoming increasingly important. Therefore, the objective of the present study was to assess the statistical power of the cumulative volume of enhancing lesions as a primary outcome measure in MS clinical trials. First, a systematic literature search for treatment efficacies on enhancing-lesion number and volume was performed. Second, we proposed a statistical model for the distribution of enhancing-lesion volume. Then, sample size calculations based on the range of reported treatment effects and the proposed statistical distribution were performed to estimate the sample sizes required for parallel grouped placebo-controlled clinical trials, by using the volume of enhancing lesions as a primary outcome measure, and we compared the results with the number of required patients for trials by using the number of enhancing lesions.
Materials and Methods
Literature Search
A literature search in the MEDLINE data base was performed to obtain the range of treatment effects on enhancing-lesion number and enhancing-lesion volume. It required placebo-controlled clinical trials that used both the number of Gd-enhancing lesions and the cumulative volume of Gd-enhancing lesions as outcome measures. On the basis of titles and abstracts, we selected full reports and evaluated them for inclusion. Trials of interest were those examining the efficacy of an immunomodulatory therapy in a placebo-controlled manner, by using a serial monthly MR imaging protocol and reporting both the effect on the number of enhancing lesions and the volume of enhancing lesions.
Patient Cohorts
New enhancing-lesion data from 2 datasets without a treatment effect were at our disposal. Baseline demographics and characteristics are shown in Table 1. Dataset A (the Oral Interferon Beta-1a Study4) was a cohort of 169 patients with RRMS who received varying doses of oral interferon beta-1a or a placebo orally every other day for 7 months. The cohort was regarded as a natural history cohort because no clinical or MR imaging effect of any dose of oral interferon beta-1a was observed. Patients were included when there were at least 2 clearly documented relapses within 24 months before study entry in conjunction with 7 T2 lesions on the screening scan or at least 1 clearly documented relapse within 24 months before study entry in conjunction with at least 1 Gd-enhancing lesion and at least another 3 T2 lesions on the screening MR imaging. Dataset B (the Oral Temsirolimus Study5) was the placebo arm of a double-blind placebo-controlled multicenter trial and included 69 patients, among whom were 12 patients with early SPMS with continued relapses.
Table 1:
Baseline descriptives and MR imaging characteristics
| Characteristics | Dataset A (n = 169) | Dataset B, Placebo (n = 69) |
|---|---|---|
| Patient | ||
| Female/male | 123:46 | 50:19 |
| RRMS/SPMS with relapses | 169:0 | 57:12 |
| Mean age (SD) | 35.4 (8.4) | 38.5 (9.1) |
| Mean disease duration in years (SD) | 6.4 (5.3) | 5.9 (5.9) |
| Median baseline EDSS (IQR) | 2.0 (1.5–3.5) | 2.5 (1.5–3.5) |
| MR imaging | ||
| % Inactive patients | 41.4% | 69.6% |
| Mean number of enhancing lesions (SD) | 2.4 (4.1) | 1.3 (0.4) |
Note:—EDSS indicates Expanded Disability Status Scale; IQR, interquartile range.
Patients were included if there was at least 1 documented relapse in the preceding 12 months before screening or at least 1 documented relapse in the preceding 24 months before screening in conjunction with at least 1 Gd-enhancing lesion on the screening or baseline scan.
MR Imaging Analysis
MR imaging data in datasets A and B were obtained from 6 and 9 monthly follow-up scans, respectively. All scans were obtained in accordance with published guidelines for the use of MR imaging in clinical trials.6 A radiologist marked all MS lesions on the original films, after which a trained technician manually outlined the lesions on each section of the scan by using purpose-developed software (Show-Images), by using the markings as a reference. The volume of enhancing lesions, measured in cubic millimeters, was determined by the sum of all lesion areas in a given scan, multiplied by the intersection distance.
Statistical Methods
Statistical Modeling of Enhancing Lesion Volumes.
The cumulative volume of enhancing lesions was considered as the primary outcome variable.
A known characteristic of the frequency distribution of lesion-volume data (as visualized by a frequency histogram) is its positive skewness, which typically is converted to a normal distribution by transformation of the original variable by, for example, a cubic root transformation.7 With enhancing-lesion volumes however, a problem arises due to the presence of a considerable amount of zero lesion volumes in patients who develop no enhancing lesions at all, which is not amenable to transformation. In the present study, enhancing-lesion volume was modeled by using a 2-component or mixture model. The first component determines the occurrence of inactive patients and models the proportion of patients developing zero enhancing lesions during the study period by the NB distribution. The second component focuses on the cumulative enhancing-lesion volume that active patients developed during the study period. To determine the best-fitting distribution for modeling the cumulative volume of enhancing lesions in active patients, we fitted a selection of 6 conceivable continuous distributions on the subset of active patients in both datasets: the γ, Weibull, log-normal, normal, normal after cube root transformation, and inverse Gaussian distribution. All models are basic and well-known distributions, generally applicable in practice and characterized by 2 parameters.8 The goodness of fit was assessed by means of the Anderson-Darling and the Kolmogorov-Smirnov tests.
Sample Size Calculations.
The statistical distribution determined in section A (statistical modeling of enhancing lesion volumes), with its parameters based on an untreated cohort of patients with MS, was implemented in a sample size calculation procedure designed by Sormani et al9 by using Matlab, Version 2007a (MathWorks, Natick, Massachusetts). The distribution serves as an infinite population of patients with MS and allows the simulation of parallel-grouped placebo-controlled clinical trials. For each simulated trial, a placebo arm is created by sampling a number of patients from the chosen distribution. A treatment arm, however, requires the simulation of a treatment effect because the cumulative lesion volume of a treated patient is expected to be lower than that of an untreated patient. In our methodology, treated and untreated patients were sampled from the same type of distribution, but for treated patients, the mean lesional volume of the distribution was shifted toward lower volumes. Because our model separated inactive patients from active ones, we determined the proportion of inactive patients by sampling from the binomial distribution and subsequently determined the cumulative volume of enhancing lesions for active patients by sampling from the chosen continuous distribution.
For the treatment arms, a treatment effect was simulated by sampling both the proportion of inactive patients from a binomial distribution with an altered parameter πtreated = πplacebo × (1-treatment effect) and the cumulative volume of lesions for active patients from the chosen distribution with an altered parameter μtreated = μplacebo × (1-treatment effect), with treatment effect ranging from 0 to 0.5. In this way, treated patients were sampled from a binomial distribution with a 0%–50% increase in proportion of inactive patients and a chosen distribution with a 0%–50% decrease in mean lesion volume, respectively.
A total of 1000 trials were simulated for a large range of sample sizes and a statistical power of 80%. The sample size to obtain a statistically significant effect was determined by the proportion of trials yielding a significant result and thus required 800 of the 1000 simulated trials to yield a statistically significant result in either a significant increase in inactive patients or a significant decrease in mean enhancing-lesion volume for active patients. (Significance was determined by a Wilcoxon rank sum test at a 2-sided test level of .05). For comparison, the number of required patients for trials by using the number of enhancing lesions as a primary outcome measure was calculated with the methodology developed by Sormani et al,10 with the parameters of the required and validated NB distributions derived from dataset A.
Results
Literature Search
A total of 29 MR imaging−monitored clinical MS trials from 1999 to 2008 was identified as potentially relevant. Twenty-five studies were excluded after examining the full published articles: Four studies did not include enhanced T1 imaging, 16 studies did not assess or report enhancing-lesion volumes, 1 study reported enhancing-lesion volumes but no enhancing-lesion counts, and 4 studies were not placebo-controlled. The results of the reports that met the specified inclusion criteria are shown in Table 2.5,11–13 Overall, the treatment efficacy measured by the percentage increase in inactive patients ranged from approximately 0% to 40%, and the reduction of cumulative enhancing-lesion volume, from 30% to 90%. However, when the effects on enhancing-lesion volumes were recalculated for the active patients in isolation (thus patients truly responsible for the cumulative lesion volume), the effect range for enhancing-volume reduction was an approximately 10%–60% reduction. We noted that the range of effects for the volume of enhancing lesions runs approximately parallel with the range of treatment effects for the number of enhancing lesions (overall mean effect of 56% and 58% reduction, respectively).
Table 2:
Results of literature searcha
| Study | No.b | FU Time (mo) | % Inactive Patients (Placebo) | Efficacy Measure |
|||
|---|---|---|---|---|---|---|---|
| Absolute % Increase in Inactive Patients | Lesion No. (All Patients) | Lesion Volume (All Patients) | Lesion Volume (Active Patients) | ||||
| Oral temsirolimus | 120 | 9 | 25% | +2% | −26% | −29% | −26% |
| Glatiramer acetate | 239 | 9 | 5% | −2% | −33%c | −42% | −43% |
| Natalizumab | |||||||
| 3 mg | 139 | 6 | 32% | +43% | −88% | −87% | −64% |
| 6 mg | 145 | 6 | 32% | +33% | −82% | −76% | −54% |
| Oral fingolimod | |||||||
| 1.25 mg | 164 | 6 | 47% | +30% | −43% | −50% | +16% |
| 5 mg | 158 | 6 | 47% | +35% | −61% | −63% | +10% |
| Overall mean effect | 13% | 56% | 58% | 27% | |||
Note:—FU indicates follow-up.
Effects shown are the percentage increase in active patients, the percentage change in mean or median number of lesions, the percentage change in mean lesion volume in the complete cohort, and the percentage change in mean lesion volume in active patients.
Total number of participating patients in trial.
Median lesion number.
Statistical Modeling
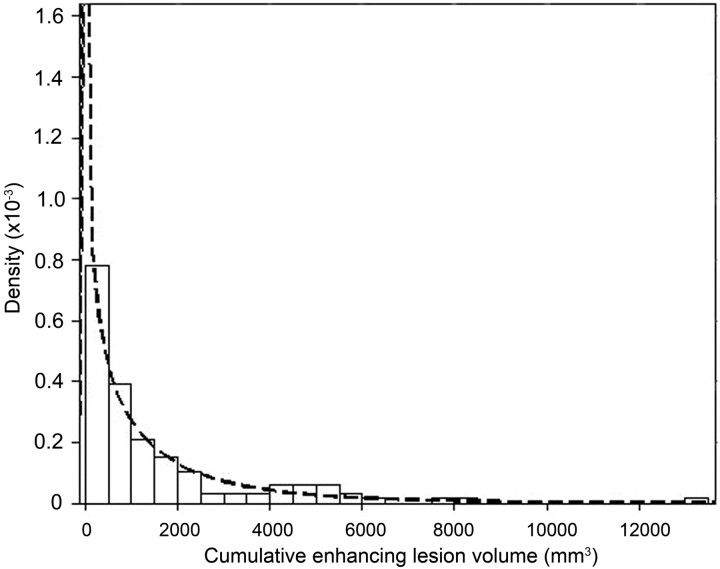
Table 3 shows the results of the Anderson-Darling and Kolmogorov-Smirnov goodness of fit tests for the continuous distributions considered for describing the cumulative enhancing-lesion volume of patients (Easyfit 4.3, Mathwave Technologies). In both datasets, the normal and inverse Gaussian distributions proved a poor fit for enhancing-lesion volume data, whereas small differences were found between the remaining Weibull, γ, log-normal, and normal (after cubic root transformation) distributions. Overall, the Weibull distribution performed best and was elected to model the enhancing-lesion volume of the patients. Its fit is depicted in Fig 1. While the parameters of dataset A were applied in our sample size calculations, comparison of the estimated shape parameter of the Weibull distribution on dataset B showed little difference between both datasets (shape = 0.76 and shape = 0.83 respectively), which strengthened our choice.
Table 3:
Goodness of fit of conceivable continuous distributionsa
| Distributions | Anderson-Darling |
Kolmogorov-Smirnov |
||
|---|---|---|---|---|
| Dataset A | Dataset B | Dataset A | Dataset B | |
| Weibull | >.2 | >.2 | .77 | .77 |
| γ | >.2 | .1 < P < .2 | .88 | .12 |
| Log-normal | 0.1 < P < .2 | >.2 | .06 | .99 |
| Normal (cube root transformation) | >.2 | >.2 | .60 | .36 |
| Normal (Natural logarithm transformation) | 0.1 < P < .2 | >.2 | .06 | .99 |
| Normal (Log10 transformation) | 0.1 < P < .2 | >.2 | .06 | .99 |
| Normal | <.01 | <.01 | <.01 | <.01 |
| Inverse Gaussian | <.01 | <.05 | <.01 | .49 |
Results of the Anderson-Darling and Kolmogorov-Smirnov goodness-of-fit test for the cumulative volume of enhancing lesions in active patients in datasets A (n = 133) and B (n = 44). Data are P values.
Fig 1.
Visualization of the fit of the Weibull distribution on cumulative enhancing volume data of patients with enhancing-lesion volumes in dataset A, by means of a probability attenuation function (attenuation on the y-axis describes the probability for enhancing-lesion volume to occur at a given point).
Sample Size Calculations
Table 4 displays the results of the sample size calculations based on the cumulative enhancing-lesion volume as a primary outcome measure. A treatment effect on the Weibull distribution was defined according to alteration of the scale parameter, and the shape parameter was kept constant, in line with the methodology of Sormani et al,10 in which the shape parameter of the NB distribution was kept constant. To strengthen this choice, comparison of the estimated shape parameter for the Weibull distribution of the treatment arm of dataset B (shape = 0.76, data not shown) with the shape parameter of datasets A and B, 0.76 and 0.83, respectively, showed minor-to-no difference in the shape of the distribution as a result of treatment.
Table 4:
Sample size estimatesa
| % Inactive Patients in Placebo Group | % Decrease in Mean Lesion Volume of Active Patients | Absolute % Increase in Inactive Patientsb |
|||||
|---|---|---|---|---|---|---|---|
| 0% | 10% | 20% | 30% | 40% | 50% | ||
| 10 | 0 | – | – | – | 435 | 225 | 124 |
| 10 | 518 | 309 | 204 | 139 | 86 | 65 | |
| 20 | 128 | 101 | 82 | 65 | 47 | 38 | |
| 30 | 56 | 50 | 43 | 35 | 30 | 27 | |
| 40 | 31 | 28 | 24 | 22 | 21 | 19 | |
| 50 | 20 | 19 | 18 | 17 | 16 | 16 | |
| 40 | 0 | – | – | – | – | – | 580 |
| 10 | 470 | 369 | 315 | 251 | 199 | 153 | |
| 20 | 121 | 115 | 94 | 83 | 75 | 66 | |
| 30 | 49 | 44 | 44 | 40 | 37 | 36 | |
| 40 | 25 | 24 | 23 | 24 | 21 | 20 | |
| 50 | 15 | 15 | 15 | 15 | 14 | 15 | |
Number of patients per treatment arm necessary to perform parallel-group-designed trials with a statistical power of 80%, to detect treatment effects ranging from 0% to 50% increase in inactive patients and a 0%–50% reduction in mean enhancing-lesion volume in active patients.
– Indicates percentage increase of patients developing no/zero enhancing lesions during follow-up.
Shown are the required number of patients per treatment arm in a placebo-controlled clinical trial for the 2 effects responsible for changes in enhancing-lesion volume: the percentage increase in inactive patients and the percentage decrease in mean volume in active patients.
When patients in the placebo group are assumed to be highly active (percentage of inactive patients, 10%), approximately 82 patients are required to significantly detect a mean percentage decrease in enhancing-lesion volume and a percentage increase in inactive patients of 20%, whereas for the same treatment effects, 94 patients are required when patients in the placebo group are assumed to be moderately active (percentage of inactive patients, 40%). In both scenarios, sample sizes decrease at a faster rate for an increase in lesional volume effects than for the increase in effect on inactive patients.
For comparison, Table 5 displays the sample size estimates obtained for the number of enhancing lesions as the primary outcome measure for placebo-controlled clinical trials, obtained with the parametric resampling and simulation procedure based on the NB distribution.10 With the NB-parameter estimates based on dataset A (μ = 7.4, dispersion = 0.45), the calculations show approximately 129 patients required for detecting a 50% reduction in the mean number of enhancing lesions, fitting in with previous estimated numbers.9
Table 5:
Number of patients per treatment arm necessary to perform parallel grouped placebo-controlled clinical trialsa
| % Decrease in Mean Number of Enhancing Lesions | No. |
|---|---|
| 50 | 129 |
| 60 | 80 |
| 70 | 47 |
| 80 | 28 |
| 90 | 12 |
To detect a percentage decrease in the mean number of enhancing lesions ranging from 50% to 90%, for a power of 80%.
Discussion
The cumulative volume of enhancing lesions is a potentially attractive and conceivable alternative for measuring the amount of ongoing inflammation in patients with MS. To our knowledge, this is the first study addressing the statistical distribution of new enhancing-lesion volumes and its statistical power as a primary outcome measure in MS clinical trials. We found that the distribution of cumulative enhancing-lesion volumes is adequately described by a mixture of the binomial distribution and the Weibull distribution, and we found enhancing-lesion volumes to be a potentially advantageous outcome measure compared with enhancing-lesion counts in terms of study power.
To our knowledge, there is no explicit literature validating the use of enhancing-lesion volume as a surrogate outcome for clinical outcome measures. However, there are several reasons why the volume of enhancing lesions is a plausible marker for the disease. First, given the same number of lesions, it is imaginable that a larger lesion volume leaves more damage and induces more decrease in functional brain volume than a smaller lesion volume.
Second, the volume of enhancing lesions also predict the viability of the tissue affected by inflammation since larger lesions are more likely to become a chronic black hole which is a known marker of axonal degeneration.14 Although the use of volumes as a continuous measure will increase the statistical power of a trial, the outlining of lesional volumes might introduce more inter- and intrarater variability, which might lessen the benefit.
When the estimated sample sizes are considered, it becomes apparent that a decrease in lesion volume in active patients has a more favorable effect on the required sample size compared with an increase in patients without enhancing lesions and that a more active cohort does not require more patients. Because both processes are likely to occur in parallel, these findings show that a decrease in measurable lesion volume lowers the detectability of treatment effects with a subsequent decrease in the study power and confirms the expected advantage of selecting active patients for clinical trials.
A limitation of our study is the use of a statistical model that needs to describe both patients without enhancing lesions and those who do develop enhancing lesions during the follow-up period. Due to the separation of the overall treatment effect into 2 effects (both parameters of the binomial-Weibull mixture are affected by treatment), the resulting sample size estimates are reported in tabulated form to encompass both treatment effects. A formal comparison with sample-size estimates for enhancing-lesion counts, therefore, becomes less “intuitive.” Still, when the current sample size estimates for volumes and counts are considered, the order of magnitude of the sample sizes for enhancing-lesion volumes is considerably smaller than the estimates for enhancing-lesion counts, even when there is no increase in inactive patients and the treatment effects are driven solely by a decrease in enhancing volume within active patients (Table 4, first column, 0% increase in inactive patients).
This study is a first approach at statistically modeling enhancing-lesion volumes in MS. Ultimately, its parameterization would allow parametric analyses of treatment effects in clinical trials with subsequent estimation of treatment effects (instead of P values) and adjustment for the effect of confounding variables in multivariate regression models. The chosen Weibull distribution is well-known in statistical literature and is frequently applied for positive continuous data in numerous fields of research (eg, survival analyses).8 In theory, the Weibull distribution is applicable in the framework of a generalized linear model, with a logistic regression model describing the occurrence of an active or an inactive patient, and the Weibull distribution modeling the enhancing-lesion volumes in active patients. Although both datasets indicate that the Weibull distribution is the optimal fit, the differences in fit with the γ distribution, the log-normal distribution, and the normal distribution on the cubic root-transformed data are small. A definite choice for a model, therefore, can only be validated when the fit is able to show consistent results in other datasets.
Although currently the Weibull distribution proved the most promising distribution for describing enhancing-lesion volumes, the present data also showed that the log-normal distribution was not substantially inferior to the Weibull distribution, and it could prove a feasible alternative, as recently shown with the application of a zero-inflated log-normal model in human sperm cell DNA data, taking into account both inter- and intrasubject variations and the use of longitudinal data.15 A disadvantage of the mixture approach is not being able to cope with the mixture of both discrete and continuous distributions concurrently. A promising approach in this regard is the Tweedie distribution, which has recently been found to model rainfall data and fishery catch processes.16,17 When applied to enhancing-lesion volumes, instead of considering lesional volumes as 2 separate circumstances (eg, inactive patients and volumes in active patients) as proposed in this study, the Tweedie distribution models both processes concurrently in a single simplified model. In addition, the Tweedie distribution models processes by using generalized estimating equations, allowing adequate modeling of dependent and longitudinal data. Future analyses should prove whether this model adequately fits enhancing-lesion volume data and is practically applicable.
Conclusions
In this study, we aimed to assess the distribution and statistical power by means of the required sample size of the volume of enhancing lesions compared with the number of enhancing lesions as a primary outcome measure in MS clinical trials. We proposed the mixture of the binomial and Weibull distribution to model the volume of enhancing lesions in patients with RRMS and showed a smaller number of patients required for clinical trials in MS using lesion volume as an outcome measure compared with trials using lesion numbers as outcome measures.
ABBREVIATIONS
- Gd
gadolinium
- MS
multiple sclerosis
- NB
negative binomial
- RRMS
relapsing-remitting multiple sclerosis
- SPMS
secondary-progressive multiple sclerosis
Footnotes
Disclosures: Ivo van den Elskamp, Research Support (including provision of equipment or materials): Bayer Schering, Pharma/Wyeth, Details: Both provided a dataset for our analyses and no support otherwise (eg, scientific/financial). Bernard M.J. Uitdehaag, Consultant: Merck Serono, Novartis, Synthon. Frederik Barkhof, Research Support (including provision of equipment or materials): Dutch MS Research Foundation, Image Analysis Center, Details: The Dutch MS Research Foundation and Image Analysis Center sponsored the study. Bayer Schering and Wyeth kindly provided data for the analysis but did not sponsor the study, Consultant: Novartis, Bayer Schering, Merck-Serono, Sanofi-Aventis, Synthon, Biogen-Idec, Roche, Genzyme, Details: member of the steering committee or data-safety-monitoring committee.
References
- 1. Filippi M. Enhanced magnetic resonance imaging in multiple sclerosis. Mult Scler 2000;6:320–26 [DOI] [PubMed] [Google Scholar]
- 2. Di Rezze S, Gupta S, Durastanti V, et al. An exploratory study on interferon beta dose effect in reducing size of enhancing lesions in multiple sclerosis. Mult Scler 2007;13:343–47 [DOI] [PubMed] [Google Scholar]
- 3. Gupta S, Solomon JM, Tasciyan TA, et al. Interferon-beta-1b effects on re-enhancing lesions in patients with multiple sclerosis. Mult Scler 2005;11:658–68 [DOI] [PubMed] [Google Scholar]
- 4. Polman C, Barkhof F, Kappos L, et al. , the European Oral Interferon Beta-1a in Relapsing-Remitting MS Study Group. Oral interferon beta-1a in relapsing-remitting multiple sclerosis: a double-blind randomized study. Mult Scler 2003;9:342–48 [DOI] [PubMed] [Google Scholar]
- 5. Kappos L, Barkhof F, Desmet A. The effect of oral temsirolimus on new magnetic resonance imaging scan lesions, brain atrophy, and the number of relapses in multiple sclerosis: results from a randomised, controlled clinical trial. J Neurol 2005;252(suppl 2):46 (abstract 158) [Google Scholar]
- 6. Miller DH, Albert PS, Barkhof F, et al. Guidelines for the use of magnetic resonance techniques in monitoring the treatment of multiple sclerosis: US National MS Society Task Force. Ann Neurol 1996;39:6–16 [DOI] [PubMed] [Google Scholar]
- 7. Sormani MP, Filippi M. Statistical issues related to the use of MRI data in multiple sclerosis. J Neuroimaging 2007;17:56S–59S [DOI] [PubMed] [Google Scholar]
- 8. Lindsey JK. Models for Repeated Measurements. 2nd ed. Oxford, UK: Oxford University Press; 1999 [Google Scholar]
- 9. Sormani MP, Miller DH, Comi G, et al. Clinical trials of multiple sclerosis monitored with enhanced MRI: new sample size calculations based on large data sets. J Neurol Neurosurg Psychiatry 2001;70:494–99 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Sormani MP, Bruzzi P, Miller DH, et al. Modelling MRI enhancing lesion counts in multiple sclerosis using a negative binomial model: implications for clinical trials. J Neurol Sci 1999;163:74–80 [DOI] [PubMed] [Google Scholar]
- 11. Comi G, Filippi M, Wolinsky JS. European/Canadian multicenter, double-blind, randomized, placebo-controlled study of the effects of glatiramer acetate on magnetic resonance imaging–measured disease activity and burden in patients with relapsing multiple sclerosis. Ann Neurol 2001;49:290–97 [PubMed] [Google Scholar]
- 12. Miller DH, Soon D, Fernando KT, et al. MRI outcomes in a placebo-controlled trial of natalizumab in relapsing MS. Neurology 2007;68:1390–401 [DOI] [PubMed] [Google Scholar]
- 13. Kappos L, Antel J, Comi G, et al. Oral fingolimod (FTY720) for relapsing multiple sclerosis. N Engl J Med 2006;355:1124–40 [DOI] [PubMed] [Google Scholar]
- 14. van den Elskamp IJ, Lembcke J, Dattola V, et al. Persistent T1 hypointensity as an MRI marker for treatment efficacy in multiple sclerosis. Mult Scler 2008;14:764–69 [DOI] [PubMed] [Google Scholar]
- 15. Li N, Elashoff DA, Robbins WA, et al. A hierarchical zero-inflated log-normal model for skewed responses. Stat Methods Med Res 2011;20:175–89 [DOI] [PubMed] [Google Scholar]
- 16. Dunn PK. Occurrence quantity of precipitation can be modeled simultaneously. Int J Climatology 2004;24:1231–39 [Google Scholar]
- 17. Shono H. Application of the Tweedie distribution to zero-catch data in CPUE analysis. Fisheries Research 2008;93:154–62 [Google Scholar]