Generalized versus Patient-Specific Inflow Boundary Conditions in Computational Fluid Dynamics Simulations of Cerebral Aneurysmal Hemodynamics

Abstract

BACKGROUND AND PURPOSE:

Attempts have been made to associate intracranial aneurysmal hemodynamics with aneurysm growth and rupture status. Hemodynamics in aneurysms is traditionally determined with computational fluid dynamics by using generalized inflow boundary conditions in a parent artery. Recently, patient-specific inflow boundary conditions are being implemented more frequently. Our purpose was to compare intracranial aneurysm hemodynamics based on generalized versus patient-specific inflow boundary conditions.

MATERIALS AND METHODS:

For 36 patients, geometric models of aneurysms were determined by using 3D rotational angiography. 2D phase-contrast MR imaging velocity measurements of the parent artery were performed. Computational fluid dynamics simulations were performed twice: once by using patient-specific phase-contrast MR imaging velocity profiles and once by using generalized Womersley profiles as inflow boundary conditions. Resulting mean and maximum wall shear stress and oscillatory shear index values were analyzed, and hemodynamic characteristics were qualitatively compared.

RESULTS:

Quantitative analysis showed statistically significant differences for mean and maximum wall shear stress values between both inflow boundary conditions (P < .001). Qualitative assessment of hemodynamic characteristics showed differences in 21 cases: high wall shear stress location (n = 8), deflection location (n = 3), lobulation wall shear stress (n = 12), and/or vortex and inflow jet stability (n = 9). The latter showed more instability for the generalized inflow boundary conditions in 7 of 9 patients.

CONCLUSIONS:

Using generalized and patient-specific inflow boundary conditions for computational fluid dynamics results in different wall shear stress magnitudes and hemodynamic characteristics. Generalized inflow boundary conditions result in more vortices and inflow jet instabilities. This study emphasizes the necessity of patient-specific inflow boundary conditions for calculation of hemodynamics in cerebral aneurysms by using computational fluid dynamics techniques.

It has been estimated that the prevalence of intracranial aneurysms in the adult population is between 1% and 5%.¹ Although most aneurysms go undetected, acute rupture resulting in subarachnoid hemorrhage is associated with high morbidity and fatality rates.^2,3 Ruptured aneurysms are treated by coiling or clipping to prevent rebleed. The indication for preventive treatment of unruptured aneurysms is, however, not straightforward.^4,5 The risk of treatment has to be carefully balanced against the risk of rupture. At present, rupture-risk assessment of unruptured intracranial aneurysms and the decision to treat or wait and scan are mainly based on size, location, and growth of the aneurysm.⁶ It is, however, clear that the predictive value of these characteristics is limited.^1,6–8 It is therefore crucial to search for additional and more predictive parameters for aneurysm rupture risk assessment.

Aneurysmal hemodynamics, in particular wall shear stress (WSS) and vortex instability, have been proposed as additional risk factors for aneurysm growth and rupture.^9,10 It has been shown that the combination of vortex instability and high or low WSS within the aneurysm is more prevalent in ruptured cases.^11–13

In many studies, computational fluid dynamics (CFD) is used to simulate aneurysmal hemodynamics. CFD is traditionally performed by using generalized inflow boundary conditions based on typical flow rates in a healthy adult.^14–27 Recently, several studies have replaced these generalized inflow boundary conditions by patient-specific velocity measurements in the vessels proximal to the aneurysm.^{10,12,28–32} In these studies, either 2D phase-contrast MR imaging (PC-MR imaging) or transcranial Doppler sonography was used to measure the flow. So far, only 3 studies have compared patient-specific with generalized inflow boundary conditions in a total of 14 aneurysms.^28–30 Evidently, the necessity of using patient-specific inflow boundary conditions has not been elucidated to the full extent. In this study, we assessed the effects of patient-specific inflow boundary conditions in a group of 36 patients.

Materials and Methods

Patient Selection

Image data of 36 aneurysms in 36 patients who presented at the Academic Medical Center, Amsterdam, The Netherlands with ruptured or unruptured aneurysms from January 2009 to October 2011 were retrospectively selected from a cohort of 164 patients in an ongoing study of aneurysm hemodynamics. This was done on the basis of the high signal quality of inflow velocity measurements. Of the selected aneurysms, 9 were located in the medial cerebral artery; 7 in the carotid artery; 6 in the anterior communicating artery; 6 in the posterior communicating artery; 3 in the basilar artery; 2 in the pericallosal artery; 1 in the anterior cerebral artery; 1 in the vertebral artery; and 1 in the ophthalmic artery. Six aneurysms were ruptured. Aneurysm size ranged from 3.2 to 12.4 mm. Dome-to-neck ratio ranged from 0.72 to 2.32. A Glasgow Outcome Score of ≥4 for patients with ruptured aneurysms was mandatory.³³ Exclusion criteria were contraindications for MR imaging, including treatment of the aneurysm by surgical clipping. The study was approved by the local ethics committee. Written informed consent was obtained from all patients.

Imaging

All patients underwent high-resolution 3D rotational angiography as part of the standard clinical work-up with de novo aneurysms. This was done in either the awake state (in the case of unruptured aneurysms) or during endovascular treatment with the patient under general anesthesia (in the case of ruptured aneurysms). A single-plane angiographic unit was used (Integris Allura Neuro; Philips Healthcare, Best, the Netherlands). Twenty-one milliliters of contrast agent was administered at 3 mL/s (iodixanol, Visipaque; GE Healthcare, Cork, Ireland). This resulted in a 256³ isotropic image volume. Following this, 3D velocity measurements proximal to the aneurysm were obtained with PC-MR imaging. A single-section PC-MR imaging was performed on a 3T scanner (Intera; Philips Healthcare). Scan resolution was 0.64 × 0.65 × 3 mm. Further imaging parameters were the following: TE/TR/flip angle, 5.7 ms/8.5 ms/10°; receiver bandwidth, 172 kHz; imaging volume, 200 × 200 × 3 mm in 1 section; parallel imaging factor, 2. The velocity-encoding was 100 cm/s in all directions. The number of measured cardiac phases (ie, temporal resolution) depended on the heart rate and ranged between 23 and 36 cardiac phases, to keep the scanning time close to 3 minutes 30 seconds. The view-sharing factor for the retrospective sorting of acquired k-lines was set to 1.8.

Because patients with ruptured aneurysms were treated within 24 hours after onset, MR imaging velocity measurements to assess inflow boundary conditions could not be performed before the coiling procedure. Therefore, for this patient group, postprocedural PC-MR images were obtained at the standard follow-up 6 months after coiling. Patients with unruptured aneurysms were requested to undergo an additional preprocedural PC-MR imaging study at admission.

Geometric Vascular Models

To generate vascular models that were usable for CFD, we segmented the aneurysm and its connected arteries in 3D rotational angiography images by using a level-set algorithm by using the Vascular Modeling Toolkit, VMTK Version 0.9.0 (http://www.vmtk.org). Subsequently, the segmented volumes were converted to volumetric meshes consisting of approximately 1,000,000 tetrahedral elements.

Computational Fluid Dynamics

For each aneurysm, we performed 2 CFD simulations: one applying spatiotemporal patient-specific inflow boundary conditions, acquired by PC-MR imaging velocity measurements, and the other applying generalized inflow boundary conditions.³⁴ The generalized inflow velocity profile was defined by predetermined Womersley profiles for fully developed pulsatile flow.^35,36 The flow was scaled so that the total generalized inflow equaled the measured inflow rate as determined by PC-MR imaging. Zero pressure boundary conditions were prescribed at all outlets. A no-slip boundary was set, and rigid walls were assumed. Transient Navier-Stokes equations were solved by using a pressure-based, 3D double-precision solver following the Semi-Implicit Method for Pressure Linked Equations.³⁷ Blood was modeled with an attenuation of 1040 kg/m³ and a dynamic viscosity of 0.004 Pa/s. CFD simulations were performed with Fluent software (ANSYS, Canonsburg, Pennsylvania). Three cardiac cycles were simulated to account for the transient character. Only the third complete cycle was used for analysis.³⁶

Quantitative Assessment of Hemodynamic Features

The mean WSS, maximum WSS, mean oscillatory shear index, and maximum oscillatory shear index values were calculated. Paired differences between the generalized and patient-specific inflow boundary conditions were analyzed by using paired t test statistics. Results with P values of <.05 were considered statistically significant.

Qualitative Assessment of Hemodynamic Features

Velocity-based streamlines and WSS patterns within the aneurysm during 1 cardiac cycle were visualized as movie clips with ParaView software (Kitware; Los Alamos National Laboratory, Los Alamos, New Mexico). On the basis of these movie clips, hemodynamic characteristics were scored in consensus by 2 neuroradiologists with >10 years of experience. The cases were randomly presented to the observers, who were blinded to the method of inflow boundary conditions used.

We assessed the following hemodynamic characteristics: inflow jet concentration, inflow jet stability, number of vortices, vortex stability, location of the highest WSS, and location of the deflection zone. If the aneurysm contained a lobulation, WSS on the lobulation sac and on the ostium of the lobulation were also assessed, as well as the direction of the main inflow jet toward the lobulation.

The inflow jet was defined as an isosurface of 25% of the maximum velocity magnitude within the aneurysm. It was considered “concentrated” when interpreted as smaller than half the size of the aneurysm neck, and “diffuse” if larger. In the event of the flow pattern deteriorating or changing considerably during the cardiac cycle, it was labeled as “unstable.” The number of vortices was defined as the number of flow structures within the aneurysm and, if present, in the lobulation. The location of the highest WSS and deflection zone were classified according to their position as dome, body, or neck.³⁶ The “deflection zone” was defined as the area of divergence of the inflow jet on the aneurysm wall. For each hemodynamic parameter, differences between the 2 inflow boundary conditions were assessed and the amount of difference was rated between 1 and 5, with 5 representing a large difference. Differences between the scores of the observers were discussed in an additional meeting to reach a consensus.

Results

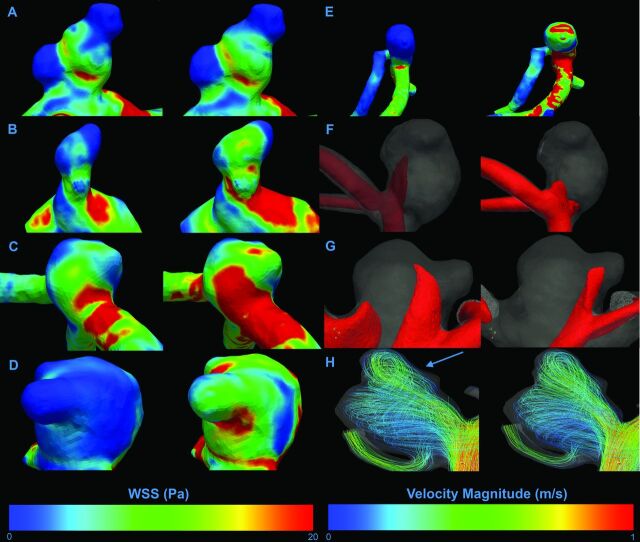
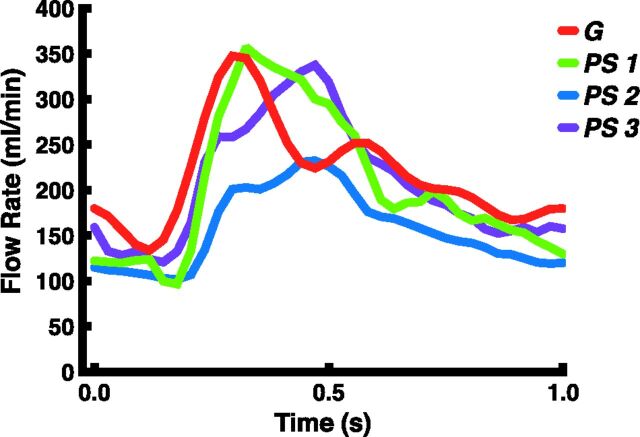
Figure 1 presents differences in hemodynamic characteristics between generalized or patient-specific inflow boundary conditions in the same aneurysm. For each scored hemodynamic characteristic, 1 example is given. An example of the flow rate curve for both methods is displayed in Fig 2.

Fig 1.

Examples of visualized differences in hemodynamic characteristics. The left column shows patient-specific inflow boundary conditions; the right column shows generalized boundary conditions. A–H, Differences in distribution for all assessed WSS characteristics. A, No difference in any characteristic. B, High WSS area on the ostium of lobulation. C, High WSS location on the primary aneurysm. D, High WSS on the lobulation sac. E, Deflection zone. F and G, Isosurface projections of inflow jet characteristics. F, Inflow jet concentration. G, Inflow jet aim in the lobulation. H, Visualization of intra-aneurysmal flow structures represented by velocity magnitude streamlines. On this figure, a difference in the number of vortices can be appreciated, with an additional vortex for the patient-specific inflow boundary conditions (blue arrow).

Fig 2.

Examples of the applied flow-rate pattern during 1 heart cycle for both methods. PS indicates patient-specific flow rate curves of 3 separate cases (blue, purple, and green); G, generalized flow-rate curve (red).

Quantitative Assessment of Hemodynamic Features

Table 1 displays the mean and maximum WSS and oscillatory shear index values per method, including their relative differences. Mean WSS was larger for the generalized inflow boundary conditions, with an average of 3.5 Pa (P < .001). The maximum WSS was also larger for the generalized approach with an average of 65 Pa (P = .0013). The differences for mean or maximum oscillatory shear index values were not statistically significant (P = .42 and P = .65, respectively). In On-line Table 1, all measured values per case used in the quantitative assessment, including their relative differences, are displayed.

Table 1:

Quantitative values for mean and maximum WSS and OSI^a

Method	Mean WSS (Pa)			Max WSS (Pa)			Mean OSI (Pa)			Max OSI (Pa)
	PS	G	Δ	PS	G	Δ	PS	G	Δ	PS	G	Δ
Median	2.1	2.9	−28%	38	54	−11%	0.013	0.011	18%	0.40	0.36	11%
Average	2.5	3.5	−29%	43	64	−33%	0.020	0.017	18%	0.36	0.35	0.3%
SD	1.7	2.7	−29%	27	44	−39%	0.024	0.021	14%	0.11	0.10	1%

Note:—PS indicates patient-specific inflow boundary conditions; G, generalized inflow boundary conditions; Δ, (PS−G)/G × 100%; Max, maximum; OSI, oscillatory shear index.

^aRelative differences are presented as percentages.

Qualitative Assessment of Hemodynamic Features

Table 2 displays the number of differences in hemodynamic characteristics as scored during the qualitative assessment. In 21 of 36 aneurysms, at least 1 of the characteristics was scored differently for the 2 inflow boundary conditions. Seven aneurysms with differences in WSS characteristics showed no differences in vortex and inflow jet characteristics (eg, patient 16). Six patients with no differences in WSS characteristics showed distinct differences in vortex and inflow jet characteristics (eg, patient 27). Furthermore, aneurysms showing differences in vortex and inflow jet characteristics were more often assessed as unstable for the generalized inflow boundary conditions. This was seen in 7 of 9 aneurysms with differences in vortex characteristics and all aneurysms with differences in inflow jet characteristics. In On-line Table 2, a detailed overview of the qualitative assessment is given, in which each case can be appreciated for which hemodynamic characteristic differences between the 2 methods were scored.

Table 2:

Qualitative assessment: number of cases for each scored hemodynamic characteristic showing a difference between the patient-specific inflow boundary conditions and the generalized inflow boundary conditions

	Inflow Jet		Vortex		WSS Location		Lobulation
	Concentration	Stability	No.	Stability	High WSS	Deflection	WSS	Jet Aim	Ostium WSS
No.	1	7	5	6	9	3	9	2	8

Discussion

We showed that the choice of general or patient-specific inflow boundary conditions results in large differences in WSS magnitude and distribution. Differences in vortex and inflow jet characteristics occurred less frequently. The approach by using generalized inflow boundary conditions led to considerably more unstable vortices and inflow jets, suggesting that inflow jet and vortex instability are sensitive to inflow boundary conditions. These data indicate that previous findings on vortex instability by using generalized inflow boundary conditions should be considered with caution.³⁸

Both patient-specific and generalized inflow boundary conditions are traditionally used for CFD analysis of cerebral aneurysm hemodynamics. However, only 2 authors have so far compared both approaches.^28–30 The large differences in WSS magnitude and WSS distribution found in our study are in line with findings of a smaller study in 6 patients by Karmonik et al,²⁸ who pointed out differences in both WSS values and in WSS distribution between the 2 inflow boundary conditions. In addition, Venugopal et al³⁹ showed that WSS distributions are sensitive to changes in flow-rate distribution in the proximal artery. Marzo et al³⁰ also reported differences in WSS magnitude but did not report changes in WSS distribution outside the order of physiologic variations.

Twenty-one of 36 aneurysms showed at least 1 difference in a hemodynamic characteristic for the 2 inflow boundary conditions. Most of these were WSS-related, such as high WSS location and level of WSS on the lobulation sac. Fewer differences were found in vortex- or inflow jet–related characteristics. This discrepancy could be explained by findings of Cebral et al,³⁶ who have shown that variations of up to 25% in blood flow rate do not affect the flow patterns inside the aneurysm.

There are several limitations related to the design of this study. It did not address the role of outflow boundary conditions and flow divisions distal to the aneurysm, which could influence the accuracy of the results. In addition, for patients with a ruptured aneurysm, postprocedural PC-MR imaging velocity measurements were used for the inflow boundary conditions to simulate preprocedural hemodynamics. The embolization itself may alter the local hemodynamics, resulting in an inadequate representation of pre-embolization hemodynamics. However, we have compared pre- and postprocedural PC-MR imaging measurements of the parent artery in a small number of patients (with unruptured aneurysms) and did not detect notable differences. Finally, vascular compliance and fluid-wall interaction were not incorporated in this model. Disregarding these effects may have influenced the resulting hemodynamic characteristics and may have led to an overestimation of mean and maximum WSS values.¹⁰

The findings of this study emphasize that running simulations with generalized boundary conditions may result in variations in WSS magnitude and distribution and may overestimate vortex instability. These variations could greatly influence the association of hemodynamics with the rupture of cerebral aneurysms. Therefore, interpretation of WSS profiles should be applied with great caution when generalized inflow boundary conditions are used for this purpose. More research is also needed to further investigate the influence of other boundary conditions on CFD in aneurysms, ideally incorporating the effect of wall and outflow boundary conditions.

Conclusions

Patient-specific and generalized inflow boundary conditions in CFD-based simulations of aneurysmal hemodynamics resulted in large differences in WSS magnitudes. In addition, 21 of 36 aneurysms showed differences in hemodynamics characteristics. Aneurysms showing differences in vortex and inflow jet characteristics were more often assessed as unstable when generalized inflow boundary conditions were applied. This study emphasizes the necessity of the use of patient-specific inflow boundary conditions for the calculation of hemodynamics in cerebral aneurysms by using CFD techniques.

ABBREVIATIONS:

CFD

computational fluid dynamics

PC-MR imaging

2D phase-contrast MR imaging

WSS

wall shear stress