Differential Diagnosis of Normal Pressure Hydrocephalus by MRI Mean Diffusivity Histogram Analysis

Abstract

BACKGROUND AND PURPOSE:

Accurate diagnosis of normal pressure hydrocephalus is challenging because the clinical symptoms and radiographic appearance of NPH often overlap those of other conditions, including age-related neurodegenerative disorders such as Alzheimer and Parkinson diseases. We hypothesized that radiologic differences between NPH and AD/PD can be characterized by a robust and objective MR imaging DTI technique that does not require intersubject image registration or operator-defined regions of interest, thus avoiding many pitfalls common in DTI methods.

MATERIALS AND METHODS:

We collected 3T DTI data from 15 patients with probable NPH and 25 controls with AD, PD, or dementia with Lewy bodies. We developed a parametric model for the shape of intracranial mean diffusivity histograms that separates brain and ventricular components from a third component composed mostly of partial volume voxels. To accurately fit the shape of the third component, we constructed a parametric function named the generalized Voss-Dyke function. We then examined the use of the fitting parameters for the differential diagnosis of NPH from AD, PD, and DLB.

RESULTS:

Using parameters for the MD histogram shape, we distinguished clinically probable NPH from the 3 other disorders with 86% sensitivity and 96% specificity. The technique yielded 86% sensitivity and 88% specificity when differentiating NPH from AD only.

CONCLUSIONS:

An adequate parametric model for the shape of intracranial MD histograms can distinguish NPH from AD, PD, or DLB with high sensitivity and specificity.

Normal pressure hydrocephalus is a reversible cause of dementia, incontinence, and gait disturbance in the elderly.¹ Accurate and timely diagnosis is essential to its successful treatment.² Diagnosis of NPH can be difficult because the clinical symptoms associated with NPH are common in the elderly and can overlap those of age-related neurodegenerative disorders such as Alzheimer and Parkinson diseases.² Nonobstructive enlargement of the cerebral ventricles in NPH can be difficult to distinguish from age- and disease-related ex-vacuo ventricular enlargement by conventional CT and MR imaging techniques. Expert clinical evaluations performed in specialized centers can achieve up to 90% accuracy in identifying shunt-responsive patients with NPH³; however, diagnosis of NPH in general practice is much less successful. It has been estimated recently that only 10%–20% of patients with NPH get the appropriate specialized treatment.⁴ Recognition of NPH in general practice could be improved if more objective and quantitative imaging methods were available for differential diagnostic and prognostic purposes.^5–9

Brain imaging is an integral part of NPH diagnosis. To meet the criteria for probable NPH by international consensus guidelines, one must use brain imaging to document an Evans index (the ratio of the widest diameter of the anterior horn of the lateral ventricle to the transverse intracranial diameter) of ≥0.3.² Another imaging sign that has been validated recently as an adjunct to the diagnosis of NPH is disproportionate enlargement of the inferior subarachnoid spaces with tight high-convexity subarachnoid spaces.⁹ A number of quantitative imaging biomarkers have also been proposed as aids to NPH diagnosis, such as phase-contrast aqueductal flow measurements,¹⁰ aqueductal stroke volume measurements,¹¹ the ratios of ventricular volume to cortical thickness,⁷ increased DTI fractional anisotropy of periventricular white matter and the basal ganglia,¹² CSF and blood flow,¹³ and temporal changes in the apparent diffusion coefficient during the cardiac cycle.¹⁴ The use of these techniques has largely been confined to research studies in specialty centers, and none have been proved to improve the diagnosis of NPH in routine clinical practice.

Alterations in brain-water diffusivity in NPH were first reported nearly 20 years ago.¹⁵ It has been recently reported that region-of-interest-based DTI techniques can distinguish shunt-responsive NPH from other dementias with higher specificity than the Evans index (95% versus 80%).⁶ Tract-based spatial statistics methods were reported to achieve sensitivity for NPH classification of >90% with a specificity between 80% and 85%.¹⁶ However, these methods require operator-defined regions of interest, which are subjective and prone to inter-rater variability issues and/or require image registration to normative images. Identifying all registration errors is almost impossible,¹⁷ and registration is especially problematic for conditions with large anatomic deformations such as NPH. Problems with registration of patients with NPH have already been reported.¹⁸

We hypothesized that radiologic differences between NPH and AD/PD can be captured by a robust and objective DTI technique that does not require intersubject image registration or operator-defined regions of interest. To that end, we developed a parametric fitting model for the shape of a whole-brain mean diffusivity histogram applicable in the differential diagnosis of NPH. Histogram approaches are attractive, compared with other diffusion MR imaging analysis methods because of their robustness and reproducibility.¹⁹ These approaches typically do not depend on intersubject registration of images or tissue segmentation and smoothing. Consequently, they are not susceptible to many of the common pitfalls of DTI analysis.¹⁷ NPH is well-suited for MD histogram analysis because transependymal fluid shifts in NPH affect a large number of brain voxels in a way that is directly detectable by MD. Ulug et al²⁰ were the first to apply an MD histogram approach to hydrocephalus and reported that MD of periventricular brain-water was increased in obstructive hydrocephalus. Our method is a generalization of the modeling approach developed by Dyke et al²¹ for analyzing MD histograms in late infantile neuronal lipofuscinosis. The generalization captures distinctive features present in the MD histograms of patients with NPH.

Materials and Methods

Subjects

This research protocol was approved by the Weill Cornell Institutional Review Board and informed consent was obtained from all the subjects. The subjects were accrued consecutively, from the Weill Cornell Memory Disorders Program clinical service. The clinical diagnoses were established by 2 neurologists (N.R. and M.L. with 21 and 16 years of experience, respectively). Probable idiopathic NPH was diagnosed in accordance with the international consensus guidelines.² AD,²² PD,²³ and dementia with Lewy bodies²⁴ were diagnosed in accordance with published criteria. The subjects of this retrospective study included 15 patients with probable idiopathic NPH (7 women and 8 men; mean age, 77.0 years; age range, 63–89 years), 9 patients with AD (5 women and 4 men; mean age, 77.2 years; age range, 63–85 years), and 16 patients with either PD or DLB (7 women and 9 men; mean age, 73.6 years; age range, 51–86 years). Two additional subjects diagnosed with a combination of NPH and AD were also included (women, ages 77 and 78 years). All patients with NPH had an Evans index of ≥0.3. All except 2 patients with AD also had an Evans index of ≥0.3. Five of 16 non-NPH non-AD patients had an Evans index of >0.3.

Subjects with secondary NPH, obstructive hydrocephalus, or shunts were not considered. Five patients with infarcts of >1 cm in major vascular territories were excluded. Lacunes and smaller infarcts were not exclusionary because this comorbidity is frequently present in patients with suspected NPH.

Image Acquisition and Preprocessing

DWI was acquired on a 3T Signa Excite scanner (GE Healthcare, Milwaukee, Wisconsin) by using 33-direction echo-planar diffusion-weighted scans at b = 1000 s/mm² and 1 at b = 0 s/mm². TE was 70–80 ms; TR, 8.2 seconds. The whole brain was covered with sixty 2.5-mm-thick sections with no gap between sections. The voxel size was 1.8 × 1.8 × 2.5 mm³.

Eddy current correction and motion correction were performed by linear registration of the gradient volumes to low gradient (B0) volume,²⁵ followed by corresponding adjustment of the encoding vectors. The automatic skull stripping²⁶ was followed by manual corrections when needed. DTI fitting and MD calculations were performed with the FMRIB Software Library (http://fsl.fmrib.ox.ac.uk/fsl).²⁷ MD values were placed in the 250 bins of normalized histograms with unit area.

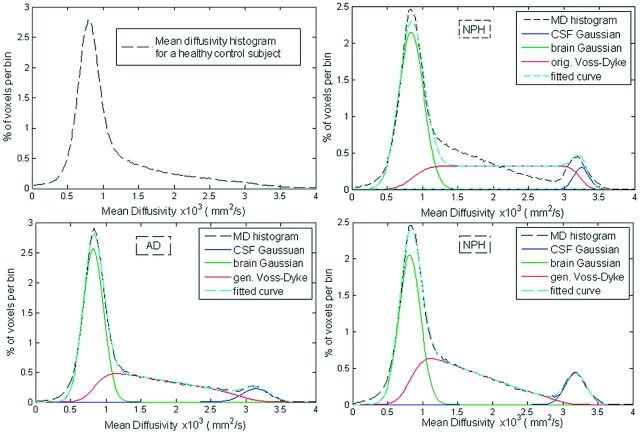
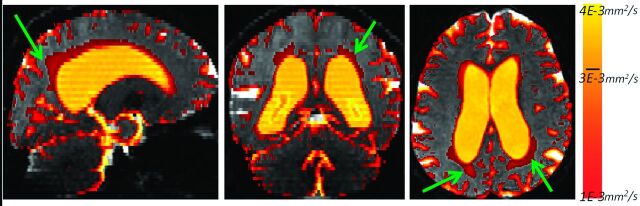
The major feature of the DTI histograms is a peak below 1E-3 mm²/s, consisting primarily of voxels in the brain parenchyma.²⁸ In subjects with enlarged ventricles, a distinctive second peak appears in the MD region above 3E-3 mm²/s (Fig 1, upper right). We observed that the region between 1E-3 mm²/s and 3E-3 mm²/s frequently has a steeper slope in subjects with NPH compared with patients with NPH. This is a consequence of extracellular water accumulated within white matter of patients with NPH (Fig 2). For the overall MD distribution, see On-line Fig 1. The parametric histogram fitting presented in this article is designed to quantify this difference in the histogram slope.

Fig 1.

The MD histograms of a healthy subject (top left), a patient with AD (bottom left), and a patient with NPH (top and bottom right). MD histogram of the same patient with NPH was fitted with the original Voss-Dyke function (top right) and with the proposed generalized Voss-Dyke function (bottom right).

Fig 2.

The voxels with MD values between 1E-3 mm²/s and 4E-3 mm²/s for a patient with NPH. Notice the area of increased MD in the periventricular white matter (green arrows). Values above 3E-3 mm²/s correspond mostly to ventricles, whereas values below 1E-3 mm²/s are primarily within the brain parenchyma (gray).

Analysis Methods

The parametric model for fitting of the histograms is a modification of the multicomponent model developed by Dyke et al²¹ for analyzing pediatric DTI data. The normalized histograms were fitted by a weighted sum of 3 functions representing the brain, CSF, and the brain-CSF partial volume voxels together with brain voxels with high MD:

where

and, here introduced, the generalized Voss-Dyke function:

where μ_θ(t) = t^θμ_brain + (1 − t^θ)μ_CSF and

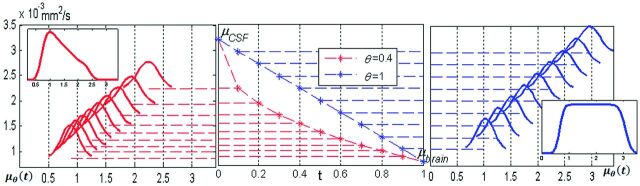
Here f_brain, f_CSF and f_mix, correspond to histogram fractions of brain parenchyma, CSF, and mixed voxels respectively; μ_brain and σ_brain(μ_CSF, σ_CSF) are the mean and SD of the brain (CSF) Gaussian. The parameter θ did not exist in the original Voss-Dyke equation¹⁷ and is introduced here. This parameter encodes the slope of the generalized Voss-Dyke function, as explained below.

The integral on the unit interval in the definition of the generalized Voss-Dyke function, P_VD(MD), was approximated by a Gaussian quadrature on 100 points. This integral can be thought of as a sum of 100 Gaussian distributions representing a homotopy from the Gaussian function P_CSF(MD) to the Gaussian function P_brain(MD). Smaller values of θ indicate a higher percentage of voxels with MD values close to those of the brain. This parameter creates the possibility of achieving unequal partial volume voxel distributions. In the original Voss-Dyke function, all fractions of partial volume voxels are necessarily equally likely (Fig 3).

Fig 3.

The original Voss-Dyke function is in blue; the generalized function is in red. In the center is homotopy mapping μ_θ(t) = t^θμ_brain + (1 − t^θ)μ_CSF. Right, for the original Voss-Dyke function, case θ = 1. The intermediate Gaussian distributions are equally between P_CSF(MD) and P_brain(MD). Left, in the case θ = 0.4, the intermediate distributions are skewed toward P_brain(MD), giving the slope to the generalized Voss-Dyke function. The inserts on the left and right represent the Voss-Dyke functions resulting as the sum of the corresponding Gaussians.

Note that patients with NPH have a disproportionally high number of voxels with elevated MD values (but lower than that of the free water in the CSF compartment).^6,18,20 Patients with AD and PD, on the other hand, have an increased number of partial volume voxels (higher f_mix) and a more proportional distribution of those voxels (higher θ).This results in a steeper slope of the middle part of the histogram fit for patients with NPH compared with those with AD and PD (Fig 1) and makes it possible to distinguish patients with NPH from those with AD and PD.

The form of the function P_VD(MD) was chosen so that the function P(MD) is differentiable with respect to θ, because it is with the respect to the other fitting parameters, so the Jacobian is defined. The total number of optimization parameters was 8: f_brain, f_CSF, f_mix, μ_brain, μ_CSF, σ_CSF and θ. Histogram fitting was performed by in-house-developed software based on the Levenberg-Marquardt algorithm implemented in C.²⁹ The Levenberg-Marquardt algorithm was iterated until the difference in fitted curves between 2 consecutive iterations was <0.1%, and it considered fitting adequate (successful) if the absolute difference between a subject's measured histogram and fitted curve was <5% of the total measured data. We initially experimented with modeling the MD histogram by a 9-parameter model consisting of 3 Gaussian functions (one component for brain parenchyma, a second for partial volume voxels, and a third for the CSF compartment),^20,30 but this model failed to adequately model the partial volume component in most patients with NPH. The original Voss-Dyke model²¹ improves over the 3-Gaussian model but does not fully capture the shape of the partial volume voxels in adults with NPH (Fig 1, upper right). The effects of the generalization of the Voss-Dyke fitting method in a subject with NPH is shown in the bottom right of Fig 1.

Classifying Methods

Fitting parameters θ and f_mix were used to construct 2D linear classifiers, one comparing NPH with AD only (group 1: NPH; group 2: AD) and another comparing NPH with all other conditions (group 1: NPH; group 2: AD, PD, DLB). Receiver operating characteristic analysis was performed with a publically available Matlab package (MathWorks, Natick, Massachusetts).³¹ The reported sensitivity and specificity values are those that maximize the Youden index.

For the sake of completeness, binary classifiers based on all 8 fitting parameters and average MD over the whole brain were also considered. In On-line Tables 1 and 2, we also report negative and positive predictive values, calculated on the basis of disease prevalence in our patient population, which may not be representative of any other clinical population.

Results

Generalized Voss-Dyke fitting was successful for all subjects (ie, the absolute difference between the subject's measured histogram and fitted curve was <5% of the total measured histogram). The basic statistics on all of the fitting parameters and average MD (over the whole histograms) are shown in Table 1.

Table 1:

Mean values for all fitting parameters and average MD

	fbrain	μbrain (×e-4 mm2/s)	σbrain (×e-4 mm2/s)	fCSF	μCSF (×e-3 mm2/s)	σCSF (×e-4 mm2/s)	fmix	θ	Average MD
NPH	0.436 ± 0.043	7.87 ± 0.24	1.5 ± 0.29	0.086 ± 0.022	3.2 ± 0.1	1.9 ± 0.16	0.478 ± 0.061	0.57 ± 0.16	1.4 ± 0.12
AD	0.435 ± 0.071	7.88 ± 0.25	1.5 ± 0.21	0.080 ± 0.023	3.2 ± 0.3	1.5 ± 0.29	0.484 ± 0.068	0.71 ± 0.14	1.5 ± 0.14
PD, DLB	0.501 ± 0.062	8.08 ± 0.35	1.6 ± 0.18	0.051 ± 0.039	3.1 ± 0.2	2.1 ± 0.17	0.446 ± 0.044	0.70 ± 0.12	1.3 ± 0.13

Classification Power

We compared 2 variants of binary classifiers: comparing patients with NPH with patients with AD only,¹ and comparing patients with NPH with all other patient groups jointly (group 1: NPH; group 2: AD, PD, DLB).² The 2 patients diagnosed both with NPH and AD were excluded from the classification analysis.

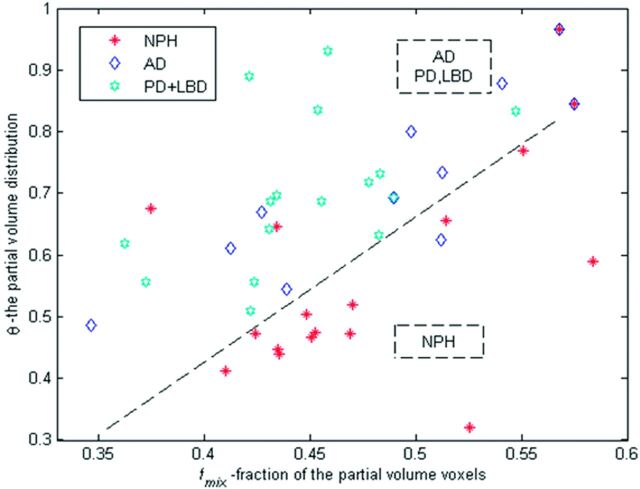
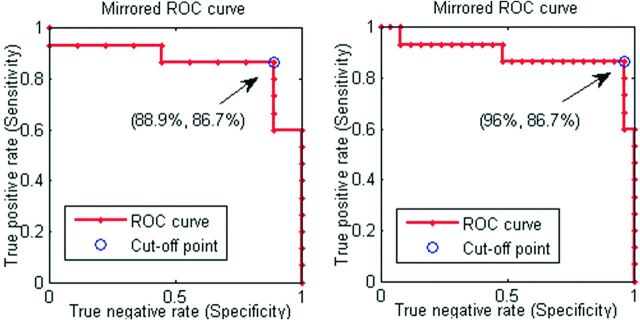
The classification power for the best one 1D and the best three 2D classifiers are shown in Tables 2 and 3. Overall, the best differentiation of NPH from the control groups, in both classifier variants, was achieved with the combination of parameters f_mix and θ (Fig 4). Estimates on achievable specificity and sensitivity for the best classifier are given by receiver operating characteristic curves in Fig 5. Complete tables of all 1D classifiers are in On-line Tables 1 and 2. Similar tables for thirty-six 2D classifiers are omitted for brevity.

Table 2:

Three 1D classifiers and three 2D classifiers with the highest Youden index, for the binary classification with group 1: NPH; and group 2: AD^a

	fCSF	fbrain	θ	(fCSF, θ)	(σbrain, θ)	(fmix, θ)
Sensitivity	0.73 (11/15)	1.00 (15/15)	0.73 (11/15)	0.73 (11/15)	0.73	0.87 (13/15)
Specificity	0.56 (5/9)	0.33 (3/9)	0.78 (7/9)	0.89 (8/9)	0.92	0.89 (8/9)
Y-index	1.29	1.33	1.51	1.62	1.65	1.76

^aThe numbers in parentheses represent the numerators and denominators for the given fractional values.

Table 3:

Three 1D classifiers and three 2D classifiers with the highest Youden index, for the binary classification with group 1: NPH; group 2: AD, PD, DLB^a

	fCSF	fbrain	θ	(fCSF, θ)	(σbrain, θ)	(fmix, θ)
Sensitivity	0.87 (13/15)	0.73 (11/15)	0.87 (13/15)	0.80 (12/15)	0.87 (13/15)	0.87 (13/15)
Specificity	0.52 (13/25)	0.80 (20/25)	0.68 (17/25)	0.84 (21/25)	0.88 (22/25)	0.96 (23/25)
Y-index	1.39	1.53	1.55	1.64	1.75	1.83

^aThe numbers in parentheses represent numerators and denominators for the given fractional values.

Fig 4.

Fraction of the midrange MD voxels (f_mix) versus θ. Lower values of θ mean a higher number of voxels, with MD values closer to parenchyma MD values and a lower number of the voxels with MD values closer to CSF. The classification line presented on the graph is θ_out = −0.4 + 2.1 * f_mix.

Fig 5.

The receiver operating characteristic curves for the patients with NPH classification against patients with AD only (left) and the joint AD, PD, and LBD group (right). The receiver operating characteristic points presented are for the cutoff lines of the form θ_out = −0.4 + β * f_mix, β ∈ (1, 3.5), with the best cutoff obtained by β = 2.1.

The 2 patients with both NPH and AD appear at the top right corner of Fig 4. These patients have a relatively flat distribution of MD values, coming from a combined effect of cerebral atrophy and high MD within the brain parenchyma.

Outliers

The patient with NPH in the top left corner of the Fig 3, misclassified by our method, is an 82-year-old man with a small hemorrhagic infarct in the left thalamus and an atrophic left hippocampus. The other misclassified patient with NPH was a relatively young (63 years of age) female patient with extensive microvascular ischemic disease. The patient with AD within the NPH region in Fig 4 is the oldest one in the patients with AD cohort: an 85-year-old woman with comorbid cerebrovascular disease.

Other Fitting Parameters

The most conspicuous parameter of the MD histograms, location of the raw data histogram peak, was, on average, at the same position for the patients with NPH (mean, 8.05E-4 ± 2.5E-5 mm²/s), AD (mean, 8.02E-4 ± 3.0E-5 mm²/s), and PD + DLB (mean, 8.08E-4 ± 3.5E-5 mm²/s) and did not yield specificity in distinguishing NPH.

Parameter f_CSF was elevated in NPH and AD compared with patients with PD + DLB (Table 1). This parameter alone yielded relatively good results in differentiating NPH from all the other conditions (sensitivity, 87%; specificity, 68%) but was not a particularly good indicator of NPH compared with AD (sensitivity, 73%; specificity, 56%). This is in line with results reported in Klassen and Ahlskog,⁵ in which a more detailed analysis of ventricle size was performed, and it was argued that the ratio of ventricular volume to cortical thickness is required to distinguish ventricular enlargement in NPH from ex-vacuo expansion in AD.

Parameter μ_CSF had a mean value of 3.1E-3 ± 1.6E-4 mm²/s over the entire subject population. This corresponds to the well-known MD value for unrestricted water.²⁷ We found no relationship between the patient diagnoses and μ_CSF (Table 1).

Discussion

The pathophysiology of NPH includes alterations in the distribution of water between and within the brain parenchymal and CSF compartments. Increased transependymal movement of CSF from the ventricles into the interstitial spaces of the brain may account for the alterations of white matter MD previously reported,^16,18,20,30 as well as the changes in the MD histogram observed in the present study. Other contributors may include increased intraparenchymal CSF production and decreased cerebral perfusion or physical distortion of brain tissue secondary to ventriculomegaly. Further studies are needed to better understand the origins of altered intracerebral water diffusivity in NPH.

MD Histogram Fitting

An often-cited downside of the MD histogram approaches is CSF “contamination,”¹⁷ (ie, inadvertent inclusion into histograms of partial volume voxels with variable amounts of parenchymal and CSF contributions). However, this is actually valuable information for NPH diagnostics because cerebral atrophy and the abnormal intermingling of free water and brain parenchyma occurs to a pathologic degree in NPH. This can be readily appreciated from a comparison of the MD histograms of a healthy control, a patient with NPH, and a patient with AD (Fig 1).

As explained in the “Materials and Methods” section, the original Voss-Dyke method operates under the assumption that all partial volume fractions are possible and equally likely. This adequately modeled MD data from children with late infantile neuronal lipofuscinosis,²¹ in whom ventricle size is actually larger (relative to the brain size) than that in the NPH population. Furthermore, in the case of patients with NPH, there are voxels fully within white matter with elevated MD values^6,18,20 but still closer to the MD values for the rest of parenchyma than to the MD values of unrestricted water (Fig 2). This situation is better modeled with the generalized form of the Voss-Dyke function.

Classification

The misclassified patients were at the extremes of their patient group age range, suggesting that age should be considered as a predictor variable. It has been argued recently, in several large studies,^31,32 that effects of aging on MD obey a quadratic law (MD ∼ α + β₁ * age + β₂ * age²), with MD decreasing from birth to approximately 40 years of age and then increasing after 40 years of age. Although our data sample was too small for a rigorous age- and sex-matched analysis, we performed multivariate first order θ_est = α + β₁ * f_mix + β₂ * age and second-order θ_est = α + β₁ * f_mix + β₂ * age + β₃ * age² regression analysis to test for possible dependence of θ on patient ages and f_mix as independent predictors. As expected, these models did not achieve the necessary P value (.05) to justify introduction of age and age² as predictor variables. With linear regression, the coefficients for the NPH group were θ_MPH = −0.25 + 1.37 * f_VD + 0.002 * age, and for AD θ_AD = −0.68 + 1.91 * f_mix + 0.006 * age, indicating potentially stronger dependence on age in patients with AD.

One limitation of this study is that it did not include age-matched healthy subjects or patients with certain other disorders that could affect MD (stroke, uncontrolled hypertension, chronic kidney disease, and so forth). Studying a larger set of healthy and disease controls will allow developing a regression model for the effects of aging. A prospective validation study is needed to rigorously determine the positive and negative predictive values of this method. The effects of different magnetic field strengths and other acquisition parameters remain to be studied but are unlikely to alter the fundamental findings.

It is quite likely that method accuracy can be further improved with a more sophisticated classification model that would include other proposed NPH biomarkers obtainable from diffusion MR imaging and T1 MR imaging data.^{6–12,14–16,18,32–36} However, higher model sophistication also leads to higher probability of undetected processing errors. Note that the proposed method is fully programmable and does not require user intervention. Most of the previously proposed quantitative NPH imaging biomarkers are operator-dependent and/or have less classification power than is obtained with the generalized Voss-Dyke function.

Conclusions

We developed a novel parametric model for the DTI MD histogram fitting, named the generalized Voss-Dyke function, which is highly successful in segregating patients with NPH from potential confounders without reliance on operator-dependent region-of-interest analyses or intersubject registration. While additional prospective validation is needed and some of the important confounders such as advanced vascular disease have to be considered separately, the presented results provide considerable cause for optimism that this technique can be used to summarize diffusivity changes in NPH and help distinguish NPH from neurodegenerative disorders and other potential diagnostic confounders.

ABBREVIATIONS:

AD

Alzheimer disease

DLB

dementia with Lewy bodies

NPH

normal pressure hydrocephalus

MD

mean diffusivity

PD

Parkinson disease