Quantitative CT Densitometry for Predicting Intracerebral Hemorrhage Growth

Abstract

BACKGROUND AND PURPOSE:

Intracerebral hemorrhage growth independently predicts disability and death. We hypothesized that noncontrast quantitative CT densitometry reflects active bleeding and improves predictive models of growth.

MATERIALS AND METHODS:

We analyzed 81 of the 96 available baseline CT scans obtained <3 hours post-ICH from the placebo arm of the phase IIb trial of recombinant factor VIIa. Fifteen scans could not be analyzed for technical reasons, but baseline characteristics were not statistically significantly different. Hounsfield unit histograms for each ICH were generated. Analyzed qCTD parameters included the following: mean, SD, coefficient of variation, skewness (distribution asymmetry), and kurtosis (“peakedness” versus “flatness”). These densitometry parameters were examined in statistical models accounting for baseline volume and time-to-scan.

RESULTS:

The coefficient of variation of the ICH attenuation was the most significant individual predictor of hematoma growth (adjusted R² = 0.107, P = .002), superior to BV (adjusted R² = 0.08, P = .006) or TTS (adjusted R² = 0.03, P = .05). The most significant combined model incorporated coefficient of variation, BV, and TTS (adjusted R² = 0.202, P = .009 for coefficient of variation) compared with BV and TTS alone (adjusted R² = 0.115, P < .05). qCTD increased the number of growth predictions within ±1 mL of actual 24-hour growth by up to 47%.

CONCLUSIONS:

Heterogeneous ICH attenuation on hyperacute (<3 hours) CT imaging is predictive of subsequent hematoma expansion and may reflect an active bleeding process. Further studies are required to determine whether qCTD can be incorporated into standard imaging protocols for predicting ICH growth.

ICH is the most devastating and least treatable stroke subtype. Hematoma growth is an important independent predictor of mortality and poor outcome and is a promising therapeutic target.¹ It occurs in >70% of patients studied within 3 hours of the onset of ICH.¹ Hemostatic studies by using rFVIIa have demonstrated approximately 50% less growth compared with a placebo.^2,3 Despite this potent biologic effect, discordant clinical results were found between an initial phase IIb proof-of-concept trial² and a pivotal phase III trial.³ However, post hoc analyses of enriched patient subgroups from the phase III trial suggest that the utility of hemostatic therapy may be improved by the appropriate identification of patients at high risk for hematoma growth.⁴

As a result, there is a critical need to establish imaging predictors of ICH growth that are rapidly and easily accessible.^5,6 Established imaging predictors of hematoma growth include baseline ICH volume and time to baseline CT scan.^7,8 With contrast CT, the CTA “spot sign” has more recently been identified as an independent predictor of hematoma growth and outcome^9–11 and is being prospectively validated in multiple centers worldwide.¹² While the sign is reasonably easily identified and may be readily applied in practice, caution is needed in the exclusion of spot sign mimics.¹³ In addition, spot sign identification requires a contrast CT scan and interpretive skill. Hemostatic agent trials based on spot sign treatment selection are being conducted in North America (NCT00810888, NCT01359202) and Australia (NCT01702636).

Noncontrast CT is the standard investigation tool in acute stroke, given its widespread availability, relatively low cost, rapid acquisition time, and safety. We first described the qualitative categorization of density heterogeneity as an independent predictor of hematoma growth, according to specific growth definitions.¹⁴ However, qualitative assessment has a number of limitations, including reliance on operator-dependent methodology and limited representation of the extent of attenuation variation.¹⁴

We therefore set out to create new predictive models of hematoma growth on the basis of noncontrast CT, by using CT densitometry, and compared a variety of models with existing predictors, BV and TTS. We hypothesized that qCTD would enhance the prediction of hematoma growth and would be able to do so rapidly and with minimal operator intervention.

Materials and Methods

The dataset used was the baseline CT scans from the placebo group of the proof-of-concept trial of rFVIIa.² Briefly, this randomized, double-blind, placebo-controlled trial involved 399 patients with spontaneous ICH, diagnosed by baseline CT within 3 hours of onset, who were randomized to placebo (n = 96) or 1 of 3 dose regimens of rFVIIa. Of the 96 placebo patients, 81 were available for analysis. Fifteen scans were either unsuccessfully transferred for technical reasons or had been digitized from hard copy films with loss of true Hounsfield unit densities. Baseline characteristics, BV (defined as baseline ICH volume on diagnostic NCCT) and TTS (defined as the time from symptom onset to baseline NCCT), of the unavailable scans were compared with those included to detect any baseline imbalances. We used the ROIs for each patient's hematoma and the corresponding ICH volumes manually outlined by 1 of the 2 neuroradiologists for the trial by using computer-assisted planimetrics (Analyze, Version 9.0; Mayo Clinic, Minneapolis, Minnesota). Scans were assessed in random order, and the reader was blinded to treatment assignment. Detailed methodology and reliability studies of imaging analysis in this trial have been published demonstrating within and between-rater intraclass correlation coefficients of >0.95.¹⁵

For our study, ICH growth was defined by using a continuous scale and 3 binary definitions based on previous studies of hematoma growth: any growth; ≥33% or ≥12.5 mL growth; and >1-mm radial growth (median radial growth of the baseline scans).^1,7,8,16 Each baseline CT scan and its ROIs were loaded into a graphic user interface created in Matlab (Version R2008b; MathWorks, Natick, Massachusetts). Hounsfield unit attenuation distributions were sampled from every voxel within each patient's entire ICH as defined by the Analyze ROIs, and densitometry variables were calculated directly from this sample, as described below.

Heterogeneity of ICH attenuation was analyzed in several ways. The 4 moments of a distribution or their commonly applied derivatives were calculated as descriptors of the distributions of ICH densities. We calculated the mean attenuation (first moment), SD (square root of variance, the second moment), coefficient of variation (CV, SD/mean), skewness (S, third moment), and kurtosis (K, fourth moment).¹⁷ Skewness is a measure of the asymmetry of a distribution around its mean. Kurtosis is a measure of its “peakedness,” or its tendency to cluster around a mean value compared with a more flattened distribution. Skewness and kurtosis, which are dimensionless quantities, were calculated from Hounsfield unit attenuation samples directly as a function within Matlab, according to the standard definitions.¹⁸

The dependent variable, volume change from baseline at 24 hours, was cube root transformed to satisfy normality assumptions applied to the residuals of the models used. With growth on a continuous scale, we used multiple linear regression, starting with known predictors for hematoma growth, namely BV and TTS, and sequentially adding individual densitometry variables as independent variables 1 at a time. No individual model incorporated >3 variables, and no more than 1 densitometry variable was included within any model, avoiding collinear coefficients. A set of predictive models was also constructed with the exclusion of TTS, because this parameter is frequently unknown (eg, in wake-up stroke), to examine the predictive performance of qCTD in this setting. Model-predicted values for the dependent variables required back-transformation to the original scale.

The various predictive models generated were compared by using the adjusted R² statistic (between 0 and 1). Adjusted R² provides an indication of the goodness of fit of the predictive linear model to the ICH growth data or the extent to which the variability in the outcome is explained by the model, adjusting for the number of explanatory terms included. The models were run within the Statistical Package for the Social Sciences (SPSS, Chicago, Illinois) to generate predicted 24-hour growth values for each patient, by using a dataset generated by leave-one-out cross-validation.^19,20 This technique avoids overestimation of model significance caused by testing a model on its derivation dataset. These predictions were compared with actual growth values, and an absolute difference was calculated. A time-interaction term was explored across 2 time epochs, <1.5 hours and ≥1.5 hours, for TTS.

Predictive models of hematoma growth as defined by the 3 binary outcome measures were created by using binary logistic regression, starting with known predictors (BV, TTS) and sequentially adding individual densitometry variables. The resulting models were compared by establishing the predicted probability of growth for each patient within a validation dataset created by using leave-one-out cross-validation, converting these to binary predictions of the binary growth outcome by using a probability cutoff of .5, and calculating the proportion of patients correctly predicted. The best models were examined further by using receiver operating characteristic curve, with an optimized cut-point identified by calculation of the Youden index.^21,22 In all cases, a P value < .05 was considered statistically significant. Analyses were performed by using SPSS, Version 16.0.

Results

Baseline Data

Median ICH BV was 14.1 mL (interquartile range [IQR], 27.4). Median TTS was 101 minutes (IQR, 37.5). Median ICH growth was 2.1 mL (IQR, 10.9). With binary growth definitions, 64 (79%) cases underwent any growth, 29 (36%) grew ≥33% or ≥12.5 mL, and 35 (43%) demonstrated radial expansion of >1 mm.

Baseline ICH volume and TTS of the 15 patients excluded from the study did not vary from those included.

The densitometry values of the ICH attenuation distributions are summarized in Table 1.

Table 1:

Densitometry values of the ICH density distributions

qCTD Parameter	Average Value (SD, range)
Mean	56.4 (±6.16, 37.7–73.2)
SD	59.6 (±16.4, 28.3–119)
Coefficient of variation	1.05 (±0.25, 0.56–1.67)
Skewness	−0.21 (±0.25, −0.84–0.33)
Kurtosis	2.21 (±0.39, 1.65–3.68)

Growth on a Continuous Scale

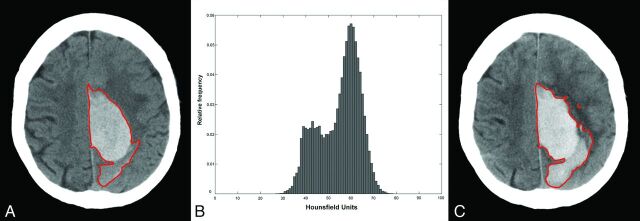
In multiple linear regression modeling (On-line Table), cube root transformation of the dependent variable satisfied assumptions of normality and constant variance for each model fitted. Of the predictors examined, coefficient of variation was the most significant individual predictor, with an adjusted R² of 0.107 (P = .002), which was greater than either BV or TTS and almost as high as their combination. A model incorporating BV, TTS, and coefficient of variation accounted for more data variability (adjusted R² = 0.202, P = .003 for coefficient of variation) than a model involving BV and TTS alone (adjusted R² = 0.115), with a 47% improvement in the number of predictions correct to within ±1 mL (28/81 versus 19/81, respectively). In the model including BV, TTS, and coefficient of variation, time was a significant interaction term when considered across 2 time epochs, <1.5 hours and ≥1.5 hours from onset to baseline CT, with a greater magnitude of increase in volume-per-unit decrease in coefficient of variation in the group scanned earlier (P = .016). An illustrative case is presented in Fig 1.

Fig 1.

A, Baseline CT scan obtained 85 minutes post-ictus with a volume of 62 mL (region of interest in red). B, Hounsfield unit histogram (mean, 54.9; SD, 41; coefficient of variation, 0.75; skewness, −0.47; kurtosis, 2.27). C, Follow-up 24-hour CT scan, with 16-mL total ICH growth, predicted to within 5 mL of actual growth by a model based on BV/TTS and within 1 mL of actual growth by a model based on BV/TTS/coefficient of variation. Note that overall study results are tested on a cross-validation-derived dataset (see text).

In models excluding TTS as an independent variable, the inclusion of either SD of the attenuation distribution (adjusted R² = 0.147, P = .01 for SD) or coefficient of variation of the attenuation distribution (adjusted R² = 0.171, P = .003 for coefficient of variation) proved to be superior to a model based on BV alone (adjusted R² = 0.082), with an extra 5 and 3 cases correctly predicted to within ±1 mL, respectively.

Binary Growth Definitions

With a growth definition of “any growth,” so many scans were designated growers (79%) that none of the predictive models were found to be significant. With a growth definition of ≥33% or ≥12.5 mL, models including BV, TTS, and either SD or coefficient of variation produced small receiver operating characteristic curve improvements but with minimal impact on the proportion of cases correctly predicted in the cross-validated dataset (4 extra correct cases, 5%). However, with a definition of >1 mm radial growth, models including BV (P < .02) and either SD (P < .02) or coefficient of variation (P = .007) were statistically significant. The densitometric model incorporating BV, TTS, and coefficient of variation achieved a 5.5% improvement in the ROC area under the curve (AUC = 0.729, Fig 2A) over a model based on BV and TTS alone (AUC = 0.691, Fig 2B), with a similar percentage increase in correct growth predictions and statistical significance of the densitometric term (P = .006 for coefficient of variation). The area under the curve in Fig 2A indicates that in a random sample of patients with ICH, 73 of 100 who undergo ICH growth will have a more positive predictive model output than those without ICH growth. The Youden index (J statistic) of 0.404 indicated an optimized sensitivity of 60% and a specificity of 80%. The negative predictive value was 100%, and the positive predictive value was 49%. An alternative point on the receiver operating characteristic curve yielded a sensitivity of 80% and a specificity of 54%. The most correct predictions occurred by using the BV and coefficient of variation model (58% correct), with no significant effect relating to time category (<1.5 hours versus ≥1.5 hours) as an interaction term in the model (P = .317).

Fig 2.

Receiver operating characteristic curves by using a binary growth definition of >1-mm radial expansion, with a binary logistic regression model incorporating BV, TTS, and coefficient of variation of ICH attenuation (A) and BV and TTS only (B).

Discussion

This study demonstrated that qCTD can be used to improve predictive models of ICH growth beyond known predictors, namely BV and TTS, increasing predictions within a cross-validation-derived dataset within ±1 mL of actual growth by up to 47%, with statistical significance of the densitometric variable in some models. In isolation, coefficient of variation was a superior predictor (by using adjusted R²) to either BV or TTS and was statistically significant. With a continuous growth scale, a predictive model incorporating qCTD accounted for >20% of variability in cube root volume change. This result represents a 76% improvement in adjusted R² compared with a model based on BV and TTS alone. Calculation of qCTD was fully automated, with measurements performed in a few seconds.

Early studies found CT densities to be helpful in the description of hemorrhage morphology, intracranially and elsewhere.^23,24 CT densitometry has been used in the assessment of intracerebral hematoma appearance in the setting of low hematocrit and thrombocytopenia²⁵ and in the prediction of hemorrhage following tPA administration in acute ischemic stroke.²⁶

The dynamic expansion of ICH was recognized in the pre-CT era,²⁷ and subsequently, by using CT, was shown to be maximal in the first few hours following symptom onset.²⁸ A primary hemorrhagic insult to the brain occurs at ictus with fresh, hypoattenuated liquid blood rapidly clotting to appear hyperattenuated on CT.²⁹ Larger bleeds have been shown to be more heterogeneous in attenuation at baseline CT.¹⁴ Kim et al¹¹ found that a low-attenuation “swirl sign” within hematomas on noncontrast CT was associated with increased mortality on univariate but not multivariate analysis. Secondary neural damage is then brought about by edema and blood-breakdown products.³⁰

Considerable attention has been given to the CTA spot sign, an independent predictor of hematoma growth characterized by uni- or multifocal contrast enhancement within the ICH at sites of active bleeding.^9–11 Densitometry has been incorporated into refined criteria for the spot sign.³¹

Although the phenomenon of wake-up stroke is more common in ischemic stroke,^32,33 ICH takes place during sleep in 15% of patients, and these patients have a significantly higher baseline hematoma volume and 1-month mortality.³⁴ The current study provides support for the supposition that in the absence of TTS information, qCTD might be substituted to improve predictive models, in particular the SD and coefficient of variation of the attenuation distribution.

The current results expand on previous findings regarding qualitative density heterogeneity¹⁴ and show that significant prognostic information is available from qCTD of NCCT. The strengths of this study include the use of a high-quality CT dataset and scans obtained within 3 hours of symptom onset, the time most likely to demonstrate ICH growth. Multiple growth definitions were explored, including growth as a continuous variable and using several binary definitions applied in the literature. The qCTD approach involves rapid automated calculations by using Matlab, which are operator-independent, eliminating issues of interobserver reliability. qCTD models may be calculated at the time of diagnostic CT, with or without the input of TTS information, to derive a prediction of hematoma growth at 24 hours. Automation enabled our analyses to be performed in <5 seconds per patient, excluding region-of-interest generation, but this function can also be fully automated.³⁵ Leave-one-out cross-validation was used to test the predictive models, serially excluding each patient in the dataset from analysis, thereby establishing a validation dataset and avoiding overestimation of model significance.

Furthermore, this technique examines the full range of attenuation information available from each patient's entire ICH, improving the limited “largest section” qualitative approach.¹⁴ In the setting of absolute or relative contrast contraindications, qCTD may provide an alternative to CTA methods of ICH growth-risk prediction, with less radiation exposure. However, CTA provides vascular and other information not available from NCCT.

There are several limitations of this study. Potential exists for improvement of these predictive models, with examination of larger datasets. In particular, examination of binary outcome measures is impaired by using such small numbers with predictive capacity limited to correct prediction of nongrowth by using 1 binary definition in this study. The binary definition of “any growth” is prone to inclusion of patients on the basis of measurement error. While cross-validation was used to test predictive models, an external validation dataset is necessary. We relied on a post hoc data analysis by using proprietary software. The Hounsfield unit scale is theoretically constant across all CT scanners; however, this assumes correct calibration and identical technical factors (eg, kilovolts, milliamperes) of each scanner from each trial center, representing a potential source of error. As such, a future validation study ideally should be performed on 1 scanner with identical technical factors for all patients. In this analysis, this error was mitigated by the fact that coefficient of variation, skewness, and kurtosis are resistant to left or right shifts in the distribution (translation), where used. In addition, a review of scan data revealed minor heterogeneity of scanning parameters, particularly kilovolts. Overall, the improvements in the predictive models were small, but they were started from a low baseline. If validated, predictive models such as these are potentially useful in the assessment of general patient status and risk of deterioration. These models could further enhance patient selection for trials that evaluate potential ICH treatments but should, of course, be complemented by clinical measures in decision-making for individual patients.

Anticoagulated patients were excluded from this hemostatic agent trial.² Hence, these findings cannot be extrapolated to warfarin-related hemorrhages, without another study. This study was limited to CT image analysis in the sub-3-hour time epoch. Association with clinical variables and outcome was not possible because hypertension, Glasgow Coma Scale, and other clinical variables also known to be of prognostic significance were not available. The density of ICH is affected by hematocrit; low-hematocrit ICHs can be isointense to brain.²⁵ Hematologic data were not available for this analysis.

CONCLUSIONS

This study demonstrates that qCTD, in particular the densitometry parameter coefficient of variation, can be used to predict ICH growth and accounts for more variability than a model based solely on established growth predictors, BV and TTS, with statistical significance. In contrast to the previously described qualitative assessment of density heterogeneity and the CTA spot sign, these models are rapidly calculated and operator-independent. On the basis of noncontrast CT, qCTD could be widely applicable, if replicated. Clinical utility could be maximized by incorporation of predictive models of ICH growth such as qCTD into CT workstations. qCTD prediction of hematoma growth should be validated in larger separate datasets at different scan times and correlated with other predictive techniques, such as the CTA spot sign.

ABBREVIATIONS:

BV

baseline ICH volume

ICH

intracerebral hemorrhage

qCTD

quantitative CT densitometry

rFVIIa

recombinant activated factor VII

TTS

time-to-scan (from ictus)