Mind the Gap: Impact of Computational Fluid Dynamics Solution Strategy on Prediction of Intracranial Aneurysm Hemodynamics and Rupture Status Indicators

Abstract

BACKGROUND AND PURPOSE:

Computational fluid dynamics has become a popular tool for studying intracranial aneurysm hemodynamics, demonstrating success for retrospectively discriminating rupture status; however, recent highly refined simulations suggest potential deficiencies in solution strategies normally used in the aneurysm computational fluid dynamics literature. The purpose of the present study was to determine the impact of this gap.

MATERIALS AND METHODS:

Pulsatile flow in 12 realistic MCA aneurysms was simulated by using both high-resolution and normal-resolution strategies. Velocity fields were compared at selected instants via domain-averaged error. We also compared wall shear stress fields and various reduced hemodynamic indices: cycle-averaged mean and maximum wall shear stress, oscillatory shear index, low shear area, viscous dissipation ratio, and kinetic energy ratio.

RESULTS:

Instantaneous differences in flow and wall shear stress patterns were appreciable, especially for bifurcation aneurysms. Linear regressions revealed strong correlations (R² > 0.9) between high-resolution and normal-resolution solutions for all indices except kinetic energy ratio (R² = 0.25) and oscillatory shear index (R² = 0.23); however, for most indices, the slopes were significantly <1, reflecting a pronounced underestimation by the normal-resolution simulations. Some high-resolution simulations were highly unstable, with fluctuating wall shear stresses reflected by the poor oscillatory shear index correlation.

CONCLUSIONS:

Typical computational fluid dynamics solution strategies may ultimately be adequate for augmenting rupture risk assessment on the basis of certain highly reduced indices; however, they cannot be relied on for predicting the magnitude and character of the complex biomechanical stimuli to which the aneurysm wall may be exposed. This impact of the computational fluid dynamics solution strategy is likely greater than that for other modeling assumptions or uncertainties.

Hemodynamic forces, notably wall shear stresses (WSSs), are thought to contribute to wall adaptation and remodeling.¹ Computational fluid dynamics (CFD) can nominally describe the hemodynamic environment to which the wall is exposed and, therefore, predict the presence of abnormal wall shear stress as a plausible surrogate marker of focal wall weakening. Using highly automated algorithms, recent CFD studies have been successful in retrospectively classifying hundreds of aneurysms according to their rupture status.^2–4 Although it has been questioned whether these simulations are really patient specific owing to the various modeling assumptions and uncertainties,⁵ CFD is, arguably, a promising tool for future clinical use.^6,7

Key factors that determine the accuracy of a particular CFD simulation are the temporal and spatial discretizations specified by the operator. In principle, these are chosen in anticipation of the expected hemodynamics and then must be demonstrated to converge to within some desired error tolerance via methodical refinement studies.⁸ In practice however, discretizations are usually constrained by available computational resources and/or desired solution times, and rarely are proper convergence studies performed or reported. Moreover, commercial CFD solvers tend to use low-order stabilization terms as the default^9,10 to ensure a result, even for otherwise-inadequate discretizations; this tendency amounts to adding artificial viscosity or dissipation to the solution. These are not minor technical issues because inexperienced individuals can now readily use commercial CFD solvers; solutions are being sought within clinical timeframes: and CFD can have an impact on clinical decision-making.^11–13

To illustrate the potential gap between what may be termed normal-resolution (NR) and high-resolution (HR) solution strategies, consider that the broadest CFD-based studies of aneurysm rupture status have reported using 100 time-steps per cardiac cycle with meshes of 1 to 5 million tetrahedra¹⁴ or 1000 time-steps per cycle with 300,000 to 1 million elements.² On the other hand, recent case studies using tens of thousands of time-steps per cardiac cycle and tens of millions of tetrahedral elements (or the equivalent) have reported the presence of highly unstable and possibly turbulent flows,^15–18 consistent with clinical observations¹⁹ but seemingly at odds with most published aneurysm CFD studies. The impact of the solution strategy was also evident in a recent CFD Challenge,²⁰ which highlighted, for the same aneurysm case, a wide variety of aneurysm inflow patterns contributed by 25 groups, most using a range of NR strategies.

Nevertheless, discrimination of aneurysm rupture status tends to rely on hemodynamic indices that reduce complex velocity and WSS fields to a single number or category via integration over the cardiac cycle and/or aneurysm dome, with the potential for ameliorating differences in velocity and WSS fields predicted by HR-versus-NR strategies. The aim of the present study was, therefore, to investigate the impact of solution strategy on the prediction of aneurysm velocity and WSS fields, to determine whether NR solution strategies may be sufficient for hemodynamic indices commonly used for discrimination of rupture status. Not having access to the datasets of other groups, we achieved this by performing a controlled numeric experiment wherein a representative HR and NR solution strategy was applied to the same set of aneurysm cases.

Materials and Methods

Patients and Imaging

The original cohort consisted of 20 consecutive patients with MCA aneurysms treated at the Department of Neurosurgery, University Hospital of North Norway. Of these patients, 12 were suitable for image-based CFD modeling and, by convention, are identified by their original case numbers, between 1 and 20. The register was approved by the local ethics committee and the data inspectorate; included patients gave consent for use of imaging and clinical data. 3D imaging of the intracranial arteries and aneurysms was obtained on a 16-multidetector row spiral CT scanner with 0.3- to 0.5-mm resolution. The resulting cases included both sidewall and bifurcation aneurysm types and stable and unstable flow types. Further details, including morphologic characterizations, are provided elsewhere.¹⁸

HR-versus-NR Solution Strategies

To ensure as controlled a numeric experiment as possible, we performed simulations by using solvers developed and validated within the same open-source finite-element method library, FEniCS (http://fenicsproject.org/)²¹: for HR, a minimally dissipative solver; for NR, a solver using a standard stabilization scheme. Most important, both HR and NR simulations were performed by using the same finite-element mesh for each case; the only difference was the use of quadratic-versus-linear elements for HR versus NR, or better than a 2× increase in spatial resolution or an 8× increase in linear elements.

For HR simulations, we used a conditionally stable incremental pressure-correction scheme,^18,21 based on Stanford's well-known CDP solver widely used in high-performance CFD research.²² For our solver, we used second-order Taylor-Hood tetrahedral elements and a second-order semi-implicit time-stepping scheme. The number of time-steps per cardiac cycle was set to 20,000 to minimize artificial diffusion and capture possible flow instabilities.¹⁸

For the NR set of simulations, we used an unconditionally stable implicit PSIO (pressure implicit with splitting of operators') scheme, widely used in commercial CFD solvers. The number of time-steps per cardiac cycle was set to 1000, the finer of the time-step sizes from the 2 largest rupture-status CFD studies.^2,3 At such temporal resolutions, the CFD solver needs to be stabilized because numeric stability criteria are not met. We used a first-order streamline-upwind/Petrov-Galerkin stabilization, which is the default approach in commercial solvers like Fluent (ANSYS, Canonsburg, Pennsylvania) and Star-CD (CD-adapco, Melville, New York).^9,10 We used first-order accurate continuous Galerkin elements for both the velocity and pressure and advanced the solution in time by using a fully implicit first-order scheme. This solution strategy is representative of most aneurysm CFD studies published in the clinical literature, and most solutions contributed to a recent aneurysm CFD Challenge.²⁰

Common Solution Parameters

The CT-imaged aneurysms were digitally segmented and meshed by using the Vascular Modeling ToolKit (www.vmtk.org). We included as much as possible from the surrounding arteries, and vessels were extended by 10 diameters to reduce boundary effects. Mesh density was chosen to be highest in the vicinity of the aneurysm sac, where the tetrahedron side length was 0.12 mm on average (eg, compared to Cebral et al,¹⁴ who reported a minimum resolution between 0.2 and 0.1 mm). Two layers of boundary elements were used throughout the domain, with a total thickness set equal to one-quarter of the tetrahedron side length. The number of tetrahedral elements was 1.44 million on average, ranging from 1.1 to 2.0 million elements. As a result, the HR meshes, by using second-order elements, were at least equivalent to linear tetrahedral meshes with 8.8- to 16-million elements and a side length of 0.06 mm.

We assumed rigid walls, a blood viscosity of 0.0035 Pa · s, and blood density of 1025 kg/m³. A fully developed Womersley velocity profile was applied at the inlet on the basis of a representative older adult ICA flow waveform²³ damped by 30% to account for the reduced pulsatility at the MCA.²⁴ A cycle-averaged cross-sectional mean velocity of 0.37 m/s was applied to the inlet in all cases, under the assumption that flow rate scales approximately with cross-sectional area. The resulting peak systolic cross-sectional mean velocity was 0.55 m/s. To represent the downstream vasculature, we applied resistance boundary conditions²⁵ to ensure a physiologic outflow division. Simulations were run until the flow exhibited cycle-to-cycle convergence or 4 cycles, whichever came first. We assumed a period of 1 second, and the analysis was based on the output from 100 uniformly spaced time-steps from the third cycle.

All simulations were performed on dual 2.5GHz quad-core processors (Xeon L5420; Intel, Santa Clara, California). Simulations performed using our highly optimized HR solver required an average of 5 days per cardiac cycle (range, 3–9 days). The NR solver, implemented for the purpose of this study and so not optimized, typically required <1 day per cycle.

Hemodynamic Indices

Velocity fields were compared quantitatively at selected instants via the L₂ error of the velocity (‖HR − NR‖_L2/‖HR‖ _L2), based on the entire CFD model. We computed the following normalized hemodynamic indices defined by Xiang et al,² which we refer to as “reduced” because they are vector quantities reduced to magnitudes that are further averaged over both time and space: cycle-averaged mean and maximum WSS, oscillatory shear index (OSI), and low shear area. We also computed the viscous dissipation ratio and kinetic energy ratio as defined by Cebral et al.³ For the indices of Xiang et al, the normalizing WSS was based on integrating the cycle-averaged parent artery WSS starting from an automatically identified “clipping point” proximal to the sac²⁶ and ending 1 diameter upstream. The aneurysm dome over which WSS, OSI, and low shear area were determined was defined as the portion of the aneurysm sac above an automatically defined ostium plane.²⁶ For viscous dissipation ratio and kinetic energy ratio, the extent of the “near-vessel region” was defined as locations below and within 10 mm of the centroid of the aforementioned ostium plane. Agreement between HR- and NR-derived hemodynamic indices was quantified via linear regression.

Results

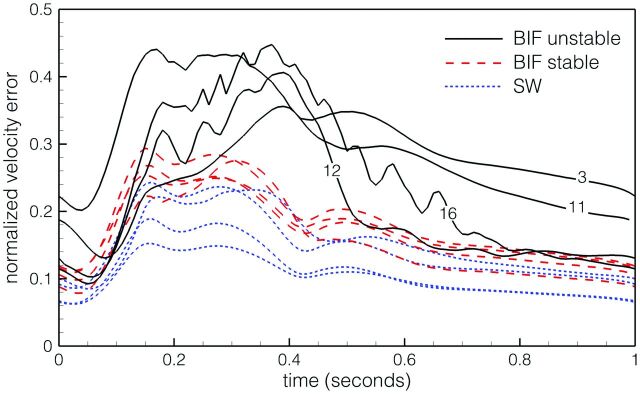
As shown in Fig 1, domain-averaged velocity differences between HR and NR simulations were up to 44%. Point-wise errors, especially within the, sac were higher, often exceeding 100%. All NR simulations showed a smooth and laminar flow, with convergence between the second and third cycle. For the HR simulations, cycle-to-cycle convergence was reached for all except 2 bifurcation cases (numbers 12 and 16). Inspection of selected velocity traces revealed unstable flow, starting just after peak systole, for these 2 cases as well as 2 other bifurcation cases (numbers 3 and 11), broadly consistent with what was previously reported under steady inflow conditions.¹⁸ As demonstrated by Fig 1, the 4 unstable-flow bifurcation cases exhibited the largest differences between NR and HR solutions, followed by the stable-flow bifurcation cases, then the (stable-flow) sidewall cases.

Fig 1.

Instantaneous domain-averaged velocity errors in NR solutions, by using the HR solutions as a reference standard. The 12 cases are divided into sidewall (SW) and bifurcation (BIF) types, the latter subdivided into cases exhibiting stable and unstable flows. Note the identification numbers for the BIF unstable cases.

The large errors in velocity and WSS patterns for NR simulations of the unstable-flow bifurcation cases are evident in Fig 2A. In particular, velocity isosurfaces for the HR simulations were more complicated and showed deeper penetration into the aneurysm sac (cases 11, 12, and 16) or more dynamic flow at the ostium (case 3). Cycle-averaged WSS distributions were surprisingly similar in light of the large-velocity errors; however, OSI was substantially underpredicted by the NR simulations. (As discussed later, this is a consequence of large instantaneous and/or point-wise differences in WSS predicted by HR-versus-NR simulations.) For stable-flow bifurcation cases (Fig 2B), marked differences in NR-versus-HR velocity patterns were evident for all except case 20. Cycle-averaged WSS and OSI patterns were broadly consistent for NR versus HR; however, WSS levels for NR simulations were substantially lower for cases 9 and 18. Differences in velocity and WSS patterns were less evident for the NR-versus-HR sidewall cases (Fig 2C), with the exception of velocity patterns for case 1 and OSI levels for case 5.

Fig 2.

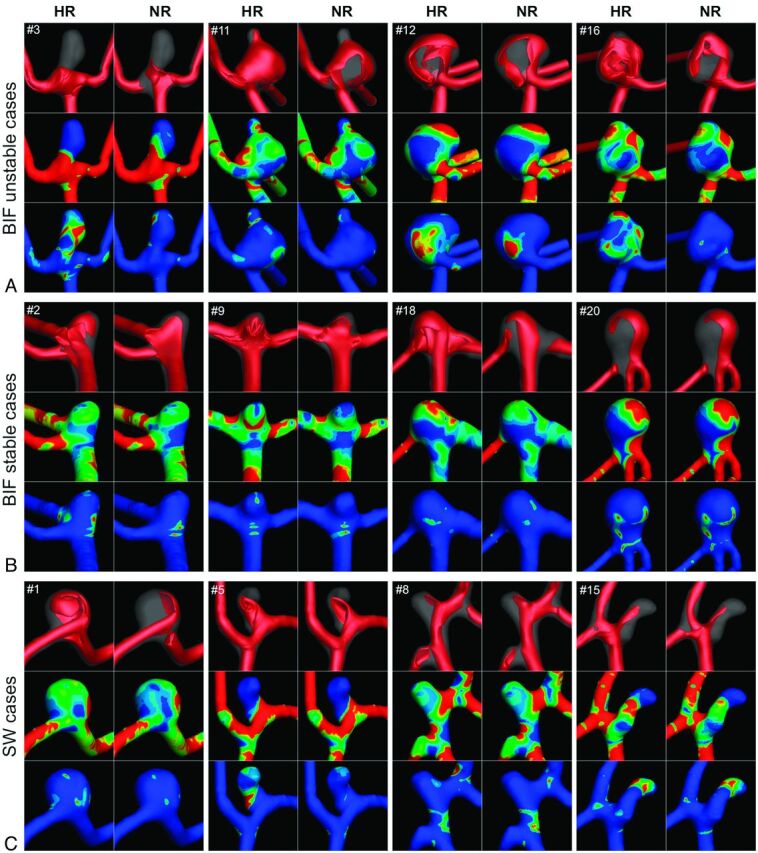
Qualitative differences in HR-versus-NR velocity and WSS fields for bifurcation cases with unstable flows (A), bifurcation cases with stable flows (B), and sidewall cases (C). For each case, the top row compares the isovelocity surfaces at the time of maximum domain-averaged error, the middle row compares the cycle-averaged WSS distributions, and the bottom row compares the OSI distributions.

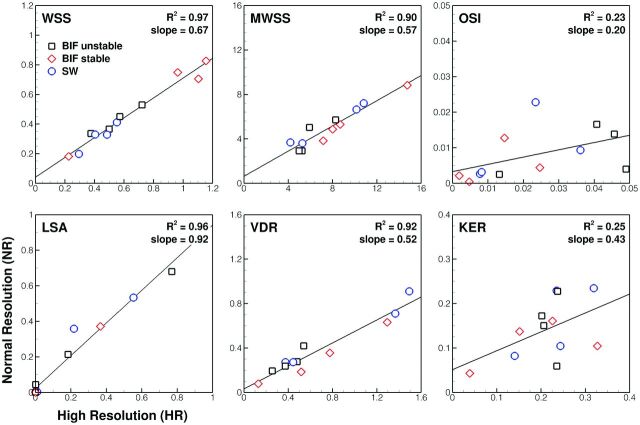
Linear regressions of the reduced hemodynamic indices for NR-versus-HR simulations (Fig 3) showed varying levels of correlation. Whereas WSS, maximum WSS, low shear area, and viscous dissipation ratio were highly correlated and thus could be relied on to stratify cases similarly whether based on NR or HR simulations, OSI and kinetic energy ratio showed weak correlation. When one looks at the slopes of the regression lines, however, it is clear that, with the exception of low shear area, NR simulations substantially underpredicted the value of a given hemodynamic index. This outcome was confirmed by paired t tests, which showed that NR indices were significantly lower than corresponding HR indices (P < .005) for all except the low shear area.

Fig 3.

Comparison of various normalized hemodynamic indices determined from HR-versus-NR solutions. The top left of each plot identifies the index. The top right shows the coefficient of determination (R²) and the slope of the linear regressions as measures of correlation and agreement, respectively. Note that different symbols are used to highlight the 3 different groups of cases, per the legend of the top left plot; KER indicates kinetic energy ratio; LSA, low shear area; VDR, viscous dissipation ratio; MWSS, maximum wall shear stress.

Discussion

We have demonstrated, in a numeric experiment intended to be as simple as possible, that the CFD solution strategy can have a substantial impact on intracranial aneurysm flow patterns and the magnitude of reduced hemodynamic indices. On the basis of Fig 2, we can conclude that NR simulations, representative of many of the strategies reported in the aneurysm CFD literature, can provide only a limited understanding of aneurysm flow, especially for bifurcation aneurysms. Moreover, NR simulations cannot be relied on for predicting the magnitude of hemodynamic forces to which the aneurysm wall is exposed. HR simulations are necessary for detecting flow instabilities, describing proper jet penetration, and calculating absolute values of hemodynamic quantities. Although certain highly reduced indices seem to be relatively robust to the solution strategy, our results suggest that HR strategies may be essential for gaining insights into the mechanobiology of wall remodeling in aneurysms.

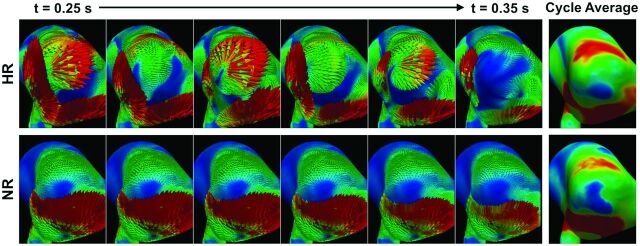
Arguably the most striking finding was the gap between predictions of OSI by NR-versus-HR simulations, whereas there was much better correspondence for WSS. For HR simulations, inspection of Fig 2 reveals that sites of low WSS tended to correlate with sites of high OSI. This finding reflects the fact that particularly for the unstable bifurcation cases, HR simulations revealed instantaneously high shear in these regions with strong oscillations, in both magnitude and direction, over the cardiac cycle, whereas NR simulations predicted persistently low shear and underestimated its temporal and directional variations (ie, OSI). An example of this is shown in Fig 4 and the On-line Video. Thus, in cases in which such dynamic flows are present, NR simulations could lead to a conclusion that low WSS is a stimulus for pathologic wall remodeling leading to rupture, whereas the mechanistic link to rupture status might not necessarily be low WSS, but rather temporally high fluctuating WSS that is low on average. In this context, in the odds ratio equation proposed by Xiang et al,² the OSI term actually contributes very little to the discrimination of rupture compared with the WSS term. In other words, mischaracterization of WSS dynamics might be at the root of ongoing debates about whether low or high WSS is correlated with aneurysm rupture status.⁵ This scenario is particularly true for bifurcation aneurysms, where we have clearly demonstrated a strong impact of solution strategy on the predicted hemodynamics, as opposed to sidewall aneurysms, for which NR simulations were largely adequate. Baharoglu et al²⁷ recently reported a dichotomy between sidewall and bifurcation aneurysms (ie, morphologic discriminants were accurate for sidewall aneurysms, but not for bifurcation aneurysms). This finding suggests that there may be a different mechanistic link to rupture in bifurcation aneurysms.

Fig 4.

Top: HR simulations of bifurcation unstable case 16 demonstrate large variations in WSS vectors during a brief (0.1 second) period of postsystolic flow deceleration. Bottom: Corresponding NR simulations show negligible variations during this same period, despite having comparable cycle-averaged WSS distributions (right column). See the On-line Video for a comparison during the entire cardiac cycle.

Another potentially important gap is the detection of flow instabilities, which are thought to be the ultimate source of aneurysm bruits.^19,28 Our pulsatile HR simulations detected highly unstable flow during and after systolic deceleration for certain of the bifurcation aneurysm cases, namely those for which flow instabilities were previously reported under stationary inflow conditions¹⁸; however, no such features were evident from the NR simulations. Indeed, there is now independent evidence for such flow instabilities based on high-resolution particle image velocimetry of realistic flow in a compliant model of a patient-specific aneurysm, which revealed transitional flow phenomena during the deceleration phase,²⁹ consistent with data presented in the current study. Hence, as has previously been argued on the basis of HR CFD findings^17,18 and as the authors of the particle image velocimetry study also emphasized,²⁹ though there is a widely held conception that aneurysm flow is laminar (ie, stable, or with periodic instabilities and/or vortex shedding; as opposed to turbulent flows or laminar/transitional flows, with high-frequency, non-periodic instabilities having small spatial and temporal scales), evidence suggests that this a priori assumption, which is often used implicitly or explicitly to rationalize NR solution strategies, must be reconsidered.

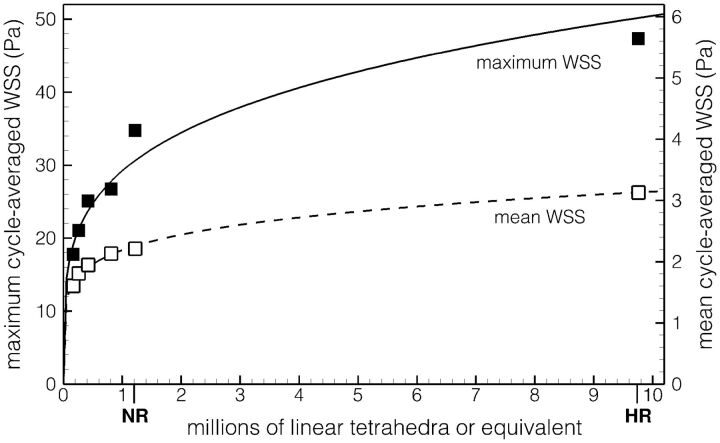
Irrespective of the nature of aneurysm flow, Fig 3 highlights another gap between NR and HR simulations, namely a consistent underestimation of all of the reduced hemodynamic indices that were assessed, with the exception of low shear area. When one considers absolute values (ie, not normalized by the parent artery WSS) of cycle-averaged WSS and maximum WSS, for example, HR predictions were, on average, 30% higher for WSS (3.96 ± 2.00 Pa versus 3.03 ± 1.41 Pa) and 60% higher for maximum WSS (49.2 ± 14.6 Pa versus 30.7 ± 10.6 Pa). In other words, point-wise WSS magnitudes are more challenging to properly resolve than dome-integrated values; and high WSS may be disproportionately underestimated by NR strategies compared with low WSS values. To illustrate this further, in Fig 5 we plot mean and maximum WSS for sidewall case 15 from our HR and NR solutions; but also from additional NR simulations, which we performed using coarser meshes ranging from 810,000 down to 170,000 elements. It can be seen that convergence, particularly for maximum WSS, is difficult to justify for meshes even around 1 million elements.

Fig 5.

Impact of mesh resolution on the sac maximum and mean cycle-averaged WSS for case 15. Symbols identify data from individual simulations; the lines show power-law fits through the respective data. Note the identification of the NR and HR resolutions on the x-axis.

The above example highlights the importance of performing proper convergence studies to prove that a numeric solution is independent of the chosen parameters, such as mesh size and time-step. When dealing with nonlinear equations such as those that govern fluid flow, convergence studies become even more important because a linear convergence cannot be expected (eg, it was previously demonstrated for stationary flow of a normal left anterior descending artery that a uniform mesh refinement strategy did not show a consistent decrease in WSS errors and that an extreme mesh convergence strategy was necessary to obtain convergence³⁰). Although most published CFD studies of aneurysms claim spatial and temporal convergence, neither the criteria nor results are normally presented. Even in the CFD studies in which refinement studies are mentioned, the general approach is to increase the number of elements by 50% and evaluate the change in some reduced hemodynamic index, typically with a tolerance of a few percent. However, in 3D, a 50% increase in elements is roughly equivalent to only a 14% decrease in cell side length (ie, 1.50^(1/3) = 1.14) along a given direction and should be considered just the first step of a refinement study.

These “routine” convergence studies appear to fall significantly short of what is needed, as may be deduced from the aneurysm CFD convergence study reported by Hodis et al,⁸ in which it was concluded that “the grid convergence errors showed oscillatory behavior; therefore, each patient-specific model required its own grid convergence study to establish the accuracy of the analysis.” The impact on hemodynamic indices was not addressed in that study, and for our HR simulations, the average element side length in the aneurysm sac was 0.06 mm, well below the 0.08 mm reported for the converged solutions of Hodis et al.⁸

The pronounced impact of the CFD solution strategy on the magnitude of derived hemodynamic indices implies that the solution strategy must be acknowledged as an additional source of variability, especially if and when the findings of different groups, potentially using a wide range of strategies, are compared or analyzed together. In striving for more patient-specific simulations, most studies have focused on the impact of other assumptions or uncertainties such as inflow/outflow conditions,³¹ non-Newtonian rheology,³² compliance,³³ and choice of imaging technique.^34,35 Although it is difficult to draw a direct comparison between their findings and the results of the present study, inspection of figures from those studies suggests that the qualitative differences due to those assumptions are less than the differences due to choice of CFD solution strategy as demonstrated in our study. By evaluating point-wise differences, we found changes on the order of hundreds of percent (in both space and time) in some cases, suggesting that adequate CFD resolution is a central issue that cannot be ignored if patient-specific simulations are desired. It is also possible that those other sources of variability need to be revisited in light of the more complex and dynamic flows evident from HR simulations versus the NR strategies used previously to infer their influence.

The present results are also interesting in the light of the previously expressed frustration of Kallmes⁵ over the many hemodynamic parameters and indices clinicians have to understand and relate to. We found it difficult to find a consistent definition for what constituted the aneurysm dome over which WSS quantities were integrated or the parent artery region used to determine the normalizing WSS. Moreover, we found that the reduced hemodynamic indices were often imprecisely or variously defined (eg, maximum WSS and low shear area,^2,3), suggesting a further source of variability that must be resolved by a standardization of definitions and parameters before meta-analyses or multicenter studies can be considered.

A limitation of our study is that the change in solution strategy involved 2 aspects: resolution and stabilization. The latter was unavoidable because coarsening the resolution causes the numeric stability criteria to no longer be met by a minimally dissipative solver such as the one we used for the HR simulations. For the NR simulations we did, however, choose a widely used stabilized solution strategy that is the default in several commercial CFD solvers used in the aneurysm CFD literature. To minimize the likelihood of overestimating the impact of solution strategy, we consciously chose the highest of the mesh and, separately, temporal resolutions reported by the 3 largest clinical studies to date^2–4; a cursory inspection of other aneurysm CFD studies recently published in the clinical literature^34–39 suggests that the resolutions of our NR simulations are, if anything, on the high side. Nevertheless, as noted by a recent aneurysm CFD Challenge,²⁰ it is difficult to compare node spacing, element types, and sizes from one study to another; there are simply not enough details provided about the solver parameters and cell distributions to exactly reproduce what other groups are using. Nevertheless, our NR simulations are likely finer than those of most of the above-mentioned studies, particularly because we concentrated our elements in the vicinity of the aneurysm rather than assuming a uniform mesh density throughout the domain. Our demonstrated impact of solution strategy can also be considered conservative because of our choice of flow rates. For example, a recently published CFD study of MCA aneurysms³⁷ reported using a mean inlet Reynolds number of 500 (versus our Reynolds number of 260) and a common carotid artery flow waveform (versus our deliberate choice of a damped waveform more representative of the reduced pulsatility at the MCA).

Like most image-based CFD studies of intracranial aneurysms, we cannot exclude the possibility that the ostium area might have been overestimated⁴⁰ because we did not have 2D DSA to compare against. As a result, assuming the same boundary conditions, the effect of the solution strategy may have been overestimated in sidewall aneurysms but underestimated in bifurcation aneurysms. We made the standard assumption of rigid walls and Newtonian fluid, and we did not have the patient-specific waveforms and flow rates. Our sample size was small and limited to 1 vascular territory (MCA). Furthermore, we do not claim that the HR simulations are fully resolved, but we are confident that they capture the correct flow states and eddies with the most energy. The smallest scales of the flow are therefore not resolved, but on the other hand, the continuum hypothesis breaks down at some point, and how to deal with this is an open question.⁴¹

Conclusions

The CFD solution strategy has a pronounced effect on the prediction of intracranial aneurysm hemodynamics, likely more so than other modeling assumptions or uncertainties. Retrospective discrimination of rupture status based on certain highly reduced hemodynamic indices may therefore be considered relatively immune to solution strategy, but only if the same strategy is used for all cases. On the other hand, NR simulations might well mask clinically relevant correlations for indices that do require HR strategies, such as OSI. Moreover, regions of dynamic WSS are more likely to be mistaken for regions of persistently low WSS by NR strategies. In short, clinically expedient CFD solution strategies might prove useful when and if they are eventually incorporated into clinical rupture-risk assessment, but HR strategies are required to elucidate the underlying mechanisms of aneurysmal wall remodeling and rupture.

ABBREVIATIONS:

CFD

computational fluid dynamics

HR

high-resolution

NR

normal-resolution

OSI

oscillatory shear index

WSS

wall shear stress