Effect of Bifurcation Angle Configuration and Ratio of Daughter Diameters on Hemodynamics of Bifurcation Aneurysms

Abstract

BACKGROUND AND PURPOSE:

EL associated with ruptured aneurysms is higher than that for unruptured aneurysms. In this study, the effect of arterial morphologic variation of bifurcation aneurysms on EL was investigated in idealized models of middle cerebral artery aneurysms.

MATERIALS AND METHODS:

Bifurcation angle configuration and DA ratio were evaluated in 6 idealized numeric models. Type A and B bifurcation models were defined with symmetric and asymmetric bifurcation angles of 136°, and 57° and 79°, respectively. Three models with DA ratios of 1, 1.3, and 2 were constructed for each type. EL was calculated as the energy difference between aneurysm inflow and outflow at the aneurysm neck. Three growth paths (R1, R2, and R3) were proposed.

RESULTS:

The highest EL and influx occurred in bifurcations with DA ratios of 1 for both types A and B. As the DA ratio increases, flow distribution between branches becomes more asymmetric, resulting in a reduction of EL and intra-aneurysmal flow. No strong relation was found between bifurcation angle configuration, inflow flux, and EL. EL decreased with an increase in the AR and DA ratio and increased with an increase in the AR and reduction of DA ratio.

CONCLUSIONS:

EL determined in idealized models is less dependent on bifurcation angle configuration than on DA ratio, and the stability of the aneurysm strongly depends on variation of the daughter artery morphology after aneurysm growth.

Hemodynamics is recognized as having an important role in cerebral aneurysm formation, development, and rupture. Computational hemodynamic technologies have been used extensively to explain these mechanisms by using vascular structures from patient-specific 3D angiography.^1–4 To date on the basis of current hemodynamic parameters, no method has been found to be effective at predicting the risk of aneurysm growth and rupture. Thus, investigating additional parameters would be necessary.

Various types of aneurysm morphology simulations have been used for assessing the role of morphology in predicting the risk of rupture.^5,6 By improving the generation of idealized bifurcation models,⁷ classifying the saccular intracranial aneurysm,⁸ and conducting in vitro analysis of bifurcation aneurysms, simulation methods become more effective.^9,10 However, a study on the effect of hemodynamic parameters such as WSS in 20 MCA aneurysms has suggested the pathogenic effect of high WSS in the initiation of aneurysms and of low WSS in the growth and rupture of cerebral aneurysms.¹¹ Any changes in intra-aneurysmal flow due to the appearance of a vortex and stagnation affect the EL of the entire system. Thus, calculating EL at the neck on the basis of the difference between energy transport to the aneurysm by inflow and energy loss by the outflow can provide information about the system and represents the power of collision applied by hemodynamic forces. Because this concept has already been used by cardiovascular surgeons to evaluate the outcome of surgery, it was assumed that EL can be used to explain the growth of aneurysms. A further study concentrating on EL of 4 ruptured and 26 unruptured ICA–posterior communicating artery aneurysms found that the EL of ruptured cases was 5 times higher than that of unruptured cases.¹²

Moreover, a study of 210 cerebral aneurysms showed the presence of a higher kinetic energy ratio in ruptured aneurysms compared with unruptured ones.¹³ A study of 26 aneurysms also indicated that a larger region of low WSS was associated with ruptured aneurysms.¹⁴

Because morphologic analysis and hemodynamic parameters alone could not adequately explain why aneurysms develop or rupture at the apex of bifurcations, novel approaches were used to investigate the role of both morphology and hemodynamic parameters on aneurysm rupture.¹⁵ A previous study of 44 unruptured aneurysms selected from 1612 patients showed that aneurysms located at bifurcations, especially the anterior communicating artery and the middle cerebral artery, bleed easily compared with those located at the branching and bending points.¹⁶ Therefore, due to the high sensitivity of bifurcation aneurysms to variations of flow pattern and morphology, the hemodynamic parameter EL was used to evaluate the growth and rupture of this type of aneurysm. The aim of this study was to elucidate the relationship between the morphologic parameters of bifurcation aneurysms, including the bifurcation angle configuration; DA ratio; and hemodynamic parameters of EL and abnormal low WSS. Because of the high risk of rupture, not enough information is available for the study of long-term follow-up of cerebral aneurysm morphologies. In a study of 22 MCA aneurysms, 7 cases were found to be located at the midline (4 ruptured and 3 unruptured).¹⁷ Among those aneurysms, only 1 ruptured aneurysm had symmetric bifurcation angles. Therefore, the present study addresses the effect of bifurcation configuration on EL and low WSS associated with rupture. In addition, 3 possible growth paths based on 3 discrete combinations of aspect ratios and DA ratios were investigated to elucidate the relation between aneurysm evolution and daughter artery morphology.

Materials and Methods

Idealized Bifurcation Aneurysm Model

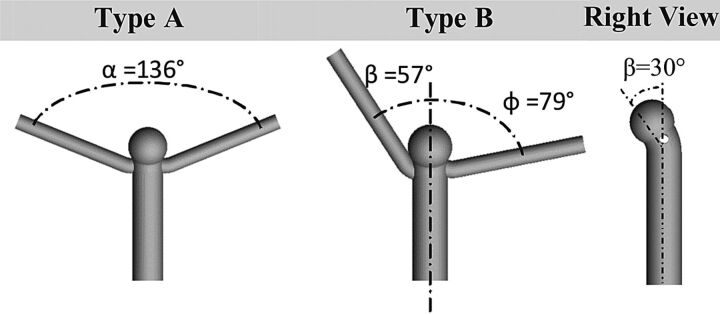
Symmetric and asymmetric numeric phantoms of bifurcation aneurysms were created to evaluate the effect of bifurcation configuration on hemodynamic parameters. Values of bifurcation angles for idealized models were determined from an MCA bifurcation ruptured aneurysm of a male patient, 51 years of age. The bifurcation angles of this patient located at the midline of the parent artery were measured as 57° and 79°.¹⁷ In the present study, we considered 2 types of bifurcation models: a symmetric bifurcation angle of 136° (type A) and a bifurcation angle set asymmetrically at 57° and 79° in reference to the midline (type B, Fig 1). Parent artery and branch geometries were selected as described in the clinical literature with a proximal inlet diameter of 4.0 mm and both distal outlet diameters of 2.0 mm.¹⁸ The size of the bifurcation aneurysm was reported as 4.3 mm.¹⁷ Although the size of this aneurysm was not considered in the large aneurysm category with higher risk of rupture,¹⁹ it was reported as ruptured. Hence, a spheric aneurysm shape with a size of 4.2 mm and a neck width of 4 mm was set for both models. Previous studies have shown that the flow pattern in bifurcation aneurysms, in which the aneurysms have zero degree relative to the parent artery with equal flow-division outlets, was highly unstable¹⁰ and very sensitive to the type of blood flow model (Newtonian versus non-Newtonian).²⁰ In addition, measurement of the aneurysm angle relative to the parent artery in our patient-specific clinical data base for the MCA showed that this angle varied between 30° and 60°. Hence, the angle of the aneurysm dome relative to the parent artery was considered 30° in this study (Fig 1). The DA ratio was defined as the ratio of the diameter of the larger branch to the diameter of the smaller branch. Models A-I, A-II, and A-III with symmetric angles of 136° were constructed with DA ratios of 1, 1.3, and 2, respectively. Models B-I, B-II, and B-III with asymmetric angles of 57° and 79° were also created with the same DA ratios.

Fig 1.

Idealized bifurcation aneurysm models at DA ratio = 1. Types A and B represent symmetric and asymmetric bifurcation angles of α = 136°, β = 57°, ϕ = 79° respectively. The right side view shows 30° between the aneurysm and parent artery.

A straight entry tube of 20 times the parent artery diameter was attached to the inlet to remove inlet effects on the computed flow field and to ensure a fully developed boundary layer at the region of entry.²¹ The outlet boundary was located 50 times the branch artery diameter from the bifurcation to eliminate the effect of boundary condition locations on the flow inside the artery.²² Aneurysm growth was simulated by constructing 3 spheric-shaped aneurysms of 4.2, 6.3, and 8.2 mm. The neck width was 4 mm for all models. Hence, the AR (aneurysm size/neck width) of the aneurysm was 1.1, 1.6 and 2.1, respectively. Three possible growth paths were investigated as described in Table 1.

Table 1:

Configuration of 3 proposed growth paths of R1, R2, and R3 in bifurcation aneurysms^a

	AR = 1.1	AR = 1.6	AR = 2.1
R1	DA ratio = 1	DA ratio = 1.3	DA ratio = 2
R2	DA ratio = 2	DA ratio = 1.3	DA ratio = 1
R3	DA ratio = 1	DA ratio = 1	DA ratio = 1

^aFlow rate was considered constant during the growth paths.

Blood Flow Modeling and Boundary Conditions

The major purpose of this study is to estimate the difference between various bifurcation angle configurations and aneurysm sizes. Our previous study indicated that there is no significant difference between the average volume of pulsatile flow and steady flow.¹² Thus in this study, calculations were performed with a steady flow rate (218 mL/min) at the parent artery inlet for idealized models by using the peak flow rate in the MCA.²³ To characterize the flow regimen in the parent artery and branches, we calculated the Reynolds number, indicating the occurrence of laminar blood flow in all models (at the inlet and outlet, the Reynolds number based on maximum velocity was 340 and 360, respectively). Secondary flow at the inlet zone would undoubtedly influence the intra-aneurysm hemodynamics. However, at similar levels of Reynolds number, the effect of secondary flow on results is relatively negligible. In this study, an incompressible steady-state laminar flow model was considered for the simulation. In large arteries (diameter > 0.5 mm), the non-Newtonian behavior of the blood flow is negligible, so blood was assumed to be a Newtonian fluid²⁴ with blood flow density and dynamic viscosity of 1050 kg/m³ and 0.0035 Pa·s, respectively.⁷ By adopting the conventional assumption of lack of resistance in the cerebral circulation, we set the outlet boundary conditions to zero pressure.²⁵ Along the artery and aneurysm wall, a no-slip flow boundary condition was imposed at the inner lumen of the vessel, and arteries were assumed to be rigid.

Computational Tools

ICEM 13.0 (ANSYS, Lebanon, New Hampshire) was used for grid generation. The models were constructed with unstructured tetrahedral and prismatic mesh. The grid independency test showed that when the grid number was increased to 1.5 × 10⁶, the EL at the aneurysm neck converged to a constant value. To increase the accuracy of WSS calculation near wall regions, we generated 5 prismatic layers with an average nodal space increasing by a ratio of 1.2 where the distance of the first layer to the vessel was fixed at 0.01 mm. The CFD simulations were performed by using commercial finite-volume software (CFX.13.0; ANSYS) to analyze the flow model.

Energy Loss Calculation

Energy loss due to the presence of the aneurysm at the apex of the bifurcation can be calculated as follows:

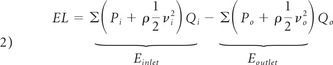where P and v are the static pressure and velocity, respectively; i indicates the inflow to the aneurysm through aneurysm neck; and o, the outflow of the aneurysm through the aneurysm neck. E_inlet and E_outlet are the spatially averaged energy values over the cross-section of the neck. Dependency of the energy loss on the pressure and velocity of the blood flow entering the aneurysm as shown in equation 2 indicates that this parameter is strongly dependent on geometry.

WSS varies in the aneurysm and arteries due to differences in size. Therefore, the mean WSS of the parent artery was assumed as a reference value to compare with the WSS of the aneurysm. The abnormally low WSS region (A_l) was calculated as an area of the aneurysm with a WSS smaller than 10% of the reference value.¹⁴ LSA quantifies the region of the aneurysm that is exposed to the abnormally low WSS and can be defined as a percentage of the area ratio¹³:

where A_a is the aneurysm sac area.

Results

Effect of Bifurcation Angle and DA Ratio on Flow Pattern

Figure 2 shows the velocity profiles at the aneurysm neck of type A and B models, in which the main flow from the parent artery divides into 3 sections. Two portions of the blood flow enter directly into the branches. The third goes to the aneurysm from the anterior side of the neck and exits from the posterior side to the branches for both models. Red represents the inflow velocity; yellow in A-I, A-II, B-I, and B-II; and green in A-III and B-III represent the outflow regions. The outflow regions were 43% larger than the inflow regions for all models (8.1 versus 5.6 mm²) except for A-III and B-III, which increased to 48%. Calculation of the influx magnitude into the aneurysm indicated that the intra-aneurysmal flow does not depend on bifurcation angle configuration. However, increasing the DA ratio from 1 to 2 for both types A and B changed the blood flow distribution between branches as shown in Table 2. The results show that with the larger DA ratio, the difference is greater between flow rates of branches. Therefore, the influx magnitude into the aneurysm reduced 31% from A-I and B-I to A-III and B-III, respectively.

Fig 2.

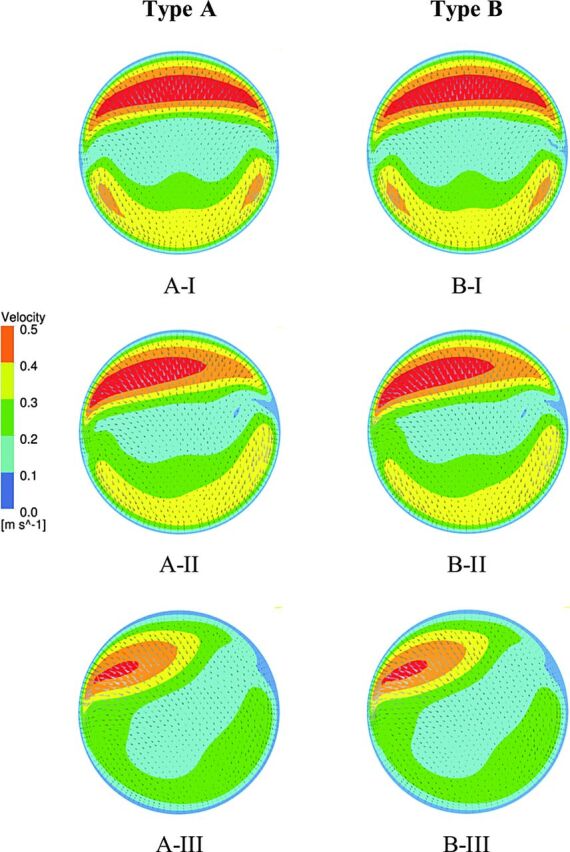
Velocity profile at the aneurysm neck for type A and B models. Increasing the DA ratio causes the flow distribution to become asymmetric, and less flow enters the aneurysm, as shown in A-III and B-III.

Table 2:

Comparison of flow distribution between branches at different DA ratios^a

	DA = 1		DA = 1.3		DA = 2
	Larger Branch (%)	Smaller Branch (%)	Larger Branch (%)	Smaller Branch (%)	Larger Branch (%)	Smaller Branch (%)
Type A	50	50	72	28	91	9
Type B	50	50	72	28	91	9

^aThe results show that the larger the DA ratio is, the more difference there is between flow rates at branches.

Effect of Bifurcation Angle and DA Ratio on EL and WSS

Energy loss at the aneurysm neck due to circulation of the blood inside the aneurysm was calculated for types A and B. As shown in Fig 3A, similar to flow patterns, a strong association is not found between the configuration of the bifurcation angle (symmetric and asymmetric) and the EL, though the EL difference increases to 4.3% for larger DA ratios. However, asymmetric flow distribution between branches leads to a larger portion of the main flow to the larger branches. Due to reduction of inflow to the aneurysm, the EL decreased by 38% from A-I to A-III and by 34.5% from B-I to B-III (Fig 3B).

Fig 3.

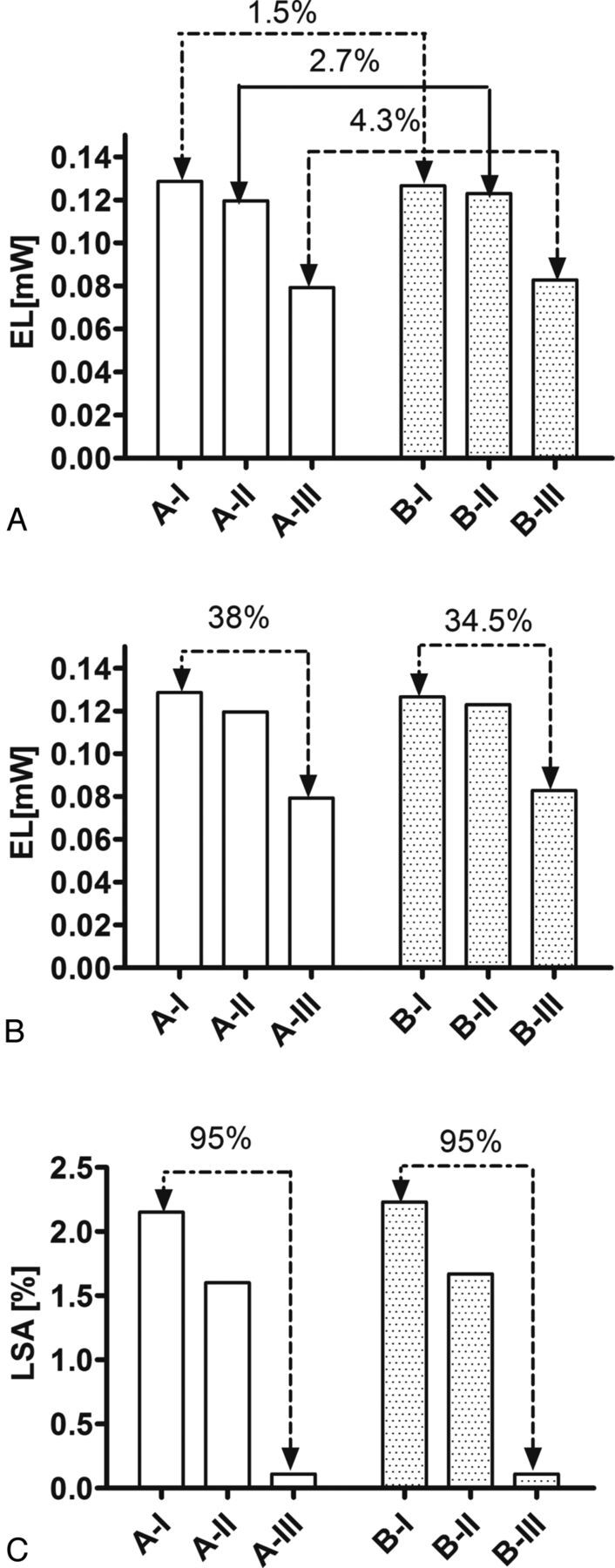
Comparison of EL calculated at the aneurysm neck of type A and B models based on bifurcation angle configuration (A) and different DA ratios (B). C, LSA calculation in both type A and B models at different DA ratios.

LSA was calculated for all scenarios. The results demonstrated that for EL, there is only a 3.7% difference between the LSA of types A and B (2.15% for A-I and 2.23% for Type B-I). However, a 95% difference in LSA was found as the DA ratio increased from 1 to 2 for both types of A and B models (Fig 3C).

Effect of Aneurysm Growth on Daughter Artery Bifurcation

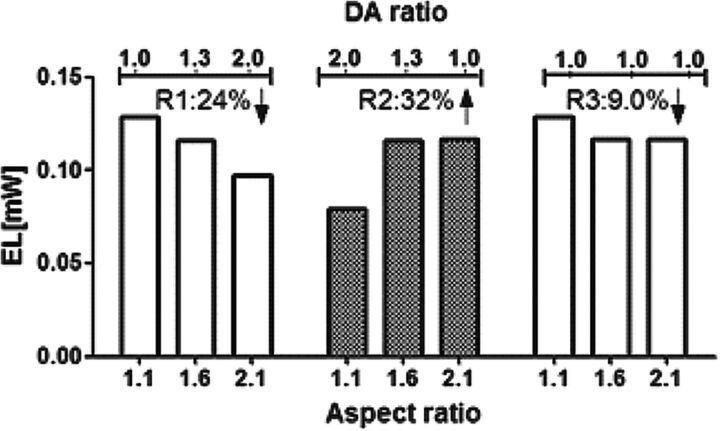
The potential of numeric simulation in creating an idealized model based on patient-specific images is being increasingly recognized.²⁶ In the present study, we propose 3 possible growth paths: growth path R1, growth path R2, and growth path R3. The EL of bifurcation aneurysms was calculated for growth paths R1, R2, and R3 as shown in Fig 4. The results indicated that if the aneurysm grows according to growth path R1, there is a reduction of 24% in EL from AR = 1.1 and DA ratio = 1 to AR = 2.1 and DA ratio = 2. In contrast, development of the aneurysm based on growth path R2 showed a 32% increase of EL from AR = 1.1 and DA ratio = 2 to AR = 1.6 and DA ratio = 1. Furthermore, growth path R3 showed only a reduction of 9.0% from AR = 1.1 to AR = 2.1 if there is no change in the morphology of the daughter arteries due to development of the aneurysm (DA ratio of 1 for all ARs).

Fig 4.

EL calculated for the proposed 3 growth paths of bifurcation aneurysms. In growth path R1, there is 24% reduction in EL by increasing the AR and DA ratio. In growth path R2, a 32% increase can be seen in EL as the AR increases and the DA ratio decreases. Growth path R3 shows that if the DA ratio does not change during the aneurysm evolution, the EL decreases by 9.0% from AR = 1.1 to AR = 2.1.

A decrease of EL in growth paths R1 and R3 suggests that if the growth of the aneurysm is associated with an increase or constant DA ratio, the aneurysm may remain stable. However, if the growth of the aneurysm follows growth path R2 with an increase of EL as the DA ratio decreases, the intra-aneurysmal flow becomes unstable and the aneurysm may be at high risk. This result is in agreement with our clinical observations from follow-up of MCA aneurysms on 3 sequential CT scans, demonstrating a variation of the DA ratio from 2.5 to 1.8 as the aneurysm grows.

Discussion

The flow pattern and energy loss of a bifurcation aneurysm at 2 types of bifurcation angle and a variety of DA ratios are presented in the current study. The results show that the DA ratio significantly affected the flow pattern and EL at the aneurysm neck for both types of bifurcation angle configurations. However, no strong correlation was found between this angle configuration and EL.

Our results are in agreement with the findings of Sadatomo et al,²⁷ who measured the AR and DA ratio of 20 unruptured and 24 ruptured MCA aneurysms. Morphologic measurements identified a higher AR and a lower DA ratio among the ruptured compared with the unruptured groups (AR: 2.24 ± 0.75 for ruptured and 1.56 ± 0.8 for unruptured; DA: 1.53 ± 0.54 for ruptured and 2.14 ± 0.8 for unruptured). They concluded that even branch diameter and aneurysm neck located at the center of the bifurcation might be related to aneurysm rupture. The present results confirmed that the highest rate of inflow and EL occurs at a DA ratio of 1, when the diameters of both branches are similar and symmetric flow distribution is observed between these branches (model A-I: 0.128 mW and B-I: 0.126 mW). A similar pattern was found at a DA ratio of 1.3, with a 6.9% difference between the EL of A-I and A-II and 2.9% between B-I and B-II. The significance of the DA ratio decreases when the bifurcation angle is asymmetric. However, at a DA ratio of 2, the flow distribution between branches changes to 90:10, which affects the influx inside the aneurysm and EL, accordingly. The reduction of the EL for a DA ratio of 2 suggested that with the more even branch diameter with a lower DA ratio, the risk of rupture was higher.

The effect of the morphology of the aneurysm and parent and daughter arteries on aneurysm growth is generally poorly understood due to lack of access to follow-up patient-specific models. Previous studies have investigated the effect of scaling the parent artery²⁸ or removing the bleb from the aneurysm²⁹ on the growth pattern. In the present study, we found that as the bifurcation aneurysm grows, any change in morphology of the daughter artery affects intra-aneurysmal flow and EL. Considering 3 possible growth paths (R1, R2, and R3) suggested that measurement of daughter artery diameter during the follow-up of the aneurysm can provide useful information about the stability of the aneurysm. Further investigations in patient-specific follow-up models are needed to confirm these observations.

A previous study of 26 intracranial aneurysms reported that the characteristics of WSS distribution are more dependent on the morphology of the aneurysm than on the flow rate and waveforms.¹⁴ Thus, measuring LSA in a consistent way at a single time point will not affect the results of the current study. A study of 119 aneurysms (38 ruptured and 81 unruptured) showed that ruptured aneurysms had larger LSAs and lower WSS magnitudes than those in the unruptured group.¹⁵ Our results have shown that even daughter artery diameters are associated with larger EL and LSA. Although EL is a global parameter that can evaluate the loss of energy in the system due to the appearance of a vortex, stagnation and intra-aneurysmal variations and LSA only represent areas locally affected by stagnation flow. No strong association was found between bifurcation angle configuration and both hemodynamic parameters of EL and LSA.

Because there is no agreement regarding the relation between available hemodynamic parameters such as WSS and the growth or rupture of aneurysms, in this study, EL was introduced as a possible new parameter that may improve the current knowledge of the risk of rupture. Once the sensitivity of EL to morphologic variations becomes clear, the next step will be categorizing the patient-specific models to evaluate the current results.

Conclusions

Morphologic study of bifurcation aneurysms with different bifurcation angle configurations and DA ratios has shown that the EL of the aneurysm is mostly dependent on the DA ratio, whereas the flow distribution between daughter arteries is affected by the branch diameter. The highest EL for bifurcation aneurysms was calculated for the symmetric branch diameter with even flow distribution. The results of this study indicate that measurement of the daughter artery diameter of bifurcation aneurysms by CT or MR imaging can provide valuable information about the intra-aneurysmal flow pattern, flow distribution, and EL, all of which may be useful in the prediction of the risk of aneurysm rupture. Simulation of 3 proposed growth paths for bifurcation aneurysm evolution demonstrated that the stability of the aneurysm strongly depends on variation of the daughter artery morphology after aneurysm growth. Further investigation is necessary to evaluate this result in larger clinical databases.

ABBREVIATIONS:

AR

aspect ratio

DA

daughter artery diameter

EL

energy loss

LSA

low shear stress area

R1

increasing the AR and DA ratio

R2

increasing the AR and reducing the DA ratio

R3

increasing the AR with a constant DA ratio

WSS

wall shear stress