Automatic Quantification of Subarachnoid Hemorrhage on Noncontrast CT

Abstract

BACKGROUND AND PURPOSE:

Quantification of blood after SAH on initial NCCT is an important radiologic measure to predict patient outcome and guide treatment decisions. In current scales, hemorrhage volume and density are not accounted for. The purpose of this study was to develop and validate a fully automatic method for SAH volume and density quantification.

MATERIALS AND METHODS:

The automatic method is based on a relative density increase due to the presence of blood from different brain structures in NCCT. The method incorporates density variation due to partial volume effect, beam-hardening, and patient-specific characteristics. For validation, automatic volume and density measurements were compared with manual delineation on NCCT images of 30 patients by 2 radiologists. The agreement with the manual reference was compared with interobserver agreement by using the intraclass correlation coefficient and Bland-Altman analysis for volume and density.

RESULTS:

The automatic measurement successfully segmented the hemorrhage of all 30 patients and showed high correlation with the manual reference standard for hemorrhage volume (intraclass correlation coefficient = 0.98 [95% CI, 0.96–0.99]) and hemorrhage density (intraclass correlation coefficient = 0.80 [95% CI, 0.62–0.90]) compared with intraclass correlation coefficient = 0.97 (95% CI, 0.77–0.99) and 0.98 (95% CI, 0.89–0.99) for manual interobserver agreement. Mean SAH volume and density were, respectively, 39.3 ± 31.5 mL and 62.2 ± 5.9 Hounsfield units for automatic measurement versus 39.7 ± 32.8 mL and 61.4 ± 7.3 Hounsfield units for manual measurement. The accuracy of the automatic method was excellent, with limits of agreement of −12.9–12.1 mL and −7.6–9.2 Hounsfield units.

CONCLUSIONS:

The automatic volume and density quantification is very accurate compared with manual assessment. As such, it has the potential to provide important determinants in clinical practice and research.

Despite improvements, the treatment of SAH is associated with high fatality rates and affects fairly young adults: up to half of all cases of SAH are fatal within 30 days, and the mean age of presentation is 55 years.^1–5 There is strong agreement among studies that the amount of subarachnoid blood on initial NCCT has a highly predictive value regarding patient outcome and the incidence of vasospasm and concomitant delayed cerebral ischemia.^3,4,6–9 Hemorrhagic density may be of equal importance in predicting patient outcome, but this has not been validated properly.^3,10–12 Currently several grading systems are used to assess the initial clinical and radiologic features of SAH.^7,8,13–15 However, there is still an ongoing discussion about the optimal method of grading SAH on NCCT.^3,7,16–18 The 2 most commonly used scales of Fisher et al⁷ and Hijdra et al⁸ have come under criticism; authors referred to these scales as rather gross estimators, difficult to apply, lacking quantification, and cumbersome in the clinical setting.^3,17,19–22 Moreover, hemorrhage density is not considered in these scales. A quantitative volume and density measurement may reduce interobserver variability in comparison with current scales and would provide physicians with a potentially valuable tool for outcome prediction and treatment guidance.²³ As such, the aim of this study was to design and validate a reliable and easy-to-apply automatic measurement for subarachnoid hemorrhage quantification.

Materials and Methods

Patient Selection

This study is a substudy of a larger project evaluating the outcome of patients with ruptured middle cerebral artery aneurysms. NCCT image data of 50 consecutive patients with ruptured MCA aneurysms who were admitted to the Academic Medical Center hospital from January 2003 to March 2011 were retrospectively enrolled in this study. A subset of 20 consecutive patients was selected to form a training set for optimization of our method. The remaining 30 patients were used for validation. The inclusion criteria were the following: clinical diagnosis of SAH, available NCCT obtained within 72 hours after initial hemorrhage, and 18 years of age or older. Patients with previous aneurysm treatment by clipping or coiling, craniectomy, or craniotomy were excluded. A summary of the patient clinical and radiographic information is presented in Table 1. Informed consent was waived by the medical ethics committee.

Table 1:

Clinical and radiographic characteristics of the study population

Characteristics	Test Set (No.) (%)	Training Set (No.) (%)
Sex
Male	12 (40)	5 (75)
Female	18 (60)	15 (25)
Age (yr)
45 or younger	7 (23)	5 (25)
46–60	16 (53)	11 (55)
Older than 60	7 (23)	4 (20)
IVH
Yes	16 (53)	4 (20)
No	14 (47)	16 (80)
ICH
Yes	19 (63)	12 (60)
No	11 (37)	8 (40)
MCA location
Left	14 (47)	18 (10)
Right	16 (53)	2 (90)
WFNS at admission
Grade I	11 (37)	9 (45)
Grade II	2 (7)	2 (10)
Grade III	2 (7)	4 (20)
Grade IV	8 (27)	3 (15)
Grade V	7 (23)	2 (10)
History of hypertension
Yes	3 (10)	7 (35)
No	22 (73)	13 (65)
Aneurysm size
≤5 mm	9 (30)	6 (30)
6–10 mm	14 (47)	12 (60)
11–15 mm	3 (10)	2 (10)
>15 mm	3 (10)	–
Signs of DCI
No	21 (70)	19 (95)
Yes	9 (30)	1 (5)
Paresis	1 (3)	1 (5)
Decreased consciousness	4 (13)	–
Hemiparesis and aphasia	3 (10)	–
Vasospasm	1 (3)	–

Note:—IVH indicates intraventricular hemorrhage; ICH, intracerebral hemorrhage; DCI, delayed cerebral ischemia; WFNS, World Federation of Neurosurgical Societies.

Imaging Protocol

Whole-brain NCCT was performed on a Sensation 64 scanner (Siemens, Erlangen, Germany) and a Sensation 4 scanner (Siemens) with the following parameters: 120 kV, 380 mAs, reconstruction kernel = H40s, and 5-mm section thickness, resulting in volumes with 23–34 sections. The image data were anonymized.

Overview

Our proposed method for detection and quantification of blood after SAH is based on a relative density increase in NCCT images due to the presence of blood. The process started with an atlas-based segmentation to classify different brain structures, followed by a compensation for partial volume effect in the vicinity of the skull. Hereafter, evaluation of density was assessed to set a tissue-specific threshold for density-based segmentation of blood. A region-growing algorithm included subtle attenuated parts of the hemorrhagic areas.

Atlas-Based Segmentation

Atlas-based segmentation requires a reference image with a corresponding atlas, which classifies structures in this image. An experienced neuroradiologist (C.B.M.) selected an NCCT image of a healthy subject as a reference image, ensuring that no pathologies or image artifacts were present. Because the proposed hemorrhage detection method is based on a relative density increase in NCCT images, brain structures with different densities on NCCT images should be recognized. As such, brain tissue was labeled as the following: 1) GM, 2) WM, and 3) CSF.

The Laboratory of Neuro Imaging Probabilistic Brain Atlas (LPBA40)²⁴ was used for the labeling. The LPBA40 dataset provides the following: 1) average-intensity skull-stripped T1-weighted MR brain image; 2) probabilistic MR imaging tissue maps of WM, GM, and CSF; and 3) probabilistic maps for 56 delineated structures in the brain. The LPBA40 Atlas was registered with the reference image to produce the CT-based atlas.

Skull-Stripping.

Because the LPBA40 images are without skull, skull stripping of the NCCT reference image was required before registration. The skull-stripping started with thresholding to select and exclude the skull by using an established threshold of 100 Hounsfield units (HU). This threshold assured that calcifications were excluded and any hemorrhage was included.^25,26 After a 2D erosion with a disk-structuring element in each section, the remaining structures were detected by using 2D-connected component analysis. To discriminate brain tissue from other soft tissues, we excluded connected components with small areas. When multiple connected components were present in a section, the component with its centroid closest to the centroid of the superior section was selected as brain tissue. Here we assume that superior sections only contain a single connected component because of the absence of soft tissues other than brain in the cranial part of the head. After selection of brain tissue, we performed a morphologic closing and dilation, resulting in the final brain mask.

Generation of a CT-Registered Atlas.

All registrations were performed by using the open-source software Elastix (Version 4.6; http://elastix.isi.uu.nl).²⁷ First, the average-density LPBA40 MR brain image was registered to align with the skull-stripped reference image. Because multimodal images needed to align, mutual information was set as a similarity measure for registration. Registration was performed by a rigid and affine transformation first to correct for major differences in position, orientation, and size. Subsequently, a nonrigid B-spline registration was applied to correct for remaining differences in brain shape, and the result was inspected by a trained observer (A.M.B). Using the transformation from this registration, we transformed the anatomically labeled maps of the LBPA40 data with the use of Transformix (Version 4.6; http://elastix.isi.uu.nl)²⁷ to align with the reference CT image, resulting in the CT-registered atlas images used in the remainder.

Atlas-Based Segmentation of Patient Images.

The CT-based atlas was used to label different brain tissue types in all patient images. By registration of the reference image with patient images, the CT-based atlas also aligned with patient data. Similar to the registration of the reference image with the LBPA40 atlas, this process was started with skull stripping. The regions of the patient images were classified by applying this transformation to the CT-based atlas. Because hemorrhages induce density changes, again, mutual information was set as a similarity measure in the registration to label patient NCCT images into GM, WM, and CSF.

Partial Volume Effect

The used image data with relatively thick sections of 5 mm had partial volume effects, resulting in higher density in the skull-brain transition zone. As a result, healthy tissue close to the skull may have density similar to that of blood. This makes it difficult separate images of true hemorrhage near the skull from artifacts, due to partial volume effects. There is however, a noticeable change in the width of the transition zone of healthy brain tissue and skull; this transition is wider in the presence of hemorrhage.

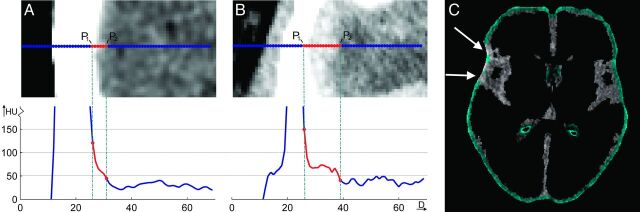
To differentiate hemorrhagic tissue from healthy tissue with partial volume effects, we estimated the density gradient at the transition of skull to healthy brain tissue, in which the gradient for hemorrhagic tissue is lower than that for healthy tissue with partial volume effects. This density gradient (ν) is defined as the density difference (in Hounsfield units) between the skull and healthy brain tissue divided by the Euclidean distance between these points. The location of the points was found by selecting 2 positions on an orthogonal line over the transition of the brain and skull. The pixel closest to the brain tissue with a density of >100 HU was selected as the first point (P₁), and the pixels closest to the skull with a density of <50 HU, as a second point (P₂). The typical density gradients for partial volume effect and hemorrhagic brain tissue near the skull are illustrated in Fig 1. Using this separation, we excluded voxels with high densities and high gradients from further processing.

Fig 1.

Illustration of differentiation between partial volume effect and hemorrhage in the vicinity of the skull. A, Calculation of the density gradient of an NCCT image with high hypodensities near the skull. High gradients are expected to be caused by partial volume effects in contrast to hemorrhages, which result in low gradients as seen in B and C. The pixels corresponding to low gradients (blue) are excluded from further segmentation. The white arrows mark the areas with high gradients present in the CSF image.

Correction for Patient-Specific Density Differences

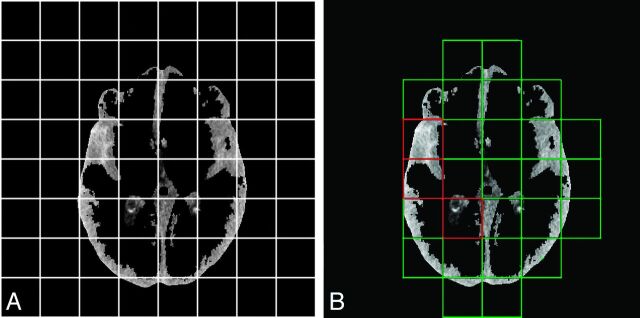
Relative density differences of normal and hemorrhagic voxels can vary from patient to patient. These variations are mainly caused by partial volume effects in upper and lower sections and beam-hardening but may also be caused by differences in scanner type and brain tissue composition (old infarct, atrophy) and blood composition (age of hemorrhage, hematocrit). Because our method is based on relative density changes, this offset needed to be corrected, to come to an optimal threshold to discriminate blood from normal brain tissue. To estimate these small offsets, we divided recognized tissue types in each section into equal tiles in which the SD of the density was calculated. After visual inspection of an alternating number of tiles, the optimal number of tiles was established (n = 64). Tiles with a small SD were expected to be free of blood. The densities in these tiles were used to estimate the mean density of that specific tissue type in that section. This process is illustrated in Fig 2. The “offset” was defined as the difference of the mean density of that tissue type and the values of the reference image. After correction for this offset, a first estimation of hemorrhage was defined as all voxels with a density higher than the adjusted threshold, which was defined by the mean density of the reference image per tissue type ± the SD.

Fig 2.

Illustration of the correction for patient-specific density differences. A, Each section of a specific tissue type (here CSF) is divided into 64 tiles, and the SDs of the density were calculated. B, Green tiles represent those with a low SD of the density and are expected to be free of a substantial amount of extravasated blood and therefore mainly consist of healthy brain tissue, whereas tiles with a high SD (red tiles) are more likely to contain hemorrhage. The densities in the green tiles were included in the calculation of the mean density of that tissue type. Comparison with the mean density of that tissue type in the reference image resulted in a density offset, which was corrected.

In the interhemispheric fissure, the falx cerebri can be mistaken for blood and therefore requires additional analysis. The interhemispheric fissure was localized by using anatomic atlas regions adjacent to the midline. A blood-free segment of the falx was selected as the segment with a small SD of densities. K-means clustering was used to partition the area into 2 structures: normal brain tissue or the falx. Subsequently, the threshold to segment blood in the interhemispheric fissure was adjusted to the normal hyperattenuated falx.

Region Growing

The threshold, as described above, does not include subtle attenuated parts of the hemorrhage. To correct for this underestimation of blood volume, we used initial segmented hemorrhages as seeds for a region-growing algorithm. This algorithm examined all voxels in the vicinity of the initial segmented hemorrhage to determine whether these voxels should be included in the segmentation. A voxel was included if the difference in its density and the average density of the segmented volume was smaller than a predefined threshold of mean density − 1.5 times the SD.

Hemorrhage Volume and Density Estimation

The volume of blood was determined as the multiplication of the segmented voxels by voxel size. For every segmented region of blood, there is a distribution of densities. Because the average density may be sensitive to small overestimations of the segmentation, which would include low-density voxels, the hemorrhage density was defined as the third quartile of the density distribution of the segmented volume.

Manual Hemorrhage Segmentation

The hemorrhage volume of 20 patients with SAH was selected for training and was manually delineated by radiologist I.A.Z. (with 8 years of experience) by using ITK-SNAP 2.4.0 (http://sourceforge.net/projects/itk-snap/files/itk-snap/2.4.0/).²⁸ The 30 hemorrhage volumes in the test set were delineated twice by radiologists I.A.Z. and R.v.d.B. (with >15 years of experience) and were used for validation. Both observers were blinded to all clinical information and each other's results.

Fisher and Hijdra Grading

Each patient was graded according to the Fisher and Hijdra scales by I.A.Z. and C.S.G. Both observers were blinded to all clinical data and reached a consensus. The sum score of the ventricles and cisterns was combined to obtain the final Hijdra score, ranging from 0 to 42.

Statistical Analysis

The manual measurements of a single observer (I.A.Z.) were used as a reference standard to evaluate the accuracy of the automatic method. The difference in hemorrhage volume between the automatic and manual assessment and the interobserver variability of the manual hemorrhage segmentation was evaluated by a number of tests. At first, scatterplots were presented, and the interclass correlation coefficient (ICC) and its 95% CI with absolute agreement definition were calculated. The ICC was assessed according to the case 3 form of Shrout and Fleiss,²⁹ in which a 2-way ANOVA model is used for analysis. Additionally, a Bland-Altman analysis was performed to assess the bias and limits of agreement, in which the “bias” was defined as the mean paired difference and limits of agreement.³⁰ Furthermore, the Dice coefficient³¹ was calculated to determine the overlap of the volumes, and the ICC and its 95% CI of the hemorrhage density were assessed.

In addition, Fisher and Hijdra scale scores were compared with manual-delineated and automatic-determined volumes by constructing scatterplots and calculating, respectively, the Spearman rank correlation coefficient and the Pearson correlation coefficient and their 95% CIs.

Results

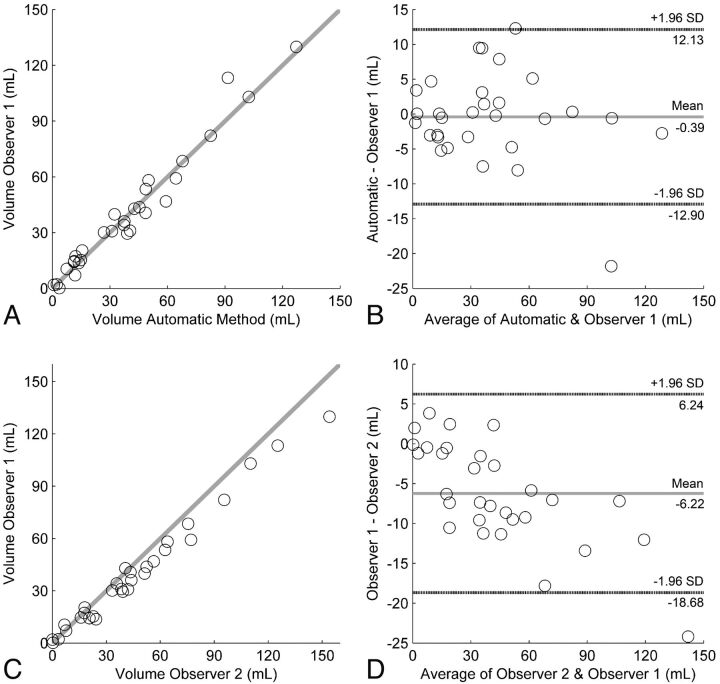
The test set included 30 patients, with a mean age of 55 ± 12 years, and 60% were women. The mean SAH volume was 39.71 ± 32.84 mL and 39.33 ± 31.49 mL, according to the manual and automatic methods, respectively. The ICC of the volume measurement between the automatic and manual measurements was 0.98 (95% CI, 96%–99%). The ICC of the volume-measurement interobserver agreement was 0.97 (95% CI, 77%–99%). Bland-Altman analysis indicated an average difference in SAH volume of −0.39 mL between the automatic and manual measurements, with limits of agreement ranging from −12.90 to 12.10 mL. For the 2 observers, the Bland-Altman analysis resulted in a bias of −6.22 mL, with limits of agreement ranging from −18.70 to 6.20 mL. The Dice coefficient of the manual and automatic measurements was 0.55 ± 0.24 and ranged from 0.00 to 0.83, in comparison with 0.64 ± 0.20 between the 2 observers.

The interobserver and accuracy measures are shown in Table 2 and Fig 3. The mean SAH density was 61.43 ± 7.26 HU and 62.23 ± 5.89 HU, according to the manual and automatic methods, respectively. The ICC of the hemorrhage density between the observers was 0.98 (95% CI, 89%–99%) and 0.80 (95% CI, 62%–90%) for the comparison of the manual reference and automatic method. In 1 case, observer 2 detected no hemorrhage; this case was excluded from the calculation of the manual interobserver variability regarding the density measurement only. Bland-Altman analysis indicated an average difference in SAH density of 0.80 HU between the automatic and manual measurements, with limits of agreement ranging from −7.58 to 9.18 HU. For the 2 observers, the Bland-Altman analysis resulted in a bias of 0.96 HU, with limits of agreement ranging from −1.52 to 3.44 HU.

Table 2:

Interobserver variability of manual SAH volume measurement and comparison of the manual and automatic methods

	ICC Volumea (95% CI)	Bland-Altman Volume Limits of Agreement (mL)	ICC Densitya (95% CI)	Bland-Altman Density Limits of Agreement (HU)	Dice Coefficient (Mean and Range)	No.b
Automatic interobserver	0.98 (0.96–0.99)	−12.90–12.13	0.80 (0.62–0.90)	−7.58–9.18	0.55 (0.00–0.83)	30
Manual interobserver	0.97 (0.77–0.99)	−18.68–6.24	0.98 (0.89–0.99)c	−1.52–3.44c	0.64 (0.00–0.86)	30

^aCase 3 intraclass correlation coefficients using an absolute agreement definition.

^bNumber of NCCT scans included in the calculation.

^cNumber of NCCT scans included for calculation = 29.

Fig 3.

The accuracy of the volume measurement of the automatic method compared with that in observer 1. A, Accuracy depicted as a scatterplot. B, Accuracy shown by the Bland-Altman plot. Interobserver variability of the manual hemorrhage volume measurement depicted as C, scatterplot, and D, Bland-Altman analysis.

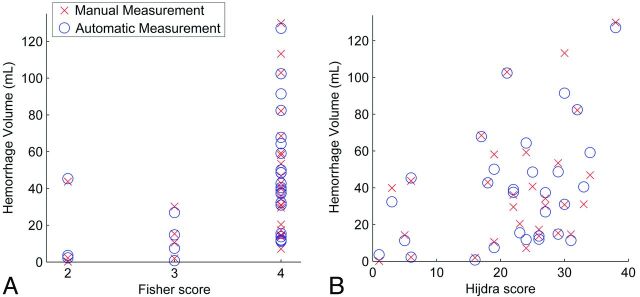
The Fisher score was 2 in 3 patients (10%), 3 in 4 patients (13%), and 4 in 23 patients (77%). The Hijdra score ranged from 1 to 38, with a median and third quartile of 24 and 29, respectively. The correlation of the hemorrhage volume with the Fisher score and Hijdra score is shown in Fig 4. The Pearson correlation coefficient of the Hijdra score with manual volume measurement was 0.39 (95% CI, 0.04–0.63; P <.05), and with automatic measurement, 0.42 (95% CI, 0.08–0.65; P < .05). The Spearman rank correlation coefficient of the Fisher score with a manual volume measurement was 0.49 (95% CI, 0.10–0.74; P <.01), and with automatic measurement, 0.50 (95% CI, 0.14–0.74; P < .01).

Fig 4.

Correlation of the Hijdra score and Fisher score with hemorrhage volume after SAH assessed with scatterplots. A, The Fisher score with automatic volume measurement (blue) and manual volume measurement (red). B, The Hijdra score with automatic volume measurement (blue) and manual volume measurement (red).

Discussion

In this study, we have presented a novel method for automatic hemorrhage volume and density quantification in NCCT scans of patients with SAH. Comparison with manual delineations in 30 patients with SAH with manual assessment showed an excellent agreement in blood volume and a good agreement in blood density.

Despite the general acceptance that the volume of blood after SAH provides information regarding prognostic outcome and guidance for treatment decisions, no method to estimate the real amount of blood so far has been successful. Sato et al²³ proposed an automated measurement on 3D CT to quantify SAH on the basis of thresholding between 40 and 80 HU, which could rapidly measure SAH volume. However, the time needed to manually exclude the scalp and subcutaneous tissue was not taken into account. Furthermore, errors in volume of approximately 10 mL were unavoidable, partly because the volume was calculated by subtracting a mean value for tissues between 40 and 80 HU of healthy subjects from the patient image. Other computer-aided detection methods have been proposed for intracranial hemorrhages; however, these are not suitable to automatically quantify SAH. For instance, the method of Chan³² is based on the symmetry of the ventricles, which are segmented by thresholding only. Here, the assumption is made that no blood is present in the ventricles, which is often not the case in patients with SAH.

The Fisher scale has become the current historical standard for this purpose on NCCT. It was designed to predict cerebral vasospasm; however, its clinical utility has been questioned.^11,14,19,33 The Fisher scale is not comprehensive enough to serve as a primary grading system for SAH and to predict clinical outcome.³ In this study, the Fisher scale fails to differentiate among hemorrhages with a small, moderate, or substantial amount of blood by categorizing grade 4 in 77% of the cases within a large range of 12–130 mL. Finding no blood on CT is rare, as is clot <1 mm in true thickness, making grades 1 and 2 quite uncommon. The correlation of this scale with hemorrhage volume was moderate (0.49). Because there is strong agreement among studies that the amount of subarachnoid blood has highly predictive value regarding patient outcome, we believe that our proposed volumetric measurement has added value above the Fisher scale.^3,4,6–9 Moreover, Fig 4 illustrates the large range of hemorrhage volumes within single Fisher scales. Because of the low number of patients in Fisher grades 1 and 2, we could not perform any valuable statistical analysis.

Even though the method by Hijdra et al⁸ is more comprehensive than the Fisher scale, the correlation with the measurements of hemorrhage volume in this study was poor in comparison with our proposed method (0.39 versus 0.98). The Hijdra scale assigns grade 3 to a fissure or cistern when it is completely filled with blood, which does not indicate a certain volume. In addition, assessment of the Hijdra scale is a tedious task and may be impractical in an emergency setting.

Recently, Wilson et al³⁴ proposed the Barrow Neurological Institute scale, a simple and quantitative method to grade the amount of blood and predict vasospasm. This scale categorized patients with SAH into 5 more evenly distributed classes than the Fisher scale and showed better inter- and intraobserver agreement. However, the clinical value has not been confirmed by other studies. Although this scale appears promising for the prediction of vasospasm, associations with SAH volume have not been reported.

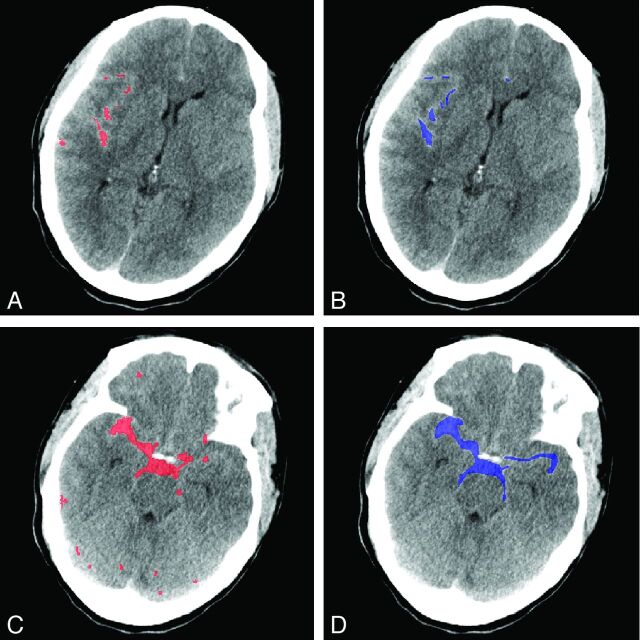
An example of the volume measurements is shown in Fig 5. The concordance of the automatic method with manual reference was excellent, despite a moderate Dice coefficient. This disagreement can partly be attributed to the tortuous shape of the cisterns. The observers perceived an image on the screen and delineated it by hand; this hand method results in smooth edges, whereas the automated method segments the image on a voxel-by-voxel basis, which results in ragged edges.

Fig 5.

Example of the results of the automatic segmentation of extravasated blood after SAH and manual measurement. A, NCCT image, shown in red, with results of the automatic method of a relatively small hemorrhage. B, The same NCCT image and hemorrhage as delineated by observer 1 (blue). C, NCCT image with beam-hardening in an extreme degree. The automatic method, in red, shows deviations of the hemorrhage volume as delineated by observer 1 (D) in blue.

Another limitation for the current grading scales is that hemorrhage density, which may be equally important, is not considered.^3,10–12 This limitation addresses an additional advantage of the proposed automatic method, which reports a good ICC of the hemorrhage density measurement with the manual reference. This ICC was, however, approximately 18% lower than the interobserver variability. Retrospective analysis showed that this difference was mainly caused by low agreement in patients with small hemorrhage volumes. When we included only SAH volumes >5 mL (3 patients excluded), the ICC of the hemorrhage density of the automatic measurement and manual reference increased to 0.95 (95% CI, 87%–98%). This increase can be partly explained by the difference in procedures regarding small hemorrhages; in the manual comparison, the observers delineated on the basis of personal experience and by using the contralateral hemisphere for comparison. Here, only slightly hyperattenuated blood could be detected, in contrast to the automatic method, which is threshold-based. No restrictions are to be expected regarding SAH quantification for such small hemorrhages.

In this study, the third quartile was chosen for the hemorrhage-density estimation. We believe that a measurement such as the mean is more sensitive to errors in the segmentation due to the difference in segmentation technique (voxel-by-voxel-based versus delineation by hand). The third quartile is, however, a heuristic approach.

SAH often is accompanied by intraventricular hemorrhage or intracerebral hemorrhage as seen in Table 1. The automatic method in this study was designed to include all blood present in the brain after SAH. Therefore, we believe this method has the potential to serve as a quantification measurement in other types of hemorrhagic strokes. As future work, it could be beneficial to differentiate among locations of hemorrhage to investigate the role of blood distribution in patients with SAH. This study was performed on image data of a population of patients who had SAH due to rupture of an MCA aneurysm. As a result, this study may be affected by a selection bias because these patients, especially, present with bleeding around the temporal and insular regions; however, in most patients, there was extension into the interhemispheric fissure and to the lower pontine cistern. All included NCCT images were obtained on 2 scanner types, with 1 reconstruction kernel. We do, however, expect no problems when using different scanner types because the automatic method corrects for these density differences.

The duration of manual segmentation was recorded for 19 patients only. The manual segmentation ranged between 5 and 23 minutes with a median of 15 minutes, which was considerably longer than the 2–5 minutes required for the Fisher and Hijdra grading. The automatic SAH assessment took an average of 5 minutes per patient on a modern computer. The computation times should be further reduced to make an approach as presented here available for clinical practice.

Furthermore, the automatic method may not recognize aneurysms and large vessels and categorizes them as part of the hemorrhage. Using the proposed method to quantify only the amount of extravasated blood may therefore lead to an overestimation of this volume. A solution for this issue could be to subtract a CTA from the NCCT image.

In this study, a method was designed to correct for partial volume and beam-hardening artifacts, which are more prominent in the anterior fossa near the skull base and in the posterior fossa. Despite these corrections, other CT artifacts, such as patient motion, may cause the automatic SAH quantification to fail. In addition, when beam-hardening is present in an extreme extent, the automatic segmentation may underestimate the hemorrhage volume because the artifacts are approached as a patient-specific density variation as seen in Fig 5. Furthermore, high-attenuated areas may be seen as hemorrhage. Although physics-based artifacts cannot be eliminated, techniques have been developed to correct for these quantitative and visual errors and could be beneficial for improvement of our method.^35,36

Another point is that the threshold values used in the algorithm are dependent on the standard value in the images. Therefore, the method may be dependent on the image quality. Validation on different scanners and reconstruction techniques is therefore required.

We designed and validated our method to align the real hemorrhage volume and density after SAH. Evaluation with patient outcome is beyond the scope of this study because multiple factors other than radiographic evidence contribute to the prediction of patient outcome, including clinical scales such as those of Hunt and Hess¹³ and the World Federation of Neurosurgical Societies.^3,15,37 A future study in which hemorrhage volume and density are combined with other factors is necessary to validate the full utility of this method as a predictor for patient outcome.

Conclusions

We have presented a fully automatic method for blood volume and density quantification in NCCT scans of patients with SAH. The automatic method showed an excellent accuracy and strong correlation with the manual reference standard. This approach is an easy-to-use (fully automatic) and observer-independent solution in assessing the volume and density and, as such, has the potential to assist in predicting patient outcome, guiding treatment decisions, and standardizing hemorrhage assessment across medical centers in multicenter studies.

ABBREVIATIONS:

ICC

intraclass correlation coefficient

LPBA40

Laboratory of Neuro Imaging Probabilistic Brain Atlas