Wall Shear Stress Distribution Inside Growing Cerebral Aneurysm

Abstract

BACKGROUND AND PURPOSE:

Hemodynamic stimulation has been suggested to affect the growth of cerebral aneurysms. The present study examined the effects of intra-aneurysmal hemodynamics on aneurysm growth.

MATERIALS AND METHODS:

Velocity profiles were measured for 2 cases of AcomA aneurysms. Realistically shaped models of these aneurysms were constructed, based on CT angiograms. Flow fields and WSS in the models were measured by using particle image velocimetry and LDV. In 1 case, hemodynamic changes were observed in 4 stages of growth over a 27-month period, whereas no development was observed in the other case.

RESULTS:

The growing model had a smaller and more stagnant recirculation area than that in the nongrowth model. The WSS was markedly reduced in the enlarging region in the growing models, whereas extremely low WSS was not found in the nongrowth model. In addition, a higher WSSG was consistently observed adjacent to the enlarging region during aneurysm growth.

CONCLUSIONS:

The results indicated that the flow structure of recirculation itself does not necessarily lead to high likelihood of cerebral aneurysm. However, WSSG and WSS were distinctly different between the 2 cases. Higher WSSG was found surrounding the growing region, and extremely low WSS was found at the growing region of the growing cerebral aneurysm.

It is conceivable that intra-aneurysmal hemodynamics may be related to the degeneration of the aneurysm wall, leading to rupture.^1,2 A precise understanding of intra-aneurysmal hemodynamics may provide new criteria to predict the risk of aneurysm rupture. To determine the role of hemodynamics in cerebral aneurysm degeneration, it is necessary to analyze the intra-aneurysmal flow, based on clinical images. Tateshima et al³ identified the significance of intra-aneurysmal flow obtained with a realistic vascular model of a basilar tip aneurysm, and they highlighted the significance of WSS affecting the aneurysmal wall. Ujie et al⁴ reported a recirculating flow pattern in ruptured aneurysms and proposed that the presence of a recirculation region may be related to an increased risk of aneurysm rupture. Shojima et al⁵ reported lower WSS on the walls of ruptured aneurysms, consistent with the observations of Ujie et al.⁴ However, these studies had difficulty in verifying the role of hemodynamics in aneurysm degeneration, because they focused on only 1 stage of cerebral aneurysm growth.

Cerebral aneurysm growth is an important indicator of aneurysm wall degeneration. A previous study evaluated the flow pattern and WSS distribution in middle cerebral artery aneurysms before and after growth⁶ and indicated reduced WSS in the enlarging area of the aneurysm bleb. The hemodynamic changes were needed to distinguish the possibility of aneurysm growth. Thus, it is important to observe hemodynamic changes during growth.

The purpose of the present study was to identify hemodynamic factors related to aneurysm growth, by evaluating consecutive hemodynamic changes at each stage during growth. We selected a case of cerebral aneurysm in which chronologic CT images were available for a 27-month period, corresponding to aneurysm growth.

Materials and Methods

Aneurysm Models

CT data for 4 stages were available for a growing AcomA aneurysm over an observation period of 27 months, at UCLA Medical Center. We also used CT data of an AcomA aneurysm with no growth over a 12-month follow-up period. We constructed 5 realistic silicone aneurysm models, based on these CT images. Although the silicone models do not have compliant walls, velocity distribution and WSS profiles in the compliant model were confirmed to be close to those of the rigid model.^7,8

There are normally 2 inflow arteries into an AcomA aneurysm, called A1, and 2 outflow arteries, called A2. However, there was only one A1 and the contralateral A1 was either hypoplastic or aplastic in the case examined. Thus, only 1 inflow artery was present in both cases. Figure 1A shows a 3D view of the growth model, based on STL data. The model has 3 outflow arteries designated as left A2 (A2–1), middle A2 (A2–2), and right A2 (A2–3). Figure 1B shows the STL view of the nongrowth model.

Fig 1.

A, STL view of the growing model and an enlarged view of the growing area. The growing area was detected by alignment of the aneurysm geometry. The alignment was assessed with the matching of surfaces in nonaneurysmal vessel segments between each model. B, STL view of the nongrowth model.

Development of Aneurysm in Growth Case

Figure 1A also shows the enlarged region of the aneurysm, detected by superimposing 4 consecutive STL datasets. To estimate the regions of aneurysm enlargement, we aligned the geometric model, based on the corresponding of the parent arteries. The alignment was assessed so that there was matching of surfaces in nonaneurysmal vessel segments between model 1 and 2, 2 and 3, and 3 and 4. Preferable matching could be seen near the neck area, not only at the nonaneurysmal vessel, and a difference was found around the aneurysm apex.

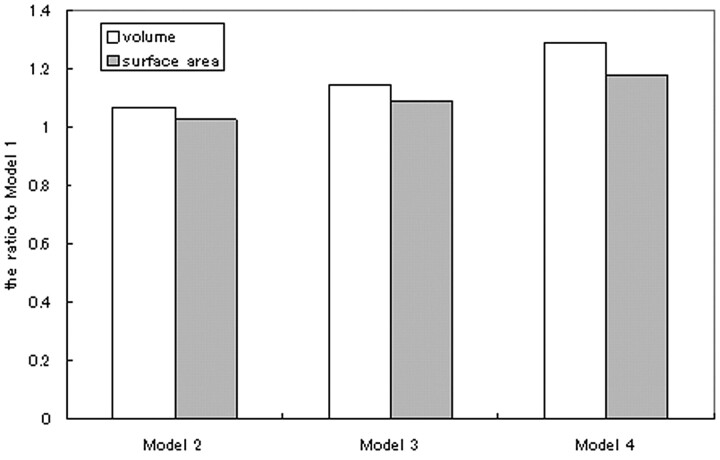
The inner volume and surface area of the aneurysms were computed from the geometry stored in the STL. Figure 2 shows the relative changes in the inner volume and surface area of the aneurysm. The volume and surface of the aneurysm increased significantly during the 2-year follow-up period.

Fig 2.

Calculated volume and the surface area of each growing model.

Flow Conditions

The refractive index of the working fluid should be matched to that of silicone resin to measure the velocity profile in PIV, by eliminating the optical distortion at the interface between the working fluid and the silicone resin. A 58% (by weight) solution of glycerin (viscosity, μ = 8.2 × 10⁻³ Pa-s; attenuation, ρ = 1.14 × 10³ kg/m³; refractive index, n = 1.41) was used as a working fluid. The effect of Newtonian behavior is very slight in cerebral arteries around 5 mm in diameter.⁹ Thus, the glycerin solution is appropriate for mimicking blood.

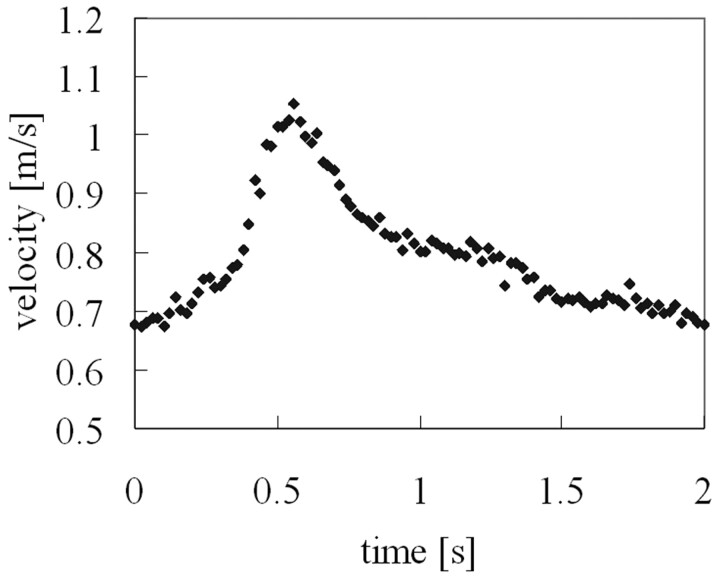
The Reynolds number and Womersley number were set to the in vivo conditions. The Reynolds number is expressed as Re = UL/v, where U and L are characteristic velocity and length scales of the flow, respectively, and ν is kinematic viscosity of the flow. Because the blood flow waveform was not acquired in the patient's cerebral artery, we set the inflow condition based on the typical waveform at the AcomA measured by transcranial Doppler sonography.¹⁰ The Womersley number is expressed as α = (D/2)(ν/ω)^1/2, where D is the diameter of the tube, and ω is the angular velocity of the flow. The Reynolds number and Womersley number at the ACA were found to be 450–800 and 3.5, respectively. To mimic the pulsatile flow in the human cerebral artery, pulsation generated by a positioning-controlled servomotor (VBLS-A11012; Toei Electric, Tokyo, Japan) was added to the steady gravity flow (Fig 3).

Fig 3.

Inflow waveform, measured by LDV. The inflow condition was set by referencing the typical blood flow waveform at the ACA.

Flow Field Measurement with PIV

The PIV system (La Vision, Bielefeld, Germany) consisted of a laser sheet for visualization of the flow field, a CCD camera for image acquisition, and a computer for analysis. A MINI YAG Nd:YAG laser (TSI, Minneapolis, Minnesota) was used as the light source, and the laser beam was transformed into a 1-mm thick light sheet to illuminate the explored planes. The laser sheet was pulsed at intervals of 150 μs, and particle images on the sheet were acquired with the CCD camera (1376 × 1040 pixels) with the trigger signal intensity synchronized to the laser pulse. The velocity vector field was calculated from the double-frame acquired images based on the path of the particle. This PIV analysis was performed with the DAVIS 7.1 software (La Vision).

WSS Measurement with LDV

WSS was determined from the velocity gradient measured by LDV according to Newton's viscosity law (equation 1), where τw is WSS, μ is viscosity of working fluid, and ∂u/∂y is the velocity gradient:

First, we determined the median point of the minimum triangle unit, constructing the STL surface as the WSS measurement object. Then, the normal vector was calculated, based on the coordinates of the triangle. Finally, we determined the position 500 μm tangentially from the median point as the measurement point. The velocity at the measurement point was measured by using an LDV system (TSI), consisting of a 500-mW Ar-ion laser (model 500A; Ion Laser Technology, Frankfort, Illinois) with an ellipsoid measurement area with axes of 45.0, 43.8, and 198 μm, and a Digital Burst Correlator (model IFA 650; TSI) by using the analysis software supplied by the manufacturer (Find ver4.03; TSI). The LDV is a measurement device that requires precise positioning. In this study, a 3-axis stage controller, which enables positioning to within 5 μm, was used to attain the desired measurement accuracy at a 500-μm distance from the silicone wall of the ×3 magnified model. The details of WSS measurement by using the LDV can be found in our previous studies.^6,11

Results

Intra-Aneurysmal Flow Structure

On-line Figure 1A–D shows the velocity vectors and path lines acquired by PIV for the intra-aneurysmal flow during the aneurysm progression stage. On-line Figure 1A shows representative velocity vectors and path lines of model 1 in 2 planes, A and B, that are perpendicular to each other.

In plane A, a small recirculation flow appeared at the apex of the aneurysm. The zone of recirculating flow corresponds to the enlarged region shown in Fig 1. In addition, recirculating flow was observed in many cases of ruptured aneurysms,⁴ and such recirculating flow seems to be related to the extent of the aneurysm wall. The rotational direction of the recirculating flow was almost parallel to plane A, and recirculation could not be identified in the flow fields of plane B.

On-line Figure 1A–D shows similar velocity profiles, but the flow structures in the recirculating zones show noticeable progressive changes from On-line Fig 1A to D.

On-line Figure 1E shows the velocity profiles in the nongrowth aneurysm, and the presence of recirculating flow near the apex of the dome should be noted. In the past study,⁶ such recirculating flow structure had been linked to aneurysm growth or rupture. It is necessary to clarify whether the existence of recirculating flow has a role on the aneurysm growth.

Recirculation Area

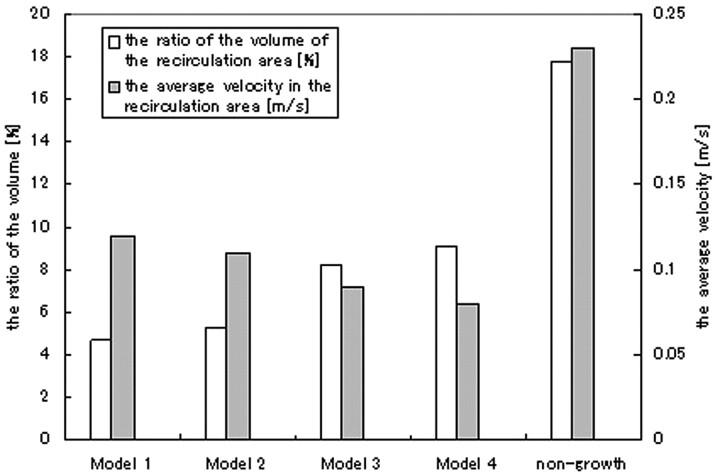
In this study, recirculating flow was observed near the apex of the aneurysm in all of the models, and the recirculation zone was exposed to the enlarging area of the aneurysm. On-line Figure 2 shows the velocity vector distribution and vorticity fields in plane A of each model. The vorticity profile is represented by the gray mapping. The direction of the recirculation in the growing aneurysm was clockwise and was observed near the enlarging area, whereas counterclockwise recirculation was observed in the nongrowing model. The vorticity in the recirculation was negative in the growing model and positive in the nongrowing model (On-line Fig 2). Thus, the recirculating zone can be distinguished by the direction of vorticity in On-line Fig 2, and the area of negative vorticity in the growing model expanded with the progression of aneurysm growth. Thus, we defined the recirculating zone in each model determined by vorticity mapping; the zone with negative vorticity in each of the growing models was defined as the recirculation area. For the nongrowing model, the recirculating zone was determined by the positive vorticity. Then, recirculating volume was calculated for each model, integrating the recirculation area with the thickness between each measurement plane, where recirculating area could be defined. The ratio of recirculating volume to the volume of the aneurysm is shown in Fig 4. For the growing models, the ratio of recirculating volume increased, from 4.7% to 9.1%. Although the increase of recirculating volume means the extent of flow stagnant area, the ratio of the recirculation volume in the nongrowing model was higher than that of model 4. Thus, the existence of a recirculation area by itself or the size of the area is not necessarily sufficient to diagnose a risk of rupture or growth.

Fig 4.

Ratio of recirculating volume to that of aneurysms and the average velocity in the recirculation area in each model.

WSS Distribution

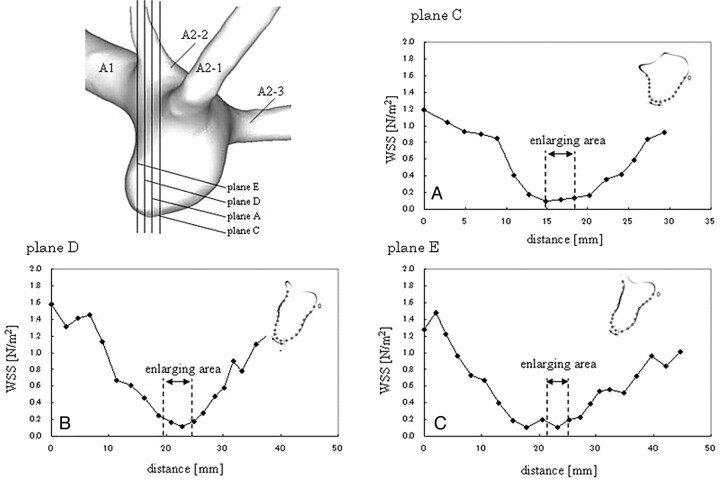
On-line Figure 3 shows the WSS in the growing aneurysm at plane A designated in On-line Fig 1, and the enlarging region is indicated in the figure by an arrow. It should be noted that the WSS tended to be low at the enlarging region in all of the models, and higher WSS was observed away from the enlarging area. Furthermore, the enlarging area increased sequentially and the WSS was much lower in this region. On-line Figure 3 also shows the WSS in the nongrowing model at plane A, and the arrow indicates the recirculation zone. Although low WSS appeared in the nongrowth model at the apex area, the overall WSS was much higher than the WSS in the growing model. Figure 5 shows the WSS in the other planes parallel to plane A, where the enlarging area was recognized in model A. In these planes, extremely low WSS was observed at the enlarging area as in plane A. In contrast, in the nongrowth model, low WSS was not observed at the recirculating zone (On-line Fig 4).

Fig 5.

WSS distribution on the planes where the enlarging region was observed in model 1. The enlarging region on each plane is shown.

WSSG Estimation

We focused on the distribution of the WSS gradient, another important mechanical parameter affecting the vessel wall. The curve showing the WSS distribution was smoothed by the moving average deviations, and spline interpolation was applied to the smoothed curve. On-line Figure 5 shows the smoothed curve for the WSS distribution and the WSSG calculated from the smoothed WSS distribution. Although the WSSG in the nongrowth model was <0.10 Pa/mm, a WSSG >0.15 Pa/mm was seen adjacent to the enlarging area in the growing models. Furthermore, the WSSG in the growing area increases with the progression of aneurysmal growth. In the area of high WSSG that was consistently present adjacent to the growing area, we also observed that the fluctuation range of the WSS during the cardiac cycle was larger than that found in the growing area (On-line Fig 6).

Discussion

A flow structure of recirculation has been identified as a risk factor for rupture.⁴ The velocity is generally low in areas of recirculation, and this low velocity has been suggested to be associated with growth. Low-velocity blood flow leads to increased leukocyte adhesion to endothelial cells, resulting in lesions in the arterial wall.¹² Low velocity causes an increased residence time of circulating particles in the region and mass transfer, thereby enhancing the interactions between circulating leukocytes and vascular endothelial cells.¹³ Furthermore, Yamaguchi et al¹⁴ reported that slow circulating flow contributed to thrombus formation, and they linked the process of fibrinolysis after thrombus formation to aneurysm wall digestion.¹⁵ However, the flow structure of recirculation alone may be insufficient to explain the hemodynamic conditions responsible for cerebral aneurysm growth, because recirculating flow was observed not only in the growing model but also in the nongrowing model.

The most important part of our study pertains to the hemodynamic changes during the process of aneurysm growth in an individual patient. Information on hemodynamic change has led to the significant result that higher WSSG occurs in the region adjacent to the growing area, where the WSS tends to be lower. Based on these findings, we hypothesize that both high WSSG and low WSS are responsible for the growth of cerebral aneurysms. Some previous studies have discussed the individual roles of WSS or WSSG. For example, Watton et al¹⁶ demonstrated continuous aneurysm enlargement, due to low WSS or high WSSG. In our study, the consecutive changes in hemodynamic events indicate the consistent presence of high WSSG in the region surrounding the growing area. This region of high WSSG could produce the initial arterial degeneration, leading to the extension of the flow stagnant region, where the WSS is low. In addition, the lower WSS could be responsible for further expansion of the aneurysm dome.

High WSSG could be an important mechanistic link between hemodynamics and vessel wall pathobiology. Meng et al¹⁷ artificially created arterial bifurcation and observed the initial arterial degeneration that leads to aneurysm formation in the area of high WSSG. These findings indicate that WSSG plays a role in the expansion of the pregrowth region, resulting in the initial bulging that could lead to a stagnant flow area. High WSSG increases the migration of ECs,¹⁸ and EC migration causes a decrease in MMP inhibitors, such as GM6001 or MMP-2–9-inhibitor III.¹⁹ MMP-2 and MMP-9 are responsible for preventing the arterial wall in a cerebral aneurysm from being weakened by the degeneration of the extracellular matrix components elastin and collagen IV.²⁰ Thus, high WSSG also could be a hemodynamic factor in cerebral aneurysm initiation, causing impairment of the IEL.

Low WSS could be related to the thinning of the media in a cerebral aneurysm. Under conditions of low WSS, THP-1 cells, which differentiate into macrophages, prominently adhere to ECs stimulated by tumor necrosis factor-α.¹⁷ The increase of infiltrated macrophages in the aneurysmal wall causes the apoptosis of SMCs, resulting in the thinning of the media.²¹ Thus, fragile media could lead to the development of the aneurysm wall under low WSS conditions.

Tateshima et al⁶ measured WSS distribution in middle cerebral artery aneurysms with an enlarged bleb, and low WSS appeared at the bleb area. Boussel et al²² demonstrated that aneurysm growth was likely to occur in regions where the endothelial layer lining the vessel wall was exposed to abnormally low WSS. Although a relationship between high WSS and aneurysm rupture can be inferred from the fact that higher WSS has appeared in rupture cases (compared with unruptured cases)^23,24 during the growing stage of a cerebral aneurysm, low WSS also could contribute to arterial weakening.

Furthermore, the WSS in the area of high WSSG exhibits a larger fluctuation during the cardiac cycle. Shimogonya et al²⁵ found that a high GON, which is a hemodynamic index dependent on the special WSSG, appeared at the location where the aneurysm is removed in computational fluid dynamics. Such temporal change in WSS or WSSG might have a significant role on cerebral aneurysm growth. However, more research is needed to clarify which parameter, for example, temporal differentiation or integration, would be significant for aneurysm growth on the point of time variation of WSS or WSSG.

Assuming the above-mentioned statements were true, the following hypothesis might be leaded. At the area with high WSSG, IEL is destroyed by MMPs, resulting in the initial bulge that causes stagnant flow with low WSS. Then, at the low WSS region, the fragility of the aneurysm wall is accelerated through SMC apoptosis by the inflammatory cells, resulting in the thinning of media. Therefore, these 2 mechanisms, high WSSG and low WSS for the aneurysm growth, are not mutually contradictory. High WSSG could create a pregrowth area, that leads to further expansion of stagnent flow (low WSS) area. Adding to the magnitude of WSSG or WSS, other hemodynamic parameters have been proposed as driving determinants for cerebral aneurysm formation, such as time-averaged magnitude, oscillatory shear index, aneurysm formation indicator (the cosine of the angle between the instantaneous WSS vector and the time-averaged WSS vector), and the GON.

Furthermore, such empirical diagnoses as a history of hypertension and cigarette smoking could be considered to be risk factors for aneurysm rupture. Thus, the risk for aneurysm generation, growth, and rupture would be influenced by multiple factors, including hemodynamics. Therefore, the aneurysm growth could not be explained solely by a temporal hemodynamic parameter. However, our results indicated that the location of low WSS is identical to that of growing aneurysm and that a hemodynamic factor could be one of the possible mechanisms for aneurysm growth.

Although our speculation linked aneurysm growth with arterial degeneration due to hemodynamic stress, some biomechanical calculations suggested that the microstructure of evolving aneurysm tends to return intramural stress back toward baseline values. Humphrey²⁶ and Kroon and Holzapfel²⁷ modeled an initial and instant loss of media and IEL, though fluid dynamic and mechanochemical processes were not modeled explicitly. From these reports, it seems that the enlargement of a cerebral aneurysm may be a protective or adaptive response to initial insult that is driven in large part by mechanical stimuli.²⁸ Such a mechanism of arterial remodeling could be difficult to explain with hemodynamics alone. Therefore, to clarify the aneurysm growth mechanism, studies on the role of wall mechanics, matrix biology, and cell biology need to be processed, adding to the complementary hemodynamic role. Furthermore, to affirm the hemodynamic role, hemodynamics should be evaluated in more cases.

In the PIV measurement, the interval of laser sheet pulse of 150 μs was set so the particle displacement was <10 pixels. Our previous experience indicated that displacement within 10 pixels produced a stable result, but a displacement >30 pixels resulted in an erratic velocity vector. This is consistent with the ‘‘one-quarter rule,” which states that the maximal displacement should be less than one-quarter of the size of the fixed interrogation spot.¹¹ However, because a little scattering light at the boundary between the silicone model and working fluid could not be avoided even with the refraction matching, particle images could not be acquired near the wall region. Furthermore, although there are PIV techniques of WSS estimation by using the velocity data distant from the targeting wall, the calculated value is variable due to the difference of the number of sampling data or the weighting function. Therefore, LDV was used for WSS measurement in this study. In our LDV experiment, the laser scattering was very small so that the calculated WSS from equation 1 would be adequate to be evaluated in the realistic cerebral aneurysm model.^9,11

Conclusions

In this study, hemodynamics was evaluated during the process of a growing aneurysm, comparing a growing case to a nongrowth case. The results indicate that the flow structure of recirculation itself does not necessarily lead to high likelihood of a cerebral aneurysm. However, WSSG and WSS were distinctly different between the 2 cases. Higher WSSG was found surrounding the growing region, and extremely low WSS appeared at the growing region of the cerebral aneurysm.

Abbreviations

ACA

anterior cerebral artery

CCD

charge-coupled device

AcomA

anterior communicating artery

EC

endothelial cell

GON

gradient oscillatory number

IEL

internal elastic lamina

LDV

laser Doppler velocimetry

MMP

matrix metalloproteinase

PIV

particle image velocimetry

SMC

smooth muscle cell

STL

stereolithography

WSS

wall shear stress

WSSG

spatial WSS gradient