Generation of Individualized Thalamus Target Maps by Using Statistical Shape Models and Thalamocortical Tractography

Abstract

BACKGROUND AND PURPOSE:

Neurosurgical interventions of the thalamus rely on transferring stereotactic coordinates from an atlas onto the patient's MR brain images. We propose a prototype application for performing thalamus target map individualization by fusing patient-specific thalamus geometric information and diffusion tensor tractography.

MATERIALS AND METHODS:

Previously, our workgroup developed a thalamus atlas by fusing anatomic information from 7 histologically processed thalami. Thalamocortical connectivity maps were generated from DTI scans of 40 subjects by using a previously described procedure and were mapped to a standard neuroimaging space. These data were merged into a statistical shape model describing the morphologic variability of the thalamic outline, nuclei, and connectivity landmarks. This model was used to deform the atlas to individual images. Postmortem MR imaging scans were used to quantify the accuracy of nuclei predictions.

RESULTS:

Reliable tractography-based markers were located in the ventral lateral thalamus, with the somatosensory connections coinciding with the VPLa and VPLp nuclei; and motor/premotor connections, with the VLpv and VLa nuclei. Prediction accuracy of thalamus outlines was higher with the SSM approach than the ACPC alignment of data (0.56 mm versus 1.24; Dice overlap: 0.87 versus 0.7); for individual nuclei: 0.65 mm, Dice: 0.63 (SSM); 1.24 mm, Dice: 0.4 (ACPC).

CONCLUSIONS:

Previous studies have already applied DTI to the thalamus. As a further step in this direction, we demonstrate a hybrid approach by using statistical shape models, which have the potential to cope with intersubject variations in individual thalamus geometry.

The thalamus is a target structure for stereotactic surgical interventions for several functional brain disorders by means of ablative therapies or deep-brain stimulation. The main concept is to modify or retune stereotactically accessible groups of neurons (ie, nuclei) or processing pathways that play a role in relaying and integrating sensory/motor thalamocortical circuits.^1–3 Various methods have been developed to map, organize, and use the prior topographic information of thalamic subdivisions that are provided by anatomic stereotactic atlases.^4–8 In parallel to the effort of providing stereotactic atlases that incorporate clinical imaging-based anatomic correspondences,⁹ it is desirable to optimize MR imaging sequences and image-processing techniques for the direct identification of thalamic nuclei.^10–12 A promising technique to noninvasively chart the human thalamus is diffusion tensor imaging¹³ and subsequent probabilistic tractography, which can be applied to map the networks of thalamocortical connectivity.^14–16 Such methods are based on the fact that various thalamic nuclei present differential interconnections; therefore, this information can be used to subdivide the thalamus into domains that have different dominant connections with preselected cortical domains.^17–21

A crucial step during indirect neurosurgical targeting is the transfer of atlas coordinates to the patient's reference space, which is commonly achieved by a linear transformation that shifts landmarks (ie, anterior commissure or posterior commissure) to match the individual geometry; however, nonlinear atlas-to-patient registration methods have also been suggested.²² Here we propose the application of SSMs to predict the structure of thalamic nuclei. SSMs are typically used to describe the shape of complex structures in the presence of sparse observations (ie, predictors of shape). Such prediction is performed through a linear combination of training shapes (eg, individual subject data), of which the coefficients are optimized to best match the visible data. The SSM approach has, therefore, optimal attributes for the analysis and prediction of subcortical brain structures because it performs the interpolation of unobserved parts of the anatomy and constrains it to statistically plausible morphologies based on multiple samples.^23–26

We exploit recent results of the fusion of multiple histologic atlases to generate a 3D statistical model of the human thalamus.²⁶ Our study was designed to develop and evaluate a workflow that augments the conventional indirect neurosurgical targeting method with complementary information about the thalamic geometry, extracted from MR images. We hypothesize that the correlation between the MR imaging observable thalamic outlines and the internal structures (nuclei) can feasibly determine the functions that transfer coordinates from a statistical shape model to the individual subject space more accurately than determination traditionally performed with the rigid registration of a single atlas. Furthermore, we propose the use of probabilistic diffusion tractography to independently and complementarily confirm the locations of the atlas-based predictions for selected nuclei with specific thalamocortical connectivity and the implementation of such subject-specific connectivity-based intrathalamic markers into the individualization workflow of the atlas. The clinical implementation of such workflow must be preceded by validations that are based on the parallel histologic work-up and postmortem MR imaging to reveal fine-grained anatomy.

Materials and Methods

Postmortem Data: Subjects, Imaging Protocol, and Image Processing

A 2-fold approach was used for subject selection: postmortem and in vivo evaluations. For postmortem evaluation, we accessed the high-resolution structural MR imaging scans of the 3 brains on which the statistical atlas generation was based (for further description on the histologic work-up and atlas construction, see the relevant works by Morel⁷ and Krauth et al²⁶); these were complemented by 2 additional specimens. Before histologic processing, high-resolution postmortem MR imaging was performed on 3T or 7T scanners (Intera Achieva; Philips Healthcare, Best, the Netherlands), though with heterogeneous MR imaging sequences (Table 1). The images most feasible for delineating thalamic nuclei of interest were accessed, and borders of nuclei were manually drawn by using the Slicer 3D software (http://www.slicer.org/).²⁷ It was only possible to select a limited number of nuclei that are sufficiently clearly distinguishable and can be used for quantitative evaluations of atlas-to-patient registrations. For each specimen, the MR imaging protocol and the delineated nuclei are summarized in Table 1.

Table 1:

Postmortem imaging protocol and the delineated thalamic nuclei^a

Brain Specimen No.	Processed Hemispheres	MRI Scanner	Sequence Used for Nuclei Depiction	TE/TR (ms), Averages	Voxel Dimensions (mm), Acquisition Matrix Size	Delineated Thalamic Nuclei
1	Left and right	Philips Achieva 3T	Axial, T2WI, TSE	80/3000, 4 averages	0.21 * 0.21 * 2, matrix: 400 * 394	AV
2	Left and right	Philips Achieva 3T	Axial, PDWI, TSE	24/3000, 30 averages	0.16 * 0.16 * 1.25, matrix: 528 * 525	AV, MDmc, MDpc + pl, CM, MGN
3	Left	Philips Achieva 3T	Sagittal, PDWI, TSE	24/3500, 30 averages	0.15 * 0.15 *2, matrix: 532 * 530	AV, CM, MGN, LGN
4	Left and right	Philips Achieva 3T	Axial, T1WI, IR, TSE	20/2000, TI: 800 ms, 8 averages	0.28 * 0.28 * 0.3, matrix: 784 * 784	AV
5	Left	Philips Achieva 7T	3D, PDWI, SE	14/900, 1 scan	0.14 * 0.14 * 0.14, matrix: 768 * 768	AV, CM, MGN

Note:—IR indicates inversion recovery; AV, anterior ventral nucleus; MDmc, mediodorsal nucleus magnocellular part; MDpc, mediodorsal nucleus parvocellular part; MDpl, mediodorsal nucleus paralamellar segment; CM, Centre médian nucleus; MGN, medial geniculate nucleus; LGN, lateral geniculate nucleus; PDWI, proton-density weighted imaging.

^aAbbreviations of thalamic nuclei are in accordance with the nomenclature used by Morel.^7,9

In Vivo Data: Subjects, Imaging Protocol, and Image Processing

Forty healthy adults were recruited to demonstrate the applicability of the developed thalamus atlas individualization workflow (female/male, 21:19; subject age, 33.8 ± 12.7 years). In vivo imaging examinations were preceded by the informed written consent of the subjects, while all the other experiments in this report were approved by the relevant institutional review boards. Images were obtained by using a clinical 1.5T MR imaging system (Siemens Magnetom Vision Plus; Siemens, Erlangen, Germany) equipped with an 8-channel phased-array head coil. Anatomic scans of the whole brain (0.45 × 0.45 × 0.83 mm voxel size) were acquired with a T1-weighted magnetization-prepared rapid acquisition of gradient echo sequence. Diffusion-weighted images were acquired by using a single-shot pulsed-gradient spin-echo EPI sequence (TR = 10,000 ms, TE = 118 ms); 12 different directions of diffusion-encoding magnetic gradients were used (b-value, 1000 s/mm²). Each volume consisted of 55 transverse sections (section thickness: 3 mm; voxel size: 0.97 × 0.97 mm).

Identification of Thalamic Connectivity Domains by Using Probabilistic Tractography

Spatial standardizations of in vivo MR images were performed by using a nonlinear deformation algorithm. To map the DTI space to the standard neuroimaging space, we registered fractional anisotropy images with the FMRIB58 FA template (http://www.fmrib.ox.ac.uk/), while T1 anatomic images were registered with the MNI152 T1 template. For each in vivo validation subject, probabilistic tractography was initiated from the entire visible thalamus volume, as delineated on the T1-weighted template. Fiber tracking was performed in the DTI space. Only the seed masks and the results were transferred to the standard space; hence, no reorientation of the tensors was necessary. The connection strength between each seed voxel and every remote brain voxel was estimated as the probability of tracts reaching their target through a trajectory guided by the model of local diffusion characteristics. For each thalamic voxel, a counter variable increased when the emitted tracing samples entered any of the cortical masks, consequently resulting in 53 back-projected probability maps, corresponding to 53 cortical territories delineated by using the Harvard-Oxford Atlas (http://www.fmrib.ox.ac.uk/fsl/data/atlas-descriptions.html#ho, for more details on this procedure, see the relevant works cited.^14,18–20) The templates, atlas, and registration algorithms are distributed with the FMRIB Software Library.²⁸ COM points were determined for interconnections with each cortical region marking the geometric center of the distribution of connections within the thalamus; this was done by averaging the thalamic voxel coordinates with weights derived from the connectivity strength. The 10 most reproducible COM points were defined as intrathalamic DTI-based landmarks and were transformed to the subject's anatomic images.

Statistical Shape Model–Based Registration of Atlas Data

SSMs enable the exploitation of prior knowledge about the interindividual variability of the morphology of an organ.²³ Compared with purely continuity- or smoothness-based constraints, these models authorize an interpolation of unobserved parts of the anatomy, which is statistically plausible with respect to a set of training shapes. High-resolution 3D models of 7 histologically processed thalami were available as training samples for a statistical shape model (point-distribution model), describing the morphologic variability of the thalamus and its nuclei among these 7 samples. While the outlines of the thalamus were determined from the histologic data and can consequently be used for guiding registrations, the inclusion of DTI-based landmarks required additional hypotheses to be formulated. We assumed that the average coordinates of the connectivity centers measured in the MNI space on a cohort of 40 healthy volunteers coincide with the matching shape from the SSM. Second, we relied on numeric interpolation to propagate the location of these connectivity centers from the MNI space back to each of the original training samples of the SSM. This resulted in augmenting the previous statistical shape model with DTI landmark data.

The registration procedure was carried out by minimizing the distance between the model and the observation data, measured as the average distance between pairs of corresponding points between both datasets. The correspondences were estimated by matching the closest points between the observed contours and the outer boundaries of the current SSM model. On the basis of the estimated correspondences, we derived simultaneously the pose (by using a similarity transform—that is, translations, rotations, and isotropic scaling) and shape parameters by relying on regularized least-squares regression, as proposed by Blanz et al.²⁹ The correspondence establishment and parameter estimation was iterated until no significant changes occurred, in an iterative closest point-like algorithm.³⁰

Study Rationale

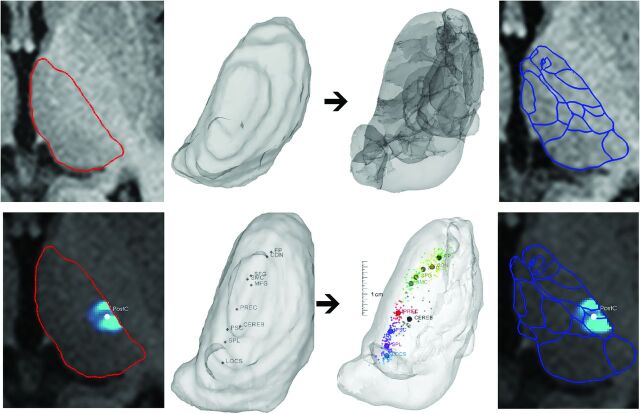
We propose 2 methods to use the above-mentioned sources of information when creating individualized target maps: 1) an outline-based SSM method by using the visible thalamus outlines as predictors of thalamic structure, and 2) a hybrid SSM method by using a combination of the outlines and DTI-based internal landmarks, with a weighting factor to balance evenly the contribution of the 2 types of predictors. The former can be tested in the in vivo and postmortem datasets, while the latter was tested only on in vivo data. Figure 1 demonstrates the single-level subject information of thalamus anatomy used, including the MR imaging–visible borders and the intrathalamic landmarks.

Fig 1.

Atlas-to-patient registration by the outline-based SSM and the hybrid SSM method. First row: alignment of atlas data (image 3) to the subject's gross, visible thalamus outlines through a statistical shape model–based registration (image 1, red outlines: thalamus borders; image 2: 3D visualization). Second row: atlas-to-patient registration by using the hybrid SSM method. Matching is guided by the weighted contribution of the gross visible thalamus borders and the DTI-based intrathalamic markers of connectivities (panel 1: visible outlines and the center-of-mass point of the connectivity map to the postcentral gyrus in panel 2; panel 3: alignment of thalamus outlines and DTI markers). The resulting thalamus maps are given in the rightmost panel. Abbreviations of the connectivity-based landmarks are given according to the cortical target areas used. FP indicates frontal pole; MFG, middle frontal gyrus; SFG, superior frontal gyrus; CDN, caudate nucleus; SMC, supplementary motor cortex; PREC, precentral gyrus; PSC, postcentral gyrus; SPL, superior parietal lobule; CEREB, cerebellum; LOCS, lateral occipital cortex, superior division.

In the On-line Appendix, we provide detailed supporting technical descriptions of the methods used for the thalamus shape-model construction and shape model–based registrations and give formulations to incorporate connectivity-based landmarks into the SSM.

Evaluation of Prediction Accuracy

For the evaluation of the accuracy of predicting various structures, surface-to-surface distances were determined with a dedicated software tool (MeshValmet; http://www.ia.unc.edu/dev/download/MeshValmet/MeshValmet.html).³¹ We compared the hand-segmented ground truth thalamus contours (which served as a reference standard) with the predicted borders for in vivo and postmortem samples. Furthermore, the Dice coefficient was used for reporting volumetric overlaps. Nuclei were manually outlined on postmortem MR images and tested for accuracy by using the outline-based SSM. The contrasts were eligible for delineating such nuclei; comparisons with histologic sections are provided in On-line Fig 1. Three of the validation brains were used for creating the mean 3D atlas and the SSM; hence, to avoid bias, we propose the use of leave-one-out cross-validation (ie, each validation brain is left out of the SSM when we evaluated accuracies on that particular brain). This approach quantifies the error for new observations. To compare the prediction accuracy with more traditional atlas-to-patient alignments, we applied the same evaluations after performing a rigid transformation that matches the anterior commissure and posterior commissure points of the atlas and the subject's MR images. Additionally, an affine surface-based registration was performed that matched the thalamic contours of the atlas and subject images.

We hypothesized that DTI-based mapping of thalamocortical connections represents independent and complementary predictors for the location of individual groups of nuclei and that this information can be used to have visual control over the locations of predicted nuclei. Ten selected intrathalamic markers were mapped back to the individual SSM training samples (On-line Appendix); their predicted locations can be compared with the individually acquired ground truth data. Another option was to test the connectivity-nuclei correspondences; this step required the putative coupling of atlas-defined nuclei and cortical regions of known interconnections to the selected nuclei. We measured the sum of tractography tracing samples (C) to a cortical region (eg, precentral gyrus) emerging inside the predicted nucleus (eg, VA or VL) and from the total thalamic volume. The C_inside/C_total ratio would give an estimated overlap of the atlas-based and DTI-based borders, referred to as the correspondence index. We assumed that overlap increases if the applied registration method is more efficient in predicting individual thalamic topography.

Results

Outline-Based SSM Alignment of Atlas Data

With the outline-based SSM method, the mean distance between the manually delineated reference and predicted thalamus outlines was 0.56 ± 0.09 mm; after the alignment by ACPC points, it was 1.24 ± 0.44 mm and 0.71 ± 0.07 mm for the surface-based affine registration. This improvement was significant compared with either the ACPC or surface-registration methods (paired Student t test, P < .001); no interhemispheric difference of accuracies was found.

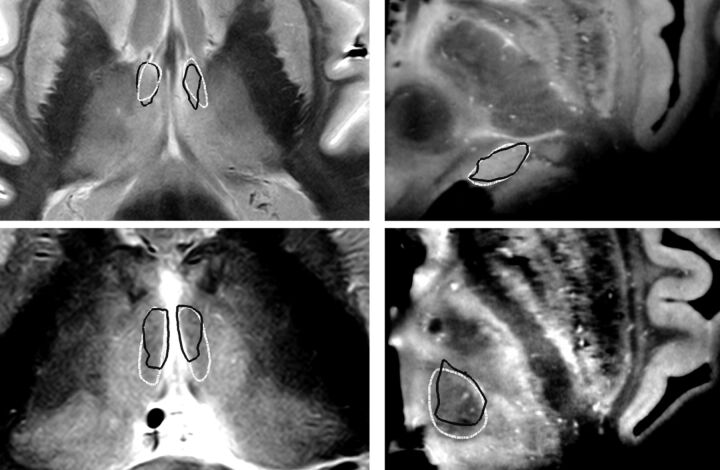
The results of the same evaluation for postmortem thalamus outlines were the following: outline-based SSM: 0.45 ± 0.07 mm; ACPC alignments: 1.49 ± 0.25 mm; and affine registration of a single atlas: 0.54 ± 0.06 mm (significance of improvement: P < .001). If we averaged across all the delineated nuclei, the prediction error of their borders was the following: outline-based SSM: 0.65 ± 0.32 mm; ACPC matching: 1.24 ± 0.68 and 1.07 ± 0.72 mm when using the affine registration described earlier. When evaluating the improvement by the Dice coefficient, we observed similar trends. Detailed results for individual nuclei are summarized in Table 2 and in On-line Table 1. Figure 2 illustrates the postmortem evaluations.

Table 2:

Evaluation of accuracy of various atlas-to-patient registration methods on postmortem samples^a

Structure	No.	Outline-Based SSM Registration	12 df Surface Matching	ACPC Matching
AV	8	0.77 mm D: 0.53	1.05 mm D: 0.41	1.91 mm D: 0.2
MDmc	2	0.93 mm D: 0.46	1.99 mm D: 0.41	0.73 mm D: 0.52
MDpc	2	0.52 mm D: 0.73	0.87 mm D: 0.62	0.92 mm D: 0.53
MGN	4	0.46 mm D: 0.64	1.09 mm D: 0.48	0.75 mm D: 0.57
LGN	1	1.19 mm D: 0.72	0.46 mm D: 0.39	0.91 mm D: 0.44
CM	4	0.41 mm D: 0.78	0.90 mm D: 0.57	0.92 mm D: 0.54
Thalamus outline	8	0.45 mm D: 0.89	0.54 mm D: 0.87	1.49 mm D: 0.71

Note:—D indicates the Dice coefficient of overlaps; AV, anterior ventral nucleus; MDmc, mediodorsal nucleus magnocellular part; MDpc, mediodorsal nucleus parvocellular part; CM, Centre médian nucleus; MGN, medial geniculate nucleus; LGN, lateral geniculate nucleus.

^aWe were able to perform such validations on a limited number of reference images. Geometric errors are given as median vertex distances measured between the reference standard (manual delineation of MRI data) and the predicted meshes and as the Dice coefficient of overlaps. For predictions, we have applied the outline-based SSM, conventional ACPC matching, and a surface-based 12 df registration method. Abbreviations of thalamic nuclei are in accordance with the nomenclature used by Morel.^7,9

Fig 2.

Postmortem evaluation of the SSM-based target map prediction method: examples for the delineation of individual visible nuclei. The generation of thalamic nuclei was performed by using visible thalamus outlines as predictors of individual geometry. Left panels: axial sections proton attenuation–weighted MR images (brain specimen 2); right panels: axial sections, T1-weighted ex situ MR images (brain specimen 5). White outlines: manual reference nuclei borders; black outlines: SSM-based prediction of nuclei borders. Top left: anterior ventral nucleus. Top right: medial geniculate nucleus. Bottom left: mediodorsal nucleus, magnocellular part. Bottom right: centromedian nucleus.

Hybrid SSM Method, Individualization by Using DTI-based Intrathalamic Landmarks

We selected 10 DTI-based intrathalamic landmarks with the lowest spatial scatter, and data were projected into the space of the shape models, hence forming the training samples for the hybrid method. The SD of locations in the standard space was, on average, 1.54 mm for the left thalamus and 1.47 mm for the right. The following tractography-based markers were used, each named according to the remote target territory used during probabilistic tractography and by using the nomenclature of the Harvard-Oxford Atlases: frontal pole, superior and middle frontal gyri, pre- and postcentral gyrus, supplementary motor cortex, superior parietal lobule, lateral occipital cortex, caudate nucleus, and cerebellum. Three aspects were considered when using individual DTI thalamocortical connectivity data: 1) to use DTI landmarks as the reference standard of individual patterns of structural connectivities within the thalamus and observe the predicted nuclei, keeping in mind the known biologic correspondences; 2) to calculate the location (COM points) of internal landmarks as they are determined from the SSM and to compare them with the DTI-based ground truth localizations; and 3) to evaluate whether embedding DTI-based landmark data is improving the accuracy of the prediction of thalamic structures.

With the hybrid method, the error for the in vivo group's thalamus outlines was 0.83 ± 0.18 mm. The accuracy was significantly higher than after ACPC-based registrations but lower than the outline-based SSM registration (P < .001).

Pair-wise distances of predicted internal landmarks and ground truth were the following: ACPC alignments: 3.21 ± 1.98 mm; affine registration: 2.87 ± 1.42 mm. Results improved significantly (P < .001) with the use of SSM: outline-based SSM: 2.46 ± 1.42 mm; hybrid SSM: 1.48 ± 1.01 mm.

The correspondence between the individual thalamocortical connectivity maps and nuclei was calculated; we report results for 7 selected nuclei-connectivity map pairs in Table 3. The correspondence indices significantly improved when using outline-based SSM and the hybrid SSM.

Table 3:

Testing the correspondences between the predicted thalamic nuclei locations and biologically coupled DTI-based thalamocortical connection maps^a

Cortical Connection Area	Frontal Pole	Superior Frontal Gyrus	Precentral Gyrus	Postcentral Gyrus	Postcentral Gyrus	Cerebellum	Lateral Occipital Cortex	Overall Results
Associated nucleus	VA	VLa	VLpv	VPLa	VPLp	VLpv	PuL
ACPC registration	0.46 ± 0.14	0.31 ± 0.16	0.38 ± 0.2	0.14 ± 0.12	0.3 ± 0.19	0.09 ± 0.09	0.08 ± 0.08	0.25 ± 0.2
Outline-based SSM	0.49 ± 0.12	0.38 ± 0.15	0.41 ± 0.16	0.14 ± 0.12	0.44 ± 0.15	0.14 ± 0.09	0.16 ± 0.1	0.31 ± 0.19
Hybrid SSM	0.5 ± 0.12	0.41 ± 0.15	0.44 ± 0.14	0.17 ± 0.11	0.48 ± 0.13	0.15 ± 0.08	0.13 ± 0.1	0.33 ± 0.2
Difference between outline-based SSM and ACPC registration	6.9%b (P = .021)	22.29%c (P < .001)	7.7% (P = .212)	5.3% (P =.666)	47.7%c (P < .001)	52.8%c (P < .001)	97.2%c (P < .001)	23.3c (P < .001)
Difference between hybrid SSM and ACPC registration	9.1%b (P = .011)	31.1%c (P < .001)	15.1%b (P =. 012)	24.6% (P = 056)	59.6%c (P < .001)	58.5c (P < .001001)	54.0%c (P < .001)	28.8%c (P < .001)
Difference between hybrid SSM and outline-based SSM registration	2.0% (P = .214)	7.3%b (P = .023)	6.8% (P = .056)	18.3%b (P = 013)	8.0%b(P =. 019)	3.7% (P = .562)	−21.9%c (P < .001)	4.5%c (P < .001)

Note:—PuL indicates lateral pulvinar.

^aCorrespondence indices (mean ± SD) are given as the ratio of tractography samples reaching 1 particular cortical area from the voxels of a nucleus and from the entire thalamus volume. Comparisons of alignment methods were tested by using a paired Student t test.

^bResult is significant at the .01 < P < .05 level.

^cResult is significant at the P < .01 level.

Detailed numeric data of the prediction accuracies (including results for individual nuclei and images) are given in the On-line Appendix (On-line Tables 1 and 2). The described method allowed us to project the mean 3D representation of the thalamus atlas to the MNI152 reference space with standardized meshes and volumetric representations (On-line Fig 2).

Discussion

The impetus of our study was to present a new design of atlas-to-patient registrations for image-guided surgical therapies that feature an intermediate step from indirect atlas-based targeting toward the direct image-based determination of target loci. Many studies adapted DTI-based tracking of thalamocortical connections as a noninvasive in vivo method to depict the internal topography of the thalamus.^18–20 As a further step in this direction, we developed a target map–generation method for the human thalamus, which combines 3 main sources of information: 1) previous knowledge about human thalamus anatomy in the form of a statistical 3D atlas combining 7 different histologic atlases, 2) single-subject-level imaging information on visible geometry of the thalamus, and 3) individual in vivo maps of thalamocortical connectivities.

As suggested by others,⁸ an ideal representation of brain anatomy as a digital atlas should provide a multidimensional set of data incorporating the uncertainty of shape, knowing that this uncertainty mainly originates from interindividual variability. We demonstrated a way to use multidimensional data by both incorporating multiple atlases and including multiple modalities (eg, histologic and functional or connectivity data). Postmortem evaluations of individual nuclei localization demonstrated the feasibility of using the outline as a predictor of internal structure, with the outline-based predictive capabilities of the SSMs in good agreement between the aligned data and nuclei borders. When predicting the outlines of in vivo thalami, we revealed median errors of 0.56–0.83 mm, which are comparable with the resolution of anatomic imaging protocols. Outline-based SSM was found superior to the ACPC-based or surface-based affine matching of the mean atlas. This finding can be explained by the few degrees of freedom that the ACPC method offers and also the limited correspondence between anatomic landmarks and the actual thalamus shape.

Atlas-to-patient matching by nonlinear registrations was previously evaluated for anatomic precision; however, such tests have a lack of criterion standards, and direct comparison of evaluations is also problematic due to the different validation metrics used. D'Haese et al³² investigated the accuracy of a nonlinear registration method for the STN and revealed distances from the group centroid of 2.16–2.22 mm. Castro et al³³ describe the estimation errors for the location of the STN with automatic algorithms; additionally, a comparison is made between expert-driven localization and registration techniques. The estimation error was 1.96 mm when using an ACPC alignment strategy and 1.72–1.77 mm with nonlinear matching algorithms. A study by Chakravarty et al³⁴ revealed that the Talairach coordinate–based targeting misplaced the thalamus outlines by 2.44 ± 0.68 mm. There is converging evidence that image-based atlas-to-patient alignment tools outperform methods like the ACPC alignment technique; this was also indicated by our postmortem evaluations. Other studies provided a way to directly depict the subthalamic nucleus and the basal ganglia³⁵; however, to the best of our knowledge, this is the first study to evaluate the precision of predicting thalamic nuclei (ie, not the subthalamic nucleus) by using postmortem high-resolution imaging as a standard reference.

To provide an in vivo assessment of the reliability in terms of predicting individual nuclei or groups of nuclei, we used DTI-based landmarks. In agreement with the results of a study by Traynor et al,²¹ we reported the lateral regions of the thalamus to be more reproducible landmarks for probabilistic mapping; the COM points of the connections to the precentral gyrus, postcentral gyrus, supplementary motor cortex, and frontal gyri showed the smallest spatial spread. The medial regions of the thalamus tend to have more divergent and less specific distribution to the cortex than the lateral parts¹⁸; these findings are in agreement with well-known observations in experimental animals, including primates.³⁶ We provided a method to compare the correspondence of cortical connectivity within the thalamus and the actual nuclei after various alignments of atlas data (Table 3.). The small correspondence indices (8%–50%) hallmarked the fact that connectivity distributions from 1 cortical domain do not respect the cyto- or myeloarchitectural borders of the nuclei but cover larger nuclear groups. The hybrid-SSM method turned out to be a compromise between the accuracy observed on the outlines and the correspondence of internal structures evaluated by quantifying the overlap between thalamocortical connections and selected nuclei (measured by the correspondence index). While the outline prediction accuracy was reduced, the agreement with connectivity data increased. Similar connectivity-nuclei correspondences were evaluated to test the applicability of DTI-based connectivity maps as a direct visualization of intrathalamic topography; this evaluation confirmed our observation of limited correspondence for some nuclei.^37,38 Preoperative DTI in the neurosurgical setting has been suggested as a marker of individual organization within the thalamus.³⁹ We conclude that better understanding of the correspondence between DTI-based and cytoarchitectural subdivisions would require validation studies with consecutive postmortem DTI imaging and histology.

Our study had several limitations. The observed accuracies of predicting individual nuclei were determined on high-resolution postmortem images, and the protocols of such scans were different from those of routine imaging settings; these features make the evaluation of clinical feasibility problematic. To examine the correspondences between imaging-based information (nuclei borders, DTI-based subdivisions) and the actual underlying cytoarchitecture, one should access postmortem in situ images, including DTI, and perform consecutive histologic processing on the same sample. We were only able to perform this for 3 brains and without an option for DTI; however, we expect to perform a preliminary study on the probabilistic tractography-based and histologic evaluation of the same sample. The acquired diffusion tensor images were compromised by the anisotropic dimensionality of voxels, which could account for the observed larger scatter of DTI-based landmarks. Only 1 fiber population per voxel was modeled; this could raise the possibility of incorrectly assessing the probability of interconnection to a particular cortical area or, for instance, the cerebellum. However, a study suggested that during the connectivity-based segmentation of the thalamus, secondary or higher level fibers become less important.¹⁵

Conclusions

Using multidimensional atlas data and subject-specific information provided by clinically feasible MR imaging and DTI protocols, the proposed method potentially reduces the uncertainty of target localization and results in submillimeter accuracy. Two approaches were developed that use statistical shape model–based registration of atlas data, constrained by MR imaging–visible thalamus borders and a weighted contribution of DTI-based landmarks and outlines. Novel image-guided therapeutic modalities like transcranial MR imaging–guided focused ultrasound surgery⁴⁰ necessitate the paradigm shift from indirect probabilistic targeting toward such frameworks offering higher spatial accuracy and using information of individual geometry or function. Our quantitative evaluations of accuracy presumably facilitate the acceptance of such atlas-matching techniques by neurosurgeons.

ABBREVIATIONS:

ACPC

anterior/posterior commissure

COM

center of mass

MNI

Montreal Neurological Institute

SSM

statistical shape model

STN

subthalamic nucleus

VA

ventral anterior nucleus, parvocellular part

VL

ventral lateral nucleus

VLa

ventral lateral nucleus, anterior part

VPLa

ventral posterior lateral nucleus, anterior part

VPLp

ventral posterior lateral nucleus, posterior part

VLpv

ventral lateral nucleus, posteroventral part