Recent developments in empirical atomistic force fields for nucleic acids and applications to studies of folding and dynamics

Abstract

Nucleic acids play critical roles in carrying genetic information, participating in catalysis, and preserving chromosomal structure. Despite over a century of study, efforts to understand the dynamics and structure-function relationships of DNA and RNA at the atomic level are still ongoing. Molecular dynamics (MD) simulations augment experiments by providing atomistic resolution and quantitative relationships between structure and conformational energy. Steady advancements in computer hardware, software, and atomistic force fields (FFs) over 40 years have facilitated new discoveries. Here, we review nucleic acid FF development with emphasis on recent refinements that have improved descriptions of important nucleic acid properties. We then discuss several key examples of successes and challenges in modeling nucleic acid structure and dynamics using the latest FFs.

Nonpolarizable nucleic acid force field development

Nucleic acid dynamics are governed by many interconnected properties, namely base stacking, hydrogen bonding, interactions with water and ions, sugar puckering, glycosidic torsion (χ) rotation, and phosphodiester backbone conformational sampling. For accurate modeling in MD simulations, a FF must be well balanced to capture these effects. Backbone properties are particularly challenging as each torsion in the phosphodiester backbone (Figure 1 a) is coupled. Accurate electrostatics are also key for modeling interactions of highly charged nucleic acids with water and ions. As such, most FF development and refinement has focused on accurately modeling these interactions.

Figure 1.

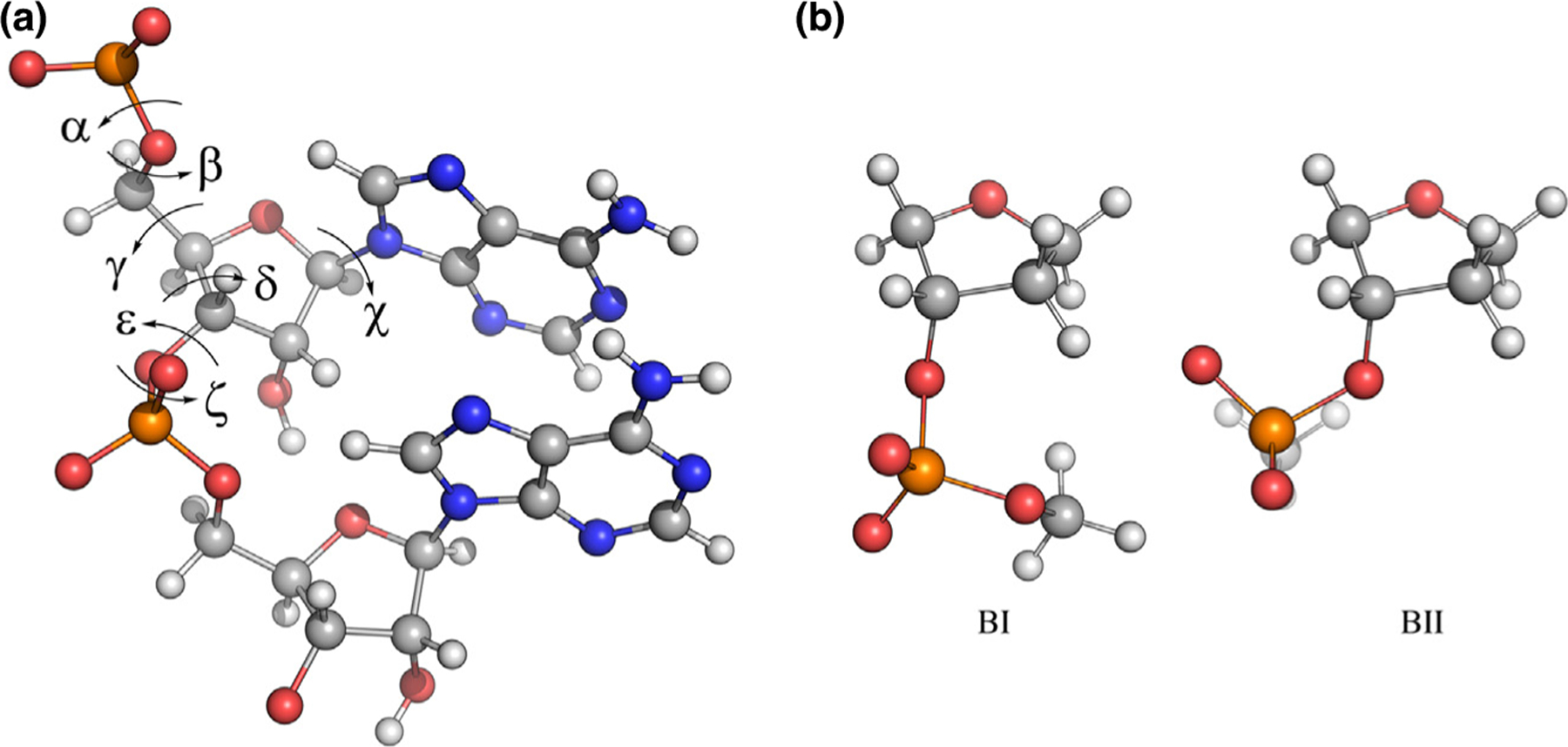
Key dihedrals and conformations in nucleic acids. (a) r(AA) dinucleotide with backbone and glycosidic torsions labeled. (b) BI and BII substates of DNA as represented by a model compound encompassing the deoxyribofuranose ring and 3’-methylphosphate group.

Most FFs applied in MD simulations to date have relied on a pairwise-additive approximation to treating electro-statics, neglecting explicit electronic polarization and instead assigning partial atomic charges assuming a mean-field polarization effect. The two most popular nonpolarizable FF families for simulating nucleic acids are AMBER and CHARMM. Here, we review key milestones in the development of each FF.

The first all-atom nucleic acid FF in the AMBER lineage, ff94, was introduced in 1995 by Cornell et al. [1] A key feature of ff94 was the assignment of partial charges by fitting to the quantum mechanical (QM) electrostatic potential (ESP) around model compounds [1]. The use of symmetry constraints in parametrization, referred to as restrained ESP (RESP) fitting [1], is central to the success of AMBER nucleic acid FFs and was used in subsequent refinement [2]. The ff98 [3] and ff99 [4] AMBER parameter sets added DNA-specific torsional parameters and improved duplex geometric properties. ff99 sufficiently described hydrogen bonding, base stacking, and base pairing on short time scales (<10 ns) [5–8]. However, longer simulations (>50 ns) with ff99 revealed incorrect modeling of γ-trans backbone conformers that resulted in B-DNA collapse and non-native RNA helical twist [9]. The parmbsc0 parameter set reparametrized the α and γ dihedrals to reduce non-native α/γ conformations and helical twisting, at the expense of overpenalizing γ-trans conformations that do occur in nucleic acids [10,11]. Another major issue in the ff99 FF lineage was the adoption of ‘ladder-like’ RNA structures that were attributed to incorrect χ sampling. The ff99bsc0x_OL3 FF was developed to prevent incorrect χ shifts and resulting non-native RNA helical twist, but the γ-trans penalty still destabilizes many noncanonical nucleic acid structures [11]. The AMBER parmbsc1 FF was built upon parmbsc0 by refining sugar puckering and χ, ε, and ζ dihedrals [12], and showed convincing improvement over parmbsc0 in exhaustive simulations of A-DNA, B-DNA, and Z-DNA. Different AMBER FFs may be combined with various water models to simulate specific nucleic acid systems [12,13]. Examples of such efforts will be described below. Further information on AMBER DNA and RNA FF parametrization and validation has been reviewed elsewhere [2,13,14].

The CHARMM FF is also widely used in simulating nucleic acids. The first parameter set, CHARMM22 (C22), was introduced in 1995 [15]. Subnanosecond MD simulations of DNA duplexes were stable, however, C22 overstabilized A-form DNA [16–18]. Foloppe et al. subsequently developed the CHARMM27 (C27) FF in 2000 [19,20] by refining backbone dihedrals, sugar puckering, and the glycosidic linkage to reproduce macromolecular target data from model compounds [19]. C27 yielded an improved model for B-DNA and RNA hairpins, and early simulations (<5 ns) yielded expected behaviors in hydrogen bonding, backbone dihedrals, and sugar puckering [20]. Limitations of C27 included modeling properties like groove width, overpopulation of the BI backbone substate in DNA (Figure 1b), and opening of Watson-Crick base pairs in RNA, prompting the development of CHARMM36 (C36) [21,22]. For DNA, C36 optimization focused on ε and ζ backbone dihedral angles as well as deoxyribose sugar puckering [21], while optimization of the RNA parameters focused on 2′-hydroxyl dihedral sampling [23]. More recently, longer C36 simulations have revealed that this FF may still suffer from aberrant base-pair opening [23] and possibly RNA helix fraying [2].

As is clear from the progressive refinement of the AMBER and CHARMM FFs, achieving adequate balance in the FF, especially in critical backbone conformational sampling, remains a challenge. Despite these shortcomings, both the AMBER and CHARMM nucleic acid FFs have been applied to investigations of many diverse structures and have provided important insights on their dynamics. Still, targeted improvements can be made. Recently, Kührová et al. developed and applied a generalized interaction-specific variant (gHBfix), that can fine-tune select nonbonded interactions like hydrogen bonding to improve the accuracy of simulated RNA structural properties [24]. This strategy was used to improve upon ff99bsc0x_OL3 and has been extended to improve hydrogen bonds involving terminal nucleotides (tHBfix) [24,25]. Both gHBFix and tHBfix have improved the conformational ensembles of RNA tetranucleotides and tetraloops in the AMBER FF and are promising strategies to improve nucleic acid FF performance without extensive refinement that may introduce new imbalances to the model [24,25]. Such select tuning can, in a sense, be viewed as another type of approximation of an electrostatics model that includes directionality, that is, induced polarization.

Polarizable force fields for nucleic acids

Polarizable FFs that explicitly account for electronic polarization have recently emerged as promising tools for modeling nucleic acids. The AMOEBA FF [26] is a multipole-induced dipole model in which each atom is assigned dipole and higher-order multipole moments. Inductive effects are calculated between ‘polarization groups’ that interact via permanent electrostatics and induced dipoles. The classical Drude oscillator FF [27] represents electronic degrees of freedom via negatively charged auxiliary particles (Drude oscillators) that are connected to non-hydrogen atoms via harmonic springs.

Both the AMOEBA [28] and Drude [29–32] FFs have complete parameter sets for nucleic acids, and the underlying approach to parametrization of both was similar. Parameter fitting in the AMOEBA FF targeted the QM ESP of model compounds and conformational energetics of sugar puckering and other dihedral rotations [28,33]. A key element of the AMOEBA FF parametrization was the inclusion of solvent effects in the QM calculations using a polarizable continuum model (PCM). The Drude FF targeted similar quantities (molecular dipole and polarizability, conformational energetics, base stacking, and hydrogen bonding) but did not utilize PCM in its QM calculations. Instead, the solvent response is incorporated into the FF by targeting scaled molecular polarizabilities and explicit water interactions with model compounds. The current Drude FF for nucleic acids is denoted Drude-2017 [30–32] and is a revision of Drude-2013 [29], the first polarizable FF for DNA. Extended simulations (>200 ns) with Drude-2013 revealed instability in duplex DNA that was attributed to systematically weak base-stacking interactions that were rectified in the Drude-2017 parameter set by explicitly targeting QM stacking energies [31], yielding stable microsecond simulations of A-DNA, B-DNA, and Z-DNA duplexes [32].

Both the AMOEBA and Drude nucleic acid FFs have been validated in microsecond simulations of duplex DNA and RNA, as well as prototypical RNA secondary structure motifs [32,34–37]. Both of these FFs yield good agreement with experimental properties such as base pairing, base stacking, backbone torsions, sugar puckering, groove geometries, and the conversion between A-form and B-form DNA in response to changes in solvent [28]. The main limitation in using polarizable FFs is reduced simulation speed; however, the implementation of AMOEBA in Tinker-HP, an MPI-enabled parallel package for MD simulations [38], and in the graphical processing unit (GPU)-accelerated OpenMM software [39], has made these polarizable simulations more accessible. Similarly, the Drude model is available in a wide range of high-performance simulation software, including CHARMM [40], NAMD [41], GROMACS [42], and OpenMM [43]. The use of GPU hardware greatly accelerates polarizable simulations and further reduces barriers to their routine implementation in MD studies on nucleic acids.

Simulations of water and ion interactions with nucleic acids

Hydration patterns around nucleic acids are of interest because water molecules help stabilize DNA and RNA structure and modulate ion binding [44]. Canonical A-form RNA is stabilized by a water-mediated hydrogen bond between the 2’-hydroxyl group and the nitrogenous bases; release of this water with concomitant rotation of the 2’-hydroxyl toward backbone atoms is associated with flexibility and the adoption of noncanonical geometries [45]. Recently, Bergonzo and Grishaev assessed explicit and implicit solvent models in simulations of a model RNA helix. They showed that judicious inclusion of NMR restraints with MD simulations can improve accuracy, regardless of the choice of solvent representation, though for unbiased simulations, the choice of water model is particularly important for achieving agreement with NMR observables [46]. Their study indicates that the FFs applied are robust and demonstrates that combining modern FFs and experimental data can help refine experimental structures to improve descriptions of nucleic acid dynamics [46]. Another interesting simulation study focused on nucleobase-water interactions to understand the contributions of lone pair–π and OH–π interactions, which are generally considered weak, in stabilizing RNA structural motifs [47]. Using the C36 FF and QM calculations, Kalra et al. showed that these interactions are uniformly favorable and are related to the ESP of all four nucleobases, a principle that may be broadly applicable to highly ordered nucleic acid structures [47].

Like water, monovalent and divalent ions play an integral role in governing the folding and dynamics of nucleic acids. Accurately modeling ion interactions with nucleic acids in MD simulations is of critical importance and has been a persistent challenge in the field. One particular aspect of this challenge is delineating the roles of divalent metal ions like Mg²⁺, which often have specific structural roles in folded RNA, from general screening effects of monovalent ions. Fischer et al. showed that Mg²⁺ and Na⁺ interactions differ at high and low concentrations and in simulations of helical and complex folded RNA [48]. At lower concentrations, both ions showed increased direct interactions, but overall, Mg²⁺ ions better stabilized these RNA structures via close, water-mediated interactions at experimentally determined binding sites. These findings demonstrate the importance of salt concentration and Mg²⁺:RNA interactions in MD simulations. Further, Nguyen et al. recently employed a coarse-grained RNA model with a reference interaction site model (RISM) for Mg²⁺:phosphate interactions while treating monovalent cation effects implicitly [49]. With this approach, they were able to calculate folding free energies of RNA in agreement with experimental findings, particularly due to strong interactions of Mg²⁺ with partially folded RNA intermediates. This study serves as a strong foundation for future theoretical work on ion-induced nucleic acid folding [49].

The development of the Drude FF explicitly included fine-tuning of ion interactions with nucleic acids against QM target data, including common monovalent (Li⁺, Na⁺, K⁺, and Rb⁺) and divalent (Mg²⁺) ions [50,51]. As a result, MD simulations with the Drude FF have reproduced experimental solution X-ray scattering profiles for duplex DNA in solutions of Li⁺, Na⁺, K⁺, and Rb [52], as well as proposing a mechanism by which water-mediated interactions between solvated cations and DNA perturb minor groove widths [52]. Further, mutual polarization between nucleobases and water was critical to computing accurate free-energy barriers to DNA base flipping [53]. Together, these findings suggest that subtle effects of ions and base hydration are modeled accurately using this polarizable FF and the Drude model may serve as the basis for new insights into nucleic acid structure and dynamics.

RNA folding simulations

Exploring RNA folding with MD simulations has been a longstanding challenge, as a reliable description of folding pathways and the native-state conformational ensembles depends on balance among base-base, base-backbone, and base-water interactions. Further, noncanonical hydrogen-bonding interactions are prevalent in many RNA motifs that are not often targeted during FF development. Here, we focus on simulations of RNA tetraloops (e.g. the four-nucleotide sequences that comprise the loops of stem-loop structures) and tetramers as representative examples of particularly challenging systems for MD simulations.

In 2013, Chen and Garcia investigated the folding of hyperstable r(UUCG), r(GCAA), and r(CUUG) RNA tetraloops [54]. Their simulations employed a modified ff99 parameter set in which they (1) refined the Lennard-Jones radii to better balance base stacking and base-water interactions, and (2) adjusted the χ dihedral parameters to achieve better syn/anti balance. With this modified FF, replica-exchange simulations recovered the native fold of the three tetraloops within 1–3 Å RMSD of the experimental structures. This result highlights the critical role of balanced interactions in nucleic acid FFs (and any FF, in general). Despite this success in folding RNA, subsequent investigations revealed that the modified parameters led to overly strong base-base hydrogen bonding and distorted structures [55,56], indicating that while the proposed refinements were suitable for RNA folding, they do not represent a transferable nucleic acid FF.

RNA tetramers are also difficult to model in MD simulations. Condon et al. carried out a systematic analysis of ff99-derived FFs in systems of r(AAAA), r(CAAU), r(GACC), and r(UUUU) using MD simulations and NMR spectroscopy [57]. Each of the FFs produced long-lived structures with incorrect, intercalated base stacking, suggesting an intrinsic inaccuracy in base hydration that leads to nonspecific collapse of the oligonucleotide chain. Bergonzo and Cheatham approached the same question of tetramer folding using a modified version of parmbsc0 with an additional χ refinement [10] and reoptimized Lennard-Jones radii [58] on phosphate oxygens [59]. Their simulations systematically evaluated different water models in lieu of the conventional TIP3P that is often used with AMBER FFs, with the OPC model [60] producing the best results. As such, their approach was to rebalance RNA-water and intra-RNA interactions to improve the description of tetramer conformational ensembles. Their modified parmbsc0+OPC model was suitable for r(GACC) but not for r(CCCC). Thus, the results of these studies indicate that there are intrinsic imbalances in several AMBER FFs that may be remedied in some cases by minor refinement or use of different water models, but as yet there is not a general solution for producing RNA tetramer ensembles that agree with NMR data.

In validating the AMOEBA nucleic acid FF, Zhang et al. also simulated r(CAAU), r(GACC), and r(AAAA) tetramers, finding that their conformers showed only small deviations from NMR data and few incidences of inter-calation [28]. These findings suggest that use of a polarizable FF may alleviate some of the imbalances in the AMBER FFs noted above as the electronic structure of the oligonucleotide, particularly the bases, respond to changes in stacking, solvation, and hydrogen bonding in ways that nonpolarizable FFs cannot. It may also be possible that the success of the AMOEBA FF is due to more comprehensive parameter fitting and use of higher-quality QM target data. Further investigations with different polarizable models, like the Drude FF, should be undertaken to determine if polarizable FFs represent a general solution to issues faced in simulating RNA tetramers.

Simulations of highly ordered nucleic acids

Noncanonical nucleic acids serve functional roles in many biological processes and are often implicated in disease states. In the context of MD simulations, these noncanonical structures serve as stringent FF tests since their stabilizing interactions are different from those found in canonical nucleic acids normally targeted for FF parametrization and validation. As such, improved accuracy in modeling four-way junctions [61], G-quadruplexes (GQs) [36], i-motifs [62], hairpins [63,64], pseudoknots [47], and riboswitches [65] (Figure 2) reflects the maturity of modern nucleic acid FFs. GQs are an important example of noncanonical nucleic acids to focus on here because (1) they form in DNA and RNA, (2) their highly ordered structures are governed by interactions with water and ions, and (3) they have been the subject of many simulation studies with both additive and polarizable FFs.

Figure 2.

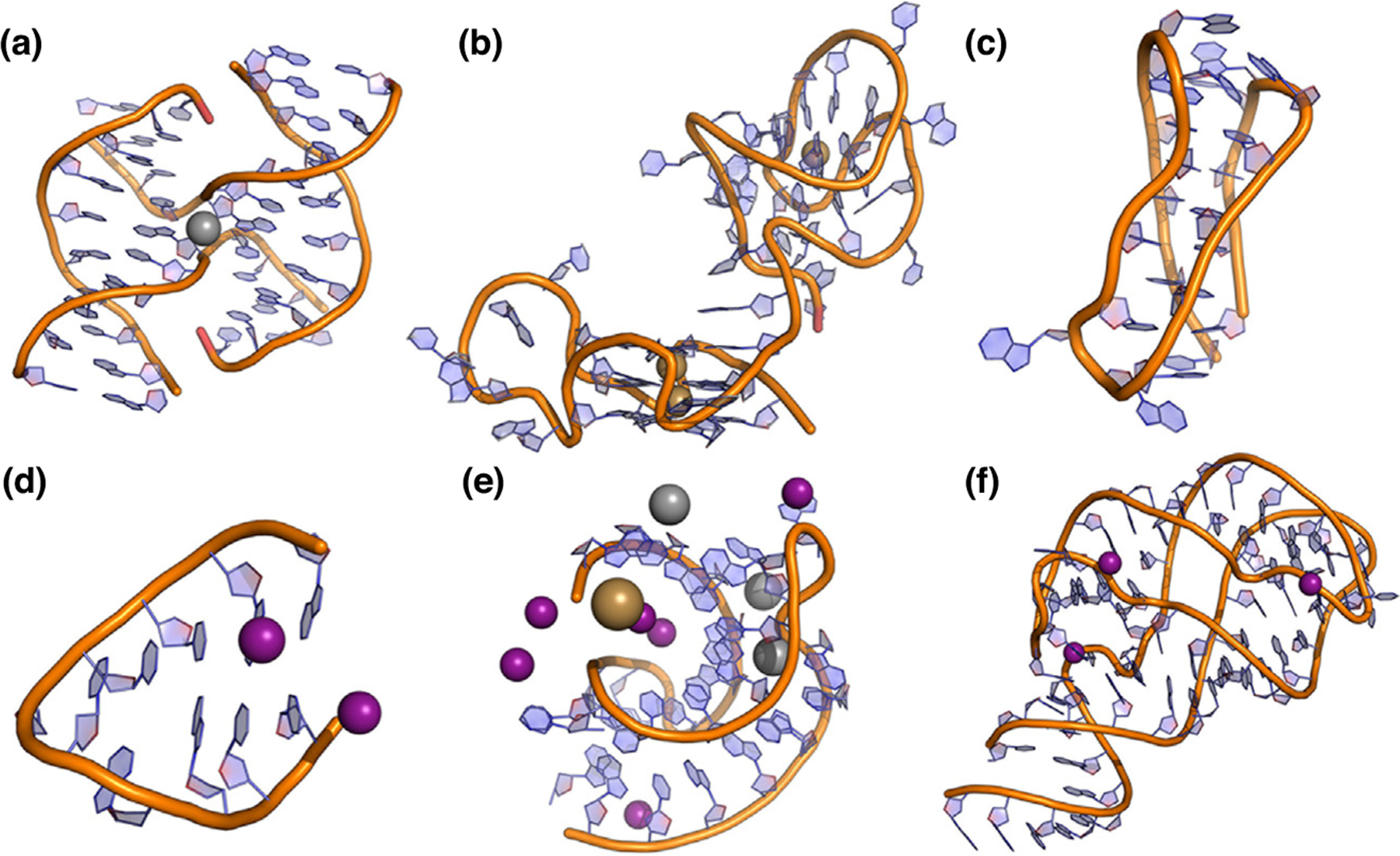
Examples of the diverse types of nucleic acids studied with MD simulations. Highly ordered DNA structures studied include the (a) Holliday junction structure of d(CCGGTACCGG), (b) linked c-kit2/c-kit* GQs, and (c) human telomeric i-motif. RNA structures include (d) UUCG hairpins, (e) viral RNA pseudoknots, and (f) add adenine riboswitch. Ions participating in these structures include K⁺ (tan), Na⁺ (grey), and Mg²⁺ (purple).

GQ sequences self-associate into four-stranded helical structures that are characterized by stacked tetrads, each consisting of a square planar arrangement of Hoogsteen hydrogen-bonded guanines [66]. GQs typically have three stacked guanine tetrads, resulting in twelve inward-facing carbonyl oxygen atoms, four in each tetrad (Figure 3). This configuration forms a strongly electronegative channel that requires cation stabilization [67]. Broadly speaking, interactions with other proteins, ions, and water govern the folded topology and dynamics of GQs, which in turn influence their function [68–70]. MD simulations with AMBER, CHARMM, and Drude FFs have provided valuable insights into GQs [35–37,70–79]. For example, simulations provided the first description of the rigid tetrad core and destabilization in the absence of coordinated ions [78], identified possible GQ folding intermediates [79], and proposed folding pathways [73]. In general, recent simulations have yielded stable GQ structures in reasonable agreement to experimental data but have not provided complete descriptions of ion coordination and ion-ion energetics in the tetrad core, shortcomings that have been largely attributed to the nonpolarizable nature of the FFs that have typically been employed [75–77]. Specifically, charge-charge repulsion between core ions in nonpolarizable simulations hinders descriptions of ion binding and coordination in the tetrad core [77]. However, the inclusion of dipole-dipole interactions between ions can smooth electrostatic repulsion and stabilize ion binding [75]. While one simulation study showed it is possible to find system-specific combinations of water models and ion parameters to improve descriptions of GQ-ion interactions [71], use of a polarizable FF may be a more general approach to overcoming these longstanding challenges.

Figure 3.

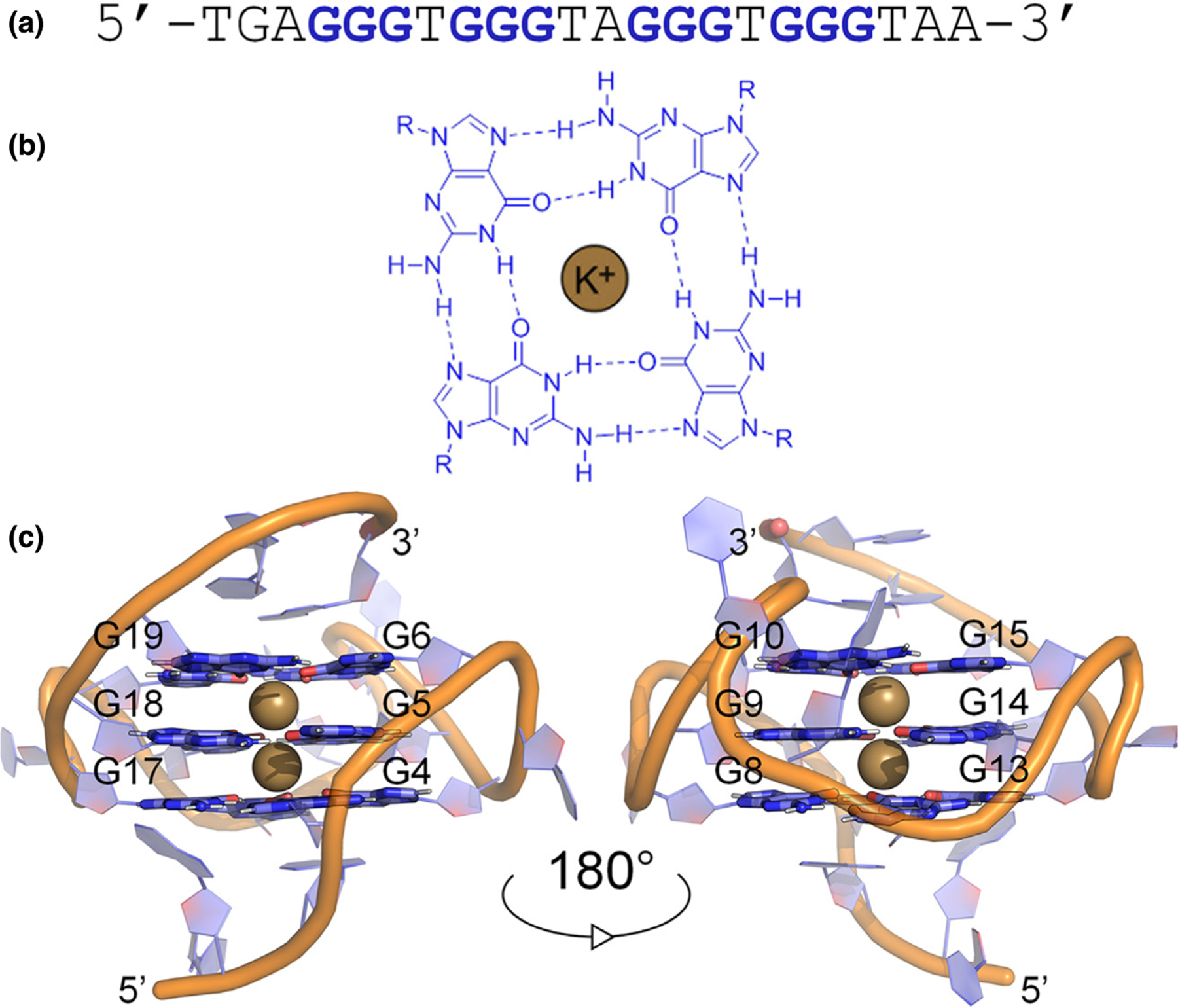
Details of the structural hierarchy of the major GQ structure formed in the human c-MYC promoter. (a) Guanine-rich sequences with four runs of at least three guanines self-associate into tetrads, consisting of a square planar arrangement of (b) Hoogsteen hydrogen-bonded guanines. (c) Monovalent metal ions, typically K⁺ (tan), stabilize the tetrad core and the highly ordered structure.

We have recently employed the Drude FF to investigate DNA and RNA GQs [35–37], finding that the polarizable model improves descriptions of GQ-ion interactions and that the nucleobase dipole moments in GQs differ from canonical DNA and RNA [35–37]. The variation in nucleobase dipole moments is a function of ion type and coordination, hydration, and primary and secondary structure, all which influence conformational sampling and core energetics [35–37]. For example, in studying the stacked c-kit2/c-kit* GQs (Figure 2b), we showed that the interplay of the two GQs and upstream and downstream regions modulates secondary structure, ion sampling, and core-ion interaction energies [36]. Though these systems were large (238 323 atoms), simulations of 500 ns were computational tractable through the use of GPU acceleration. However, extending the time scales of these simulations further is important as other studies have shown that unbiased simulations of telomeric GQs may not be converged within even 10 μs [72,74]. The combination of including sufficient flanking (non-GQ) nucleotides, increasing time scales, and achieving adequate sampling, is an emerging challenge in GQ simulations. Meeting this challenge requires careful attention to FF parametrization and reporting possible deficiencies in models, the latter of which requires high-quality experimental data for these systems. Despite these challenges, recent simulations of GQs have benefited from improved FF descriptions of water, ions, and polarization; therefore, their successes mark considerable progress in nucleic acid simulations.

Conclusions and outlook

The quality and scope of nucleic acid simulations have progressed dramatically over the past four decades, providing important atomistic insights into DNA and RNA structure and dynamics. These successes have been driven by the development, assessment, and progressive refinement of atomistic FFs, which have made use of increasing repositories of experimental and QM target data (Figure 4). Employing polarizable FFs is a promising approach to overcoming longstanding issues regarding hydration and ion interactions with nucleic acids. However, more investigations of diverse nucleic acid structures are needed to further assess the quality of these polarizable models. Further, recent efforts combining experiments and simulations show promise for improving the accuracy of nucleic acid FFs. To achieve better agreement with experimental data, future work may require well-characterized model systems from experimental and computational perspectives. Finally, multi-μs simulations show that sampling is still an issue in some nucleic acid simulations, so extending simulation time scales and exploring efficient enhanced sampling methods are an important future endeavor. Together, these efforts will drive improvements to atomistic FFs and ultimately our understanding of nucleic acid structure, dynamics, and function.

Figure 4.

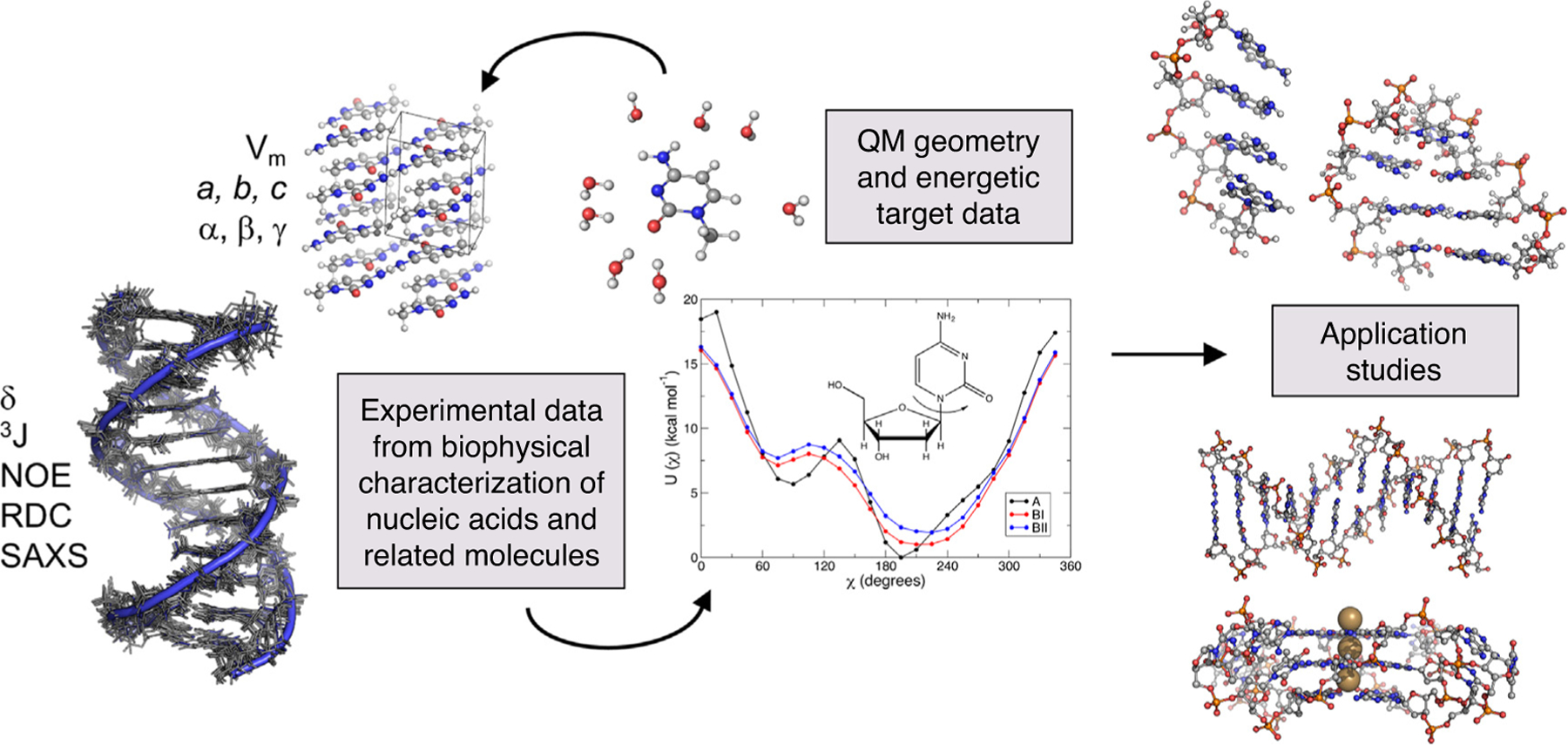
Overview of nucleic acid FF development and applications. Refinement of FFs is driven by comparisons to available experimental data on nucleic acids and suitable model compounds, as well as QM calculations that describe intermolecular interactions, electrostatic properties, and conformational energetics, and so on. Application studies on canonical and noncanonical nucleic acid structures can be performed after sufficiently rigorous FF parametrization and validation toward a greater understanding of nucleic acid structure-function relationships.